平面直角坐标系知识点题型【最全面】总结
平面直角坐标系重难点题型(四大题型)(原卷版)

专题05 平面直角坐标系重难点题型(四大题型)【题型1 两点间距离】【题型2 求平面直角坐标系中动点问题的面积】【题型3 平面直角坐标系中规律题探究】【题型4 等腰三角形个数讨论问题】【题型1 两点间距离】1.在平面直角坐标系中,有A(﹣2,a+1),B(a﹣1,4),C(b﹣2,b)三点.(1)当AB∥x轴时,求A、B两点间的距离;(2)当CD⊥x轴于点D,且CD=1时,求点C的坐标.2.已知平面直角坐标系内的三点:A(a﹣1,﹣2),B(﹣3,a+2),C(b﹣6,2b).(1)当直线AB∥x轴时,求A,B两点间的距离;(2)当直线AC⊥x轴,点C在第二、四象限的角平分线上时,求点A和点C 的坐标.3.先阅读一段文字,再回答下列问题:已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴时,两点距离公式可简化成|x1﹣x2|或|y2﹣y1|.(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;(2)已知A,B在平行于y轴的直线上,点A的纵坐标为6,点B的纵坐标为﹣4,试求A,B两点的距离;(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),找出三角形中相等的边?说明理由.4.先阅读一段文字,再回答下列问题:已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为:p1p2=,例如:点(3,2)和(4,0)的距离为.同时,当两点所在的直线在坐标轴上或平行于x轴或平行于y轴距离公式可简化成:p1p2=|x1﹣x2|或p1p2=|y1﹣y2|.(1)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为2,则A,B两点的距离为;(2)线段AB平行于x轴,且AB=3,若点B的坐标为(2,4),则点A的坐标是;(3)已知A(3,5),B(﹣4,4),A,B两点的距离为;(4)已知△ABC三个顶点坐标为A(3,4),B(0,5),C(﹣1,2),请判断此三角形的形状,并说明理由.5.先阅读下列一段文字,再解答问题:已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,4),B(﹣2,1),则AB=;(2)已知点C,D在平行于y的直线上,点C的纵坐标为3,点D的纵坐标为﹣2,则CD=;(3)已知点M和(1)中的点A有MA∥x轴,且MA=3,则点M的坐标为;(4)已知点P(3,1)和(1)中的点A,B,则线段P A,PB,AB中相等的两条线段是.6.先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(1,3),B(﹣3,﹣5),试求A,B两点间的距离;(2)已知线段MN∥y轴,MN=4,若点M的坐标为(2,﹣1),试求点N 的坐标.7.先阅读下列一段文字,再回答后面的问题.已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;(2)已知A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离.8.阅读材料:两点间的距离公式:如果平面直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB=,则AB2=(x1﹣x2)2+(y1﹣y2)2.例如:若点A(4,1),B(3,2),则AB=,若点A(a,1),B(3,2),且AB=,则.根据实数章节所学的开方运算即可求出满足条件的a的值.根据上面材料完成下列各题:(1)若点A(﹣2,3),B(1,2),则A、B两点间的距离是.(2)若点A(﹣2,3),点B在x轴上,且A、B两点间的距离是5,求B 点坐标.9.在平面直角坐标系中,有A(﹣2,a+1),B(a﹣1,4),C(b﹣2,b)三点.(1)当点C在y轴上时,求点C的坐标;(2)当AB∥x轴时,求A,B两点间的距离;(3)当CD⊥x轴于点D,且CD=1时,求点C的坐标.10.先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.【题型2 求平面直角坐标系中动点问题的面积】11.如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).(1)在平面直角坐标系中画出△ABC,则△ABC的面积是;(2)若点D与点C关于原点对称,则点D的坐标为;(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.12.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.(1)填空:a=,b=;(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.13.如图,在平面直角坐标系内,已知点A的坐标为(3,2),点B的坐标为(3,﹣4),点P为直线AB上任意一点(不与A、B重合),点Q是点P 关于x轴的对称点.(1)在方格纸中标出A、B,并求出△ABO的面积;(2)设点P的纵坐标为a,求点Q的坐标;(3)设△OP A和△OPQ的面积相等,且点P在点Q的上方,求出此时P点坐标.14.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足a2+2a+1+|3a+b|=0.(1)填空:a=,b=;(2)若存在一点M(﹣2,m)(m<0),点M到x轴距离,到y轴距离,求△ABM的面积(用含m的式子表示);(3)在(2)条件下,当m=﹣1.5时,在y轴上有一点P,使得△MOP的面积与△ABM的面积相等,请求出点P的坐标.15.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.16.如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO =8,OA=OB,BC=10,点P的坐标是(﹣6,a),(1)求△ABC三个顶点A、B、C的坐标;(2)连接P A、PB,并用含字母a的式子表示△P AB的面积(a≠2);(3)在(2)问的条件下,是否存在点P,使△P AB的面积等于△ABC的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+=0.(1)求a,b的值;(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积恒成立?若存在,请直接写出符合条件的点M的坐标.18.如图,直线AB与x轴,y轴分别相交于点A(6,0),B(0,8),M是OB上一点,若将△ABM沿AM折叠,则点B恰好落在x轴上的点B'处.求:(1)点B'的坐标;(2)△ABM的面积.19.如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a,b,c的值.(2)求四边形AOBC的面积.(3)是否存在点P(x,﹣x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.20.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)(1)求△ABC的面积;(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.21.如图,在平面直角坐标系中,A(2,2),B(﹣1,0),C(3,0)(1)求△ABC面积;(2)在y轴上存在一点D,使得△AOD的面积是△ABC面积的2倍,求出点D的坐标;(3)在平面内有点P(3,m),是否存在m值,使△AOP的面积等于△ABC 面积的2倍?若存在,直接写出m的值;若不存在,请说明理由.22.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(0,4),C(﹣3,2).(1)如图1,求△ABC的面积.(2)若点P的坐标为(m,0),①请直接写出线段AP的长为(用含m的式子表示);②当S△P AB =2S△ABC时,求m的值.(3)如图2,若AC交y轴于点D,直接写出点D的坐标为.23.如图,在平面直角坐标系中,点A(﹣3b,0)为x轴负半轴上一点,点B (0,4b)为y轴正半轴上一点,其中b满足方程:3(b+1)=6.(1)求点A、B的坐标;(2)点C为y轴负半轴上一点,且△ABC的面积为12,求点C的坐标;(3)在(2)的条件下,在x轴上是否存在点P,使得△PBC的面积等于△ABC的面积的一半?若存在,求出相应的点P的坐标;若不存在,请说明理由.【题型3 平面直角坐标系中规律题探究】24.如图,动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),…,按这样的运动规律,则第2021次运动到点()A.(2021,1)B.(2021,2)C.(2020,1)D.(2021,0)25.有一组数,按照下列规律排列:1,2,3,6,5,4,7,8,9,10,15,14,13,12,11,16,17,18,19,20,21,……数字5在第三行左数第二个,我们用(3,2)点示5的位置,那点这组成数里的数字100的位置可以表示为()A.(14,9)B.(14,10)C.(14,11)D.(14,12)26.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A.(1,﹣1)B.(﹣1,1)C.(﹣1,﹣2)D.(1,﹣2)27.如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳动1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是()A.(﹣24,49)B.(﹣25,50)C.(26,50)D.(26,51)28.如图,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点.按如此规律走下去,当机器人走到A6点时,离O点的距离是()A.10m B.12m C.15m D.20m29.如图,将正整数按有图所示规律排列下去,若用有序数对(n,m)表示n 排从左到右第m个数.如(4,3)表示9,则(10,3)表示.30.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(﹣1,3)…,根据这个规律探索可得,第90个点的坐标为.31.如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,﹣2),A4(4,0),…根据这个规律,探究可得点A2017坐标是.32.如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m 到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时是位置.33.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是.【题型4 等腰三角形个数讨论问题】34.如图,在平面直角坐标系中,点A的坐标是(6,6),点B在坐标轴上,且△OAB是等腰直角三角形,则点B的坐标不可能是()A.(0,6)B.(6,0)C.(12,0)D.(0,﹣6)35.如图,在平面直角坐标系中,A,B两点的坐标分别为(﹣4,0),(0,3),连接AB,点P在第二象限,以点P,A,B为顶点的等腰直角三角形有个,任意写出其中一个点P坐标为.36.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.(1)观察每次变换前后的三角形的变化规律,若将△OA3B3变换成△OA4B4,则A4的坐标是,B4的坐标是.(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是,B n的坐标是.(3)若按第(1)题找到的规律将△OAB进行n次变换,得到△OA n B n,则△OA n B n的面积S为37.如图,方格纸中小正方形的边长均为1个单位长度,A、B均为格点.(1)在图中建立直角坐标系,使点A、B的坐标分别为(3,3)和(﹣1,0);(2)在(1)中x轴上是否存在点C,使△ABC为等腰三角形(其中AB为腰)?若存在,请直接写出所有满足条件的点C的坐标.38.如图,在平面直角坐标系中,已知点A(﹣2,0),B(2,0).(1)画出等腰三角形ABC(画一个即可);(2)写出(1)中画出的三角形ABC的顶点C的坐标.。
平面直角坐标系知识点归纳及例题

纳及5 j平面直角坐标系知识点归纳在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系; 坐标平面上的任慧一点P 的坐标,都和惟一的一对对(a.h ) ——对应;其中,d 为横坐标,h 为纵坐标坐标;x 轴上的点,纵坐标等于0;y 轴上的点,横坐标等于0;坐标轴上的点丕屋壬任何象限;4、 四个象限的点的坐标具有如下特征:小限横、纵坐标 正负性;(2)点P(x,y 所在的数84 横、纵坐标X 、y 中必有一数为5、 在平面直角坐标系中,已知点P ⑺上),则(1)点P 到A-轴的距离为问;(2 )点P 到y 轴的距离为 (3)点P 到原点0的距离为P0 =6、 平行直线上的点的坐标特征:一a)在与X 轴平行的直线上,所有点的纵坐标相等;,Y川F 点A 、B 的纵坐标都等于加;-------- ► X与y 轴平行的直线上,所有点的横坐标相等;点C 、D 的横坐标都等于《 ;对!睦征: 点POs)关于X 轴的对称点为片(心-”),即横坐标不变,纵坐标互为相反数; 』卩(也时关于$轴的对称点为卩2(-加“)Z 即纵坐标不变,横坐标互为相反 数; 象限 横坐标龙纵坐标y 第一象限 正 正 第 象限 负 正 第二象限 负 负 第四象限正负1. 2♦P(%b)(N ] b所在的魚》 a X X 、y 的取值的7;— D ,a, b)C)a点P ("")关于原点的对称点为出(-山,-"),即横、4 XP4/P▼ 1▼ 1I入1 1------ *-► X 1 1 1纵坐标都互为相反数;y ----- ♦Po关于X 轴对称 关于y 轴对称 关于原点对称8、 两条坐标轴夹角平分线上的点的坐标的特征: a) 若点P( ”” )在第一、三象限的角平分线上,则加=“,即横、纵坐标相等;b) 若点P( “5 )在第二 四象限的角平分线上,则怖=-",即横、纵坐标互为 相反数;点B 与C 的横坐标与纵坐标分别相等D ・点B 与C 的横坐标.纵坐标都不相等若点P(X, y)的坐标满足Q = 0则点P 必在 原点 B ・X 轴上 C ・y 轴上 D . X 轴或y 轴上 点P 在X 轴上,且到y 轴的距离为5,则点P 的坐标是A ・(5, 0)B ・(0, 5)C ・(5, 0)或(-5, 0)D . (0, 5)或(0, -5) 4.平面上的点(2,-1)通过上下平移不能与之重合的是A ・(2,-2)B ・(-2,-1)C . (2, 0)D . 2,-3) 5•将△ABC 各顶点的横坐标分别减去3,纵坐标不变,得到的^ ABC 相应顶点的坐 标,则 AA B C 可以看成△ABC 6・线段CD 是由线段AB 平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-l)的对 应点D 的坐标是A ・(2,9)B ・(5, 3)C ・(1,2)D . (-9,-4)in, nin, n在第一、分线上Is 在平面直角线段BC 〃x 轴,则曉角平分线上点B 与C 的横坐标相等 八、、B ・点B 与C 的纵坐标相等A.向左平移3个单位长度得到B ・向右平移三个单位长度得到C.向上平移3个单位长度得到D.向下平移3个单位长度得到 在第二p7 .在坐标系内,点P (2,-2)和点Q (2,4)之间的距离等于 段PQ 和中点坐标是 8・将点M(2,-3)向左平移2个单位长度,再向下平移1个单位长度,得到的点的坐标为 9•在直角坐标系中,若点P ⑺-2b + 5)在y 轴上,则点P 的坐标为 10.已知点P(-2<), Q©3),且PQ 〃天轴,则0 = 11 .将点P(_3』)向下平移3个单位,并向左平移2个单位后得到点Q(x.-l),则12•则坐标原点0 (0,0) , A (-2,0) ,B(-2,3)三点围成的△ABO 的面积为 13・点?(a.h)在第四象限,则点Q(/?,-«)在第.14 .已知点P 在第二象限两坐标轴所成角的平分线上,且到X 轴的距离为3,则点P 的 坐标为 15 .在同一坐标系中.图形a 是图形b 向上平移3个单位长度得到的,如果在图形a 中 点A 的坐标为(5-3),则图形b 中与A 对应的点A 的坐标为 16・在平面直角坐标系中,将坐标为(0,0), (2,0), (3,4), (1,4)的点用线段依次连接起 来形成一个图像,并说明该图像是什么图形。
八上数学平面直角坐标系必背知识点总结

第三章平面直角坐标系
1、在平面内,确定一个物体的位置一般需要两个数据。
①列数和排数,(列数,排数)
②方位角和距离,(方位角以南北开头)
③经度和纬度
④区域定位法,如A2
2、平面直角坐标系
定义:在平面内,两条互相垂直且有公共原点重合的数轴组成平面直角坐标系
.......。
x轴与y轴的交
点为平面直角坐标系的原点
..(.0.,.0.).。
水平的数轴叫x.轴或横轴
....;x轴取向右为正方向。
竖直的数
轴叫y.轴或纵轴
....;y轴取向上为正方向。
坐标表示(横坐标,纵坐标)
象限:第一象限(+,+)第二象限(-,+)
第三象限(-,-)第四象限(+,-)
坐标轴(x轴或y轴)上的点不属于任何一个象限.
x轴正半轴(+,0),x轴负半轴(-,0);
y轴正半轴(0,+),y轴负半轴(0,-);
3、性质:
①位于x轴上的点,纵坐标等于0 ;
位于y轴上的点,横坐标等于0 .
②点(x , y)到x轴的距离等于纵坐标的绝对值(即|y|),
到y轴的距离等于横坐标的绝对值(即|x|)。
③ 与x轴平行(或与y轴垂直)的直线上的点,纵坐标相等;
与y轴平行(或与x轴垂直)的直线上的点,横坐标相等;
④关于x轴对称的两个点的坐标,横坐标相等,纵坐标互为相反数;
关于y轴对称的两个点的坐标,纵坐标相等,横坐标互为相反数;
关于原点对称的两个点的坐标,横坐标互为相反数,纵坐标互为相反数;第一象限(+,+)
第二象限(-,+)
第三象限(-,-)第四象限(+,-)。
八年级上册数学第三章知识点

八年级上册数学第三章知识点八年级上册数学第三章知识点一、平面直角坐标系:在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系。
二、知识点与题型总结:1、由点找坐标:A 点的坐标记作A( 2,1 ),规定:横坐标在前, 纵坐标在后。
2、由坐标找点:例找点B( 3,-2 ) ?由坐标找点的方法:先找到表示横坐标与纵坐标的点,然后过这两点分别作x轴与y轴的垂线,垂线的交点就是该坐标对应的点。
3、各象限点坐标的符号:① 若点P(x,y)在第一象限,则x 0,y 0 ;② 若点P(x,y)在第二象限,则x 0,y 0 ;③ 若点P(x,y)在第三象限,则x 0,y 0 ;④ 若点P(x,y)在第四象限,则x 0,y 0 。
典型例题:例1、点P的坐标是(2,-3),则点P在第四象限。
例2、若点P(x,y)的坐标满足xy0,则点P在第一或三象限。
例3、若点A 的坐标为(a^2+1, -2–b^2) ,则点A在第四象限。
4、坐标轴上点的坐标符号:坐标轴上的点不属于任何象限。
① x 轴上的点的纵坐标为0,表示为(x,0),② y 轴上的点的横坐标为0,表示为(0,y),③ 原点(0,0)既在x轴上,又在y轴上。
例4、点P(x,y ) 满足xy = 0, 则点P 在x 轴上或y 轴上。
.5、与坐标轴平行的两点连线:① 若AB‖ x 轴,则A、B 的纵坐标相同;② 若AB‖ y 轴,则A、B 的横坐标相同。
例5、已知点A(10,5),B(50,5),则直线AB 的位置特点是(A )A、与x 轴平行B、与y 轴平行C、与x 轴相交,但不垂直D、与y 轴相交,但不垂直6、象限角平分线上的点:① 若点P 在第一、三象限角的平分线上, 则P( m, m );② 若点P 在第二、四象限角的平分线上,则P( m, -m )。
例6、已知点A(2a+1,2+a)在第二象限的平分线上,试求A 的坐标。
解:由条件可知:2a+1 +(2+a)=0 ,解得a = -1 ,∴ A(-1,1)。
(完整版)平面直角坐标系知识点总结(可编辑修改word版)

温馨提示(a , b )与(b , a )顺序不同,含义就不同。
例如:用(3 , 5) 表示第 3 列的第 5 位同学,那么(5 , 3) 就表示第 5 列的第 3 位同学。
夯实基础平面直角坐标系平面直角坐标系的有关概念一.有序数对在日常生活中,可以用有序数对来描述物体的位置,这样可以用含有两个数的组合来表示一个确定的位置,其中两个数各自表示不同的含义,我们把这种有顺序的两个数 a 与b 组成的数对,叫做有序数对,记作(a , b )。
例 1:(1)在一层的电影院内如何找到电影票上所指的位置?(2)在电影票上, 如果把“5 排 8 号”简记为(5,8),那么“4 排 9 号”如何表示?(8,3)表示什么含义?二.平面直角坐标系相关概念具体内容平面直角坐标系定义在平面内画两条互相垂直并且原点重合的数轴,这样就建立了平面直角坐标系两轴水平的数轴叫做 x 轴或横轴,取向右为正方向;垂直的数轴叫做 y 轴或纵轴,取向上为正方向 原点 两轴的交点O 为平面直角坐标系的原点 坐标平面坐标系所在的平面叫做坐标平面三.象限x 轴和 y 轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限,如图。
y第二象限第三象限第一象限Ox第四象限y b • Oax例 2:设M (a , b ) 为平面直角坐标系中的点。
(1) 当a > 0, b < 0 时,点M 位于第几象限?(2) 当ab > 0 时,点M 位于第几象限?四.点的坐标对于坐标平面内的任意一点 A ,过点 A 分别向 x 轴、 y 轴作垂线,垂足在 x 轴、 y 轴上对应的数 a 、b 分别叫做点 A 的横坐标和纵坐标,有序数对(a , b )叫做点 A 的坐标,记作A (a , b ) ,如图。
1. 已知坐标平面内的点,确定点的坐标先由已知点 P 分别向 x 轴、 y 轴作垂线,设垂足分别为 A 、 B ,再求出垂足 A 在 x 轴上的坐标 a 与垂足 B 在 y 轴上的坐标b ,最后按顺序写成(a , b )即可。
(完整版)平面直角坐标系知识点总结

平面直角坐标系二、知识要点梳理知识点一:有序数对比如教室中座位的位置,常用“几排几列”来表示,而排数和列数的先后顺序影响座位的位置,因此用有顺序的两个数a与b组成有序数时,记作(a,b),表示一个物体的位置。
我们把这种有顺序的两个数a与b组成的数对叫做有序数对,记作: (a,b).要点诠释:对“有序”要准确理解,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,表示不同位置。
知识点二:平面直角坐标系以及坐标的概念1.平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系。
水平的数轴称为x 轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1)。
注:我们在画直角坐标系时,要注意两坐标轴是互相垂直的,且有公共原点,通常取向右与向上的方向分别为两坐标轴的正方向。
平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的。
2.点的坐标点的坐标是在平面直角坐标系中确定点的位置的主要表示方法,是今后研究函数的基础。
在平面直角坐标系中,要想表示一个点的具体位置,就要用它的坐标来表示,要想写出一个点的坐标,应过这个点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是a,垂足N在y轴上的坐标是b,我们说点A的横坐标是a,纵坐标是b,那么有序数对(a,b)叫做点A的坐标.记作:A(a,b).用(a,b)来表示,需要注意的是必须把横坐标写在纵坐标前面,所以这是一对有序数。
注:①写点的坐标时,横坐标写在前面,纵坐标写在后面。
横、纵坐标的位置不能颠倒。
②由点的坐标的意义可知:点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离。
知识点三:点坐标的特征l.四个象限内点坐标的特征:两条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别叫做第一、二、三、四象限,如图2.这四个象限的点的坐标符号分别是(+,+),(-,+),(-,-),(+,-).2.数轴上点坐标的特征:x轴上的点的纵坐标为0,可表示为(a,0);y轴上的点的横坐标为0,可表示为(0,b).注意:x轴,y轴上的点不在任何一个象限内,对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上。
第七章 平面直角坐标系(单元总结)(解析版)
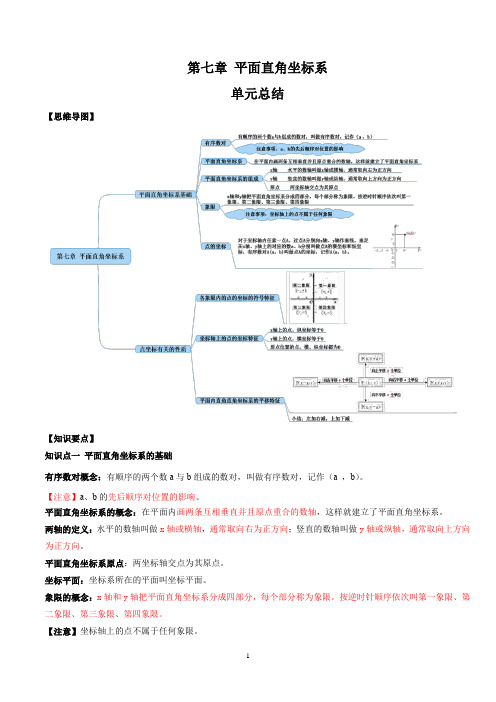
第七章平面直角坐标系单元总结【思维导图】【知识要点】知识点一平面直角坐标系的基础有序数对概念:有顺序的两个数a与b组成的数对,叫做有序数对,记作(a ,b)。
【注意】a、b的先后顺序对位置的影响。
平面直角坐标系的概念:在平面内画两条互相垂直并且原点重合的数轴,这样就建立了平面直角坐标系。
两轴的定义:水平的数轴叫做x轴或横轴,通常取向右为正方向;竖直的数轴叫做y轴或纵轴,通常取向上方向为正方向。
平面直角坐标系原点:两坐标轴交点为其原点。
坐标平面:坐标系所在的平面叫坐标平面。
象限的概念:x轴和y轴把平面直角坐标系分成四部分,每个部分称为象限。
按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限。
【注意】坐标轴上的点不属于任何象限。
点的坐标:对于坐标轴内任意一点A ,过点A 分别向x 轴、y 轴作垂线,垂足在x 轴、y 轴上的对应的数a 、b 分别叫做点A 的横坐标和纵坐标,有序数对A(a ,b)叫做点A 的坐标,记作A(a ,b)。
题型一 用有序数对表示位置典例1(2019·甘肃省榆中县兰山中学初二期中)兰州是古丝绸之路上的重镇,以下准确表示兰州市的地理位置的是( ) A .北纬3403︒' B .在中国的西北方向C .甘肃省中部D .北纬3403︒',东经10349︒' 【答案】D 【详解】根据地理上表示某个点的位的方法可知北纬3403︒',东经10349︒'可以准确表示兰州市的地理位置. 故选:D .变式1-1(2019·花都区期末)若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( ) A .(2,1) B .(3,3) C .(2,3) D .(3,2)【答案】C 【详解】∵(1,2)表示教室里第1列第2排的位置, ∴教室里第2列第3排的位置表示为(2,3), 故选C.变式1-2 (2019·北城片区期中)会议室“4排 6号”记作()4,6,那么“3排 2号”记作( ) A .()2,3 B .()3,2 C .()2,3-- D .()3,2--【答案】B【详解】解:会议室“4排 6号”记作()4,6,那么“3排 2号”记作()3,2, 故选:B .变式1-3 (2019·广西壮族自治区初二期中)下列数据中,不能确定物体位置的是( ) A .1单元201号 B .南偏西60°C .学院路11号D .东经105°,北纬40°【答案】B 【详解】解:A 、1单元201号,是有序数对,能确定物体的位置,故正确; B 、南偏西45°,不是有序数对,不能确定物体的位置,故错误;C 、学院路11号,“学院路”相当于一个数据,是有序数对,能确定物体的位置,故正确;D 、东经105°北纬40°,是有序数对,能确定物体的位置,故正确. 故选B.变式1-4 (2019·萍乡市期中)如图1是一局围棋比赛的几手棋.为记录棋谱方便,横线用数字表示,纵线用字母表示,这样,黑棋的位置可记为(B,2),白棋②的位置可记为(D,1),则白棋⑨的位置应记为( )A .(C ,5)B .(C ,4)C .(4,C)D .(5,C)【答案】B 【解析】 试题分析:∵黑棋的位置可记为(B ,2),∴白棋⑨的位置应记为(C ,4). 故选B .变式1-5 (2019·白银市期中)某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )A .第3组第2排B .第3组第1排C .第2组第3排D .第2组第2排 【答案】C 【详解】解:某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是第2组第3排,所以C 选项是正确的.知识点二 点的坐标的有关性质(考点) 性质一 各象限内点的坐标的符号特征性质二 坐标轴上的点的坐标特征 1.x 轴上的点,纵坐标等于0; 2.y 轴上的点,横坐标等于0; 3.原点位置的点,横、纵坐标都为0. 性质三 象限角的平分线上的点的坐标1.若点P (n m ,)在第一、三象限的角平分线上,则n m =,即横、纵坐标相等; 2.若点P (n m ,)在第二、四象限的角平分线上,则n m -=,即横、纵坐标互为相反数;在第一、三象限的角平分线上 在第二、四象限的角平分线上 性质四 与坐标轴平行的直线上的点的坐标特征 1.在与x 轴平行的直线上, 所有点的纵坐标相等;点A 、B 的纵坐标都等于m ;2.在与y 轴平行的直线上,所有点的横坐标相等;象限 横坐标x 纵坐标y 第一象限 正 正 第二象限 负 正 第三象限 负 负 第四象限正负XyPOyPOX点C 、D 的横坐标都等于n ;性质六 点到坐标轴距离在平面直角坐标系中,已知点P ),(b a ,则 1.点P 到x轴的距离为b ; 2.点P 到y 轴的距离为a ;3.点P 到原点O 的距离为PO = 22b a +性质七 平面直角坐标系内平移变化性质八 对称点的坐标1、点P ),(n m 关于x 轴的对称点为),(1n m P -, 即横坐标不变,纵坐标互为相反数;P ()2、点P ),(n m 关于y 轴的对称点为),(2n m P -, 即纵坐标不变,横坐标互为相反数;3、点P ),(n m 关于原点的对称点为),(3n m P --,即横、纵坐标都互为相反数;小结:题型二 点到坐标轴的距离典例2(2020·厦门市期中)点()3,4-到x 轴上的距离为( ) A .3 B .4 C .5 D .6【答案】B 【详解】 ∵点()3,4-,∴点()3,4-到x 轴上的距离为4, 故选:B.变式2-1(2019·济南市期中)在平面直角坐标系中,点()4,3M -到x 轴的距离是( )A .3B .4C .5D .-3【答案】A 【详解】在平面直角坐标系中,点P (4,-3)到x 轴的距离为:3-=3 故选A .变式2-2 (2019·织金县三塘中学初二期中)点A 到x 轴的距离是3,到y 轴的距离是6,且点A 在第二象限,则点A 的坐标是( ) A .(-3,6) B .(-6,3)C .(3,-6)D .(6,-3)【答案】B 【详解】∵点A 到x 轴的距离是3,到y 轴的距离是6,且点A 在第二象限, ∴点A 的横坐标为−6,纵坐标为3, ∴点A 的坐标是(−6,3). 故选B.题型三 判断点的象限典例3(2019·合肥市期中)点()3,2P -在平面直角坐标系内的位置是( ) A .x 轴上 B .第二象限C .y 轴上D .第四象限【答案】B 【详解】点P (-3,2)在平面直角坐标系中所在的象限是第二象限, 故选:B .变式3-1(2020·济宁市期末)下列坐标点在第四象限内的是( ) A .(1,2) B .(﹣1,﹣2)C .(﹣1,2)D .(1,﹣2)【答案】D 【详解】解:由第四象限内的点的横坐标大于零,纵坐标小于零,得在第四象限内的是(1,-2), 故选:D .变式3-2(2019惠州市期中)在平面直角坐标系中,点(-2,5)所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】B 【详解】∵第二象限内的点横坐标<0,纵坐标>0, ∴点(-2,5)所在的象限是第二象限. 故选:B .变式3-3(2019·淮南市期末)已知点P (0,m )在y 轴的负半轴上,则点M (﹣m ,1)在( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A 【详解】解:∵点P (0,m )在y 轴的负半轴上, ∴m <0, ∴﹣m >0,∴点M (﹣m ,1)在第一象限, 故选:A .题型四 直角坐标系点的坐标典例4(2019·青岛市期末)点(3,1)P m m +-在y 轴上,则点P 的坐标为( ) A .(0,4)- B .(3,0)-C .(3,1)-D .(4,0)【答案】A 【详解】∵点()31P m m +-,在y 轴上, ∴30m +=, 解得:3m =-, ∴1314m -=--=-,∴点P 的坐标为()04-,. 故选:A .变式4-1(2019·东营市期中)若点P (m +3,m -2)在直角坐标系的x 轴上,则点P 的坐标为( ) A .(0,5)B .(5,0)C .(-5,0)D .(0,-5)【答案】B 【解析】由题意得m -2=0,m =2,所以P (5,0),故选B.变式4-2 (2019·抚顺市期末)在平面直角坐标系中,点P (x+1,x -2)在x 轴上,则点P 的坐标是( ) A .(3,0) B .(0,-3)C .(0,-1)D .(-1,0)【答案】A 【详解】解:∵点P (x+1,x -2)在x 轴上, ∴x -2=0, ∴x=2, ∴x+1=3,∴点P 的坐标为(3,0), 故选:A .变式4-3 (2019·广西壮族自治区初二期中)点P 的横坐标是一3,且到x 轴的距离为5,则点P 的坐标是( ) A .()3,5- B .()3,5--C .()5,3-或()3,5-D .()3,5-或()3,5--【答案】D 【详解】解:∵点P 到x 轴的距离为5, ∴P 点的纵坐标是5或−5, ∵点P 的横坐标是−3, ∴P 点的坐标是(−3,5)或(−3,−5). 故选D .题型五 实际生活中用坐标表示点的位置典例5(2020·揭阳市期末)如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,3),棋了“马”的坐标为(1,3),则棋子“炮”的坐标为( )A.(3,2)B.(3,1)C.(2,2)D.(﹣2,2)【答案】A【详解】解:如图所示:棋子“炮”的坐标为(3,2).故选:A.变式5-1(2019·石家庄市期末)小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是()A.(5,30)B.(8,10)C.(9,10)D.(10,10)【答案】C【详解】如图,过点C作CD⊥y轴于D,∴BD=5,CD=50÷2-16=9,OA=OD-AD=40-30=10,∴P(9,10);故选C.变式5-2 (2019·晋中市期中)中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(3,﹣2),则“兵”位于点()A.(﹣1,1)B.(﹣2,﹣1)C.(﹣3,1)D.(﹣2,1)【答案】D【详解】如图所示,根据题意可建立如图所示平面直角坐标系,则“兵”位于点(﹣2,1),故选D.变式5-3(2019·江西省初二期末)如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是()A.(1,0)B.(1,2)C.(2,1)D.(1,1)【答案】D【详解】根据两个标志点A(3,1),B(2,2)可建立如下所示的坐标系:由平面直角坐标系知,“宝藏”点C的位置是(1,1),故选:D.题型六由平移确定点的坐标典例6(2019·深圳市期末)在平面直角坐标系中,将点P(3,2)向右平移2个单位长度,再向下平移2个单位长度,所得到的点坐标为()A.(1,0)B.(1,2)C.(5,4)D.(5,0)【答案】D【详解】将点P(3,2)向右平移2个单位长度得到(5,2),再向下平移2个单位长度,所得到的点坐标为(5,0).故选D.变式6-1(2019·东营市期中)在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是()A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)【答案】D【解析】解:在坐标系中,点(﹣3,2)先向右平移5个单位得(2,2),再把(2,2)向下平移3个单位后的坐标为(2,﹣1),则A 点的坐标为(2,﹣1).故选D .变式6-2 (2019·广西壮族自治区初二期中)在直角坐标系中,ABC ∆的顶点()1,5A -,()3,2B ,()0,1C ,将ABC ∆平移得到A B C '''∆,点A 、B 、C 分别对应A '、B '、C ',若点()1,4A ',则点C '的坐标是( ). A .()2,0-B .()2,2-C .()2,0D .()5,1 【答案】C【详解】由点A 平移得到点A '可知,先向右平移2个单位,再向下平移1个单位,则点C 平移后的点C '坐标为()2,0, 故选:C.变式6-3(2019·唐山市期末)将点P (m+2,2m+1)向左平移1个单位长度到P′,且P′在y 轴上,那么P′的坐标是( )A .(0,﹣1)B .(0,﹣2)C .(0.﹣3)D .(1,1) 【答案】A【详解】P (m+2,2m+1)向左平移1个单位长度到P′(m+1,2m+1),∵P′在y 轴上,∴m+1=0,∴m=﹣1,∴P′(0,﹣1),故选A .变式6-4 (2018·滁州市期末)已知线段AB 是线段CD 平移得到的,点()C 1,2-,()B 3,3,()D 2,5,则点C 的对应点A 的坐标为( )A .()0,0B .()1,1C .()3,1D .()2,1--【答案】A【详解】解:由点()D 2,5的对应点B 的坐标为()3,3知,线段AB 是由线段CD 向右移1个单位、向下平移2个单位得到的,所以点()C 1,2-的对应点A 的坐标为()11,22-+-,即()0,0,故选:A .变式6-5 (2019·德州市期末)如图,A ,B 的坐标为()1,0,()0,2,若将线段AB 平移至11A B ,则a b -的值为( )A .1B .1-C .0D .2【答案】C【解析】 试题解析:由B 点平移前后的纵坐标分别为2、4,可得B 点向上平移了2个单位, 由A 点平移前后的横坐标分别是为1、3,可得A 点向右平移了2个单位,由此得线段AB 的平移的过程是:向上平移2个单位,再向右平移2个单位, 所以点A .B 均按此规律平移,由此可得a =0+2=2,b =0+2=2,∴a −b =0,故选C.。
平面直角坐标系复习讲义(知识点+典型例题)

D、第四象限.
【例 3】点 P(m,1)在第二象限内,则点 Q(-m,0)在( )
A.x 轴正半轴上 B.x 轴负半轴上 C.y 轴正半轴上 D.y 轴负半轴上
【例 4】(1)在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,则 a= ,点的坐标为
。
(2)当 b=______时,点 B(-3,|b-1|)在第二、四象限角平分线上.
电量为 8 千瓦时,则应交电费 4.4 元;④若所交电费为 2.75 元,则用电量为 6 千瓦时,其中正确的有( )
A.4 个 B.3 个 C.2 个 D.1 个
【例 7】小明骑自行车上学,开始以正常速度匀速行驶,途中自行车出了故障,他只好停下来修车.车修好后,因怕
耽误上课,故加快速度继续匀速行驶赶往学校.如图是行驶路程 S(米)与时间 t(分)的函数图象,那么符合小明骑
D. .
11、星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离 y(千米)与时间 t(分钟)的关系如图所示.根 据图象回答下列问题:
2
2
巩固练习
5
1、下列 各曲线中表示 y 是 x 的函数的是( )
A.
B.
C.
D.
2、下列平面直角坐标系中的图象,不能表示 y 是 x 的函数的是( )
A.
B.
C.
D.
3、下列四个选项中,不是 y 关于 x 的函数的是( )
A.|y|=x﹣1 B.y=
C.y=2x﹣7 D.y=x2
4、下列四个关系式:(1)y=x;(2) y x2 ;(3) y x3 ;(4) y x ,其中 y 不是 x 的函数的是( )
.
【例 8】在坐标系内,点 P(2,-2)和点 Q(2,4)之间的距离等于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面直角坐标系知识点归纳总结
1、 在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系;
2、 坐标平面上的任意一点P 的坐标,都和惟一的一对 有序实数对(b a ,)一一对应;其中,a 为横坐标,
b 为纵坐标坐标;
3、x 轴上的点,纵坐标等于0;y 轴上的点,横坐标等于0; 坐标轴上的点不属于任何象限;
4、 四个象限的点的坐标具有如下特征:
小结: (1)点P (y x ,)所在的象限
横、纵坐标x 、y 的取值的正负性; (2)点P (y x ,)所在的数轴 横、纵坐标x 、y 中必有一数为零;
5、 在平面直角坐标系中,已知点
P ),(b a ,则
(1) 点P 到x 轴的距离为b ; (2) 点
P 到y 轴的距离为a ; 6、 平行直线上的点的坐标特征:
a) 在与x 轴平行的直线上, 所有点的纵坐标相等;点A 、B
的纵坐标都等于m ;
b) 在与y 轴平行的直线上,所有点的横坐标相等; 点C 、D 的横坐标都等于n ;
7、 对称点的坐标特征:
a) 点P
),(n m 关于x 轴的对称点为),(1n m P -, 即横坐标不变,纵坐标互为相反数; b) 点P
),(n m 关于y 轴的对称点为),(2n m P -, 即纵坐标不变,横坐标互为相反数;
c) 点P ),(n m 关于原点的对称点为),(3n m P --,即横、纵坐标都互为相反数;
-2
X
X
P X
-
8、 两条坐标轴夹角平分线上的点的坐标的特征:
a) 若点P (n m ,)在第一、三象限的角平分线上,则n m =,即横、纵坐标相等; b) 若点P (n m ,)在第二、四象限的角平分线上,则n m -=,即横、纵坐标互为相反数;
在第一、三象限的角平分线上 在第二、四象限的角平分线上 习题考点归纳
考点一——平面直角坐标系中点的位置的确定
已知坐标系中特殊位置上的点,求点的坐标
【例1】下列各点中,在第二象限的点是 ( )
A .(2,3)
B .(2,-3)
C .(-2,3)
D .(-2, -3) 【例2】已知点M(-2,b)在第三象限,那么点N(b, 2 )在 ( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 【例3】 若点P (x ,y )的坐标满足xy=0(x ≠y),则点P 在( )
A .原点上
B .x 轴上
C .y 轴上
D .x 轴上或y 轴上
【例4】点P (x,y )位于x 轴下方,y 轴左侧,且 x =2,y =4,点P 的坐标是( )
A (4,2)
B .(-2,-4)
C .(-4,-2)
D .(2,4)
【例5】点P (0,-3),以P 为圆心,5为半径画圆交y 轴负半轴的坐标是 ( )
A .(8,0)
B .( 0,-8)
C .(0,8)
D .(-8,0) 【例6】点
E (a,b )到x 轴的距离是4,到y 轴距离是3,则有( )
A .a=3, b=4
B .a=±3,b=±4
C .a=4, b=3
D .a=±4,b=±3 【例7】已知点P (a,b ),且ab >0,a +b <0,则点P 在( )
X
A .第一象限
B .第二象限
C .第三象限
D .第四象限
【例8】如果点M 到x 轴和y 轴的距离相等,则点M 横、纵坐标的关系是( )
A . 相等
B .互为相反数
C .互为倒数
D .相等或互为相反数
【例9】在坐标系内,点P (2,-2)和点Q (2,4)之间的距离等于 个单位长度。
线段PQ 的中点的坐标是________________。
【例10】点P (a-1,2a-9)在x 轴负半轴上,则P 点坐标是 。
【例11】点P(m+2,m-1)在y 轴上,则点P 的坐标是 . 考点二——平面直角坐标系中对称点的问题
【例1】点A (﹣1,2)关于y 轴的对称点坐标是 ;点A 关于原点的对称点的坐
标是 。
点A 关于x 轴对称的点的坐标为 。
【例2】已知点M ()y x ,与点N ()3,2--关于x 轴对称,则______=+y x 。
【例3】已知点P ()3,3b a +与点Q ()b a 2,5+-关于x 轴对称,___________==b a 。
【例4】将三角形ABC 的各顶点的横坐标都乘以1-,则所得三角形与三角形ABC 的关系( )
A .关于x 轴对称
B .关于y 轴对称
C .关于原点对称
D .将三角形ABC 向左平移了一个单位
考点三——平面直角坐标系中平移问题
【例1】线段CD 是由线段AB 平移得到的。
点A (–1,4)的对应点为C (4,7),则点B
(–4,–1)的对应点D 的坐标为______________。
【例2】在平面直角坐标系内,把点P (-5,-2)先向左平移2个单位长度,再向上平移4
个单位长度后得到的点的坐标是 。
【例3】将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x ,-1),则xy=__。
【例4】点P 在x 轴上对应的实数是3 ,则点P 的坐标是 ,若点Q 在y 轴上对应的
实数是
3
1
,则点Q 的坐标是 , 考点四——平面直角坐标系中平行线问题
【例1】已知AB ∥x 轴,A 点的坐标为(3,2),并且AB =5,则B 的坐标为 。
【例2】过A (4,-2)和B (-2,-2)两点的直线一定( )
A .垂直于x 轴
B .与Y 轴相交但不平于x 轴 B . 平行于x 轴 D .与x 轴、y 轴平行
【例3】已知点A (m ,-2),点B (3,m-1),且直线AB ∥x 轴,则m 的值为 。
【例4】已知:A(1,2),B(x,y),AB ∥x 轴,且B 到y 轴距离为2,则点B 的坐标是 . 【例5】平行于x 轴的直线上的点的纵坐标一定( )
A .大于0
B .小于0
C .相等
D .互为相反数
【例6】若点(a ,2)在第二象限,且在两坐标轴的夹角平分线上,则a= . 【例7】已知点P (x 2-3,1)在一、三象限夹角平分线上,则x= . 【例8】过点A (2,-3)且垂直于y 轴的直线交y 轴于点B ,则点B 坐标为( ).
A .(0,2)
B .(2,0)
C .(0,-3)
D .(-3,0)
【例9】如果直线AB 平行于y 轴,则点A ,B 的坐标之间的关系是( ).
A .横坐标相等
B .纵坐标相等
C .横坐标的绝对值相等
D .纵坐标的绝对值相等
考点五——平面直角坐标系中对角线上的问题
【例1】已知P 点坐标为(2-a ,3a +6),且点P 到两坐标轴的距离相等,则点P 的坐标__。
【例2】已知点A (-3+a ,2a+9)在第二象限的角平分线上,则a 的值是____________。
【例3】已知点P (x ,-y )在第一、三象限的角平分线上,由x 与y 的关系是________。
考点六——平面直角坐标系中面积的求法,图形的平移
【例1】如图所示的直角坐标系中,三角形ABC 的顶点坐标分别是A (0,0)、B (6,0)、
C (5,5)。
求:(1)求三角形ABC 的面积;
(2)如果将三角形ABC 向上平移3个单位长度,得三角形A 1B 1C 1,再向右平移2个单位长度,得到三角形A 2B 2C 2。
分别画出三角形A 1B 1C 1和三角形A 2B 2C 2。
并试求出A 2、B 2、C 2的坐标?
【例2】如图,正方形ABCD 以(0,0)为中心,边长为4,求各顶点的坐标.
【例3】三角形ABC 三个顶点A 、B 、C 的坐标分别为A(2,-1)、B(1,-3)、C(4,-3.5).把三角
形A 1B 1C 1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC ,试写出三角形A 1B 1C 1三个顶点的坐标,并在直角坐标系中描出这些点;在平面直角坐标系中,将点M (1,0)向右平移3个单位,得到点1M ,则点1M 的坐标为________.
A
C
x
y
B。
