随机过程第6章课件
合集下载
随机过程-第六章 鞅与停时

E (Yn ) 0 E , Y (n ) ; X 0 0, X n Yi ,则 { X n , n 0} 关于 {Yn , n 0} 是鞅。
i 1
n
-1-
例 6.2 ( 独 立 同 分 布 变 量 之 积 ) 设 Y0 1 , {Yn , n 1} 服 从 独 立 同 分 布 , 且
3、若 { X n , n 0} 关于 {Yn , n 0} 是(上)鞅, g 是关于 Y0 , Y1 ,, Yn 的(非负)函数, 则
6.1 离散鞅的定义
定义 6.1 鞅:随机过程 { X n , n 0} 是鞅,如果 n 0 有
(1) E ( X n ) ; (2) E ( X n1 X 0 , X1 ,, X n ) X n , a.s. 鞅是公平赌博的一种推广。 假设我们把 X n 解释为第 n 次赌博后的赌资, 则根据定义 6.1, 第 n 1 次赌博后的平均赌资恰好等于 X n ,无论之前发生怎样的情况,即每次赌博胜负机会 均等。 对(2)式两边取期望得
f ( y) f ( z )dF ( z y)
则称 { X n n f (Yn ), n 0} 是一个鞅。 例 6.4 和例 6.5 将马尔可夫链与鞅这两个重要的随机过程有机地联系起来,在今后的实 际研究中应用广泛。 例 6.6 波利亚(Polya)坛子抽样模型:考虑一个装有红、黄两色球的坛子。假设最初 坛子中装有红黄两色各一个球,每次都按如下规则有放回地随机抽取:如果拿出的是红球, 则放回的同时再加一个同色的球;如果拿出的是黄色的球也采取同样的做法。以 Yn 第 n 次 抽取后坛子中的红球数,则 Y0 1 , Yn 是一个非时齐的马尔可夫链,转移概率为
a0 (Y1 ) a0 , E[ f (Z0 ) Y1 ] E[ f (Z0 )] ,令
北大随机过程课件:第 6 章 第 1 讲 最小均方误差线性估计汇编

sˆ(t) = ax(t) ,且
a = E{s(t )x(t)}/ E{x(t) x(t)} = Rss (0) /[Rss (0) + Rnn (0)]
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t) − sˆ(t) 2 = E{[s(t) − ax(t)]s(t)}
为了使均方误差最小,
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
a = E{s(t )x(t)}/ E{x(t) x(t)} = Rss (0) /[Rss (0) + Rnn (0)]
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t) − sˆ(t) 2 = E{[s(t) − ax(t)]s(t)}
为了使均方误差最小,
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
第6章信号处理简介

机电工程学院 Sun Chuan 68215 第6章 信号处理简介
随机信号分类
随机信号可分为平稳的和非平稳的。如果随机 信号的特征参数不随时间变化,则称为平稳的,否
则为非平稳的。一个平稳随机信号,若一次长时间
测量的时间平均值等于它的统计平均值(或称集合平 均值),则称这样的随机信号是各态历经的。通常把 工程上遇到的随机信号均认为是各态历经的。
X(k ) x(n)e j2πkn/N
n 0
N 1
(2.4.1)
1 N 1 x(n) X(k )e j2πkn/N N k 0
机电工程学院 Sun Chuan 68215 第6章 信号处理简介
上述的离散傅里叶变换对将N个时域采样点x(n)与N 个频率采样点X((k)联系起来,建立了时域与频域的关 系,提供了通过计算机作傅里叶变换运算的一种数学 方法。利用计算机进行离散傅里叶变换可查阅相关文 献。
机电工程学院 Sun Chuan 68215 第6章 信号处理简介
图2.4.3 采样频率不同时的频谱波形
机电工程学院 Sun Chuan 68215 第6章 信号处理简介
3. 量化及量化误差
(1) 量化 将采样信号的幅值经过四舍五入的方法离散化的 过程称为量化。 (2) 量化电平 若采样信号可能出现的最大值为A,令其分 为B个间隔,则每个间隔Δx=A/B,Δx称为量化电平,每个量 化电平对应一个二进制编码。 (3) 量化误差 当采样信号落在某一区间内,经过四舍五入 而变为离散值时,则产生量化误差,其最大值是±0.5Δx。 量化误差的大小取决于A/D转换器的位数,其位数越高, 量化电平越小,量化误差也越小。比如,若用8位的A/D转换 器,8位二进制数为28=256,则量化电平为所测信号最大幅值 的1/256,最大量化误差为所测信号最大幅值的±1/512。
随机过程课件PPT资料(正式版)

应怎样分才合理呢➢?」
☞随机事件:样本空间的子集,常记为 A ,B ,…它是满足某些条件的样本点所组成的集合.
排队和服务系统 ◙A∩勤B 奋⇔、A刻B :苦A、与合➢B作的、积探事索件;; 更新过程 为从事科学研究打下坚实的基础;
☞抽取的是精装中➢文版数学书 ⇒
➢ 时间序列分析
➢ 鞅过程
绪论
《随机过程》基础
概率(或然率或几率) ——随机事件出现的可能 性的量度;
概率论其起源与博弈、 、天气预报等问题有 关
⊕16世纪意大利学者开始研究掷骰子等赌博 中的一些问题;
⊕17世纪中叶,「现有两个赌徒相约赌若干 局,谁先赢S局就算赢了,当赌徒A赢K局(K<S), 而赌徒B赢L局(L<S)时,赌博中止,赌资应怎 样分才合理呢?」
随机过程课件
《随机过程》
➢ 教材: ◙ 张卓奎,陈慧婵,随机过程.西安电子科技大 学.2003.
➢ 主要参考文献: ◙ 胡奇英编著,随机过程.西安电子科技大学.1998. ◙ 周荫清 ,随机过程习题集. 清华大学出版社, 2004. ◙ 林元纟金烈 ,应用随机过程. 清华大学出版社, 2002.
……
➢ 随机过程理论在社会科学中例如在社会统计, 学、经 济、金融工程、管理中也得到极其广泛的应用。
➢ 为从事科学研究打下坚实的基础;
绪论
教学目标
➢ 充分理解、熟练掌握教材的内容 ◙ 熟练掌握基本的数学概念和定理;
◙ 熟练掌握随机过程研究对象的数学描述;
Hale Waihona Puke ➢ 通过学习和练习,具备一定的分析、解决本专业具体 问题的能力;
☞拉普拉斯曾说:“生活中最重要的问题,其中 绝大多数在实质上只是概率的问题”。
☞概率论是研究随机现象数量规律的数学分支。 在实际中,人们往往还需要研究在时间推进中某 一特定随机现象的演变情况,描述这种演变的就 是概率论中的随机过程。
☞随机事件:样本空间的子集,常记为 A ,B ,…它是满足某些条件的样本点所组成的集合.
排队和服务系统 ◙A∩勤B 奋⇔、A刻B :苦A、与合➢B作的、积探事索件;; 更新过程 为从事科学研究打下坚实的基础;
☞抽取的是精装中➢文版数学书 ⇒
➢ 时间序列分析
➢ 鞅过程
绪论
《随机过程》基础
概率(或然率或几率) ——随机事件出现的可能 性的量度;
概率论其起源与博弈、 、天气预报等问题有 关
⊕16世纪意大利学者开始研究掷骰子等赌博 中的一些问题;
⊕17世纪中叶,「现有两个赌徒相约赌若干 局,谁先赢S局就算赢了,当赌徒A赢K局(K<S), 而赌徒B赢L局(L<S)时,赌博中止,赌资应怎 样分才合理呢?」
随机过程课件
《随机过程》
➢ 教材: ◙ 张卓奎,陈慧婵,随机过程.西安电子科技大 学.2003.
➢ 主要参考文献: ◙ 胡奇英编著,随机过程.西安电子科技大学.1998. ◙ 周荫清 ,随机过程习题集. 清华大学出版社, 2004. ◙ 林元纟金烈 ,应用随机过程. 清华大学出版社, 2002.
……
➢ 随机过程理论在社会科学中例如在社会统计, 学、经 济、金融工程、管理中也得到极其广泛的应用。
➢ 为从事科学研究打下坚实的基础;
绪论
教学目标
➢ 充分理解、熟练掌握教材的内容 ◙ 熟练掌握基本的数学概念和定理;
◙ 熟练掌握随机过程研究对象的数学描述;
Hale Waihona Puke ➢ 通过学习和练习,具备一定的分析、解决本专业具体 问题的能力;
☞拉普拉斯曾说:“生活中最重要的问题,其中 绝大多数在实质上只是概率的问题”。
☞概率论是研究随机现象数量规律的数学分支。 在实际中,人们往往还需要研究在时间推进中某 一特定随机现象的演变情况,描述这种演变的就 是概率论中的随机过程。
随机振动--第6章-傅里叶变换

傅立叶变换的10大性质: j F ( ) f ( ) e d (5) 对称性定理: F [ F (t )] 2f ( ) 把F(w)的变量换成t, (6)时域微分定理 d n f (t ) n
F[ dt
t
倒频谱
n
] ( j ) F ( )
1 F [ f (at )] F ( ) a a
3、狄拉克δ函数(δ函数)
是一个广义函数,没有普遍意义下的函数值。 定义:满足下列条件的函数称为δ函数。
0 (1) (t ) (2) (t ) dt 1
当t 0 当t 0
推论一下:
0 (1) (t t 0) (2) (t t 0)dt 1
x (t )
n
c e
n
jnt
1 其中:c n T
T 2 T 2
x (t ) e
jnt
dt
2、傅立叶变换
狄氏条件: (1)函数f(t)连续或只有有限个第一 类间断点;(2)函数f(t) 只有有限个极值点。
傅立叶变换F ( )
f ( )e
j
d
1、傅立叶级数
1)傅立叶级数的实数形式
任一周期函数x(t),如在[-T/2,T/2] 区 间满足狄利克雷(狄氏)条件,都可 展开成傅立叶级数(傅氏级数)
狄氏条件:
(1)函数连续或只有有限个第一类间断点; (2)函数只有有限个极值点。
设一周期函数x(t ),周期为T,满足狄氏条件,则可将其展开成傅氏级数: a0 [ a n cos nt bn sin nt ] x(t ) 2 n 1
随机数学 第9讲 第六章平稳过程(1)

2 C X (τ ) = COV [ X (t ), X (t − τ )] = RX (τ ) − mX
2 C X (0) = DX ( t ) = RX (0) − mX .
则称 { X ( t ), t ∈ T }为宽平稳过程 , 或广义平稳过程 . 以下讨论中,若没有特别说明,平稳即指宽平稳。
第六章 平稳过程随机过程 6.1 平稳过程概念 平稳过程是指过程的统计特性不随时间的推移而变 化的随机过程。 一般,为了便于研究,我们只考虑随机过程的数字 特征特性的平稳性,即有如下宽平稳过程的 定义:
注1 平稳过程数字特征的特点
(1) 平稳过程的所有样本曲 线都在水平直线
x(t ) = mX 上下波动 , 平均偏离度为 σ X .
平稳过程X(t) 的“平均功率”
此式表明:
自相关 (自协方差 )函数都在 τ = 0处取到最大值 .
RX (0) ≥ 0.
RX (−τ ) = RX (τ ) ,
2 证明: RX (0) = E[ X (t ) X (t )] = E X (t ) 2 = Ψ X ≥ 0.
e − λt ( λt ) , k = 0,1, 2, k!
k
若随机点在[0,t]内出现偶数次 ,则
若随机点在[0,t]内出现奇数次 ,则 X ( t ) = −1; (1)计算 mX ( t ) , C X ( t1 , t2 )
⎛ ( λt )0 ( λt )2 ( λt )4 ⎞ = e − λt ⎜ + + + ⎟ ⎜ 0! ⎟ 2! 4! ⎝ ⎠ λt − λt −2 λ t ⎞ 1+ e − λt ⎛ e + e [0,t]内随机 = e ⎜ ⎟ = 2 2 ⎝ ⎠ 点出现奇数次
计量经济学第6章时间序列分析

则一个时间序列是“弱平稳的”,通常情况下,我们所 说的平稳性指的就是弱平稳。
三、五种经典的时间序列类型
1.白噪声( White noise)
白噪声通常用εt表示,是一个纯粹的随机过程,满足: (1)E(εt) = 0 , 对所有t成立; (2)V ar(εt) = σ2,对所有t成立; (3)Cov (εt, εt+k) = 0,对所有t和k≠0成立。
而与α、β无关。
2. ADF检验
在DF检验中,实际上是假定了时间序列是由具有白噪声 随机误差项的一阶自回归过程AR(1)(见教材式6.3.2)生成的。 但在实际检验中,时间序列可能由更高阶的自回归过程生成 的,或者随机误差项并非是白噪声的,为了保证DF检验中随 机误差项的白噪声特性,Dicky和Fuller对DF检验进行了扩充,
第六章 时间序列分析
6.1 时间序列分析的基本概念 6.2 平稳性检验 6.3 ARIMA模型 6.4 协整与误差修正模型 6.5* 向量自回归(VAR)模型
第一节 时间序列分析的基本概念
一、时间序列与随机过程
随机变量组成的一个有序序列称为随机过程,记为{X t ,t T }
的两个模型分别进行检验,可以得到同样的结论。
第三节 ARIMA模型
ARIMA 模 型 ( autoregressive integrated moving average model ),又称为 Box-Jenkins 模型,简称为 BJ 模 型。它是单变量时间序列在同方差情况下进行线性建模的 最常用的方法。 ARIMA 模型实质上是差分运算与 ARMA 模型 的组合,它不同于经济计量模型的两个主要特点是:第一, 这种建模方法不以经济理论为依据,而是依据变量自身的 变化规律,利用外推机制描述时间序列的变化;第二,明 确考虑时间序列的非平稳性,如果时间序列非平稳,建立 模型之前应先通过差分把它变换成平稳的时间序列,再考 虑建模问题。
《数学随机过程》PPT课件
所以X与Y不相关。 故 (X,Y )=0 X与Y不相关
几何直观意义
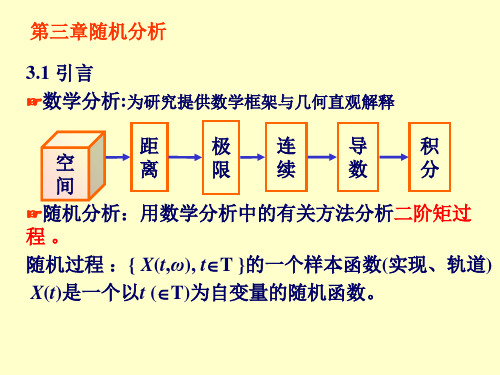
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
马尔可夫过程是理论和实际应用都十分重要的一类随 机过程。在工程系统中的噪声和信号分析、通信网络 和输送现象的模拟、统计物理学、生物学、数字计算 方法、经济管理和市场预测等领域中都有十分重要的
作用和广泛应用。
2013-4-26 胡朝明 26-4
§3.1 马尔可夫过程的概念
给定随机过程{X(t),tT},如果对于参数中任意n个时 刻ti,i=1,2,…,n,t1<t2<…<tn有 P{X(tn)<xn|X(t1)=x1,X(t2)=x2,…,X(tn-1)=xn-1} =P{X(tn)<xn|X(tn-1)=xn-1} (3.1) 则称随机过程{X(t),tT}为马尔可夫过程,简称马氏过程。 具有(3.1)式性质称为具有马尔可夫性、无后效性或无记忆性。 由条件分布函数的定义,(3.1)等价于 F(xn;tn|x1,x2,…,xn-1;t1,t2,…,tn-1)=F(xn;tn|xn-1;tn-1)。 如果概率密度函数存在,它等价于 f(xn;tn|x1,x2,…,xn-1;t1,t2,…,tn-1)=f(xn;tn|xn-1;tn-1)。 随机过程具有马尔可夫性质是说:当给定X(t1), X(t2), …,X(tn-1)时,X(tn)的条件分布只依赖于X(tn-1)的已知值, 而与在tn-1以前X(t)的取值无关。
26-21
转移矩阵:
2013-4-26
胡朝明
3.带有两个反射壁的随机游动
状态空间E={1,2,3,4,5}。转移概率: p11=0,p12=1,p1j=0,j=3,4,5; p55=0,p54=1,p5j=0,j=1,2,3; pi,i-1=q,pi,i+1=p,i=2,3,4; pij=0,ji-1,i+1,i=2,3,4。 状态1和5永远不能停留,称为反射壁。
iu
更新计数过程 相关函数 R(s,t)=min(s,t)+2st。
2013-4-26 胡朝明 26-2
等待时间序列n服从参数为的n阶爱而朗分布; 协方差函数 C(s,t)=min(s,t);
本讲主要内容
马尔可夫过程
• • • • • 马尔可夫过程的概念 马尔可夫过程的分类 离散参数马氏链 k步转移概率、 k步转移矩阵 齐次马尔可夫链
2013-4-26 胡朝明 26-5
转移概率
给定马氏过程{X(t),tT},条件概率 p(s,t;x,y)=P{X(t)<y|X(s)=x} 称为马氏过程的转移概率。
若转移概率与s无关,则此过程称为齐次(时)马 氏过程。
马氏过程{X(t),tT}中,X(t)的取值x称为状态, X(t)=x表示过程在时刻t处于状态x,过程所取状 态的全体 E={x:X(t)=x,tT} 称为状态空间。
p
j E
ij
( k ) 1;
p
j E
ij
1。
2013-4-26
胡朝明
26-17
例1 贝努里序列
如上节例2所述,贝努里序列是一个齐次 马氏链,其转移矩阵为
q P q p p
一般地,独立同分布的离散随机变量序列 {X(n),n=0,1,2,…}都是齐次马氏链。
状态空间E={1,2,3,4,5}。转移概率 p11=p55=1;p1j=0,j1;p5j=0,j5; pi,i-1=q,pi,i+1=p,i=2,3,4; pi,j=0,ji-1,i+1。 质点运动到1,5时,永远留在那里,称状态1,5为 吸收壁(状态)。
1 q P 0 0 0 0 0 q 0 0 0 p 0 q 0 0 0 p 0 0 0 0 0 p 1
t1<t2<…<tn,有 P{X(tn)<xn|X(t1)=x1,X(t2)=x2,…,X(tn-1)=xn-1} =P{X(tn)-X(tn-1)<xn-xn-1|X(t1)-X(t0)=x1, X(t2)-X(t1)=x2-x1,…,X(tn-1)-X(tn-2)=xn-1-xn-2} =P{X(tn)-X(tn-1)<xn-xn-1} =P{X(tn)<xn|X(tn-1)=xn-1} 马氏性成立,故独立增量过程{X(t),t0}是马尔可夫过程。
转移矩阵: P 0 0 0 q 0 0 0 q 0 p 0 q 0 p 0 0 0 p 0 0 0
2013-4-26
胡朝明
26-20
2.两个吸收壁随机游动
2013-4-26 胡朝明 26-6
马尔可夫过程的分类
参数集T 离散 连续 连续参数马氏链 离散 离散参数马氏链
状态空间E
连续 离散参数马氏序列 连续参数马氏过程
2013-4-26
胡朝明
26-7
例1 一维随机游动
在直线上非负整数点作随机游动的质点,当时 刻n时处于位置i(i0),时刻n+1时处于i+1的概率为 p i ,处于i-1的概率为q i ,不动的概率为r i (p i +q i +r i =1),若以X(n)表示时刻n质点的位置,那么{X(n), n=0,1,2,…}离散参数马氏链。 这是因为,当X(n)=i时,X(n+1),X(n+2),… 等以后的行为只与X(n)=i有关,而与质点在n以前 如何到达i是无关的。它的状态空间E={0,1,2,…}。
为马氏链{X(n),n=0,1,…}在m时刻的k步转移矩阵。 一步转移矩阵P(m,1)简称转移矩阵。 由转移概率的定义,显然有:
p ij ( m , k ) 0
2013-4-26
p
j E
ij
(m , k ) 1
26-16
胡朝明
齐次马尔可夫链
若马氏链{X(n),n=0,1,2,…}的转移概率pij(m,k)与m 无关,即 pij(m,k)=P{X(m+k)=j|X(m)=i}=pij(k); pij(m,1)=P{X(m+1)=j|X(m)=i}=pij(1)=pij; 则称{X(n),n=0,1,2,…}为齐次马尔可夫链,简称齐次马氏 链。 齐次马氏链的k步转移矩阵记为: P(m,k)=P(k)=(pij(k))i,jE 一步转移矩阵,简称转移矩阵,记为: P(m,1)=P(1)=P=(pij)i,jE 齐次马氏链的转移概率具有如下性质: 0pij(k)1, 0pij1,
2013-4-26 胡朝明 26-11
二项计数过程
设{X(n),n=1,2,…}是贝努里随机序列,X(0) =0,X(n),n=1,2,…是相互独立同分布的贝努里随 机变量,设
Y (n )
k 1
n
X (k ), n 1,2 , , Y ( 0 ) 0
称{Y(n),n=0,1,2,…}为二项计数过程(广义随机游 动),它是平稳独立增量过程,因而是离散参数 马氏链。
成立,则称{X(n),n=0,1,2,…}为离散参数马尔可 夫链,简称马氏链。
2013-4-26 胡朝明 26-14
k步转移概率
设{X(n),n=0,1,2,…}为马氏链,E={0,1,2, …},称条件概率 pij(m,k)=P{X(m+k)=j|X(m)=i} 为马氏链{X(n),n=0,1,…}在m时刻的k步转移概率. k步转移概率的直观意义是:质点在时刻m时 处于状态i,再经过k步(k个单位时间)处于状态j 的条件概率。 特别地,k=1时, pij(m,1)=P{X(m+1)=j|X(m)=i} 称为一步转移概率,简称转移概率。
2013-4-26 胡朝明 26-15
k步转移矩阵
称矩阵 P ( m , k )
( p ij ( m , k )) i , j E p 01 ( m , k ) p 11 ( m , k ) p n1 (m , k ) p 0n (m , k ) p 1n (m , k ) p nn (m , k ) p 00 ( m , k ) p 10 ( m , k ) p (m , k ) n0
此,随机游动{X(n),n=0,1,2,…}是齐次马氏链。
随机游动的统计特征由它在边界的特点决定, 下面给出几种特殊的情形。
2013-4-26 胡朝明 26-19
1.自由(无限制)随机游动
状态空间E={…,-2,-1,0,1,2,…}两端无限
制。转移概率:
pi,i-1=q,pi,i+1=p,其余pi,j=0,ji-1,i+1
2013-4-26 胡朝明 26-9
贝努里随机序列
特例 贝努里随机序列,即X(n),n=0,1,
2,…是相互独立同分布的贝努里随机变量,
X(n) P 0 q 1 p
0<p<1,p+q=1 n=1,2,…
{X(n),n=0,1, 2,…}是离散参数马氏链。
2013-4-26
胡朝明
26-10
例3
独立增量过程{X(t),t0},(X(0)=0)是马尔可夫过程。 证明 设 {X(t),tT}是独立 增 量过程 , X(0)=0,对任意
2013-4-26
胡朝明
26-18
例2 随机游动
一质点在数轴上的整数点上作随机游动的, 以X(n)表示时刻n质点的位置。质点在某一时刻m
时处于状态i,即X(m)=i,则下一步以概率q左移
到状态i-1,即p i,i-1 (m,1)=q;而以概率p右移到状 态i+1,即p i,i+1 (m,1)=p。因而质点将来所处的状 态X(m+1),X(m+2),…,X(m+k)等仅与现在所处的 状态X(m)=i有关,而与过去所处的状态无关。因
2013-4-26
胡朝明
26-8
作用和广泛应用。
2013-4-26 胡朝明 26-4
§3.1 马尔可夫过程的概念
给定随机过程{X(t),tT},如果对于参数中任意n个时 刻ti,i=1,2,…,n,t1<t2<…<tn有 P{X(tn)<xn|X(t1)=x1,X(t2)=x2,…,X(tn-1)=xn-1} =P{X(tn)<xn|X(tn-1)=xn-1} (3.1) 则称随机过程{X(t),tT}为马尔可夫过程,简称马氏过程。 具有(3.1)式性质称为具有马尔可夫性、无后效性或无记忆性。 由条件分布函数的定义,(3.1)等价于 F(xn;tn|x1,x2,…,xn-1;t1,t2,…,tn-1)=F(xn;tn|xn-1;tn-1)。 如果概率密度函数存在,它等价于 f(xn;tn|x1,x2,…,xn-1;t1,t2,…,tn-1)=f(xn;tn|xn-1;tn-1)。 随机过程具有马尔可夫性质是说:当给定X(t1), X(t2), …,X(tn-1)时,X(tn)的条件分布只依赖于X(tn-1)的已知值, 而与在tn-1以前X(t)的取值无关。
26-21
转移矩阵:
2013-4-26
胡朝明
3.带有两个反射壁的随机游动
状态空间E={1,2,3,4,5}。转移概率: p11=0,p12=1,p1j=0,j=3,4,5; p55=0,p54=1,p5j=0,j=1,2,3; pi,i-1=q,pi,i+1=p,i=2,3,4; pij=0,ji-1,i+1,i=2,3,4。 状态1和5永远不能停留,称为反射壁。
iu
更新计数过程 相关函数 R(s,t)=min(s,t)+2st。
2013-4-26 胡朝明 26-2
等待时间序列n服从参数为的n阶爱而朗分布; 协方差函数 C(s,t)=min(s,t);
本讲主要内容
马尔可夫过程
• • • • • 马尔可夫过程的概念 马尔可夫过程的分类 离散参数马氏链 k步转移概率、 k步转移矩阵 齐次马尔可夫链
2013-4-26 胡朝明 26-5
转移概率
给定马氏过程{X(t),tT},条件概率 p(s,t;x,y)=P{X(t)<y|X(s)=x} 称为马氏过程的转移概率。
若转移概率与s无关,则此过程称为齐次(时)马 氏过程。
马氏过程{X(t),tT}中,X(t)的取值x称为状态, X(t)=x表示过程在时刻t处于状态x,过程所取状 态的全体 E={x:X(t)=x,tT} 称为状态空间。
p
j E
ij
( k ) 1;
p
j E
ij
1。
2013-4-26
胡朝明
26-17
例1 贝努里序列
如上节例2所述,贝努里序列是一个齐次 马氏链,其转移矩阵为
q P q p p
一般地,独立同分布的离散随机变量序列 {X(n),n=0,1,2,…}都是齐次马氏链。
状态空间E={1,2,3,4,5}。转移概率 p11=p55=1;p1j=0,j1;p5j=0,j5; pi,i-1=q,pi,i+1=p,i=2,3,4; pi,j=0,ji-1,i+1。 质点运动到1,5时,永远留在那里,称状态1,5为 吸收壁(状态)。
1 q P 0 0 0 0 0 q 0 0 0 p 0 q 0 0 0 p 0 0 0 0 0 p 1
t1<t2<…<tn,有 P{X(tn)<xn|X(t1)=x1,X(t2)=x2,…,X(tn-1)=xn-1} =P{X(tn)-X(tn-1)<xn-xn-1|X(t1)-X(t0)=x1, X(t2)-X(t1)=x2-x1,…,X(tn-1)-X(tn-2)=xn-1-xn-2} =P{X(tn)-X(tn-1)<xn-xn-1} =P{X(tn)<xn|X(tn-1)=xn-1} 马氏性成立,故独立增量过程{X(t),t0}是马尔可夫过程。
转移矩阵: P 0 0 0 q 0 0 0 q 0 p 0 q 0 p 0 0 0 p 0 0 0
2013-4-26
胡朝明
26-20
2.两个吸收壁随机游动
2013-4-26 胡朝明 26-6
马尔可夫过程的分类
参数集T 离散 连续 连续参数马氏链 离散 离散参数马氏链
状态空间E
连续 离散参数马氏序列 连续参数马氏过程
2013-4-26
胡朝明
26-7
例1 一维随机游动
在直线上非负整数点作随机游动的质点,当时 刻n时处于位置i(i0),时刻n+1时处于i+1的概率为 p i ,处于i-1的概率为q i ,不动的概率为r i (p i +q i +r i =1),若以X(n)表示时刻n质点的位置,那么{X(n), n=0,1,2,…}离散参数马氏链。 这是因为,当X(n)=i时,X(n+1),X(n+2),… 等以后的行为只与X(n)=i有关,而与质点在n以前 如何到达i是无关的。它的状态空间E={0,1,2,…}。
为马氏链{X(n),n=0,1,…}在m时刻的k步转移矩阵。 一步转移矩阵P(m,1)简称转移矩阵。 由转移概率的定义,显然有:
p ij ( m , k ) 0
2013-4-26
p
j E
ij
(m , k ) 1
26-16
胡朝明
齐次马尔可夫链
若马氏链{X(n),n=0,1,2,…}的转移概率pij(m,k)与m 无关,即 pij(m,k)=P{X(m+k)=j|X(m)=i}=pij(k); pij(m,1)=P{X(m+1)=j|X(m)=i}=pij(1)=pij; 则称{X(n),n=0,1,2,…}为齐次马尔可夫链,简称齐次马氏 链。 齐次马氏链的k步转移矩阵记为: P(m,k)=P(k)=(pij(k))i,jE 一步转移矩阵,简称转移矩阵,记为: P(m,1)=P(1)=P=(pij)i,jE 齐次马氏链的转移概率具有如下性质: 0pij(k)1, 0pij1,
2013-4-26 胡朝明 26-11
二项计数过程
设{X(n),n=1,2,…}是贝努里随机序列,X(0) =0,X(n),n=1,2,…是相互独立同分布的贝努里随 机变量,设
Y (n )
k 1
n
X (k ), n 1,2 , , Y ( 0 ) 0
称{Y(n),n=0,1,2,…}为二项计数过程(广义随机游 动),它是平稳独立增量过程,因而是离散参数 马氏链。
成立,则称{X(n),n=0,1,2,…}为离散参数马尔可 夫链,简称马氏链。
2013-4-26 胡朝明 26-14
k步转移概率
设{X(n),n=0,1,2,…}为马氏链,E={0,1,2, …},称条件概率 pij(m,k)=P{X(m+k)=j|X(m)=i} 为马氏链{X(n),n=0,1,…}在m时刻的k步转移概率. k步转移概率的直观意义是:质点在时刻m时 处于状态i,再经过k步(k个单位时间)处于状态j 的条件概率。 特别地,k=1时, pij(m,1)=P{X(m+1)=j|X(m)=i} 称为一步转移概率,简称转移概率。
2013-4-26 胡朝明 26-15
k步转移矩阵
称矩阵 P ( m , k )
( p ij ( m , k )) i , j E p 01 ( m , k ) p 11 ( m , k ) p n1 (m , k ) p 0n (m , k ) p 1n (m , k ) p nn (m , k ) p 00 ( m , k ) p 10 ( m , k ) p (m , k ) n0
此,随机游动{X(n),n=0,1,2,…}是齐次马氏链。
随机游动的统计特征由它在边界的特点决定, 下面给出几种特殊的情形。
2013-4-26 胡朝明 26-19
1.自由(无限制)随机游动
状态空间E={…,-2,-1,0,1,2,…}两端无限
制。转移概率:
pi,i-1=q,pi,i+1=p,其余pi,j=0,ji-1,i+1
2013-4-26 胡朝明 26-9
贝努里随机序列
特例 贝努里随机序列,即X(n),n=0,1,
2,…是相互独立同分布的贝努里随机变量,
X(n) P 0 q 1 p
0<p<1,p+q=1 n=1,2,…
{X(n),n=0,1, 2,…}是离散参数马氏链。
2013-4-26
胡朝明
26-10
例3
独立增量过程{X(t),t0},(X(0)=0)是马尔可夫过程。 证明 设 {X(t),tT}是独立 增 量过程 , X(0)=0,对任意
2013-4-26
胡朝明
26-18
例2 随机游动
一质点在数轴上的整数点上作随机游动的, 以X(n)表示时刻n质点的位置。质点在某一时刻m
时处于状态i,即X(m)=i,则下一步以概率q左移
到状态i-1,即p i,i-1 (m,1)=q;而以概率p右移到状 态i+1,即p i,i+1 (m,1)=p。因而质点将来所处的状 态X(m+1),X(m+2),…,X(m+k)等仅与现在所处的 状态X(m)=i有关,而与过去所处的状态无关。因
2013-4-26
胡朝明
26-8
