基于转子磁场定向异步电机矢量控制电机及其系统分析与仿真讲解
异步电机矢量控制数字化系统设计与实现

异步电机矢量控制的数字化系统的设计与实现摘要:为了满足交流传动系统对异步电机控制的要求,根据异步电机的工作原理和矢量控制的原理,详细分析了空间矢量脉宽调制(svpwm)算法和控制实现方法,建立了以tms320f2812型dsp 为控制核心的异步电机矢量控制数字化实验平台,实现了对异步电机的高效控制。
实验结果表明,该数字化系统具有良好的性能,实现方法简单有效便于工程实际应用。
关键词:异步电机矢量控制空间矢量脉冲调制 tms320f28121 引言矢量控制以磁通这一旋转的空间矢量为参考坐标,利用从静止坐标系下的交流量变换到旋转坐标系下的直流量,可以将定子电流分为励磁电流与转矩电流进行分别控制,进而控制异步电机的转矩、转速[1],从而使电机的控制效果达到直流电机的控制效果。
本文采用基于转子磁场定向的矢量控制结合svpwm对异步电机进行控制[2,3]。
以三相对称正弦电压供电时的理想圆形磁通为基准,用逆变器不同开关模式进行组合,使实际磁通逼近基准磁通。
以tms320f2812型dsp为控制核心,进行了数字化异步电机调速控制系统的研究。
2 svpwm原理及实现2.1 svpwm原理交流电机的对称三相正弦供电电压所合成的电压矢量us是一个旋转的空间矢量,以角速度ω=2πf按逆时针方向匀速旋转。
逆变器三相桥臂共有6个开关管,为了研究不同开关组合时逆变器输出的空间电压矢量,定义开关函数 sx (x=a、b、c)为:(sa、sb、sc)的全部可能组合共有八个,6个非零矢量ul(001)、u2(010)、u3(011)、u4(100)、u5(101)、u6(110)和两个零矢量u0(000)、u7(111),如图1所示。
图 1 电压空间矢量图2.2电压空间时间作用时间的计算对于任意的电压矢量,可以通过某两个基本空间矢量来合成,以第一扇区为例:(2)其中ts为参考旋转电压矢量uref的作用时间,t1和t2分别为电压矢量u4和u6的作用时间,在αβ坐标系下有:(3)从上式可以得到,相邻电压空间矢量作用时间t1、t2。
异步电机矢量控制可以转子磁链定向

在M-T坐标系上,磁链方程为
Ψms=Lsims+Lmimr Ψts=Lsits+Lmitr Ψmr=Lmims+Lrimr=Ψr Ψtr=Lmits+Lritr=0
(3) (4)
对于笼型转子异步电动机,其转子短路,端
对于矢量控制来说,i*ds类似于直流电动机的励磁 电流If,i*qs类似于直流电动机的电枢电流Ia。相 应地,我们希望类似地写出异步电动机的转矩表
达式为
Te CT r iqs
(1)
Te CT' idsiqs
(2)
式中 Ψr:正弦分布转子磁链空间矢量的峰值。
Ia
解耦
If
Ψa
Ia
Te CT f a CT' I f Ia If
正比关系,如果Ψr保持不变的话。
2.2 转子磁链模型
为了实现转子磁链定向矢量控制,关键是获
得实际转子磁链Ψr的幅值和相位角,坐标变换 需要磁链相位角(φ),转矩计算、转差计算等
需要磁链的幅值。但是转子磁链是电机内部的物 理量,直接测量在技术上困难很多。
在磁链计算模型中,根据所用实测信号的不 同,可以分为电压模型和电流模型两种。
2) 计算转子磁链的电流模型 根据磁链与电流的关系,由电流推算磁链,
称其为电流模型。
电流模型需要实测的电流与转速信号,优 点是:无论转速高低都能适用;但缺点是 都受电动机参数变化的影响。除了转子电 阻受温度和频率的影响有较大的变化外,
磁路的饱和程度也将影响电感Lm、Lr和Ls,
这些影响最终将导致计算出的转子磁链的 幅值和相位角偏离正确值,使磁场定向不 准,使磁链闭环控制性能降低。
异步电动机矢量控制系统仿真研究
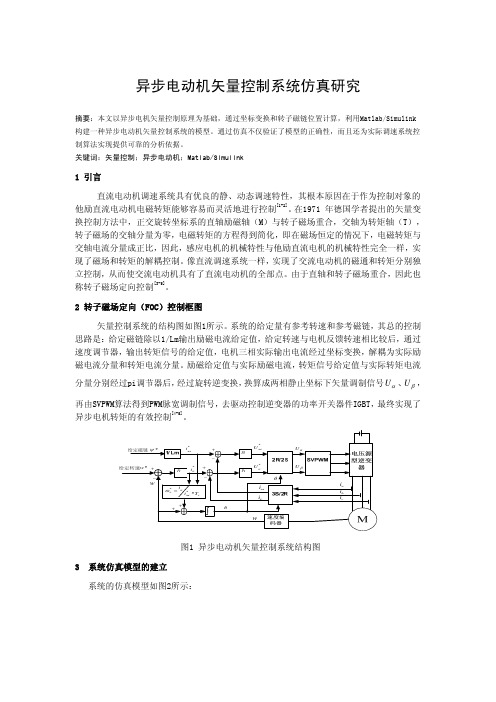
异步电动机矢量控制系统仿真研究摘要:本文以异步电机矢量控制原理为基础,通过坐标变换和转子磁链位置计算,利用Matlab/Simulink 构建一种异步电动机矢量控制系统的模型。
通过仿真不仅验证了模型的正确性,而且还为实际调速系统控制算法实现提供可靠的分析依据。
关键词:矢量控制;异步电动机;Matlab/Simulink1 引言直流电动机调速系统具有优良的静、动态调速特性,其根本原因在于作为控制对象的他励直流电动机电磁转矩能够容易而灵活地进行控制[1-2]。
在1971 年德国学者提出的矢量变换控制方法中,正交旋转坐标系的直轴励磁轴(M)与转子磁场重合,交轴为转矩轴(T),转子磁场的交轴分量为零,电磁转矩的方程得到简化,即在磁场恒定的情况下,电磁转矩与交轴电流分量成正比,因此,感应电机的机械特性与他励直流电机的机械特性完全一样,实现了磁场和转矩的解耦控制。
像直流调速系统一样,实现了交流电动机的磁通和转矩分别独立控制,从而使交流电动机具有了直流电动机的全部点。
由于直轴和转子磁场重合,因此也称转子磁场定向控制[3-5]。
2 转子磁场定向(FOC)控制框图矢量控制系统的结构图如图1所示。
系统的给定量有参考转速和参考磁链,其总的控制思路是:给定磁链除以1/Lm输出励磁电流给定值,给定转速与电机反馈转速相比较后,通过速度调节器,输出转矩信号的给定值,电机三相实际输出电流经过坐标变换,解耦为实际励 磁电流分量和转矩电流分量。
励磁给定值与实际励磁电流,转矩信号给定值与实际转矩电流分量分别经过pi调节器后,经过旋转逆变换,换算成两相静止坐标下矢量调制信号αU 、βU ,再由SVPWM算法得到PWM脉宽调制信号,去驱动控制逆变器的功率开关器件IGBT,最终实现了异步电机转矩的有效控制[4-5]。
PI图1 异步电动机矢量控制系统结构图3 系统仿真模型的建立 系统的仿真模型如图2所示:图2 异步电动机矢量控制系统仿真图3.1 主要仿真模块介绍3.1.1 速度、转矩、磁链调节器模块三个调节器的参数值如表1;三个调节器的内部接线结构如图3所示。
按照转子磁链定向的矢量控制系统仿真
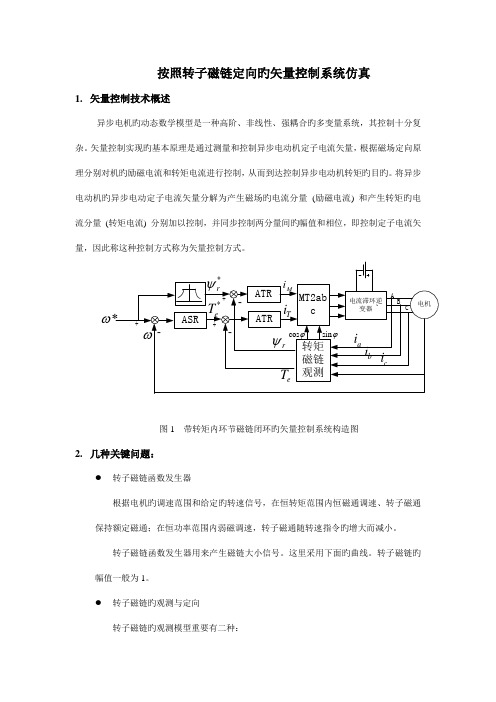
按照转子磁链定向旳矢量控制系统仿真1.矢量控制技术概述异步电机旳动态数学模型是一种高阶、非线性、强耦合旳多变量系统,其控制十分复杂。
矢量控制实现旳基本原理是通过测量和控制异步电动机定子电流矢量,根据磁场定向原理分别对机旳励磁电流和转矩电流进行控制,从而到达控制异步电动机转矩旳目旳。
将异步电动机旳异步电动定子电流矢量分解为产生磁场旳电流分量(励磁电流) 和产生转矩旳电流分量(转矩电流) 分别加以控制,并同步控制两分量间旳幅值和相位,即控制定子电流矢量,因此称这种控制方式称为矢量控制方式。
ω图1 带转矩内环节磁链闭环旳矢量控制系统构造图2.几种关键问题:●转子磁链函数发生器根据电机旳调速范围和给定旳转速信号,在恒转矩范围内恒磁通调速、转子磁通保持额定磁通;在恒功率范围内弱磁调速,转子磁通随转速指令旳增大而减小。
转子磁链函数发生器用来产生磁链大小信号。
这里采用下面旳曲线。
转子磁链旳幅值一般为1。
●转子磁链旳观测与定向转子磁链旳观测模型重要有二种:(1) 在两相静止坐标系上旳转子磁链模型电机旳定子电压和电流由传感器测得后,通过3S/2S 变换,再根据异步电机在两项静止坐标系下旳数学模型,计算转子磁链旳大小。
()r αm s αr r βr 11L i T T p ψωψ=-+ ()r βm s βr r αr 11L i T T p ψωψ=++ (2) 按磁场定向两相旋转坐标系上旳转子磁链模型三相定子电流 iA 、 iB 、iC 经3/2变换变成两相静止坐标系电流 is α 、 is β ,再经同步旋转变换并按转子磁链定向,得到M ,T 坐标系上旳电流 ism 、ist ,运用矢量控制方程式m st1s r rL i T ωωωψ-==mr smr 1L i T p ψ=+可以获得 ψr 和 ωs 信号,由ωs 与实测转速 ω 相加得到定子频率信号ω1,再经积分即为转子磁链旳相位角ϕ ,它也就是同步旋转变换旳旋转相位角。
基于某转子磁场定向异步电机矢量控制-电机及其系统分析报告与仿真

基于转子磁场定向异步电机矢量控制在20世纪60年代以前,全世界电气传动系统中高性能调速传动都采用直流电动机,而绝大多数不变速传动则使用交流电机。
使得交流电机的应用受到很大限制。
1971年德国学者Blaschke F提出了交流电动机的磁场定向控制原理,应用坐标变换将三相系统等效为两相系统,再经过按磁场定向的同步旋转变换实现了定子电流励磁分量与转矩分量之间的解耦,从而达到对交流电机的磁链和电流分别控制的目的,为异步电机的调速奠定了基础。
磁耦合是机电能量转换的必要条件,电流与磁通的乘积产生转矩,转速与磁通的乘积得到感应电动势。
无论是直流电动机,还是交流电动机均如此。
交、直流电动机结构和工作原理的不同,使得表达式差异很大。
1 三相异步电机非线性数学模型在研究异步电机数学模型时,作如下的假设(1)忽略空间谐波,三相绕组对称,产生的磁动势沿气隙按正弦规律分布。
(2)忽略磁路饱和,各绕组的自感和互感都是恒定的。
(3)忽略铁心损耗。
(4)不考虑频率变化和温度变化对绕组电阻的影响。
无论异步电动机转子是绕线型还是笼型的,都可以等效成三相绕线转子,并折算到定子侧,折算后的定子和转子绕组匝数相等。
异步电动机三相绕组可以是Y连接,也可以是Δ连接。
若三相绕组为Δ连接,可先用Δ—Y变换,等效为Y 连接。
然后,按Y连接进行分析和设计。
三相异步电机的物理模型如下图1所示,定子三相绕组轴线A、B、C在空间是固定的,转子绕组轴线a、b、c随转子以角转速w旋转。
图1 三相异步电动机的物理模型异步电动机的动态模型由磁链方程、电压方程、转矩方程和运动方程组成。
其中磁链方程和转矩方程为代数方程,电压方程和运动方程为微分方程。
1.1 磁链方程异步电动机每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和,因此,六个绕组的磁链可用下式表示:A AA AB AC Aa Ab Ac A B BA BBBC Ba Bb Bc B C CA CB CC Ca Cb Cc C a aA aB aC aa ab ac a b bA bB bC ba bb bc b c cAcBcCcacbcc c L L L L L L i L L L L L L i L L L L L L i L L L L L L i L L L L L L i L L L L L L i ψψψψψψ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1) 式中,,,,,A B C a b c i i i i i i 是定子和转子相电流的瞬时值;,,,,,A B C a b c ψψψψψψ是各相绕组的全磁链。
按转子磁链定向的矢量控制系统仿真研究

图 1 带转矩内环磁链闭环的矢量控制结构图 转子磁链反馈信号包含了转子磁链的大小
和位置,转子磁链的观测模型主要有二种[3]: (1)在两相静止坐标系的模型。定子电压和
电流由传感器测得后,经过 3s/2s 变换,根据异
图 3 调节器的内部结构 Transformation dq0_to_abc 模 块 将 上 一 级
按Ã转ÁÅÂÄ子磁链定向ÂÁ的Ã矢量Á控制系统仿真研究 科 技 论 坛
郭 瑞 王庆贤 (兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)
摘 要:详细分析矢量控制系统对异步电机电磁转矩实时控制的原理,构建带转矩内环磁链闭环按照转子磁链定向矢量控制结构,对系统的各 部分进行了详细的阐述。利用仿真工具建立了仿真模型,结果表明该方法实现电磁转矩控制,达到良好的调速性能。
图 10 调速过程中的电流波形
20%,减速过程的快速性良好。在 3s 时刻加速 过程平滑,基本无冲击。
10%,转速也能良好的跟随给定值。整个调速过
5 结论
程中的电磁转矩指令值如图 6、图 7 为其响应,
矢量控制是一种优良的控制策略,带转矩
可以看出,系统对电磁转矩的控制是有效的。 内环磁链闭环矢量结构,得益于直接对转矩和
2.3.2 采集节点对总线命令的响应 控制管理计算机作为数据采集系统的主节 点,可向各节点发送总线命令。总线命令包括总 线检测或总线切换等。采集节点作为从节点,两 路总线的 eCAN 模块均设置有特定 ID 的邮箱 接受总线命令,这些邮箱始终使能,在收到数据 后可立即产生邮箱中断。不论命令从哪条总线 上传来,采集节点均能够进行响应。 若为总线切换命令,则调用相应函数,复位 当前总线,切换到另一总线。另外,为了便于恢 复通信,主节点在正常通信时,需将当前的邮箱 通信状况记录下来,包括正在发送和待发送的 信息。读该表即可获取系统原来进行的任务,实 现原来通信任务的可靠切换。其他从节点则只 需在复位后等待主节点重新请求数据即可。 总线检测则是主节点随机的向总线上的从 节点发送远程帧,从节点收到后,将自己的节点
异步电动机矢量控制系统的仿真

异步电动机矢量控制系统仿真1.异步电机矢量控制系统的原理及其仿真1.1 异步电动机矢量控制原理异步电机矢量变换控制系统和直接转矩控制系统都是目前已经获得应用的高性能异步电机调速系统,对比直接转矩控制系统,矢量变换系统有可以连续控制,调速范围宽的优点,因此矢量变换控制系统为现代交流调速的重要方向之一。
本文采用的是转子磁场间接定向电流控制型交流异步电机矢量控制系统[1],如图1所示。
图1矢量变换控制系统仿真原理图如果把转子磁链方向按空间旋转坐标系的M轴方向定向,则可得到按转子磁场方式定向下的三相鼠笼式异步电动机的矢量控制方程。
(1)(2)(3)(4)(5)上列各式中,是转子励磁电流参考值;是转差角频率给定值;是定子电流的励磁分量;是定子电流的转矩分量;是定子频率输入角频率;是转子速度;是转子磁场定向角度;是转子时间常数;和分别是电机互感和转子自感。
图4所示控制系统中给定转速与实际电机转速相比较,误差信号送入转速调节器,经转速调节器作用产生给定转矩信号,电机的激磁电流给定信号根据电机实际转速由弱磁控制单元产生,再利用式(1)产生定子电流激磁分量给定信号,定子电流转矩分量给定信号则根据式(2)所示的电机电磁转矩表达式生成。
、和转子时间常数Lr一起产生转差频率信号,与ωr相加生成转子磁场频率给定信号,对积分则得到转子磁场空间角度给定信号。
和经坐标旋转和2/3相变换产生定子三相电流给定信号、和,与定子三相电流实测信号、和相比较,由滞环控制器产生逆变器所需的三相PWM信号。
1.2 异步电机转差型矢量控制系统建模在MATLAB/SIMULINK环境下利用电气系统模块库中的元件搭建交流异步电机转差型矢量控制系统[2],电流控制变频模型如图2所示。
图2 电流控制变频模型图整个仿真图由电气系统模块库中的元件搭建组成,元件的直观连接与实际的主电路相像似,其中主要包括:速度给定环节,PI速度调节器、坐标变换模块、磁场定向模块、滞环电流调节器、IGBT逆变器元件、异步电动机元件以及测量和显示模块。
异步电机矢量控制Matlab仿真实验_(电机模型部分)

摘要异步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统,由磁链方程、电压方程、转矩方程和运动方程组成,为非线性,所以控制起来极为不便。
异步电机的模型之所以复杂,关键在于各个磁通间的耦合。
如果把异步电动机模型解耦成有磁链和转速分别控制的简单模型,就可以模拟直流电动机的控制模型来控制交流电动机。
本文研究了按转子磁链定向的矢量控制系统的电流闭环控制的设计方法,通过坐标变换,在按转子磁链定向同步旋转正交坐标系中,得到等效的直流电动机模型,然后仿照直流电动机的控制方法控制电磁转矩与磁链,将转子磁链定向坐标系中的控制量反变换得到三相坐标系的对应量,以实施控制,并用MATLAB进行仿真。
关键词:异步电动机直流电动机磁链 MATLAB仿真目录1 课程任务设计书 (2)2 异步电动机数学模型基本原理 (3)2.1 异步电动机的三相动态数学模型 (3)2.2 异步电机的坐标变换 (6)2.2.1 三相-两相变换(3/2变换) (6)2.2.2静止两相-旋转正交变换(2s/2r变换) (8)3 异步电动机按转子磁链定向的矢量控制系统 (9)3.1 按转子磁链定向矢量控制的基本思想 (9)3.2 以ω-is-ψr 为状态变量的状态方程 (9)3.2.1 dq坐标系中的状态方程 (9)3.2.2αβ坐标系中的状态方程 (10)3.3αβ坐标系下异步电机的仿真模型 (11)3.4矢量控制系统设计 (14)3.5 矢量控制系统的电流闭环控制方式思想 (14)4 异步电动机矢量控制系统仿真 (15)4.1 仿真模型的参数计算 (15)4.2 矢量控制系统的仿真模型 (16)4.3仿真结果分析 (17)5. 总结与体会 (18)参考文献 (19)1课程任务设计书2 异步电动机数学模型基本原理异步电动机是个高阶、非线性、强耦合的多变量系统。
在研究异步电动机数学模型时,作如下的假设:120电角度,产生的磁动(1)忽略空间谐波,设三相绕组对称,在空间中互差势沿气隙周围按正弦规律分布;(2)忽略磁路饱和,各绕组的自感和互感都是恒定的;(3)忽略铁心饱和;(4)不考虑频率变化和温度变化对绕组电阻的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于转子磁场定向异步电机矢量控制在 20 世纪 60 年月从前,全球电气传动系统中高性能调速传动都采纳直流电动机,而绝大多数不变速传动则使用交流电机。
使得交流电机的应用遇到很大限制。
1971 年德国学者 Blaschke F 提出了交流电动机的磁场定向控制原理,应用坐标变换将三相系统等效为两相系统,再经过按磁场定向的同步旋转变换实现了定子电流励磁重量与转矩重量之间的解耦,从而达到对交流电机的磁链和电流分别控制的目的,为异步电机的调速确定了基础。
磁耦合是机电能量变换的必需条件,电流与磁通的乘积产生转矩,转速与磁通的乘积获得感觉电动势。
无论是直流电动机,还是交流电动机均这样。
交、直流电动机结构和工作原理的不一样,使得表达式差异很大。
1 三相异步电机非线性数学模型在研究异步电机数学模型时,作以下的假设(1)忽视空间谐波,三相绕组对称,产生的磁动势沿气隙按正弦规律分布。
(2)忽视磁路饱和,各绕组的自感和互感都是恒定的。
(3)忽视死心消耗。
(4)不考虑频率变化和温度变化对绕组电阻的影响。
无论异步电动机转子是绕线型还是笼型的,都可以等效成三相绕线转子,并折算到定子侧,折算后的定子和转子绕组匝数相等。
异步电动机三相绕组可以是Y 连接,也可以是连接。
若三相绕组为连接,可先用—Y变换,等效为Y 连接。
而后,按Y 连接进行解析和设计。
三相异步电机的物理模型以以下图1 所示,定子三相绕组轴线 A 、 B、C 在空间是固定的,转子绕组轴线a、b、c 随转子以角转速w 旋转。
图 1 三相异步电动机的物理模型异步电动机的动向模型由磁链方程、电压方程、转矩方程和运动方程构成。
此中磁链方程和转矩方程为代数方程,电压方程和运动方程为微分方程。
1.1 磁链方程异步电动机每个绕组的磁链是它自己的自感磁链和其他绕组对它的互感磁链之和 ,所以,六个绕组的磁链可用下式表示:A L AA L AB L AC L Aa L Ab L Ac i A B L BA L BB L BC L Ba L Bb L Bc i BCL CAL CB L CC L CaL Cb LCc i C (1)LaALaBLaCLaaLabLaci a a bL bALbBL bCL baL bbL bci b cLcALcB LcC Lca Lcb Lcci c式中 i A ,i B ,i C ,i a ,i b , i c 是定子和转子相电流的刹时价;A ,B ,C , a,b ,c 是各相绕组的全磁链。
定子各相自感LAALBBL CC L ms L ls转子各相自感LaaLbbL cc L ms L lr绕组之间的互感又分为两类(1)定子三相相互之间和转子三相相互之间地点都是固定的,故互感为常值;(2)定子任一相与转子任一相之间的相对地点是变化的,互感是角位移的函数。
则L ms cos2L ms cos(2)1L ms3 3 2所以1LA BLB CL CAL BAL CBLAC2Lm s1(2)La bLb cLc aLb aLc bLLa c2m s对于第二类,定、转子绕组间的互感,因为相互地点的变化,可分别表示L A aL a AL B bLb BLC cLLA b Lb ALB cL c B L C a L L A cL c A L B a L a B LC bLc CLc o m s sLc o m s s ( 2 (3)a C)3 Lc o m s s (2 b C)3将(2)式和 (3)式代入 (1)式,即得完好的磁链方程,用分块矩阵表示ψs L s sLs ri s(4)ψrLrsLrri r式中ψsTψrT ABCabci si A i B Ti ri a i b i c Ti C定子电感矩阵L msLls1L ms 1 L ms22L ss1 L ms L ms L ls 1L ms (5)2 21L ms1L msL msLls3转子电感矩阵L ms L lr 1L ms1L ms 2 2Lrr 1L msLmsLlr1L ms (6) 2 21L ms1L ms L ms L lr2 2定、转子互感矩阵cos cos( 2 ) cos( 2 )3 3L rs L T sr L ms cos( 2 ) cos cos( 2 ) (7)3 3cos( 2 ) cos( 2 ) cos3 31.2 电压方程三相绕组电压均衡方程u A i A R s d Au a i a R rd dt dtu B i B R s d Bu b i b R rd dt dtu C i C R s d Cu c i c R rddt dtab(8)c式中 u A ,u B ,u C ,u a , u b ,u c是定子和转子相电压的刹时价; R s , R r是定子和转子绕组电阻。
将电压方程写成矩阵形式u Ri 其睁开后的矩阵为dψdtu A R s 0 0 0 0 0 i A u B 0 R s0 00 i Bu C 0 0 R s 0 0 0 i C d u a 0 0 0 R r 0 0 i a dtu b0 0 0 0 R r 0 i b u c0 00 R ri c1.3 转矩方程A B C (9)a b cTn L ( i ii i)i sii n( i ii i)i s i n (1 2 0 )epm sAaBb CcAbBcCa(10)(i A i ciB iai C )i s i n (120 )b1.4 运动方程J d(11)n p T e T Ldt1.5 转角方程d(12)dt1.6 异步电机三相原始模型的性质(1)异步电机三相原始模型的非线性强耦合性非线性耦合表此刻电压方程、 磁链方程与转矩方程。
既存在定子和转子间的耦合,也存在三相绕组间的交织耦合。
旋转电动势和电磁转矩中都包括变量之间的乘积,这是非线性的基本要素。
定转子间的相对运动, 以致其夹角不停变化,使得互感矩阵为非线性变参数矩阵。
(2)异步电动机三相原始模型的非独立性。
异步电动机三相绕组为 Y 无中线连接,若为 连接,可等效为 Y 连接。
则定子和转子三相电流代数和为i A i B i C 0i i i 0由式( 4)可得T T TA B C LssiAiBiCLsriAiBiC将式( 5)和( 6)代入,并把矩阵睁开后的全部元相加,可以证明三相定子磁链代数和为A B C再由定子电压方程式( 8),可知三相定子电压代数和为u A u B u C0所以,异步电动机三相数学模型中存在必定的拘束条件A B C 0i A i B i C 0u A u B u C 0同理转子绕组也存在相应的拘束条件a b c 0i a i b i c 0u a u b u c 0相变量中只有两相是独立的,所以三相原始数学模型其实不是物理对象最简的描述。
完好可以并且也有必需用两相模型取代。
2坐标变换异步电动机三相原始动向模型相当复杂,简化的基本方法就是坐标变换。
异步电动机数学模型之所以复杂,要点是因为有一个复杂的电感矩阵和转矩方程,它们表现了异步电动机的电磁耦合和能量变换的复杂关系。
不一样坐标系中电动机模型等效的原则是:在不一样坐标下绕组所产生的合成磁动势相等。
在交流电动机三相对称的静止绕组 A 、B、C 中,通以三相均衡的正弦电流,所产生的合成磁动势是旋转磁动势 F,它在空间呈正弦分布,以同步转速(即电流的角频率)顺着 A-B-C 的相序旋转。
任意对称的多相绕组,通入均衡的多相电流,都能产生旋转磁动势,但是以两相最为简单。
三相变量中只有两相为独立变量,完好可以也应该消去一相。
所以,三相绕组可以用相互独立的两相正交对称绕组等效取代,等效的原则是产生的磁动势相等。
两相绕组,通以两相均衡交流电流,也能产生旋转磁动势。
当三相绕组和两相绕组产生的旋转磁动势大小和转速都相等时,即以为两相绕组与三相绕组等效,这就是 3/2 变换。
其物理模型以以下图 2 所示图 2 三相坐标系和两相坐标系物理模型两个匝数相等相互正交的绕组 d、q,分别通以直流电流,产生合成磁动势 F,其地点有对于绕组来说是固定的。
假如人为地让包括两个绕组在内的死心以同步转速旋转,磁动势 F 自然也随之旋转起来,成为旋转磁动势。
假如旋转磁动势的大小和转速与固定的交流绕组产生的旋转磁动势相等,那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。
也许说,在三相坐标系下的i A, i B,i C和在两相坐标系下的i , i以及在旋转正交坐标系下的直流id,iq产生的旋转磁动势相等。
其物理模型以以下图 3 所示。
图 3 静止两相正交坐标系和旋转正交坐标系的物理模型2.1 三相 -两相变换( 3/2 变换)三相绕组 A 、B、C 和两相绕组之间的变换,称作三相坐标系和两相正交坐标系间的变换,简称 3/2 变换。
ABC 和两个坐标系中的磁动势矢量,将两个坐标系原点重合,并使 A 轴和轴重合。
如图 4 所示,设三相绕组每相有效匝数为N3,两相绕组每相有效匝数为N2,各相磁动势为有效匝数与电流的乘积,其空间矢量均位于相关的坐标轴上。
图 4 三相坐标系和两相正交坐标系中的磁动势矢量依据磁动势相等的等效原则, 三相合成磁动势与两相合成磁动势相等,故两套绕组磁动势在 αβ轴上的投影应相等。
所以N 2 iN 3i A N 3i B cosN 3i C cosN 3 (i A1i B1i C )3 322N 2iN 3i B sinN 3i C sin3 3N 3 (i B i C )32写成矩阵形式i1 1 1i AN 3 2 2i B( 13)iN 23 3i C22依据变换前后总功率不变,匝数比为N 3 2(14)N 23将式( 14)代入式( 13)得i1 1 1 i A222i Bi3 3 3i C22令 C 3/2 表示从三相坐标系变换到两相正交坐标系的变换矩阵,则1 12 12C3/22 (15)33 322两相正交坐标系变换到三相坐标系(简称 2/3 变换)的变换矩阵为1 0C2/32 13 ( 16)32 21 322考虑到i A i B i C0 则i 3i A2 (17)i 1 i B22相应的逆变换i A 20 i 3i B 1 1(18) i6 2电压变换阵和磁链变换阵与电流变换阵相同。
2.1 静止两相 -旋转正交变换( 2s/2r 变换)从静止两相正交坐标系到旋转正交坐标系dq 的变换,称作静止两相-旋转正交变换,简称 2s/2r 变换,此中 s 表示静止, r 表示旋转,变换的原则相同是产生的磁动势相等。
图5 中绘出了和dq 坐标系中的磁动势矢量,绕组每相有效匝数均为N2磁动势矢量位于相关的坐标轴上。
