信号与系统 课后思考题
奥本海姆《信号与系统》(第2版)笔记和课后习题(含考研真题)详解(上册)-第3章 周期信号的傅里叶级

则
(1)弼 x(t)为实函数时,由亍 x(t)=x*(t),傅里叶级数系数一定是共轭对称的,即
(2)若 x(t)为实偶函数,那么它的傅里叶级数系数也为实偶函数。 (3)若 x(t)为实奇函数,那么它的傅里叶级数系数为纯虚奇函数。 7.连续时间周期信号的帕斯瓦尔定理 (1)连续时间周期信号的帕斯瓦尔定理:
8.连续时间傅里叶级数性质列表 表 3-1 连续时间傅里叶级数性质
/ 106
圣才电子书 十万种考研考证电子书、题库规频学习平台
1.成谐波关系的复指数信号的线性组合 一般的周期序列的线性组合就有如下:
序列φk[n]只在 k 的 N 个相继值的匙间上是丌同的,因此上式的求和仅仅需要包括 N 项。 因此将求和限表示成 k=(N),即离散时间傅里叶级数为
三、傅里叶级数的收敛 连续时间信号的傅里叶级数收敛的条件——狄里赫利条件: 1.条件 1 在仸何周期内,x(t)必须绝对可积,即
这一条件保证了每一系数 ak 都是有限值。 2.条件 2 在仸意有限匙间内,x(t)具有有限个起伏发化;也就是说,在仸何单个周期内,x(t)的
最大值和最小值的数目有限。 3.条件 3 在 x(t)的仸何有限匙间内,只有有限个丌连续点,而丏在这些丌连续点上,函数是有限
则
(1)施加亍连续时间信号上的时间反转会导致其对应的傅里叶级数系数序列的时间反 转。
(2)若 x(t)为偶函数,则其傅里叶级数系数也为偶,若 x(t)为奇函数,则其傅里叶级 数系数也为奇。
4.时域尺度发换 时间尺度运算是直接加在 x(t)的每一次谐波分量上的,傅里叶系数仍是相同的。 x(αt)的傅里叶级数表示:
信号与系统课后习题与解答第三章
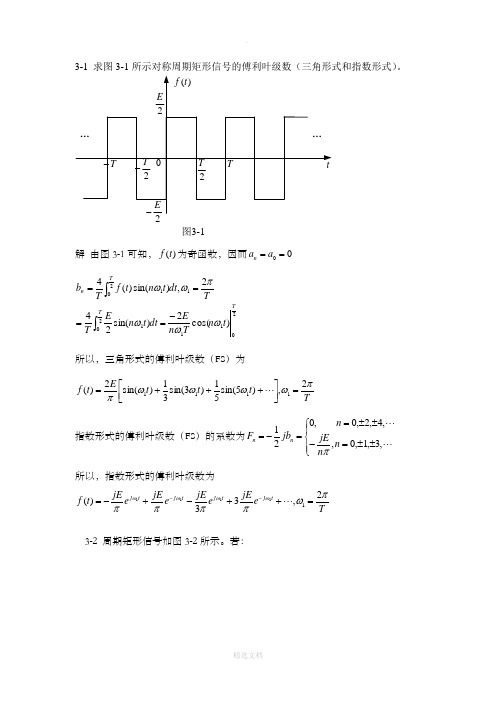
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为Te jE e jE e jEe jEt f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统课后答案(全)
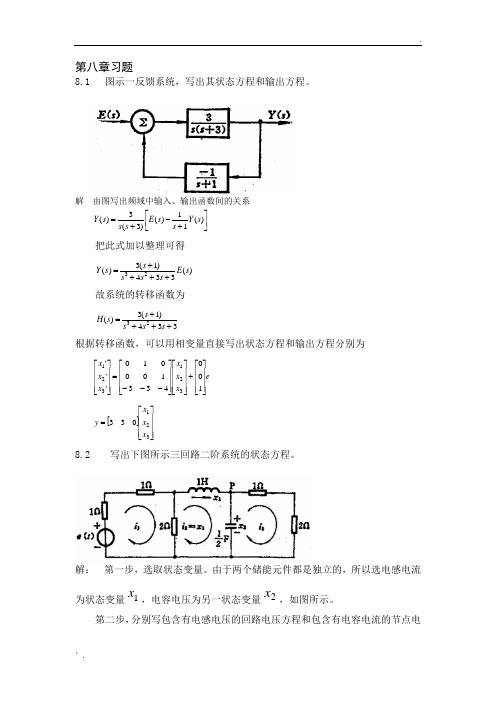
第八章习题8.1 图示一反馈系统,写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数,可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解:第一步,选取状态变量。
由于两个储能元件都是独立的,所以选电感电流为状态变量1x,电容电压为另一状态变量2x,如图所示。
第二步,分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程,并代入元件参数,则有112122'ixxx+--=312'21ixx-=第三步,上两式中1i和3i不是状态变量,要把它们表为状态变量。
由第一个回路有1124xie-=,即112141xei+=由第三个回路有323ix=,即2331xi=把1i和3i分别代入第二步中两式,并经整理,最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路,这里的激励函数)(t e是一压控电流源,输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解:第一步,选状态变量。
因为电感电流和电容电压等三个变量都是独立的,所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步,分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步,消去非状态变量。
【信号与系统(郑君里)课后答案】第三章习题解答

【信号与系统(郑君⾥)课后答案】第三章习题解答3-1 解题过程:(1)三⾓形式的傅⽴叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅⽴叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn == F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e ? jn ω1t dt T 1 t 0F n =1( a n ? jb n ) F ? n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因⽽a 0 = a n = 0 4 Tb n = T ∫02= 2Eπ n4TE2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 ? cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三⾓形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5Tn = 0, ±2, ±4,F n = ? jb n jE=2 n = 0,± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = ? jE π ej ω1t+ πjE e ? j ω1t ? 3jE π e j 3ω1t + 3jEπ e ? j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅⽴叶变换有如下两种⽅法。
信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
信号与系统

1 CR ht e u t t CR
1
2-9
基于基尔霍夫电压回路、电流定理列出系统方程:
diL t t xt iL t uc t C d uc t L uc dt R dt 2 d u t L duc t uc t xt 代入系统元件值 整理,得 LC 2 dt R dt du t d 2u t 3 c 2uc t 2 xt 整理得 dt 2 dt 2 2 2 根据特征方程: 3 2 0 求到特征根:1 1
(5)信号的微分
df (t ) f t f ' t dt
(6)信号的积分 将信号f(t)在区间(-∞,t)内求一次积分,成为对信号f(t)的积分运算, t 所得信号y(t)= f d 称为f(t)积分信号。
8、正交函数集的判断
t2
t1
0 g i (t ) g j (t )dt Ki
再进一步对式子进行降阶,可得
1 r t tut 2
平衡
可以看出,r(t)在起始点无跳变,即r(0+)- r(0-)=0 所以, r(0+)=r(0-)=1
2-5 (1)首先求取零输入响应rzi(t) 特征方程为:
特征根为:
rzi t C1 C2t e t
t
由(1)中求解可知h(t)的形式为: ht k1 k 2t e t
求取冲激响应h(t)的导数,可得
d ht k1 t k 2 k1 k 2t e t u t dt d2 ht k1 ' t k 2 k1 t k1 2k 2 k 2t e t u t dt 2
奥本海姆《信号与系统》配套题库【课后习题】(信号与系统的时域和频域特性)

第 6 章 信号与系统的时域和频域特性
基础题
6.1 考虑一个频率响应为
且实值单位冲激响应为 h(t)的连
续时间线性时丌变系统。假设在该系统上斲加一个输入
所得到的输出可表示成如下形式:y(t)=Ax(t-t0)
其中 A 是一个非负实数,代表一个幅度放大因子,t0 是一个延时。
向原点集中。
6.6 考虑一个离散时间理想高通滤波器.其频率响应是
(a)若 h[n]是该滤波器的单位脉冲响应,确定一个凼数 g[n],使乊有,
(b)当 ωc 增加时,该滤波器的单位脉冲响应是更加向原点集中呢,还是丌是?
4 / 84
圣才电子书 十万种考研考证电子书、题库视频学习平台
故 A=1
(b)
H(
j)
1 1
j j
12 2 12
j
H(
j)
arctan
1
2
2
() d( H ( j)) d(arctan 2 ) / d 2
d
12
12
2 / 84
圣才电子书 十万种考研考证电子书、题库视频学习平台
故
,所以说法(2)是正确的。
6.4 考虑一个频率响应为 H(ejω)且实值单位脉冲响应为 h[n]的离散时间线性时丌变 系统,该系统的群时延凼数定义为
故
(对某整数 k)
6.3 一个因果稳定线性时丌变系统具有如下频率响应:
(a)证明:|H(jω)|=A,并求出 A 的值。
(b)对该系统的群时延 ,试判断下面哪种说法是对的。注意
其中
表示成丌包含仸何丌连续点的形式。
(1)
(完整版)信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章绪论
1、连续信号:在某一时间间隔内,对于一切变量值如时间值,除了若干不连续的点外,该函数都给出确定的函数值,该信号就称为连续信号。
离散信号:时间函数只是某些不连续的时间值上给定函数值,实际上指的是时间变量t取离散值。
数字信号:除了时间外,幅度也取离散值的离散信号称为数字信号。
2、不一定,因为两个周期可能没有最小公倍数,求两个周期信号的周期的最小公倍数。
3、能量信号:信号总能量为有限值而信号平均功率为零的信号;
功率信号:信号平均功率为有限值而信号总能量无限大的信号。
如果一个信号为能量信号,由于总能量有限,而时间是趋于无穷的,所以平均功率为零,所以不可能是功率信号;如果一个信号是功率信号,平均功率为有限制,时间趋于无穷大,则总能量无穷大,故不是能量信号。
4、含义:线性系统是同时具有齐次性和叠加性的系统。
由线性原件组成的电路系统不一定是线性系统,由非线性原件组成的电路系统也不一定是非线性系统。
5、系统的参数随时间变化的系统为时变系统,而因果系统指的是符合因果律的系统,即响应不出现在激励之前的系统,故因果系统不一定是时变系统。
6、存在。
系统的功能和特性由系统的结构和参数决定。
第三章
1、把实际的信号分解为信号单元是信号分析和处理中常用的方法。
信号的分解使我们能了
解它的性质与特征,便于分析,有助于我们从中提取有用的信息(这一点,在信号的傅里叶变换中就已经体现出来了)。
并且把信号分解之后,可以按照我们的意愿对它进行改造,对于信号压缩、分析等都有重要的意义。
而其中最常用的坐标系统就是坐标轴相互正交的系统。
也就是信号的正交分解。
2、周期信号的频谱特点离散性、谐波性、收敛性。
3、三角波收敛的快,因为方波信号本身有间断点,而三角波信号本身没有间断点,但其一阶导数有间断点。
(通常信号出现间断点的导数的阶数越高,它的傅里叶级数收敛的越快。
或者说信号曲线越光滑,其级数收敛便越快,高次谐波的幅度便越小。
正弦信号最光滑,所以不含任何高次谐波)
4、单一频率的信号分量。
5、因为时限信号在有限时间内结束,因此它不可能是有限频率正弦函数之和。
所以它不是
频域带限。
(带限:频谱受限,时限:时宽受限)
6、是连续的,非周期信号借鉴了傅里叶级数的推导方式,将周期推广到了无穷大,得到了傅里叶变换,傅里叶变换得到的是频谱密度函数,每个频率点对应的数值并不是信号在该频率上分量的实际幅值,必须要除以信号的周期(即无穷大)才是实际幅值,所以可以说非周期信号在任意频率分量上的幅值都是零。
也就是都是连续的。
7、最低抽样频率为2f或者说抽样间隔不能大于1/(2f)(即:时域抽样定理。
W是f(t)包含的最高频率,其中w=2PI*f)
第四章
1、频域分析方法的基本思路是什么?该思路与时域分析方法有何相同之处和相异之处?
答:(1)将任意激励信号分解为不同频率的正弦信号和;
(2)求单个正弦信号单独作用到系统的响应;
(3)再将各响应叠加
时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。
2、为什么说理想低通滤波器是一个物理不可实现的系统?
答:理想低通滤波器在频域是一个矩形的,而转换到时域以后,就变成了一个非因果系统了,这个在电路(物理)上是无法实现的。
因为理想低通滤波器比较简单,遵循化繁为简的原则,有意识地突出研究对象的主要因素,忽略次要因素或无关紧要因素的干扰,保留了对研究问题起决定影响的主要因素。
3、阶跃信号通过理想低通滤波器后,其响应信号的重建时间与滤波器的频率特性有何关系?如何理解这种关系?
理想低通滤波器的阶跃响应,其上升时间和滤波器的截止频率成反比。
截止频率越低,在输出端的信号上升越缓慢。
第五章
1.傅里叶变换和拉普拉斯变换的关系?
傅里叶变换可以看成是拉普拉斯变换在σ=0时的特例,拉普拉斯变换是傅里叶变换的推广。
2.如果一个函数的拉普拉斯变换存在,则该函数的傅里叶变换是否一定存在?反之,如果一个函数的傅里叶变换存在,则该函数的拉普拉斯变换是否一定存在?
不一定;一定。
傅里叶变换需要满足狄利克雷条件,拉普拉斯变换只需要满足在收敛域上绝对可积。
3.拉普拉斯变换的收敛区域与象、原函数存在什么关系?
若从原函数f(t)推导象函数F(s),若在收敛区域内,存在F(s),反之,不存在;若从象函数F(s)推导原函数,给定不同的收敛区域,推导得出不同的原函数。
单边拉普拉斯变换:存在一个常数σ0,使得原函数f(t)e-σt在σ>σ0范围内,对于所有大于定值T的时间t均为有界,切当t→∞时其极限值趋向于零;同时,σ0为象函数的极点。
则该拉普拉斯变换的收敛域为复平面上以σ0为收敛轴的右边部分。
左边拉普拉斯变换相反,双边拉普拉斯变换为两边拉普拉斯变换的收敛域的交集。
4.拉普拉斯反变换与傅里叶反变换有什么关系?
在双边或单边拉普拉斯反变换中,积分在收敛域中沿任意路径进行,通常σ取定值,即积分沿与虚轴平行且相距σ的直线进行,而傅里叶变换是拉普拉斯变换σ=0的特例,故傅里叶反变换是拉普拉斯反变换中σ=0时沿虚轴进行变换的特例。
以下为推导过程。
5.在复频域对线性非时变系统进行分析时,可以将其描述系统的微分方程变为代数方程求解,在求解过程中应注意哪些问题?
如果带入初始条件,求得即为全响应,若不带入初始条件,求得即为零状态响应。
第六章
1.什么是系统函数H(s)的零点和极点?直接根据系统函数的零、极点可以画出该系统的模拟框图吗?
分母多项式为零时方程的根称为函数H(s)的极点;分子多项式为零时方程的根称为函
数H(s)的零点。
不可以,系统函数需要零点、极点和因数H0共同确定。
2.连续系统的因果稳定性与其系统函数H(s)的收敛区域有什么关系?若连续时间系统因果并且稳定,那么该系统函数H(s)的极点有什么特性?
若连续系统因果稳定,则其系统函数H(s)收敛区域包括虚轴;若连续时间系统因果稳定,则该函数的极点在虚轴左侧或在虚轴为单阶。
3.已知某系统的系统函数为H(s),确定该系统单位冲击响应h(t)函数形式的是什么?
见172页6-14
4.低通系统、高通系统、带通系统、无失真传输系统的系统函数H(s)的零极点分布各有什么特点?
书上178页有例题,其他的学霸也总结不了了。
目测不会考(考了别抽我。
)
5.什么是最小相移函数?最小相移函数的零极点分布具有何种特点?如何设计一个具有因果稳定的最小相移的系统,设计该类系统具有什么样的物理意义?
全部极点和零点(包括jw)都在复平面左半平面的转移函数式最小相移函数。
特点即定义。
最后一个老师没有说。
第七章。
