高三下学期文科数学限时训练(十二)
广东省广雅中学高三文科数学限时训练题(二)

广东省广雅中学高三文科数学限时训练题(二)1.(本题满分12分)在△ABC 中,已知A=450,54cos =B . (I)求sinC 的值; (II)若BC=10,求△ABC 的面积.2.(本题满分14分)已知正项等差数列{a n }的前n 项和为S n ,若S 3=12,且2a 1,a 2,a 3+1成等比数列.(I)求{a n }的通项公式: (II)记n n n a b 3=的前n 项和为T n ,求T n .3.(本题满分14分)如图,已知直四棱柱ABCD-A 1B 1C 1D 1的底面是直角梯形,AB⊥BC,AB//CD ,E ,F 分别是棱BC,B 1C 1上的动点,且EF//CC 1 ,CD=DD 1=1 AB=2,BC=3(I)证明:无论点E 怎样运动,四边形EFD 1D 都为矩形;(II)当EC=1时,求几何体A-EFD 1D 的体积.4.(本题满分14分) 椭圆)0(12222>≥=+b a by a x 上任一点P 到两个焦点的距离的和为6,焦距为24,A ,B 分别是椭圆的左右顶点.(I)求椭圆的标准方程;(II)若P 与A ,B 均不重合,设直线PA 与PB 的斜率分别为k 1,k 2,证明:21k k ⋅为定值:(III)设C(x ,y)(0<x<a )为椭圆上一动点,D 为C 关于y 轴的对称点,四边形ABCD 的面积为S (x),设3)()(2+=x x S x f ,求函数f(x)的最大值.参考答案1.(本题满分12分)解:(I)54cos =B 且,53cos 1sin 2=-=∴B B .....2分 )135sin()180sin(sin B B A C -=--= ………3分B B sin 135cos cos 135sin -=102753)22(5422=⋅--⋅=……6分 (II)由正弦定理得C AB A BC sin sin =,即21072210AB =,解得AB=14 ....10分 则△ABC 的面积4253141021sin ||||21=⨯⨯⨯==B BC AB S …………12分 2.解:(I)123=S ,即a 1+a 2+a 3=12∴3a 2=12,所以a 2=4,..........2分∵2a 1,a 2,a 3+1成等比数列,)1(23122+⋅=∴a a a , 即)1()(22222++⋅-=d a d a a ..........4分 解得,d=3或d=-4(舍去),∴a 1=a 2-d=1,故a n =3n-2; …………7分(II)法1:n n n n n n n a b 31)23(3233⋅-=-==, +⨯+⨯=∴2314311n T n n 31)23(3173⨯-++⨯ , ① ①31⨯得,43231731431131⨯+⨯+⨯=n T 131)23(31)53(+⨯-+⨯-++n n n n ② ①-②得,323133133132⨯+⨯+=n T n 3133134⨯++⨯+ 131)23(+⨯--n n ---⨯+=-311)311(3133112n 6531)23(|=⨯-+ n n )23(31211--⨯--n n 131+⨯n 2314145-⨯-=∴n n T 4531223=⨯--n n n n 31456⨯+- ……14分 法2:=-==n n n n n a b 3233 n n n 312311⨯-⋅-, 设23133121⨯+⨯+=n A 1331314-⨯++⋅⨯+n n , ① 则323133123131⨯+⨯+=n A n n 313144⨯++⨯+ , ② ①-②得,32313131132+++=n A n n n 313.11⨯-++----=311311n n n n n 31)23(2331⨯+-=⨯311)311(312--⨯⨯-=∴n n n A T ,n n 31)2349(49⨯+-=45)311(=--n n n 31456⨯+- …14分3.解:(I)在直四棱柱ABCD-A 1B 1C 1D 1中,DD 1//CC 1∵EF//CC 1,EF//DD 1 ..........2分又∵平面ABCD//平面A 1B 1C 1D 1平面ABCD∩平面EFD 1D=ED平面A 1B 1C 1D 1∩平面EFD 1D=FD 1∴ED//FD 1,∴四边形EFD 1D 为平行四边形, ……4分 ∵侧棱DD 1⊥底面ABCD ,又⊂DE 平面ABCD 内,∴DD 1⊥DE,∴四边形EFD 1D 为矩形; (6)∵四棱柱ABCD-A1B1C1D1为直四棱柱,(II)证明:连结AE ,∵四棱柱ABCD-A 1B 1C 1D 1为直四棱柱, ∴侧棱DD 1⊥底面ABCD ,又⊂AE 平面ABCD 内,AE DD ⊥∴1 ……8分在Rt△ABE 中,AB=2,BE=2,则22=AE …9分存Rt△CDE 中,EC=1,CD=1,则2=DE ………10分 在直角梯形中ABCD ,.2210)(=-+=CD AB BC AD ; 222AD DE AE =+∴,即AE⊥ED,又D DD ED =⋂1 ,∴AE⊥平面EFD 1D ; ………12分 由(I)可知,四边形EFD 1D 为矩形,且2=DE ,DD 1=1, ∴矩形EFD 1D 的面积为211=⋅=DD DE S D EFD , ∴几何体A-EFD 1D 的体积为AE V DSEFD D EFD A ⋅=-11313422231=⨯⨯=.……14分4.解:(I)由题意得,2a=6,∴a=3, ……1分又242=c ,22=∴c ,1222=-=c a b , 故椭圆的方程为1922=+y x ………3分 (II)设)0)(,(000=/y y x P ,A(-3,0), B(3,0),则192020=+y x ,即912020x y -=, 则3,3002001-=+=x y k x y k ……4分 即9202021-=⋅x y k k 919)9(9199120202020-=--=--=x x x x 21k k ⋅∴为定值91- …………8分 (Ⅲ)由题意可知,四边形ABCD 是梯形,则y x x S ⋅+=)26(21)(,且9122x y -=,……9分 于是3)()(2+=x x S x f 3)91()3(22+-+=x x x )91)(3(2x x -+=+--=3923x x )30(3<<+x x ……10分 1323)('2+--=x x x f ,令f'(x)=0,解之得x 1=1,或x=-3(舍去)………11分 当0<x<1,f'(x)>0,函数f(x)单调递增; ………12分 当1<x<3,f'(x)<0,函数f(x)单调递减;…………13分 所以f (x )在x=1时取得极大值,也是最大值932 ……14分。
高三文科数学限时训练(十)

高三文科数学限时训练(十)一、选择题. 1.已知集合2M x x,103x N xx ⎧+⎫=<⎨⎬-⎩⎭,则集合N M 等于( ) A .{}2-<x xB .{}3>x xC .{}21<<-x xD .{}32<<x x2.若函数3()()f x x x R =∈,则函数()y f x =-在其定义域上是( ) A .单调递减的偶函数 B.单调递减的奇函数 C .单凋递增的偶函数 D .单调递增的奇函数 3. 已知函数sin ,4()6(1),4x x f x f x x π⎧<⎪=⎨⎪-≥⎩,则(5)f 的值为( )A .12B .C .D .14. 函数)3sin()2cos(x x y -++=ππ具有性质( )A. 最大值为3,图象关于直线6π=x 对称 B. 最大值为1,图象关于直线6π=x 对称C. 最大值为3,图象关于)0,6(π对称 D. 最大值为1,图象关于)0,6(π对称5.函若22)4sin(2cos -=-παα,则ααcos sin +的值为( ) A. B . 12-C . 12D6.已知x x f 2cos )(cos =,则f(︒15sin )的值等于( )A.21 B.21- C.23 D.23-7. 函数()cos 22sin f x x x =+的最小值和最大值分别为( )A .1-,1B .2-,2C .3-,32D .2-,328. 已知平面α⊥平面β,l αβ=,点A α∈,A l ∉,直线AB l ∥,直线AC l ⊥,直线m m αβ∥,∥,则下列四种位置关系中,不一定...成立的是( ) A .AB m ∥B .AC m ⊥C .AB β∥D .AC β⊥9. 函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )10. 定义一种运算⎩⎨⎧>≤=⊗ba b b a a b a ,,,令()()45sin cos 2⊗+=x x x f ,且⎥⎦⎤⎢⎣⎡∈2,0πx ,则函数⎪⎭⎫⎝⎛-2πx f 的最大值是( ) A .45B .1C .1-D .45-姓名 班级 分数二、填空题11. 函数13)(23+-=x x x f 的极小值是 .12. 在△ABC 中,若 60,75,3=∠=∠=ACB ABC AB ,则BC = .13.若函数f (x )的图象与函数x y ln =的图象关于直线x -y =0对称,则=)2(f .14已知函数())cos()f x x x ωϕωϕ=+-+(0πϕ<<,0ω>)为偶函数, 且函数()y f x =图象的两相邻对称轴间的距离为π2,则π8f ⎛⎫⎪⎝⎭= .x xA .B .C .D .。
高三下学期数学文科限时训练1.

高三文科数学限时练1班级姓名学号得分BD O=l=,证明:的中点,求三棱锥P BCE-BCE.1(本小题满分12分)解(1)当x =7时,由茎叶图可知,乙组同学去图书馆学习次数是:7,8,9,12,所以平均数为;9412987=+++=x …………………3分方差为.27])912()99()98()97[(4122222=-+-+-+-=s ……………6分(2)记甲组3名同学为A 1,A 2,A 3,他们去图书馆学习次数依次为9,12,11;乙组4名同学为B 1,B 2,B 3,B 4,他们去图书馆学习次数依次为9,8,9,12;从学习次数大于8的学生中人选两名学生,所有可能的结果有15个,它们是:A 1A 2,A 1A 3,A 1B 1,A 1B 3,A 1B 4,A 2A 3,A 2B 1,A 2B 3,A 2B 4,A 3B 1,A 3B 3,A 3B 4, B 1 B 3,B 1B 4,B 3B 4. …………………9分用C 表示:“选出的两名同学恰好在两个图书馆学习且学习的次数和大于20”这一事件,则C 中的结果有5个,它们是:A 1B 4,A 2B 4,A 2B 3,A 2B 1,A 3B 4,故选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20概率为.31155)(==C P …………………12分 2(Ⅰ)证明:因为//,,AB DC AB PDC DC PDC ⊄⊂平面平面,所以AB PDC //平面. (2分) 又平面ABP平面DCP l =,且AB ABP ⊂面,所以//l AB . (4分) (Ⅱ)解:因为底面是菱形,所以BD AC ⊥. (5分) 因为PB PD =,且O 是BD 中点,所以BD PO ⊥. (6分) 又POAC O = ,所以BD PAC ⊥面.所以BO 是三棱锥B PCE -的高. (7分)因为AO 为边长为2的等边△ABD的中线,所以AO =因为PO 为边长为2的等边△PBD的中线,所以PO =. 在△POA中,PA =AO =PO =所以222AO PO PA +=,所以PO AO ⊥. (8分) 所以132PAC S AC PO ∆==, (9分) 因为E 是线段PA 的中点,所以1322PCE PAC S S ∆∆==. (10分) 所以1132P BCE B PCE PCE V V S BO --∆==⨯⨯=. (12分)。
2021-2022年高三12月份限时训练数学理含答案

2021-2022年高三12月份限时训练数学理含答案一、选择题:每小题5分,共60分.在给出的四个选项中,只有一项是符合要求的.1.若,则= A. B. C. D.2.已知集合,,则A. B. C. D.3.已知向量, ,如果向量与垂直,则的值为A. B. C. D.4.函数的图像为5.如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①; ②;③; ④.其中“同簇函数”的是 A.①② B.①④ C.②③ D.③④6.若数列的前项和,则数列的通项公式A. B. C. D.7.已知命题;命题,则下列命题中为真命题的是A. B. C. D.8.已知,满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若的最小值为,则A. B.C. D. 9.在中,角的对边分别为,且22cos cos sin()sin 2A B B A B B --- .则 A . B . C . D .10.函数是上的奇函数,1212()[()()]0x x f x f x --<,则的解集是 A . B.C. D.11. 等比数列中,,,128()()()()f x x x a x a x a =--⋅⋅⋅-,为函数的导函数,则( )A .0B .C .D .12.空间中,、、是三条不同的直线,、、是三个不同的平面,则下列结论错误的是A.若则B.若则C.若,则D.若,,,,,m l n l m l n αββγγα===⊥⊥则二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡中相应题的横线上.13.= .14.已知圆锥的母线长为5cm ,侧面积为15πcm 2,则此圆锥的体积为 cm 3.15.在中,,,,则 .16.已知命题p :x 2+2x -3>0;命题q :,若“非q 且p ”为真,则x 的取值范围是____________________.三、解答题:本大题共6小题,共74分. 把解答写在答题卡中.解答应写出文字说明,证明过程或演算步骤.17.记函数的定义域为集合,函数的定义域为集合.(1)求和;(2)若A C p x x C ⊆<+=},04|{,求实数的取值范围.18.(本小题满分12分)已知(2cos ,2sin )(cos ,sin )a b ααββ==,,. (Ⅰ)若,求的值;(Ⅱ)设,若,求的值.19.(本小题满分12分)已知函数和的图象关于轴对称,且.(Ⅰ)求函数的解析式;(Ⅱ)解不等式20. (本小题满分12分)已知数列{a n }中,a 1=1,a n+1=a n +2n +1,且n ∈N *。
(文数)高三下学期文科数学综合训练
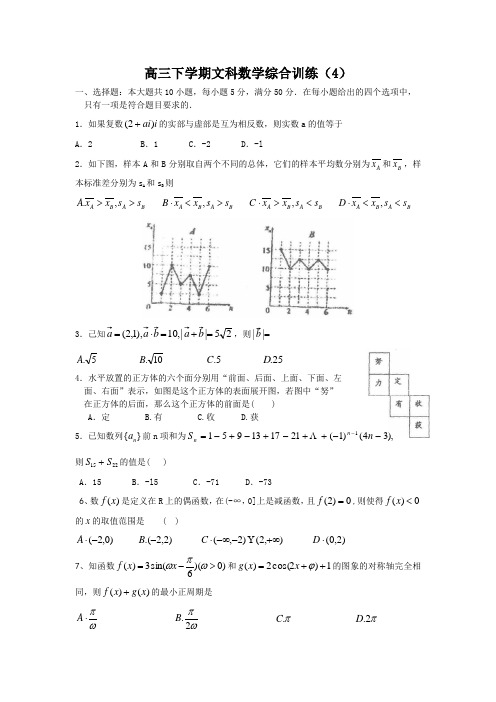
高三下学期文科数学综合训练(4)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.1.如果复数i ai )2(+的实部与虚部是互为相反数,则实数a 的值等于 A .2 B .1 C .-2 D .-l2.如下图,样本A 和B 分别取自两个不同的总体,它们的样本平均数分别为A x 和B x ,样本标准差分别为s A 和s B 则B A B A s s x x A >>,. B A B A s s x x B ><⋅, B A B A s s x xC <>⋅, B A B A s s x xD <<⋅,3.己知25||,10),1,2(=+=⋅=b a b a a ,则=||b5.A 10.B 5.C 25.D4.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左 面、右面”表示,如图是这个正方体的表面展开图,若图中“努” 在正方体的后面,那么这个正方体的前面是( ) A .定 B.有 C.收 D.获5.已知数列}{n a 前n 项和为),34()1(2117139511--++-+-+-=-n S n n Λ则2215S S +的值是( )A .15B .-l5C .-71D .-736、数)(x f 是定义在R 上的偶函数,在(-∞,0]上是减函数,且0)2(=f ,则使得0)(<x f 的x 的取值范围是 ( ))0,2(-⋅A )2,2.(-B ),2()2,(+∞--∞⋅Y C )2,0(⋅D7、知函数)0)(6sin(3)(>-=ωπωx x f 和1)2cos(2)(++=ϕx x g 的图象的对称轴完全相同,则)()(x g x f +的最小正周期是ωπ⋅A ωπ2.B π.C π2.D8、已知函数⎩⎨⎧≥+<+=.1,,1,23)(2x ax x x x x f ,若a f f 4))0((=,则实数=a2.-A 32.B 1.C 2.D9.函数)(x f 的导函数为)(x f ',若0)()1(>'⋅+x f x 则下列结论中正确的一项为( )1,-=x A 一定是函数)(x f 的极大值点1.-=x B 一定是函数)(x f 的极小值点 1.-=x C 不是函数)(x f 的极值点 1.-=x D 不一定是函势)(x f 的极值点10.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成”函数。
高三下学期数学(文科)模拟考试卷(带参考答案与解析)

高三下学期数学(文科)模拟考试卷(带参考答案与解析)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答选择题时,则选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,则将答案写在答题卡上。
写在本试卷上无效。
3.本试卷共22题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1.已知向量(2,1)a =和(3,2)b =,则()a a b ⋅-=( ) A .-5 B .-3C .3D .52.不等式312x >+的解集为( ) A .{1,2}x x x <≠- B .{1}x x >C .{21}x x -<<D .{21}x x x <->或3.直线x +ay -3=0与直线(a +1)x +2y -6=0平行,则a =( )A .-2B .1C .-2或1D .-1或24.古希腊科学家阿基米德发明了享誉世界的汲水器,称为阿基米德螺旋泵,两千多年后的今天,左图所示的螺旋泵,仍在现代工农业生产中使用,其依据是“阿基米德螺线”.在右图所示的平面直角坐标系xOy 中点A 匀速离开坐标系原点O ,同时又以固定的角速度绕坐标系原点O 逆时针转动,产生的轨迹就是“阿基米德螺线”,该阿基米德螺线与坐标轴交点依次为A 1(-1,0),A 2(0,-2),A 3(3,0),A 4(0,4),A 5(-5,0),…按此规律继续,若四边形123n n n n A A A A +++的面积为220,则n =( )A .7B .8C .9D .105.△ABC 中AC =,BC =和60A =︒,则cos B =( )A .2±B .12±C .12D .26.设函数()f x 满足(1)()0f x f x ++=,当0≤x <1时,则1()2xf x -=,则()0.5log 8f =( ) A .-2B .12-C .12D .27.若cos 0,2(sin 2)1cos2αααα≠+=+,则tan2α=( ) A .43-B .34-C .34D .438.设函数()y f x =由关系式||||1x x y y +=确定,函数(),0,()(),0.f x xg x f x x -≥⎧=⎨-<⎩,则( )A .g (x )为增函数B .g (x )为奇函数C .g (x )值域为[1,)-+∞D .函数()()y f x g x =--没有正零点二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
江西新高考数学文科二轮复习作业精练精析专题限时集训(十二)(含答案详析)

专题限时集训(十二)[第12讲 简单空间几何体](时间:45分钟)1视图的是( )-X12-2.[2012·江西卷] 若一个几何体的三视图如图X12-3所示,则此几何体的体积为( ) A.112 B .5 C.92D .4-3图X12-43.已知某几何体的三视图如图X12-4所示,则该几何体的表面积为( ) A .24 B .20+4 2 C .28 D .24+4 24.已知一个三棱锥的三视图如图X12-5所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )-5A .1B .2C .3D .45.某几何体的主视图与俯视图如图X12-6所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A.203B.43C .6D .4图X12-76.若正三棱柱的三视图如图X12-7所示,则该三棱柱的表面积是( )A .6+2 3 B.9 32C .6+3 D. 37.某四棱锥的底面为正方形,所示,则该四棱锥的体积等于( )A .1B .2C .3 D.2图X12-8图X12-98.某几何体的三视图如图X12-9所示,该则几何体的表面积为()A.28+6 5 B.30+6 5C.56+12 5 D.60+12 59.X12-10已知四棱锥P-ABCD的三视图如图X12-10所示,则此四棱锥的四个侧面的面积中最大的是()A.2B.3C.13D.3 210.一个三棱锥的三视图是三个直角三角形,如图X12-11所示,则该三棱锥的外接球的表面积为________.图X12-11图X12-1211.某几何体的三视图如图X12-12所示,则它的体积为________.12.某正三棱柱的三视图如图X12-13所示,其中主视图是边长为2的正方形,该正三棱柱的表面积是________.-13图X12-1413.如图X12-14所示的是一几何体的三视图,则该几何体的体积是________.14.如图X12-15所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF15.如图X12-16所示,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,F为AB上一点.该四棱锥的主视图和左视图如图X12-17所示,则四面体P-BFC 的体积是________.X12-16X12-1716.如图X12-18所示,在四棱锥P-ABCD中,△PBC为正三角形,PA⊥底面ABCD,其三视图如图X12-19所示,俯视图是直角梯形.(1)求主视图的面积;(2)求四棱锥P-ABCDX12-18图X12-19专题限时集训(十二)1.C [解析] 若俯视图为C ,则与左视图矛盾,其他三者均有可能.2.D [解析] 该几何体是直六棱柱,由左视图知其高为1,由主视图和俯视图知其底面面积S =(1+3)×1=4,因此其体积为4,故选D.3.B [解析] 由几何体的三视图知该几何体的上部是底面边长为2高为1的正四棱锥,该几何体的下部是边长为2的正方体,所以该几何体的表面积为S =5×22+4×12×2×2=20+4 2.4.D [解析] 由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示,利用长方体模型可知,此三棱锥的四个面都是直角三角形.5.A [解析] 由三视图知,该几何体为一个正方体挖掉一个正四棱锥,其中正方体的棱长为2,正四棱锥的底面为正方体的上底面,高为1,所以该几何体的体积为V =2×2×2-13×2×2×1=203. 6.A [解析] 由三视图可知,三棱柱的高为1,底面正三角形的高为3,所以正三角形的边长为2,所以三棱柱的侧面积为2×3×1=6,两底面积为2×12×2×3=2 3,所以表面积为6+2 3.7.D [解析] 由三视图可知该四棱锥有一侧棱与底面垂直,底面面积为2,高为1,所以V =13×2×1=23.8.B [解析] 如图所示,该几何体的表面积为S =⎝⎛⎭⎫12×5×4×3+12×2 5×(41)2-(5)2=30+6 5.9.D [解析] 由三视图可知该是四棱锥顶点在底面的射影是底面矩形的一个顶点,底面边长分别为3,2,后面是直角三角形,直角边分别为3,2,所以后面的三角形的面积为12×2×3=3.左面三角形是直角三角形,直角边长分别为2,2,三角形的面积为12×2×2=2.前面三角形是直角三角形,直角边长分别为3,2 2,其面积为12×3×2 2=3 2.右面也是直角三角形,直角边长为2,13,三角形的面积为12×2×13=13.所以四棱锥P -ABCD的四个侧面中面积最大的是前面的三角形,面积为3 2,选D.10.29π [解析] 借助长方体画出直观图,该三棱锥的外接球即是长方体的外接球,所以该球的半径为R =1222+32+42=292,其表面积为29π.11.16 [解析] 由三视图可知该几何体的底面是下底为4,上底为2,高为4的直角梯形,该几何体是高为4的四棱锥,顶点在底面的射影是底面直角梯形高的中点,几何体的体积为V =13×2+42×4×4=16.12.12+2 3 [解析] 由三视图可知,正三棱柱的高为2,底面边长为2,所以底面积为2×12×22×32=2 3,侧面积为3×2×2=12,所以正三棱柱的表面积是12+2 3.13.56[解析] 由三视图可知该几何体是一个正方体去掉一角,其直观图如图所示,其中正方体的棱长为1,所以正方体的体积为1.去掉的三棱锥的体积为13×12×1×1×1=16,所以该几何体的体积为1-16=56.14.16 [解析] 因为E 点在线段AA 1上,所以S △DED 1=12×1×1=12,又因为F 点在线段B 1C 上,所以点F 到平面DED 1的距离为1,即h =1,所以VD 1-EDF =VF -DED 1=13·S△DED 1·h =13×12×1=16.15.23 [解析] 由左视图可得F 为AB 的中点,所以△BFC 的面积为S =12×1×2=1.因为PA ⊥平面ABCD ,所以四面体P -BFC 的体积为V 四面体P -BFC =13S △BFC ·PA =13×1×2=23.16.解:(1)如图所示,过A 作AE ∥CD 交BC 于E ,联结PE.根据三视图可知,E 是BC 的中点,且BE =CE =1,AE =CD =1, 又∵△PBC 为正三角形,∴BC =PB =PC =2,且PE ⊥BC. ∴PE 2=PC 2-CE 2=3.∵PA ⊥平面ABCD ,AE 平面ABCD ,∴PA ⊥AE , ∴PA 2=PE 2-AE 2=2,即PA =2,∴主视图的面积为S =12×2×2= 2.(2)由(1)可知,四棱锥P -ABCD 的高PA =2,底面积为S =AD +BC 2·CD =1+22×1=32.∴四棱锥P -ABCD 的体积V 四棱锥P -ABCD =13S ·PA =13×32×2=22.。
2021年高三下学期统一练习(二)文科数学 含解析

2021年高三下学期统一练习(二)文科数学含解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 复数的虚部为(A)3 (B)(C)4 (D)【答案】A【解析】,所以虚部为3,选A.2. 若a∈R,则“a=1”是“”的(A)充要条件(B)必要而不充分条件(C)充分而不必要条件(D)既不充分又不必要条件【答案】C【解析】若,则。
所以“a=1”是“”的充分而不必要条件,选C.3. 设向量a=(4,x),b=(2,-1),且a⊥b,则x的值是(A)8 (B)-8 (C)2 (D)-2【答案】A【解析】因为,所以设,解得,选A.4. 双曲线的离心率为(A)(B)(C)(D)【答案】C【解析】由双曲线的方程可知,所以,即离心率,选C.5. 下列四个函数中,最小正周期为,且图象关于直线对称的是(A)(B)(C)(D)【答案】D【解析】因为函数的周期是,所以,解得,排除A,B.当时,为最大值,所以图象关于直线对称,选D.6.某几何体的三视图如图所示,则该几何体的表面积为(A)24 (B)20+4(C)28 (D)24+ 4【答案】B【解析】由几何体的三视图知该几何体的上部是底面边长为2高为1的正四棱锥,该几何体的下部是边长为2的正方体,所以该几何体的表面积为,.选B.7.在平面区域内任取一点,若满足的概率大于,则的取值范围是(A)(B)(C)(D)【答案】D【解析】其构成的区域D如图所示的边长为2的正方形,面积为S1=4,满足所表示的平面区域是以原点为直角坐标顶点,以b为直角边长的等腰直角三角形,其面积为,所以在区域D 内随机取一个点,则此点满足的概率,由题意令,解得,选D.8. 已知偶函数f(x)(x∈R),当时,f(x)=-x(2+x),当时,f(x)=(x-2)(a-x)().关于偶函数f(x)的图象G和直线:y=m()的3个命题如下:①当a=2,m=0时,直线与图象G恰有3个公共点;②当a=3,m=时,直线与图象G恰有6个公共点;③,使得直线与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A) ①②(B) ①③(C) ②③(D) ①②③【答案】D【解析】设,则,故,所以当时,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开始 ()
()0
f x f x +-=结束
是
是
否
否
()f x 存在零点? 输入函数()f x
输出函数()f x
左视图
主视图高三下学期文科数学限时训练(十二)
一、选择题
1.设集合2
{|1},{|1}M x x P x x =>=>,则下列关系中正确的是( )
A .M ∪P=P
B .M=P
C .M ∪P=M
D .M ∩P=P
2.复数
1+2i
i (i 是虚数单位)的虚部是( ) A .i 51 B .25 C .15- D .15
3.学校为了调查学生在课外读物方面的支出情况,抽出了一 个容量为n 的样本,其频率分布直方图如右图所示,其中 支出在[50,60)元的同学有30人,则n 的值为( ) A .90 B.100
C .900
D .1000
4.已知(,0)2π
α∈-
,3cos 5α=
,则tan()4π
α+=( )
A .17-
B .7-
C .7
D .17
5.已知21,e e 是互相垂直的单位向量,21212,e e e e -=+=λ, 且a 垂直,则下列各式正确的是( )
A .1=λ
B .2=λ
C .3=λ
D .4=λ
6.如右图,一个空间几何体的主视图、左视图是周长为4,一个内角
为060的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为( )
A .2
π
B .π
C .23π
D .π2
7.两个正数b a ,的等差中项是9
2
,一个等比中项是25
且,b a >则双曲线
12
22
2=-
b
y a
x 的离心率为( )
A .
415
B .
414 C .53 D .
5
3
8.某程序框图如图所示,现输入如下四个函数, 则可以输出的函数是( )
A .2
()f x x = B .1
()f x x
=
C .()x
f x e = D .()sin f x x =
9.函数x
x g x x f -=+=122)(log 1)(与在同一直角坐标系下的图象大致是( )
元
频率
组距
20 30 40 50 60
0.01
0.036 0.024
10.一批物资要用11辆汽车从甲地运到360千米外的乙地,若车速为ν千米/时,两车的距离不能小于2
)10
(
v 千米. 则运完这批物资至少需要( ) A .10小时
B .11小时
C .12小时
D .13小时
姓名 班级 分数
二、填空题
11.已知函数23,0
() 1.0
x x f x x x -⎧>⎪=⎨-≤⎪⎩,则[(2)]f f -= .
12.△ABC 的内角A 、B 、C 的对边分别为c b a ,,,若︒===120,6,2B b c ,则a = . 13.与直线020102=+-y x 平行且与抛物线2
x y =相切的直线方程是 . 14.在直角坐标系xOy 中,已知曲线C 的参数方程是⎩⎨
⎧+==1
sin ,
cos θθy x (θ是参数),
若以O 为极点,x 轴的正半轴为极轴,则曲线C 的极坐标方程可写为 .。
