非理想流动模型
合集下载
第四章-停留时间分布

可见,F(t)与C(t)有相同的变化趋势,二者仅差常数C0。
3.脉冲法测定E( t )
0,t < 0
V0
示 踪
剂M
反应器
VR
检测器
C( t )
V0
注入刺激浓度 C = C0,t = 0 0,t > 0
C0
脉冲刺激
C0
应答曲线
Δt Δt
0
t
0
t
示踪剂物料衡算式,在dt 时间内, V0
排出量为V0C(t)dt,总量为
整理得
dC(t) dt
V0 VR
[C0
C(t)]
1 tm
[C0
C(t)];
或
dC(t) dt ; C0 C(t) tm
积分得 F (t) C(t) 1 et tm ; E(t) dF (t) 1 et tm
C0
dt tm
F( t ) E( t )
1.0
1 et tm
0
t
1 et tm
1
tm
示
M 0 V0C(t)dt
踪
剂M
反应器
VR
检测器
C( t )
V0
于是 1 V0 C(t)dt, 与归一化式
E(t)dt 1
比较,得
0M
0
E(t) V0 C(t) ( 停留时间分布密度函数公式) M
在实际实验中,脉冲注入示踪剂的量可从实验数据中求得:
M V0 0 C(t)dt,
停留时间分布密度可写成: E(t) 因停留时间分布函数为
时间t (s) 0 120 240 360 480 600 720 840 960 1080
示踪剂浓度 0 6.5 12.5 12.5 10.0 5.0 2.5 1.0 0.0 0.0 C(g / m3)
第二章 理想流动与非理想流动1

第二章
理想流动与非理想 流动反应器
流体在反应器中的流动情况影响着反应速率、反应选择率, 直接影响反应结果,研究反应器的流动模型是反应器选型、设计 和优化的基础。 流动模型可以抽象出两种极限的情况:一种是完全没有返混 的活塞流反应器;另一种是返混达到极大值的全混流反应器。 实际生产中的多数管式反应器及固定床催化反应器等可作活 塞流反应器处理,多数槽式反应器可作全混流反应器处理。
对活塞流反应器,物料质点是平推着向前流动的,物料质点在反 应器中的逗留时间相同不产生返混。而在全混流反应器中,不同 年龄的质点达到完全混合,有的逗留时间很短,有的却很长,返 混程度最大。 活塞流与全混流是两种理想流型:前者理想置换,没有返混;后 者理想混合,返混最大。而介于两者之间的流型,是非理想流型, 存在着不同程度的返混现象。
2 全混流模型 亦称理想混合模型或连续搅拌槽式反应器模型,如图2-1(c)所 示,是一种返混程度为无穷大的理想化流动模型。
全混流假定反应物料以稳定流率流入反应器,在反应器中,刚进 入反应器的新鲜物料与存留在器内的物料在瞬间达到完全混合。 反应器中所有空间位置的物料参数都是均匀的,等于反应器出口 处的物料性质,即反应器内物料温度、浓度均匀,与出口处物料 温度、浓度相等。而物料质点在反应器中的逗留时间参差不齐, 有的很短,有的很长,形成一个逗留时间分布。 搅拌十分强烈的连续搅拌槽式反应器中的流体流动可视为全混流。
(2)热量衡算 热量衡算以能量守恒与转化定律为基础,在计算反应速率时必须 考虑反应物系的温度,通过热量衡算可以计算反应器中温度的变 化。与物料衡算相仿,对反应器或其一微元体积进行反应物料的 热量衡算,基本式为 (带入的热焓)=(流出的热焓)十(反应热)十(热量的 累积)十(传向环境的热量) (2-2) 式中反应热项,放热反应时为负值,吸热反应时为正值。
理想流动与非理想 流动反应器
流体在反应器中的流动情况影响着反应速率、反应选择率, 直接影响反应结果,研究反应器的流动模型是反应器选型、设计 和优化的基础。 流动模型可以抽象出两种极限的情况:一种是完全没有返混 的活塞流反应器;另一种是返混达到极大值的全混流反应器。 实际生产中的多数管式反应器及固定床催化反应器等可作活 塞流反应器处理,多数槽式反应器可作全混流反应器处理。
对活塞流反应器,物料质点是平推着向前流动的,物料质点在反 应器中的逗留时间相同不产生返混。而在全混流反应器中,不同 年龄的质点达到完全混合,有的逗留时间很短,有的却很长,返 混程度最大。 活塞流与全混流是两种理想流型:前者理想置换,没有返混;后 者理想混合,返混最大。而介于两者之间的流型,是非理想流型, 存在着不同程度的返混现象。
2 全混流模型 亦称理想混合模型或连续搅拌槽式反应器模型,如图2-1(c)所 示,是一种返混程度为无穷大的理想化流动模型。
全混流假定反应物料以稳定流率流入反应器,在反应器中,刚进 入反应器的新鲜物料与存留在器内的物料在瞬间达到完全混合。 反应器中所有空间位置的物料参数都是均匀的,等于反应器出口 处的物料性质,即反应器内物料温度、浓度均匀,与出口处物料 温度、浓度相等。而物料质点在反应器中的逗留时间参差不齐, 有的很短,有的很长,形成一个逗留时间分布。 搅拌十分强烈的连续搅拌槽式反应器中的流体流动可视为全混流。
(2)热量衡算 热量衡算以能量守恒与转化定律为基础,在计算反应速率时必须 考虑反应物系的温度,通过热量衡算可以计算反应器中温度的变 化。与物料衡算相仿,对反应器或其一微元体积进行反应物料的 热量衡算,基本式为 (带入的热焓)=(流出的热焓)十(反应热)十(热量的 累积)十(传向环境的热量) (2-2) 式中反应热项,放热反应时为负值,吸热反应时为正值。
化学反应工程第三章反应器内的流体流动

物料的浓度变化。
如测定数据属于离散型, 则:
3.2.3 寻求停留时间分布的实验方法
在实验时,时间间隔可以取成等值,得:
平均停留时间和散度可按下式计算:
当 为定值时,
散度
3.2.3 寻求停留时间分布的实验方法
例3-2 在稳定操作的连续搅拌式反应器的进料中脉冲
m 50g
注入染料液(
),测出出口液中示踪剂浓度随时
多级混合模型是由N个容积为V的全混釜串联组成,从一 个釜到下一个釜的管道内无返混且不发生化学反应,示 意如图3-8:
图3-8 多级混合模型
3.4.1 多级混合模型
经推导可得该多级混合模型的停留时间分布规律为:
F ( ) cN 1 1 1 1 1 exp( N )[1 ( N ) ( N ) 2 ( N ) 3 (N ) N 1 ] c0 1 ! 2 ! 3! (N 1 )!
(t);另一部分是阶跃输入前的物料量为Vc0-中时间
大于t的示踪剂,其量为Vc0-[1-F(t)] 。即:
即得:
(3-15)
如果阶跃输入前进口物料中不含示踪剂,即 ,则上 c F ( t ) 式可以改写成: (3-16) c0
3.2.3 寻求停留时间分布的实验方法
例3-1 测定某一反应器停留时间分布规律,采用阶跃输 入法,输入的示踪剂浓度 ,在出口处测定响应曲线得到 的数据如下表3-1所示:
占的分率。依此定义,E(t)和F(t)之间应具有如下关
系: 以及
3.2.1 停留时间分布的定量描述
在t=0时 F(0)=0和t=∞时 ,关于E(t)、F(t)曲线以及它 们之间的关系示于图3-2中。
图3—2 停留时间分布曲线
反应器基础知识—流体流动
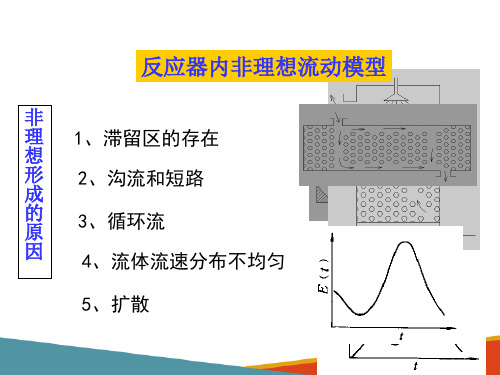
改善措施
1、增大流体在设备内的湍流程度,以消除轴向扩散而造
非 理
成的停留时间分布不均匀的现象。
想 2、在反应器内装设填充物,以改变设备内速度分布和浓
流 动
度分布,从而使停留时间分布趋于均一化。但要注意避免
的 沟流和短路现象的发生。
改
善 3、增加设备级数或在设备内增设挡板。
4、采用适当的气体分布装置,或调节各组反应管的阻力,
停留时间描述
理 想 混 合 流 动 模 型
E(t) 1 et /
F (t) 1 et /
e d 1 0
2
2e d
1 1
0
流体流动
流体的流动特征:
指反应器内流体的流动状态和混合情况,它们随反应器的几何结 构(包括内部构件)和几何尺寸不同发生变化。由于反应流体在反 应器内流动的复杂性导致反应器内不仅存在流体流速的分布,更重 要的是还存在浓度和温度的分布。使得反应器内存在不同停留时间 的流体粒子以及不同停留时间流体粒子之间的混合即返混,从而导 致反应器内反应物料处于不同的温度和浓度下进行反应。影响反应 速率和反应选择性,使反应结果发生变化。
t≤0, F(t)=0 0<t<∞,0<F(t)<1 t=∞, F(t)=1。
E(t) dF(t) dt
1、数学期望
停
留 时 间
1.0
t 0 tdF(t) 0 tE(t)dt
分
布 的 2、方差
特
征 值
2 t
(t t)2 E(t)dt
0
t 2 E(t)dt t 2
0
停
脉冲法:
留
流体流动的描述
1、停留时间分布密度函数
停
非理想流动

(3)停留时间分布函数
在稳定连续流动系统中,同
时进入反应E器(t) 的N个流体粒子
F(t)
中,其停留时间小于t的面积那= 0 E部(t)dt 1.0 1.0
分粒子占总E粒(t1) 子数N的分率。
F(t1)
F(t1)
F (t) t dN
0N
t1
t
很显然: 当t=0时,F(t) 0;
E(t)
F(t) 0 E(t)dt 1.0
• 多级全混流串联模型的停留时间分布:
假设反应器总体积为VR,现由N个体积相等的全混釜串联组成。 对系统施加脉冲示踪剂A后,现对示踪剂A作物料衡算:
对第一釜 (i=1)应有:
0 v0CA1
dV1CA1 dt
①
CA0
0
CA1
C
dt V1 dCA1 t dCA1
v0 CA1
CA1
rA1
CA2
F (t) CA CA0
F (t)
dF (t)
1
t
dt
0 1 F (t) t 0
ln[1 F (t)] t t NhomakorabeaF(t) 1 exp[ t ]
E(t) dF (t) d [1 exp( t )] 1 exp( t )
t
dt dt
tt
t
E(t)
F (t)
1 t
1.0
0.632
t
t
t
(2)停留时间分布
理想反应器内所有反应物料的停留时间都是一样的。而 非理想流动使得反应物料的各个微元在反应器中的停留 时间长短不一,存在着一个停留时间的分布问题。
停留时间的长短直接影响反应的效果,停留时间越长, 反应进行得越完全。所以,对于非理想流动系统,我们 必须了解其停留时间的分布问题。本节主要讨论:阐明 流动系统的停留时间分布的定量描述及其实验测定方法。
10__第二章_反应器内流体流动与混合--非理想流动__297-2003(0)

间,调节釜数N就可以在全混釜与平推流反应
器之间确定某一种性能状态。
非理想连续流动的返混程度介于两种流动之间。
多釜串联模型把一个非理想流动的实际反
应器等价为N 个体积相同的全混釜串联反 应器,每个釜内达到完全混合,釜间没有
返混。
实际非理想流动反应器的停留时间分布等
价为釜数为 N 的串联全混釜的停留时间分
应器的管径较小、较长,物料在其中的流
速较快时,返混程度很小,此时可近似按
平推流进行分析与设计。
平推流反应器中所有物料质点的停留时间
都相同,且等于整个物料的平均停留时间。
采用脉冲示踪法测定平推流的停留时间分
布密度函数 E(t)
C(t)
C0 E(t)
t=0
t=0 t=0
t t tt
激励曲线
S
C 2 (t )
1
S
C1 (t )
1
S
(1 e
t
S
)
此一阶常微分方程可用积分因子法求解。
C 2 (t ) 1 e F2 (t ) C 2 (t ) C0
t
S
(1
t
S
t
) (1 t
C 2 (t ) 1 e
S
S
)
对第三釜作物料衡算,可得:
同样的停留时间分布可以是不同的返混造 成的。 不能直接用测定的停留时间分布来描述返 混的程度,必须借助于模型方法。
数学模型方法
分析器内复杂的实际流动状况,进行
合理的简化,通过数学方法来表述或关联 返混与停留时间分布的定量关系,然后再 进行求解。
建立流动模型的基本思想: 根据实测的停留时间分布,假设一种流动 状态,令这种流动状态下的停留时间分布 与实测结果一致,并根据假设的流动状态 的模型参数,结合在其中进行反应的特征
理想流动非理想流动理想流动反应器的分类和应用

➢气液鼓泡反应器 因为气泡搅动所造成旳液体反向流动,形成很大旳液相循环
流量。所以,其液相流动十分接近于理想混合。 ①放置填料 ②设置多孔多层横向挡板,把床层提成若干级 ③设置垂直管
理想流动反应器旳分类和应用
分类 ➢ 理想混合流反应器 ➢ 理想平推流反应器 应用
实际生产中,连续操作釜式反应器能够近似看作是理 想混合流,连续操作管式反应器能够近似看作是理想平 推流。
降低返混程度旳措施
返混对反应器旳意义 ➢ 对反应过程产生不同程度旳影响 在返混对反应不利旳情况下,要使反应过程由间歇操作转 为连续操作时,应该考虑返混可能造成旳危害。选择反应器旳 型式时,应尽量防止选用可能造成返混旳反应器,尤其应该注 意有些反应器内旳返混程度会随其几何尺寸旳变化而明显增强。
➢ 在工程放大中产生旳问题
➢ 连续操作旳搅拌釜式反应器 为降低返混,工业上常采用多釜串联旳操作。当串联釜 数足够多时,连续多釜串联旳操作性能就很接近理想置 换反应器旳性能。(横向纵向?)
➢ 流化床 因为气泡运动造成气相和固相都存在严重旳返混。为了 限制返混,对高径比较大旳,常在其内部装置横向挡板 以降低返混;而对高径比较小旳流化床反应器,则可设 置垂直管作为内部构件(横向纵向?)
➢ 间歇反应器中不存在返混 ➢ 理想置换反应器不存在返混 ➢ 理想混合反应器返混到达极限状态 ➢ 非理想流动反应器存在不同程度旳返混
返混对反应过程旳影响
➢ 返混带来旳最大影响是反应器进口处反应物高浓度区旳消 失或减低。 ➢ 返混变化了反应器内旳浓度分布,使器内反应物旳浓度下 降,反应产物旳浓度上升。但是,这种浓度分布旳变化对反 应旳利弊取决于反应过程旳浓度效应。 ➢ 返混是连续反应器中旳一种主要工程原因,任何过程在连 续化时,必须充分考虑这个原因旳影响,不然不但不能强化 生产,反而有可能造成生产能力旳下降或反应选择率旳降低。
理想流动非理想流动理想流动反应器的分类和应用

➢滞留区的存在 ➢存在沟流与短路 ➢循环流 ➢流体流速分布不均匀 ➢扩散
上述是造成非理想流动的几种常见原因,对一个流 动系统可能全部存在,也可能是其中的几种,甚至有 其它的原因。
返混及其对反应过程的影响
返混含义:专指不同时刻进入反应器的物料之间的混合, 是逆向的混合,或者说是不同年龄质点之间的混合。
理想流动 非理想流动 理想流动反应器的分类和应用
反应器内流体的流动特征主要指反应器内反应流体的流动状 态、混合状态等,它们随反应器的几何结构和几何尺寸而异。
反应流体在反应器内不仅存在浓度和温度的分布,而且还存在流 速分布。这样的分布容易造成反应器内反应物处于不同的温度和浓 度下进行反应,出现不同停留时间的微团之间的混合,即返混。
长径比较大和流速较高的连续操作管式反应器中的流体流 动可视为理想置换流动。
理想混合流动模型
含义:理想混合流动模型也称为全混流模型。反应物料以稳 定的流量进入反应器,刚进入反应器的新鲜物料与存留在其中 的物料瞬间达到完全混合。反应器内物料质点返混程度为无穷 大。
特点:所有空间位置物料的各种参数完全均匀一致,而且出 口处物料性质与反应器内完全相同。
种,其中重要的是__________。 连续搅拌釜式反应器为减少返混,工业上常采用________的操作
由于放大后的反应器中流动状况的改变,导致了返混程度 的变化,给反应器的放大计算带来很大的困难。因此,在分析 各种类型反应器的特征及选用反应器时都必须把反应器的返混 状况作为一项重要特征加以考虑。
降低返混程度的措施
降低返混程度的主要措施是分割,通常有横向分割和纵向分 割两种,其中重要的是横向分割。
理想置换流动模型
含义:理想置换流动模型也称作平推流模型或活塞流模型。 与流动方向相垂直的同一截面上各点流速、流向完全相同, 即物料是齐头并肩向前运动的。
上述是造成非理想流动的几种常见原因,对一个流 动系统可能全部存在,也可能是其中的几种,甚至有 其它的原因。
返混及其对反应过程的影响
返混含义:专指不同时刻进入反应器的物料之间的混合, 是逆向的混合,或者说是不同年龄质点之间的混合。
理想流动 非理想流动 理想流动反应器的分类和应用
反应器内流体的流动特征主要指反应器内反应流体的流动状 态、混合状态等,它们随反应器的几何结构和几何尺寸而异。
反应流体在反应器内不仅存在浓度和温度的分布,而且还存在流 速分布。这样的分布容易造成反应器内反应物处于不同的温度和浓 度下进行反应,出现不同停留时间的微团之间的混合,即返混。
长径比较大和流速较高的连续操作管式反应器中的流体流 动可视为理想置换流动。
理想混合流动模型
含义:理想混合流动模型也称为全混流模型。反应物料以稳 定的流量进入反应器,刚进入反应器的新鲜物料与存留在其中 的物料瞬间达到完全混合。反应器内物料质点返混程度为无穷 大。
特点:所有空间位置物料的各种参数完全均匀一致,而且出 口处物料性质与反应器内完全相同。
种,其中重要的是__________。 连续搅拌釜式反应器为减少返混,工业上常采用________的操作
由于放大后的反应器中流动状况的改变,导致了返混程度 的变化,给反应器的放大计算带来很大的困难。因此,在分析 各种类型反应器的特征及选用反应器时都必须把反应器的返混 状况作为一项重要特征加以考虑。
降低返混程度的措施
降低返混程度的主要措施是分割,通常有横向分割和纵向分 割两种,其中重要的是横向分割。
理想置换流动模型
含义:理想置换流动模型也称作平推流模型或活塞流模型。 与流动方向相垂直的同一截面上各点流速、流向完全相同, 即物料是齐头并肩向前运动的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xA
1 exp
0
kt c
c
1
0.3347
0.6653
多级串联槽模型
• 物理模型: • 反应器是由若干大小相等的全混流反应器
串联而成。 • 这些全混流反应器之间没有返混,没有反
应。 • 定常态操作。
平推流与全混流的比较
1 (-rA )
平推流
= VR
V0
=cA0
dx xAf
A
0 (-rA )
Nc3
Nc2
Nc0
1
e N
1
N
解得:
c3
c0 1
e N
1
11!N
1 N
2!
2
依此类推:
cN
c0 1 eN
1 11!N
1 N
2!
2
......
N
1
1!
N
N1
cN
c0 1 eN
1 11!N
1 N
2!
2
......
N
1
1!
N
N1
由定义:
cN F
c0
因此:
F
1
e N
1
11!N
1 2!
N
2
......
N
1
1!
N
N
1
由E dF
d
E
Ne N
1
11!N
1 N
2!
2
......
N
1
1!
N
N 1
Ne N
1
11!N
1 2!
N
2
......
N
1
2!
N
N 2
E
N
N 1!
N
e N 1 N
N N e N 1 N
N 1!
E d
0
0
NNN1!
N
e
N
d
流出
ATu
cA
cA l
dl
反应
rA ATdl
积累
cA t
ATdl
轴E向扩clA 散AT出
• 整理得:
E
2cA l 2
u
cA l
cA t
rA
0
对示踪实验,rA 0,因此
cA t
=E
2cA l 2
u
cA l
无因次化: 令c cA , t , z l
cA0
L
c
E uL
2c z 2
• N等于某一值,意味着该反应器的返混程 度相当于N个理想混合反应器的串联。
• N只是一个虚拟值,因此,N可以是整数
也可以是小数。
2 θ
1 N
• 停留时间分布密度函数的散度为槽数的 倒数。
• 小数的阶乘由Γ函数解决。
z u z1eudu 0
n 1 n!
x x 1,
x
x x 1x 1
NVRi
V0
t
则:
由Vci1
Vci
VRi
dci dt
得:
dci
d
Nci
Nci1
BC : 0t 0, ci 0
对第一槽 解得:
dc1
d
Nc1
Nc0
c1 c0 1 eN
对第二槽
dc2
d
Nc2
Nc1
Nc0
1
e N
解得: c2 c0 1 eN 1 N
对第三槽
dc3
d
凝集流模型
• 物理模型: • 流体以流体团的方式流过反应器,这些流
体团彼此之间不发生混合,每个流体团相 当于一个小反应器。由于返混的作用,流 体团在反应器内的停留时间不同,达到的 转化率因而不同,在反应器出口处的宏观 转化率,就是各不同停留时间的流体团达 到的转化率的平均值。
• 这样就把流体的停留时间分布与反应转 化率联系起来了,每个流体团都作为一 个间歇反应器,它的反应时间由停留时 间分布决定。而流体团在停留时间内达 到的转化率由反应动力学决定。最后, 将二者结合起来,在出口处加权平均, 得到最终转化率。
xneaxdx
0
n!
a
n1
所以:
NN
N 1!
N! N N 1
1
2
0
2 E d
2 E
d
2
0
2
NN
2
N 1eN d
0 N 1!
NN
N 1eN d 1
0 N 1!
NN
N 1!
N
N
1!
N 2
1
N N 1 1
N2
1 N
• N=1,全混流
• N ,平推流
• 相当于若干平推流反应器或间歇反应器 的并联,将非理想流动对反应的影响明 显化了。
• 写成数学公式:
停留时间在t和t t之 停留时间在t和t t
xAf t0 间的微元达到的转化率 之间的微元的分率 如果是连续函数:
xAf
0
xA
E
t
dt
或
xAf
1 0
xAdF
t
xA--单个微元的转化率,当然是t的函数。
• 例3-3某非理想流动反应器,其停留时间分 布规律同例3-2。在该反应器内进行一级反 应,动力学方程为-rA=3.33×10-3cA,请确 定该反应器的出口转化率(反应物A的化学 计量系数为1)。
• 解:采用凝集流模型进行计算。
• 对于一级反应,在间歇反应器中转化率 与反应时间关系如下:
t
• 费克扩散定律(Fick’s law):
NA
E
dcA dl
NA : kmol m-2s-1
E : m2s1
• 在有化学反应时对反应物做物料衡算:
ATucA
AT
u
cA
cA l
dl
E
cA l
AT
dl
E
l
cA
cA l
dl
AT
流入 ATucA
E
轴向扩散入
l
cA
cA l
dl
AT
c z
L :反应器总长
令: Pe uL 彼克列Peclet 数
E c 1 2c c
Pe z2 z
Pe的物理意义:流动量与扩散量的比值, 数值越大返混程度越小。 扩散系数E ,则Pe 0,全混流 扩散系数E 0,则Pe ,平推流 不同的边界条件会有不同的结果。 依流体进出反应器时是否发生流型变化, 共有四种边界条件
cA0
xA 0
dxA rA
cA0
xA 0
dxA kcA0 1 xA
1 ln k
1
xA
xA 1 exp kt
xA
0
xAiF t
1
0
exp
k tF t
1
exp
0
kt
c
c
时间 t/s
0 120 240 360 480 600 720 840 960 1080 Σ
示踪剂浓度 c/g.m-3
全混流
VR V0
cA0
xAf xA1 rA f
xA
• 用阶跃法测定第i个反应器的停留时间分布
V0, c0,
V1,c1,
V2,c2,
Vi,ci,
Vn,cn
t时刻,对第i个反应器的示踪剂做物料衡算:
输入量 Vci1
输出量 Vci
积累量
VRi
dci dt
恒容且每个CSTR的容积为VRi ,总容积为NVRi ,
0 6.5 12.5 12.5 10.0 5.0 2.5 1.0 0 0 50
ΔF(t)
0 0.13 0.25 0.25 0.20 0.10 0.05 0.02
0 0
exp
kt
c
c
0 0.0872 0.1124 0.0754 0.0464 0.0136 0.0045 0.0012
0 0 0.3347
称函数递推公式。
手册可查1 x 2的函数值,
其余通过递推公式求得。
• 解题步骤:
停留时
t
2 t
2 θ
N
对等温一级不可逆反应,前一章有:
xAN
1
1
1
k i
N
式中: i N
轴向扩散模型
• 物理模型:
• 1 主体流动为平推流,但叠加一涡流扩 散。
• 2 涡流扩散遵循费克扩散定律且在整个 反应器内扩散系数为常数。
