第四章 非理想流动模型 答案
合集下载
化学反应：第四章 非理想流动
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
实际的工业装置
在实际的工业装置中由于物料在反应器内的流 动速率不均匀、或因内部构件的影响造成物料出现 与主体流动方向相反的逆向流动、死角等都会导致 偏离理想流动。
对于所有偏离平推流和全混流的流动模式 统称为非理想流动。
本章将利用停留时间分布定量地对非理想流动 进行讨论，并考察这些非理想流动对反应器性能的 影响。
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
假如示踪剂改用红色流体，连续检测出口中红色
流体的浓度，如果将观测的时间间隔缩到非常小，
得到的将是一条连续的停留时间分布曲线。
4.1 反应器中的返混现象与停留时间分布
(1) 停留时间分布密度函数的定义
第四章 非理想流动
定义：在稳定连续流动系统中，同时进入反应器的N 个流体粒子中，其停留时间介于t～t+dt的那部分粒 子dN占总粒子数N的分率记作：
第四章 非理想流动
1. 停留时间分布密度函数E(t)
实验： 在连续反应器内，如果在某一瞬间 (t = 0) 极快地 向入口物流中加入 100 个红色粒子，同时在系 统的出口处记下不同时间间隔流出的红色粒子数， 结果如下表。
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动
以时间 t 为横坐标，出口流中红色粒子数为 纵坐标，将上表作图如下：
流体的流动速率和方向带有一定的随机性。反应器内的流动状态实际是 随机变化的。
根据概率理论，我们可以借用两种概率分布以定量地描绘物料在流动系统中的 停留时间分布，这两种概率分布就是停留时间分布密度函数 E (t)和停留时间 分布函数 F (t)。
4.1 反应器中的返混现象与停留时间分布
第四章 非理想流动反应器设计
t2
1
最后由模型参数计算非理想反应器的平均结果。
第四章 非理想流动反应器设计
4.1 流体物料粒子的停留时间分布函数和分布密度函数 4.2 停留时间分布（RTD）的数字特征及无量纲化
4.3 理想流动模型
4.4 非理想流动模型 4.5 非理想流动反应器设计 4.6 混合质量对反应的影响
第四章 非理想流动反应器设计
第四章 非理想流动反应器设计
（3）计算分布函数F 根据F (t) 与 E(t) 关系： F (t )
E (t )dt
0
t
（4-4）
当上式用于实验数据计算时，应转换成下列形式：
F (t ) E (t )t
由此就可以计算出不同时间下的 F(t) 值，例如 当 t=5 min 时， F (5) tE (t ) 1 (0.05 0.1 0.16 0.2 0.16) 0.64 当 t=12 min 时，
计算举例：
n0~ 2 F (2) F (0) 0 0 0 N n F (4 ~ 6) 4~ 6 F (6) F (4) 0.38 0.08 0.30 N F (0 ~ 2)
同理可计算其它各时间段的分布函数值，见上表。
第四章 非理想流动反应器设计
（2）停留时间分布密度函数E(t) 定义：停留时间分布函数 F(t) 在某时间段 t→t+dt 内的平
用一定的方法将示踪剂加到反应器进口，然后在反应器出 口物料中检验示踪剂信号，以获得示踪剂在反应器中停留
时间分布的实验数据。
1、不与主流体反应； 2、物理性质相近；
选择示踪剂的原则
3、有别于主流体的可测性； 4、多相检测不发生相转移； 5、易于转变为光、电信号。
化学反应工程第四章答案
4-1 在定态操作反应器的进口物料中脉冲注入示踪物料。
出口处示踪物浓度随时间变化的情况如下。
假设在该过程中物料的密度不发生变化，试求物料的平均停留时间与=100⎰∞=-=-=02222971.8187.625.47)(t dt t E t tσmin 24-2 无量纲方差表达式的推导 （1）推导无量纲方差222/ttσσθ=；（2）推导CSTR 的22tt=σ。
1. τθt=2. ττtet E -=1)(证明： 4-3 设()θF 及()θE 分别为闭式流动反应器的停留时间分布函数及停留时间分布密度函数，θ为对此停留时间。
（1）若该反应器为平推流反应器，试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) （2）若该反应器为全混流反应器，试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) （3）若该反应器为非理想流动反应器，试求 ①F(∞); ②F(0);③E(∞);④E(0);⑤⎰∞0)(θθd E ；⑥⎰∞)(θθθd E解1平推流模型 2 全混流θθ-=e E )( ， θθ--=e F 1)(3非理想流动模型a 多釜串联 θθθN N N e N N E ---=1)!1()(， 0)(C C F N =θ4-4 C(t)t/min4-18图用阶跃法测定某一闭式流动反应器的停留时间分布，得到离开反应器的示踪剂浓度与时间的关系，如图4-18所示。
试求 （1）该反应器的停留时间分布函数)(θF 及分布密度函数)(θE ；（2）数学期望θ 及方差2θσ；（3）若用多釜串联模型来模拟该反应器，则模型参数是多少？ （4）若用轴向扩散模型来模拟该反应器，则模型参数是多少？（5）若在此反应器内进行1级不可逆反应，反应速率常数1min 1-=k ，且无副反应，试求反应器出口转化率。
解（1）.()()θF c t c t F ==0)(⎪⎩⎪⎨⎧-=12)(t t c 3322〉≤≤≤t t t()⎪⎩⎪⎨⎧-==∴120)(0t c t c t F 3322〉≤≤≤t t t ，()θF t F =)(⎪⎩⎪⎨⎧=∆∆=010)(0t c c t E3322〉≤≤≤t t t ，()t t E E =)(θ（2）.1==-ttθ（3）. 多釜串联模型 (4). 轴向扩散模型 试差 Pe=0.001 (5).4-5. 为了测定某一闭式流动反应器的停留时间分布，采用脉冲输入法，反应（1）反应物料在该反应器中的平均停留时间t 及方差2θσ（2）停留时间小于4.0min 的物料所占的分率。
第四章非理想流动反应器(201204)
Vc(t )dt c(t ) F (t ) Vc()dt c()
降 阶 法
(不讲)
c(0)
c(0) c(t)
c0(t) 0
t=0 输入曲线
0 t
响应曲线
t
Vc(t )dt Vc(0) dt
停留时间大于 t 的示踪剂量 示踪剂输入量
t→t +dt
1-F(t)
c( t ) F (t ) 1 c ( 0)
t E (t )t t
2 t 2 0 2
• 取样为等时间间隔时： (t t ) E (t ) t t E (t ) t t E (t )t E (t )t
2 2 2 t
2
t E (t ) t E (t )
2
2
(4)无因次化对比时间及函数
(4) 脉冲法和阶跃法的比较
脉冲法 阶跃法
示踪剂 注入方 法
在原有的流股中加入 示踪剂，不改变原流 股流量
可直接测得
将原有流股换成流量与 其相同的示踪剂流股
dF (t ) dC (t ) E（t ) dt C0 dt
E(t)
F(t)
C (t )dt F (t ) C (t )dt C (t )dt
0
E（t )dt 1
• 停留时间分布函数F(t):停留时间0-t范围内的物料（停留 时间小于t的质点）占进料的分率。 t 有： t=0, F(t)=0, t=∞, F(t)=1,F(t)是单调增函数
F (t ) E（t )dt
0
在某一时间t时， E(t)和F(t)之间的关系为： dF (t ) t E（t ) F (t ) E（t )dt dt 0
第四章 非理想流动模型 答案
0
t20 10tic 2c ii tm 2171 2 1 2 6 .4 61.4272.5275736.374256.31480(s2)
0
无因次方差
θ2tm 2t2217428.5 020.01990.02 ( 接近 PFR )
求平均转化率
（1） 根据一级反应转化率的本征动力学公式： 在该反应器出口处的平均转化率为
F ( t ) 5 0 0 0 .0 0 2 e x p ( 0 .0 0 2 t ) d t e x p ( 0 .0 0 2 t) 5 0 0
2 0 0
2 0 0
11 e 0 .4 e 0 .6 7 0 0 .3 6 8 0 .3 0 2 3 0 .2 %
E(t)
0 .0 0 2 4 0 .0 0 2 2 0 .0 0 2 0 0 .0 0 1 8 0 .0 0 1 6 0 .0 0 1 4 0 .0 0 1 2 0 .0 0 1 0 0 .0 0 0 8 0 .0 0 0 6 0 .0 0 0 4 0 .0 0 0 2 0 .0 0 0 0
第四章 非理想流动模型 答案
② 停留时间在0 ～ tm 的物料所占总料量的百分数为
F (tm )0 tm E (t)d t 0 .0 0 2 0 tm e x p ( 0 .0 0 2 t) d t ( tm= 500 s )
5 0 0 e x p ( 0 .0 0 2 t) d ( 0 .0 0 2 t) e x p ( 0 .0 0 2 t)5 0 0
0
1 0
c i 0 0 0 0 .1 0 .5 1 0 .0 8 .0 4 .0 0 0 2 2 .6
i 1
1 0
t ic i 0 0 0 1 4 .4 9 6 .0 2 4 0 0 2 3 0 4 1 3 4 4 0 0 6 1 5 8 .4
第四章. 非理想流动[1]
![第四章. 非理想流动[1]](https://img.taocdn.com/s3/m/ec0f2f87e53a580216fcfe1c.png)
12
4.1.2 概率函数的定义与性质
4.1.2.1 RTD密度函数E（t）的定义与性质 • （1）定义：流体以稳定流量进入设备而 不发生化学变化时，任意瞬间（记为t=0） 进入设备的数量为N的流体微元中，从出 口流出的停留时间介于tt+dt的流体微 N d 元数占总数的分率 N ，用统计规律的概 率方法表示时为概率密度与随机变量的 N d 变化值的乘积E（t）dt，即 N =E（t） dt。为时间的函数，称RTD密度函数。
E t dt 1
t 0
t 0
N
即
0
E t dt 1
（4-1）式
15
②E（t）t的图形
图中直方阴影的面 积dS=E(t)dt,密度随 时间的变化曲线与 横坐标围城的面积 是无数个小直方面 积的加和，即
S dS E t dt 1
i
i
13
对离散型数据：（Ni/N）=E（t）t，或：
N i N E t t
因此上述实验（t1=t2==2）得：
N i N
0 100
2 100 6 100 12 100
18 100
22 100
17 100 17 200
12 100
6 100
4 100 4 200
4
（4）. 三种理想反应器RTD的定性说明 • BSTR.间歇操作，无流型可言，故不存在 停留时间分布问题； • PFR. 所有流体微元停留时间相同，集中 在同一时间点=VR/V0，就是说PFR的 RTD是均一的或RTD范围集中在一点。 • CSTR.流体微元停留时间从0应有尽 有，RTD范围最宽。
24
4.1.2 概率函数的定义与性质
4.1.2.1 RTD密度函数E（t）的定义与性质 • （1）定义：流体以稳定流量进入设备而 不发生化学变化时，任意瞬间（记为t=0） 进入设备的数量为N的流体微元中，从出 口流出的停留时间介于tt+dt的流体微 N d 元数占总数的分率 N ，用统计规律的概 率方法表示时为概率密度与随机变量的 N d 变化值的乘积E（t）dt，即 N =E（t） dt。为时间的函数，称RTD密度函数。
E t dt 1
t 0
t 0
N
即
0
E t dt 1
（4-1）式
15
②E（t）t的图形
图中直方阴影的面 积dS=E(t)dt,密度随 时间的变化曲线与 横坐标围城的面积 是无数个小直方面 积的加和，即
S dS E t dt 1
i
i
13
对离散型数据：（Ni/N）=E（t）t，或：
N i N E t t
因此上述实验（t1=t2==2）得：
N i N
0 100
2 100 6 100 12 100
18 100
22 100
17 100 17 200
12 100
6 100
4 100 4 200
4
（4）. 三种理想反应器RTD的定性说明 • BSTR.间歇操作，无流型可言，故不存在 停留时间分布问题； • PFR. 所有流体微元停留时间相同，集中 在同一时间点=VR/V0，就是说PFR的 RTD是均一的或RTD范围集中在一点。 • CSTR.流体微元停留时间从0应有尽 有，RTD范围最宽。
24
1024 第4章 非理想流动1(1)
E(t)
平行流动
表明反应器内有两股平行 的流体存在
t
接近平推流的 E 曲线形状
10
反 应 工 程 第 四 章 非 理 想 流 动 ·
接近全混流的几种E曲线形状
11
反 应 工 程 第 四 章 非 理 想 流 动 ·
接近全混流的曲线，也同样有着正常形状、出峰太早、 内循环、出峰太晚、由于仪表滞后而造成时间的推迟等。 总之，测定停留时间分布曲线的目的，在于对反应器内 的流动状况作出定性的判断，以确定是否符合工艺要求 或提出相应的改善方案。求取数学期望和方差，以作为 返混的量度，进而求取模型参数N。
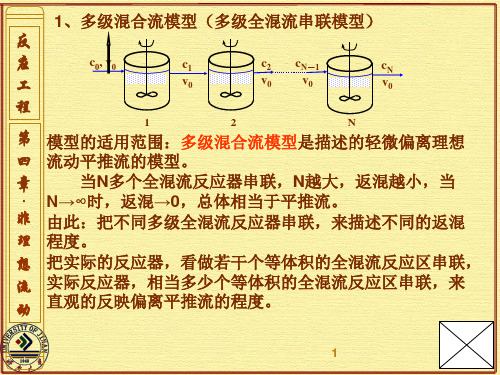
1、多级混合流模型（多级全混流串联模型） 反 应 工 程
c0, v0 c1 v0
1 2
c2 v0
cN－1 v0
N
cN v0
第 模型的适用范围：多级混合流模型是描述的轻微偏离理想 四 流动平推流的模型。 当N多个全混流反应器串联，N越大，返混越小，当 章 N→∞时，返混→0，总体相当于平推流。 非 由此：把不同多级全混流反应器串联，来描述不同的返混 理 程度。 想 把实际的反应器，看做若干个等体积的全混流反应区串联， 流 实际反应器，相当多少个等体积的全混流反应区串联，来 动 直观的反映偏离平推流的程度。 ·
c AN N t N 1 N t / t E( t ) ( ) e c0 ( N 1 )! t t t t N ti ,ti N
N
4
反 应 工 程 第 四 章 非 理 想 流 动 ·
无因次化令
t t
上式简化为：
NN E( ) t E( t ) N 1e N ( N 1 )! N 1 max N
因此，对于第N个全混区
第四章非理想流动作业1(1)
பைடு நூலகம்
形成非理想流动的根源 ① 操作条件：温度、压力、流量、物料组成 ② 流体性质：粘度、重度、扩散系数等 ③ 设备型式及结构
病态流动是指：设计、制造不良，即反应设备缺陷 引起的非理想流动，如死角、短路等
2. 什么是E(t) 、F(t)、 、σt2、σθ2 ？ E(t)dt 和F(t) 物理意义？ 答： E(t) 是停留时间密度分布函数：定常态下的连
4. 示踪剂有何要求（选取原则）？ 答：采用何种示踪剂，要根据物料的物态、
相系及反应器的类型等情况而定。
1.不与主流体发生反应（无化学反应活性）。 2.与所研究的流体完全互溶，除了显著区别
于主流体的某一可检测性质外，二者应具 有尽可能相同的物理性质
便于检测：应具有或易于转变为电信号 或光信号的特点，且浓度很低时也能 检测。
第四章
第四组 组长：钟美弟 组员：韩平、杨丹、 马梦华、郭慧春、曾召名、 曾凡林、土孙江、包生璞
1.非理想流动的起因是什么？其根源有哪些？ 什么是病态流动?
答：起因有两个
1.设备内不均匀的速度分布。包括：死角、沟流、 短路、层流流动、截面突变引起的收缩膨胀等。
2.与物料主体流动方向相反的流动。例如：管式反 应器：扩散、局部循环流动、压差、流体与固体 间的摩擦等引起；釜式反应器：搅拌引起流体循 环运动等。
或：流过反应器的物料中停留时间小于 t (介 于0 ~ t 之间)的质点所占的分率。
σt2停留时间分布分散程度的量度。数学上指 对于平均停留时间的二次矩。
σθ2 是无因此散度 E(t)dt：表示同时进入反应器的N个流体质点
中，停留时间介于t 与t+dt 间的质点所占分 率dN/N。
F(t)：表示出口流体中停留时间小于t 的物料 （ 0~t 范围内的质点）占进料的分率。
形成非理想流动的根源 ① 操作条件：温度、压力、流量、物料组成 ② 流体性质：粘度、重度、扩散系数等 ③ 设备型式及结构
病态流动是指：设计、制造不良，即反应设备缺陷 引起的非理想流动，如死角、短路等
2. 什么是E(t) 、F(t)、 、σt2、σθ2 ？ E(t)dt 和F(t) 物理意义？ 答： E(t) 是停留时间密度分布函数：定常态下的连
4. 示踪剂有何要求（选取原则）？ 答：采用何种示踪剂，要根据物料的物态、
相系及反应器的类型等情况而定。
1.不与主流体发生反应（无化学反应活性）。 2.与所研究的流体完全互溶，除了显著区别
于主流体的某一可检测性质外，二者应具 有尽可能相同的物理性质
便于检测：应具有或易于转变为电信号 或光信号的特点，且浓度很低时也能 检测。
第四章
第四组 组长：钟美弟 组员：韩平、杨丹、 马梦华、郭慧春、曾召名、 曾凡林、土孙江、包生璞
1.非理想流动的起因是什么？其根源有哪些？ 什么是病态流动?
答：起因有两个
1.设备内不均匀的速度分布。包括：死角、沟流、 短路、层流流动、截面突变引起的收缩膨胀等。
2.与物料主体流动方向相反的流动。例如：管式反 应器：扩散、局部循环流动、压差、流体与固体 间的摩擦等引起；釜式反应器：搅拌引起流体循 环运动等。
或：流过反应器的物料中停留时间小于 t (介 于0 ~ t 之间)的质点所占的分率。
σt2停留时间分布分散程度的量度。数学上指 对于平均停留时间的二次矩。
σθ2 是无因此散度 E(t)dt：表示同时进入反应器的N个流体质点
中，停留时间介于t 与t+dt 间的质点所占分 率dN/N。
F(t)：表示出口流体中停留时间小于t 的物料 （ 0~t 范围内的质点）占进料的分率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
50
1 1 1 0.135 0.865 1 0.0075 (272.5 / 50)
可见方法（1）与方法（2）得到相同的结果。
（3） 选用PFR流动模型，平均停留时间tm 为 272.5 s
xA 1 exp(ktm ) 1 exp(0.0075 272.5) 1 0.13 0.870
1 exp(0.002t ) 500 s 0.002 0
② 停留时间在0 ～ tm 的物料所占总料量的百分数为
F (tm ) E (t )dt 0.002 exp(0.002t )dt
0 0
tm
tm
( tm= 500 s )
500
500
0
exp(0.002t )d(0.002t ) exp(0.002t ) 0
10
0 0 0
0 0 0
0 0 0
0.004 14.4 2073.6
0.027 96.0 18432
0.469 2400 576000
0.823 2304 663552
1.00 1344 451584
1.00 0 0
1.00 0 0
c
i 1
i
0 0 0 0.1 0.5 10.0 8.0 4.0 0 0 22.6
10
i
C
i 1
2 tm
i
将相关数据列于下表
t/s
c (g / m3)
0
0 0
48
0 0
96
0 0
144
0.1 0.1
192
0.5 0.6
240
10.0 10.6
288
8.0 18.6
336
4.0 22.6
384
0 22.6
432
0 22.6
c
i 1
10
i
F( ti ) t ic i t i2 c i
θ2
t2
2 tm
1480 0.0199 0.02 ( 接近 PFR ) 2 272.5
求平均转化率
（1） 根据一级反应转化率的本征动力学公式： 在该反应器出口处的平均转化率为
xA 1 exp(kt )
xA
0
xA E (t )dt
0
E (t )dt
1 exp(kt )E (t )dt E (t )dt
200
0.002exp(0.002t )dt exp(0.002t ) 200
1 1 0.4 0.670 0.368 0.302 30.2% e e
0.0024 0.0022 0.0020 0.0018
63.2%
E(t)
0.0016 0.0014 0.0012 0.0010 0.0008 0.0006 0.0004 0.0002 0.0000 0 200 400 600 800 1000 1200 1400 1600 1800 2000
30.2%
E(t)=0.002exp(-0.002t)
tm
t (s)
4-3 t/s c (g / m3)
用脉冲法测得某反应器的示踪剂浓度为 0 0 48 0 96 0 144 0.1 192 0.5 240 10.0 288 8.0 336 4.0 384 0 432 0
计算平均停留时间。在反应器中进行一级反应 A → P, k = 7.5×10-3 s-1, 求平均转 化率。若此反应分别在CSTR和PFR中进行，具有相同的平均停留时间，反应结果 如何？
t c
i 1 10 i 1
10
i i
0 0 0 14.4 96.0 2400 2304 1344 0 0 6158.4
2 t i ci 0 2073.6 18432 576000 663552 451584 0 1711641.6
解： ①
tm
由求平均停留时间公式
0 0
tE (t )dt E (t )dt
tE (t )dt 0.002t exp(0.002t )dt
0 0
t exp(0.002t ) 0 exp(0.002t )dt
0
t exp(0.002t ) 0
i 1 i
10
i
c
i 1
10
i
192 0.5
240 10.0
288 8.0
336 4.0
384 0
432 0
xi ci
10
0
0
0
0.066
0.382
8.347
7.077
3.678
0
0
x c
i 1
A i
0 0 0 0.066 0.382 8.347 7.077 3.678 0 0 19.55
0 0
因为 E (t )
V0 c(t ), M
将其代入后，得
xA
1 exp(kt ) c(t )dt c(t )dt
0 0
对于离散型的实验数据，上式又写成
1 exp(kti ) ci
t c
0 0 48 0 96 0 144 0.1
xA
1 exp(kt ) c
解： 根据计算离散型停留时间分布函数公式
F (t )
Ci ti
1 10 i 1 i i
i
C t C
i 1
Ci
1 10 i
i
; tm
tiCi ti
i 1 10
10
C t
i 1 i
tiCi
i 1 10
10
i
C
i 1
; t2
2 t i Ci i 1 10
平1 exp(kt ) c
i 1 10 i i
10
10
c
i 1
i 1
i
i
i
c
i 1
10
19.55 0.865 22.6
i
（2）选用 m-CSTR 非理想流动模型，模型参数 m 为
m
1
θ2
m
1 50 0.02
m
1 1 xA 1 1 1 k 1 k ( t / m ) m
第四章 非理想流动模型
4-1 有一反应器的停留时间密度函数为
E (t ) 0.002exp(0.002t )
（时间单位为s）
试求：① 平均停留时间（即数学期望）tm是多少？
② 停留时间在0 ～ tm 的物料所占总料量的百分数？ ③ 停留时间在 200s 到 500s 的物料所占总料量的百分数？
（4） 选用CSTR流动模型，平均停留时间tm为272.5 s
1 xA 1 1 k
1 1 0.671 1 0.0075 272.5
结论： 1. 根据实验数据计算出的方差为0.02，流型很接近于PFR；
2. 无论采用何种求算反应器出口平均转化率，均有相同的结果， 出口平均转化率为0.865； 3. 相同反应和相同平均停留时间， 在PFR 的出口转化率为0.870，
e1 1 0.632 63.2%
③ 停留时间在200 s ～ 500 s的物料所占总料量的百分数为
F (t ) F (500) F (200) F (t )
500
500
0
E (t )dt
200
0
E (t )dt
500
500
200
E (t )dt
平均停留时间
tm
方差
t c c
0 0 10 i
10
i i
6158.4 272.5 (s) 22.6
t2
t c c
0 0 10 i
10
2 i i
2 tm
1711641.4 272.52 75736.3 74256.3 1480 (s2 ) 22.6
无因次方差
说明该反应器的确接近于PFR；
4. 相同反应和相同平均停留时间， 在CSTR的出口转化率为0.671。
1 1 1 0.135 0.865 1 0.0075 (272.5 / 50)
可见方法（1）与方法（2）得到相同的结果。
（3） 选用PFR流动模型，平均停留时间tm 为 272.5 s
xA 1 exp(ktm ) 1 exp(0.0075 272.5) 1 0.13 0.870
1 exp(0.002t ) 500 s 0.002 0
② 停留时间在0 ～ tm 的物料所占总料量的百分数为
F (tm ) E (t )dt 0.002 exp(0.002t )dt
0 0
tm
tm
( tm= 500 s )
500
500
0
exp(0.002t )d(0.002t ) exp(0.002t ) 0
10
0 0 0
0 0 0
0 0 0
0.004 14.4 2073.6
0.027 96.0 18432
0.469 2400 576000
0.823 2304 663552
1.00 1344 451584
1.00 0 0
1.00 0 0
c
i 1
i
0 0 0 0.1 0.5 10.0 8.0 4.0 0 0 22.6
10
i
C
i 1
2 tm
i
将相关数据列于下表
t/s
c (g / m3)
0
0 0
48
0 0
96
0 0
144
0.1 0.1
192
0.5 0.6
240
10.0 10.6
288
8.0 18.6
336
4.0 22.6
384
0 22.6
432
0 22.6
c
i 1
10
i
F( ti ) t ic i t i2 c i
θ2
t2
2 tm
1480 0.0199 0.02 ( 接近 PFR ) 2 272.5
求平均转化率
（1） 根据一级反应转化率的本征动力学公式： 在该反应器出口处的平均转化率为
xA 1 exp(kt )
xA
0
xA E (t )dt
0
E (t )dt
1 exp(kt )E (t )dt E (t )dt
200
0.002exp(0.002t )dt exp(0.002t ) 200
1 1 0.4 0.670 0.368 0.302 30.2% e e
0.0024 0.0022 0.0020 0.0018
63.2%
E(t)
0.0016 0.0014 0.0012 0.0010 0.0008 0.0006 0.0004 0.0002 0.0000 0 200 400 600 800 1000 1200 1400 1600 1800 2000
30.2%
E(t)=0.002exp(-0.002t)
tm
t (s)
4-3 t/s c (g / m3)
用脉冲法测得某反应器的示踪剂浓度为 0 0 48 0 96 0 144 0.1 192 0.5 240 10.0 288 8.0 336 4.0 384 0 432 0
计算平均停留时间。在反应器中进行一级反应 A → P, k = 7.5×10-3 s-1, 求平均转 化率。若此反应分别在CSTR和PFR中进行，具有相同的平均停留时间，反应结果 如何？
t c
i 1 10 i 1
10
i i
0 0 0 14.4 96.0 2400 2304 1344 0 0 6158.4
2 t i ci 0 2073.6 18432 576000 663552 451584 0 1711641.6
解： ①
tm
由求平均停留时间公式
0 0
tE (t )dt E (t )dt
tE (t )dt 0.002t exp(0.002t )dt
0 0
t exp(0.002t ) 0 exp(0.002t )dt
0
t exp(0.002t ) 0
i 1 i
10
i
c
i 1
10
i
192 0.5
240 10.0
288 8.0
336 4.0
384 0
432 0
xi ci
10
0
0
0
0.066
0.382
8.347
7.077
3.678
0
0
x c
i 1
A i
0 0 0 0.066 0.382 8.347 7.077 3.678 0 0 19.55
0 0
因为 E (t )
V0 c(t ), M
将其代入后，得
xA
1 exp(kt ) c(t )dt c(t )dt
0 0
对于离散型的实验数据，上式又写成
1 exp(kti ) ci
t c
0 0 48 0 96 0 144 0.1
xA
1 exp(kt ) c
解： 根据计算离散型停留时间分布函数公式
F (t )
Ci ti
1 10 i 1 i i
i
C t C
i 1
Ci
1 10 i
i
; tm
tiCi ti
i 1 10
10
C t
i 1 i
tiCi
i 1 10
10
i
C
i 1
; t2
2 t i Ci i 1 10
平1 exp(kt ) c
i 1 10 i i
10
10
c
i 1
i 1
i
i
i
c
i 1
10
19.55 0.865 22.6
i
（2）选用 m-CSTR 非理想流动模型，模型参数 m 为
m
1
θ2
m
1 50 0.02
m
1 1 xA 1 1 1 k 1 k ( t / m ) m
第四章 非理想流动模型
4-1 有一反应器的停留时间密度函数为
E (t ) 0.002exp(0.002t )
（时间单位为s）
试求：① 平均停留时间（即数学期望）tm是多少？
② 停留时间在0 ～ tm 的物料所占总料量的百分数？ ③ 停留时间在 200s 到 500s 的物料所占总料量的百分数？
（4） 选用CSTR流动模型，平均停留时间tm为272.5 s
1 xA 1 1 k
1 1 0.671 1 0.0075 272.5
结论： 1. 根据实验数据计算出的方差为0.02，流型很接近于PFR；
2. 无论采用何种求算反应器出口平均转化率，均有相同的结果， 出口平均转化率为0.865； 3. 相同反应和相同平均停留时间， 在PFR 的出口转化率为0.870，
e1 1 0.632 63.2%
③ 停留时间在200 s ～ 500 s的物料所占总料量的百分数为
F (t ) F (500) F (200) F (t )
500
500
0
E (t )dt
200
0
E (t )dt
500
500
200
E (t )dt
平均停留时间
tm
方差
t c c
0 0 10 i
10
i i
6158.4 272.5 (s) 22.6
t2
t c c
0 0 10 i
10
2 i i
2 tm
1711641.4 272.52 75736.3 74256.3 1480 (s2 ) 22.6
无因次方差
说明该反应器的确接近于PFR；
4. 相同反应和相同平均停留时间， 在CSTR的出口转化率为0.671。