相遇与追及教案
初中相遇,追及应用题教学设计

教师活动
教学目标
教学说明
预习相关概念及定理。
思考并回答。
学生同步回答
学生以小组形式进行讨论
小组讨论完成后请小组代表起来公布各个小组的答案。
学生观察并思考。
学生运用直尺进行绘图。
画完的学生举手,等待老师的提问。
学生观察黑板上两位同学的线段图,并以小组形式进行讨论。
学生观察思考,以小组形式谈论。
先让学生理解题意。
先让学生自己动手操作把复杂的题目用简单的图形来表达。
关注不同成绩和层次学生的思考能力。然后再进行总结,使得掌握各个层次学生的思考能力。
学生能更容易接受新知识。
先让学生掌握解应用题中审题的步骤。
让学生体会合作和竞争的关系。
让学生掌握怎么列相遇问题的方程和解方程。
解一道应用题前首先能够判断这题属于‘相遇’还是‘追及’?
初中数学双语教学设计数学应用题“相遇,追及问题”
西藏日喀则市桑珠孜区第二中学格桑德吉
课型:新授课
日期:2017
教材分析:
1、数学应用题“相遇,追及问题”在初中六本书中没有单独的列出一章。但是在方程与不等式的应用题中经常出现“相遇,追及问题”。
2、由于这类问题与实际问题紧密相联,所以考试中出现次数很多。
准备工作:1、制作讲学稿,上课之前发给每一位学生。
2、学生课前分小组预习,上课时按小组落座。
3、学生准备好直尺,为了方便画图。
教学设计策略:依据教学目标和学生的特点,依据教学时间和效率的要求,在此课教学方法和教学模式的设计中我主要体现了以下的设计思想和策略:
1、回归学生主体,一切围绕着学生的学习活动和当堂的反馈程度安排教学过程。
学生观察体验,领会怎么列方程,解方程。
相遇、追及问题教学设计

相遇、追及问题教学设计教学目标1.知识与能力会画物体运动图,能分析不同类型的相遇、追及问题中的位移和速度关系,列出方程,解决问题。
2.过程与方法通过活动引导学生积极参与、合作探究,使学生进一步掌握解决追及与相遇问题的方法步骤。
3.情感态度与价值观让学生感受到物理与生活息息相关,增加其对物理学习的兴趣,并通过小组合作,加强学生之间的交流以及团结互助的精神。
教学重点找到相遇、追及问题中的等量关系,列出方程。
教学难点寻找相遇、追及问题中的等量关系。
教学过程师生活动设计意图一.观看猎豹追羚羊和汽车追尾视频,导入新课。
观看视频提出问题思考问题激发学生学习兴趣二.例题分析,掌握新知(一)追及问题1、追及问题中两者速度大小与两者距离变化的关系。
思考1.匀加速追匀速,追上的条件是什么?观看图片总结结论:当两物体在同一时刻到达同一位置时,则表示追上。
思考2.在追赶的过程中,两者之间的距离如何变化?结合V-t图像,总结:在匀加速直线运动追赶匀速直线运动中,当两物体速度相等时,有最大距离。
学生思考,教师点拨培养学生分析问题解决问题的能力例1:一辆执勤的警车停在公路边。
当警员发现从他旁边以v0=8m/s的速度匀速行驶的货车有违章行为时,立即前去追赶。
警车以加速度a=2m/s2做匀加速运动。
试问:(1)警车要多长时间才能追上违章的货车?(2)在警车追上货车之前,两车间的最大距离是多大?总结解追及、相遇问题的思路:1.根据对两物体运动过程的分析,画出两物体运动的示意图;2.根据两物体的运动性质,分别列出两个物体的速度和位移方程,注意要将两物体运动时间的关系反映在方程中;3.由运动示意图找出两物体位移间的关联方程,这是关键;4.联立方程求解,并对结果进行简单分析.三、变式练习,巩固新知1.一辆值勤的警车停在公路边,当警员发现从他旁边以v0=8 m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,经t0=2.5 s,警车发动起来,以加速度a=2 m/s2做匀加速运动.试问:(1)警车要多长时间才能追上违章的货车?(2)在警车追上货车之前,两车间的最大距离是多大?(二)避免相撞问题思考1:在躲避的过程中,两者之间的距离如何变化?思考2:在躲避的过程中,如何保证两者不相撞?安排学生讲解教师总结点拨。
高中物理——相遇和追及问题教案
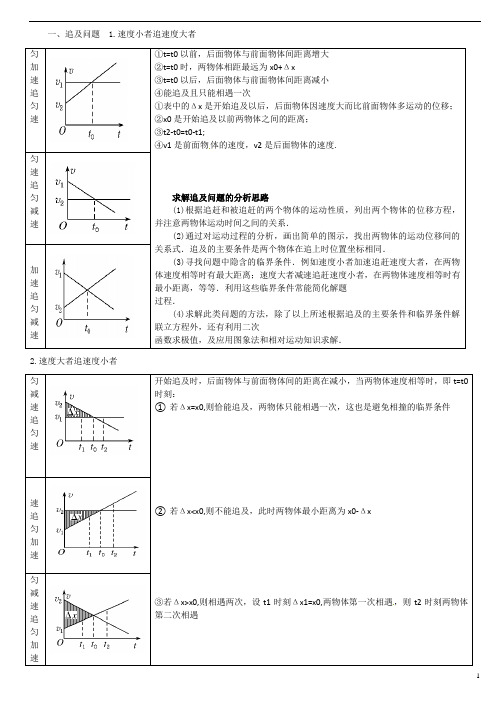
一、追及问题 1.速度小者追速度大者匀加速追匀速①t=t0以前,后面物体与前面物体间距离增大②t=t0时,两物体相距最远为x0+Δx③t=t0以后,后面物体与前面物体间距离减小④能追及且只能相遇一次①表中的Δx是开始追及以后,后面物体因速度大而比前面物体多运动的位移;②x0是开始追及以前两物体之间的距离;③t2-t0=t0-t1;④v1是前面物体的速度,v2是后面物体的速度.求解追及问题的分析思路(1)根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物体运动时间之间的关系.(2)通过对运动过程的分析,画出简单的图示,找出两物体的运动位移间的关系式.追及的主要条件是两个物体在追上时位置坐标相同.(3)寻找问题中隐含的临界条件.例如速度小者加速追赶速度大者,在两物体速度相等时有最大距离;速度大者减速追赶速度小者,在两物体速度相等时有最小距离,等等.利用这些临界条件常能简化解题过程.(4)求解此类问题的方法,除了以上所述根据追及的主要条件和临界条件解联立方程外,还有利用二次函数求极值,及应用图象法和相对运动知识求解.匀速追匀减速匀加速追匀减速2.速度大者追速度小者匀减速追匀速开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0时刻:①若Δx=x0,则恰能追及,两物体只能相遇一次,这也是避免相撞的临界条件②若Δx<x0,则不能追及,此时两物体最小距离为x0-Δx③若Δx>x0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇匀速追匀加速匀减速追匀加速。
追及和相遇问题专题教案

追及问题和相遇问题专题学习目标:1.知道两种问题的各种处理方法2.能归纳两种问题的临界条件3.理解数学方法和图象法在处理物体问题中的重要性课时安排:1课时教学过程追及问题的实质就是:当两物体在同一直线上运动,分析讨论两物体在同一时刻是否能达到同一空间位置的问题.在分析追及问题时,必须明确以下几点:一个条件,两个关系,三种解题方法.1. 一个条件即两物体的速度相等,它往往是追上追不上(两物体间距离有极值(最大值,最小值))的的临界条件,也是分析判断此类问题的切入点.2.两个关系即两物体运动的时间关系和位移关系.(1)若两物体同时开始运动则运动时间相等,若不同时开始运动则应找出时间关系.(2)若两物体从同一位置开始运动则追上的位移关系是s1=s2;若开始运动时两物体相距s0,则追上的位移关系是s1-s2=s03.三种解题方法解这类问题一般可用物理分析法,数学极值法,图象法.(1)物理分析法 基本的解题思路是:①分别对两物体研究②画出运动过程示意图③列出位移方程④找出时间关系速度关系,位移关系⑤解出结果,必要时进行讨论.例1. 甲物体作匀速直线运动的速度是5m/s ,经过乙物体时,乙物体从静止开始以1m/s 2的加速度追赶甲物体,求:①乙在追上甲之前,经过多长时间甲乙相距最远?此距离是多少?②什么时候乙追上甲?此时乙物体的速度是多少?解析:①乙物体运动后速度由零逐渐增大,而甲的速度不变,在乙的速度小于甲物体的速度前,二者间的距离将越来越大,一旦乙的速度超过甲物体的速度时两物体间的距离就将缩小,因此当两物体的速度相等时,两物体相距最远.因此有:甲乙乙v t a v == ∴s 5s 15a v t ===乙甲t v x 甲甲= 2at 21x =乙 由位移关系:乙甲x x x -=∆ 带入数据得Δx =12.5m②设经过t1时间乙追上甲,此时甲乙的位移相等. 则121t v at 21甲= s 10a v 2t 1==∴甲s /m 10at v 1==乙 (2)数学极值法运用物理规律将物理问题转化成数学问题,通过函数运算得出结果.上题也可以用数学极值法求解.解析:①设乙在追上甲之前经t时间两物体相距最远.乙甲x x x -=∆=2at 21t v -甲=5t-0.5t2 由二次函数求极值公式知:当s 5a2b t ==时Δs最大,代入数据得Δx =12.5m ②同物理分析法②(3)图象法①甲乙的v-t图像如图所示,根据速度图像的物理意义,图像与坐标轴所围面积表示位移的大小由图像可看出:在乙追上甲之前的t 时刻,两物体的速度相等,甲的位移(矩形面积)与乙的位移(三角形的面积)之差(画斜线部分)达最大,所以:甲乙乙v t a v == ∴s 5s 15a v t ===乙甲乙甲s s x -=∆=S 矩形-S 三角形 =12.5m②由图像可知:在t 时刻后,由甲与乙的速度图线所围三角形的面积与阴影三角形的面积相等时,两物体的位移相等(即追上),所以由图可得:乙追上甲时,t '=2t=10s , 10v 2v ==甲乙m/s 点评:(1)追和被追两者的速度相等常是能追上、追不上、二者距离有极值的临界条件。
物理知识点高一物理专题一追及与相遇教案【精品教案】

t,
则
t (v1 v2 ) a
s1
(v1 v2 )t 2
s2 v2t
s1 s2 (v1 v2 )t (v1 v 2 ) 2 s
2
2a
a ( v1 v2 ) 2 2s
解法二: 以前车为参照系,后车的速度为 v (v1 v2 ) ,当后车的速度减为零时,其位移
小于 s,两车不会相撞,即
2
2
(v1 v 2 )
直观,物理图景清晰,便于分析研究。
② 分析研究对象的运动过程,搞清整个运动过程按运动性质的转换可分为哪几个运动阶
段,各个阶段遵循什么规律,各个阶段间存在什么联系。
特别是,若被追赶的物体做匀减速运动,一定要注意追上前该物体是否停止运动。 ③ 仔细审题,注意抓住题目中的关键字眼,充分挖掘题目中的隐合条件,如“刚好”、
( 1)最多能有几个小球同时在空中? ( 2)设在 t=0 时第一个小球被抛出,那么它应在哪些时刻和以后抛出的小球在空中相遇
而过?( g 10m / s2 )
t 2v0 6s
解: v0 30m / s ,小球在空中运动的时间为
g
t 0 0 时,将第一个小球抛出,它在第 6s 末回到原处,同时第七个小球即将被抛出。在
t 当 t 2s时,
1
30
2
s 4s
2
10
,这是与第三个小球相遇而过的时刻;
当 t 3s 时, t 4.5s ,这是与第四个小球相遇而过的时刻;
当 t 4s时, t 5s ,这是与第五个小球相遇而过的时刻;
当 t 5s 时, t 5.5s ,这是与第六个小球相遇而过的时刻。
除上述分析计算法之外,还可用图像法解决本题。根据题意,定性画出
高中物理——相遇和追及问题教案

1.物体A、B同时从同一地点,沿同一方向运动,A以10m/s的速度匀速前进,B以2m/s2的加速度从静止开始做匀加速直线运动,求A、B再次相遇前两物体间的最大距离.3.(2011·新课标全国卷)甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。
在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半。
求甲乙两车各自在这两段时间间隔内走过的总路程之比。
4.一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ.初始时,传送带与煤块都是静止的.现让传送带以恒定的加速度α0开始运动,当其速度达到v0后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动.求此黑色痕迹的长度.5.甲、乙两物体相距s,同时同向沿同一直线运动,甲在前面做初速度为零、加速度为a1的匀加速直线运动,乙在后做初速度为υ0,加速度为a2的匀加速直线运动,则()A.若a1=a2,则两物体可能相遇一次B.若a1>a2,则两物体可能相遇二次C.若a1<a2,则两物体可能相遇二次D.若a1>a2,则两物体也可相遇一次或不相遇6.A、B两棒均长1m,A棒悬挂于天花板上,B棒与A棒在一条竖直线上,直立在地面,A棒的下端与B棒的上端之间相距20m,如图1-5-3所示,某时刻烧断悬挂A棒的绳子,同时将B棒以v0=20m/s的初速度竖直上抛,若空气阻力可忽略不计,且g=10m/s2,试求:(1)A、B两棒出发后何时相遇?(2)A、B两棒相遇后,交错而过需用多少时间?7.经检测汽车A的制动性能:以标准速度20m/s在平直公路上行驶时,制动后40s停下来。
现A在平直公路上以20m/s的速度行驶发现前方180m处有一货车B以6m/s的速度同向匀速行驶,司机立即制动,能否发生撞车事故?8.(2011·长沙模拟)在平直公路上,自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移随时间变化的规律为:汽车x=10t-t2,自行车x=5t,(x的单位为m,t的单位为s),则下列说法正确的是( ) A.汽车做匀加速直线运动,自行车做匀速直线运动B.经过路标后的较短时间内自行车在前,汽车在后C.在t=2.5 s 时,自行车和汽车相距最远D.当两者再次同时经过同一位置时,它们距路标12.5 m9.(2011·东北三校联考)从同一地点同时开始沿同一直线运动的两个物体Ⅰ、Ⅱ的速度—时间图象如图所示.在0~t 2时间内,下列说法中正确的是( )A .Ⅰ物体所受的合外力不断增大,Ⅱ物体所受的合外力不断减小B .在第一次相遇之前,t 1时刻两物体相距最远C .t 2时刻两物体相遇D .Ⅰ、Ⅱ两个物体的平均速度大小都是v 1+v 2210.两辆游戏赛车在a 、b 在两条平行的直车道上行驶.t =0时两车都在同一计时线处,此时比赛开始.它们在四次比赛中t v -图像的如图1-2-8图像所示.哪些图对应的比赛中,有一辆赛车追上了另一辆( ) 12..甲、乙两汽车在一条平直的单行道上乙前甲后同向匀速行驶.甲、乙两车的速度分别为m/s 4001=v 和m/s 2002=v ,当两车距离接近到=s 250 m 时两车同时刹车,已知两车刹车时的加速度大小分别为210.1m/s =a 和223/1m/s =a ,问甲车是否会撞上乙车?13..A 、B 两辆汽车在平直公路上朝同一方向运动,如图6所示为两车运动的速度—时间图象,对于阴影部分的说法正确的是( )A .若两车从同一点出发,它表示B 车追上A 车前两车的最大距离B .若两车从同一点出发,它表示B 车追上A 车前的最小距离C .若两车从同一点出发,它表示B 车追上A 车时离出发点的距离D .表示两车出发前相隔的距离14..两辆完全相同的汽车,沿水平直路一前一后匀速行驶,速度均为v 0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中所行的距离为s ,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为:A.sB.2s C.3s D.4s15.经检测汽车A 的制动性能:以标准速度20m/s 在平直公路上行使时,制动后40s 停下来.现A 在平直公路上以20m/s 的速度行使发现前方180m 处有一货车B 以6m/s 的速度同向匀速行使,司机立即制动,能否发生撞车事故?0 t/s 5 10 15 20 25 30 10 v /(m/s) 5 A a b 0 t/s 5 10 15 20 25 30 10 v /(m/s) 5 B a b 0 t/s 5 10 15 20 25 30 10 v /(m/s) 5 C a b 0 t/s 5 10 15 20 25 30 10 v /(m/s) 5D a b 图6。
追击和相遇教案

0
解得t1=0;t2=20s。 t1=0表示开始两
车从同一位置出发, t2=20s表示经20s
汽车追上自行车,此时两车行驶的距离,
S=100m。汽车的速度v=10m/s。
开始,v自 v汽 ,两车距离不断增大,当
汽车速度增大到 v汽 v自 ,两车的距离将
逐渐减小,所以 v汽 v自 时,两车距离
关系为: s车+s0= s人
即: at2/2 + s0= v人t
由此方程求解t,若有解,则可追上;若 无解,则不能追上。 代入数据并整理得:t2-12t+50=0
△=b2-4ac=122-4×50×1=-56<0 所以,人追不上车。
两物体在同一直线上追及、相遇或避免 碰撞问题中的条件是:两物体能否同时 到达空间某位置。因此应分别对两物体 研究,列出位移方程,然后利用时间关 系、速度关系、位移关系而解出。
(一)追赶问题
1、追赶问题的特征:“追及”主要条件 是两个物体在追赶过程中处在同一位置。 常见的情形有三种:
①初速度为零的匀加速运动的物体甲追 。
赶同方向的匀速运动的物体乙,一定能 追上,追上前有最大距离的条件:两物 体速度相等,即v甲=v乙
②匀速运动的物体甲追赶同向匀加速运 动的物体乙,存在一个能否追上的问题。 判断方法是若当两者速度相同时甲的位 置在乙之前,即可追及;若在同一位置, 即此时恰追上;若在乙之后则不可能追 及,此时物体间距离最小。
最大。v汽 v自 ,v at ,t v 5 1( 0 s)
a 0.5
最远距离Svt1a2t25m
2
追上时,s自 s汽 ,v t 1 a t 2 , t 2v2520s
行驶的距离
2
(完整版)相遇问题与追及问题

相遇与追及问题一、学习目标1.理解相遇与追及的运动模型,掌握相遇与追及这两种情况下路程、时间、速度这三个基本量之间的关系.会利用这个关系来解决一些简单的行程问题.2.体会数形结合的数学思想方法.二、主要内容1.行程问题的基本数量关系式:路程二时间X速度;速度二路程F时间;时间二路程F速度.2.相遇问题的数量关系式:相遇路程二相遇时间X速度和;速度和二相遇路程F相遇时间;相遇时间二相遇路程F速度和.3.追及问题的数量关系式:追及距离二追及时间X速度差;速度差二追及距离F追及时间;追及时间二追及距离F速度差.4.能熟练运用路程、时间、速度这三个基本量的关系,结合图形分析,解决一些简单的行程问题.三、例题选讲例1两辆汽车同时分别从相距500千米的A,B两地出发,相向而行,速度分别为每小时40千米和每小时60千米.求几小时后两车相遇.例2甲车在乙车前200千米,同时出发,速度分别为每小时40千米与60千米.问多少小时后,乙车追上甲车.例3一辆公共汽车和一辆小轿车同时从相距598千米的两地相向而行.公共汽车每小时行40千米,小轿车每小时行52千米,问几小时后两车相距138千米?例4甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇.求东、西两地相距多少千米?例6一辆卡车和一辆摩托车同时从A、B两地相对开出,两车在途中距A地60千米处第一次相遇•然后,两车继续前进,卡车到达B地,摩托车到达A地后都立即返回,两车又在途中距B地30千米处第二次相遇.求A、B两地相距多少千米?例7甲、乙、丙三人进行100米赛跑•当甲到达终点时,乙离终点还有20米,丙离终点还有40米.如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多远?例8小明步行上学,每分行75米,小明离家12分后,爸爸骑单车去追,每分行375米.问爸爸出发多少分后能追上小明?例9解放军某部快艇追击敌舰,追到A岛时,敌舰已逃离该岛15分钟,已测出敌舰每分钟行驶1000米,解放军快艇每分钟行驶1360米,在距离敌舰600米处可开炮射击.问解放军快艇从A岛出发经过多少分钟就可以开炮射击敌舰?例10甲、乙两人在环形跑道上以各自的不变速度跑步,如果两人同时从同地相背而行乙跑4分钟后两人第一次相遇,已知甲跑一周需6分钟,那么乙跑一周需要多少分钟?例11两名运动员在湖周围环形道上练习长跑,甲每分跑250米,乙每分跑200米,两人同时从两地同向出发,经过45分甲追上乙,如果两人同时同地反向出发,经过多少分两人相遇?例12甲、乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果她们同时分别从直路两端点出发,跑了6分,那么,这段时间内,两人共迎面相遇了多少次?巩固练习:1、甲、乙两站相距980千米,两列火车由两站相对开出,快车每小时行50千米,慢车每小时行多少千米,两车经10小时能相遇?2、甲车每小时行60千米,1小时后,乙车紧紧追赶,速度为每小时80千米,几小时后乙车可追上甲车?3、早晨6时,有一列货车和一列客车同时从相距360千米的甲、乙两城相对开出,中途相遇,这期间,货车停车一次60分钟,客车停车两次各30分钟,已知货车每小时行42千米,客车每小时行78千米,问两车在几点钟相遇?4、东、西两镇相距240千米,一辆客车从上午8时从东镇开往西镇,一辆货车在上午9时从西镇开往东镇,到正午12点,两车恰好在两镇间的中点相遇,如果两车都从上午8时由两地相向开出,速度不变,到上午10时,两车还相距多少千米?5、骑单车从甲地到乙地,以每小时10千米的速度行进,下午1点到,以每小时15千米的速度行进,上午11点到.如果希望中午12点到,那么应以怎样的速度行进呢?6、某人由甲地去乙地,如果他从甲地先骑摩托车行了12小时,再换骑自行车行9小时,恰好到达乙地.如果他从甲地先骑自行车行了21小时,再换骑摩托车行8小时,也恰好到达乙地.问:全程骑摩托车需要多少小时才能到达乙地?7、兄妹两人同时由家上学,哥哥每分钟走90米,妹妹每分钟走60米,哥哥到校门口时,发现忘了带课本,立即沿原路返回去取,行至离校门口180米处与妹妹相遇,他们家离学校多少米?8、兄妹两人在周长300米的圆形水池边玩.从同一地点同时背向饶水池而行.哥哥每分钟走13米,妹妹每分钟走12米.他们第5次相遇时,哥哥共走了多长的路?课后作业:1.甲以每小时4千米的速度步行去学校,乙比甲晚4小时骑自行车从同一地点出发去追甲,乙每小时行12千米,乙多少小时可追上甲?2.小张从家到公园,原打算每分钟走50米,为了提早10分钟到,他把速度加快,每分钟走75米.小张家到公园有多少米?3.父亲和儿子都在某厂工作,他们从家里出发步行到工厂,父亲用40分钟,儿子用30分钟.如果父亲比儿子早5分钟离家,问儿子用多少分钟可赶上父亲?4.解放军某部小分队,以每小时6千米的速度到某地执行任务,途中休息30分后继续前进,在出发5.5小时后,通讯员骑摩托车以56千米的速度追赶他们。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相遇与追及
知识要点
相遇与追及是最常见的行程问题。
相遇问题的基本公式是:相遇路程÷速度和=相遇时间
追及问题的基本公式是:追及路程÷速度差=追及时间
典题解析
例1、南京到上海的水路长392千米,同时从两港各开出一艘轮船相对而行,从南京开出的船每小时行28千米,从上海开出的船每小时行21千米,经过几小时两船相遇?
1,甲乙两艘轮船分别从A、B两港同时出发相向而行,甲船每小时行驶18千米,乙船每小时行驶15千米,经过6小时两船在途中相遇。
两地间的水路长多少千米?
2,一辆汽车和一辆摩托车同时分别从相距900千米的甲、乙两地出发,汽车每小时行40千米,摩托车每小时行50千米。
8小时后两车相距多少千米?
3,甲乙两车分别从相距480千米的A、B两城同时出发,相向而行,已知甲车从A城到B 城需6小时,乙车从B城到A城需12小时。
两车出发后多少小时相遇?
例2、甲车在乙车前500千米,同时同向发车,甲车的速度为每小时40千米,乙车的速度为每小时60千米,多少小时后,乙车追上甲车?
4、两辆汽车相距120千米,甲车在乙车前面,甲车每小时行70千米,乙车每小时行90千
米,乙车追上甲车需要几个小时?
5、甲每小时行4千米,乙每小时行3千米。
甲动身时,乙已走出了9千米。
问经几小时甲能追上乙?例3、好马每天走120千米,劣马每天走75千米,劣马先走12天,好马几天能追上劣马?
6、我人民解放军追击一股逃窜的敌人,敌人在下午16点开始从甲地以每小时10千米的速
度逃跑,解放军在晚上22点接到命令,以每小时30千米的速度开始从乙地追击。
已知甲乙
两地相距60千米,问解放军几个小时可以追上敌人?
7、甲车每小时行50千米,走3小时后,乙车以每小时80千米的速度去追,几小时能追上?
例4、王欣和陆亮两人同时从相距2000米的两地相向而行,王欣每分钟行110米,陆亮每
分钟行90米。
如果一只狗与王欣同时同向而行,每分钟行500米,遇到陆亮后,立即回头
向王欣跑去;遇到王欣后再回头向陆亮跑去。
这样不断来回,直到王欣和陆亮相遇为止,狗
共行了多少米?
8,甲乙两队学生从相隔18千米的两地同时出发相向而行。
一个同学骑自行车以每小时15千米的速度在两队之间不停地往返联络。
甲队每小时行5千米,乙队每小时行4千米。
两队相遇时,骑自行车的同学共行多少千米?
9,甲、乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米。
一个人骑摩托车以每小时行80千米的速度在两车队中间往返联络,问两车队相遇时,摩托车行驶了多少千米?
例5、货车和客车同时从东西两地相向而行,货车每小时行48千米,客车每小时行42千米,两车在距中点18千米处相遇。
东西两地相距多少千米?
10,甲、乙两人同时分别从两地骑车相向而行,甲每小时行20千米,乙每小时行18千米。
两人相遇时距全程中点3千米,求全程长多少千米。
11,快车和慢车同时从南北两地相对开出,已知快车每小时行40千米,经过3小时后,快车已驶过中点25千米,这时慢车还相距7千米。
慢车每小时行多少千米?
例6、小李和小刘在周长为400米的环形跑道上跑步,小李每秒钟跑5米,小刘每秒钟跑3米,他们从同一地点同时出发,(1)如果反向而跑,他们几秒相遇?(2)如果是同向而跑,他们多少秒相遇?
12、甲,乙两人在一条长400米的环形跑道上跑步,甲的速度是360米/分,乙的速度是240米/分.(1)两人同时同地同向跑,问第一次相遇时,两人一共跑了几圈?(2)两人同时同地同向跑,问几秒后两人第一次相遇时?
13、环形跑道的周长是800米,甲、乙两名运动员同时顺时针自起点出发,甲的速度是每分钟400米,乙的速度是每分钟375米,多少分钟后两人第一次相遇?甲、乙两名运动员各跑了多少米?甲、乙两名运动员各跑了多少圈?
例7、两名运动员在湖周围环形道上练习长跑,甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙,如果两人同时同地反向出发,经过多少分钟相遇?
14、两人在环形跑道上跑步,两人从同一地点出发,小明每秒跑3米,小雅每秒跑4米,反向而行,45秒后两人相遇。
如果同向而行,几秒后两人再次相遇?
15、一条环形跑道长为400米,小明每分钟跑300米,小红每分钟跑250米,两人同时同地同向出发,,经过多长时间,小明第一次追上小红?。
