垂线练习题
过一点作垂线 作图操作题专项练习40题 有答案 (7+12页 )
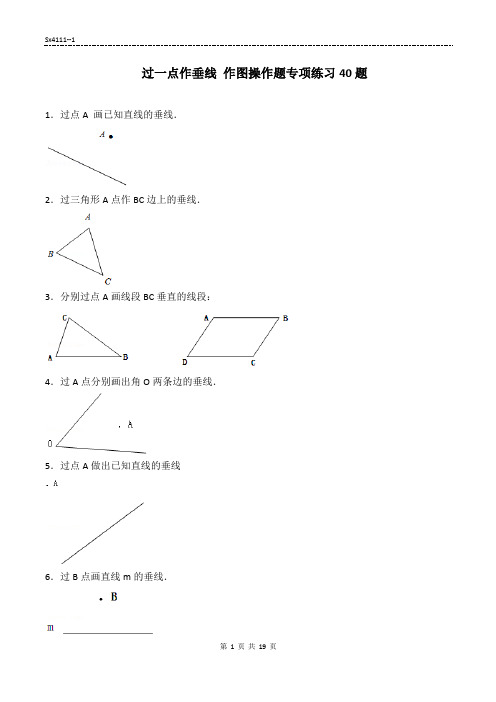
过一点作垂线作图操作题专项练习40题1.过点A 画已知直线的垂线.2.过三角形A点作BC边上的垂线.3.分别过点A画线段BC垂直的线段:4.过A点分别画出角O两条边的垂线.5.过点A做出已知直线的垂线6.过B点画直线m的垂线.7.过B点作直线n的垂线.8.过p点画出已知直线的垂线.9.新华村要修一条通村公路(从国道到新华村),以便于农副产品的运输.你认为怎样设计最近?画一画.10.A是BC上一点,过点A分别作BC和CD的垂线.11.过A点画已知直线的垂线.12.过直线上或直线外一点,画已知直线的垂线.13.如图,你知道点A到直线a、b的距离各是多少吗?怎样量?画一画.14.过点A画已知直线的垂线.15.如下图,要从幸福镇(用A点表示)修一条通往公路的小路,怎样修最近呢?画一画,并说明理由.16.分别过直线上的点A和直线外的点B画已知直线的垂线.17.过C点分别作OA和OB的垂线.18.过A点作这条直线的垂线.20.经过点P分别画OA的平行线和OB的垂线.21.过点A画BC的垂线.22.画一画.过点A画已知直线的垂线.23.画一画.(1)过A点画线的垂线.(2)过P点,向角两边画垂线.25.过B点分别画出两条直线的垂线.26.过B点分别作已知角的两条边的垂线.27.过点A画已知直线的垂线.28.过P点作四条边的垂线.29.过点A画BC的垂线.31.如图,过A点作直线m的垂线,过B点作直线m的垂线,这两条垂线32.如图,过点A分别作直线BC的垂线(MN)和平行线(EF).33.过三角形ABC的顶点B画它对边AC的垂线BD.34.过三角形内一点作这个三角形三边的垂线.35.过A点作两条直线的垂线.36.过点B分别向角的两条边画垂线.37.过直线上或直线外一点画已知直线的垂线.38.过A点画角的两边的垂线.39.过A、B两点分别画已知直线的垂线,再填空.两条垂线的关系:.40.过A点画出两条直线的垂线过一点作垂线作图操作题40题参考答案:1.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:2.【分析】把三角板的一条直角边与BC重合,沿BC移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向BC画直线即可.【解答】解:画图如下:3.【分析】把三角板的一条直角边与线段BC重合,沿线段BC移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向线段BC画垂直的线段即可.【解答】解:画图如下:4.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:5.【分析】用三角板的一条直角边与已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A点沿直角边向已知直线画直线即可.【解答】解:根据分析画图如下:6.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和B点重合,过B点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:7.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和B点重合,过B点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:8.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和P点重合,过P点沿三角板的直角边,向已知直线画直线即可.【解答】解:9.【分析】根据垂直线段的性质:从直线外一点向已知直线画垂直线段和斜线,垂线段最短.把公路看作一条直线,新华村看作一个点,由点向直线画垂直线段即可.【解答】解:根据分析画图如下:10.【分析】(1)用三角板的一条直角边与BC重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A点沿直角边向BC画直线即可.(2)用三角板的一条直角边与CD重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A点沿直角边向CD画直线即可.【解答】解:11.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:12.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和直线外一点重合,过直线外一点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:13.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画垂线段,然后用直尺测量即可.【解答】解:点A到直线a、b的距离分别是0.7厘米和1厘米.14.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:15.【分析】根据垂直线段的性质,从直线外一点到这条直线的连线中,垂直线段最短,过点A作公路所在的直线的垂直线段,沿这条垂直线段修小路最近.【解答】解:如图沿公路所在的直线的垂直线段AB修这条小路最近.理由:从直线外一点到这条直线的连线中,垂直线段最短.16.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点(或B点)重合,过A点(或B点)沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:17.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和C点重合,过C点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:18.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.【解答】解:画图如下,19.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.【解答】解:根据分析画图如下:20.【分析】(1)把三角板的一条直角边与已知直线OA重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和p点重合,过P点沿三角板的直角边画直线即可;(2)把三角板的一条直角边与已知直线OB重合,沿直线移动三角板,使三角板的另一条直角边和p点重合,过p点沿三角板的直角边,向已知直线画直线即可.【解答】解:由分析作图如下:21.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知线段BC画垂线即可.【解答】解:画图如下:22.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.【解答】解:根据分析画图如下:23.【分析】把三角板的一条直角边与已知直线重合,另一条直角边与直尺重合,然后把直角三角板向A(或P)点平移,再过A(或P)点作直线即可.【解答】解:(1)(2)24.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:25.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和B点重合,过B点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:26.【分析】把三角板的一条直角边与已知的角的边重合,沿角的边移动三角板,使三角板的另一条直角边和B点重合,过B点沿三角板的直角边,向角的边画直线即可.【解答】解:画图如下:27.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:28.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和P点重合,过P点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:29.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:30.【分析】把三角板的一条直角边与已知直线重合,沿三角板的另一直角边,向已知直线画线段即可.【解答】解:画图如下:31.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可;同理过B点也可以作出直线m的垂线;然后根据在同一平面内垂直于同一条直线的两条垂线互相平行;由此解答即可.【解答】解:由图可知:过A点作直线m的垂线,过B点作直线m的垂线,这两条垂线互相平行;故答案为:互相平行.32.【分析】(1)用三角板的一条直角边与已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可;(2)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可.【解答】解:作图如下:33.【分析】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和B点重合,过B点沿三角板的直角边画直线即可.【解答】解:画图如下:二.解答题(共7小题)34.【分析】用直角三角板的一条直角边与三角形的某一条边重合,沿重合的边平移三角板,使另一条直角边与已知点重合,过这个点沿直角边画直线即可.【解答】解:根据题干分析画图如下:35.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.【解答】解:画图如下:36.【分析】用三角板的一条直角边与已知直线中的其中一条重合,沿重合的直线平移三角板,使三角板的另一条直角边和B点重合,过B沿直角边向已知直线画直线即可;利用同样的方法即可画出另外一条已知直线的垂线.【解答】解:由分析作图如下:37.【分析】用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.【解答】解:作图如下:38.【分析】将三角板的一条直角边和角的一边重合,然后平移三角板,让其另一条直角边与A点重合,过A点和三角板的直角顶点作直线,就是这条边的垂线;同样的方法即可作出过A点的角的另一条边的垂线.【解答】解:如图所示,即为所要求作的垂线:.39.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A(或B)点重合,过A(或B)点沿三角板的直角边,向已知直线画直线即可.根据垂直与平行的性质可知,所画的两条直线都与已知直线垂直,则两条垂线的关系是平行.【解答】解:画图如下:两条垂线的关系:平行;故答案为:平行.40.【分析】(1)用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和A点重合,过A沿直角边向已知直线画直线即可.(2)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可.【解答】解:画图如下:。
画垂线的练习题

画垂线的练习题垂线,顾名思义指与另一条线段或者平面相交且与其垂直的线段。
画垂线的练习题在几何学中非常常见,有助于培养学生的观察能力和几何直觉。
通过不同形状和难度级别的练习题,学生可以加深对垂线性质的理解,并且提高画垂线的技巧。
本文将介绍几个画垂线的练习题,并给出详细解答。
练习题1:画垂线连接点与线段题目描述:给定一条线段 AB 和一点 C,画一条垂线通过点 C 并与线段 AB 相交于点 D。
解答:1. 首先,用直尺将线段 AB 画出来,记作 AB。
2. 确定点 C 的位置,并在该位置处画一个点,记作 C。
3. 将直尺的一端放置在点 C 上,另一端沿着线段 AB 平行移动。
4. 在直尺的移动过程中,观察是否存在一个位置使得直尺与线段AB 相交。
如果存在,将该位置标记为点 D。
5. 连接点 C 和点 D,得到一条垂线 CD。
练习题2:画垂线连接平面内两条线段题目描述:给定平面内两条线段 AB 和 CD,画一条垂线连接线段 AB 和线段CD,并确定垂线与两条线段的交点。
解答:1. 首先,用直尺将线段 AB 和线段 CD 画出来,记作 AB 和 CD。
2. 确定线段 AB 和线段 CD 之间的最短距离,即两条线段的最短连线,记作 line。
3. 在最短距离线段上选择一个点 E,与线段 CD 的一个端点连线,记作 AE。
4. 在点 E 的同侧,选择一个与线段 AB 平行的线段 EF。
5. 在线段 CD 上选择一个点 G,使得线段 EG 的长度等于线段 EF 的长度。
6. 连接点 E 和点 G,得到一条垂线 EG。
垂线 EG 和线段 AB、CD 分别相交于点 F 和点 H。
练习题3:画垂线连接两条平面内的直线题目描述:给定平面内两条不相交的直线 l1 和 l2,画一条垂线连接直线 l1 和直线 l2,并确定垂线与两直线的交点。
解答:1. 首先,用直尺将直线 l1 和直线 l2 画出来。
2. 选取直线 l1 上一点 A 和直线 l2 上一点 B。
四年级下册垂线性质练习题

四年级下册垂线性质练习题垂线性质练习题是四年级下册数学学习的重要内容之一,通过掌握垂线的定义和性质,不仅可以加深对几何概念的理解,还能够培养学生的逻辑思维和几何推理能力。
下面我将为您提供一些垂线性质的练习题,请您具体参考。
练习题一:1. 在平面上,如何判断一条线段与给定的直线相垂直?2. 请画出两条分别与直线相垂直和平行的线段。
3. 若两条线段相垂直,它们之间的夹角是多少?请用图形表示。
4. 若两条线段相垂直,它们之间的夹角是否会受到线段长度的影响?请进行说明。
5. 给定一个直线和一个点,在不使用量角器的情况下,如何在该点上作一条与直线垂直的线段?练习题二:1. 在平面上给出一条直线AB和一点C,如何画出一条通过点C且垂直于直线AB的线段?2. 若一条直线与另一条直线相垂直,那么它们之间的夹角是多少?3. 若一条直线与一条平面相垂直,那么它在该平面上的投影线段是什么?4. 已知一条直线和一点,如何作出通过该点且垂直于给定直线的线段?5. 如何判断两条直线是否垂直?练习题三:1. 在长方形ABCD中,AE是BC的垂线,若BE的长度为8cm,BC的长度为12cm,求AE的长度。
2. 若矩形的长和宽分别为8cm和4cm,求其对角线的长度。
3. 若直角三角形的两条直角边分别为3cm和4cm,求斜边的长度。
4. 若直角梯形的上底和下底分别为6cm和10cm,高为8cm,求斜边的长度。
5. 如何判断一个四边形是否为矩形?以上为四年级下册垂线性质的一些练习题,通过解答这些题目,可以提高学生对垂线性质的理解和运用能力。
希望对您有所帮助!。
小学数学垂直线练习题

小学数学垂直线练习题练习题一:1. 请用直尺和铅笔,在纸上画出一条垂直线段。
2. 画图中的线段是否垂直?为什么?3. 斜线和垂直线有什么区别?4. 请给出一个垂直线段的例子。
5. 请用文字和符号表示垂直线段的特征。
练习题二:1. 在纸上画出一条垂直线段,并标记为AB。
2. 设C为AB线段上一点,画出AC线段。
3. 请说明AC线段与AB线段的关系。
4. 设D为AC线段上一点,画出BD线段。
5. 请说明BD线段与AC线段和AB线段的关系。
6. 如果BD线段长度为5 cm,AC线段长度为3 cm,求AB线段的长度。
练习题三:1. 如图所示,AC和BD是相交的线段。
如果AC线段与BD线段垂直,那么AB线段和CD线段是否垂直?2. 如果AB线段和CD线段垂直,那么AC线段和BD线段是否垂直?3. 给出垂直线段的定义。
4. 判断以下线段是否垂直,并给出理由:EF,GH,IJ。
5. 请用文字和符号表示两条垂直线段。
练习题四:1. 如图所示,矩形ABCD中的AC和BD是相交于O点的对角线。
判断AC和BD线段是否垂直,并给出理由。
2. 如果AC和BD线段垂直,那么矩形ABCD的两条对边是否垂直?3. 如果矩形ABCD的两条对边垂直,那么AC和BD线段是否垂直?4. 给出矩形的定义。
5. 请用文字和符号表示矩形的性质。
练习题五:1. 请用直尺和铅笔,在纸上画出一个等腰直角三角形。
2. 画图中的三条线段分别是什么关系?3. 请证明等腰直角三角形的两条直角边是垂直的。
4. 设等腰直角三角形的直角边长度为a,斜边长度为b,求斜边的表达式。
5. 请用文字和符号表示等腰直角三角形的性质。
以上是一份关于小学数学垂直线的练习题,希望对你有帮助!。
(完整版)垂线练习题

二、垂线一、填空题1.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线______,其中一条直线叫做另一条直线的______线,它们的交点叫做______.2.垂线的性质性质1:平面内,过一点____________与已知直线垂直.性质2:连接直线外一点与直线上各点的_________中,_________最短.3.直线外一点到这条直线的__________________叫做点到直线的距离.4.如图,直线AB,CD互相垂直,记作______;直线AB,CD互相垂直,垂足为O点,记作____________;线段PO的长度是点_________到直线_________的距离;点M到直线AB的距离是_______________.二、按要求画图5.如图,过A点作CD⊥MN,过A点作PQ⊥EF于B.图a 图b 图c6.如图,过A点作BC边所在直线的垂线EF,垂足是D,并量出A点到BC边的距离.图a 图b 图c7.如图,已知∠AOB及点P,分别画出点P到射线OA、OB的垂线段PM及PN.图a 图b 图c8.如图,小明从A村到B村去取鱼虫,将鱼虫放到河里,请作出小明经过的最短路线.综合、运用、诊断一、判断下列语句是否正确(正确的画“√”,错误的画“×”)9.两条直线相交,若有一组邻补角相等,则这两条直线互相垂直. ( )10.若两条直线相交所构成的四个角相等,则这两条直线互相垂直. ( )11.一条直线的垂线只能画一条. ( )12.平面内,过线段AB 外一点有且只有一条直线与AB 垂直. ( )13.连接直线l 外一点到直线l 上各点的6个有线段中,垂线段最短. ( )14.点到直线的距离,是过这点画这条直线的垂线,这点与垂足的距离. ( )15.直线外一点到这条直线的垂线段,叫做点到直线的距离. ( )16.在三角形ABC 中,若∠B =90°,则AC >AB . ( )二、选择题17.如图,若AO ⊥CO ,BO ⊥DO ,且∠BOC =α,则∠AOD 等于( ).(A)180°-2α (B)180°-α (C)α2190+︒ (D)2α-90° 18.如图,点P 为直线m 外一点,点P 到直线m 上的三点A 、B 、C 的距离分别为PA =4cm ,PB =6cm ,PC =3cm ,则点P 到直线m 的距离为( ).(A)3cm (B)小于3cm (C)不大于3cm (D)以上结论都不对19.如图,BC ⊥AC ,CD ⊥AB ,AB =m ,CD =n ,则AC 的长的取值范围是( ).(A)AC <m (B)AC >n (C)n ≤AC ≤m (D)n <AC <m20.若直线a 与直线b 相交于点A ,则直线b 上到直线a 距离等于2cm 的点的个数是( ).(A)0 (B)1 (C)2 (D)321.如图,AC ⊥BC 于点C ,CD ⊥AB 于点D ,DE ⊥BC 于点E ,能表示点到直线(或线段)的距离的线段有( ).(A)3条 (B)4条 (C)7条 (D)8条(第17题) (第18题) (第19题) (第21题)三、解答题22.已知:OA ⊥OC ,∠AOB ∶∠AOC =2∶3.求∠BOC 的度数.23.已知:如图,三条直线AB ,CD ,EF 相交于O ,且CD ⊥EF ,∠AOE =70°,若OG平分∠BOF .求∠DOG .。
垂线精选练习题

垂线精选题39道一.选择题(共17小题)1.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为()A.1个B.2个C.3个D.4个8.过点B画线段AC所在直线的垂线段,其中正确的是()A.B.C.D.4.已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是()A.B.C.D.2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为()A.35°B.45°C.55°D.65°3.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为()A.35°B.45°C.55°D.65°5.如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=()A.36°B.44°C.50°D.54°6.在同一平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为()A.20°B.55°C.20°或125°D.20°或55°7.如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=142°,∠BOD:∠BOF=1:3,则∠AOF的度数为()A.138°B.128°C.117°D.102°9.如图,直线AD、BE相交于点O,CO⊥AD于点O,OF平分∠BOC,若∠AOB=32°,A.29°B.30°C.31°D.32°10.如图,直线AB、CD相交于点O,EO⊥CD.下列说法错误的是()A.∠AOD=∠BOC B.∠AOE+∠BOD=90°C.∠AOC=∠AOE D.∠AOD+∠BOD=180°11.如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC =()A.150°B.140°C.130°D.120°12.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()A.相等B.互余C.互补D.互为对顶角13.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BOD=70°,A.35°B.45°C.55°D.65°14.如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为()A.36°B.44°C.46°D.54°15.已知:OA⊥OC,∠AOB:∠AOC=2:3,则∠BOC的度数为()A.30°B.60°C.150°D.30°或150°16.如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是()A.①②B.①③C.②③D.①②③17.如图,若AB,CD相交于点O,过点O作OE⊥CD,则下列结论不正确的是()A.∠1与∠2互为余角B.∠3与∠2互为余角C.∠3与∠AOD互为补角D.∠EOD与∠BOC是对顶角二.填空题(共14小题)18.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为.19.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是.20.如图,直线AB、CD交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD=度.21.已知:OA⊥OC,∠AOB:∠AOC=2:3.则∠BOC的度数为.22.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为.23.如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有(只填写正确结论的序号).24.如图,直线AB,CD相交于O,OE⊥AB,O为垂足,∠COE=34°,则∠BOD=度.25.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于.26.如图,已知BO⊥AD于点O,∠COE=90°,且∠BOC=4∠AOC,则∠BOE的度数为度.27.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC =°.28.如图,已知OA⊥OC,OB⊥OD,∠3=24°,则∠1=.29.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=3:2,则∠AOD=.30.如图,若OA⊥OB,OC⊥OD,且∠AOC:∠BOD=1:2,则∠BOD=°.31.如图,直线AB、CD相交于点O,OF⊥CD,∠DOE:∠BOD=3:2,若∠AOC=28°,则∠EOF的度数为.三.解答题(共8小题)32.如图,∠AGF=∠ABC,∠1+∠2=180°.(1)试判断BF与DE的位置关系,并说明理由;(2)若BF⊥AC,∠2=150°,求∠AFG的度数.33.如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF 平分∠DOB,求∠EOF的度数.34.如图,AB与CD相交于O,OE平分∠AOC,OF⊥AB于O,OG⊥OE于O,若∠BOD =40°,求∠AOE和∠FOG的度数.35.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数.36.如图,直线AB、CD相交于点O,OM⊥AB.(1)若∠1=∠2,证明:ON⊥CD;(2)若∠1=13∠BOC,求∠BOD的度数.37.如图所示,直线AB、CD相交于点O,OM⊥AB.(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;(2)若∠1=14∠BOC,求∠MOD的度数.38.如图,直线AB、CD相交于点O,OE⊥CD,∠AOC=50°.求∠BOE的度数.39.如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11、(1)求∠COE的度数;(2)若OF⊥OE,求∠COF的度数.。
垂线的专项练习30题有答案ok

垂线专项练习30题(有答案)1.如图,①过点Q作QD⊥AB,垂足为D,②过点P作PE⊥AB,垂足为E,③过点Q作QF⊥AC,垂足为F,④连P、Q两点,⑤P、Q两点间的距离是线段_________的长度,⑥点Q到直线AB的距离是线段_________的长度,⑦点Q到直线AC的距离是线段_________的长度,⑧点P到直线AB的距离是线段_________的长度.2.如图,点P是∠AOB的边OB上的一点过点P画OB的垂线,交OA于点C;(1)过点P画OA的垂线,垂足为H;(2)线段PH的长度是点P到_________的距离,_________是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是_________(用“<”号连接)3.(1)画出表示点B到直线CD的距离的线段,结论:_________(2)A、C两点之间的距离为线段_________的长;(3)画出表示两条平行线AD、BC之间的距离的线段,结论:_________.4.如图,DE∥BC,AF⊥DE于G,DH⊥BC于H,且AG=4cm,DH=4cm,试求点A到BC的距离.5.如图,过点A作BC的垂线,并指出那条线的长度是表示点A到BC的距离?6.如图,∠C=90°,AB=5,AC=4,BC=3,则点A到直线BC的距离为_________,点B到直线AC的距离为_________,A、B间的距离为_________,AC+BC>AB,其依据是_________,AB>AC,其依据是_________.7.如图所示,村庄A、村庄B分别要从河流L引水入庄,各需修筑一水渠,请你画出修筑水渠的路线图.8.如图,要把水渠中的水引到C点,在渠岸AB的什么地方开沟,才能使沟最短?画出图形,并说明理由.9.如图,王林和李明同学骑自行车同时从各自的家中出发去学校.如果他们的骑车速度相同,那么谁先到达学校?为什么?10.如图,是一条河,C是河边AB外一点:(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)11.如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.(1)从火车站到码头怎样走最近,画图并说明理由;(2)从码头到铁路怎样走最近,画图并说明理由;(3)从火车站到河流怎样走最近,画图并说明理由.12.如图,计划在河边建一水厂,可过C点引CD⊥AB于D,在D点建水厂,可使水厂到村庄C的路程最短,这种设计的依据是_________.13.如图,点P处有一个工厂,现拟修一条通往大路口a的公路,应如何修才能使所修之路最短,试说明理由.14.如图,直线AD和BE相交于点O,∠COD=90°,∠COE=60°,求∠AOB的度数.15.如图,OF平分∠AOC,OE⊥OF,AB与CD相交于O,∠BOD=130°,求∠EOB的度数.16.如图所示,已知∠AOB=∠COD=90°,(1)若∠BOC=45°,求∠AOC与∠BOD的度数;(2)若∠BOC=25°,求∠AOC与∠BOD的度数;(3)由(1)、(2)你能得出什么结论?说说其中的道理.17.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM的度数.18.如图,直线AB与CD相交于点O,OP是∠AOD的平分线,OF⊥CD,如果∠BOD=30°.求:(1)∠AOF的度数;(2)∠POF的度数.19.如图所示,OA丄OB,OC丄OD,OE为∠BOD的平分线,∠BOE=15°,求∠BOD和∠AOC的度数.20.已知:如图,直线AB、CD、EF相交于点0,∠1=20°,∠BOC=90°.求∠2的度数.21.说出日常生活现象中的数学原理:日常生活现象相应数学原理有人和你打招呼,你笔直向他走过去两点之间直线段最短要用两个钉子把毛巾架安装在墙上桥建造的方向通常是垂直于河两岸人去河边打水总是垂直于河边方向走22.如图所示,修一条路将A,B两村庄与公路MN连起来,怎样修才能使所修的公路最短?画出线路图,并说明理由.23.如图,点P是∠AOB的边OB上的一点.(1)过点P画OB的垂线,交OA于点C,(2)过点P画OA的垂线,垂足为H,(3)线段PH的长度是点P到_________的距离,线段_________是点C到直线OB的距离.(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是_________(用“<”号连接)24.已知:如图所示,∠1=∠2,∠3=∠4,GF⊥AB于G点,那么CD与AB是否互相垂直?试判断并说明理由.25.如图,已知OA⊥OB,∠1与∠2互补,求证:OC⊥OD.26.你能用折纸的方法过一点作已知直线的垂线吗?27.先拿一张长方形的白纸,按如图所示的方式将∠A、∠E折叠,使A′B与BE′重合,则BC与BD有什么关系?说明理由.28.分别过点P作线段MN的垂线.29.如图,∠AOE与∠BOF互余,那么AO与BO是否垂直?试说明理由.30.对于平面上垂直的两条直线a和b,称(a,b)为一个“垂直对”,而a和b都是属于这个“垂直对”的直线.那么当平面上有二十条直线时最多可组成多少个“垂直对”?参考答案:1.①②③④作图如图所示:⑤根据两点之间距离即可得出P、Q两点间的距离是线段PQ的长度,⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度,⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度,⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度,故答案为PQ,QD,QF,PE.2.(1)如图:(2)线段PH的长度是点P到直线OA的距离,线段CP的长度是点C到直线OB的距离,根据垂线段最短可得:PH<PC<OC,故答案为:OA,线段CP,PH<PC<OC3.(1)过B点作DC的垂线,交CD的延长线于E点,如,则线段BE的长为点B到直线CD的距离;所以过直线外一点作直线的垂线,垂线段长就是这个点到直线的距离;(2)A、C两点之间的距离为线段AC的长;(3)过C点作AD的垂线,垂足为F点,如图,则线段CF的长即为两条平行线AD、BC之间的距离.故答案为过直线外一点作直线的垂线,垂线段的长就是这个点到直线的距离;AC;两条平行线之间的距离就是一条直线上任意一点到另一条直线的距离.4.∵AF⊥DE,DE∥BC,∴AF⊥BC,∵DE∥BC,∴四边形DHFG是平行四边形,∴DH=GF=4cm,∴AF=AG+GF=4cm+4cm=8cm,即点A到BC的距离是8cm.5.过点A作BC的垂线,交CB的延长线于E,根据点到直线的距离的定义:从直线外一点到这条直线的垂线段长度,叫点到直线的距离.可得AE的长度即为点A到BC的距离.答:AE的长度即为点A到BC的距离.6.∵∠C=90°,AB=5,AC=4,BC=3,∴点A到直线BC的距离为4,点B到直线AC的距离为3,A、B间的距离为5,AC+BC>AB,其依据是三角形任意两边之和大于第三边长度,AB>AC,其依据是直角三角形中斜边长度大于直角边长度.7.如图所示,AE、BF就是村庄A、村庄B修筑水渠的路线图.8.如图,过C作CD⊥AB,垂足为D,在D处开沟,则沟最短.因为直线外一点与直线上各点连线的所有线段中,垂线段最短.9.根据垂线段定理,可知王林先到达学校.因为从他家到学校是垂线段,路程最短.10.如图:(1)过点C画一平行线平行于AB.(2)过点C作CD垂直于AB交AB于点D.然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.11.如图所示(1)沿AB走,两点之间线段最短;(2)沿BD走,垂线段最短;(3)沿AC走,垂线段最短.12.∵CD⊥AB,∴线段CD的长度就是点C到直线AB的最短距离.故答案为:垂线段最短.13.如图,过点P作PD⊥a于D,则由点P沿着PD修路,能使所修之路最短.14.∵已知∠COD=90°,∠COE=60°,∴∠DOE=90°﹣60°=30°,又∵∠AOB与∠DOE是对顶角,∴∠AOB=∠DOE=30°.15.∵∠AOC=∠BOD,∠BOD=130°,∴∠AOC=130°.∵OF平分∠AOC,∴∠AOF=∠FOC=65°.∵OE⊥OF,∴∠EOF=90°.∴∠BOE=180°﹣∠AOF﹣∠EOF=180°﹣65°﹣90°=25°16.(1)∵∠AOB=∠COD=90°,且∠BOC=45°,∴∠AOC=∠AOB﹣∠BOC=45°,∠BOD=∠COD﹣∠BOC=45°;(2)∵∠AOB=∠COD=90°,且∠BOC=25°,∴∠AOC=∠AOB﹣∠BOC=65°,∠BOD=∠COD﹣∠BOC=65°;(3)∠AOC=∠BOD,等角的余角相等.17.∵OE平分∠BON,∴∠BON=2∠EON=40°,∴∠COM=∠BON=40°,∴∠AOM=90°﹣∠COM=90°﹣40°=50°.18.(1)∵∠AOC=∠BOD=30°,OF⊥CD,∴∠AOF=90°﹣30°=60°;(2)∵OP是∠AOD的平分线,∴∠AOP=∠AOP=(180°﹣∠BOD)=(180°﹣30°)=75°,∴∠POF=∠AOP﹣∠AOF=75°﹣60°=15°19.∵OE为∠BOD的平分线,∴∠BOE=∠BOC,即∠BOD=2∠BOE=2×15°=30°;∵OA丄OB,OC丄OD,∴∠AOB=∠COD=90°,∴∠AOC=360°﹣90°﹣90°﹣30°=150°.20.∵∠1=20°,∠BOC=90°,∴∠BOE=∠BOC﹣∠1=90°﹣20°=70°,∴∠2=∠BOE=70°.21.这几种实际问题用数学原理解释分别是:两点确定一条直线;夹在两平行线间的线段中,垂线段最短;连接直线外一点与直线上各点的所有线段中,垂线段最短.22.连接AB,作BC⊥MN,C是垂足,线段AB和BC 就是符合题意的线路图.因为从A到B,线段AB最短,从B到MN,垂线段BC最短,所以AB+BC最短.23.(1)如图(2)如图,(3)直线0A、PC的长.(4)PH<PC<OC.24.相互垂直.理由:∵GF⊥AB,∴∠2+∠4=90°,而∠1=∠2,∠3=∠4,∴∠1+∠3=90°,∴∠1+∠2=180°,∵OA⊥OB,∴∠AOB=90°,∴∠COD=360°﹣(∠1+∠2)﹣∠AOB=360°﹣180°﹣90°=90°,∴OC⊥OD26.先沿已知直线折一下,再在已知点处对折即可.27.垂直;根据题意可得∠ABC=∠A′BC,∠FBE=∠FBE′,∵∠ABC+∠A′BC+∠E′BF+∠FBE=180°,∴∠A′BC+∠E′BF=90°,∴BC⊥FB28.①延长NM,过点P作NM所在直线的垂线.②延长NM,过点P作NM所在直线的垂线.③过点P作NM所在直线的垂线.④延长NM,过点P作NM所在直线的垂线.29.AO与BO垂直.理由如下:∵∠AOE与∠BOF互余,∴∠AOE+∠BOF=90°,又∵∠AOE+∠AOB+∠BOF=180°,∴∠AOB=90°,∴AO⊥BO,即AO与BO垂直30.当二十条直线有10条互相平行;另10条不仅互相平行而且与前10条垂直时垂直对最多.答案是100对.。
《垂线》练习题(含答案)

《垂线》练习题(含答案)5.1.2垂线1.(2014·贺州)如图,OA⊥OB,若∠1=55°,则∠2的度数是()A.35°B.40°C.45°D.60°2.如图,直线AB与直线CD相交于点O,已知OE⊥AB,∠BOD=45°,则∠COE的度数是()A.125°B.135°C.145°D.155°3.过线段外⼀点,画这条线段的垂线,垂⾜在()A.这条线段上B.这条线段的端点C.这条线段的延长线上D.以上都有可能4.如图所⽰,AD⊥B D,B C⊥C D,A B=a,B C=b,则BD的范围是__________,理由是____________________.5.如图,⽥径运动会上,七年级⼆班的⼩亮同学从C点起跳,假若落地点是 D.当AB与CD__________时,他跳得最远.6.(2014·厦门)已知直线AB,CB,l在同⼀平⾯内,若AB⊥l,垂⾜为B,CB⊥l,垂⾜也为B,则符合题意的图形可以是()CD7.如图,当∠1与∠2满⾜条件__________时,OA⊥OB.8.(2014·河南改编)如图,直线AB,相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为__________.9.如图所⽰,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.(1)判断OF与OD的位置关系;(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.10.如图所⽰,⼀辆汽车在直线形的公路AB上由A向B⾏驶,C,D分别是位于公路AB两侧的村庄.(1)该汽车⾏驶到公路AB上的某⼀位置C′时距离村庄C最近,⾏驶到D′位置时,距离村庄D最近,请在公路AB上作出C′,D′的位置(保留作图痕迹);(2)当汽车从A出发向B⾏驶时,在哪⼀段路上距离村庄C越来越远,⽽离村庄D越来越近?(只叙述结论,不必说明理由)参考答案1.A2.B3.D4.b<BD<a垂线段最短5.垂直6.C7.∠1+∠2=90°8.55°9.(1)因为OF平分∠AOE,所以∠AOF=∠EOF=12∠AOE.1⼜因为∠DOE=∠BOD=∠BOE,211所以∠DOE+∠EOF=(∠BOE+∠AOE)=×180°=90°,22即∠FOD=90°.所以OF⊥OD.(2)设∠AOC=x°,因为∠AOC∶∠AOD=1∶5,所以∠AOD=5x°.因为∠AOC+∠AOD=180°,所以x+5x=180,x=30.所以∠DOE=∠BOD=∠AOC=30°.⼜因为∠FOD=90°,所以∠EOF=90°-30°=60°.10.(1)图略.过点C作AB的垂线,垂⾜为C′,过点D作AB的垂线,垂⾜为D′.(2)在C′D′上距离村庄C越来越远,⽽离村庄D越来越近.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂练习 练习一:达标测试
1、下列说法是否正确:
两条直线相交,有一条角是直角,则两条直线互相垂直。
两条直线相交,有一对对顶角互补,则两条直线互相垂直。
两条直线相交,四个角都相等,则两条直线互相垂直。
两条直线相交,有一组邻补角相等,则两条直线互相垂直。
2、如图一所示,当∠1与∠2满足 时,能使OA ⊥OB 3、如图二所示,从河中向稻田A 处引水,为使水渠最短,可过A 做AB ⊥CD 于点B ,沿线段AB 修渠最短,其根据是:( ) 4、过一条线段外一点画这条线段的垂线,垂足在( ) A 、这条线段 B 、这条线段的端点上 C 、这条线段的延长线上 D 、以上都有可能
B
C
D
O 图一
5、如图三所示,已知ON⊥L,OM⊥L,所以OM与ON重合,其理由是( )
A.过两点有且只有一条直线B、过一点只能作一条直线C、在同一平面内,经过一点有且只有一条直线与已知直线垂直D、垂线段最短
6、点直线的距离是指:( )
A、直线外一点到该直线的垂线的长度
B、直线外一点到该直线的垂线段的长度
C、直线外一点与直线外一点间的距离
D、从直线外一点向该直线所画的垂线段
7、
A处,要到路的右侧,怎样走最近?
B处,怎样走最近,为什么?
图三
O
L
A
B
路
图四
8、如图五所示,AB ⊥CD ,垂足为
AOE=35°
求∠BOE 、∠COE
的度数。
练习二:开拓思维
9、①请画出∠AOB 的角平分线OC ,
图五
O B
②在OC 上任取一点P ,过点P 画OA 、OB 的垂线,垂足分别为点E 、F
③量出点P 到OA 、OB 的距离,你有什么发现? ④把你发现的结论用一句话描述出来。
10、如图六所示,一辆汽车在直线型的公路AB 上有A 向B 行驶,MN 分别是位于公路AB 两侧的村庄
①设汽车行驶到公路AB 上点B 的位置是,距离村庄M 最近,行驶到Q 位置时,距离村庄N 最近,请在图中的公路上分别画出点P 、Q 的位置
②当汽车从A 出发向B 行驶时,在公路AB 的哪一段路上,距离M 、N 两村庄距离都越来越近?在哪一段路上,距离村庄N 越来越近,而离村庄M 却越来越远?(用文字表述你的结论)
B
A
M
N
图六。
