【2013大兴一模】北京市大兴区2013届高三一模文科数学Word版含答案
【推荐】北京2013届高三文科试题分类汇编(含9区一模及上学期期末试题)专题12:算法
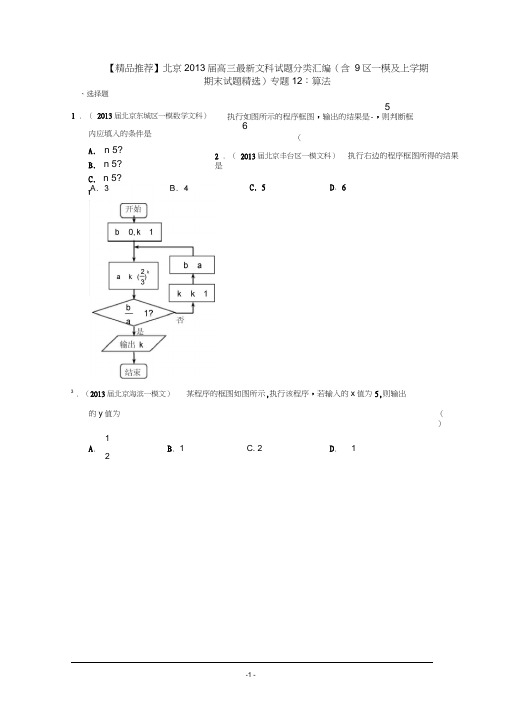
【精品推荐】北京2013届高三最新文科试题分类汇编(含 9区一模及上学期期末试题精选)专题12:算法、选择题5执行如图所示的程序框图,输出的结果是-,则判断框6(2 . ( 2013届北京丰台区一模文科) 执行右边的程序框图所得的结果是3. (2013届北京海滨一模文)某程序的框图如图所示,执行该程序,若输入的x 值为5,则输出的y 值为 ()1A .B . 1 C. 2 D . 121 . ( 2013届北京东城区一模数学文科)内应填入的条件是A.n 5? B. n 5? C. n 5? D.n 5?C. 5D . 64 . (2013届北京大兴区一模文科)执行如图所示的程序框图5 .(2013届北京西城区一模文科)执行如图所示的程序框图A. -42B. -21C. 11D. 43n A.- 6 B.nC.-3D..若n 4,则输出s的值是.若输出y .3,则输入角F y=审口1 f/输缶〃6 . (2013届房山区一模文科数学)执行如图所示的程序框图.若输出S 15,可以填入A. n4B. n8C. n16 则框图中①处()D. n 167 .(北京市石景山区2013届高三上学期期末考试数学文试题)3, 则可输入的实数X值的个数为A. 1B. 2C. 3执行右面的框图, 若输出结果为()D. 48 .(北京市朝阳区2013届高三上学期期末考试数学文试题)执行如图所示的程序框图. 若输入x 3,则输出k的值是x=x+5f t*箱束QA. 3B. 4 c. 5 D. 69 .(北京市东城区2013届高三上学期期末考试数学文科试题)执行如图所示的程序框图,()输出10.11 .12. 的k的值为A. 4(北京市丰台区的S值为. A. 3(北京市海淀区序,若输入的/馆出七/B. 5C. 6 2013届高三上学期期末考试数学文试题)B. 6C. 7 2013届高三上学期期末考试数学文试题)p为24,则输出的n,S的值分别为A. n 4,S 30 C. n 5,S 30D. 7执行如图所示的程序框图,()则输出D. 10某程序的框图如图所示,()执行该程■开始n 1, S 0入PS =•n___S是' 1 r1 /输岀n,S /t ___结束B. n 4,SD. n 5,S4545(北京市通州区2013届高三上学期期末考试数学文试题)执行如图所示的程序框图, 输出的13.(北京市西城区2013S=S^C. 251 1D. 250 1届高三上学期期末考试数学文科试题)执行如图所示的程序框图, 则输/辑出占/. a•结東.A. 2、填空题B. 6C. 15D. 3114 . (2013届北京市延庆县一模数学文)执行如图的程序框图,如果输入p 6 ,则输出的15. (2013届北京门头沟区一模文科数学)如右图所示的程序框图,执行该程序后输出的结果是开始i 1,s 2| H = 74■厂16.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)(7W5=97=1^=1 (文)试题)某程序框图如图所示,该程序运行后输出的n的值是S=S+T17.(北京市昌平区2013届高三上学期期末考试数学文试题)已知某算程图如图所示,则程序运行结束时输出的结果为___________ .TET 工—■]即=7¥+ H/输出邸/法的流18.(北京市房山区2013届高三上学期期末考试数学文科试题(解析版)运行相应的程序,则输出n的值为•)阅读右边的程序框图,【精品推荐】北京 2013届高三最新文科试题分类汇编(含9区一模及上学期期末试题精选)专题12:算法参考答案选择题 A A A C D ; B 【答案】Cx ? 1x2解:本程序为分段函数 y' ,当x 2时,由x 2 1 3得,x 2 4,所以log 2x, x 2x 2。
北京市2013届高三最新文科数学模拟试题分类汇编3:三角函数

北京2013届高三最新文科模拟试题分类汇编3:三角函数一、选择题错误!未指定书签。
.(2013届北京大兴区一模文科)函数()f x =( )A .在ππ(,)22-上递增 B .在π(,0]2-上递增,在π(0,)2上递减 C .在ππ(,)22-上递减D .在π(,0]2-上递减,在π(0,)2上递增【答案】D错误!未指定书签。
.(2013届北京门头沟区一模文科数学)为得到函数sin (π-2)y x =的图象,可以将函数πsin (2)3y x =-的图象 ( )A .向左平移3π个单位 B .向左平移6π个单位 C .向右平移3π个单位D .向右平移6π个单位【答案】B错误!未指定书签。
.(2013届北京门头沟区一模文科数学)若△ABC 的内角A . B .C 所对的边a 、b 、c 满足422=-+c b a )(,且C =60°,则ab 的值为 ( )A .348-B .1C .34D .32 【答案】C错误!未指定书签。
.(2013北京丰台二模数学文科试题及答案)下列四个函数中,最小正周期为π,且图象关于直线12x π=对称的是 ( )A .sin()23x y π=+B .sin()23x y π=-C .sin(2)3y x π=-D .sin(2)3y x π=+【答案】 D .错误!未指定书签。
.(2013北京朝阳二模数学文科试题)函数()sin()4f x x π=-(x ∈R )的图象的一条对称轴方程是 ( )A .0x =B .π4x =- C .π4x =D .π2x =【答案】B .错误!未指定书签。
.(北京市石景山区2013届高三一模数学文试题)函数y=2sin(3x π-)(0≤x≤π)的最大值与最小值之和为( )A .0B .2C .-1D .-l【答案】B 二、填空题错误!未指定书签。
.(2013北京房山二模数学文科试题及答案)已知角A 为三角形的一个内角,且3cos 5A =,则tan A =____,tan()4A π+=____.【答案】4,73- 错误!未指定书签。
北京市2013届高三最新文科数学模拟试题分类汇编3:三角函数

北京2013届高三最新文科模拟试题分类汇编3:三角函数一、选择题1 .(2013届北京大兴区一模文科)函数()f x =( )A .在ππ(,)22-上递增 B .在π(,0]2-上递增,在π(0,)2上递减 C .在ππ(,)22-上递减D .在π(,0]2-上递减,在π(0,)2上递增【答案】D2 .(2013届北京门头沟区一模文科数学)为得到函数sin (π-2)y x =的图象,可以将函数πsin (2)3y x =-的图象( )A .向左平移3π个单位B .向左平移6π个单位 C .向右平移3π个单位D .向右平移6π个单位【答案】B3 .(2013届北京门头沟区一模文科数学)若△ABC 的内角A . B .C 所对的边a 、b 、c 满足422=-+c b a )(,且C =60°,则ab 的值为( )A .348-B .1C .34D .32 【答案】C4 .(2013北京丰台二模数学文科试题及答案)下列四个函数中,最小正周期为π,且图象关于直线12x π=对称的是 ( )A .sin()23x y π=+B .sin()23x y π=-C .sin(2)3y x π=-D .sin(2)3y x π=+【答案】 D .5 .(2013北京朝阳二模数学文科试题)函数()sin()4f x x π=-(x ∈R )的图象的一条对称轴方程是 ( )A .0x =B .π4x =- C .π4x =D .π2x =【答案】B .6 .(北京市石景山区2013届高三一模数学文试题)函数y= 2sin(3x π-)(0≤x≤π)的最大值与最小值之和为 ( )A .0B .2C .-1D .-l【答案】B 二、填空题7 .(2013北京房山二模数学文科试题及答案)已知角A 为三角形的一个内角,且3cos 5A =,则tan A =____,tan()4A π+=____.【答案】4,73- 8 .(2013届房山区一模文科数学)在△ABC 中,角A B C,,所对的边分别为,,a b c ,24A a c π===,,则角C 的大小为____.【答案】6π或30︒9 .(2013北京顺义二模数学文科试题及答案)设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且1cos ,,534A B b π=∠==,则sin _____,C ABC =∆的面积S =__________.【答案】4100,69++; 10.(2013届北京大兴区一模文科)函数f x x x()s i nc o s =的最小正周期是________________ 【答案】π11.(2013届北京丰台区一模文科)若3cos ,tan 05x x =<,则sin x =________. 【答案】45-; 12.(2013届北京西城区一模文科)在△ABC 中,内角A ,B ,C 的对边边长分别为a ,b ,c ,且cos 3cos 4A bB a ==.若10c =,则△ABC 的面积是______. 【答案】24;13.(2013北京丰台二模数学文科试题及答案)若tan()2x π-=,则tan 2x 的值是_______.【答案】34; 14.(2013北京海淀二模数学文科试题及答案)已知函数()sin(2)(01)6f x x πωω=-<<的图象经过点(,0)6π,则ω= ______,()f x 在区间[0,]π上的单调递增区间为________.【答案】12 ; 2[0,]3π15.(2013北京昌平二模数学文科试题及答案)在△ABC 中,若4,5,a b c ==则C ∠的大小为_________.【答案】 120︒ ;16.(北京市石景山区2013届高三一模数学文试题)在△ABC 中,若∠B=4π,b=,则∠C=__________________.【答案】712π17.(2013届北京海滨一模文)在ABC ∆中,若4,2,a b ==1cos 4A =,则______.c =【答案】418.(2013北京西城高三二模数学文科)在△ABC 中,2BC =,AC ,3B π=,则AB =______;△ABC 的面积是______.【答案】 19.(北京市朝阳区2013届高三第一次综合练习文科数学)在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对的边,且满足7sin b a B =,则sin A =_______,若60B = ,则sin C =_______.【答案】17 ;131420.(2013届北京东城区一模数学文科)函数()sin()3f x x π=-的图象为C ,有如下结论:①图象C 关于直线56x π=对称;②图象C 关于点4(,0)3π对称;③函数)(x f 在区间5[,]36ππ内是增函数,其中正确的结论序号是____.(写出所有正确结论的序号)【答案】①②③21.(2013北京东城高三二模数学文科)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且+2A C B =. 若1a =,b =,则c 的值为___.【答案】3π, 2; 22.(2013届北京市延庆县一模数学文)在ABC ∆中,c b a ,,依次是角C B A ,,的对边,且c b <.若6,32,2π===A c a ,则角=C _______.【答案】120 三、解答题23.(2013届北京海滨一模文)已知函数2()2cos )f x x x =--.(Ⅰ)求π()3f 的值和()f x 的最小正周期; (Ⅱ)求函数在区间ππ[,]63-上的最大值和最小值.【答案】解:(I)2π1()2)132f =-=因为2()2cos )f x x x =--222(3sin cos cos )x x x x =-+-22(12sin )x x =-+212sin x x =-cos2x x =π= 2sin(2)6x + 所以 ()f x 的周期为2π2ππ||2T ω=== (II)当ππ[,]63x ∈-时, π2π2[,]33x ∈-,ππ5π(2)[,]666x +∈- 所以当6x π=-时,函数取得最小值()16f π-=- 当6x π=时,函数取得最大值()26f π=24.(2013北京丰台二模数学文科试题及答案)本小题13分) 已知ABC ∆的三个内角分别为A,B,C,且22sin ()2.B C A + (Ⅰ)求A 的度数;(Ⅱ)若7,5,BC AC ==求ABC ∆的面积S.【答案】解: (Ⅰ)22sin ()2.B C A +22sin cos A A A ∴=,sin 0,sin ,tan A A A A ≠∴∴ 60,0=∴<<A A π °(Ⅱ)在ABC ∆中,60cos 2222⨯⨯-+=AC AB AC AB BC ,7,5,BC AC ==,525492AB AB -+=∴8,02452=∴=--∴AB AB AB 或3-=AB (舍),31023852160sin 21=⨯⨯⨯=⨯⨯=∴∆ AC AB S ABC 25.(2013北京昌平二模数学文科试题及答案)已知函数2()3s i n (2)2c o s 1,Rf x x x x π=--+∈. (Ⅰ)求()2f π;(Ⅱ)求)(x f 的最小正周期及单调递增区间.【答案】解:(Ⅰ) 2()2)2cos 12cos 22sin(2)6f x x x x x x ππ=--+=-=-∴1()2sin()21262f πππ=-=⨯=(Ⅱ)()2sin(2)6f x x π=-的最小正周期T π=,又由222(Z)26263k x k k x k k πππππππππ-≤-≤+⇒-≤≤+∈可得函数)(x f 的单调递增区间为,(Z)63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦26.(2013届北京西城区一模文科)已知函数()sin cos f x x a x =+的一个零点是3π4. (Ⅰ)求实数a 的值;(Ⅱ)设22()[()]2sin g x f x x =-,求()g x 的单调递增区间.【答案】(Ⅰ)解:依题意,得3π()04f =,即 3π3πsincos 04422a +=-=, 解得 1a = (Ⅱ)解:由(Ⅰ)得 ()sin cos f x x x =+22()[()]2sin g x f x x =- 22(sin cos )2sin x x x =+-sin 2cos 2x x =+π)4x =+由 πππ2π22π242k x k -≤+≤+, 得 3ππππ88k x k -≤≤+,k ∈Z 所以 ()g x 的单调递增区间为3ππ[π,π]88k k -+,k ∈Z 27.(2013北京朝阳二模数学文科试题)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且()f A =2cossin()22A A π-22sin cos 22A A+-. (Ⅰ)求函数()f A 的最大值;(Ⅱ)若()0,,12f A C a 5π===求b 的值. 【答案】(Ⅰ)22()2cos sin sin cos 2222A A A A f A =+-sin cos )4A A A π=-=-. 因为0A <<π,所以444A ππ3π-<-<.则所以当42A ππ-=,即34A π=时,()f A 取得最大值,(Ⅱ)由题意知())04f A A π=-=,所以sin()04A π-=.又知444A ππ3π-<-<,所以04A π-=,则4A π=.因为12C 5π=,所以712A B π+=,则3B π=.由sin sin a b A B =得,sinsin 33sin sin 4a Bb A π===π 28.(2013北京西城高三二模数学文科)如图,在直角坐标系xOy 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A ,且,)62ππ∈(α.将角α的终边按逆时针方向旋转3π,交单位圆于点B .记),(),,(2211y x B y x A . (Ⅰ)若311=x ,求2x ;(Ⅱ)分别过,A B 作x 轴的垂线,垂足依次为,C D .记△AOC 的面积为1S ,△BOD 的面积为2S .若122S S =,求角α的值.(Ⅰ)解:由三角函数定义,得 1cos x =α,2cos()3x π=+α 因为 ,)62ππ∈(α,1cos 3=α,所以 sin 3==α所以 211cos()cos 3226x π-=+==αα-α (Ⅱ)解:依题意得 1sin y =α,2sin()3y π=+α. 所以 111111cos sin sin 2224S x y ==⋅=ααα, 2221112||[cos()]sin()sin(2)223343S x y πππ==-+⋅+=-+ααα依题意得 2sin 22sin(2)3π=-+αα, 整理得 cos 20=α因为 62ππ<<α, 所以 23π<<πα,所以 22π=α, 即 4π=α29.(2013北京房山二模数学文科试题及答案)已知函数()sin()(00)f x x ωϕωϕ=+><<π,的最小正周期为π,且图象过点1(,)62π. (Ⅰ)求,ωϕ的值;(Ⅱ)设()()()4g x f x f x π=-,求函数()g x 的单调递增区间.【答案】(Ⅰ)由最小正周期为π可知 22==Tπω, 由1()62f π=得 1sin()32πϕ+=, 又0ϕπ<<,333πππϕπ<+<+所以536ππϕ+=,2πϕ=, (Ⅱ)由(Ⅰ)知 ()sin(2)cos 22f x x x π=+=所以()cos 2sin[2()]cos 2sin 242g x x x x x ππ=⋅-+=1sin 42x = 解24222k x k ππππ-≤≤+得(Z)2828k k x k ππππ-≤≤+∈ 所以函数()g x 的单调增区间为[,] (Z)2828k k k ππππ-+∈ 30.(北京市石景山区2013届高三一模数学文试题)已知函数f(x)=sin(2x+6π)+cos 2x.(Ⅰ)求函数f(x)的单调递增区间.(Ⅱ)在△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c,已知,a=2,B=3π,求△ABC 的面积.【答案】31.(2013北京顺义二模数学文科试题及答案)已知函数1()2f x =+.(Ⅰ)求()3f π的值;(Ⅱ)求函数()f x 的最小正周期及单调递减区间.【答案】解(Ⅰ)2sin )sin 1333()322cos 3f πππππ-=+112221222-=+⨯102=+12=(Ⅱ)由cos 0()2x k k Z ππ≠≠+∈得故()f x 的定义域为,2x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭因为sin )sin 21()2cos 2x x x f x x -=+1sin sin )2x x x =-+212sin 2x x =-+1cos 21222x x -=-+12cos 22x x =+sin(2)6x π=+所以()f x 的最小正周期为22T ππ== 因为函数sin y x =的单调递减区间为32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 由3222,()2622k x k x k k Z πππππππ+≤+≤+≠+∈ 得2,632k x k x k ππππππ+≤≤+≠+ 所以()f x 的单调递减区间为2,,,()6223k k k k k Z ππππππππ⎡⎫⎛⎤++++∈⎪ ⎢⎥⎣⎭⎝⎦32.(2013届北京门头沟区一模文科数学)已知函数)-2π(cos cos sin )(2x x x x f +=. (Ⅰ)求)3π(f 的值;(Ⅱ)求函数()f x 的最小正周期及值域.【答案】解:(I)由已知,得2πππππ()sincos cos()33323f =+-π313()34224f =+⨯ (II)2()sin cos sin f x x x x =+1cos 2sin 222x x -=+ 111sin 2cos 2222x x =-+π1)42x =-+ 函数)(x f 的最小正周期T π=值域为 33.(2013北京东城高三二模数学文科)已知函数()sin sin )f x x x x =-.(Ⅰ)求()f x 的最小正周期; (Ⅱ)当2(0)3x π∈,时,求()f x 的取值范围.【答案】(共13分)解:(Ⅰ)因为()sin sin )f x x x x =-2cos sin x x x =-=21cos 2sin )2x x x-11=2cos 2)22x x +- 1sin(2)62x π=+-. 所以()f x 的最小正周期2T π==π2. (Ⅱ) 因为203x π<<, 所以32662x πππ<+<. 所以()f x 的取值范围是31(,]22- 34.(2013北京海淀二模数学文科试题及答案)已知点 D 为ΔABC 的边 BC 上一点.且 BD =2DC,ADB ∠=750,∠ACD=30°,AD =2.(I)求CD 的长;(II)求ΔABC 的面积【答案】解:(I)因为75ADB ∠= ,所以45DAC ∠=在ACD ∆中,AD =根据正弦定理有sin45sin30CD AD = 所以2CD =(II)所以4BD =又在ABD ∆中,75ADB ∠=,sin75sin(4530)=+=所以1sin7512ADB S AD BD ∆=⋅⋅所以32ABC ABD S S ∆∆== 法2:同理,根据根据正弦定理有sin105sin30AC AD = 而sin105sin(4560)=+=所以1AC = 又4BD =,6BC =所以1sin302ABC S AC BC ∆=⋅⋅= 35.(2013届北京大兴区一模文科)在∆A B C 中,角A ,B ,C 的对边分别为a ,b ,c ,3cos 5=A ,π4B =,b =.(Ⅰ)求a 的值; (Ⅱ)求sin C 及∆A B C的面积. 【答案】解:(Ⅰ)因为 ABC ,53cos 内角是∆=A A ,所以,54sin =A 由正弦定理:B b A a sin sin =知4πsin 54a = 得: 58=a (Ⅱ)在 AB C ∆中, )sin()](sin[sin B A B A C +=+-=π102722532254sin cos cos sin =⨯+⨯=+=B A B A ABC ∆的面积为:2528102725821sin 21=⨯⨯⨯==C ab s 36.(2013届北京丰台区一模文科)已知函数22()(sin cos )2cos .f x x x x =+-(Ⅰ)求()f x 的最小正周期和单调递增区间;(Ⅱ)求函数()f x 在3[,]44ππ上的值域. 【答案】已知函数22()(sin cos )2cos .f x x x x =+-(Ⅰ)求()f x 的最小正周期和单调递增区间;(Ⅱ)求函数()f x 在3[,]44ππ上的值域.解:(Ⅰ)2()1sin 22cos )4f x x x x π=+-=-, ∴最小正周期T=π, 单调增区间3[,]()88k k k Z ππππ-+∈, (Ⅱ)33,24422x x ππππ≤≤∴≤≤ ,52444x πππ∴≤-≤,∴()f x 在3[,]44ππ上的值域是[1-37.(2013届房山区一模文科数学)已知函数2()2cos cos 1f x x x x =+-.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间[0,]2π上的最小值和最大值.【答案】(Ⅰ)1cos sin 32cos 2)(2-+=x x x x fx x 2sin 32cos +=)2sin 232cos 21(2x x += )62sin(2π+=x 周期为2.2T ππ== (Ⅱ) 20π≤≤x ∴67626πππ≤+≤x∴当262ππ=+x 时,1)62sin(=+πx 此时2)(max =x f ∴当6762ππ=+x 时,21)62sin(-=+πx 此时min ()1f x =- 38.(2013届北京市延庆县一模数学文)已知x x x f 2sin 22sin 3)(-=.(Ⅰ)求)(x f 的最小正周期和单调递增区间;(Ⅱ)若]6,0[π∈x ,求)(x f 的最小值及取得最小值时对应的x 的取值. 【答案】解:(Ⅰ)12cos 2sin 3)(-+=x x x f1)62sin(2-+=πx ππ==22T ,)(x f ∴最小正周期为π 由πππππk x k 226222+≤+≤+-)(Z k ∈,得ππππk x k 232232+≤≤+-ππππk x k +≤≤+-63)(x f ∴单调递增区间为)](6,3[Z k k k ∈++-ππππ(Ⅱ)当]6,0[π∈x 时,]2,6[62πππ∈+x , )(x f ∴在区间]6,0[π单调递增, 0)0()]([min ==∴f x f ,对应的x 的取值为039.(北京市朝阳区2013届高三第一次综合练习文科数学)已知函数21()sin 22x f x x ωω=-+(0ω>)的最小正周期为π. (Ⅰ)求ω的值及函数()f x 的单调递增区间;(Ⅱ)当[0,]2x π∈时,求函数()f x 的取值范围.【答案】解:(Ⅰ)1cos 1()22x f x x ωω-=-+1cos 2x x ωω=+ sin()6x ωπ=+ 因为()f x 最小正周期为π,所以2ω=于是()sin(2)6f x x π=+. 由222262k x k ππππ-≤+≤π+,k ∈Z ,得36k x k πππ-≤≤π+. 所以()f x 的单调递增区间为[,36k k πππ-π+],k ∈Z (Ⅱ)因为[0,]2x π∈,所以72[,]666x πππ+∈, 则1sin(2)126x π-≤+≤ 所以()f x 在[0,]2π上的取值范围是[1,12-]. 40.(2013届北京东城区一模数学文科)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,且sin cos b A B =.(Ⅰ)求角B ;(Ⅱ)若b =求ac 的最大值.【答案】(共13分)解:(Ⅰ)因为sin cos b A B =,由正弦定理可得sin sin cos B A A B =,因为在△ABC 中,sin 0A ≠,所以tan B =又0B <<π, 所以3B π=. (Ⅱ)由余弦定理 2222cos b a c ac B =+-,因为3B π=,b =所以2212a c ac =+-.因为222a c ac +≥,所以12ac ≤.当且仅当a c ==,ac 取得最大值12.。
【2013大兴一模】北京市大兴区2013届高三一模 文科数学

大兴区2013年高三统一练习数学(文科)一、选择题(1)复数2(1i)+的值是(A )2 (B )2- (C )2i (D )2i - 【答案】C22(1)122i i i i +=++=,选C.(2)设集合2{|1}=>A x x ,2{|log 0|}=>B x x ,则ÇA B 等于(A )}1|{>x x (B )}0|{>x x (C )}1|{-<x x (D ){|11},或x x x <-> 【答案】A{11}A x x x =><-或,{1}B x x =>,所以{1}A B x x =>,选A.(3)执行如图所示的程序框图.若4n =,则输出s(A )-42 (B ) -21 (C ) 11 (D ) 43【答案】C第一次循环,11(2)1,2s i =+-=-=;第二次循环,21(2)3,3s i =-+-==;第三次循环,33(2)5,4s i =+-=-=;第四次循环,5,11)2(5s 4==-+-=i ,此时不满足条件,输出11s =,所以选C.(4)设0.70.45 1.512314,8,()2y y y -===,则 (A )312y y y >> (B )213y y y >> (C )123y y y >> (D )132y y y >>【答案】A0.7 1.4142y ==,0.45 1.35282y ==, 1.5 1.531()22y -==,所以312y y y >>,选A.(5)已知平面βα,,直线n m ,,下列命题中不.正确的是 (A )若α⊥m ,β⊥m ,则α∥β (B )若m ∥n ,α⊥m ,则α⊥n (C )若m ∥α,n =βα ,则m ∥n (D )若α⊥m ,β⊂m ,则βα⊥. 【答案】CC 中,当m ∥α时,m 只和过m 平面与β的交线平行,所以C 不正确。
北京市2013各区数学一模试题--数列及解析几何

2013年北京市各区高三一模试题编--数列一填空选择(2013年东城一模文科)(7)对于函数)(x f y =,部分x 与y 的对应关系如下表:x 1 2 3 4 5 6 7 8 9 y7 4 5 8 1 3 5 2 6数列}{n x 满足21=x ,且对任意*n ∈N ,点),(1+n n x x 都在函数)(x f y =的图象上,则201320124321x x x x x x ++++++ 的值为(A )9394 (B )9380 (C )9396 (D )9400 (2013年东城一模文科理科)(14)数列{a n }的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若n n a a =(0)a ≠, 则位于第10行的第8列的项等于 ,2013a 在图中位于 .(填第几行的第几列)(2013年东城一模理科)(5)已知数列{}n a 中,12a =,120n n a a +-=,2log n n b a =,那么数列{}n b 的前10项和等于(A )130 (B )120 (C )55 (D )50(2013西城一模文科理科)4.设等比数列{}n a 的公比为q ,前n 项和为n S ,且10a >.若232S a >,则q 的取值范围是(A )1(1,0)(0,)2- (B )1(,0)(0,1)2-(C )1(,1)(,)2-∞-+∞(D )1(,)(1,)2-∞-+∞(2013西城一模文科)14.已知数列{}n a 的各项均为正整数,其前n 项和为n S .若1, ,231,,nn n nn a a a a a +⎧⎪=⎨⎪+⎩是偶数是奇数且329S =,则1a =______;3n S =______. (2013西城一模理科)10.设等差数列{}n a 的公差不为0,其前n 项和是n S .若23S S =,0k S =,则k =______.(2013海淀一模文科)2.等差数列{}n a 中, 2343,9,a a a =+= 则16a a 的值为 A. 14 B. 18 C. 21 D.2(2013海淀一模理科)10.等差数列{}n a 中,34259,18a a a a +==, 则16_____.a a = (2013丰台一模文科理科)3. 设n S 为等比数列{}n a 的前n 项和,3420a a +=,则31S a ( )(A) 2 (B) 3 (C) 4 (D) 5(2013年石景山一模文科理科)11.在等差数列{a n }中,a l =-2013,其前n 项和为S n ,若10121210S S -=2,则2013S 的值等于 。
北京2013届高三最新文科试题分类汇编(含9区一模及上学期期末试题精选)专题3三角函数

【精品推荐】北京2013届高三最新文科试题分类汇编(含9区一模及上学期期末试题精选)专题3:三角函数一、选择题1 .(2013届北京门头沟区一模文科数学)为得到函数sin (π-2)y x =的图象,可以将函数πsin (2)3y x =-的图象 ( )A .向左平移3π个单位 B .向左平移6π个单位 gkstk C .向右平移3π个单位D .向右平移6π个单位2 .(2013届北京门头沟区一模文科数学)若△ABC 的内角A . B .C 所对的边a 、b 、c 满足422=-+c b a )(,且C =60°,则ab 的值为 ( )A .348-B .1C .34D .323 .(2013届北京大兴区一模文科)函数()cos f x x=( )A .在ππ(,)22-上递增 B .在π(,0]2-上递增,在π(0,)2上递减 C .在ππ(,)22-上递减D .在π(,0]2-上递减,在π(0,)2上递增4 .(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(文)试题)在ABC ∆中,内角CB A ,,所对边的长分别为c b a ,,,若C c B b A a sin sin sin <+,则ABC ∆的形状是( )A .锐角三角形B .钝角三角形C .直角三角形D .不确定5 .(北京市丰台区2013届高三上学期期末考试数学文试题)函数2sin()y x ωϕ=+在一个周期内的图象如图所示,则此函数的解析式是( )A .2sin(2)4y x π=-B .2sin(2)4y x π=+C .32sin()8y x π=+D .72sin()216x y π=+6 .(北京市海淀区2013届高三上学期期末考试数学文试题)已知函数sin , sin cos ,()cos , sin cos ,x x x f x x x x ≥⎧=⎨<⎩则下面结论中正确的是 ( )A .()f x 是奇函数B .()f x 的值域是[1,1]-C .()f x 是偶函数D .()f x 的值域是[2-二、填空题7 .(2013届北京市延庆县一模数学文)在ABC ∆中,c b a ,,依次是角C B A ,,的对边,且c b <.若6,32,2π===A c a ,则角=C _______.8 .(2013届北京东城区一模数学文科)函数()sin()3f x x π=-的图象为C ,有如下结论:①图象C 关于直线56x π=对称;②图象C 关于点4(,0)3π对称;③函数)(x f 在区间5[,]36ππ内是增函数,其中正确的结论序号是____.(写出所有正确结论的序号)9 .(2013届北京丰台区一模文科)若3cos ,tan 05x x =<,则sin x =________.10.(2013届北京海滨一模文)在ABC ∆中,若4,2,a b ==1cos 4A =,则______.c =11.(2013届北京大兴区一模文科)函数f x x x()s i nc o s =的最小正周期是________________12.(2013届北京西城区一模文科)在△ABC 中,内角A ,B ,C 的对边边长分别为a ,b ,c ,且cos 3cos 4A bB a ==.若10c =,则△ABC 的面积是______.13.(2013届房山区一模文科数学)在△ABC 中,角A B C ,,所对的边分别为,,a b c ,24A a c π==,,则角C 的大小为____.14.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(文)试题)已知32sin =α,则()απ2cos -的值等于_______________.15.(北京市石景山区2013届高三上学期期末考试数学文试题)在ABC ∆中,若2,60,a B b =∠=︒=,则c = .16.(北京市昌平区2013届高三上学期期末考试数学文试题)在ABC △中,若3b =,1c =,1cos 3A =,则a =17.(北京市朝阳区2013届高三上学期期末考试数学文试题)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且222b c a bc +-=,则A = .18.(北京市东城区2013届高三上学期期末考试数学文科试题)若3sin 5α=-,且tan 0α>,则cos α= .19.(北京市丰台区2013届高三上学期期末考试数学文试题)已知ABC ∆中,BC=1,,则AC 等于______.20.(北京市海淀区2013届高三上学期期末考试数学文试题)tan225的值为________.21.(北京市西城区2013届高三上学期期末考试数学文科试题)已知函数π()sin()6f x x =+,其中π[,]3x a ∈-.当2a π=时,()f x 的值域是______;若()f x 的值域是1[,1]2-,则a 的取值范围是______. 22.(北京市房山区2013届高三上学期期末考试数学文科试题(解析版))在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,,1,3,3===b a A π则=c ,ABC ∆的面积等于 .三、解答题23.(2013届北京市延庆县一模数学文)已知x x x f 2sin 22sin 3)(-=.(Ⅰ)求)(x f 的最小正周期和单调递增区间;(Ⅱ)若]6,0[π∈x ,求)(x f 的最小值及取得最小值时对应的x 的取值. 24.(2013届北京东城区一模数学文科)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,且sin cos b A B =.(Ⅰ)求角B ;(Ⅱ)若b =,求ac 的最大值.25.(2013届北京丰台区一模文科)已知函数22()(sin cos )2cos .f x x x x =+-(Ⅰ)求()f x 的最小正周期和单调递增区间; (Ⅱ)求函数()f x 在3[,]44ππ上的值域.26.(2013届北京海滨一模文)已知函数2()2cos )f x x x =--.(Ⅰ)求π()3f 的值和()f x 的最小正周期;(Ⅱ)求函数在区间ππ[,]63-上的最大值和最小值.27.(2013届北京门头沟区一模文科数学)已知函数)-2π(cos cos sin )(2x x x x f +=. (Ⅰ)求)3π(f 的值;(Ⅱ)求函数()f x 的最小正周期及值域.28.(2013届北京大兴区一模文科)在∆A B C中,角A ,B ,C 的对边分别为a ,b ,c ,3cos 5=A ,π4B =,b =.(Ⅰ)求a 的值; (Ⅱ)求sin C 及∆A B C 的面积.29.(2013届北京西城区一模文科)已知函数()sin cos f x x a x =+的一个零点是3π4. (Ⅰ)求实数a 的值;(Ⅱ)设22()[()]2sin g x f x x =-,求()g x 的单调递增区间.30.(2013届房山区一模文科数学)已知函数2()2cos cos 1f x x x x =+-.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间[0,]2π上的最小值和最大值.31.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(文)试题)已知函数()())2,0,0(sin πϕωϕω<>>+=A x A x f 的图象的一部分如图所示.(Ⅰ)求函数()x f 的解析式; (Ⅱ)求函数())44c os(2ππ++=x x f y ])32,6[(--∈x 的最大值和最小值.32.(北京市石景山区2013届高三上学期期末考试数学文试题)已知函数sin 2(sin cos )()cos x x x f x x+=.(Ⅰ)求)(x f 的定义域及最小正周期; (Ⅱ)求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ,上的最大值和最小值.33.(北京市昌平区2013届高三上学期期末考试数学文试题)(本小题满分13分)已知函数()2cos )cos 1f x x x x =-⋅+.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间[,]42ππ上的最值. gkstk34.(北京市朝阳区2013届高三上学期期末考试数学文试题)已知函数2()sincos cos 1222x x xf x =+-. (Ⅰ)求函数()f x 的最小正周期及单调递减区间; (Ⅱ)求函数()f x 在[,]π3π42上的最小值.35.(北京市东城区2013届高三上学期期末考试数学文科试题)已知函数2()cos cos f x x x x =+.(Ⅰ)求()f x 的最小正周期; (Ⅱ)求()f x 在区间[,]63ππ-上的最大值和最小值.36.(北京市丰台区2013届高三上学期期末考试数学文试题)(本题共13分)如图,在平面直角坐标系中,角α和角β的终边分别与单位圆交于A ,B 两点. (Ⅰ)若点A 的横坐标是35,点B 的纵坐标是1213,求sin()αβ+的值; (Ⅱ) 若∣AB ∣=32, 求OA OB ⋅的值.37.(北京市海淀区2013届高三上学期期末考试数学文试题)已知函数21()cos cos 2f x x x x =-+,ABC ∆三个内角,,A B C 的对边分别为,,,a b c 且()1f A =. (I ) 求角A 的大小;(Ⅱ)若7a =,5b =,求c 的值.38.(北京市通州区2013届高三上学期期末考试数学文试题)已知函数()21sin cos cos 2f x x x x =+-. (Ⅰ)求()f x 的最小正周期; (Ⅱ)求函数()f x 在ππ,82⎡⎤-⎢⎥⎣⎦的最大值和最小值.39.(北京市西城区2013届高三上学期期末考试数学文科试题)在△ABC 中,内角,,A B C 的对边分别为,,a b c ,且cos2cos 0B B +=.(Ⅰ)求角B 的值; gkstk (Ⅱ)若b =,5a c +=,求△ABC 的面积.40.(北京市房山区2013届高三上学期期末考试数学文科试题(解析版))(本小题满分13分)已知函数sin 2cos 21()2cos x x f x x++=.(Ⅰ)求函数)(x f 的定义域;(Ⅱ)若523)4(=+παf ,求αcos 的值.【精品推荐】北京2013届高三最新文科试题分类汇编(含9区一模及上学期期末试题精选)专题3:三角函数参考答案一、选择题 1. B 2. C 3. D 4. B 5. 【答案】B解:由图象可知52882T πππ=-=,所以函数的周期T π=,又2T ππω==,所以2ω=。
【VIP专享】北京2013届大兴区高三数学一模文科试题及答案

11、已知矩形 ABCD 中, AB = 2 , AD = 1 ,E、F 分别是 BC、CD 的中点,则 ( AE + AF )×AC 等于
一、选择题 1、复数 (1+ i)2 的值是
(A)2
(B) - 2
(C) 2i
北京市大兴区 2013 年高三统一练习
2、设集合 A = {x | x2 > 1} , B = {x | log2 x > 0 |} ,则 A Ç B 等于 (A){x | x 1} (B){x | x 0} (C){x | x 1} (D){x | x 1,或x 1}
2
2
i≤n?
否 输出 s
i i 1
s = s + (- 2)i 是
一个如图所示的旋
一个面恰好与旋转
体的开口面平齐,则此正方体的棱长是
(A)1
二、填空题
9、函数 f (x) siC) 2 2
3
10、已知中心在原点,焦点在 x 轴上的双曲线的离心率为 ,实轴长为 4,则双曲线的方程是
3、执行如图所示的程序框图.若 n 4 ,则输出 s 的值是
开始
(A)-42 (B) -21 (C) 11 (D) 43
4、设
y1
40.7 , y2
(A) y3 > y1 > y2 (B ) y2 > y1 > y3
80.45 , y3
5、已知平面 , ,直线 m, n ,下列命题中不正确的是
(C)在 ( π , π ) 上递减 22
数学(文科)
(D) - 2i
(C) y1 > y2 > y3
输入 n
s=1,i=1
(D) y1 > y3 > y2
2013年北京市高考数学试卷(文科)(附答案解析)

2013年北京市高考数学试卷(文科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合A={−1, 0, 1},B={x|−1≤x<1},则A∩B=()A.{0}B.{−1, 0}C.{0, 1}D.{−1, 0, 1}2. 设a,b,c∈R,且a>b,则( )A.ac>bcB.1a <1bC.a2>b2D.a3>b33. 下列函数中,既是偶函数又在区间(0, +∞)上是单调递减的是()A.y=1xB.y=e−xC.y=−x2+1D.y=lg|x|4. 在复平面内,复数i(2−i)对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限5. 在△ABC中,a=3,b=5,sin A=13,则sin B=()A.1 5B.59C.√53D.16. 执行如图所示的程序框图,输出的S值为( )A.1B.23C.1321D.6109877. 双曲线x2−y2m=1的离心率大于√2的充分必要条件是()A.m>12B.m≥1C.m>1D.m>28. 如图,在正方体ABCD−A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有()A.3个B.4个C.5个D.6个二、填空题共6小题,每小题5分,共30分.若抛物线y2=2px的焦点坐标为(1, 0),则p=________;准线方程为________.某四棱锥的三视图如图所示,该四棱锥的体积为________.若等比数列{a n}满足a2+a4=20,a3+a5=40,则公比q=________;前n项和S n=________.设D为不等式组{x≥02x−y≤0x+y−3≤0表示的平面区域,区域D上的点与点(1, 0)之间的距离的最小值为________.函数f(x)={log12x,x≥12x,x<1的值域为________.已知点A(1, −1),B(3, 0),C(2, 1).若平面区域D 由所有满足AP →=λAB →+μAC →(1≤λ≤2, 0≤μ≤1)的点P 组成,则D 的面积为________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.已知函数f(x)=(2cos 2x −1)sin 2x +12cos 4x . (1)求f(x)的最小正周期及最大值;(2)若α∈(π2,π),且f(α)=√22,求α的值.如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.(1)求此人到达当日空气重度污染的概率;(2)求此人在该市停留期间只有1天空气重度污染的概率;(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)如图,在四棱锥P −ABCD 中,AB // CD ,AB ⊥AD ,CD =2AB ,平面PAD ⊥底面ABCD ,PA ⊥AD .E 和F 分别是CD 和PC 的中点,求证:(1)PA ⊥底面ABCD ;(2)BE // 平面PAD ;(3)平面BEF ⊥平面PCD .已知函数f(x)=x 2+x sin x +cos x .(1)若曲线y =f(x)在点(a, f(a))处与直线y =b 相切,求a ,b 的值;(2)若曲线y =f(x)与直线y =b 有两个不同交点,求b 的取值范围.直线y =kx +m(m ≠0)与椭圆W:x 24+y 2=1相交于A ,C 两点,O 是坐标原点.(1)当点B 的坐标为(0, 1),且四边形OABC 为菱形时,求AC 的长;(2)当点B 在W 上且不是W 的顶点时,证明:四边形OABC 不可能为菱形.给定数列a 1,a 2,…,a n .对i =1,2,…,n −1,该数列前i 项的最大值记为A i ,后n −i 项a i+1,a i+2,…,a n 的最小值记为B i ,d i =A i −B i .(1)设数列{a n }为3,4,7,1,写出d 1,d 2,d 3的值;(2)设a 1,a 2,…,a n−1(n ≥4)是公比大于1的等比数列,且a 1>0.证明:d 1,d 2,…,d n−1是等比数列; (3)设d 1,d 2,…,d n−1是公差大于0的等差数列,且d 1>0.证明:a 1,a 2,…,a n−1是等差数列.参考答案与试题解析2013年北京市高考数学试卷(文科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.【答案】B【考点】交集及其运算【解析】找出A与B的公共元素,即可确定出两集合的交集.【解答】解:∵A={−1, 0, 1},B={x|−1≤x<1},∴A∩B={−1, 0}.故选B.2.【答案】D【考点】不等式的基本性质【解析】对于A、B、C可举出反例,对于D利用不等式的基本性质即可判断出.【解答】解:A,令a=3,b=2,c=−1,则3×(−1)<2×(−1),即ac<bc,故A不正确;B,令a=1,b=−2,而1>−12,故B不正确;C,令a=−1,b=−2,而(−1)2<(−2)2,故C不正确;D,∵a>b,∴a3>b3,成立,故D正确.故选D.3.【答案】C【考点】函数奇偶性的判断函数的单调性及单调区间【解析】根据函数y=1x是奇函数,得A项不符合题意;根据函数y=e−x是非奇非偶函数,得B项不符合题意;根据二次函数y=−x2+1的图象是开口向下的抛物线且关于y轴对称,得到C项符合题意;根据对数函数的单调性,得函数y=lg|x|在(0, +∞)上是增函数,可得D项不符合题意.【解答】解:对于A,函数y=1x 满足f(−x)=−1x≠f(x),可得函数不是偶函数,故A项不符合题意;对于B,函数y=e−x满足f(−x)=e x≠f(x),得函数不是偶函数,故B项不符合题意;对于C,函数y=−x2+1满足f(−x)=−(−x)2+1=−x2+1=f(x),∴函数y=−x2+1是R上的偶函数.又∵函数y=−x2+1的图象是开口向下的抛物线,关于y轴对称,∴当x∈(0, +∞)时,函数为减函数.故C项符合题意;对于D,当x∈(0, +∞)时,函数y=lg|x|=lg x,底数10>1,∴函数y=lg|x|在区间(0, +∞)上是单调递增的函数,故D项不符合题意.故选C.4.【答案】A【考点】复数的代数表示法及其几何意义【解析】首先进行复数的乘法运算,得到复数的代数形式的标准形式,根据复数的实部和虚部写出对应的点的坐标,看出所在的象限.【解答】解:∵复数z=i(2−i)=−i2+2i=1+2i,∴复数对应的点的坐标是(1, 2),这个点在第一象限.故选A.5.【答案】B【考点】正弦定理【解析】由正弦定理列出关系式,将a,b及sin A的值代入即可求出sin B的值.【解答】解:∵a=3,b=5,sin A=13,∴由正弦定理得:sin B=b sin Aa=5×133=59.故选B.6.【答案】C【考点】程序框图【解析】从框图赋值入手,先执行一次运算,然后判断运算后的i的值与2的大小,满足判断框中的条件,则跳出循环,否则继续执行循环,直到条件满足为止. 【解答】解:框图首先给变量i 和S 赋值0和1. 执行S =12+12×1+1=23,i =0+1=1;判断1≥2不成立,执行S =(23)2+12×23+1=1321,i =1+1=2;判断2≥2成立,算法结束,跳出循环,输出S 的值为1321. 故选C . 7.【答案】 C【考点】根据充分必要条件求参数取值问题 双曲线的离心率 【解析】根据双曲线的标准形式,可以求出a =1,b =√m ,c =√1+m .利用离心率e 大于√2建立不等式,解之可得 m >1,最后利用充要条件的定义即可得出正确答案. 【解答】 解:双曲线x 2−y 2m=1,说明m >0,∴ a =1,b =√m ,可得c =√1+m , ∵ 离心率e >√2等价于 ca =√1+m 1>√2⇔m >1,∴ 双曲线x 2−y 2m=1的离心率大于√2的充分必要条件是m >1.故选C . 8.【答案】 B【考点】点、线、面间的距离计算 【解析】建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,即可得到各顶点的坐标,利用两点间的距离公式即可得出. 【解答】解:建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=3,则A(3, 0, 0),B(3, 3, 0),C(0, 3, 0),D(0, 0, 0),A 1(3, 0, 3),B 1(3, 3, 3),C 1(0, 3, 3),D 1(0, 0, 3), ∴ BD 1→=(−3, −3, 3), 设P(x, y, z),∵ BP →=13BD 1→=(−1, −1, 1), ∴ DP →=DB →+(−1,−1,1)=(2, 2, 1).∴ |PA|=|PC|=|PB 1|=√12+22+12=√6, |PD|=|PA 1|=|PC 1|=√22+22+12=3, |PB|=√3,|PD 1|=√22+22+22=2√3.故P 到各顶点的距离的不同取值有√6,3,√3,2√3共4个. 故选B .二、填空题共6小题,每小题5分,共30分. 【答案】 2,x =−1 【考点】 抛物线的性质 【解析】由抛物线的性质可知,知p2=1,可知抛物线的标准方程和准线方程. 【解答】解:∵ 抛物线y 2=2px 的焦点坐标为(1, 0), ∴ p2=1,p =2, 抛物线的方程为y 2=4x , ∴ 其标准方程为:x =−1.故答案为:2;−1. 【答案】 3【考点】由三视图求体积 【解析】利用三视图判断几何体的形状,然后通过三视图的数据求解几何体的体积.【解答】解:几何体为底面边长为3的正方形,高为1的四棱锥,所以体积V=13×32×1=3.故答案为:3.【答案】2,2n+1−2【考点】等比数列的前n项和等比数列的通项公式【解析】利用等比数列的通项公式和已知即可得出{a1q+a1q3=20a1q2+a1q4=40,解出即可得到a1及q,再利用等比数列的前n项和公式即可得出S n=a1(q n−1)q−1.【解答】解:设等比数列{a n}的公比为q,∵a2+a4=a2(1+q2)=20①a3+a5=a3(1+q2)=40②∴ ①②两个式子相除,可得到a3a2=4020=2,即等比数列的公比q=2,将q=2带入①中可求出a2=4,则a1=a2q =42=2,∴数列{a n}时首项为2,公比为2的等比数列.∴数列{a n}的前n项和为:S n=a1(q n−1)q−1=2×(2n−1)2−1=2n+1−2.故答案为:2;2n+1−2.【答案】2√5【考点】求线性目标函数的最值【解析】首先根据题意作出可行域,欲求区域D上的点与点(1, 0)之间的距离的最小值,由其几何意义为点A(1, 0)到直线2x−y=0距离为所求,代入点到直线的距离公式计算可得答案.【解答】解:如图可行域为阴影部分,由其几何意义为点A(1, 0)到直线2x−y=0距离,即为所求,由点到直线的距离公式得:d=√4+1=2√55,则区域D上的点与点(1, 0)之间的距离的最小值等于2√55.故答案为:2√55.【答案】(−∞, 2)【考点】函数的值域及其求法【解析】通过求解对数不等式和指数不等式分别求出分段函数的值域,然后取并集得到原函数的值域.【解答】解;当x≥1时,f(x)=log12x≤log121=0;当x<1时,0<f(x)=2x<21=2.所以函数f(x)={log12x,x≥12x,x<1的值域为(−∞, 2).故答案为:(−∞, 2).【答案】3【考点】简单线性规划向量的加法及其几何意义点到直线的距离公式【解析】设P的坐标为(x, y),根据AP→=λAB→+μAC→,结合向量的坐标运算解出{λ=23x−13y−1μ=−13x+23y+1,再由1≤λ≤2、0≤μ≤1得到关于x、y的不等式组,从而得到如图的平行四边形CDEF及其内部,最后根据坐标系内两点间的距离公式即可算出平面区域D的面积.【解答】解:设P 的坐标为(x, y),则AB →=(2, 1),AC →=(1, 2),AP →=(x −1, y +1),∵ AP →=λAB →+μAC →,∴ {x −1=2λ+μ,y +1=λ+2μ, 解之得{λ=23x −13y −1,μ=−13x +23y +1,∵ 1≤λ≤2,0≤μ≤1,∴ 点P 坐标满足不等式组{1≤23x −13y −1≤2,0≤−13x +23y +1≤1, 作出不等式组对应的平面区域,得到如图的平行四边形CDEF 及其内部,其中C(4, 2),D(6, 3),E(5, 1),F(3, 0) ∵ |CF|=√(4−3)2+(2−0)2=√5, 点E(5, 1)到直线CF:2x −y −6=0的距离为d =√5=3√55∴ 平行四边形CDEF 的面积为S =|CF|×d =√5×3√55=3,即动点P 构成的平面区域D 的面积为3.故答案为:3.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 【答案】解:(1)因为f(x)=(2cos 2x −1)sin 2x +12cos 4x=12sin 4x +12cos 4x =√22sin (4x +π4) ∴ T =2π4=π2,函数的最大值为:√22.(2)∵ f(x)=√22sin (4x +π4),f(α)=√22, ∴ sin (4α+π4)=1,∴ 4α+π4=π2+2kπ,k ∈Z , ∴ α=π16+kπ2,又∵ α∈(π2,π), ∴ α=916π. 【考点】二倍角的正弦公式 两角和与差的正弦公式 正弦函数的周期性 三角函数的最值 正弦函数的定义域和值域【解析】(1)利用二倍角的正弦函数以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,通过周期公式求f(x)的最小正周期,利用三角函数的最值求出函数的最大值;(2)通过α∈(π2,π),且f(α)=√22,求出α的正弦值,然后求出角即可. 【解答】解:(1)因为f(x)=(2cos 2x −1)sin 2x +12cos 4x=12sin 4x +12cos 4x =√2sin (4x +π) ∴ T =2π4=π2,函数的最大值为:√22. (2)∵ f(x)=√22sin (4x +π4),f(α)=√22, ∴ sin (4α+π4)=1,∴ 4α+π4=π2+2kπ,k ∈Z , ∴ α=π16+kπ2,又∵ α∈(π2,π), ∴ α=916π.【答案】解:(1)由图看出,1日至13日13天的时间内,空气重度污染的是5日、8日共2天.由古典概型概率计算公式得,此人到达当日空气质量重度污染的概率P=213.(2)此人在该市停留期间两天的空气质量指数为(86, 25),(25, 57),(57, 143),(143, 220),(220, 160),(160, 40),(40, 217),(217, 160),(160, 121),(121, 158),(158, 86),(86, 79),(79, 37)共13种情况, 其中只有1天空气重度污染的是(143, 220),(220, 160),(40, 217),(217, 160)共4种情况,所以,此人在该市停留期间只有1天空气重度污染的概率P=413.(3)因为方差越大,说明三天的空气质量指数越不稳定,由图看出从5日开始连续5,6,7三天的空气质量指数方差最大.【考点】列举法计算基本事件数及事件发生的概率极差、方差与标准差古典概型及其概率计算公式【解析】(Ⅰ)由图查出13天内空气质量指数大于200的天数,直接利用古典概型概率计算公式得到答案;(Ⅱ)用列举法写出此人在该市停留两天的空气质量指数的所有情况,查出仅有一天是重度污染的情况,然后直接利用古典概型概率计算公式得到答案;(Ⅲ)因为方差越大,说明三天的空气质量指数越不稳定,由图直接看出答案.【解答】解:(1)由图看出,1日至13日13天的时间内,空气重度污染的是5日、8日共2天.由古典概型概率计算公式得,此人到达当日空气质量重度污染的概率P=213.(2)此人在该市停留期间两天的空气质量指数为(86, 25),(25, 57),(57, 143),(143, 220),(220, 160),(160, 40),(40, 217),(217, 160),(160, 121),(121, 158),(158, 86),(86, 79),(79, 37)共13种情况, 其中只有1天空气重度污染的是(143, 220),(220, 160),(40, 217),(217, 160)共4种情况,所以,此人在该市停留期间只有1天空气重度污染的概率P=413.(3)因为方差越大,说明三天的空气质量指数越不稳定,由图看出从5日开始连续5,6,7三天的空气质量指数方差最大.【答案】证明:(1)∵PA⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴由平面和平面垂直的性质定理可得,PA⊥平面ABCD.(2)∵AB // CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点,∴AB=//12CD=DE,∴四边形ABED为平行四边形,故有BE // AD.又AD⊂平面PAD,BE不在平面PAD内,故有BE // 平面PAD.(3)平行四边形ABED中,由AB⊥AD可得,ABED为矩形,故有BE⊥CD①.由PA⊥平面ABCD,可得PA⊥AB,再由AB⊥AD可得AB⊥平面PAD,∴CD⊥平面PAD,故有CD⊥PD.再由E、F分别为CD和PC的中点,可得EF // PD,∴CD⊥EF②.而EF和BE是平面BEF内的两条相交直线,故有CD⊥平面BEF.由于CD⊂平面PCD,∴平面BEF⊥平面PCD.【考点】平面与平面垂直的判定直线与平面垂直的判定直线与平面平行的判定【解析】(1)根据条件,利用平面和平面垂直的性质定理可得PA⊥平面ABCD.(2)根据已知条件判断ABED为平行四边形,故有BE // AD,再利用直线和平面平行的判定定理证得BE // 平面PAD.(3)先证明ABED为矩形,可得BE⊥CD①.现证CD⊥平面PAD,可得CD⊥PD,再由三角形中位线的性质可得EF // PD,从而证得CD⊥EF②.结合①②利用直线和平面垂直的判定定理证得CD⊥平面BEF,再由平面和平面垂直的判定定理证得平面BEF⊥平面PCD.【解答】证明:(1)∵PA⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴由平面和平面垂直的性质定理可得,PA⊥平面ABCD.(2)∵AB // CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点,∴AB=//12CD=DE,∴四边形ABED为平行四边形,故有BE // AD.又AD⊂平面PAD,BE不在平面PAD内,故有BE // 平面PAD.(3)平行四边形ABED中,由AB⊥AD可得,ABED为矩形,故有BE⊥CD①.由PA⊥平面ABCD,可得PA⊥AB,再由AB⊥AD可得AB⊥平面PAD,∴CD⊥平面PAD,故有CD⊥PD.再由E、F分别为CD和PC的中点,可得EF // PD,∴CD⊥EF②.而EF和BE是平面BEF内的两条相交直线,故有CD⊥平面BEF.由于CD⊂平面PCD,∴平面BEF⊥平面PCD.【答案】解:(1)f′(x)=2x+x cos x=x(2+cos x),∵曲线y=f(x)在点(a, f(a))处与直线y=b相切,∴f′(a)=a(2+cos a)=0,f(a)=b,联立{2a+a cos a=0,a2+a sin a+cos a=b,解得{a=0,b=1,故a=0,b=1.(2)∵f′(x)=x(2+cos x).令f′(x)=0,得x=0,x,f(x),f′(x)的变化情况如表:-+(0, +∞)上单调递增,f(0)=1是f(x)的最小值.故当b>1时曲线y=f(x)与直线y=b有且只有两个不同的交点.【考点】由函数零点求参数取值范围问题利用导数研究曲线上某点切线方程利用导数研究函数的单调性【解析】(I)由题意可得f′(a)=0,f(a)=b,联立解出即可;(II)利用导数得出其单调性与极值即最值,得到值域即可.【解答】解:(1)f′(x)=2x+x cos x=x(2+cos x),∵曲线y=f(x)在点(a, f(a))处与直线y=b相切,∴f′(a)=a(2+cos a)=0,f(a)=b,联立{2a+a cos a=0,a2+a sin a+cos a=b,解得{a=0,b=1,故a=0,b=1.(2)∵f′(x)=x(2+cos x).令f′(x)=0,得x=0,x,f(x),f′(x)的变化情况如表:- +(0, +∞)上单调递增,f(0)=1是f(x)的最小值.故当b>1时曲线y=f(x)与直线y=b有且只有两个不同的交点.【答案】解:(1)∵点B的坐标为(0, 1),当四边形OABC为菱形时,AC⊥OB,而B(0, 1),O(0, 0),∴线段OB的垂直平分线为y=12,将y=12代入椭圆方程得x=±√3,因此A、C的坐标为(±√3, 12),如图,于是AC=2√3.(2)欲证明四边形OABC不可能为菱形,利用反证法,假设四边形OABC为菱形,则有OA=OC,设OA=OC=r,则A、C为圆x2+y2=r2与椭圆W:x24+y2=1的交点,故3x24=r2−1,x2=43(r2−1),则A、C两点的横坐标相等或互为相反数.从而得到点B是W的顶点.这与题设矛盾.于是结论得证.【考点】椭圆中的平面几何问题反证法椭圆的标准方程【解析】(I)先根据条件得出线段OB的垂直平分线方程为y=12,从而A、C的坐标为(±√3, 12),根据两点间的距离公式即可得出AC的长;(II)欲证明四边形OABC不可能为菱形,只须证明若OA=OC,则A、C两点的横坐标相等或互为相反数.设OA=OC=r,则A、C为圆x2+y2=r2与椭圆W:x24+y2=1的交点,从而解得3x24=r2−1,则A、C两点的横坐标相等或互为相反数.于是结论得证.【解答】解:(1)∵点B的坐标为(0, 1),当四边形OABC为菱形时,AC⊥OB,而B(0, 1),O(0, 0),∴线段OB的垂直平分线为y=12,将y=12代入椭圆方程得x=±√3,因此A、C的坐标为(±√3, 12),如图,于是AC=2√3.(2)欲证明四边形OABC不可能为菱形,利用反证法,假设四边形OABC为菱形,则有OA=OC,设OA=OC=r,则A、C为圆x2+y2=r2与椭圆W:x24+y2=1的交点,故3x 24=r2−1,x2=43(r2−1),则A、C两点的横坐标相等或互为相反数.从而得到点B是W的顶点.这与题设矛盾.于是结论得证.【答案】解:(1)当i=1时,A1=3,B1=1,故d1=A1−B1=2,同理可求d2=3,d3=6;(2)由a1,a2,…,a n−1(n≥4)是公比q大于1的等比数列,且a1>0,则{a n}的通项为:a n=a1q n−1,且为单调递增的数列.于是当k=1,2,…n−1时,d k=A k−B k=a k−a k+1,进而当k=2,3,…n−1时,d kd k−1=a k−a k+1a k−1−a k=a k(1−q)a k−1(1−q)=q为定值.∴d1,d2,…,d n−1是等比数列;(3)设d为d1,d2,…,d n−1的公差,对1≤i≤n−2,因为B i≤B i+1,d>0,所以A i+1=B i+1+d i+1≥B i+d i+d>B i+d i=A i,又因为A i+1=max{A i, a i+1},所以a i+1=A i+1>A i≥a i.从而a1,a2,…,a n−1为递增数列.因为A i=a i(i=1, 2,…n−1),又因为B1=A1−d1=a1−d1<a1,所以B1<a1<a2<...<a n−1,因此a n=B1.所以B1=B2=…=B n−1=a n.所以a i=A i=B i+d i=a n+d i,因此对i=1,2,…,n−2都有a i+1−a i=d i+1−d i=d,即a1,a2,…,a n−1是等差数列.【考点】等差数列与等比数列的综合【解析】(Ⅰ)当i=1时,A1=3,B1=1,从而可求得d1,同理可求得d2,d3的值;(Ⅱ)依题意,可知a n=a1q n−1(a1>0, q>1),由d k=a k−a k+1⇒d k−1=a k−1−a k(k≥2),从而可证d kd k−1(k≥2)为定值.(Ⅲ)依题意,0<d1<d2<...<d n−1,可用反证法证明a1,a2,…,a n−1是单调递增数列;再证明a m为数列{a n}中的最小项,从而可求得是a k=d k+a m,问题得证.【解答】解:(1)当i=1时,A1=3,B1=1,故d1=A1−B1=2,同理可求d2=3,d3=6;(2)由a1,a2,…,a n−1(n≥4)是公比q大于1的等比数列,且a1>0,则{a n}的通项为:a n=a1q n−1,且为单调递增的数列.于是当k=1,2,…n−1时,d k=A k−B k=a k−a k+1,进而当k=2,3,…n−1时,d kd k−1=a k−a k+1a k−1−a k=a k(1−q)a k−1(1−q)=q为定值.∴d1,d2,…,d n−1是等比数列;(3)设d为d1,d2,…,d n−1的公差,对1≤i≤n−2,因为B i≤B i+1,d>0,所以A i+1=B i+1+d i+1≥B i+d i+d>B i+d i=A i,又因为A i+1=max{A i, a i+1},所以a i+1=A i+1>A i≥a i.从而a1,a2,…,a n−1为递增数列.因为A i=a i(i=1, 2,…n−1),又因为B1=A1−d1=a1−d1<a1,所以B1<a1<a2<...<a n−1,因此a n=B1.所以B1=B2=…=B n−1=a n.所以a i=A i=B i+d i=a n+d i,因此对i=1,2,…,n−2都有a i+1−a i=d i+1−d i=d,即a1,a2,…,a n−1是等差数列.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大兴区2013年高三统一练习数学(理科)一、选择题(1)复数2(1i)+的值是(A )2 (B )2- (C )2i (D )2i -(2)设集合2{|1}=>A x x ,2{|log 0|}=>B x x ,则ÇA B 等于(A )}1|{>x x (B )}0|{>x x (C )}1|{-<x x(D ){|11},或x x x <-> (3)执行如图所示的程序框图.若4n =,则输出s 的值是 (A )-42 (B ) -21 (C ) 11 (D ) 43(4)设0.70.45 1.512314,8,(2y y y -===,则(A )312y y y >> (B )213y y y >> (C )123y y y >>(D )132y y y >>(5)已知平面βα,,直线n m ,,下列命题中不.正确的是 (A )若α⊥m ,β⊥m ,则α∥β (B )若m ∥n ,α⊥m ,则α⊥n (C )若m ∥α,n =βα ,则m ∥n (D )若α⊥m ,β⊂m ,则βα⊥.(6)函数()f x =(A )在ππ(,)22-上递增 (B )在π(,0]2-上递增,在π(0,)2上递减(C )在ππ(,)22-上递减 (D )在π(,0]2-上递减,在π(0,)2上递增 (7)若实数,a b 满足221a b +≤,则关于x 的方程220x x a b -++=无.实数根的概率为 (A )14 (B ) 34(C )3π24π+ (D )π24π-(8)抛物线2(22)y x x =-≤≤绕y 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是(A )1 (B )2 (C) (D )4二、填空题(9)函数f x x x ()s i nc o s =的最小正周期是 (10)已知中心在原点,焦点在x 轴上的双曲线的离心率为32,实轴长为4,则双曲线的方程是(11)已知矩形ABCD 中,2AB =,1AD =,E 、F 分别是BC 、CD 的中点,则()AE AF AC +?等于 .(12)已知数列{}n a ,1+2n n a a +=,1=1a ,数列11n n a a +禳镲镲睚镲镲铪的前n 项和为1837,则n = . (13)已知函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x 在区间[1,]m -上的最大值是1,则m 的取值范围是.(14)已知函数()f x 是定义在(0,)+?上的单调递增函数,且*ÎN x 时,()*ÎN f x ,若[()]3f f n n =,则(2)=f ;(4)(5)f f +=三、解答题(15)(本小题满分13分)在∆A B C 中,角A ,B ,C 的对边分别为a ,b ,c ,3cos 5=A ,π4B =,b =.(Ⅰ)求a 的值;(Ⅱ)求sin C 及∆A B C 的面积. (16)(本小题满分13分)一次考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩如下表:(Ⅰ)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定;(Ⅱ)从以上5名同学中选2人参加一项活动,求选中的学生中至少有一个物理成绩高于90分的概率.(17)(本小题满分13分)如图,直三棱柱ABC —A 1B 1C 1中,ABC D 是等边三角形,D 是BC 的中点. (Ⅰ)求证:直线A 1D ⊥B 1C 1;(Ⅱ)判断A 1B 与平面ADC 1的位置关系,并证明你的结论.(18)(本小题满分14分) 已知函数()(1)e x f x ax =+.(I )求函数()f x 的单调区间;(Ⅱ)当0a >时,求函数()f x 在区间[2,0]-上的最小值.19.(本小题满分14分)已知动点P 到点A (-2,0)与点B (2,0)的斜率之积为14-,点P 的轨迹为曲线C 。
(Ⅰ)求曲线C 的方程;(Ⅱ)若点Q 为曲线C 上的一点,直线AQ ,BQ 与直线x =4分别交于M 、N 两点,直线BM 与椭圆的交点为D 。
求线段MN 长度的最小值。
(20)(本小题满分13分)已知数列}{n a 的各项均为正整数,且12n a a a <<<,设集合1{|101}1,,或,或(≤≤)nk i iiiii A x x a k n λλλλ====-==∑。
性质1 若对于k x A ∀∈,存在唯一一组i λ(1,2,,i k =⋅⋅⋅)使1ki i i x a λ==∑成立,则称数列}{n a 为完备数列,当k 取最大值时称数列}{n a 为k 阶完备数列。
性质2 若记1(1≤≤)kk i i m a k n==∑,且对于任意≤k x m ,x ∈Z ,都有k x A ∈成立,则称数列}{n a 为完整数列,当k 取最大值时称数列}{n a 为k 阶完整数列。
性质3 若数列}{n a 同时具有性质1及性质2,则称此数列}{n a 为完美数列,当k 取最大值时}{n a 称为k 阶完美数列;(Ⅰ)若数列}{n a 的通项公式为12-=n a n ,求集合2A ,并指出}{n a 分别为几阶完备数列,几阶完整数列,几阶完美数列;(Ⅱ)若数列}{n a 的通项公式为110-=n n a ,求证:数列}{n a 为n 阶完备数列,并求出集合nA 中所有元素的和n S 。
(Ⅲ)若数列}{n a 为n 阶完美数列,试写出集合n A ,并求数列}{n a 通项公式。
2013年高三统一练习 高三数学(文科)参考答案一、选择题(共8小题,每小题5分,共40分)(1)C (2)A (3)C (4)A (5)C (6)D (7)D (8)B 二、填空题(共6小题,每小题5分,共30分)(9)π 154)10(22=-y x 215)11( 18)12( (](13)1,1- 15,3)14(三、解答题(共6小题,共80分) (15)(本小题共13分) 解:(Ⅰ)因为 ABC ,53cos 内角是∆=A A ,所以,54sin =A由正弦定理:B b A a sin sin =知4πs i n 54a = 得: 58=a(Ⅱ)在 AB C ∆中, )sin()](sin[sin B A B A C +=+-=π102722532254sin cos cos sin =⨯+⨯=+=B A B A ABC ∆的面积为:2528102725821sin 21=⨯⨯⨯==C ab s(16)(本小题共13分) 解:(I) 5名学生数学成绩的平均分为:93)9795939189(51=++++ 5名学生数学成绩的方差为:8])9397()9395()9393()9391()9389[(5122222=-+-+-+-+- 5名学生物理成绩的平均分为:90)9392898987(51=++++5名学生物理成绩的方差为:524])9093()9092()9089()9089()9087[(5122222=-+-+-+-+- 因为样本的数学成绩方差比物理成绩方差大,所以,估计高三(1)班总体物理成绩比数学成绩稳定.(Ⅱ)设选中的学生中至少有一个物理成绩高于90分为事件A5名学生中选2人包含基本事件有:,21A A ,31A A ,41A A ,51A A ,32A A ,42A A ,52A A ,43A A ,53A A ,54A A 共10个.事件A 包含基本事件有:,41A A ,51A A ,42A A ,52A A ,43A A ,53A A ,54A A 共7个. 107)( =A P 则所以,5名学生中选2人, 选中的学生中至少有一个物理成绩高于90分的概率为107.(17)(本小题共13分)解: (Ⅰ)在直三棱柱111C B A ABC -中,1AA ABC ⊥面,所以1AA BC ⊥, 在等边 ABC ∆中,D 是BC 中点,所以BC AD ⊥因为 在平面AD A 1中,A AD A A =⋂1,所以 1BC A AD ⊥面 又因为AD A D 11面⊂A ,所以,BC D A ⊥1在直三棱柱111C B A ABC -中,四边形11BCC B 是平行四边形,所以BC C B //11 所以,111C B D A ⊥(Ⅱ) 在直三棱柱111C B A ABC -中,四边形11ACC A 是平行四边形, 在平行四边形11ACC A 中联结C A 1,交于1AC 点O ,联结DO . 故O 为C A 1中点.在三角形CB A 1中,D 为BC 中点,O 为C A 1中点,故B A DO 1//.因为111, DO DAC A B DAC ⊂⊄平面平面,所以,11 //ADC B A 面故,11 ADC B A 与面平行 (18)(本小题共14分) 解:定义域为R)1())(1()1()('''++=+++=a ax e e ax e ax x f x x x(Ⅰ)①当0a =时,0)('>=xe xf ,则()f x 的单调增区间为),(+∞-∞②当0a >时,解0)('>x f 得, aa x 1+->,解0)('<x f 得, a a x 1+-<,则()f x 的单调增区间为),1(+∞+-a a ,()f x 的单调减区间为)1,(aa +--∞ ③当0<a 时,解0)('>x f 得, a a x 1+-<,解0)('<x f 得, a a x 1+->,则()f x 的单调增区间为)1,(a a +--∞,()f x 的单调减区间为),1(+∞+-aa (Ⅱ) ①当⎪⎩⎪⎨⎧->+->21aa a 时, 即 当1>a 时, ()f x 在)1,2(aa +--上是减函数,在)0,1(aa +-上是增函数,则函数()f x 在区间[-2,0]上的最小值为 aa ae aa f 1)1(+--=+-②当⎪⎩⎪⎨⎧-≤+->210aa a 时, 即 当10≤<a 时, ()f x 在]0,2[-上是增函数,则函数()f x 在区间[-2,0]上的最小值为221)2(eaf -=- 综上: 当1>a 时, ()f x 在区间[-2,0]上最小值为a a ae1+--当10≤<a 时, ()f x 在区间[-2,0]上最小值为221ea-(19)(本小题共14分)解:(Ⅰ)设),(y x P ,由题意知 41-=⋅BP AP k k ,即)2(4122±≠-=-⋅+x x y x y 化简得曲线C 方程为:)2( 1422±≠=+x y x (Ⅱ)思路一满足题意的直线AQ 的斜率显然存在且不为零,设其方程为)2(+=x k y ,由(Ⅰ)知41-=⋅k k QB ,所以,设直线QB 方程为k y 41-=)2(-x , 当4=x 时得N 点坐标为)21,4(kN -,易求M 点坐标为)6,4(k M 所以k k MN 216||+==|2|1|6|k k +32|2|1|6|2=⋅≥k k , 当且仅当63±=k 时,线段MN 的长度有最小值32. 思路二:满足题意的直线AQ 的斜率显然存在且不为零,设其方程为)2(+=x k y ,联立方程:⎪⎩⎪⎨⎧+==+)2(1422x k y y x消元得2222(41)161640k x k x k +++-=,设),(00y x Q ,),(),,(2211y x N y x M ,由韦达定理得:144162220+-=⋅-k k x ,所以1428220++-=k k x ,代入直线方程得14420+=k ky , 所以222284(,)1414k kQ k k -++,又2,0B() 所以直线BQ 的斜率为22240114,428214kk k k k -+=---+ 以下同思路一思路三:设),(00y x Q ,则直线AQ 的方程为00(2)2y y x x =++ 直线BQ 的方程为00(2)2y y x x =-- 当4x =,得0062M y y x =+,即006(4,)2y M x + 当4x =,得0022N y y x =-,即002(4,)2y N x - 则0000200062282224y y x MN y x x x -=-=⋅+-- 2220020284()4x MN y x -=⋅- 又220044x y +=所以220204(4)4x MN x -=-利用导数,或变形为二次函数求其最小值。
