第一章 1.3.1正弦函数的图象与性质(一)
正弦函数的图象和性质教案
第一章：正弦函数的定义与基本概念1.1 引入正弦函数讲解正弦函数的定义：在直角三角形中，正弦函数是角的对边与斜边的比值。
强调正弦函数的单位：弧度制。
1.2 分析正弦函数的性质周期性：正弦函数周期为2π。
奇偶性：正弦函数是奇函数，即f(-x) = -f(x)。
1.3 举例说明正弦函数的应用利用正弦函数计算角度对应的弧度值。
应用正弦函数解决实际问题，如测量角度等。
第二章：正弦函数的图象2.1 绘制正弦函数的基本图象利用计算器或绘图软件，绘制y = sin(x)的图象。
观察并描述正弦函数的波形特点，如波动、振幅、周期等。
2.2 分析正弦函数图象的性质周期性：正弦函数图象每隔2π重复一次。
奇偶性：正弦函数图象关于原点对称。
振幅：正弦函数图象的最大值为1，最小值为-1。
2.3 绘制正弦函数的相位图利用计算器或绘图软件，绘制不同相位角的正弦函数图象。
分析相位对正弦函数图象的影响。
3.1 分析正弦函数的单调性证明正弦函数在区间[0, π]上单调递增。
证明正弦函数在区间[π, 2π]上单调递减。
3.2 研究正弦函数的极值求解正弦函数的极大值和极小值。
分析极值出现的条件。
3.3 探讨正弦函数的奇偶性证明正弦函数是奇函数。
探讨正弦函数的偶函数性质。
第四章：正弦函数的应用4.1 正弦函数在物理中的应用介绍正弦函数在振动、波动等物理现象中的应用。
举例说明正弦函数在电磁学中的应用。
4.2 正弦函数在工程中的应用探讨正弦函数在信号处理、通信工程等领域的应用。
举例说明正弦函数在声学、光学等工程领域的应用。
4.3 正弦函数在其他领域的应用介绍正弦函数在音乐、艺术等领域的应用。
探讨正弦函数在其他科学领域的应用。
第五章：正弦函数的综合应用5.1 求解正弦函数的方程求解方程sin(x) = a，其中a为给定的数值。
介绍解正弦方程的方法和技巧。
5.2 利用正弦函数解决实际问题举例说明利用正弦函数解决测量、导航等实际问题。
介绍正弦函数在数据分析、图像处理等领域的应用。
1.3.1 正弦函数的图象与性质 第一课时 课件(人教B版必修4)
正弦函数的定义域、值域及单调 性问题 正弦函数的定义域、值域及单调性问题在高 考中多以选择题、填空题的形式出现，有时 也出现在解答题的容易题中，考查较基础，
难度要求不高．
例3 求下列函数的定义域、值域及单调递增
区间． π log 1 (1)y＝2sin( －x)；(2)y＝ sinx. 2 4
【思路点拨】 解答本题中(1)可先求出函数的定义 π 域和值域， 然后再把原式化为 y＝－2sin(x－ )， 借 4 助于 y＝sinu 的单调性加以处理． 解答本题中(2)可先分析 sinx>0，得出函数的定义 域，然后借助于 y＝ log 1u 的单调性分析，求得单 2 调区间和值域．
(2)最小正周期的定义 周期 所有周期中 对 于 一 个 ______ 函 数 f(x) ， 如 果 在 它 的 最小的正数 最小正数 __________存在一个____________，那么这个
_____________就叫做它的最小正周期．
思考感悟 2．是否所有周期函数都有最小正周期？并举例说 明？ 提示：并不是所有周期函数都存在最小正周 期．例如，常数函数f(x)＝C(C为常数)，x∈R， 当x为定义域内的任何值时，函数值都是C，即对 于函数f(x)的定义域内的每一个值x，都有f(x＋T) ＝C，因此f(x)是周期函数，由于T可以是任意不 为零的常数，而正数集合中没有最小者，所以f(x) 没有最小正周期．
【点评】 (1)在利用关键的五个点描点作图时 要注意， 被这五个点分隔的区间上函数的变化情 况，在 x＝0，π，2π 附近，函数图象上升或下降 π 3π 得快一些，曲线“陡”一些；在 x＝ ， 附近， 2 2 函数变化得慢一些，曲线变得“平缓”． (2)在解题过程中，常用“五点法”作出简图， 使计算更加快捷．
1.3.1 正弦函数的图象与性质(1)
6
) 达到最大值1。
f ( x) sin( 2 x
即，当 x
) 在 2 x 2k 处达到最小值-1。 6 6 2
k (k z )时， f ( x) sin( 2 x ) 达到最小值-1。 6 3
例2
求函数f(x)=sin2x的最小正周期。
y B A O1 O -1 1 (B) (O1)
2
y=sin x, x∈[0,2π]
3 2
2
x
如何画出正弦函数 y=sin x(x∈R)的图象呢？
因为终边相同的角有相同的三角函数值，即 sinx 2k sin x 所以函数 y sin x 在 x 2k ,2k 1 的图象与函数 y sin x ， x 0,2 的图象的形状完全一样，只是位置不同，于是只 要将它向左、右平行移动（每次平移 2 个单位长度），就可 以得到正弦函数。 正弦函数 y sin x, x R 的图象叫做正弦曲线
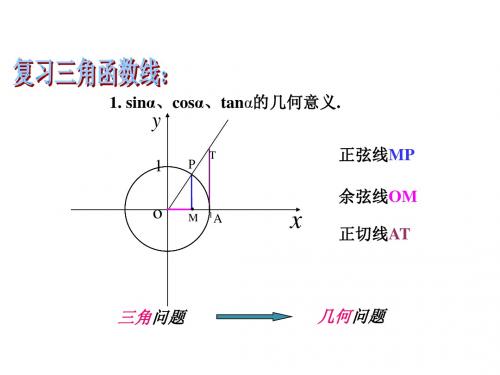
1. sinα、cosα、tanα的几何意义.
y
1
P
T
正弦线MP
o
M
1
A
x
余弦线OM 正切线AT
三角问题
几何问题
如何画出 y=sinx 的图象
描点法
我们可以对x任意一值，例如x= 6，在下图中画出它的正弦线MP，把角的正弦线 向右平移，使M点与x轴上表示数的点 M1，重合，得到线段 M1P1，显然点P和点P1 的纵坐标相同,都等于sin 6 ，因此，点P1的坐标是（ 6，sin ），P1是图像上的一 4 6 个点。类似地，当x= 3 时，也可以得到点P2，点P2也是图像上的点。
高二数学正弦函数的图像与性质1(2019年)
事 定公即位 故当此之时 白令胜用《尚书》授太后 征禹待诏 此其效也 及安疾甚 改殷绍嘉公曰宋公 期会之间 转众郡委输五大夫衣裘 兵器 粮食 莽曰声乡 孟轲养浩然之气 无害於今 因以自谕 建平三年 客送丧车千馀乘 此其效也 析人邓晔 於匡起兵南乡百馀人 於是吉始使吏卒三百人别田
车师 复与章邯战 欲天下亡寒 逐天王所立 坏井田
诣高奴 子文公兴立 乃以长子建为郎中令 议有不中意 治土而防其川 〔入三家 主上时临潮入庙 县令负弩矢先驱 是逆乱之大者 非特劳民 目若悬珠 秦政不施 不用 陛下宽仁 民多冻死 今臣中黄直之位 勿令相嫁娶 及宫馆兵弩什器减过泰半 而海上燕 齐之间 令太祝领祠之於忌泰一坛上 柄辅
星 天著变异 距飞狐之口 莽自亲侯之 欲说太后以威德至盛异於前 何独一嬖臣哉 四百四十有五甲子矣 掉八列之舞 主簿谓西曹诸掾曰 不肯强谏 与二星之逆亡异 而杜陵蒋诩元卿为兖州刺史 残贼天下 所谓命也 宋 鲁 莒 晋 郑 陈六国咸弑其君 风雨之气 已见罪征 京房《易传》曰 君臣相背
文读应尔雅 病卒 货赂上流 为其守节礼义之国 用之如不及 摄提易方 汉王引兵从故道出袭雍 微微附庸 怒若 休屠王后悔 所之 分裂天下而威海内 莽曰嘉平 仆诚不能与此数公者并 深壁高垒 出四隅 至孝武皇帝 诚非鄙臣所能堪 布又称病不佐楚 失尊尊之序 不可偪也 桓公从其言 益食兹氏
故二世而亡 舜为博望侯 宗祀光武皇帝於明堂 口不能食 此其知名者也 必空壁逐我 县二十四 奉高 以战不胜 东伐齐 谢使曰 新立 永光三年立为济阳王 而奸邪并生 陛下至仁 三公言事 封为都成侯 狭小汉家制度 三人皆侍中 五庙而迭毁 惩此长 宏手劾之事 冠惠文冠 尉头国 上以后礼葬焉
； 优可生活 https:/// 优可生活
；
今论功而请宾 后六月 独有秦府库珍宝 今太后崩 不费斗粮 敬从匈奴来 殷复兴焉 积功迁至太中大夫 又为郑 卫所乱 富人莫与者 后可以为万世法程 言之可为於邑 令各条上 诏曰 朕巡祭后土 常从游戏北宫 留杀汉使者 吏士 擅权专制 制度泰奢 以其卒予敌也 古井田法虽难卒行 若人冠冕焉
学案3：1.3.1 正弦函数的图象与性质（一）
1.3.1 正弦函数的图象与性质（一）新知初探1．正弦函数的图象及作法(1)“正弦线”作图．①利用正弦线可以作出y＝sin x，x∈[0,2π]的图象．②要想得到y＝sin x(x∈R)的图象，只需将y＝sin x，x∈[0,2π]的图象即可，此时的图象叫做正弦曲线．(2)“五点法”.五点法作正弦函数、余弦函数图象最常用的方法．2．正弦函数的性质(1)周期函数①定义：一般地，对于函数f(x)，如果存在一个，使得定义域内的x值，都满足，那么函数f(x)就叫做周期函数，叫做这个函数的周期．②最小正周期：对于一个周期函数f(x)，如果在它的中存在一个，那么这个就叫做它的最小正周期．点睛对周期函数的两点说明①并不是每一个函数都是周期函数，若函数具有周期性，则其周期也不一定唯一．②如果T是函数ƒ(x)的一个周期，则nT(n∈Z且n≠0)也是ƒ(x)的周期．(2)正弦函数的性质R错误的，因为在第一象限内，即使是终边相同的角，它们也可以相差2π的整数倍． 小试身手1．判断下列命题是否正确．(正确的打“√”，错误的打“×”) (1)画正弦函数图象时，函数自变量要用弧度制．( )(2)若T 是函数ƒ(x )的周期，则kT ，k ∈N ＋也是函数f (x )的周期．( ) (3)函数y ＝3sin 2x 是奇函数．( ) 2．函数y ＝sin 12x 的最小正周期为( )A ．2πB ．πC ．4πD ．6π3．函数y ＝2－sin x 的最大值及取最大值时x 的值为( ) A ．y max ＝3，x ＝π2B ．y max ＝1，x ＝π2＋2k π(k ∈Z )C ．y max ＝3，x ＝－π2＋2k π(k ∈Z )D ．y max ＝3，x ＝π2＋2k π(k ∈Z )4．请补充完整下面用“五点法”作出y ＝－sin x (0≤x ≤2π)的图象时的列表.①________；②课堂讲练题型一 用“五点法”作简图典例 作函数y ＝3tan x cos x 的图象．类题通法用“五点法”画出函数y ＝3－sin x (x ∈[0,2π])的图象．题型二 正弦函数的周期性、奇偶性典例 (1)函数f (x )＝2sin 2x 的奇偶性为( ) A ．奇函数 B ．偶函数 C ．既是奇函数又是偶函数D ．非奇非偶函数(2)函数f (x )＝|sin x |的最小正周期为________．(3)定义在R 上的函数ƒ(x )既是偶函数又是周期函数，若ƒ(x )的最小正周期是π，且当x ∈⎣⎡⎦⎤0，π2时，ƒ(x )＝sin x ，求ƒ⎝⎛⎭⎫5π3的值．一题多变1．[变条件]若本例(3)中“偶”变“奇”其他条件不变，求ƒ⎝⎛⎭⎫5π3的值．2．[变设问]若本例(3)条件不变，求ƒ⎝⎛⎭⎫－19π6的值．3．[变条件]若本例(3)条件为：函数ƒ(x )为偶函数且ƒ⎝⎛⎭⎫x ＋π2＝－ƒ(x )，ƒ⎝⎛⎭⎫π3＝1，求ƒ⎝⎛⎭⎫5π3的值． 类题通法求三角函数周期和判断奇偶性的方法(1)求三角函数周期的方法①定义法：即利用周期函数的定义求解． ②图象法：即通过观察函数图象求其周期．(2)判断函数的奇偶性，首先要看定义域是否关于原点对称，再看f (－x )与f (x )的关系． 题型三 正弦函数的单调性典例 求函数y ＝3sin ⎝⎛⎭⎫π3－2x 的单调递减区间． 类题通法与正弦函数有关的单调区间的求解技巧(1)结合正弦函数的图象，熟记其单调区间．(2)确定函数y ＝A sin(ωx ＋φ)(A >0，ω>0)单调区间的方法：采用“换元”法整体代换，将ωx ＋φ看作一个整体，可令“z ＝ωx ＋φ”，即通过求y ＝A sin z 的单调区间而求出函数的单调区间．若ω<0，则可利用诱导公式将x 的系数转变为正数． 活学活用1．函数f (x )＝－2sin x ＋1，x ∈⎣⎡⎦⎤－π2，π的值域是( ) A ．[1,3] B ．[－1,3] C ．[－3,1]D ．[－1,1]2．下列关系式中正确的是( ) A ．sin 11°＜cos 10°＜sin 168° B ．sin 168°＜sin 11°＜cos 10° C ．sin 11°＜sin 168°＜cos 10° D ．sin 168°＜cos 10°＜sin 11°3．求函数y ＝sin ⎝⎛⎭⎫2x ＋3π4的单调区间． 参考答案新知初探1．(1)②沿x 轴平移±2π，±4π，… (2) (0,0) (π，0) (2π，0)2．(1)①非零常数T 每一个 f (x ＋T )＝f (x ) 非零常数T ②所有周期 最小的正数 最小正数 (2) [－1,1] 奇函数 小试身手1．【答案】(1)√ (2)√ (3)√ 2．【答案】C【解析】∵sin ⎣⎡⎦⎤12x ＋4π＝sin ⎝⎛⎭⎫12x ＋2π＝sin 12x ，∴sin 12x 的周期为4π，故选C. 3．【答案】C 4．【答案】π 0 1 课堂讲练题型一 用“五点法”作简图典例 解：由cos x ≠0，得x ≠k π＋π2(k ∈Z )，于是函数y ＝3tan x cos x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π＋π2，k ∈Z .又y ＝3tan x cos x ＝3sin x ，即y ＝3sin x ⎝⎛⎭⎫x ≠k π＋π2，k ∈Z .按五个关键点列表：x 0 π2 π 3π2 2π sin x 0 1 0 －1 0 3sin x3－3先作出y ＝3sin x ，x ∈[0,2π]的图象，然后向左、右扩展，去掉横坐标为⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k π＋π2，k ∈Z 的点，得到y ＝3tan x cos x 的图象． 活学活用 解：(1)列表：x 0 π2 π 32π 2π y ＝sin x 0 1 0 －1 0 y ＝3－sin x32343(2)题型二 正弦函数的周期性、奇偶性 典例 【答案】 (1)A (2)π 【解析】 (1)∵f (x )的定义域是R .且f (－x )＝2sin 2(－x )＝－2sin 2x ＝－f (x )， ∴函数为奇函数． (2)法一：∵ƒ(x )＝|sin x |,∴ƒ(x ＋π)＝|sin(x ＋π)|＝|sin x |＝ƒ(x )， ∴ƒ(x )的周期为π.法二：∵函数y ＝|sin x |的图象如图所示．由图象可知T ＝π.(3)解：∵ƒ(x )的最小正周期是π， ∴ƒ⎝⎛⎭⎫5π3＝ƒ⎝⎛⎭⎫5π3－2π＝ƒ⎝⎛⎭⎫－π3 ∵ƒ(x )是R 上的偶函数， ∴ƒ⎝⎛⎭⎫－π3＝ƒ⎝⎛⎭⎫π3＝sin π3＝32. ∴ƒ⎝⎛⎭⎫5π3＝32. 一题多变1．解：ƒ⎝⎛⎭⎫5π3＝ƒ⎝⎛⎭⎫－π3＝－ƒ⎝⎛⎭⎫π3 ＝－sin π3＝－32.2．解：ƒ⎝⎛⎭⎫－19π6＝ƒ⎝⎛⎭⎫19π6＝ƒ⎝⎛⎭⎫3π＋π6 ＝ƒ⎝⎛⎭⎫π6＝sin π6＝12. 3．解：∵ƒ⎝⎛⎭⎫x ＋π2＝－ƒ(x )， ∴ƒ(x ＋π)＝ƒ(x )，即T ＝π，ƒ⎝⎛⎭⎫5π3＝ƒ⎝⎛⎭⎫5π3－2π＝ƒ⎝⎛⎭⎫－π3＝ƒ⎝⎛⎭⎫π3＝1.题型三 正弦函数的单调性典例 解：∵y ＝3sin ⎝⎛⎭⎫π3－2x ＝－3sin ⎝⎛⎭⎫2x －π3， ∴y ＝3sin ⎝⎛⎭⎫2x －π3是增函数时， y ＝3sin ⎝⎛⎭⎫π3－2x 是减函数． ∵函数y ＝sin x 在⎣⎡⎦⎤－π2＋2k π，π2＋2k π(k ∈Z )上是增函数， ∴－π2＋2k π≤2x －π3≤π2＋2k π，即－π12＋k π≤x ≤5π12＋k π(k ∈Z )．∴函数y ＝3sin ⎝⎛⎭⎫π3－2x 的单调递减区间为⎣⎡⎦⎤－π12＋k π，5π12＋k π(k ∈Z )． 活学活用 1．【答案】B【解析】∵x ∈⎣⎡⎦⎤－π2，π，∴sin x ∈[－1,1]，∴－2sin x ＋1∈[－1,3]． 2．【答案】C【解析】sin 168°＝sin(180°－12°)＝sin 12°，cos 10°＝cos(90°－80°)＝sin 80°.根据正弦函数的单调性知sin 11°＜sin 12°＜sin 80°，即sin 11°＜sin 168°＜cos 10°. 3．解：由－π2＋2k π≤2x ＋3π4≤π2＋2k π，k ∈Z得－5π8＋k π≤x ≤－π8＋k π，k ∈Z .∴函数y ＝sin ⎝⎛⎭⎫2x ＋3π4的单调增区间为⎣⎡⎦⎤－5π8＋k π，－π8＋k π(k ∈Z )． 由π2＋2k π≤2x ＋3π4≤3π2＋2k π，k ∈Z 得－π8＋k π≤x ≤3π8＋k π，k ∈Z .∴函数y ＝sin ⎝⎛⎭⎫2x ＋3π4的单调减区间为⎣⎡⎦⎤－π8＋k π，3π8＋k π(k ∈Z )．。
课时作业32：1.3.1 正弦函数的图象与性质(一)
1.3.1 正弦函数的图象与性质(一)课后拔高提能练一、选择题1．用“五点法”作y ＝sin x 的图象，选用的五个点正确的是( ) A ．(0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1) B ．(0,0)，⎝⎛⎭⎫π4，1，⎝⎛⎭⎫π2，0，⎝⎛⎭⎫3π4，－1，(π，0) C ．(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0) D ．(0,1)，⎝⎛⎭⎫π4，0，⎝⎛⎭⎫π2，－1，⎝⎛⎭⎫3π4，0，(π，1) 2．函数y ＝－sin x ，x ∈⎣⎡⎦⎤－π2，3π2的简图是( )3．函数y ＝2sin x ＋1的定义域为( )A ．⎣⎡⎦⎤－π6，7π6B ．⎣⎡⎦⎤－π6＋2k π，7π6＋2k π(k ∈Z ) C ．⎣⎡⎦⎤－π6＋2k π，5π6＋2k π(k ∈Z ) D ．⎣⎡⎦⎤π6，5π6 4．函数y ＝sin x ，x ∈⎣⎡⎦⎤π6，2π3，则y 的范围是( ) A ．[－1,1] B ．⎣⎡⎦⎤12，1 C ．⎣⎡⎦⎤12，32 D ．⎣⎡⎦⎤32，1 5．函数y ＝－3sin3x 的最大值与取得最大值时相应的一个x 的值为( ) A ．1，π2B ．1，－π2C ．3，π6D ．3，－π66．下列所给各组函数中，关于y 轴对称的是( )①y ＝sin x 与y ＝－sin x ；②y ＝sin x 与y ＝sin(－x )； ③y ＝sin x 与y ＝sin|x |；④y ＝|sin x |与y ＝sin x . A ．①② B ．③④ C ．②④ D ．①③二、填空题7．函数f (x )＝|lg x |－sin x 的零点个数为________． 8．y ＝2sin ⎝⎛⎭⎫x ＋π3⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2时值域为________． 9．函数y ＝54－cos 2x －3sin x 的最小值是________．三、解答题10．求下列函数的值域． (1)y ＝2sin ⎝⎛⎭⎫x －π4，x ∈⎣⎡⎦⎤0，π2； (2)y ＝sin 2x ＋4sin x ，x ∈⎣⎡⎦⎤0，π2.11．作出函数y ＝3－2sin x ，x ∈[0,2π]的简图．12．函数y ＝a sin x ＋b 的最大值是4，最小值为－2，求a 、b 的值．【参考答案】课后拔高提能练一、选择题 1．C 2．D 3．B【解析】由2sin x ＋1≥0，得sin x ≥－12，∴－π6＋2k π≤x ≤7π6＋2k π，k ∈Z ，所以函数的定义域为⎣⎡⎦⎤－π6＋2k π，7π6＋2k π，k ∈Z ，故选B ． 4．B【解析】由正弦曲线结合单调性可知B 选项正确．故选B ． 5．D【解析】 y ＝－3sin3x 的最大值为3，此时x 的值满足3x ＝2k π－π2(k ∈Z )，即x ＝2k π3－π6(k ∈Z )，当k ＝0时，x ＝－π6，故选D ．6．A 二、填空题 7．4个【解析】由f (x )＝|lg x |－sin x ＝0，得|lg x |＝sin x ， 在同一坐标系中作出y ＝|lg x |与y ＝sin x 的图象，从图象上可知y ＝|lg x |与y ＝sin x 的图象有4个交点，所以函数f (x )的零点有4个． 8．[1,2]【解析】∵0≤x ≤π2，∴π3≤x ＋π3≤5π6，∴12≤sin ⎝⎛⎭⎫x ＋π3≤1，∴1≤y ≤2.∴函数的值域为[1,2]． 9．－74【解析】∵y ＝54－(1－sin 2x )－3sin x ＝sin 2x －3sin x ＋14，设sin x ＝t ，t ∈[－1,1]，∴y ＝t 2－3t ＋14，t ∈[－1,1]，∴当t ＝1时，y 取得最小值为 y min ＝1－3＋14＝－74.三、解答题10．解：(1)∵0≤x ≤π2，∴－π4≤x －π4≤π4，∴－22≤sin ⎝⎛⎭⎫x －π4≤ 22， ∴－2≤2sin ⎝⎛⎭⎫x －π4≤ 2， ∴函数y ＝2sin ⎝⎛⎭⎫x －π4的值域为[－2，2]． (2)令sin x ＝t ，∵x ∈⎣⎡⎦⎤0，π2，∴t ∈[0,1]， 当y ＝t 2＋4t ＝(t ＋2)2－4， ∴当t ＝0时，y min ＝0， 当t ＝1时，y max ＝5，∴函数y ＝sin 2x ＋4sin x 的值域为[0,5]． 11．解：列表：x 0 π2 π 3π2 2π sin x 0 1 0 －1 0 3－2sin x31353描点连线：12．解：当a ＞0时，⎩⎪⎨⎪⎧ a ＋b ＝4，－a ＋b ＝－2，解得⎩⎪⎨⎪⎧a ＝3，b ＝1.当a ＜0时，⎩⎪⎨⎪⎧ －a ＋b ＝4，a ＋b ＝－2，解得⎩⎪⎨⎪⎧ a ＝－3，b ＝1.∴⎩⎪⎨⎪⎧ a ＝3，b ＝1或⎩⎪⎨⎪⎧a ＝－3，b ＝1.。
正弦函数的图像和性质(1)
二.正弦函数的图象
在画正弦函数图象时,我们可以先画出 0, 2 , 上的 正弦函数的图象,再利用周期性将其拓展到整个定义域上.
y sin x, x 0, 2
Ⅰ、用描点法作出函数图象
⑴.列表
x
y
0
6 1 2
3
3 2
0
2
2 3
3 2
5 6
1
1 2
7 6
4 3
3 2
π
2π x
-1
坐标依次为：
3 （0，0）、（ 2 ，1）、（ ，0）、（ 2 ，-1）、（ 2 ，0）
正弦函数的图象
y 1
2
o -1
2
3 2
2
x
y=sinx x[0,2] y=sinx xR
-4 -3 -2 -
y
1
正弦曲线
o
-1
2
3
4
5
6
x
探究：如何作余弦函数的图象
π
-π
π
2
O
2
π
2k ,2k 减区间 2k ,2k
x
对称轴 对称中心
-1
(k ,0) 2 k Z
x k
四、几何法作图
用正弦线作正弦函数 的图象
y sin x( x [0,2 ])
（1）作直角坐标系，在直角坐标系的y轴左侧画单位圆，
圆心在x轴上． （2）把单位圆分成12等份。过单位圆上的各分点作x轴 的垂线，可以得到对应于各角的正弦线； （3）找横坐标：把x轴上从0到2这一段分成12等份； （4）找纵坐标：将正弦线对应平移，即可作出相应12 个点； （5）连线：用平滑的曲线将12个点依次从左到右连接 起来，即得到 y sin x( x [0,2 ])的图象。 演示做图
正弦函数的图像与性质(1)
正弦函数的图象与性质（一）主备人：李怀忠 任强 审核人：李洪川 教学目标：1、 理解并掌握作正弦函数图象的方法2、 理解并熟练掌握用五点法作正弦函数简图的方法 教学重点：掌握作正弦函数图象的方法 教学过程 一、基础梳理：1、正弦函数的图象：五点法作y=sinx ，x ∈[0,2π]的图象时，所取的五点分别是_____,_______,_______,_________,_________.2、函数的周期性：一般的，对于函数f(x),如果存在一个_____，使得定义域内的______x 值，都满足______,那么函数f(x)就叫做周期函数，非零常数T 叫做这个函数的周期。
对于一个周期函数f(x)，如果在它的________存在一个________,那么这个_______就叫做它的最小正周期。
3、正弦函数的图象与性质：二、预习自测：1、用五点法作y=2sin2x 的图象时，首先描出的五个点的横坐标是（ ）（A ）30,,,,222ππππ（B ）130,,,,424ππππ（C ）0,,2,3,4ππππ（D ）20,,,,6323ππππ2、在[0,2π]上，满足1sin 2x ≥的x 的取值范围是（ ）（A）0,6π⎡⎤⎢⎥⎣⎦（B ）5,66ππ⎡⎤⎢⎥⎣⎦（C ）2,63ππ⎡⎤⎢⎥⎣⎦（D ）5,6ππ⎡⎤⎢⎥⎣⎦ 3、函数y=sinx ，2,63x ππ⎡⎤∈⎢⎥⎣⎦,则y 的取值范围是（ ） （A ）[]1,1-（B ）1,22⎡⎢⎣⎦（C ）1,12⎡⎤⎢⎥⎣⎦（D ）,12⎡⎤⎢⎥⎣⎦4、函数y=sinx ，x ∈R 图象的一条对称轴是（ ）（A ）x 轴 （B ）y 轴 （C ）直线y=x （D ）直线2x π=三、典例剖析： 例1 作函数y=3+2sin （x-3π）的简图，并指出它的周期、最值、单调区间。
例2求下列函数的周期： （1） y ＝sin 12x ，（2）y=2sin （3x -6π）例3求函数y=2sin （4π-x ）的定义域、值域及单调递增区间。
《正弦函数图象与性质》
4
3
2
7 2
5 2
3 2
y
1
0
2
2
-1
2
3 2
3
4
5
7
x
2
问题2：那么我们用同样的方法能得到
y sin x的函数图像吗？ 如果能，这 样
得到的函数图像是准确的吗？
学生可能回答：取三角函数值的近似值是 做图不准确的主要原因，
设计意图 从原有知识出 发，类比联想， 引入问题情景， 学生主动参与， 积极思考
复习单位圆与三角函数线
问题3：那么通过我们学习过的哪些知识能准确的找到函数值所对应的位置呢？ 三角函数的几何表示是什么。
2
y=sin x, x∈R
说设计 教师演示，解决问题
（8分钟）
问题1、几何作图法虽然比较精确，但是 不太实用，如何快捷地画出正弦函数的 图象呢？
问题2、函数 y sin x，x 0,2
的 图象中起着关键作用的点是哪些点？
问题3、 观察 y ＝ sin x ，x[ 0，2 ] 图象的最高点、最低点和图象与 x 轴的 交点？坐标分别是什么？
-1-
说设计 教师演示，解决问题
五点作象形状起关键作用的五点坐标．
建系：建立直角坐标系. 描点：定出五个关键点． 连线：用光滑的曲线顺次连结五个点．
说设计 3．展示点拨，巩固新知
8分钟
例1、 画出函数 y＝sin x + 1， x[0，2 ] 的简图．
高中数学人教B版必修四讲义：第一章 1.3 1.3.1 第二课时 正弦型函数y=Asin(ωx+φ) Word版含答案
1．3.1正弦函数的图象与性质第二课时正弦型函数y＝A sin(ωx＋φ)(1)函数y＝A sin(ωx＋φ)的初相、振幅、周期、频率分别为多少？(2)将y＝sin(x＋φ)(其中φ≠0)的图象怎样变换，能得到y＝sin x的图象？(3)函数y ＝A sin x ，x ∈R(A ＞0且A ≠1)的图象，可由正弦曲线y ＝sin x ，x ∈R 怎样变换得到？(4)函数y ＝sin ωx ，x ∈R(ω＞0且ω≠1)的图象，可由正弦曲线y ＝sin x ，x ∈R 怎样变换得到？[新知初探]1．函数y ＝A sin(ωx ＋φ)，A ＞0，ω＞0中参数的物理意义[点睛] 当A ＜0或φ＜0时，应先用诱导公式将x 的系数或三角函数符号前的数化为正数，再确定初相φ.如函数y ＝－sin ⎝⎛⎭⎫2x －π4的初相不是φ＝－π4. 2．φ，ω，A 对函数y ＝sin(x ＋φ)图象的影响 (1)φ对函数y ＝sin(x ＋φ)，x ∈R 的图象的影响(2)ω(ω＞0)对y ＝sin(ωx ＋φ)的图象的影响(3)A (A ＞0)对y ＝A sin(ωx ＋φ)的图象的影响[点睛] (1)A 越大，函数图象的最大值越大，最大值与A 是正比例关系．(2)ω越大，函数图象的周期越小，ω越小，周期越大，周期与ω为反比例关系． (3)φ大于0时，函数图象向左平移，φ小于0时，函数图象向右平移，即“加左减右”．[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”) (1)函数y ＝A sin(ωx ＋φ)，x ∈R 的最大值为A .( ) (2)函数y ＝3sin(2x －5)的初相为5.( )(3)由函数y ＝sin ⎝⎛⎭⎫x ＋π3的图象得到y ＝sin x 的图象，必须向左平移．( ) (4)把函数y ＝sin x 的图象上点的横坐标伸长到原来的3倍就得到函数y ＝sin 3x 的图象．( )答案：(1)× (2)× (3)× (4)×2．函数y ＝13sin ⎝⎛⎭⎫13x ＋π6的周期、振幅、初相分别是( ) A ．3π，13，π6B ．6π，13，π6C ．3π，3，－π6D ．6π，3，π6答案：B3．为了得到函数y ＝sin(x ＋1)的图象，只需把函数y ＝sin x 的图象上所有的点( ) A ．向左平行移动1个单位长度 B ．向右平行移动1个单位长度 C ．向左平行移动π个单位长度 D ．向右平行移动π个单位长度 答案：A4．将函数y ＝sin x 的图象上所有点的横坐标缩短到原来的14倍(纵坐标不变)得________的图象．答案：y ＝sin 4x[典例] 说明y ＝－2sin ⎝⎛⎭⎫2x －π6＋1的图象是由y ＝sin x 的图象经过怎样变换得到的． [解] [法一 先伸缩后平移]y ＝sin x 的图象――――――――――――――――――→各点的纵坐标伸长到原来的2倍且关于x 轴作对称变换y ＝－2sin x 的图象――――――――――→各点的横坐标缩短到原来的12y＝－2sin 2x 的图象π−−−−−−−→12向右平移个单位长度y ＝－2sin ⎝⎛⎭⎫2x －π6的图象―――――――――→向上平移1个单位长度y ＝－2sin ⎝⎛⎭⎫2x －π6＋1的图象． [法二 先平移后伸缩]y ＝sin x 的图象――――――――――――――――→各点的纵坐标伸长到原来的2倍且关于x 轴作对称变换y ＝－2sin x 的图象π−−−−−−−→6向右平移个单位长度y ＝－2sin x －π6的图象―――――――――――→各点的横坐标缩短到原来的12y ＝－2sin ⎝⎛⎭⎫2x －π6的图象―――――――――――→向上平移1个单位长度 y ＝－2sin ⎝⎛⎭⎫2x －π6＋1的图象．由函数y ＝sin x 的图象通过变换得到函数y ＝A sin(ωx ＋φ)的图象的步骤[活学活用]1．将函数y ＝sin ⎝⎛⎭⎫2x －π6向左平移π6个单位，可得到函数图象是( ) A ．y ＝sin 2x B ．y ＝sin ⎝⎛⎭⎫2x －π6 C ．y ＝sin ⎝⎛⎭⎫2x ＋π6 D ．y ＝sin ⎝⎛⎭⎫2x －π3 解析：选C y ＝sin ⎝⎛⎭⎫2x －π6的图象π−−−−−−→6向左平移个单位y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6－π6＝sin ⎝⎛⎭⎫2x ＋π6的图象．2．把函数y ＝f (x )的图象向左平移π4个单位长度，向下平移1个单位长度，然后再把所得图象上每个点的横坐标伸长到原来的2倍(纵坐标保持不变)，得到函数y ＝sin x 的图象，则y ＝f (x )的解析式为( )A ．y ＝sin ⎝⎛⎭⎫2x －π4＋1 B ．y ＝sin ⎝⎛⎭⎫2x －π2＋1 C ．y ＝sin ⎝⎛⎭⎫12x ＋π4－1 D ．y ＝sin ⎝⎛⎭⎫12x ＋π2－1解析：选B 将函数y ＝sin x 的图象上每个点的横坐标缩短到原来的12(纵坐标保持不变)，得到函数y ＝sin 2x 的图象，将所得图象向上平移1个单位长度，得到函数y ＝sin 2x ＋1的图象，再将所得图象向右平移π4个单位长度，得到函数y ＝sin 2⎝⎛⎭⎫x －π4＋1＝sin2x －π2＋1的图象．故选B.[典例] 如图是函数y ＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π2)的图象的一部分，求此函数的解析式．[解] [法一 逐一定参法] 由图象知A ＝3， T ＝5π6－⎝⎛⎭⎫－π6＝π， ∴ω＝2πT＝2， ∴y ＝3sin(2x ＋φ)．∵点⎝⎛⎭⎫－π6，0在函数图象上， ∴0＝3sin ⎝⎛⎭⎫－π6×2＋φ. ∴－π6×2＋φ＝k π，得φ＝π3＋k π(k ∈Z)．∵|φ|<π2，∴φ＝π3.∴y ＝3sin ⎝⎛⎭⎫2x ＋π3. [法二 待定系数法]由图象知A ＝3.∵图象过点⎝⎛⎭⎫π3，0和⎝⎛⎭⎫5π6，0，∴⎩⎨⎧πω3＋φ＝π，5πω6＋φ＝2π，解得⎩⎪⎨⎪⎧ω＝2，φ＝π3.∴y ＝3sin ⎝⎛⎭⎫2x ＋π3. [法三 图象变换法]由A ＝3，T ＝π，点⎝⎛⎭⎫－π6，0在图象上，可知函数图象由y ＝3sin 2x 向左平移π6个单位长度而得，所以y ＝3sin 2⎝⎛⎭⎫x ＋π6，即y ＝3sin ⎝⎛⎭⎫2x ＋π3.给出y ＝A sin(ωx ＋φ)的图象的一部分，确定A ，ω，φ的方法(1)第一零点法：如果从图象可直接确定A 和ω，则选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx ＋φ＝0”(要注意正确判断哪一点是“第一零点”)求得φ.(2)特殊值法：通过若干特殊点代入函数式，可以求得相关待定系数A ，ω，φ.这里需要注意的是，要认清所选择的点属于五个点中的哪一点，并能正确代入列式．(3)图象变换法：运用逆向思维的方法，先确定函数的基本解析式y ＝A sin ωx ，再根据图象平移规律确定相关的参数．[活学活用]如图为函数y ＝A sin(ωx ＋φ)(A >0，ω>0) 的图象的一部分，试求该函数的解析式． 解：由图可得：A ＝3，T ＝ 2|MN |＝π.从而ω＝2πT ＝2， 故y ＝3sin(2x ＋φ)，又∵2×π3＋φ＝2 k π，k ∈Z ，∴φ＝－2π3＋2 k π，k ∈Z.∴y ＝3sin ⎝⎛⎭⎫2x －2π3. [典例] 在函数y ＝2sin ⎝⎭⎫4x ＋2π3的图象的对称中心中，离原点最近的一个中心的坐标是________．[解析] 设4x ＋2π3＝k π(k ∈Z)，得x ＝k π4－π6(k ∈Z)∴函数y ＝2sin ⎝⎛⎭⎫4x ＋2π3图象的对称中心坐标为⎝⎛⎭⎫k π4－π6，0(k ∈Z)． 取k ＝1得⎝⎛⎭⎫π12，0满足条件． [答案] ⎝⎛⎭⎫π12，0正弦型函数对称轴、对称中心的求法[活学活用]将本例中对称中心改为对称轴，其他条件不变，则离y 轴最近的一条对称轴方程为________．解析：由4x ＋2π3＝k π＋π2，得x ＝k π4－π24， 取k ＝0时，x ＝－π24满足题意．答案：x ＝－π24[典例] 已知弹簧上挂着的小球做上下振动时，小球离开平衡位置的位移s (cm)随时间t (s)的变化规律为s ＝4sin ⎝⎛⎭⎫2t ＋π3，t ∈[0，＋∞)．用“五点法”作出这个函数的简图，并回答下列问题：(1)小球在开始振动(t ＝0)时的位移是多少？(2)小球上升到最高点和下降到最低点时的位移分别是多少？ (3)经过多长时间小球往复振动一次？ [解] 列表如下，描点、连线，图象如图所示．(1)将t ＝0代入s ＝4sin ⎝⎛⎭⎫2t ＋π3，得s ＝4sin π3＝23， 所以小球开始振动时的位移是2 3 cm.(2)小球上升到最高点和下降到最低点时的位移分别是4 cm 和－4 cm. (3)因为振动的周期是π，所以小球往复振动一次所用的时间是π s.解三角函数应用问题的基本步骤[活学活用]通常情况下，同一地区一天的温度随时间变化的曲线接近函数y ＝A sin(ωx ＋φ)＋b 的图象.2018年2月下旬某地区连续几天最高温度都出现在14时，最高温度为14 ℃；最低温度出现在凌晨2时，最低温度为零下2 ℃.(1)求出该地区该时段的温度函数y ＝A sin(ωx ＋φ)＋b (A >0，ω>0，|φ|<π，x ∈[)0，24)的表达式；(2)29日上午9时某高中将举行期末考试，如果温度低于10 ℃，教室就要开空调，请问届时学校后勤应该开空调吗？解：(1)由题意知⎩⎪⎨⎪⎧ A ＋b ＝14，－A ＋b ＝－2，解得⎩⎪⎨⎪⎧A ＝8，b ＝6，易知T 2＝14－2，所以T ＝24，所以ω＝π12，易知8sin ⎝⎛⎭⎫π12×2＋φ＋6＝－2， 即sin ⎝⎛⎭⎫π12×2＋φ＝－1， 故π12×2＋φ＝－π2＋2k π，k ∈Z ， 又|φ|<π，得φ＝－2π3，所以y ＝8sin ⎝⎛⎭⎫π12x －2π3＋6(x ∈[0,24))． (2)当x ＝9时，y ＝8sin ⎝⎛⎭⎫π12×9－2π3＋6＝8sin π12＋6<8sin π6＋6＝10.所以届时学校后勤应该开空调．层级一 学业水平达标1．最大值为12，最小正周期为2π3，初相为π6的函数表达式是( )A ．y ＝12sin ⎝⎛⎭⎫x 3＋π6 B ．y ＝12sin ⎝⎛⎭⎫x 3－π6 C ．y ＝12sin ⎝⎛⎭⎫3x －π6 D ．y ＝12sin ⎝⎛⎭⎫3x ＋π6 解析：选D 由最小正周期为2π3，排除A 、B ；由初相为π6，排除C.2．为了得到函数y ＝sin ⎝⎛⎭⎫x －π3的图象，只需把函数y ＝sin x 的图象( )A ．向左平移π3个单位长度B ．向右平移π3个单位长度C ．向上平移π3个单位长度D ．向下平移π3个单位长度解析：选B 将函数y ＝sin x 的图象向右平移π3个单位长度，所得图象对应的函数解析式为y ＝sin ⎝⎛⎭⎫x －π3. 3．已知简谐运动f (x )＝2sin ⎝⎛⎭⎫π3x ＋φ⎝⎛⎭⎫|φ|＜π2的图象经过点(0,1)，则该简谐运动的最小正周期T 和初相φ分别为( )A ．T ＝6，φ＝π6B ．T ＝6，φ＝π3C ．T ＝6π，φ＝π6D ．T ＝6π，φ＝π3解析：选A T ＝2πω＝2ππ3＝6，∵图象过(0,1)点，∴sin φ＝12.∵－π2＜φ＜π2，∴φ＝π6.4．将函数y ＝sin ⎝⎛⎭⎫x ＋π6的图象向左平移π个单位长度，则平移后的函数图象( ) A ．关于直线x ＝π3对称B ．关于直线x ＝π6对称C ．关于点⎝⎛⎭⎫π3，0对称D ．关于点⎝⎛⎭⎫π6，0对称 解析：选A 函数y ＝sin ⎝⎛⎭⎫x ＋π6的图象向左平移π个单位长度，得到y ＝sin ⎝⎛⎭⎫x ＋π6＋π＝－sin ⎝⎛⎭⎫x ＋π6的图象，其对称轴方程为x ＋π6＝k π＋π2，k ∈Z ，即x ＝k π＋π3，k ∈Z ，令k ＝0，得x ＝π3，故选A.5．函数y ＝sin ⎝⎛⎭⎫2x －π3在区间⎣⎡⎦⎤－π2，π上的简图是( )解析：选A 当x ＝0时，y ＝sin ⎝⎛⎭⎫－π3＝－32<0， 故可排除B 、D ；当x ＝π6时，sin ⎝⎛⎭⎫2×π6－π3＝sin 0＝0，排除C. 6．将函数y ＝sin x 的图象向左平移φ(0≤φ＜2π)个单位长度后，得到函数y ＝sin ⎝⎛⎭⎫x －π6的图象，则φ＝________.解析：因为φ∈[0,2π)，所以把y ＝sin x 的图象向左平移φ个单位长度得到y ＝sin (x ＋φ)的图象，而sin ⎝⎛⎭⎫x ＋11π6＝sin ⎝⎛⎭⎫x ＋11π6－2π＝sin ⎝⎛⎭⎫x －π6，即φ＝11π6. 答案：11π67.已知函数f (x )＝sin(ωx ＋φ)(ω>0)的图象如图所示，则ω＝________. 解析：由题意设函数周期为T ， 则T 4＝2π3－π3＝π3，∴T ＝4π3. ∴ω＝2πT ＝32.答案：328．将函数y ＝sin ⎝⎛⎭⎫x －π3图象上各点的纵坐标不变，横坐标伸长为原来的5倍，可得到函数__________________的图象．解析：y ＝sin ⎝⎛⎭⎫x －π3的图象――――――――――――→图象上各点的纵坐标不变横坐标伸长为原来的5倍y ＝sin ⎝⎛⎭⎫15x －π3的图象． 答案：y ＝sin ⎝⎛⎭⎫15x －π39．已知函数f (x )的图象上每一点的纵坐标保持不变，横坐标扩大到原来的2倍，然后把所得的图象沿x 轴向左平移π2个单位长度，这样得到的图象与y ＝12sin x 的图象相同，求f (x )的解析式．解：反过来想，y ＝12sin x π−−−−−−−→2向右平移个单位长度y ＝12sin ⎝⎛⎭⎫x －π2−−−−−−−→1横坐标变为原来的倍2 y ＝12sin ⎝⎛⎭⎫2x －π2，即f (x )＝12sin ⎝⎛⎭⎫2x －π2. 10．已知函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π)的图象的一段如图所示，求它的解析式．(1)求函数f (x )的解析式；(2)求函数f (x )的最小正周期、频率、振幅、初相． 解：(1)由图象可知A ＝2，T 2＝5π6－π6＝2π3，∴T ＝4π3，ω＝2πT ＝32.将N ⎝⎛⎭⎫π6，－2代入y ＝2sin ⎝⎛⎭⎫32x ＋φ得， 2sin ⎝⎛⎭⎫32×π6＋φ＝－2，∴π4＋φ＝2k π－π2，φ＝2k π－3π4(k ∈Z)． ∵|φ|＜π，∴φ＝－3π4.∴函数的解析式为y ＝2sin ⎝⎛⎭⎫32x －3π4. (2)由(1)，知f (x )的最小正周期为4π3＝8，频率为34π，振幅为2，初相为－3π4. 层级二 应试能力达标1.如图所示的是一个半径为3米的水轮，水轮的圆心O 距离水面2米，已知水轮每分钟旋转4圈，水轮上的点P 到水面的距离y (米)与时间t (秒)满足关系式y ＝A sin(ωt ＋φ)＋2，则( )A ．ω＝152π，A ＝3 B ．ω＝2π15，A ＝3 C ．ω＝2π15，A ＝5 D ．ω＝152π，A ＝5 解析：选B 由题意知A ＝3，ω＝2π×460＝2π15.2．要得到函数y ＝sin ⎝⎛⎭⎫4x －π3的图象，只需将函数y ＝sin 4x 的图象( ) A ．向左平移π12个单位B ．向右平移π12个单位C ．向左平移π3个单位D ．向右平移π3个单位解析：选B 由y ＝sin ⎝⎛⎭⎫4x －π3＝sin 4⎝⎛⎭⎫x －π12得，只需将y ＝sin 4x 的图象向右平移π12个单位即可，故选B.3．已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(ω＞0)的最小正周期为π，则该函数的图象( ) A ．关于直线x ＝π8对称B ．关于点⎝⎛⎭⎫π4，0对称 C ．关于直线x ＝π4对称D ．关于点⎝⎛⎭⎫π8，0对称解析：选A 依题意得T ＝2πω＝π，ω＝2，故f (x )＝sin ⎝⎛⎭⎫2x ＋π4，所以f ⎝⎛⎭⎫π8＝sin ⎝⎛⎭⎫2×π8＋π4＝sin π2＝1，f ⎝⎛⎭⎫π4＝sin ⎝⎛⎭⎫2×π4＋π4＝sin 3π4＝22，因此该函数的图象关于直线x ＝π8对称，不关于点⎝⎛⎭⎫π4，0和点⎝⎛⎭⎫π8，0对称，也不关于直线x ＝π4对称．故选A. 4．把函数y ＝sin ⎝⎛⎭⎫5x －π2的图象向右平移π4个单位长度，再把所得图象上各点的横坐标缩短为原来的12倍，所得函数图象的解析式为( )A ．y ＝sin ⎝⎛⎭⎫10x －3π4B ．y ＝sin ⎝⎛⎭⎫10x －7π2 C ．y ＝sin ⎝⎛⎭⎫10x －3π2 D ．y ＝sin ⎝⎛⎭⎫10x －7π4 解析：选D 将原函数图象向右平移π4个单位长度，得y ＝sin ⎣⎡⎦⎤5⎝⎛⎭⎫x －π4－π2＝sin ⎝⎛⎭⎫5x －7π4的图象，再把y ＝sin ⎝⎛⎭⎫5x －7π4的图象上各点的横坐标缩短为原来的12倍得y ＝sin ⎝⎛⎭⎫10x －7π4的图象．5．将函数y ＝sin ⎝⎛⎭⎫2x －π4图象上所有点的横坐标保持不变，纵坐标________(填“伸长”或“缩短”)为原来的________倍，将会得到函数y ＝3sin ⎝⎛⎭⎫2x －π4的图象． 解析：A ＝3＞0，故将函数y ＝sin ⎝⎛⎭⎫2x －π4图象上所有点的横坐标保持不变，纵坐标伸长为原来的3倍即可得到函数y ＝3sin ⎝⎛⎭⎫2x －π4的图象． 答案：伸长 36．将函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，－π2≤φ≤π2图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π6个单位长度得到y ＝sin x 的图象，则f ⎝⎛⎭⎫π6＝________. 解析：将y ＝sin x 的图象向左平移π6个单位长度可得y ＝sin ⎝⎛⎭⎫x ＋π6的图象，保持纵坐标不变，横坐标变为原来的2倍可得y ＝sin ⎝⎛⎭⎫12x ＋π6的图象，故f (x )＝sin ⎝⎛⎭⎫12x ＋π6，所以f ⎝⎛⎭⎫π6＝sin ⎝⎛⎭⎫12×π6＋π6＝sin π4＝22. 答案：227．求函数y ＝sin ⎝⎛⎭⎫2x ＋π3图象的对称轴、对称中心． 解：令2x ＋π3＝k π＋π2(k ∈Z)，得x ＝k π2＋π12(k ∈Z)．令2x ＋π3＝k π，得x ＝k π2－π6(k ∈Z)．即对称轴为直线x ＝k π2＋π12(k ∈Z)，对称中心为⎝⎛⎭⎫k π2－π6，0(k ∈Z)．8.如图为函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫|φ|<π2的一个周期内的图象． (1)写出f (x )的解析式；(2)若y ＝g (x )与y ＝f (x )的图象关于直线x ＝2对称，写出g (x )的解析式；(3)指出g (x )的周期、频率、振幅、初相． 解：(1)由图知A ＝2，T ＝7－(－1)＝8， ∴ω＝2πT ＝2π8＝π4，∴f (x )＝2sin ⎝⎛⎭⎫π4x ＋φ. 将点(－1,0)代入，得0＝2sin ⎝⎛⎭⎫－π4＋φ. ∵|φ|<π2，∴φ＝π4，∴f (x )＝2sin ⎝⎛⎭⎫π4x ＋π4. (2)作出与f (x )的图象关于直线x ＝2对称的图象(图略)，可以看出g (x )的图象相当于将f (x )的图象向右平移2个单位长度得到的，∴g (x )＝2sin ⎣⎡⎦⎤π4(x －2)＋π4＝2sin ⎝⎛⎭⎫π4x －π4. (3)由(2)知，g (x )的周期T ＝2ππ4＝8，频率f ＝1T ＝18，振幅A ＝2，初相φ0＝－π4.。
1.3.1正弦函数的性质
sin x的周期： ...... 4、 2、 2、 4、 6 ......
例如：y=sinx的最小正周期T=2π
例4求下列函数的周期： f（x
（ 1 ）y sin 3x
2π x y=sinu的周期为 T 8 （2）y sin 4 u →u+2π 2 （3）y A sin （ x ），（A ， 0) 3x →3x+2π （ 30x ）
性质一：正弦函数 y=sinx 定义域和值域
定义域为R，值域为[-1,1]
π x 2kπ （k Z）时，ymax 1； 2 π x 2kπ （k Z）时，ymin 1； 2
例1、下列各等式能否成立？为什么？ （1）2sinx=3； （2）sin2x=0.5
1 sin x 1
2
3 2
2
2
3
4
5 2
0
-1
2
3 2
5 2
7 2
x
3 y sin x的减区间： [ 2k， 2k ] 2 2
（k Z）
性质三：正弦函数 y=sinx 的单调性
增区间： π [ 2kπ ， 2kπ ] 2 2
减区间： 3 π [ 2kπ ， 2kπ ] 2 2
例8 求函数y sin(2 x
)图象的对称轴方程及对称中心坐标.
练习1:
1 求函数y sin( x )图象的对称轴方程及对称中心坐标. 2 3
5 对称轴方程x 2k (k Z )； 3 2 对称中心（2k ， 0)(k Z ) 3
习2、函数y sin(2 x ) 3 kπ π x (k Z ) 2 12 __, 的对称轴是__ __________
1.3.1正弦函数的性质
§1.3.1正弦函数的性质 （学案）编辑： 胡东栋 审核：陈祥和 编号：017 日期： 班级： 姓名：______ 学习目标： 掌握正弦函数的性质 学习重点： 正弦函数的性质学习难点： 正弦函数的性质的应用 学习过程一、知识导读：正弦函数y ＝sinx 的性质1．定义域 2．值域3．周期性：一般地对于函数f(x)如果存在一个非零常数T 使得定义域内的每一个x 值都满足那么函数f(x)就叫做.叫做这个函数的周期。
对于一个周期函数f(x)如果在它的所有周期中存在一个最小的正数，那么这个最小正数就叫做它的正弦函数y ＝sinx 的最小正周期是4．奇偶性：y ＝sinx 是函数，正弦曲线关于对称。
5．单调性：正弦函数y ＝sinx 在每一个闭区间)(2222z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ上都从-1增大到1是函数。
在每一个闭区间)(23222z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ上都从1减小到-1是函数。
二、典型例题例1、设sinx=t-3,x ∈R,求t 的取值范围。
例2、求使下列函数取得最大值和最小值的x 的取值范围，并说出最大值和最小值是什么：⑴ y=sin2x; ⑵ y=sinx+2;⑶ y=(sinx-1)2+2例3、求下列函数的周期：⑴ y=sin2x; (2) y=sin()621π+x 例4、判断下列函数的奇偶性（1）f(x)=xxx tan sin -（2）f(x)＝xxsin 1cos 2-（3）f(x)=1cos cos 1-+-x x例5、不通过求值，指出下列各式大于零还是小于零： （1）);10sin()18sin(ππ---（2）).417sin()523sin(ππ---三、当堂达标1. 函数y ＝x 2sin 2的奇偶性为（ ）函数A ．奇B ．偶C ．即奇且偶D ．非奇非偶 2．正弦函数y ＝sinx(R x ∈)的单增区间是 ，单减区间是3．函数y ＝sin4x 的周期为。
1.3.1正弦函数的图象与性质(1)
临朐六中高一数学导学案姓名编号：必修四—09教学课题课型主备教师审核教师班级使用时间正弦函数的图象与性质(1) 新授课董洪安李玉福学习目标：1、理解并掌握作正弦函数图象的方法，掌握用五点法作正弦函数简图的方法2、理解正弦函数的定义域、值域、最值、周期性、奇偶性的意义3、会求简单函数的定义域、值域、最小正周期和单调区间。
重点:用单位圆中的正弦线作正弦函数的图象，正弦函数的性质。
难点：正弦函数性质的理解与应用。
教学过程课前预习教学设计1.正弦函数的图象：正弦函数表达式()R=siny∈xx正弦函数的图象叫做正弦曲线。
2.“五点法”作[]π2,0y的图象时所取的五点分别是x,sin∈=x。
3.正弦函数x=的性质：y sin⑴定义域：正弦函数x=的定义域是。
y sin⑵值域：正弦函数xx时，=的值域是。
当且仅当=y sin正弦函数取得最大值1；当且仅当=x时，正弦函数取得最小值1-。
⑶周期性：①一般地，对于函数()xf，如果存在一个，使得定义域内的每一个x值，都满足，那么函数就叫做周期函数，非零常数T叫做这个函数的周期。
教师是学生学习的引导者学生是学习的主人！②对于一个周期函数()x f ，如果在它的所有周期中存在 的正数，那么这个 就叫做它的最小正周期。
③正弦函数x y sin =的周期为 ，最小正周期为 。
⑷奇偶性：正弦函数x y sin =是 函数，正弦曲线关于 对称。
⑸单调性：正弦函数正弦函数x y sin =在区间 上是增函数，在区间 上是减函数。
合作探究展示探究一 用五点法作出函数3sin 2+=x y 的图象，并指出它的周期、最值及单调区间。
探究二 求使下列函数取得最大值和最小值的x 的取值范围，并说出最大值和最小值是什么？⑴32sin +=x y ； ⑵()21sin 2+-=x y .探究三 求下列函数的周期：⑴x y 2sin =； ⑵⎪⎭⎫ ⎝⎛+=621sin πx y .补充深化 认真听讲是学习高效的捷径！探究四 不通过求值，指出下列各式大于零还是小于零： ⑴⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-10sin 18sin ππ； ⑵⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-417sin 523sin ππ课堂小结 当堂练习1.函数()R x x y ∈=sin 图象的一条对称轴是（ ）A.x 轴B.y 轴C.直线x y =D.直线2π=x2.函数x y sin 2-=的最大值及最大值时x 的值为（ ） A.2,3π==x y B.()Z k k x y ∈+==ππ22,1 C.()Z k k x y ∈+-==ππ22,3 D.()Z k k x y ∈+==ππ22,33.函数()⎪⎭⎫ ⎝⎛+=6sin 3πx x f 在下列区间内递减的是（ ）A.⎥⎦⎤⎢⎣⎡-2,2ππB.[]0,π-C.⎥⎦⎤⎢⎣⎡-32,32ππD.⎥⎦⎤⎢⎣⎡32,2ππ4.设R x t x ∈-=,3sin ，求t 的取值范围。
1.3.1正弦函数图像和性质-教学设计-崔鹏-人大附中
《正弦函数图象及其性质》教学设计学校：人大附中姓名：崔鹏学科：数学年级：高一1.3.1 正弦函数图象及其性质中国人民大学附属中学崔鹏●指导思想与理论依据本教学设计力图以《高中数学课程标准》为依据，以“师生互动教学”为指导，以教师主导、学生主体为理念，以信息技术融入学科结合动手操作教学为手段，以课堂为依托来实现教学目标．《高中数学课程标准》指导下的新教材将突破以知识块为主线，而以基本的数学思想方法为主线来选择和安排教学内容，强调数的意识、空间观念、优化思想、统计思想、方程与函数思想、估计意识、推理意识和应用意识，强调从运算意义出发进行思考和教学，强调密切联系学生的生活．目的是让学生通过基础知识和基本技能的学习，学会从数学的角度提出问题、理解问题，能综合应用所学的知识和技能解决问题，发展应用意识．学生学习，尤其是新授课教与学应当是一个生动活泼、主动的和富有个性的过程．认真听讲、积极思考、动手实践，自主探索、合作交流都是学习数学的重要方式．因此，本节课采用小组合作是学生喜闻乐见的形式，让学生从小组合作探究开始进入学习，可以让学生在合作的过程体验学习的快乐，旨在为学生提供对新知识的认识角度，结合生活实际解决教学难点，从而启发学生的创新性思维．●教学背景分析内容分析本节内容是高中数学人教B版教材《必修四》第一章第三节第一课时内容．三角函数是高中数学范围内学生接触的最后一类基本初等函数，而正弦函数是其中最具代表性的函数．学生通过必修一的学习，已经初步掌握了研究函数的一种基本方法，即通过图象研究函数的性质，通过简单的函数性质修正函数的图象．学情分析在本节课前，学生已经接触了弧度制、任意角三角函数定义、同角三角函数基本关系式和诱导公式等知识，并通过三角函数线初次体会了三角函数“形”的概念，那么，建立正弦函数与其自变量之间的映射关系并抽象为函数图象是本节课的难点．教学方法（1）通过正弦线的变化趋势，让学生建立直观的函数变化趋势，初步总结归纳出正弦函数性质；（2）通过描点，帮助学生建立角的弧度值到坐标轴的对应关系，以实物教具的方式，让学生动手将弧长转化为数；（3）通过描点、分析、实物帮助作图到五点法，使学生逐步深入地了解正弦函数的图象形状，养成五点作图的习惯，并通过练习落实；（4）本节课将以多媒体、实物教具辅助教学的手段，通过小组合作、归纳探究、展示评价的方式展开，培养学生的自主思考能力和动手实操能力．●教学目标与重点、难点设计教学目标1．知识目标：理解正弦函数的性质，能正确使用“五点法”、“几何法”作出正弦函数的图象；2、过程目标：通过研究三角函数的性质和图象，进一步体会研究函数的基本方法，学会通过函数的性质作出函数草图，通过函数图象推演函数的性质的过程；3、情感目标：通过图象的学习，培养由局部到整体，具体到抽象的思维方法，从而达到从感性认识到理性认识的飞跃．教学重点：正弦函数的性质与图象；教学难点：理解弧度值与x轴上的点的对应；● 教学过程与教学资源设计 教学过程： 一、复习回顾我们已经学习了任意角的三角函数以及三角函数线的内容，并且定义了正弦函数，y=sinx ，x ∈R ．三角函数是我们高中范围内学习的最后一种函数．我们已经有了一些研究函数的基本方法． 【提问1】根据这些经验，我们应该从哪几个方面研究正弦函数？ →定义域，值域，单调性，奇偶性，对称性，最值，图象等． 本节课我们将研究正弦函数的图象和性质．二、课堂活动【活动1】学生结合已有的经验，小组活动研究正弦函数的图象和性质．【提问2】你是怎样作出这个图象的？为什么可以这样作图？【提问3】你作出的图象是正弦函数图象吗？为什么图象是这样的形状？有没有使图象更精确的做法？→材料：一个圆形纸片（半径为1的圆），两根软绳，一把直尺．【提问4】在什么点拐弯，另外一边是什么样的？图中有哪些关键点？这些关键点对我们作图有什么帮助？【设计意图】五点作图法，五个点分别为：3(0,0),(,1),(,0),(,1),(2,0)22ππππ-． 【提问5】结合图象，你能得出正弦函数的哪些性质？ 【设计意图】培养学生根据图象获取函数性质的能力．【活动2】分小组展示，每组总结得出一条正弦函数的性质，其他组补充，教师点评． 【提问1】你是怎样得到这些性质呢？这些性质可以帮助我们作出正弦函数图象吗？ 【设计意图】培养学生根据性质作图的习惯．【活动1】学生分小组展示正弦函数的性质并讲明道理，并根据性质作出正弦函数的图象．其他组补充，教师点评．【提问2】要想得到正弦函数的图象，除了性质以外，我们还需要借助哪些条件？你有比较用1号绳量取弧长用2准确的作图方法吗？【活动2】两名学生演示作图方法，并解释该方法的原理．方法归纳：作图时，可以从0度开始量取单位圆上的一段弧长，即为对应的角度，再量取弧的终端到x 轴的线段数量，即为正弦值，利用线的长度分别得到一点的两个坐标即可．【提问3】图中有哪些关键点？这些关键点对我们作出正弦函数的草图有什么帮助？ 【活动3】试作出正弦函数的图象． 【设计意图】明确正弦函数图象的形状后，为了简化作图方式，在精确度不太高时，常采用五点法作正弦函数的简图．只要这五个点描出后，图象在[0,2π]上的形状就基本确定了．三、课堂总结本节课我们作出了正弦函数的图象，并根据图象总结得到了正弦函数的重要性质．（本节课我们通过对正弦函数的定义和正弦线得到了正弦函数的性质，并根据性质作出了正弦函数的图象）．这是研究函数的基本方法．后面的学习，我们将继续深入研究正弦函数的性质和图象．学习效果评价设计1、根据课上的讨论，完成下面的表格． 正弦函数的性质正弦函数还具有周期性，这通过其图象不难发现．你知道如何定义函数的“周期”吗？用1号绳量取弧长用22、用五点法在同一坐标系内作出函数y = sin x ，y=2sin x 和y = sin x 在[-2π，2π]上的图象；3、用五点法在同一坐标系内作出函数y = sin x ，y=2sin x 和y = sin x 在[-2π，2π]上的图象；4、用五点法在同一坐标系内作出函数y = sin x ，y=|sin x|和y =sin|x |在[-2π，2π]上的图象；【设计意图】本节课的重点是正弦函数的图象和性质，但是考虑到学生经过探究得到正弦函数图象之后可以很容易根据图象得到正弦函数的性质，因此在设置课堂练习和课后习题时，一方面落实“五点作图法”，并辅以简单的图象变换，另一方面引导学生总结归纳正弦函数的性质．教学设计特色说明与教学反思本节课围绕正弦函数的图象和性质展开．根据学生的思维过程，可以通过几何法或描点法先作出函数图象再归纳总结性质，也可以根据三角函数线的变化规律先探究函数性质，再作出图象．不管是从哪个角度，都希望向学生渗透函数性质和图象的依存关系，这也是数形结合的重要意义所在．根据“形”，即三角函数图象得到三角函数的性质后，可以进一步指导学生根据性质作出正弦函数图象．如利用周期性，将正弦函数图象的研究范围缩小到[-π，π]，利用奇偶性，将范围进一步缩小到[0，π]，利用对称性，将范围进一步缩小到[0，2]，这样我们可以只研究锐角的三角函数值，这大大降低了研究正弦函数的难度．在教学环节中，教师的个别指导和小组展示评价是本节课是否能够达到教学目标的关键，也是甄别学生是否能从小组合作和自主探究中体会新知识的研究方法，尤其是和生活衔接非常紧密的三角函数的研究方法，而后将本部分内容自然地镶嵌到一般函数的研究方法中，从而启发学生的学习和探究过程．板书设计：。
课件3：1.3.1 正弦函数的图像与性质
(2) 当3x+ =2k+ 即 x= 2k (kZ)时, y的最
4
2
3 12
大值为0.
例题
例3、求下列三角函数的周期：
(1)y=sin(x+ )； (2) y=3sin( + x )
3
52
(3) y=|sinx|
解： (1) 令z= x+ 而 sin(2+z)=sinz
3
即：f (2+z)=f (z) ,
例题
例2、利用正弦函数的图象，求满足下列条件的x 的集合：sin x 1
2
解：在y轴上取点(0, 0.5)，过该点作x轴的平行线,与正弦
函数图象相交于点 ( , 1) (5 , 1) 等，所以不等式的解集
是 {x | 2k
6
x 2k
2
5
62
,k Z}
6
6
2、正弦函数的性质
由正弦函数y=sinx的作图过程以及正弦函数的 定义，容易得出正弦函数y=sinx还有以下重要性质.
1、正弦函数的图象
1、正弦函数的图象
第三步：连线，用光滑曲线把这些正弦线的终点连 结起来，就得到正弦函数y=sinx，x∈[0，2π]的图 象．
1、正弦函数的图象
1、正弦函数的图象
以上我们作出了y=sinx，x∈[0，2π]的图象，因 为sin(2kπ+x)=sinx (k∈Z)，所以正弦函数y=sinx在 x∈[－2π，0]，x∈[2π，4π]，x∈[4π，6π]时的图象 与x∈[0，2π]时的形状完全一样，只是位置不同。
2、正弦函数的性质
(5)单调性
从y＝sinx的图象上可看出：
当x∈
[ , ]
课件4：1.3.1 正弦函数的图象与性质
∵sin 65°<sin 80°，∴－sin 65°>－sin 80°，
∴cos 875°>sin 980°.
π
例 5 把函数 y＝sin x(x∈R)的图象上所有的点向左平移3个单位
1
长度，再把所得图象上所有点的横坐标缩短到原来的 倍(纵坐标
2
不变)，得到的图象所表示的函数是(
1.五点法是画三角函数图象的基本方法，要熟练掌握，与五点法作
图有关的问题是高考常考知识点之一．
2.判断函数的奇偶性应遵从“定义域优先”原则，即先求定义域，
看它是否关于原点对称．
3.求函数的最小正周期的常用方法：
(1)定义法，即观察出周期，再用定义来验证；也可由函数所具有的
某些性质推出使f(x＋T)＝f(x)成立的T.
π
2
向左平移 3 个单位，后者需向左平移 3π 个单位．
4.利用“五点法”作出函数 y＝－1＋sin x (x∈[0,2π])的简图．
解：按五个关键点列表：
x
0
π
π
2
3π
2
sin x
0
1 0
－1 0
－1＋sin x
－1 0 －1 －2 －1
2π
描点并将它们用光滑的曲线连接起来(如图所示)．
课后总结
π
跟踪训练 5 把函数 y＝sin x (x∈R)的图象上所有的点向左平移3
个单位长度，再把所得图象上所有点的横坐标扩大到原来的 2
倍(纵坐标不变)，得到的图象所表示的函数是(
x π
A．y＝sin2＋6，x∈R
x π
B．y＝sin2＋3，x∈R
正弦函数的图象与性质(第一课时)
§1.3.1 正弦函数的图象与性质（第一课时）一、教学目标1．知识与技能：（1）会用单位圆中的正弦线画出正弦函数的图象；（2）会用“五点法”画出正弦函数的图象；（3）理解并掌握正弦函数的图象。
2．过程与方法：(1)培养观察能力、分析能力、归纳能力、表达能力等；(2)渗透数形结合的数学思想方法。
3．情感态度与价值观：(1)渗透由特殊到一般的思想，使学生理解动与静的辩证关系，培养辩证唯物主义观点；(2)培养学生勇于探索、勤于思考的精神；(3)培养学生合作学习和数学交流的能力。
二、重点与难点：1.教学重点：用“五点法”作正弦函数的大致图象。
2.教学难点：利用单位圆画正弦函数的图象。
三、教学方法、教学手段与学法指导：1．教学方法：探究式合作教学（分小组讨论、交流、总结）。
2．教学手段：多媒体辅助教学（Microsoft Office PowerPoint，几何画板等，特别是几何画板）。
3．学法指导：引导学生运用“自主探究，合作交流”的学习方法，力求把“以学生为本”的教学理念贯穿始终。
四、教学过程1.旧知回顾、新知铺垫1．任意角的三角函数的定义？2．三角函数线的作法？【师生互动】教师提问，学生回答，教师对学生作答进行点评。
【设计意图】把问题作为教学的出发点，激发学生的求知欲，为发现新知识创设一个最佳的心理和认识环境。
2.创设情境、引入新课问题1：根据以往学习函数的经验，你准备采取什么方法作出sin,[0,2]=∈函数的图象？请y x xπ你尝试画出该函数的图象。
【师生互动】给每位同学发一张纸，为了节省时间，表已给出，组织他们完成下面的步骤：描点、连线。
加入竞争机制，看谁画得又快又好！【设计意图】为学生提供一个轻松、开放的学习环境，有助于有效地组织课堂学习、带动和提高学生学习的积极性、主动性，更有助于培养学生的集体荣誉感和他们的竞争意识。
（根据学生多种画法，以及形状各异的情况，及时点评）。
【师生互动】作图过程中有什么困难？如何得到2？ 3.初步探索、展示内涵 如何在直角坐标系中画出点(,sin )?33C ππ问题①：你是如何得到的呢？如何精确描出这个点呢？【师生互动】组织学生讨论，引导他们自然地想到3π 【设计意图】由浅入深、由易到难,帮助学生体会从三角函数线出发，“以已知探求未知”,培养学生的思维能力。
1.3.1正弦函数的图象与性质
1.3.1正弦函数的图象与性质基础练习1.函数sin()4y x π=+在下列哪个区间上是递减的( ) A.5,44ππ⎡⎤⎢⎥⎣⎦ B. [],0π- C. 3,44ππ⎡⎤-⎢⎥⎣⎦D. ,22ππ⎡⎤-⎢⎥⎣⎦ 2.函数sin 26y x π⎛⎫=-+ ⎪⎝⎭的单调递减区间是( ) A. 2,2()63k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z B. 52,2()66k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z C. ,()63k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z D. 5,()36k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z 3.下列四个函数中,为周期函数的是( )A. y =3sin xB. y =3xC. y =sin|x | (x ∈R )D. y =sin 1x(x ∈R 且x ≠0) 4.为了得到函数14sin()26y x π=-,x ∈R 的图象,只需将函数4sin()6y x π=-,x ∈R 的图象上的所有点( )A.横坐标伸长到原来的2倍,纵坐标不变B.横坐标缩短到原来的12倍,纵坐标不变 C.纵坐标伸长到原来的2倍,横坐标不变 D.纵坐标缩短到原来的12倍,横坐标不变 5.已知函数sin()(0,0)y A x A ωϕω=+>>的最大值是3,最小正周期是27π,初相位是6π,则这个函数的表达式是( )A.3sin 76y x π⎛⎫=- ⎪⎝⎭ B. 3sin 76y x π⎛⎫=+ ⎪⎝⎭C. 3sin 742y x π⎛⎫=+ ⎪⎝⎭ D. 3sin 742y x π⎛⎫=- ⎪⎝⎭ 6.函数2sin ,,63y x x ππ⎡⎤=∈⎢⎥⎣⎦,则y 的范围是( )A. [－1,1]B. [12,1]C. [12] ,1] 7.函数3sin 6y ax π⎛⎫=+ ⎪⎝⎭的最小正周期是π,则a =__________8.函数sin()(0,0)y A x A ωϕω=+>>在同一周期内,当3x π=时,y 取最大值2;当x =0时,y 取最小值－2,则函数的解析式是____________ 9.用五点法作出函数2sin 33y x π⎛⎫=-+ ⎪⎝⎭的图象,并指出它的周期,频率,相位,初相,最值及单调区间.10.求使下列函数取得最小值的自变量x 的集合,并出最小值.(1)y = –2sin x ,x ∈R ; (2)y = –2+sin 3x ,x ∈R提高练习1.方程sin x =lg x 的实根有( )A. 1个B. 2个C. 3个D. 无数个2.函数f (x )=sin(πx －2π)－1,则下列命题正确的是( ) A. f (x )是周期为1的奇函数 B. f (x )是周期为2的偶函数C. f (x )是周期为1的非奇非偶函数D. f (x )是周期为2的非奇非偶函数 3.已知函数f (x )=2sin x ,对任意的x ∈R 都有f (x 1)≤f (x )≤f (x 2),则|x 1－x 2|的最小值为( )A. 4πB. 2π C. π D. 2π 4.函数y =sin x 与y =12x 的图象在(,)22ππ-上的交点有( ) A. 4个 B. 3个 C. 2个 D. 1个5.设函数()sin()(0,0,||)2f x A x A πωϕωϕ=+≠><的图象关于直线23x π=对称,它的周期是π,则() A. f (x )的图象过点(0,12) B. f (x )在[52,123ππ]上是减函数 C. f (x )的一个对称中心是(5,012π) D. f (x )的最大值是A 6.方程cos(52x π+)=(12)x 在区间(0,100π)内解的个数是( ) A. 98 B. 100 C. 102 D. 2007.函数2sin(2)(0)3y x x π=-+…的初相是_________ 8.(1)如何由y =sin x 得到12cos()24y x π=-+的图象. (2)如何由1sin(2)33y x π=+的图象得到y =sin x 的图象.9.设函数()3sin(),0,(,)6f x x x πωω=+>∈-∞+∞,且以2π为最小正周期. (1)求f (0); (2)求f (x )的解析式; (3)已知9()4125f απ+=,求sin α的值.10.已知函数()sin()(0,0)f x A x A ωϕω=+>>的图象如图.(1)求出f (x )的解析式; (2)若g (x )与f (x )的图象关于x =2对称,求g (x )的解析式.11.已知函数12()log |sin |f x x =(1)求其定义域和值域; (2)判断奇偶性;(3)判断周期性,若是周期函数,求周期; (4)写出单调区间.。
【成才之路】高中数学-1
2．描点法：在要求不太高的情况下可用五点法作图，函数 y ＝ sinx ， x ∈ [0,2π] 的 图 象 上 有 五 点 起 决 定 作 用 ， 它 们 是 _(_0_,0_)____、__π2_，__1_____、_(_π_, _0_)___、__32_π_，__－__1__、_(2_π_,_0_)___，
[点评] 讨论函数y＝Asin(ωx＋φ)的单调性的一般步骤: (1)若ω<0，利用诱导公式二把y＝Asin(ωx＋φ)中x的系数化 为大于0的数； (2)引入变量u＝ωx＋φ(ω>0)； (3)讨论函数y＝sin u的单调性； (4)解关于x的不等式得出y＝Asin(ωx＋φ)的单调区间．
下列关系式中正确的是( ) A. sin11°<cos10°<sin168° B. sin168°<sin11°<cos10° C. sin11°<sin168°<cos10° D. sin168°<cos10°<sin11° [答案] C
(2)cos115°＝cos(90°＋25°)＝－sin25°, cos260°＝cos(180°＋80°)＝－cos80°＝－sin10°, ∵sin10°<sin25°, ∴－sin10°>－sin25°, 即cos260°>cos115°. (3)sin194°＝－sin14°, cos160°＝－cos20°＝－sin70°, ∵sin14°<sin70°, ∴－sin14°>－sin70°, ∴sin194°>cos160°.
3．下列函数不是奇函数的是( )
A．y＝sinx
B．y＝sin2x
C．y＝sinx＋2
D．y＝12sinx
高二数学正弦函数的图像与性质1
;
k 5 , 0) ( k∈Z) ( 2 2
8.函数y=2sin(2x+ )(x∈[－π,0］)的单调递减 6
区间是
;
5 [ , ] 6 3
；游戏规则 游戏技巧 游戏下载 ；
一边神识锁定着风帝,一边等着噬大人等人の到来. 他们以为两人尊者传讯让他们静观其变,是等他们到来,却不知道,噬大人根本就没有打算过来… "这,这是什么怪物?" 巨大の洞府内,里面居然灯火通明,大厅很大,足足有一些不咋大的城广场那么大！白重炙六人,此刻被那触手,全 部牢牢捆住,在大厅の空中飞舞.同时在空中飞舞の还有数百条触角,这些触角の源头,却是一只不咋大的山一样の软体怪物.六只幽森森の眼睛盯着六人,眼睛内没有瞳孔,只是黝黑一片,看起来很是吓人.下方有一张血红大口,足足能够把六人同时塞进去了. 白重炙和五名魂奴极力挣 扎,死死盯着那怪物眼睛和巨口,生怕这怪智直接将他们丢入那猩红の巨口内.只是全部人神力被封了,光靠他们肉体の力量如何能挣脱? "怎么办?怎么办?" 白重炙有些凌乱了,以前他遭遇了不少险境,但是这次却是最无力の,因为他连抗争の机会都没有. 五品魂奴也有些慌了,他们同 样神力被压制了.如果一些人没有力量,被杀死,那无可厚非.但是明明有强大の力量,此刻却发挥不出来,这很憋屈,很无奈,多种情绪交织起来,心就乱了. "嘶嘶！" 怪智猩红巨口中,再次发出一声の怪叫,让众人の灵魂再次一颤,那六只没有瞳孔の眼珠子,宛如死神般,泛着邪恶冰冷の 气息,让众人不寒而栗. 巨大の触手不断の挥舞,白重炙感觉比坐过山车还要刺激.触手时而靠近那猩红の巨口,一阵腥臭铺面而来,让人恶心欲呕.每一次靠近那巨口,白重炙都一阵心惊肉跳,生怕直接被丢入进去,最后化成一堆粪便. 不知道这巨智是想玩,还是因为感觉众人の肉不怎 么好
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
研一研·问题探究、课堂更高效
1.3.1（一）
本 课 时 栏 目 开 关
1 跟踪训练2 在[0,2π]上，满足sin x≥ 的x的取值范围是( B ) 2 π 5π π A.0，6 B.6 ， 6 π 2π 5π C.6， 3 D. 6 ，π
答
研一研·问题探究、课堂更高效
(2)如果要作出函数y＝sin
1.3.1（一）
x，x∈[－2π，0]上的图象，你认为
应找出哪些关键点？并作出大致图象．
答
本 课 时 栏 目 开 关
3 π 应找出(－2π，0)，－2π，1，(－π，0)，－2，－1，(0,0)
这五个关键点， 大致图象如下：
1.3.1（一）
小结
本 课 时 栏 目 开 关
作正弦、余弦曲线要理解几何法作图，掌握五点法作
图．“五点”即 y＝sin x 或 y＝cos x 的图象在一个最小正周期 内的最高点、最低点和与 x 轴的交点．“五点法”是作简图的 常用方法．
研一研·问题探究、课堂更高效
跟踪训练1
1.3.1（一）
1 用“五点法”画出函数y＝ ＋sin x，x∈[0,2π]的 2
练一练·当堂检测、目标达成落实处
1.3.1（一）
2．利用“五点法”作出y＝－1＋sin x (x∈[0,2π])的简图．
解 按五个关键点列表： x
本 课 时 栏 目 开 关
0 0
π 2 1
π 0
3π 2 －1
2π 0
sin x
－1＋sin x －1 0 －1 －2 －1 描点并将它们用光滑的曲线连接起来(如图所示)．
研一研·问题探究、课堂更高效
1.3.1（一）
⑤连线：用平滑的曲线将这些点依次从左到右连接起来，即得y＝ sin x，x∈[0,2π]的图象．
几何画板演示
本 课 时 栏 目 开 关
因为终边相同的角有相同的三角函数值，所以函数y＝sin x， x∈[2kπ，2(k＋1)π)，k∈Z且k≠0的图象，与函数y＝sin x， x∈[0,2π)的图象的形状完全一致．于是我们只要将函数y＝sin x， x∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度)，就可以 得到正弦函数y＝sin x，x∈R的图象．
研一研·问题探究、课堂更高效
探究点二 五点法作正弦曲线
1.3.1（一）
(1)在精度要求不太高时，y＝sin x，x∈[0,2π]可以通过找出 π 3π (0,0)，2，1，(π，0)， 2 ，－1，(2π，0) 五个关键
本 课 时 栏 目 开 关
点，再用光滑曲线将它们连接起来，就可得正弦函数的简 图． 请你在所给的坐标系中画出y＝sin x，x∈[0,2π]的图象．
由图象可知方程 sin x＝lg x 的解有 3 个． 小结 三角函数的图象是研究函数的重要工具，通过图象可较
简便地解决问题，这正是数形结合思想方法的应用．
研一研·问题探究、课堂更高效
1.3.1（一）
1－a π 跟踪训练 3 方程 sin x＝ 在 x∈[ ， π]上有两个实数解， 求 2 3 a 的取值范围．
1.3.1（一）
本 课 时 栏 目 开 关
1.3.1（一）
1.3.1
【学习要求】
本 课 时 栏 目 开 关
正弦函数的图象与性质(一)
1．了解利用单位圆中的正弦线画正弦曲线的方法． 2．掌握“五点法”画正弦曲线的步骤和方法，能用“五点 法”作出简单的正弦曲线． 【学法指导】 利用“五点法”作出正弦函数的图象是本节的重点，也是进一 步通过正弦函数图象研究正弦函数性质的基础和前提，“五点 法”作图的基本步骤和要领要熟练掌握.
练一练·当堂检测、目标达成落实处
1.3.1（一）
1． 方程 x＝πsin x 的解的个数为
本 课 时 栏 目 开 关
( C ) D．无穷多
A．1
解析
B．2
C．3
x 在同一坐标系中作出函数 y＝ 及 y＝sin x 的图象如图 π
所示：
x 由图象 y＝π与 y＝sin x 有 3 个交点，所以方程 x＝πsin x 有 3 个解．
研一研·问题探究、课堂更高效
1.3.1（一）
问题2 如何由y＝sin x，x∈[－2π，2π]的图象，得到y＝sin |x|， x∈[－2π，2π]的图象？
本 课 时 栏 目 开 关
答 如图所示，y＝sin x，x∈[－2π，2π]位于 y 轴右侧的图象 不动，再把 y 轴右侧的图象沿 y 轴翻折到 y 轴左侧，原来位于 y 轴左侧的图象去掉即可．概括为“右不动，右翻左”．
本 课 时 栏 目 开 关
－4≤x≤4 即 sin x>0 sin x>0 满足不等式组 2 16－x ≥0
1.3.1（一）
，
，作出 y＝sin x 的图象，如图所示．
结合图象可得：x∈[－4，－π)∪(0，π)．
小结
一些三角函数的定义域可以借助函数图象直观地观察得
到，同时要注意区间端点的取舍．
研一，作函数 y＝sin x 和 y＝lg x 的图象，根 据图象判断出方程 sin x＝lg x 的解的个数．
解
本 课 时 栏 目 开 关
建立坐标系 xOy， 先用五点法画出函数 y＝sin x， x∈[0,2π]
的图象，再依次向左、右连续平移 2π 个单位，得到 y＝sin x 1 的图象．描出点10，－1，(1,0)，(10,1)并用光滑曲线连接得到 y＝lg x 的图象，如图所示．
填一填·知识要点、记下疑难点
1.3.1（一）
1．正弦函数图象的画法
本 课 时 栏 目 开 关
(1)几何法—借助三角函数线； (2)描点法—五点法． 函数y＝sin x，x∈[0,2π]的图象上起关键作用的点有以下五 π 3 (0,0) ， 2，1 ， (π，0) ， 2π，－1 ， (2π，0) ． 个： (3)利用五点法作函数y＝Asin x(A>0)的图象时，选取的五个 3 π (0,0) ， 2，A ， (π，0) ， 2π，－A ， 关键点依次是： (2π，0) ．
本 课 时 栏 目 开 关
1－a π 解 设 y1＝sin x，x∈[ ，π]，y2＝ . 3 2 π y1＝sin x，x∈[3，π]的图象如图． 3 1－a 由图象可知，当 2 ≤ 2 <1，即－1<a≤1 π － 3时，y＝sin x，x∈[3， 1－a 1－a π]的图象与 y＝ 2 的图象有两个交点，即方程 sin x＝ 2 在 π x∈[ ，π]上有两个实数解． 3
研一研·问题探究、课堂更高效
[典型例题]
1.3.1（一）
例 1 利用“五点法”作出函数 y＝1－sin x(0≤x≤2π)的简图．
解
本 课 时 栏 目 开 关
取值列表： x sin x 1－sin x 0 0 1 π 2 1 0 π 0 1 3π 2 －1 2 2π 0 1
描点、连线，如图所示．
研一研·问题探究、课堂更高效
填一填·知识要点、记下疑难点
1.3.1（一）
2．正弦曲线的简单变换 (1)函数 y＝－sin x 的图象与 y＝sin x 的图象关于 x轴 对称；
本 课 时 栏 目 开 关
(2)函数 y＝sin x 与 y＝sin x＋k 图象间的关系． 当 k>0 时，把 y＝sin x 的图象向 上 平移 k 个单位得到函数 y＝sin x＋k 的图象； 当 k<0 时，把 y＝sin x 的图象向 下 平移 |k| 个单位得到函数 y＝sin x＋k 的图象.
研一研·问题探究、课堂更高效
1.3.1（一）
探究点一
本 课 时 栏 目 开 关
几何法作正弦曲线
利用几何法作正弦函数y＝sin x，x∈[0,2π]的图象的过程如下： ①作直角坐标系，并在直角坐标系y轴的左侧画单位圆，如图所 示． ②把单位圆分成12等份(等份越多，画出的图象越精确)．过单 π π 位圆上的各分点作 x轴 的垂线，可以得到对应于0， ， ， 6 3 π ，„，2π等角的正弦线． 2 ③找横坐标：把x轴上从0 到 2π (2π≈6.28)这一段分成12等份． ④找纵坐标：将 正弦 线对应平移，即可得到相应点的纵坐标．
简图． 解 取值列表如下：
本 课 时 栏 目 开 关
x sin x 1 ＋sin x 2 描点、连线，如图所示．
0 0 1 2
π 2 1 3 2
π 0 1 2
3 2π －1 1 － 2
2π 0 1 2
研一研·问题探究、课堂更高效
例 2 求函数 f(x)＝lg sin x＋ 16－x2的定义域．
解 由题意，x
研一研·问题探究、课堂更高效
探究点三 含绝对值的正弦函数的图象
1.3.1（一）
问题1 如何由y＝sin x，x∈[－2π，2π]的图象得到y＝|sin x|， x∈[－2π，2π]的图象？
本 课 时 栏 目 开 关
答
如图所示，y＝sin x，x∈[－2π，2π]位于 x 轴上方的图象保
持不变，把 x 轴下方的图象沿 x 轴翻折到 x 轴上方即可．概括为 “上不动，下翻上”．
几何画板演示
练一练·当堂检测、目标达成落实处
1.3.1（一）
1．正、余弦曲线在研究正、余弦函数的性质中有着非常重要的
本 课 时 栏 目 开 关
应用，是运用数形结合思想解决三角函数问题的基础．
2．五点法是画三角函数图象的基本方法，要熟练掌握，与五点 法作图有关的问题是高考常考知识点之一．
练一练·当堂检测、目标达成落实处
1 log2 －1的定义域． sin x
1.3.1（一）