2018年初中毕业班质量检测及标准答案
2018年漳州市初中毕业班质量检测数学试题和答案
2018漳州市初中毕业班质量检测数学试题一、选择题（本大题共10小题，每小题4分，共40分） 1．如图，数轴上点M 所表示的数的绝对值是（ ）． A ．3 B ．3- C ．±3 D ．31-2．“中国天眼"FAST 射电望远镜的反射面总面积约250 000m 2，数据250 000用科学记数法表示为（ ）．A ．25×104B ．2.5×105C ．2。
5×106D ．0。
25×1063．如图是某几何体的左视图，则该几何体不可能．．．是( )． 4．下列计算，结果等于x 5的是（ )．A ．32x x + B ．32x x ⋅ C ．210x x÷ D ．（x 2)35．如图,在右框解分式方程的4个步骤中，根据等式基本性质的是( ）．A ．①②B ．②④C ．①③D ．③④6．如图，OP 平分∠AOB，PC⊥OA 于C ，点D 是OB 上的动点，若PC=6cm 则PD 的长可以是（ ）．A ．3cmB ．4cmC ．5cmD ．7 cm7．如图,点A ，B 在方格纸的格点上，将线段AB 先向右平移3格，再向下 平移2个单位，得线段DC,点A 的对应点为D ，连接AD 、BC,则关于 四边形ABCD 的对称性，下列说法正确的是（ ）． A ．既是轴对称图形,又是中心对称图形 B ．是中心对称图形，但不是轴对称图形 C ．是轴对称图形,但不是中心对称图形 D ．既不是轴对称图形,也不是中心对称图形8．甲、乙两地今年2月份前5天的日平均气温如图所示，则下列描述错误．．的是（ ）． A ．两地气温的平均数相同B ．甲地气温的众数是4℃C ．乙地气温的中位数是6℃D ．甲地气温相对比较稳定9．如图，正六边形 ABCDEF 的中心与坐标原点0重合,其中A （-2，0）． 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次，每次旋转 60°,则旋转后点A 的对应点A’的坐标是（ )． A ． （1，3）B ． （3，1）C ．(1,3-）D ．(—1,3) 10．如图，在矩形ABCD 中,点A 在x 轴上，点B 的坐标为（1，0），且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上，若在矩形ABCD左视图CBAD xyE FO C BA DxyO内随机取一点,则此点取自阴影部分的概率是（ ）． A ．21 B ．83 C ．41 D ．61二，填空题（本大题共6小题，每小题4分，共24分) 11．因式分解：a ax -2=________．12．一个不透明的袋子中装有4个红球、2个黑球，它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球"是________事件(填“必然”、 “随机”或“不可能”) 13．如图，DE 是△ABC 的中位线，若△ADE 的面积为3,则△ABC 的面积为________．14．“若实数a ,b ，c 满足a 〈b <c ，则a +b 〈c ”，能够说明该命题是假命题的一组a ，b ,c 的值依次为________． 15．如图，在□ABCD 中，点E ，F 分别在边AD 、BC 上，BF=2，∠DEF=60°将四边形EFCD 沿EF 翻折，得到四边形EFC ’D’,ED’交BC 于点G ，则△GEF 的周长为________． 16．如图，双曲线y=xk(x >0)经过A 、B 两点，若点A 的横坐标为1， ∠OAB=90°，且OA=AB ，则k 的值为________． 三、解答题(本大题共9小题，共86分） 17．（8分) 计算：91301-+-π 18．（8分）如图，在△ABC 中，∠A=80°，∠B=40°．（1）求作线段BC 的垂直平分线DE ，垂足为E ，交AB 于点D; (要求；尺规作图，保留作图痕迹，不写作法） （2)在(1)的条件下，连接CD ，求证:AC=CD ． 19．（8分)求证：对角线相等的平行四边形是矩形． （要求：画出图形，写出已知和求证,并给予证明)20．（8分)为响应市收府关于”垃圾不落地·市区更美丽"的主题宣传活动，某校随机调查了部分学生对垃圾分类知识的掌握情况．调查选项分为“A :非常了解，B ：比较了解C ：了解较少,D:不了解”四种，并将调查结果绘制成以下两幅不完整的统计图． 请根据图中提供的信息，解答下列问题： (1)把两幅统计图补充完整；（2）若该校学生数1000名，根据调查结果，估计该校“非常了解”与“比较了解”的学 生共有________名；(3)已知“非常了解”的4名男生和1名女生，从 中随机抽取2名向全校做垃圾分类的知识交流，请用画树状图或列表的方法，求恰好抽到1男1女的概率．CB A D EA B CDD ’ EF G BAxyOB CABCD ___%___%30%8%垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况A21．(8分）如图，AB 是⊙0的直径，AC 是弦，D 是BC 的中点，过点D 作EF 垂直于直线AC ，垂足为F,交AB 的延长线于点E ． (1）求证：EF 是⊙0的切线； （2)若tan A=34，AF=6，求⊙0的半径．22．（10分)某景区售票处规定：非节假日的票价打a 折售票； 节假日根据团队人数x （人）实行分段售票：若≤x 10，则按 原展价购买;若x 〉10，则其中10人按原票价购买，超过部 分的按原那价打b 折购买．某旅行社带团到该景区游览，设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示．（1）观察图象可知：a ________，b ________；(2）当x >10时，求y 2与x 之间的函数表达式；（3）该旅行社在今年5月1目带甲团与5月10日（非节假日）带乙国到该景区游览，两团合计50人，共付门票款3120元，已知甲团人数超过10人，求甲团人数与乙团人数．23．（10分）阅读：所谓勾股数就是满足方程x 2+y 2=z 2的正整数解，即满足勾股定理的三个正整数构成的 一组数．我国古代数学专著《九章算术》一书，在世界上第一次给出该方程的解为：)(2122n m x -=，y =mn ，)(2122n m z +=，其中m 〉n >0，m 、n 是互质的奇数． 应用:当n =5时,求一边长为12的直角三角形另两边的长．D24．(12分)已知抛物线c bx ax y ++=2 （a 、b 、c 是常数，0≠a )的对称轴为直线2-=x ． （1） b =______；(用含a 的代数式表示)(2)当1-=a 时，若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解，求c 的取值范围； （3)若抛物线过点(2-，2-)，当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4，求a 的值． 25．（14分）如图，在正方形ABCD 中，对角线AC 、BD 相交于点O ，E 为OC 上动点（与点0不重合), 作AF⊥BE,垂足为G ，交BC 于F,交B0于H,连接0G ，CC ． （1）求证：AH=BE ； (2）试探究：∠A GO 的度数是否为定值?请说明理由； (3)若OG⊥CG,BG=5，求△OGC 的面积．CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议一、选择题(本大题共10小题,每小题4分，共40分）1 2 3 4 5 6 7 8 9 10A B D B C D A B A C二、填空题（本大题共6小题，每小题4分,共24分)11. a(x+1）(x—1); 12. 必然; 13. 12； 14.答案不唯一,如1,2,3； 15。
2018年福建省福州市初中毕业班质量检测数学试题及答案
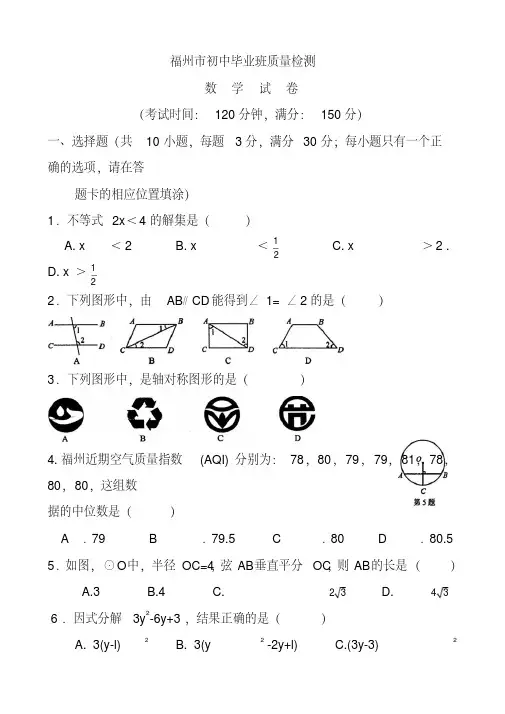
福州市初中毕业班质量检测数学试卷（考试时间：120分钟，满分：150分）一、选择题（共10小题，每题3分，满分30分；每小题只有一个正确的选项，请在答题卡的相应位置填涂）1．不等式2x＜4的解集是（）A. x＜2B. x＜1C. x＞2 .2D. x＞122．下列图形中，由AB∥CD能得到∠1= ∠2的是（）3．下列图形中，是轴对称图形的是（）4.福州近期空气质量指数(AQI)分别为：78，80，79，79，81，78，80，80，这组数据的中位数是（）A．79 B．79.5 C．80 D．80.55．如图，⊙O中，半径OC=4，弦AB垂直平分OC，则AB的长是（）A.3B.4C.6．因式分解3y2-6y+3，结果正确的是（）A. 3(y-l)2B. 3(y2 -2y+l)C.(3y-3)227．下列计算正确的是（）A. (a+b)2 =a2+b2B. a9÷a3=a3C.(ab)3=a3b3.D.(a5)2 =a78．如图，C，D是线段AB上两点，分别以点A和点B为圆心，AD，BC长为半径作弧，两弧相交于点M,连接AM,BM.测量∠AMB的度数，结果为（）A．100° B．110° C．120°D.130°9．已知y是x的函数，当x＞-1时，y随着x的增大而减小；当x＜-l时，y随着x的增大而增大．满足上述条件的函数图象可能是（）10.在△ABC中，∠C= 90°，AC=3，BC =4，D为BC边上一点，将△ACD沿AD折叠，当点C落在边AB上时，BD的长为（）A．1.5 B.2 C．2.5 D．3二、填空题（共6小题，每题4分，满分24分）11.如图，∠ABC=90°，∠CBD=40°，则∠ABD的度数是12.已知反比例函数图象过点(3，1)，则它的解析式是．13．如果2426x =-，那么13x -值是 14. 一个质地均匀的小正方体，’六个面分别标有数字“l”“2”“2”“3”“3”“3”，掷小正方体后，朝上的一面数字为2的概率是 ．15．某企业今年5月份产值为a(l - 10%)(1+15%)万元，比4月份增加了15%，4月份比3月份减少了10%，则3月份的产值是 万元．16.已知二次函数y=(x-l)2-t 2(t ≠0)，方程(x-1)2-t 2-1=0的两根分别为m ，n （m ＜n ），方程(x-l)2-t 2-2=0的两根分别为p ，q(p ＜q)，判断m ，n ，p ，q 的大小关系是 （用“＜”连接）． 三、解答题（共10小题，满分96分） 17.（7分）计算：011(2015()4--+18.（7分）化简求值：,22y x y y x x ---其中.31,31-=+=y x19．（8分）解方程：.0522=-+x x20.（8分）如图，AC ，BD 交于点D ，AB∥CD，OA= OC ． 求证：AB= CD ．21. (9分)某校政教处针对同学们对福州地铁建设情况的了解程度进行随机抽样调查，并制成如下统计图，请根据图中的信息，解答下列问题：(1)抽样调查的人数共有 人；(2)就福州地铁建设情况随机采访该校一名学生，哪部分学生最可能被采访到，为什么？22.（9分）某班去看演出，甲种票每张24元，乙种票每张18元，如果35名学生购票恰好用去750元，甲乙两种票各买了多少张？23. (10分)如图，AB为⊙O的直径，弦AC=2，∠B= 30°，∠ACB的平分线交⊙O于点D，求：(1) BC，AD的长。
2018年福建省福州市初中毕业班质量检测数学试题及答案
(1) 抽样调查的人数共有
人；
(2) 就福州地铁建设情况随机采访该校一名学生，哪部分学生最可能 被采访到，为什么？
22. （ 9 分）某班去看演出，甲种票每张 24 元，乙种票每张 18 元，如 果 35 名学生购票恰好用去 750 元，甲乙两种票各买了多少张？ 23. (10 分 ) 如图， AB 为⊙ O的直径，弦 AC=2，∠ B= 30 °，∠ ACB的 平分线交⊙ O于 点 D，求： (1) BC ， AD的长。 (2) 图中两阴影部分面积的和．
∴∠ BDE= ∠BAC= ，
∵ BD= 2BC=2sin ， ∴ BE=BD· sin =2sin .sin ∴ AE=AB-BE=l-2sin 2 ，
=2sin 2 ,
∴ cos2
AE 1 2sin 2
cos DAE
AD
1
2
1 2sin
阅读以上内容，回答下列问题： (1) 如图 l ，若 BC=1 ，则 cos =
）
＞2 .
3．下列图形中，是轴对称图形的是（
）
4. 福州近期空气质量指数 (AQI) 分别为： 78，80， 79， 79， 81， 78，
80， 80，这组数
据的中位数是（
）
A ．79
B
．79.5
C
．80
D
．80.5
5．如图， ⊙ O中，半径 OC=4，弦 AB垂直平分 OC，则 AB的长是 （ ）
3
(2) 求出 sin 2 的表达式（用含 sin
， cos2 =
；
或 cos 的式子表示） ．
25. （ 13 分）如图，△ AABC 中， AC=8， BC=6， AB =10．点 P 在 AC 边
2018年初中毕业班质量检测及答案
2018年初中毕业班质量检测语文试题（全卷共6页，23题；完卷时间120分钟；满分150分）友情提示：请把所有答案填写（涂）在答案卡上，请不要错位、越界做答！（1）窈窕淑女，。
（《诗经·关雎》）（2），悠然见南山。
（陶渊明《饮酒》）（3）会当凌绝顶，。
（杜甫《望岳》）（4）春蚕到死丝方尽，。
（李商隐《无题》）（5）乱花渐欲迷人眼，。
（白居易《钱塘湖春行》）（6），燕然未勒归无计。
（范仲淹《渔家傲·秋思》）（7）千古兴亡多少事？悠悠。
（辛弃疾《南乡子·登京口北固亭有怀》）（8）峰峦如聚，，。
（张养浩《山坡羊·潼关怀古》）（9）子曰：“，思而不学则殆。
”（《论语》）（10）我们常引用周敦颐《爱莲说》中的“，”来强调一个人应不受环境影响，保持崇高的个性节操。
2. 下列文学常识说法有误．．的一项是（2分）A．我国古代文学作品常用“桑梓”“桃李”“婵娟”分别代指家乡、老师、月亮。
B．唐诗、宋词、元曲是我国诗歌史上的三大高峰。
唐有大小李杜，宋有豪放之“苏辛”，元有四大家。
C．《从百草园到三味书屋》和《藤野先生》都是现代作家鲁迅的回忆性散文。
D．《我的叔叔于勒》选自法国作家莫泊桑的短篇小说集《羊脂球》。
3. 阅读下面文字，按要求作答。
（6分）2018平昌冬奥会闭幕式上，“北京八分钟”表演甲（A、美轮美奂B、富丽堂皇）、科技感十足，为观众献上了一场视觉盛宴。
24台移动机器人携．①（A、xié B、jiá）带“冰屏”与舞蹈演员配合完成了一系列màn ②（A、曼 B、嫚）妙复杂的舞美动作，展现了人工智能与中华文化的完美原句：在经久不息的掌声中，表明八分钟的演出完美成功。
修改句：二、阅读（70分）（一）阅读下面这首诗，完成4～5题。
（5分）送杜少府之任蜀州王勃城阙辅三秦，风烟望五津。
与君离别意，同是宦游人。
海内存知己，天涯若比邻。
无为在歧路，儿女共沾巾。
2018年漳州市初中毕业班质量检测数学试题和答案
2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题，每小题4分，共40分) 1．如图，数轴上点M 所表示的数的绝对值是（ ）． A ．3 B ．3- C ．±3 D ．31-2．“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2，数据250 000用科学记数法表示为（ ）．A ．25×104B ．2.5×105C ．2.5×106D ．0.25×1063．如图是某几何体的左视图，则该几何体不可能．．．是（ ）． 4．下列计算，结果等于x 5的是（ ）．A ．32x x + B ．32x x ⋅ C ．210x x÷ D ．(x 2)35．如图，在右框解分式方程的4个步骤中，根据等式基本性 质的是（ ）．A ．①②B ．②④C ．①③D ．③④6．如图，OP 平分∠AOB，PC⊥OA 于C ，点D 是OB 上的动点，若PC=6cm 则PD 的长可以是（ ）．A ．3cmB ．4cmC ．5cmD ．7 cm7．如图，点A ，B 在方格纸的格点上，将线段AB 先向右平移3格，再向下 平移2个单位，得线段DC ，点A 的对应点为D ，连接AD 、BC ，则关于 四边形ABCD 的对称性，下列说法正确的是（ ）． A ．既是轴对称图形，又是中心对称图形 B ．是中心对称图形，但不是轴对称图形 C ．是轴对称图形，但不是中心对称图形 D ．既不是轴对称图形，也不是中心对称图形8．甲、乙两地今年2月份前5天的日平均气温如图所示，则下列描述错误．．的是（ ）． A ．两地气温的平均数相同B ．甲地气温的众数是4℃C ．乙地气温的中位数是6℃D ．甲地气温相对比较稳定9．如图，正六边形 ABCDEF 的中心与坐标原点0重合，其中A(-2，0)． 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次，每次旋转 60°，则旋转后点A 的对应点A'的坐标是（ ）． A ． (1，3)B ． (3，1)C ．(1，3-)D ．(-1，3) 10．如图，在矩形ABCD 中，点A 在x 轴上，点B 的坐标为(1，0)，且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上，若在矩形ABCD左视图内随机取一点，则此点取自阴影部分的概率是（ ）． A ．21 B ．83 C ．41 D ．61二，填空题(本大题共6小题，每小题4分，共24分) 11．因式分解：a ax -2=________．12．一个不透明的袋子中装有4个红球、2个黑球，它们除颜色外其余都相同，从中任意搞出3个球，则事件“摸出的球至少有1个红球”是________事件(填“必然”、13．如图，DE 是△ABC 的中位线，若△ADE 的面积为3，则△ABC 的面积为________．14．“若实数a ，b ，c 满足a<b <c，则a +b <c ”，能够说明该命题是假命题的 一组a ，b ，c 的值依次为________． 15．如图，在□ABCD 中，点E ，F 分别在边AD 、BC 上，BF=2，∠DEF=60°将四边形EFCD 沿EF 翻折，得到四边形EFC ’D’，ED ’交BC 于点G ，则△GEF 的周长为________． 16．如图，双曲线y=xk(x >0)经过A 、B 两点，若点A 的横坐标为1， ∠OAB=90°，且OA=AB ，则k 的值为________． 三、解答题(本大题共9小题，共86分) 17．(8分) 计算：91301-+-π 18．(8分)如图，在△ABC 中，∠A=80°，∠B=40°．(1)求作线段BC 的垂直平分线DE ，垂足为E ，交AB 于点D ； (要求；尺规作图，保留作图痕迹，不写作法) (2)在(1)的条件下，连接CD ，求证：AC=CD ．19．(8分)求证：对角线相等的平行四边形是矩形． (要求：画出图形，写出已知和求证，并给予证明)20．(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动，某校随机调查了部分学生对垃圾分类知识的掌握情况．调查选项分为“A：非常了解，B ：比较了解C ：了解较少，D ：不了解”四种，并将调查结果绘制成以下两幅不完整的统计图． 请根据图中提供的信息，解答下列问题： (1)把两幅统计图补充完整；(2)若该校学生数1000名，根据调查结果，估计该校“非常了解”与“比较了解”的学 生共有________名；(3)已知“非常了解”的4名男生和1名女生，从 中随机抽取2名向全校做垃圾分类的知识交流，请用画树状图或列表的方法，求恰好抽到1男1女的概率．CA B CDD ’ EF G B C垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况21．(8分)如图，AB 是⊙0的直径，AC 是弦，D 是BC 的中点，过点D 作EF 垂直于直线AC ，垂足为F ，交AB 的延长线于点E ． (1)求证：EF 是⊙0的切线； (2)若tan A=34，AF=6，求⊙0的半径．22．(10分)某景区售票处规定：非节假日的票价打a 折售票； 节假日根据团队人数x (人)实行分段售票：若≤x 10，则按 原展价购买；若x >10，则其中10人按原票价购买，超过部 分的按原那价打b 折购买．某旅行社带团到该景区游览，设在非节假日的购票款为y 1元，在节假日的购票款为y 2元，y 1、y 2与x 之间的函数图象如图所示．(1)观察图象可知：a ________，b ________；(2)当x >10时，求y 2与x 之间的函数表达式；(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览，两团合计50人，共付门票款3120元，已知甲团人数超过10人，求甲团人数与乙团人数．23．(10分)阅读：所谓勾股数就是满足方程x 2+y 2=z 2的正整数解，即满足勾股定理的三个正整数构成的 一组数．我国古代数学专著《九章算术》一书，在世界上第一次给出该方程的解为：)(2122n m x -=，y =mn ，)(2122n m z +=，其中m >n >0，m 、n 是互质的奇数． 应用：当n =5时，求一边长为12的直角三角形另两边的长．24．(12分)已知抛物线c bx ax y ++=2(a 、b 、c 是常数，0≠a )的对称轴为直线2-=x ． (1) b =______；(用含a 的代数式表示)(2)当1-=a 时，若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解，求c 的取值范围； (3)若抛物线过点(2-，2-)，当01≤≤-x 时，抛物线上的点到x 轴距离的最大值为4，求a 的值．25．(14分)如图，在正方形ABCD 中，对角线AC 、BD 相交于点O ，E 为OC 上动点(与点0不重合)， 作AF⊥BE，垂足为G ，交BC 于F ，交B0于H ，连接0G ，CC ． (1)求证：AH=BE ； (2)试探究：∠A GO 的度数是否为定值?请说明理由； (3)若OG⊥CG，BG=5，求△OGC 的面积．CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议二、填空题(本大题共6小题，每小题4分，共24分)11. a（x+1）(x-1)； 12. 必然； 13. 12； 14.答案不唯一，如1,2,3； 15. 6； 16.2.三、解答题(本大题共9小题，共86分)17.（本小题满分8分）解：原式=11+133……………………………………………………………………6分=1. ……………………………………………………………………8分18.（本小题满分8分）解：（1）如图，直线DE为所求作的垂直平分线，点D，E就是所求作的点；…………4分（没标字母或字母标错扣1分）（2）连接CD.方法一：∵DE垂直平分AB,∴BD=CD，∴∠1=∠B=40°. ……………………………5分∴∠2=∠B+∠1=80°. ……………………6分∵∠A=80°,∴∠2=∠A. …………………………………………………………7分∴AC=CD.……………………………………………………………8分方法二：∵DE垂直平分AB,∴BD=CD，∴∠1=∠B=40°. ………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°.∴∠ACD=60°-40°=20°. ……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A. …………………………………7分∴AC=CD.……………………………………………………………8分已知：如图，在□ABCD 中， AC =BD . （画图2分，已知1分） ………………3分 求证：□ABCD 是矩形. …………………………………………………………4分 证明：方法一：∵四边形ABCD 是平行四边形,∴AB =CD ，AB ∥CD . …………………5分∵AC =BD ，BC =BC ,∴△ABC ≌△DCB .∴∠ABC =∠DCB . ………………………………………………6分 ∵AB ∥CD ,∴∠ABC +∠DCB =180°.∴∠ABC =11802⨯°=90°. …………………………………………7分 ∴□ABCD 是矩形. ……………………………………………………8分方法二：设AC ，BD 交于点O .∵四边形ABCD 是平行四边形,∴OA =OC ，OB =OD . ………………5分∵AC =BD ,∴OA =OC =OB .∴∠1=∠3,∠2=∠4. ……………………………………………6分∴∠ABC =∠1+∠2=11802⨯°=90°. …………………………………7分 ∴□ABCD 是矩形. ………………………………………………8分 20.（本小题满分8分）解：（1）如图所示（补充2个或3个正确，得1分）； …………………………………2分 （2）500； ………4分（3）树状图法：………………………………………6分共有12种等可能结果，其中满足条件有6种，∴P （一男一女）=12. ………………8分 （用列表法参照给分）解：（1）方法一：如图1，连接OD . ∵EF ⊥AF ,∴∠F =90°.∵D 是BC 的中点,∴BD DC =.∴∠1=∠2=12∠BOC . ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 . ………………………………………2分 ∴OD ∥AF . ∴∠EDO =∠F =90°.∴OD ⊥EF . ……………………………………………………………3分 ∴EF 是⊙O 的切线. ……………………………………………………4分方法二：如图2，连接OD ，BC .∵D 是BC 的中点,∴BD DC =.∴∠1=∠2. …………………………………………………………1分∵OB =OC ，∴OD ⊥BC . ……………………………2分∵AB 是⊙O 的直径，∴∠ACB =90°. ∵AF ⊥EF ，∴∠F =∠ACB =90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分（2）设⊙O 半径为r ,则OA =OD =OB =r .方法一：在Rt △AFE 中，tan A =43，AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴OE =10-r .∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-. ……………………………………7分 ∴r =154， 即⊙O 的半径为154. ……………………………………8分方法二：在Rt △AFE 中，tan A =43，AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴EO =10-r .∵∠A =∠1，∠E =∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r =154， 即⊙O 的半径为154. ……………………………………8分22. （本小题满分10分）解：（1）6,8； ………………………………………………………………………………2分（2）当x ﹥10时，设y 2=kx +b .∵图象过点（10,800），（20,1440）, …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) . ………………………………………………………6分 （3）设甲团有m 人，乙团有n 人.由图象，得y 1=48x . ……………………………………………………………7分 当m ﹥10时，依题意，得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答：甲团有35人，乙团有15人. ………………………………………………10分23. （本小题满分10分）解：∵n =5，直角三角形一边长为12，∴有三种情况： ① 当x =12 时，12)52122=-m （. ………………………………………………………………1分 解得m 1=7，m 2= -7（舍去）. …………………………………………………2分∴y = mn =35. ……………………………………………………………………3分 ∴222211()(75)3722z m n =+=⨯+=. ……………………………………4分 ∴该情况符合题意. ② 当y =12时，5m =12, …………………………………………………………………………5分125m =. …………………………………………………………………………6分 ∵m 为奇数， ∴125m =舍去. …………………………………………………………………7分 ③ 当z =12时，221(5)122m +=，…………………………………………………………………8分 21m =-， …………………………………………………………………9分此方程无实数解. ………………………………………………………………10分 综上所述：当n =5时, 一边长为12的直角三角形另两边的长分别为35，37. 24. （本小题满分12分）解：（1）4a ； ………………………………………………………………………………2分（2）当a = -1时,∵关于x 的方程240x x c --+=在-3< x <1的范围内有解，即关于x 的方程x 2+4x-c =0在-3< x <1的范围内有解，∴b 2-4ac =16+4c ≥0,即c ≥ -4. …………………………………………………3分 方法一：∴抛物线y= x 2+4x =（x +2）2-4与直线y = c 在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2时，y = -4，当x =1时，y = 5. ………………………………5分 由图像可知： -4≤ c < 5. …………………………………………7分方法二：∴抛物线y= x 2 +4x -c =（x +2）2-4-c 与x 轴在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2，y =0时，c = -4，当x = 1，y =0时，c = 5. …………………5分 由图像可知：-4≤ c <5. ………………………………………………7分 方法三：∵224(2) 4.c x x x =+=+-∴c 是x 的二次函数. ……………………………………………………4分当x = -2时，c = -4，当x = 1时，c = 5. ……………………………5分由图像可知： -4≤ c < 5. ………………………………………………7分 （3）∵抛物线y =ax 2+4ax +c 过点（-2，-2），∴c = 4a -2.∴抛物线解析式为：22442(2)2y ax ax a a x =++-=+-. …………………8分 方法一： ① 当a > 0时，抛物线开口向上.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而增大.∵抛物线上的点到x 轴距离的最大值为4，由图像可知：4a -2=4. ………………………………………………9分∴32a =. …………………………………………………………10分 ② 当a < 0时，抛物线开口向下.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而减小. ∵抛物线上的点到x 轴距离的最大值为4，由图像可知：4a -2= -4. ……………………………………………11分∴12a =-. …………………………………………………………12分 方法二： ∵-1≤x ≤0，∴当x = 0时，y = 4a -2；当x = -1时，y = a -2. ……………8分 ∵当-1≤x ≤0时，抛物线上的点到x 轴距离的最大值为4. ∴有两种情况：① 若424a -=，则3122a a ==-或. ……………………9分 此时1242a -=<或5242a -=<，符合题意. ………10分 ② 若24a -=，则a = 6或a = -2. ………………………11分 此时42224a -=>或42104a -=>.∴a = 6或a = -2不合题意，舍去. ………………………12分综上所述: 3122a a ==-或. 25. （本小题满分14分）解：（1）方法一:∵四边形ABCD 是正方形,∴OA =OB ，∠AOB =∠BOE =90°.…………………………………………1分∵AF ⊥BE ,∴∠GAE+∠AEG =∠OBE +∠AEG =90°.∴∠ GAE =∠OBE . ………………………2分∴△AOH ≌ △BOE . ………………………3分∴AH =BE . …………………………………4分方法二:∵四边形ABCD 是正方形,∴∠ABC =90°，AB =CB ，∠ABO =∠ECB =45°. ……………………1分∵AF ⊥BE ,∴∠BAG+∠ABG =∠CBE +∠ABG =90°.∴∠BAH =∠CBE . ………………………………………………………2分 ∴△ABH ≌△BCE . ……………………………………………………3分 ∴AH =BE . ………………………………………………………………4分（2）方法一：∵∠AOH =∠BGH =90°, ∠AHO =∠BHG ,∴△AOH ∽△BGH . ……………………5分 ∴OH AH GH BH=. …………………………6分 ∴OH GH AH BH=. …………………………7分 ∵∠OHG =∠AHB .∴△OHG ∽△AHB . ………………………………………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ……………………9分方法二：如图，取AB 中点M ，连接MO ，MG . ………6分∵∠AGB =∠AOB =90°,∴AM =BM =GM =OM . ………………………7分∴点O ，G 在以AB 为直径的⊙M 上,即点A ,B ,G ,O 四点在以AB 为直径的⊙M 上, ………………………8分 ∴∠AGO =∠ABO =45°，即∠AGO 的度数为定值. ………………………………………………9分（3）∵∠ABC =90°,AF ⊥BE ,∴∠BAG =∠FBG ,∠AGB =∠BGF =90°,∴△ABG ∽△BFG . ……………………………………………………………10分 ∴GFBG BG AG =,∴AG ·GF =BG 2 =5. …………………………………11分∵△AHB ∽△OHG ，∴∠BAH =∠GOH =∠GBF .∵∠AOB =∠BGF =90°,∴∠AOG =∠GFC . ……………………………………………………………12分 ∵∠AGO =45°,CG ⊥GO ,∴∠AGO =∠FGC =45°.∴△AGO ∽△CGF . ………………………………………………………13分 ∴CGAG GF GO =, ∴GO ·CG =AG ·GF =5.∴S △OGC =12CG ·GO =52. ……………………………………………………14分。
2018年莆田市初中毕业班质量检查试卷评分标准与参考答案
2018年莆田市初中毕业班质量检查试卷数学参考答案与评分标准说明：(一)考生的解法与“参考答案”不同时，可参考“答案的评分标准”的精神进行评分． (二)如果解答的某一步计算出现错误，这一错误没有改变后续部分的考察目的，可酌情给分，但原则上不超过后面得分数的二分之一；如果属严重的概念性错误，就不给分．(三)以下解答各行右端所注分数表示正确做完该步骤应得的累计分数． (四)评分的最小单位1分，得分和扣分都不能出现小数点．一、选择题(本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)(1) C (2) C (3) B (4) D (5) C (6) A (7) D (8) B (9) B (10) A 二、填空题(本大题共6小题，每小题4分，共24分．把答案填在答题卡上的相应位置) (11) 2 (12) 8.27⨯105 (13) 1 (14)25 (15) 43(16) 四 三、解答题(本大题共9小题，共86分．解答应写出必要的文字说明、证明过程、正确作图或演算步骤)(17) (本小题满分8分)解：原式=111)1(2+-+÷+a a a a ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分=aa a a 1)1(2+⨯+ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 =11+a ┄ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∵a ＝13-. ∴原式=33311131==+-. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (18) (本小题满分8分)(I)┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 如图所示，点D 就是所求作的点. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 (II) 在菱形ABCD 中，∠BAC =60°，OB ⊥OA ， ┄┄┄┄┄┄┄┄ ┄┄┄┄5分∴在Rt △OAB 中，tan ∠OAB =tan60°=OAOB.∵OA=1∴3=BO ，BD =32. ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分 又∵AC =2OA =2∴菱形ABCD 的面积3221=⋅=AC BD S . ┄┄┄┄┄┄┄┄┄┄┄┄┄8分(19) (本小题满分8分)(I) 120 ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄4分 (II) 解：平均保费为300)21075.1305.14025.14018085.0100(6000⨯+⨯+⨯+⨯+⨯+⨯⨯=6950(元) ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄8分 (20) (本小题满分8分)(I) △ADE 是等腰直角三角形. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分 理由：在等边△ABD 和等边△ACE 中， ∵BA =DA ，CA =EA ，∠BAD =∠CAE =60°. ∴∠BAD -∠CAD =∠CAE -∠CAD . 即∠BAC =∠EAD .∴△ABC ≌△ADE . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴AB=AD ，BC=DE ，∠ABC =∠ADE ∵ AB =BC ，∠ABC =90° ∴AD =DE ，∠ADE =90°即△ADE 是等腰直角三角形. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 (II) 连接CD ，则直线CD 垂直平分线段AE .(或连接BE ，则直线BE 垂直平分线段AC ) ┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分理由：由(I)得DA =DE . 又∵CA =CE .∴直线CD 垂直平分线段AE . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (21) (本小题满分8分)(I) 解：观察可知，售价x 与日销量y 的乘积为定值300.y 与x 之间的关系为反比例函数. ┄┄┄┄┄┄┄┄┄┄┄┄2分设函数解析式为)0( ≠=k x ky .当30,10==y x 时，300=k . ┄┄┄┄┄┄┄┄┄┄┄┄┄3分∴函数解析式为 300xy =. ┄┄ ┄┄┄┄┄┄┄┄┄┄4分 (II)解： 能达到200元.理由：依题意：200300)10(=⋅-xx .解得：30=x . ┄┄┄┄┄┄┄┄┄┄┄┄6分 经检验，30=x 是原方程的解，并且符合题意. ┄┄┄┄┄┄┄7分 答：当售价30元/kg 时，水果店销售该种水果的日利润为200元. ┄┄┄┄8分 (22) (本小题满分10分)(I)解：∵AB ⊥CD ，垂足为N∴∠BNO =90°在Rt △ABC 中，∵ON =1，BN =3∴222=+=ON BN BO ，3tan ==∠ONBNBON ┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴∠BON =60° ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分∴. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分(II)证明：如图，连接BC ∵CD 是⊙O 的直径，AB ⊥CD ，∴. ┄┄┄┄┄┄┄┄┄┄┄┄6分∴∠1=∠CAB∵AB AE AC ⋅=2，且∠A =∠A∴△ACE ∽△ABC ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 ∴∠1=∠2 ∴∠CAB =∠2∴∠CEB =∠CAB +∠2=2∠CAB . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (23) (本小题满分10分)(I)解：直线2+-=x y 经过点（2，0）与（0，2），则这两点绕原点O 顺时针旋转90°的对应点为（0，-2）与（2，0）┄┄┄2分 设直线2+-=x y 的“旋转垂线”的解析式为)0( ≠+=k m kx y ┄┄3分 把（0，-2）与（2，0）代入 m kx y +=得：⎩⎨⎧=+-=022m k b .解得⎩⎨⎧-==21m k .即直线2+-=x y 的“旋转垂线”为2-=x y ； ┄┄┄┄┄┄┄┄┄┄┄┄┄5分DC(II) 证明：直线)0( 111≠+=k x k y 经过点（11k -，0）与（0，1）， ┄┄┄┄6分 则这两点绕原点O 顺时针旋转90°的对应点为（0，11k ）与（1，0）， ┄┄8分 把（0，11k ）与（1，0）代入b x k y +=2，得⎪⎩⎪⎨⎧=+=0121b k k b∴0112=+k k ，∴121-=⋅k k . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (24) (本小题满分12分)(I)证明∵AD 平分∠BAC ， ∴∠P AQ =∠BAD∵PQ ⊥AC ，BD ⊥AD ∴∠PQA =∠BDA =90°∴△PQA ∽△BDA ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分 ∴ABAD AP AQ = ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 (II)证法一：由(I)得ABADAP AQ =又∵∠P AB =∠QAD∴△P AB ∽△QAD ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分 ∴∠APB =∠AQD∵∠APB =∠PDB +∠DBP ∠AQD =∠AQP +∠DQP ∴∠PDB =∠AQP =90°∴∠DBP =∠DQP ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分 证法二：如图，延长AC ，交BD 的延长线于点E ， 连接PE ，取PE 的中点O ，连接OD,OQ.∵∠PDE =∠PQE =90°在Rt △PDE 与Rt △PQE 中，∵O 是PE 的中点，∴PE DO 21=，PE QO 21= 即PO EO QO DO ===∴P 、D 、E 、Q 四点都在以O 为圆心，OP 为半径的⊙O 上，┄┄┄┄┄┄┄┄5分∴∠1=∠DQP ∵AD 垂直平分BE ∴PB =PE ∴∠1=∠DBP∴∠DBP =∠DQP ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分B(III)解：过点P 分别作PG ⊥AB 于点G ，PH ⊥DQ 于点H . 则PG =d 1，PH =d 2.∵AD 平分∠BAC ，PQ ⊥AC.∴d 1=PG =PQ . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 ∴PHPQ d d S ==21. 由(II)得∠DBP =∠DQP ，∵∠BDP =∠QHP =90°.∴△DBP ∽△HQP ； ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 ∴PDPB PH PQ =. 在Rt △BDP 中，BD =1，DP =t.∴12+=t PB .∴tt S 12+=. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分25．(本小题满分14分)(I) 解：∵A (-1，0)，B (3，0)，∴该二次函数图象的对称轴为1=x ，且AB =4. 过点C 作CH ⊥AB 于点H.∵△ABC 为等腰直角三角形，∴CH =21AB =2. ┄┄1∴C (1，-2)或C (1，2) ①如图1，当C (1，-2)时，可设2)1(2--=x a y .把点B (3，0)代入可得：21=a . ┄┄┄┄3分②如图2，当C (1，2)时，可设2)1(2+-=x a y .把点B (3，0)代入可得：21-=a .综上所述，21=a 或21-. ┄┄┄┄┄┄┄4分(II) 解：(i ) 当a b 2-=时，c ax ax y +-=22=a c x a -+-2)1(.┄┄┄┄┄┄┄┄5分 ∴C (1，c -a )∴B (1+c -a ，0).┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∴0)(2=-+-a c a c a .B∴0)1)((2=+--a ac a c . ∵0≠-a c ，∴aa c 1-=.∴()ax a y 112--=. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (ii ) 法一：∵31≤≤-x ，a <0，∴当x =-1或3时，y 取得最小值aa 14-，┄┄┄┄┄┄┄┄┄┄┄┄10分当x =1时，y 取得最大值a1-. ┄┄┄┄┄┄┄┄┄┄┄┄11分若以321, , y y y 为长度的三条线段能围成三角形.则aa a 1)14(2->-. ┄┄┄┄┄┄┄┄┄┄┄┄13分整理得：0182<-a . ∴042<<-a . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分 法二：依题意得：a x a y 1)1(211--=，a x a y 1)1(222--=，ax a y 1)1(233--=. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分以321, , y y y 为长度的三条线段能围成三角形.不妨设321y y y ≤≤. 则321y y y >+在31≤≤-x 范围内恒成立.∴ax a a x a a x a 1)1(1)1(1)1(232221-->--+-- 整理得：22322211)1()1()1(ax x x <---+-. ┄┄┄┄┄┄┄┄┄┄┄10分等价于232221)1()1()1(---+-x x x 最大值小于21a.当121-==x x 时，2221)1()1(-+-x x 取最大值为8； 当13=x 时，23)1(-x 取最小值为0.此时232221)1()1()1(---+-x x x 取最大值为8. ∴218a <. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分 整理得：0182<-a . ∵0<a .2-a. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分<<∴04。
2018年福州市初中毕业班质量检测试卷及答案
2018 年福州市初中毕业班质量检测（考试时间：45分钟满分：75分）可能用到的相对原子质量：H-1 C-12 O-16第Ⅰ卷选择题分。
每题只有一个选项符合题目要求30题，每题3分，共第Ⅰ卷包含101.下列福州传统工艺制作步骤中，主要发生化学变化的是（）A．糊纸伞B．酿米酒C．刻石雕D．磨牛角梳2.钨酸（HWO）中钨元素的化合价为（）42A．＋2 B．＋3 C．＋4 D．＋63.下列化学用语与其含义不相符的是（）AC—60 个碳原子．60BBaSO—硫酸钡．4C2CH—2 个甲烷分子．4+2—氯化亚铁中铁元素为+2价FeClD．24. 实验室配制稀硫酸并用其与氧化铜反应，部分操作如图1所示，其中正确的是（）D C A B 热．倾．加．取样．稀释倒1图 5. 下列关于水和冰的说法，正确的是（）B. 分子间隔相同 A. 分子质量相同D. 组成元素不同分子大小不同C.）6.下列物质的用途主要利用其化学性质的是（．稀有气体用于霓虹灯A B．干冰用于人工降雨8/ 1．石墨用作电池电极DC．熟石灰改良酸性土壤）。
下列说法正确的是年5月9日，中科院发布了四种新元素的中文名称（如表17. 2017（）A．四种元素都属于金属元素单质．“Nh”可表示B是地壳中含量最多元素．Og C D．镆原子的相对原子质量是115 1表）8. 鉴别下列各组物质所用的试剂或方法，错误的是（．硝酸铵和氯化钠A ——水B．硬水和软水——肥皂水．纯铝和硬铝C ——互相刻划D．氢氧化钠和碳酸钠——酚酞溶液9. 下列归纳正确的是（）——都属于天然纤维A．蚕丝和涤纶——都属于复合肥KNOB．和CO(NH)232——防锈原理相同C．自行车车架喷漆和链条涂油去污原理相同D．洗洁精除油污和汽油除油污——表示X10.图2为采用“数字化”实验，由传感器采集实验相关信息描绘出曲线，其中物质Y能与二氧化碳反应的某液体，纵坐标Y表示烧杯中的某个量。
下列对物质X与纵坐标）的分析正确是（物质X 纵坐标Y 选项A 水溶液的质量pH B 溶液的水氢氧化钠溶液C 溶质的质量溶液中钙元素质量 D 氢氧化钙溶液8/ 2非选择题第Ⅱ卷（10分）化学源于生活。
2018年莆田市初中毕业班质量检查数学试卷(含答案)
2018年莆田市初中毕业班质量检查试卷(满分：150分；考试时间：120分钟)注意：本试卷分为 试题”和 答题卡”两部分，答题时请按答题卡中的注意事项”认真作答，答案写在答题卡上的相应位置. 一、选择题(本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中有且只有 一个选项是正确的，答对的得 4分；答错、不答或答案超过一个的一律得0分) (1) 2018的相反数为1 1 (A) 2018 (B) — (C) -2018 (D) 2018 2018⑵下列式子运算结果为2a 的是(A) a a (B) 2 a (C) a a (D) a' “ a(3)若一个几何体的主视图、左视图、俯视图都是半径相等的圆，则这个几何体是(A)圆柱 (B)球 (C)正方体 (D) 圆锥⑷下列说法中，正确的是(A) 一组对边平行，另一组对边相等的四边形是平行四边形(B) 对角线相等的四边形是矩形(C) 对角线互相垂直的四边形是菱形(D) 有一组邻边相等的矩形是正方形⑸ 若x=1是关于x 的方程x 2 -2x • c =0的一个根，贝U c 的值为(A) 2 (B) 3 (C) 4 (D) 5⑺一组数据：2, 3, 3，4,若添加一个数据3,则发生变化的统计量是(A)平均数 (B)中位数 (C)众数 (D)方差(8) 已知一次函数y =kx ■ 1的图象经过点A ，且函数值y 随x 的增大而减小，则点A 的坐标可 能是(A) (2, 4) (B) (-1, 2) (C) (-1, -4) (D) (5, 1)(9) 如图，在四边形ABCD 中，/ A=120°,Z C=80°将厶BMN 沿着MN 翻折，得到△ FMN. 若MF // AD , FN // DC ,贝U/ F 的度数为(A) 70° (B) 80° (C) 90° (D) 100°⑹1 a OB(10) 如图，点A,B 分别在反比例函数y= —(x .0), y )(x ：：：0)的图象上若OA 丄OB,0—=2 , x x OA则a 的值为(A) -4 (B) 4 (C) -2 (D) 2二、填空题(本大题共6小题，每小题4分，共24分•把答案填在答题卡上的相应位置)(11) ___________________ 计算：18=(12) 我国五年来(2013年一2018年)经济实力跃上新台阶，国内生产总值增加到827000亿元. 数据827000亿元用科学记数法表示为 ___________________ 亿元.(14) 如图，△ ABC 中，AB=3 5，AC=4,5 .点 F 在 AC 上, AE 平分/ BAC ，AE 丄 BF 于点E .若点D 为BC 中点，贝U DE 的长为 ______ .(15) 小峰抛掷一枚质地均匀硬币两次，则事件“至少出现一次正面朝上”的概率为(16) 2010年8月19日第26届国际数学家大会在印度的海德拉巴市举行，并首次颁出陈省身奖，该奖项是首个以中国人名字命名的国际主要科学奖 .根据蔡勒公式可以得出2010年8月19日是星期 _________ .(注：蔡勒(德国数学家)公式：心；一2^土誉严“其中：W ――所求的日期的星期数(如大于7,就需减去7的整数倍)，c 所求年份的 前两位，y 所求年份的后两位，m 月份数(若是1月或2月，应视为上一年的13 月或14月，即3空m乞14)，d 日期数，a 1 表示取数a 的整数部分.)三、解答题(本大题共9小题，共86分.解答应写出必要的文字说明、证明过程、正确作图 或演算步骤)(17) (本小题满分8分)先化简，再求值：2 a "(1- 1 )，其中a = 3-1.a 2+2a+1 a+1(18) (本小题满分8分)D(13)如图，四个全等的直角三角形围成一个大正方形 ABCD ，中间阴影部分是一个小正方形EFGH 的面积为.4- C如图，等边△ ABC.(I) 求作一点D ，连接AD , CD ，使得四边形ABCD 为菱形；(要求：尺规作图，保留作 图痕迹，不写作法)(II) 连接BD 交AC 于点0,若0A=1，求菱形ABCD 的面积.(19) (本小题满分8分)保险公司车保险种的基本保费为 a (单位：元)，继续购买该险种的投保人称为续保人, 续保人本年度的保费与其上年度出险次数的关联如下表：该公司随机调查了该险种的300名续保人在一年内的出险情况，得到如下统计图:(I) 样本中，保费高于基本保费的人数为名；(II) 已知该险种的基本保费a 为6000元，估计一名续保人本年度的平均保费.(20) (本小题满分8分)如图，在△ ABC 中，AB=BC ，Z ABC=90°.分别以AB ，AC 为边在AB 同侧作等边△ ABD 和等边△ ACE ，连接DE .(I) 判断△ ADE 的形状，并加以证明；(II) 过图中两点画一条直线，使其垂直平分图中的某条线段，并说明理由.(21) (本小题满分8分)水果店在销售某种水果，该种水果的进价为10元/kg.根据以往的销售经验可知：日销量 y(单位：kg)随售价x(单位：元/kg)的变化规律符合某种函数关系.该水果店以往的销售记录如下表：(售价不低于进价)若y与x之间的函数关系是一次函数，二次函数，反比例函数中的某一种(I) 判断y与x之间的函数关系，并写出其解析式；(II) 水果店销售该种水果的日利润能否达到200元？说明理由.(22) (本小题满分10分)如图，O O的直径CD，AB是。
2018年三明市初中毕业班质量检测数学试题及答案
2018年三明市初中毕业班教学质量检测数 学 试 题（满分：150分 考试时间：5月8日下午 15:00-17:00）友情提示：1.作图或画辅助线等需用签字笔描黑.2.未注明精确度的计算问题，结果应为准确数．．．. 一、选择题（共10题，每题4分，满分40分.每题只有一个正确选项，请在答题卡．．．的相应位置填涂）BC（第6题）（第3题）（第5题）7．某校田径运动会有13名同学参加女子百米赛跑，她们预赛的成绩各不相同，取前6名参加决赛，小玥已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（▲）A ．方差B ．极差C ．平均数D ．中位数8A ．．2C ．3D ． 210．定义运算：a ⋆b =2ab ．若a ，b 是方程x 2+x -m =0(m ＞0)的两个根，则(a +1)⋆a -(b +1)⋆b 的值为（▲） A ．0B ．2C ．4m D ．-4m二、填空题（共6题，每题4分，满分24分．请将答案填在答题卡．．．的相应位置） 1112.在一个不透明的空袋子里放入3个白球和2个红球，每个球除颜色外完全相同，小乐从中任意摸出1个球，摸出的球是红球，放回后充分摇匀，又从中任意摸出1个球，摸到红球的概率是 ▲ ．13.如图，一名滑雪运动员沿着倾斜角为34°的斜坡从A 滑行至B . 已知AB =500米，则这名滑雪运动员下降的垂直高度 为▲ 米.(参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67)14．如图，AB 为半圆的直径，且AB =2，半圆绕点B 顺时针旋转40°，点A 旋转到A ′的位置，则图中阴影部分的面积为▲ (结果 保留π)．（第8题）（第14题）（第13题）DC G （第9题）15．二次函数22y x mx m =++-的图象与x 轴有▲个交点 ． 16．在Rt △ABC 中，∠ABC =90°，AB =3，BC =4，点E ，F 分别在边AB ，AC 上，将△AEF 沿直线EF 翻折，点A 落在点 P 处，且点P 在直线BC 上．则线段CP 长的取值范围是▲.三、解答题（共9题，满分86分．请将解答过程写在答题卡．．．的相应位置，解答应写出文字说明、证明过程或演算步骤.） 17.(本题满分8分）先化简，再求值：2(2)(1)2x x y x x +-++，其中1x =，1y =.18.(本题满分8分） 解方程：21133x x x-+=--.19. (本题满分8分）写字是学生的一项基本功，为了了解某校学生的书写情况，随机对该校部分学生进行测试，测试结果分为A ，B ，C ，D 四个等级.根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息，回答以下问题：(Ⅰ) 把条形统计图补充完整；(Ⅱ) 若该校共有2000名学生，估计该校书写等级为“D 级”的学生约有▲人；(Ⅲ)随机抽取了4名等级为“A 级”的学生，其中有3名女生，1名男生，现从这4名学生中任意抽取2名，用列表或画树状图的方法，求抽到的两名学生都是女生的概率.（第16题）PAFECB（第19题）调查结果扇形统计图20. (本题满分8分）如图，一次函数y=ax +b 的图象经过点A （2，0），与反比例函数ky x的图象在第四象限交于点B (4,n )，△OAB 的面积为32,求一次函数和反比例函数的表达式.21．(本题满分8分）如图，在△ABC 中，∠C ＝90°，∠B ＝30°.(Ⅰ)作边AB 的垂直平分线，交AB 于点D ，交BC 于点E (用尺规作图，保留作图痕迹，不写作法)；(Ⅱ)在(Ⅰ)的条件下，连接AE ，求证：AE 平分∠CAB .22. (本题满分10分）某乡村在开展“美丽乡村”建设时，决定购买A ，B 两种树苗对村里的主干道进行绿化改造，已知购买A 种树苗3棵，B 种树苗4棵，需要380元；购买A 种树苗5棵，B 种树苗2棵，需要400元．（Ⅰ）求购买A ，B 两种树苗每棵各需多少元？（Ⅱ）现需购买这两种树苗共100棵，要求购买A 种树苗不少于60棵，且用于购买这两种树苗的资金不超过5620元．则有哪几种购买方案？（第20题）（第21题）23.(本题满分10分）如图，在△ABC 中，∠A ＝45°，以AB 为直径的⊙O 经过AC 的中点D ，E 为⊙O 上的一点，连接DE ，BE ，DE 与AB 交于点F . （Ⅰ）求证：BC 为⊙O 的切线；（Ⅱ）若F 为OA 的中点,⊙O 的半径为2，求BE 的长.24. (本题满分12分）已知：如图①，△ABC ∽△ADE ，∠BAC ＝∠DAE ＝90°，AB ＝6，AC ＝8，点D 在线段BC 上运动.(Ⅰ) 当AD ⊥BC 时（如图②），求证：四边形ADCE 为矩形； （Ⅱ）当D 为BC 的中点时（如图③），求CE 的长；（Ⅲ）当点D 从点B 运动到点C 时，设P 为线段DE 的中点，求在点D 的运动过程中，点P 经过的路径长（直接写出结论）.25.(本题满分14分）已知直线l ：y =kx +2k +3(k ≠0)，小明在画图时发现，无论k 取何值，直线l 总会经过一个定点A .(Ⅰ)点A 坐标为___▲____； (Ⅱ)抛物线y =c bx x ++22 (c ＞0) 经过点A ，与y 轴交于点B . (ⅰ)当4＜b ＜6时，若直线l 经过点B ，求k 的取值范围．(ⅱ)当k =1时，若抛物线与直线l 交于另一点MAM ≤≤b 的取值范围.（第23题）（第24题）（图②） （图③） （图①）2018年三明市初中毕业班学业质量检测数学试卷参考答案及评分标准说明：以下各题除本参考答案提供的解法外，其他解法参照本评分标准，按相应给分点评分. 一、选择题 (每题4分，共40分)1．A 2．B 3．C 4．A 5．C 6．B 7．D 8．D 9．B 10．A 二、填空题（每题4分，共24分） 11．1)-1)((a a a + 12．5213．280 14．4π915．2 16．51≤≤CP三、解答题（共86分）17．解： 原式=x 2+2xy - (x 2+2x +1)+2x …………2分 = x 2+2xy -x 2-2x -1+2x …………4分=2xy -1.…………5分当x =13＋，y =1-3时，原式=2(13＋)(1-3)-1…………6分＝2（3－1）－1 …………7分 =3. …………8分 18.解：去分母，得2-x -1=x -3 …………3分-x -x =-3-2+1` …………4分 -2x =-4 …………5分x =2 …………6分经检验，x =2是原方程的根所以原方程的根是x =2…………8分19.解：(Ⅰ) B 级人数16人，图略； …………2分(Ⅱ) 360 ； …………4分 (Ⅲ)列表如下：………6分由上表可知，总共有12种等可能结果，其中符合要求有6种，8分 （树状图略）20．解：∵A （2，0），B (4,n )，且点B 在第四象限，∴S △OAB ＝n n -)-221=⨯⨯（. ∵S △OAB ＝23, ∴n =-23.∴B (4, -23). …………3分把B (4, -23)代入x ky =，得k =-6，∴反比例函数表达式为x y 6-=. …………5分把A （2，0），B (4,-23)代入y =ax +b ，得：⎪⎩⎪⎨⎧=+=+23-402b a b a , ∴3-43. 2a b ⎧=⎪⎪⎨⎪=⎪⎩…………7分 ∴一次函数表达式为33-42y x =+. …………8分 21. 解：(Ⅰ)…………3分DE 就是所作的边AB 的垂直平分线.…………4分(Ⅱ)∵∠C ＝90°，∠B ＝30°，∴∠CAB ＝60°. …………5分 ∵DE 垂直平分AB ， ∴AE ＝BE ，∴∠EAB ＝∠B ＝30°， …………7分 ∴∠CAE ＝∠CAB －∠EAB ＝30°， ∴∠CAE ＝∠EAB ＝30°.∴AE 平分∠BAC . …………8分22. 解：（Ⅰ）设购买A ，B 两种树苗每棵分别需x 元，y 元，则⎩⎨⎧=+=+4002538043y x y x , …………3分 解得⎩⎨⎧==5060y x . …………4分答：购买A ，B 两种树苗每棵分别需60元，50元. …………5分（Ⅱ）设购进A 种树苗m 棵，则5620)100(5060≤-+m m …………7分解得62≤m . ∵购进A 种树苗不能少于60棵，且m 为整数，∴m =60或61或62， …………8分 ∴有三种购买方案，分别为：方案一：购进A 种树苗60棵，B 种树苗40棵；方案二：购进A 种树苗61棵，B 种树苗39棵；方案三：购进A 种树苗62棵，B 种树苗38棵. …………10分23.解：（Ⅰ）解法一：连接OD ， ∵OA =OD , ∠A ＝45°， ∴∠ADO =∠A ＝45°,∴∠AOD =90°. …………………1分 ∵D 是AC 的中点，∴AD =CD .∴OD ∥BC . ……………………2分∴∠ABC =∠AOD =90°. ……………………3分∴BC 是⊙O 的切线. ……………………4分解法二：连接BD ， ∵AB 为⊙O 的直径，∴BD ⊥AC . …………………1分 ∵D 是AC 的中点，∴BC =AB .…………………2分 ∴∠C =∠A ＝45°.∴∠ABC =90°.……………………3分 ∴BC 是⊙O 的切线.……………………4分 （Ⅱ）连接OD ，由（Ⅰ）可得∠AOD =90°.∵⊙O 的半径为2, F 为OA 的中点，∴OF=1, BF =3，AD ……………5分∴DF =……………6分∵BD BD =, ∴∠E =∠A .……………7分 ∵∠AFD =∠EFB ,∴△AFD ∽△EFB.……………8分 ∴DF BFAD BE =,3BE =. ……………………9分∴BE =……………………10分 （其他解法按相应步骤给分）24. (Ⅰ)证明：∵AD ⊥BC ，∠DAE ＝90°， ∴∠ADB ＝∠ADC ＝∠DAE ＝90°，∴AE ∥CD ， ………………1分 ∵△ABC ∽△ADE ， ∴∠AED ＝∠ACB ， ∵AD ＝DA ，∴△ADC ≌△DAE .∴AE ＝DC . ………………3分 ∴四边形ADCE 为平行四边形， ∵∠ADC ＝90°，∴□ADCE 为矩形. ………………4分（其他解法按相应步骤给分）（Ⅱ）解：∵∠BAC ＝90°，AB ＝6，AC ＝8， ∴BC =10.∵D 为BC 的中点，∴AD =BD =BC 21＝5.………………5分 ∵△ABC ∽△ADE ，∴AEACAD AB ＝. ∵∠BAC ＝∠DAE ＝90°， ∴∠BAD ＝∠CAE .∴△ABD ∽△ACE.………………7分∴AC AB ＝CE BD. 即CE586＝. ∴CE ＝320. ………………8分（其他解法按相应步骤给分）（Ⅲ）325. ………………12分 25．(Ⅰ) (－2，3)； ………………3分(Ⅱ) (ⅰ) ∵抛物线y =c bx x ++22经过点A ， ∴3＝8-2b +c. ∴c =2b -5.∴B (0, 2b -5). ………………5分∵直线l 经过点B ， ∴2k +3=2b -5.∴k =4-b . ………………6分 当b =4时，k =0，当b =6时，k =2, ∵4＜b ＜6,∴0＜k ＜2. ………………8分(ⅱ) k =1时，直线l 的表达式为y =x +5，直线l 交y 轴于点F (0，5)， 当点M 在点A 右侧，过点A 作x 轴平行线交y 轴于点E ，过点M 作y 轴的平行线交AE 于点D ，∵A (-2，3)，∴AE ＝EF ＝2.∴∠EAF ＝45°. ∴当AM ＝2时，AD ＝MD ＝1.∴M (-1，4). 把M (-1，4)代入y =c bx x ++22，求得b =7,c =9. 由AM ＝42，A (-2，3)，同上可得M (2，7)，把A (-2，3)，M (2，7)代入y =c bx x ++22，求得b =1,c =－3.………………10分把A (-2，3) 代入y =c bx x ++22，得c =2b -5.又∵c ＞0，∴25>b . ∴7b 25≤<………………11分 当点M 在点A 左侧时，由AM ＝2，A (-2，3)，同上可得M (-3，2)，把A (-2，3)，M (-3，2)代入y =c bx x ++22，求得b =11,c =7， 由AM ＝42，A (-2，3)，同上可得M (－6，－1)，把A (-2，3)，M (-6，-1)代入y =c bx x ++22，求得b =17,c =29， ∴17b 11≤≤. 综上所述，7b 25≤<或17b 11≤≤. ………………14分 （其他解法按相应步骤给分）。
福建省莆田市2018年初中毕业班质量检查试卷(含答案)
2018年莆田市初中毕业班质量检查试卷数 学（满分：150分；考试时间：120分钟）注意：本试卷分为“试题”和“答题卡”两部分，答题时请按答题卡中的“注意事项”认真作答，答案写在答题卡上的相应位置．一、选择题(本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中有且只有一个选项是正确的，答对的得4分；答错、不答或答案超过一个的一律得0分) (1) 2018的相反数为(A) 2018 (B)20181 (C) 2018- (D) 20181- (2) 下列式子运算结果为2a 的是(A) a a ⋅ (B) a +2 (C) a a + (D) a a ÷3(3) 若一个几何体的主视图、左视图、俯视图都是半径相等的圆，则这个几何体是(A) 圆柱 (B) 球 (C) 正方体 (D) 圆锥 (4) 下列说法中，正确的是(A) 一组对边平行，另一组对边相等的四边形是平行四边形 (B) 对角线相等的四边形是矩形 (C) 对角线互相垂直的四边形是菱形 (D) 有一组邻边相等的矩形是正方形 (5) 若x =1是关于x 的方程022=+-c x x 的一个根，则c 的值为(A) -1 (B) 0 (C) 1 (D) 2(6) 如图，AB 是⊙O 的切线，A 为切点，连接OB 交⊙O 于点C .若OA =3,tan ∠AOB =34，则BC 的长为 (A) 2 (B) 3 (C) 4 (D) 5(7) 一组数据：2，3，3，4，若添加一个数据3，则发生变化的统计量是(A) 平均数 (B) 中位数 (C) 众数 (D) 方差(8) 已知一次函数1+=kx y 的图象经过点A ，且函数值y 随x 的增大而减小，则点A 的坐标可 能是(A) (2，4) (B) (-1，2) (C) (-1，-4) (D) (5，1)(9) 如图，在四边形ABCD 中，∠A =120°，∠C =80°.将△BMN 沿着MN 翻折，得到△FMN.若MF ∥AD ，FN ∥DC ，则∠F 的度数为(A) 70° (B) 80° (C) 90° (D) 100°(10) 如图，点A ，B 分别在反比例函数)0( ,)0( 1<=>=x x a y x x y 的图象上.若OA ⊥OB ，2=OAOB，则a 的值为(A) -4 (B) 4 (C) -2 (D) 2二、填空题(本大题共6小题，每小题4分，共24分．把答案填在答题卡上的相应位置) (11) 计算：38= .(12) 我国五年来(2013年—2018年)经济实力跃上新台阶，国内生产总值增加到827000亿元.数据827000亿元用科学记数法表示为 亿元.(13) 如图，四个全等的直角三角形围成一个大正方形ABCD ，中间阴影部分是一个小正方形EFGH ，这样就组成一个“赵爽弦图”.若AB =5，AE =4，则正方形EFGH 的面积为 .(14) 如图，△ABC 中，AB =53，AC =54．点F 在AC 上，AE 平分∠BAC ，AE ⊥BF 于点E ．若点D 为BC 中点，则DE 的长为 ．(15) 小峰抛掷一枚质地均匀硬币两次，则事件“至少出现一次正面朝上”的概率为 . (16) 2010年8月19日第26届国际数学家大会在印度的海德拉巴市举行，并首次颁出陈省身奖，该奖项是首个以中国人名字命名的国际主要科学奖． 根据蔡勒公式可以得出2010年8月19日是星期 .(注：蔡勒(德国数学家)公式：110)1(26424-+⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++-⎥⎦⎤⎢⎣⎡=d m y y c c W 其中：W ——所求的日期的星期数(如大于7，就需减去7的整数倍)，c ——所求年份的前两位，y ——所求年份的后两位，m ——月份数(若是1月或2月，应视为上一年的13月或14月，即143≤≤m )，d ——日期数，[]a ——表示取数a 的整数部分.)三、解答题(本大题共9小题，共86分．解答应写出必要的文字说明、证明过程、正确作图或演算步骤)(17) (本小题满分8分)先化简，再求值：)111(122+-÷++a a a a ，其中a ＝13-．(18) (本小题满分8分)如图，等边△ABC .(I) 求作一点D ，连接AD ，CD ，使得四边形ABCD 为菱形；(要求：尺规作图，保留作图痕迹，不写作法)(II) 连接BD 交AC 于点O ，若OA =1，求菱形ABCD 的面积.(19) (本小题满分8分)保险公司车保险种的基本保费为a （单位：元），继续购买该险种的投保人称为续保人， 续保人本年度的保费与其上年度出险次数的关联如下表：该公司随机调查了该险种的300名续保人在一年内的出险情况，得到如下统计图：(I) 样本中，保费高于基本保费的人数为 名；(II) 已知该险种的基本保费a 为6000元，估计一名续保人本年度的平均保费．(20) (本小题满分8分)如图，在△ABC 中，AB =BC ，∠ABC =90°．分别以AB ，AC 为边在AB 同侧作等边△ABD 和等边△ACE ，连接DE ．(I) 判断△ADE 的形状，并加以证明；(II) 过图中两点画一条直线，使其垂直平分图中的某条线段，并说明理由．(21) (本小题满分8分)水果店在销售某种水果，该种水果的进价为10元/kg .根据以往的销售经验可知：日销量y (单位：kg)随售价x (单位：元/kg)的变化规律符合某种函数关系． 该水果店以往的销售记录如下表：（售价不低于进价）若y 与x 之间的函数关系是一次函数，二次函数，反比例函数中的某一种. (I) 判断y 与x 之间的函数关系，并写出其解析式；(II) 水果店销售该种水果的日利润能否达到200元？说明理由.(22) (本小题满分10分)如图，⊙O 的直径CD ，AB 是⊙O 的弦，AB ⊥CD ，垂足为N .连接AC. (I) 若ON =1，BN =3.求长度；(II) 若点E 在AB 上，且AB AE AC ⋅=2.求证：∠CEB =2∠CAB .DC(23) (本小题满分10分)规定：在平面直角坐标系内，某直线l 1绕原点O 顺时针旋转90°，得到的直线l 2称为l 1的“旋转垂线”.(I) 求出直线2+-=x y 的“旋转垂线”的解析式；BC(II) 若直线)0( 111≠+=k x k y 的“旋转垂线”为直线b x k y +=2.求证：121-=⋅k k .(24) (本小题满分12分)如图，AD 平分∠BAC ，BD ⊥AD ，垂足为点D .点P 是AD 上一点，PQ ⊥AC 于点Q ，连接BP ，DQ .(I) 求证：ABADAP AQ =； (II) 求证：∠DBP =∠DQP ；(III) 若BD =1，点P 在线段AD 上运动(不与A ，D 重合)，设DP =t ，点P 到AB 的距离为d 1，点P 到DQ 的距离为d 2．记21d d S =，求S 与t 之间的函数关系式.B(25) (本小题满分14分)已知二次函数)0( 2≠++=a c bx ax y 的图象与x 轴交于A ，B 两点，顶点为C ，且△ABC 为等腰直角三角形.(I) 当A (-1，0)，B (3，0)时，求a 的值； (II) 当a b 2-=，a <0时.(i ) 求该二次函数的解析式(用只含a 的式子表示)；(ii ) 在31≤≤-x 范围内任取三个自变量321,,x x x ，所对应的的三个函数值分别为321,,y y y .若以321, , y y y 为长度的三条线段能围成三角形，求a 的取值范围.2018年莆田市初中毕业班质量检查试卷数学参考答案与评分标准说明：(一)考生的解法与“参考答案”不同时，可参考“答案的评分标准”的精神进行评分． (二)如果解答的某一步计算出现错误，这一错误没有改变后续部分的考察目的，可酌情给分，但原则上不超过后面得分数的二分之一；如果属严重的概念性错误，就不给分．(三)以下解答各行右端所注分数表示正确做完该步骤应得的累计分数． (四)评分的最小单位1分，得分和扣分都不能出现小数点．一、选择题(本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)(1) C (2) C (3) B (4) D (5) C (6) A (7) D (8) B (9) B (10) A 二、填空题(本大题共6小题，每小题4分，共24分．把答案填在答题卡上的相应位置) (11) 2 (12) 8.27⨯105 (13) 1 (14)25 (15) 43(16) 四 三、解答题(本大题共9小题，共86分．解答应写出必要的文字说明、证明过程、正确作图或演算步骤)(17) (本小题满分8分)解：原式=111)1(2+-+÷+a a a a ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分=aa a a 1)1(2+⨯+ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 =11+a ┄ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∵a ＝13-. ∴原式=33311131==+-. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (18) (本小题满分8分)(I)┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 如图所示，点D 就是所求作的点. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分(II) 在菱形ABCD 中，∠BAC =60°，OB ⊥OA ， ┄┄┄┄┄┄┄┄ ┄┄┄┄5分∴在Rt △OAB 中，tan ∠OAB =tan60°=OAOB.∵OA=1∴3=BO ，BD =32. ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分 又∵AC =2OA =2∴菱形ABCD 的面积3221=⋅=AC BD S . ┄┄┄┄┄┄┄┄┄┄┄┄┄8分(19) (本小题满分8分)(I) 120 ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄4分 (II) 解：平均保费为300)21075.1305.14025.14018085.0100(6000⨯+⨯+⨯+⨯+⨯+⨯⨯=6950(元) ┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄8分 (20) (本小题满分8分)(I) △ADE 是等腰直角三角形. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分 理由：在等边△ABD 和等边△ACE 中， ∵BA =DA ，CA =EA ，∠BAD =∠CAE =60°. ∴∠BAD -∠CAD =∠CAE -∠CAD . 即∠BAC =∠EAD .∴△ABC ≌△ADE . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴AB=AD ，BC=DE ，∠ABC =∠ADE ∵ AB =BC ，∠ABC =90° ∴AD =DE ，∠ADE =90°即△ADE 是等腰直角三角形. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 (II) 连接CD ，则直线CD 垂直平分线段AE .(或连接BE ，则直线BE 垂直平分线段AC ) ┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分理由：由(I)得DA =DE . 又∵CA =CE .∴直线CD 垂直平分线段AE . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (21) (本小题满分8分)(I) 解：观察可知，售价x 与日销量y 的乘积为定值300.y 与x 之间的关系为反比例函数. ┄┄┄┄┄┄┄┄┄┄┄┄2分设函数解析式为)0( ≠=k x ky .当30,10==y x 时，300=k . ┄┄┄┄┄┄┄┄┄┄┄┄┄3分∴函数解析式为 300xy =. ┄┄ ┄┄┄┄┄┄┄┄┄┄4分 (II)解： 能达到200元.理由：依题意：200300)10(=⋅-xx . 解得：30=x . ┄┄┄┄┄┄┄┄┄┄┄┄6分经检验，30=x 是原方程的解，并且符合题意. ┄┄┄┄┄┄┄7分 答：当售价30元/kg 时，水果店销售该种水果的日利润为200元. ┄┄┄┄8分 (22) (本小题满分10分)(I)解：∵AB ⊥CD ，垂足为N∴∠BNO =90°在Rt △ABC 中，∵ON =1，BN =3∴222=+=ON BN BO ，3tan ==∠ONBNBON ┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴∠BON =60° ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分∴. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分(II)证明：如图，连接BC ∵CD 是⊙O 的直径，AB ⊥CD ，∴. ┄┄┄┄┄┄┄┄┄┄┄┄6分∴∠1=∠CAB∵AB AE AC ⋅=2，且∠A =∠A∴△ACE ∽△ABC ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 ∴∠1=∠2 ∴∠CAB =∠2∴∠CEB =∠CAB +∠2=2∠CAB . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (23) (本小题满分10分)(I)解：直线2+-=x y 经过点（2，0）与（0，2），则这两点绕原点O 顺时针旋转90°的对应点为（0，-2）与（2，0）┄┄┄2分 设直线2+-=x y 的“旋转垂线”的解析式为)0( ≠+=k m kx y ┄┄3分 把（0，-2）与（2，0）代入 m kx y +=得：⎩⎨⎧=+-=022m k b .解得⎩⎨⎧-==21m k .即直线2+-=x y 的“旋转垂线”为2-=x y ； ┄┄┄┄┄┄┄┄┄┄┄┄┄5分 (II) 证明：直线)0( 111≠+=k x k y 经过点（11k -，0）与（0，1）， ┄┄┄┄6分 则这两点绕原点O 顺时针旋转90°的对应点为（0，11k ）与（1，0）， ┄┄8分DC把（0，11k ）与（1，0）代入b x k y +=2，得⎪⎩⎪⎨⎧=+=0121b k k b∴0112=+k k ，∴121-=⋅k k . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (24) (本小题满分12分)(I)证明∵AD 平分∠BAC ， ∴∠P AQ =∠BAD∵PQ ⊥AC ，BD ⊥AD ∴∠PQA =∠BDA =90°∴△PQA ∽△BDA ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分 ∴ABAD AP AQ = ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 (II)证法一：由(I)得ABADAP AQ =又∵∠P AB =∠QAD∴△P AB ∽△QAD ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分 ∴∠APB =∠AQD∵∠APB =∠PDB +∠DBP ∠AQD =∠AQP +∠DQP ∴∠PDB =∠AQP =90°∴∠DBP =∠DQP ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分 证法二：如图，延长AC ，交BD 的延长线于点E ， 连接PE ，取PE 的中点O ，连接OD,OQ.∵∠PDE =∠PQE =90°在Rt △PDE 与Rt △PQE 中，∵O 是PE 的中点，∴PE DO 21=，PE QO 21= 即PO EO QO DO ===∴P 、D 、E 、Q 四点都在以O 为圆心，OP 为半径的⊙O 上，┄┄┄┄┄┄┄┄5分∴∠1=∠DQP ∵AD 垂直平分BE ∴PB =PE ∴∠1=∠DBP∴∠DBP =∠DQP ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分B(III)解：过点P 分别作PG ⊥AB 于点G ，PH ⊥DQ 于点H . 则PG =d 1，PH =d 2.∵AD 平分∠BAC ，PQ ⊥AC.∴d 1=PG =PQ . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 ∴PHPQ d d S ==21. 由(II)得∠DBP =∠DQP ，∵∠BDP =∠QHP =90°.∴△DBP ∽△HQP ； ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 ∴PDPB PH PQ =. 在Rt △BDP 中，BD =1，DP =t.∴12+=t PB .∴tt S 12+=. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分25．(本小题满分14分)(I) 解：∵A (-1，0)，B (3，0)，∴该二次函数图象的对称轴为1=x ，且AB =4. 过点C 作CH ⊥AB 于点H.∵△ABC 为等腰直角三角形，∴CH =21AB =2. ┄┄1∴C (1，-2)或C (1，2) ①如图1，当C (1，-2)时，可设2)1(2--=x a y .把点B (3，0)代入可得：21=a . ┄┄┄┄3分②如图2，当C (1，2)时，可设2)1(2+-=x a y .把点B (3，0)代入可得：21-=a .综上所述，21=a 或21-. ┄┄┄┄┄┄┄4分(II) 解：(i ) 当a b 2-=时，c ax ax y +-=22=a c x a -+-2)1(.┄┄┄┄┄┄┄┄5分 ∴C (1，c -a )∴B (1+c -a ，0).┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∴0)(2=-+-a c a c a . ∴0)1)((2=+--a ac a c . ∵0≠-a c ，∴aa c 1-=.B/ ∴()a x a y 112--=. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分(ii ) 法一：∵31≤≤-x ，a <0，∴当x =-1或3时，y 取得最小值a a 14-，┄┄┄┄┄┄┄┄┄┄┄┄10分当x =1时，y 取得最大值a 1-. ┄┄┄┄┄┄┄┄┄┄┄┄11分若以321, , y y y 为长度的三条线段能围成三角形. 则a a a 1)14(2->-. ┄┄┄┄┄┄┄┄┄┄┄┄13分整理得：0182<-a . ∴042<<-a . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分 法二：依题意得：a x a y 1)1(211--=，a x a y 1)1(222--=，a x a y 1)1(233--=.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分 以321, , y y y 为长度的三条线段能围成三角形.不妨设321y y y ≤≤. 则321y y y >+在31≤≤-x 范围内恒成立. ∴a x a a x a a x a 1)1(1)1(1)1(232221-->--+-- 整理得：22322211)1()1()1(a x x x <---+-. ┄┄┄┄┄┄┄┄┄┄┄10分等价于232221)1()1()1(---+-x x x 最大值小于21a .当121-==x x 时，2221)1()1(-+-x x 取最大值为8；当13=x 时，23)1(-x 取最小值为0.此时232221)1()1()1(---+-x x x 取最大值为8. ∴218a <. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分整理得：0182<-a .∵0<a . ∴042<<-a . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分。
2018年福建省福州市初中毕业班质量检测语文试卷及参考答案[答案]
![2018年福建省福州市初中毕业班质量检测语文试卷及参考答案[答案]](https://img.taocdn.com/s3/m/fdeb740952d380eb62946d99.png)
2018年福建省福州市初中毕业班质量检测语文试卷及参考答案[答案]2018年福州市初中毕业班质量检测语文试卷参考答案及评分标准一、积累与运用(20分)1.（12分，每空1分，出现错别字本空不得分。
）（1）星汉灿烂（2）博学而笃志（3）会当凌绝顶（4）困于心衡于虑而后作（5）衔远山吞长江（6）忽如一夜春风来千树万树梨花开（7）我寄愁心与明月，随风直到夜郎西（8）不畏浮云遮望眼，自缘身在最高层2.（2分）C3.（6分)（1）惘 lǚ（2）B B（3）自己一样可以通过不懈的奋斗，拥有一份简单而充实的生活（的幸福）。
（改对即可）二、阅读（70分）（一）（5分）4.（3分）D5.（2分）自己虽然辞官，但仍会关心国家前途和命运。
（意思对即可）（二）（16分）6.（4分）（1）甘美（2）勉励（3）教（4）有时（有的）7.（2分）A8.（4分）（1）知道了自己的不足，这样以后就能自我反省。
（2）喜爱学习却不多问，不是真的喜爱学习。
9. (6分)（1）教学相长（也）君子学必好问（2）示例1：学是第一位的，只有不断学习，才能获得知识，才能知不足，才能不断完善自己；学习中需要互动和交流，教与学是可以相互促进的。
示例2：问和学是相辅相成的，不学就不能提出疑难，不问就不能增长知识。
示例3：教和学可以互相促进，问和学是相辅相成的。
在学习中交流切磋、质疑提问都可以促进学习。
（言之成理即可）参考译文：君子学习一定喜爱问。
问和学是相辅相成地进行的，不学就不能提出疑难，不问就不能增加知识。
喜爱学习却不多问，不是真的喜爱学习。
道理明白了，可是有时还不能应用于实际，认识了那些大的（原则、纲领），可是有时还不了解那些细节，（对于这些问题）除了问，还能怎么解决呢？（三）（21分）10.（3分)C11.（4分）救治海鸥，送信求援。
最终获救，善心得到回报。
12.（6分）（1）加点词写出我急于阻止爷爷杀生，突出了“我”心地善良，对生命充满关爱之情。
2018年莆田市初中毕业班质量检查试卷答案(1)
2018年莆田市初中毕业班质量检查试卷语文参考答案及评分标准评分意见与建议：①主观表述题的答案不必强求与参考答案一致，言之成理或意思对即可。
②开放性试题的答案不唯一，提供的“示例”仅是从某一角度或某一方面回答的例子而已，评卷时宜选出学生的答案实例进行分类，拟定评分等级标准。
一、积累与运用（20分）1.（12分）（1）悠然见南山（2）长风破浪会有时（3）心忧炭贱愿天寒（4）病树前头万木春（5）会挽雕弓如满月（6）柳暗花明又一村（7）宫阙万间都做了土（8）人则无法家拂士（9）受任于败军之际，奉命于危难之间（10）报君黄金台上意，提携玉龙为君死（填对一处得1分，有错别字该处不得分。
满分12分）2.（2分）B3.(6分 )(1)（2分）A 盎（每小题各1分）（2）（2分）A B（每小题各1分）（3）（2分）示例一：如一首婉转的歌曲，吟唱出抑扬顿挫的旋律。
示例二：如一幅秀丽的山水画，绘出浓墨重彩的色调。
（句式1分，内容1分）二、阅读（70分）（一）（5分）4.（3分）B5.(2分 )表达了壮志难酬的悲愤（抑扬、愤慨）之情。
（二）（16分）6.（4分）（1）偏爱（2）偶然（偶尔）（3）将要（4）违背7.（3分）C8.(5分)（1）（3分）在公共场所批评议论我的过失（1分），传到我耳朵里的（1分），可得下等奖赏（1分）。
（意思正确，句子通顺即可）（2）（2分）越国打算在吴国未发兵之前去攻打吴国。
（“伐”翻译正确1分，句意正确1分。
）9.（4分）甲文中邹忌委婉劝说，齐威王乐于纳谏，齐国大治（2分）；乙文中范蠡直言劝谏，越王不听良言，越国大败（2分）。
参考译文：越王勾践三年，勾践听说吴王夫差日夜操练士兵，将报复越国，越国打算在吴国未发兵之前去攻打吴国。
范蠡进谏说：“不行,我听说兵器是凶器，攻战是违背道德，争先打仗是事情中最下等的。
阴谋去做违背道德的事，喜爱使用凶器，亲身参与不等事，定会遭到天帝的反对，这样做绝对不利。
2018年5月福建省龙岩市初中毕业班质量检测数学试题含答案
∴ E D F 9 0 …………４ 分
∴2
4 90
又∵ 3 4 9 0
∴2
3
又∵ 1 C …………５ 分
∴ A D E ≌ C D F ( A SA ) . …………６分
（2）当 B C 与⊙ O 相切时， A D 是直径 …………７ 分
在 R t A D C 中， C 4 5 , A C
2 …………８ 分
所以 2017 年前三季度居民人均消费可支配收入平均数为
（ 2） 8.3% 360 29.88
30
2 0 3 9 5 元. …………３ 分
所以用于医疗保健所占圆心角度数为 3 0 . ………………５ 分 （ 3） 1 8.3 % 2.6 % 2 9.2 % 6.8 % 6.2 % 1 3.6 % 1 1.2 % 0.2 2 1
23 6
3
，
3
90 ，
1
显然此时点 T 和点 P 重合，即 A T A P
A B 3. …………２ 分
2
法 1： ②当点 T 在 A B 的下方， ATB 90 ，如图 24－①所示 .
在 Rt APB 中，由 AF BF ，
可得： AF BF PF 3 ，
B PF
F B P 3 0 , BFT 60 .
A． 3
4
B． 1
2
C． EDC
EFC
D ． ACD
AFE
7．实数 a , b 在数轴上的对应点位置如图所示，把
a， b , 0 按照从小到大的顺序排列，正确的是
( )． A． a 0 b C． b 0 a
B． 0 a b D． 0 b a
k
8．在同一直角坐标系中，函数 y
【答案】2018年三明市初中毕业班学业质量检测答案
2018年三明市初中毕业班学业质量检测数学试卷参考答案及评分标准说明：以下各题除本参考答案提供的解法外，其他解法参照本评分标准，按相应给分点评分.一、选择题 (每题4分，共40分)1．A 2．B 3．C 4．A 5．C 6．B 7．D 8．D 9．B 10．A二、填空题（每题4分，共24分）11．1)-1)((a a a + 12．52 13．280 14．4π9 15．2 16．51≤≤CP三、解答题（共86分）17．解： 原式= x 2+2xy - (x 2+2x +1)+2x …………2分= x 2+2xy -x 2-2x -1+2x …………4分=2xy -1. …………5分当x =13＋，y =1-3时，原式=2(13＋)(1-3)-1 …………6分＝2（3－1）－1 …………7分 =3. …………8分 18.解：去分母，得2-x -1=x -3 …………3分-x -x =-3-2+1` …………4分 -2x =-4 …………5分x =2 …………6分经检验，x =2是原方程的根所以原方程的根是x =2 …………8分 19.解：(Ⅰ) B 级人数16人，图略； …………2分(Ⅱ) 360 ； …………4分 (Ⅲ)列表如下： (6)分由上表可知，总共有12种等可能结果，其中符合要求有6种，…………8分 （树状图略）20．解：∵A （2，0），B (4,n )，且点B 在第四象限，∴S △OAB ＝n n -)-221=⨯⨯（.∵S △OAB ＝23, ∴n =-23.∴B (4, -23). …………3分把B (4, -23)代入x ky =，得k =-6，∴反比例函数表达式为x y 6-=. …………5分把A （2，0），B (4, -23)代入y =ax +b ，得：⎪⎩⎪⎨⎧=+=+23-402b a b a , ∴3-43. 2a b ⎧=⎪⎪⎨⎪=⎪⎩…………7分 ∴一次函数表达式为33-42y x =+. …………8分 21. 解：(Ⅰ)…………3分DE 就是所作的边AB 的垂直平分线. …………4分(Ⅱ)∵∠C ＝90°，∠B ＝30°，∴∠CAB ＝60°. …………5分 ∵DE 垂直平分AB ， ∴AE ＝BE ，∴∠EAB ＝∠B ＝30°， …………7分∴∠CAE ＝∠CAB －∠EAB ＝30°， ∴∠CAE ＝∠EAB ＝30°.∴AE 平分∠BAC . …………8分22. 解：（Ⅰ）设购买A ，B 两种树苗每棵分别需x 元，y 元，则⎩⎨⎧=+=+4002538043y x y x , …………3分解得⎩⎨⎧==5060y x . …………4分答：购买A ，B 两种树苗每棵分别需60元，50元. …………5分（Ⅱ）设购进A 种树苗m 棵，则5620)100(5060≤-+m m …………7分 解得62≤m . ∵购进A 种树苗不能少于60棵，且m 为整数，∴m =60或61或62， (8)分∴有三种购买方案，分别为：方案一：购进A 种树苗60棵，B 种树苗40棵；方案二：购进A 种树苗61棵，B 种树苗39棵； 方案三：购进A 种树苗62棵，B 种树苗38棵. (10)分23.解：（Ⅰ）解法一：连接OD ， ∵OA =OD , ∠A ＝45°，∴∠ADO =∠A ＝45°,∴∠AOD =90°. …………………1∵D 是AC 的中点，∴AD =CD .∴OD ∥BC . ……………………2分∴∠ABC =∠AOD =90°. ……………………3分∴BC 是⊙O 的切线. ……………………4分解法二：连接BD ，∵AB 为⊙O 的直径，∴BD ⊥AC . .....................1分 ∵D 是AC 的中点，∴BC =AB . (2)分∴∠C =∠A ＝45°.∴∠ABC =90°. ……………………3分 ∴BC 是⊙O 的切线. ……………………4分 （Ⅱ）连接OD ，由（Ⅰ）可得∠AOD =90°.∵⊙O 的半径为2, F 为OA 的中点，∴OF =1,BF =3，AD ==……………5分∴DF =……………6分∵BD BD =, ∴∠E =∠A . ……………7分 ∵∠AFD =∠EFB ,∴△AFD ∽△EFB. ……………8分 ∴DF BFAD BE =,3BE=. ……………………9分∴BE ……………………10分 （其他解法按相应步骤给分）24. (Ⅰ)证明：∵AD ⊥BC ，∠DAE ＝90°，∴∠ADB ＝∠ADC ＝∠DAE ＝90°，∴AE ∥CD ， ………………1分 ∵△ABC ∽△ADE ， ∴∠AED ＝∠ACB ， ∵AD ＝DA ，∴△ADC ≌△DAE . ∴AE ＝DC . ………………3分 ∴四边形ADCE 为平行四边形， ∵∠ADC ＝90°，∴□ADCE 为矩形. ………………4分（其他解法按相应步骤给分）（Ⅱ）解：∵∠BAC ＝90°，AB ＝6，AC ＝8， ∴BC =10.∵D 为BC 的中点，∴ AD =BD =BC21＝5. ………………5分∵△ABC ∽△ADE ，∴AE AC AD AB ＝. ∵∠BAC ＝∠DAE ＝90°， ∴∠BAD ＝∠CAE .∴△ABD ∽△ACE. ………………7分 ∴AC AB ＝CE BD . 即CE586＝. ∴CE ＝320. ………………8分（其他解法按相应步骤给分）（Ⅲ）325. ………………12分 25．(Ⅰ) (－2，3)； ………………3分 (Ⅱ) (ⅰ) ∵抛物线y =c bx x ++22经过点A ， ∴3＝8-2b +c. ∴c =2b -5.∴B (0, 2b -5). ………………5分∵直线l 经过点B ， ∴2k +3=2b -5.∴k =4-b . ………………6分 当b =4时，k =0， 当b =6时，k =2, ∵4＜b ＜6,∴0＜k ＜2. ………………8分(ⅱ)k =1时，直线l 的表达式为y =x +5，直线l 交y 轴于点F (0，5)，当点M 在点A 右侧，过点A 作x 轴平行线交y 轴于点E ，过点M 作y 轴的平行线交AE 于点D ，∵A (-2，3)，∴AE ＝EF ＝2.∴∠EAF ＝45°. ∴当AM ＝2时，AD ＝MD ＝1.∴M (-1，4). 把M (-1，4)代入y =c bx x ++22，求得b =7,c =9. 由AM ＝42，A (-2，3)，同上可得M (2，7)，把A (-2，3)，M (2，7)代入y =c bx x ++22，求得b =1,c =－3.………………10分把A (-2，3) 代入y =c bx x ++22，得c =2b -5.又∵c ＞0，∴25>b . ∴7b 25≤< ………………11分 当点M 在点A 左侧时，由AM ＝2，A (-2，3)，同上可得M (-3，2)， 把A (-2，3)，M (-3，2)代入y =c bx x ++22，求得b =11,c =7， 由AM ＝42，A (-2，3)，同上可得M (－6，－1)，把A (-2，3)，M (-6，-1)代入y =c bx x ++22，求得b =17,c =29， ∴17b 11≤≤.综上所述，7b 25≤<或17b 11≤≤. ………………14分（其他解法按相应步骤给分）。
2018年宁德市初中毕业班质量检测及答案
2018年宁德市初中毕业班质量检测数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页．满分150分．注意事项：1．答题前，考生务必在试题卷、答题卡规定位置填写本人XX号、XX等信息．考生要认真核对答题卡上粘贴的条形码的“XX号、XX”与考生本人XX号，XX是否一致．2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答，在试题卷上答题无效．3．作图可先使用2B铅笔画出，确定后必须0.5毫米黑色签字笔描黑．4．考试结束，考生必须将试题卷和答题卡一并交回．第Ⅰ卷一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．2018-的值是A．12018B．2018C．12018-D．2018-2．如图，若a∥b，∠1=58°，则∠2的度数是A．58°B．112°C．122°D．142°3．下列事件是必然事件的是A．2018年5月15日宁德市的天气是晴天B．从一副扑克中任意抽出一张是黑桃C．在一个三角形中，任意两边之和大于第三边D．打开电视，正在播广告4．由6个大小相同的小正方体拼成的几何体如图所示，则下列说法正确的是A．主视图的面积最大B．左视图的面积最大C．俯视图的面积最大D．三种视图的面积相等正面第4题图ab 第2题图21..5．不等式组10,10≤＞x x -⎧⎨+⎩的解集在数轴上表示正确的是6．在平面直角坐标系中，A ，B ，C ，D ，M ，N 的位置如图所示，若点M 的坐标为（-2 ，0）， N 的坐标为（2 ，0），则在第二象限内的点是 A ．A 点B ．B 点 C ．C 点D ．D 点7．在“创文明城，迎省运会”合唱比赛中，10位评委给某队的评分如下表所示，则下列说法正确的是A ．中位数是9.4分B ．中位数是9.35分C ．众数是3和1D ．众数是9.4分8．如图，将△OAB 绕O 点逆时针旋转60°得到△OCD ，若OA=4，∠AOB =35°，则下列结论错误的是 A ．∠BDO =60°B ．∠BOC =25° C ．OC=4D ．BD=49．某校为进一步开展“阳光体育”活动，购买了一批篮球和足球．已知购买足球数量是篮球的2倍，购买足球用了4000元，购买篮球用了2800元，篮球单价比足球贵16元．若可列方程40002800162x x=-表示题中的等量关系，则方程中x 表示的是 A ．足球的单价B ．篮球的单价C ．足球的数量D ．篮球的数量10．如图，已知等腰△ABC ，AB=BC ，D 是AC 上一点，线段BE 与BA 关于直线BD 对称，射线CE 交射线BD 于点F ，连接AE ，AF ．则下列关系正确的是A ．180∠∠AFE ABE +=︒B ．12∠∠AEF ABC =C ．180∠∠AEC ABC +=︒D ．∠∠AEB ACB =C DB DCBAO第8题图第6题图MNA BD C第10题图CFE D ABA.第Ⅱ卷注意事项：1．用0.5毫米黑色签字笔在答题卡上相应位置书写作答，在试题卷上作答，答案无效． 2．作图可先使用2B 铅笔画出，确定后必须0.5毫米黑色签字笔描黑． 二、填空题：本题共6小题，每小题4分，共24分．11．2017年10月18日，中国共产党第十九次全国代表大会在隆重召开．从全国近89 400000党员中产生的2300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为.12．因式分解：222a -= .13．小明同学在计算一个多边形的内角和时，由于粗心少算了一个内角，结果得到的总和是800°，则少算了这个内角的度数为.14.已知一次函数23(0)y kx k k =++≠，不论k 为何值，该函数的图像都经过点A ，则点A的坐标为.15．小丽计算数据方差时，使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦，则公式中x =.16．如图，点A ，D 在反比例函数(0)my m x=<的图像上，点B ，C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴，AC ∥y 轴，且AB =4，AC =3，CD =2，则n =.三、解答题：本题共9小题，共86分．17．（本题满分8分）计算：14cos302-︒+18．（本题满分8分）如图，在△ABC 中，D ，E 分别是AB ，AC 的中点，△ABC 的角平分线AG 交DE 于点F ，若∠ABC =70°，∠BAC ＝54°，求∠AFD 的度数．CFEDBAG第16题图.19．（本题满分8分）首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行，某校组织115位师生去会展中心参观，决定租用A ，B 两种型号的旅游车．已知一辆A 型车可坐20人，一辆B 型车可坐28人，经测算学校需要租用这两种型号的旅游车共5辆．学校至少要租用B 型车多少辆?20．（本题满分8分）某中学为推动“时刻听党话永远跟党走”校园主题教育活动，计划开展四项活动：A ：党史演讲比赛，B ：党史手抄报比赛，C ：党史知识竞赛，D ：红色歌咏比赛．校团委对学生最喜欢的一项活动进行调查，随机抽取了部分学生，并将调查结果绘制成图1，图2两幅不完整的统计图．请结合图XX 息解答下列问题：（1）本次共调查了名学生； （2）将图1的统计图补充完整；（3）已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生，现从这4名学生中任意抽取2名学生参加该项目比赛，请用画树状图或列表的方法，求出恰好抽到一名男生一名女生的概率．21．（本题满分8分）如图，已知矩形ABCD ，E 是AB 上一点.（1）如图1，若F 是BC 上一点，在AD ，CD 上分别截取DH =BF ，DG =BE ．求证：四边形EFGH 是平行四边形；（2）如图2，利用尺规分别在BC ，CD ，AD 上确定点F ，G ，H ，使得四边形EFGH是特殊的平行四边形.（提示：①保留作图痕迹，不写作法；②只需作出一种情况即可）图1ADFHBEGC图2图2图1项.22．（本题满分10分）若正整数a ，b ，c 满足111a b c+=，则称正整数a ，b ，c 为一组和谐整数.（1）判断2，3，6是否是一组和谐整数，并说明理由；（2）已知x ，y ，z （其中x y z ＜≤）是一组和谐整数，且1x m =+，3y m =+，用含m 的代数式表示z ，并求当24z =时m 的值.23．（本题满分10分）如图，在△ABC 中，∠ACB =90°，O 是AB 上一点，以OA 为半径的⊙O 与BC 相切于点D ，与AB 交于点E ，连接ED 并延长交AC 的延长线于点F .（1）求证：AE =AF ；（2）若DE =3，sin ∠BDE =13，求AC 的长．24．（本题满分13分）如图1，在△ABC 中，∠BAC =90°，AB =AC =4，D 是BC 上一个动点，连接AD ，以AD 为边向右侧作等腰直角△ADE ，其中∠ADE =90°． （1）如图2，G ，H 分别是边AB ，BC 的中点，连接DG ，AH ，EH ．求证：△AGD ∽△AHE ；（2）如图3，连接BE ，直接写出当BD 为何值时，△ABE 是等腰三角形； （3）在点D 从点B 向点C 运动过程中，求△ABE 周长的最小值．25．（本题满分13分）已知抛物线22(0)y ax ax c a =-+<的图像过点A （3，m ）．（1）当a =-1，m =0时，求抛物线的顶点坐标； （2）若P （t ，n ）为该抛物线上一点，且n ＜m ，求t 的取值范围；（3）如图，直线:(0)l y kx c k =+<交抛物线于B ，C 两点，点Q (x ，y )是抛物线上点B ，C 之间的一个动点，作QD ⊥x 轴交直线l 于点D ，作QE ⊥y 轴于点E ，连接DE ．设∠QED=β，当x 2≤≤4时，β恰好满足°°30≤≤60β，求a 的值． B图1ABCDE图2图3ABCDEABCDGH.2018年宁德市初中毕业班质量检测数学试题参考答案与评分标准⑴本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可参照本答案的评分标准的精神进行评分．⑵对解答题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的立意，可酌情给分．⑶解答右端所注分数表示考生正确作完该步应得的累加分数． ⑷评分只给整数分，选择题和填空题均不给中间分． 一、选择题：（本大题有10小题，每小题4分，满分40分） 1．B 2．C 3．C4．A 5．D 6．A7．B 8．D 9．D 10．B 二、填空题：（本大题有6小题，每小题4分，满分24分）11．78.9410⨯ 12．2(1)(1)a a +- 13．100 14．(-2，3) 15．1116．83三、解答题（本大题共9小题，共86分．请在答题卡．．．的相应位置作答） 17．（本题满分8分）解：原式=142+- ·························································································· 6分 =12····································································································· 8分 18．（本题满分8分）证明：∵∠BAC =54°，AG 平分∠BAC ，∴∠BAG =12∠BAC =27°． ·································· 2分 ∴∠BGA =180 °-∠ABC -∠BAG ＝83° ················· 4分 又∵点D ，E 分别是AB ，AC 的中点，∴DE ∥BC ． ····························································· 6分 ∴∠AFD =∠BGA =83°． ······································ 8分 19．（本题满分8分）解： 设租用B 型车x 辆，则租用A 型车（5-x ）辆，根据题意，得 ······················ 1分 2820(5)115≥x x +-． ··································································································· 5分 解得 158≥x ． ······································································································ 7分因为x 为整数，所以x 的最小值是2．答：学校至少租用了2辆B 型车． ············································································· 8分CFEDBAG.20．（本题满分8分）（1）40； 2分（2）图略 ················································································································· 4分 （3）列表如下： ··········································································································· 6分女生的结果有6种，所以抽到一名男生和一名女生的概率是612，即12． ··········· 8分 21．（本题满分8分）（1）证明：∵四边形ABCD 是矩形， ∴AD =BC ，AB =CD ，∠A =∠B =∠C =∠D =90°， ∵DG =BE ，DH =BF ， ∴△GDH ≌△EBF ．2分 ∴GH =EF .∵AD =BC ，AB =CD ，DH =BF ，DG =BE ， ∴AD －DH =BC －BF ，AB －BE =CD －DG ． 即AH =CF ，AE =CG ．∴△AEH ≌△CGF . ········································ 4分 ∴EH =GF .∴四边形EFGH 是平行四边形． ················ 5分 (2)作图如下：作法一：作菱形(如图2) ································································································ 7分 ∴四边形EFGH 就是所求作的特殊平行四边形． ······················································· 8分 作法二：作矩形（如图3，图4） ··············································································· 7分∴四边形EFGH 就是所求作的特殊平行四边形. ·························································· 8分ADFHBEGC.22．（本题满分10分）(1)是 ····························································································································· 1分理由如下：∵111362+=，满足和谐整数的定义，∴2，3，6是和谐整数． ······················································································ 4分(2) 解：∵x y z ＜≤， 依题意，得111y z x+=． ∵1x m =+，3y m =+，∴11111213(1)(3)z x y m m m m =-=-=++++．∴(1)(3)2m m z ++=． ································································································· 7分∵24z =，∴(1)(3)242m m ++=．解得 59，m m ==-． ·························································································· 9分 ∵x 是正整数，∴5m =． ············································································································· 10分23．（本题满分10分）解：（1）证明：连接OD .∵OD =OE ，∴∠ODE =∠OED ． ··········································· 1分∵直线BC 为⊙O 的切线， ∴OD ⊥BC ．∴∠ODB =90°． ················································· 2分 ∵∠ACB =90°，∴OD ∥AC ． ······················································ 3分∴∠ODE =∠F ．∴∠OED =∠F ． ······································································ 4分 ∴AE =AF ． ··············································································· 5分 （2）连接AD ． ∵AE 是⊙O 的直径∴∠ADE =90°． ······································································· 6分B图1.∵AE =AF ， ∴DF =DE =3. ∵∠ACB =90°．∴∠DAF +∠F =90°，∠CDF +∠F =90°， ∴∠DAF =∠CDF =∠BDE ．7分 在Rt △ADF 中，1sin sin 3∠DF DAF BDE AF ==∠=， ∴39AF DF ==．8分 在Rt △CDF 中，1sin sin 3∠CF CDF BDE DF ==∠=， ∴113CF DF ==．9分∴AC =AF -CF =8. ·············································· 10分 24．（本题满分13分）解：（1）由题意知△ABC 和△ADE∴∠B =∠DAE =45°．∵G 为AB 中点，H 为BC 中点， ∴AH ⊥BC ．∴∠BAH =45°=∠DAE ． ∴∠GAD =∠HAE ．1分在等腰直角△BAH 和等腰直角△DAE 中， AH AB ==，AE =．∴AH AE AG AD =．3分 ∴△AGD ∽△AHE ．4分（2）当BD =0△ABE 是等腰三角形.8分（注：给出0和1得2分） （3）解法一：当点D 与点B 重合时，点E 的位置记为点M .此时，∠ABM =∠BAC =90°，∠AMB =∠BAM =45°，BM =AB =AC .∴四边形ABMC 是正方形. ∴∠BMC =90°，B图1图2.∴∠AMC =∠BMC -∠AMB =45°，9分 ∵∠BAM =∠DAE =45°， ∴∠BAD =∠MAE ，在等腰直角△BAM 和等腰直角△DAE 中，AM =，AE =．∴AM AE AB AD =．∴△ABD ∽△AME ． ∴∠AME =∠ABD =45° ∴点E 在射线MC 上．10分作点B 关于直线MC 的对称点N ，连接AN 交MC 于点E ′， ∵BE +AE =NE +AE ≥AN =NE ′+AE ′=BE ′+AE ′， ∴△ABE ′就是所求周长最小的△ABE ． 在Rt △ABN 中，∵AB =4，BN =2BM =2AB =8， ∴AN=AN =∴△ABE周长最小值为4AB AN +=+． 13分解法二：取BC 的中点H ，连接AH ， 同解法一证△ACE ∽△AHD ． ∴∠ACE=∠AHD=90°．∴点E 在过点C 且垂直于AC 的直线上，记为直线l ．10分 点A 关于直线l 的对称点M ，连接BM 交直线l 于点E ′， 同解法一，△ABE ′就是所求周长最小的△ABE ． ∴△ABE 周长最小值为4AB BM +=+．13分25．（本题满分13分） 解：（1）当a =-1，m =0时，22y x x c =-++，A 点的坐标为（3，0）， ∴-9+6+c =0． 解得c =3．2分∴抛物线的表达式为223y x x =-++． 即2(1)4y x =--+．∴抛物线的顶点坐标为（1，4）．4分图2BACDE ′ MNE 图3BACDE ′MEH.（2）∵22y ax ax c =-+的对称轴为直线212a x a-==-，5分 ∴点A 关于对称轴的对称点为（-1，m ）．6分 ∵0＜a ，∴当1＜x ，y 随x 的增大而增大；当1＞x ，y 随x 的增大而减小． 又∵n ＜m ，∴当点P 在对称轴左边时，t ＜-1；当点P 在对称轴右边时，t ＞3．综上所述：t 的取值范围为t ＜-1或t ＞3．8分（3）∵点Q （x ，y ）在抛物线上，∴22y ax ax c =-+．又∵QD ⊥x 轴交直线 :(0)l y kx c k =+<于点D∴D 点的坐标为（x ，kx+c ）．又∵点Q 是抛物线上点B ，C 之间的一个动点， ∴222()(2)QD ax ax c kx c ax a k x =-+-+=-+． 10分∵QE =x ，∴在Rt △QED 中，2(2)tan 2QD ax a k x ax a k QE x -+===--β．11分 ∴tan β是关于x 的一次函数，∵a ＜0，∴tan β随着x 的增大而减小．又∵当x 2≤≤4时，β恰好满足°°30≤≤60β，且tan β随着β的增大而增大， ∴当x=2时，β=60°；当x=4时，β=30°． ∴2242a a k a a k ⎧--=⎪⎨--=⎪⎩解得 k a ⎧=⎪⎨=⎪⎩∴a =13分.。
2018年漳州初中毕业班质量检测语文参考答案(2)
2018年初中毕业班质量检测
语文参考答案
一、（20分）
1.（12分，每格1分）
（1）君子好逑
（2）采菊东篱下
（3）一览众山小
（4）蜡炬成灰泪始干
（5）浅草才能没马蹄
（6）浊酒一杯家万里
（7）不尽长江滚滚流
（8）波涛如怒山河表里潼关路
（9）学而不思则罔
（10）出淤泥而不染,濯清涟而不妖
2.（2分）A
3.（6分）
（1）（2分）① A ② A
（2）（2分）甲：A 乙：B
（3）（2分）在经久不息的掌声中，八分钟的演出完美成功。
（或“经久不息的掌声，表明八分钟的演出完美成功。
”）
二、（70分）
（一）（5分）
4.（3分）C
5.（2分）诚挚的友谊可以超越时空，缩短距离。
（二）（16分）
6.（4分）（1）出名，闻名（2）什么（3）于是（4）通“披”；披着，穿着
7.（3分）B
8.（1）（2分）没有嘈杂的音乐扰乱两耳，没有官府的公文使身体劳累。
（2）（2分）挨着的房屋都是这样，因为竹瓦价格便宜而且节省很多工序。
9.（5分）甲文叙写了环境的幽静和生活情趣的高雅，乙文着力写清韵雅趣的竹楼和幽雅飘逸的谪居生活，
都表现了作者甘居陋室、淡泊名利、安贫乐道的高尚情怀。
（三）（22分）
10.（3分）D
11.（6分）①夜归路上被轻呼“小飞鱼”
②生气、委屈
③激动、兴奋。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2０18年初中毕业班质量检测
语文试题
（全卷共6页，23题；完卷时间１20分钟；满分150分）友情提示:请把所有答案填写(涂）在答案卡上，请不要错位、越界做答！
(2）,悠然见南山。
(陶渊明《饮酒》）
（３)会当凌绝顶, 。
(杜甫《望岳》)
（４)春蚕到死丝方尽, 。
（李商隐《无题》)
(5）乱花渐欲迷人眼, 。
(白居易《钱塘湖春行》）
（6） ,燕然未勒归无计。
(范仲淹《渔家傲·秋思》）
（7）千古兴亡多少事？悠悠。
(辛弃疾《南乡子·登京口北固亭有怀》) （8）峰峦如聚，，。
(张养浩《山坡羊·潼关怀古》）
（9）子曰:“ ,思而不学则殆。
”(《论语》）
(10）我们常引用周敦颐《爱莲说》中的“ , ”
来强调一个人应不受环境影响，保持崇高的个性节操。
２. 下列文学常识说法有误
．．的一项是(２分）
A．我国古代文学作品常用“桑梓”“桃李”“婵娟”分别代指家乡、老师、月亮。
B.唐诗、宋词、元曲是我国诗歌史上的三大高峰。
唐有大小李杜，宋有豪放之“苏辛”,元有四大家。
C．《从百草园到三味书屋》和《藤野先生》都是现代作家鲁迅的回忆性散文。
D.《我的叔叔于勒》选自法国作家莫泊桑的短篇小说集《羊脂球》。
3．阅读下面文字,按要求作答。
（6分）
２0１8平昌冬奥会闭幕式上,“北京八分钟”表演甲 (Ａ、美轮美奂B、富丽堂皇）、科技感十足,为观众献上了一场视觉盛宴。
24台移动机器人携．① (A、xiéＢ、jｉá）带“冰屏”与舞蹈演员配合完成了一系列ｍàｎ② (A、曼Ｂ、嫚）妙复杂的舞美动作，展现了人工智能与中华文
原句:在经久不息的掌声中，表明八分钟的演出完美成功。
修改句:
二、阅读（7０分）
（一）阅读下面这首诗,完成4～5题。
(５分）
送杜少府之任蜀州
王勃
城阙辅三秦，风烟望五津。
与君离别意,同是宦游人。
海内存知己,天涯若比邻。
无为在歧路,儿女共沾巾。
4. 对这首诗的理解和分析不正确
．．．的一项是（3分)
A．这是一首送别诗,表达了对友人的惜别之情。
Ｂ．“城阙辅三秦,风烟望五津”写出了送行的地点和友人要赴任的地方。
Ｃ.“与君离别意，同是宦游人”写对友人的安慰，表现了诗人依依不舍的伤感之情。
D．“无为在歧路,儿女共沾巾”，这两句承上作结，表达了诗人豪迈旷达的思想感情。
５．品味“海内存知己，天涯若比邻”两句诗，简述其中所蕴涵的哲理。
(2分）
（二）阅读下面文言文，完成6～9题。
(16分)
【甲】山不在高，有仙则名．。
水不在深,有龙则灵。
斯是陋室，惟吾德馨。
苔痕上阶绿，草色入帘青。
谈笑有鸿儒，往来无白丁。
可以调素琴，阅金经。
无丝竹之乱耳,无案牍之劳形。
南阳诸葛庐,西蜀子云亭。
（《黄冈新建小竹楼记》)
[注]①椽：房椽。
②陶瓦：用泥土烧成的瓦。
③雉堞圮毁：城上矮墙倒塌毁坏。
④公退：公事完毕，回来。
⑤茶烟:指烹茶炉火的烟气。
⑥齐云、落星、井干、丽谯:都是名楼。
6. 解释下列加点词在文中的意思。
（4分)
(１）有仙则名．名:_＿＿＿______ (2）何．陋之有何:_＿_＿＿___＿＿
(3）因．作小楼二间因:___＿___＿__ （４)被．鹤氅衣被：_＿______＿_
7．下列对文中画波浪线部分的断句,正确的一项是( )（３分）
A、止于藏/歌舞非骚人之事/吾所不取
B、止于藏歌舞/非骚人之事/吾所不取
C、止于/藏歌舞非/骚人之事吾所不取
D、止于藏歌／舞非骚人/之事吾所不取
８. 把文中画横线的句子翻译成现代汉语。
(4分)
（1）无丝竹之乱耳，无案牍之劳形。
（2分)
(2）比屋皆然，以其价廉而工省也。
(2分）。