立体几何压轴题.docx
高考的立体几何压轴题精选

ABCDE F1.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四 面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一 个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为a ,则以四个氢原子为顶点 的这个正四面体的体积为( ) A,3827a3C,313a D,389a 2.夹在两个平行平面之间的球,圆柱,圆锥在这两个平面上的射影都是圆,则它们的体积之 比为( )A,3:2:1 B,2:3:1 C,3:6:2 D,6:8:33.设二面角a αβ--的大小是060,P 是二面角内的一点,P 点到,αβ的距离分别为1cm, 2cm,则点P 到棱a 的距离是( )A,3B,3cm C,23cmD,34.如图,E,F 分别是正三棱锥A -BCD 的棱AB,BC的中点,且DE ⊥EF.若BC=a ,则此正三棱锥的体积是( )A,324aB,324C,312a35.棱长为的正八面体的外接球的体积是( ) A,6πB,27C,3D,36.若线段AB 的两端点到平面α的距离都等于2,则线段AB 所在的直线和平面α 的位置关系是 .7.若异面直线,a b 所原角为060,AB 是公垂线,E,F 分别是异面直线,a b 上到A,B 距离为 2和平共处的两点,当3EF =时,线段AB 的长为 .8.如图(1),在直四棱柱1111A BC D ABCD -中,当底面四边形ABCD 满足条件时,有1A C⊥1B 1D (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)CDF ABOCD EOAA B C D P Q9.如图(2),是一个正方体的展开图,在原正方体中,有下列命题: ①AB 与EF 所连直线平行; ②AB 与CD 所在直线异面; ③MN 与BF 所在直线成060; ④MN 与CD 所在直线互相垂直.其中正确命题的序号为 .(将所有正确的都写出)10.如图,在ABC ∆中,AB=AC=13,BC=10,DE//BC 分别交AB,AC 于D,E.将ADE ∆沿 DE 折起来使得A 到1A ,且1A DE B --为060的二面角,求1A 到直线BC 的最小距离.11.如图,已知矩形ABCD 中,AB=1,BC=a (0)a >,PA ⊥平面ABCD,且PA=1.(1)问BC 边上是否存在点Q 使得PQ ⊥QD?并说明理由;(2)若边上有且只有一个点Q,使得PQ ⊥QD,求这时二面角Q PD A --的正切.12. 已知三角形ABC 的顶点分别是A (1, 2, 3)、B (3, 4, 5)、C (2, 4, 7), 求三角形ABC 的面积.A BCDA BC D图(1)A BENM 图(2)13.在正四棱柱1111ABCD A BC D -中,122AB BB==, P 为B 1C 1的中点.(1)求直线AC 与平面ABP 所成的角;(2)求异面直线AC 与B P 所成的角; (3)求点B 到平面APC 的距离.14.如图,正四棱锥P-ABCD 中,侧棱PA 与底面ABCD 所成的角的正切值为26。
立体几何压轴题
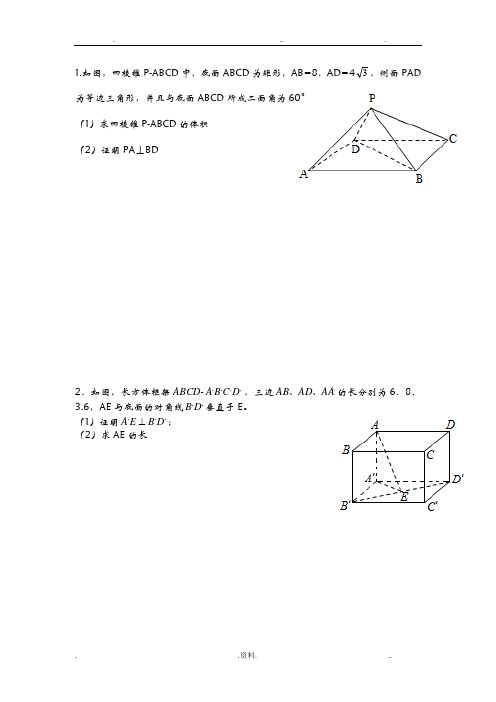
1.如图,四棱锥P-ABCD 中,底面ABCD 为矩形,AB=8,AD=43,侧面PAD 为等边三角形,并且与底面ABCD 所成二面角为60°(1)求四棱锥P-ABCD 的体积(2)证明PA ⊥BD2、如图,长方体框架ABCD -,,,,D C B A ,三边,、、AA AD AB 的长分别为6、8、3.6,AE 与底面的对角线,,D B 垂直于E 。
(1)证明,,,D B E A ;(2)求AE 的长3、如图,已知⊙O 的直径AB=3,点C 为⊙O 上异于A ,B 的一点,VC ⊥平面ABC,且VC=2,点M 为线段VB 的中点。
(1)求证:BC ⊥平面VAC;(2)若直线AM 与平面VAC 所成角为4π,求三棱锥B-ACM 的体积4、如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,CF⊥FB,BF=CF,G为BC的中点,(1)求证:FG∥平面BDE;(2)求平面BDE与平面BCF所成锐二面角的大小;(3)求四面体B-DEF的体积。
5、如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB 上的一点,且CD⊥平面PAB(1)求证AB⊥平面PCB;(2)求二面角C-PA-B的大小的余弦值。
6、ABCD为平行四边形,P为平面ABCD外的一点,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=3(1)求证:平面ACD⊥平面PAC;(2)求异面直线PC与BD所成角的余弦值;(3)设二面角A-PC-B的大小为θ,试求θtan的值。
7、如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F 为CE上的点,且BF⊥平面ACE(1)求证AE⊥平面BCE;(2)求二面角B-AC-E的正弦值;(3)求点D到平面ACE的距离。
8、如图所示,四棱锥P-ABCD 的底面ABCD 是直角梯形,BC ∥AD ,AB ⊥AD ,AB=BC=21AD ,PA ⊥底面ABCD ,过BC 的平面交PD 于M ,交PA 与N (M 与D 不重合)。
专题12 立体几何小题压轴练(原卷版)

【一专三练】 专题12 立体几何小题压轴练-新高考数学复习分层训练(新高考通用)一、单选题1.(2023·山东济宁·统考一模)已知直三棱柱111ABC A B C -,D 为线段11A B 的中点,E为线段1CC 的中点,1A E 过1AC E △的内切圆圆心,且1AD DC ⊥,CA =,2AB =,则三棱锥D ABC -的外接球表面积为( )A .27π8B .274πC .27π2D .27π 2.(2023春·湖北武汉·高三华中师大一附中校考期中)在正四棱台1111ABCD A B C D -中,112AB A B =,1AA =M 为棱11B C 的中点,当正四棱台的体积最大时,平面MBD 截该正四棱台的截面面积是( ).AB C .D .3.(2023·湖北武汉·华中师大一附中校联考模拟预测)在三棱锥D ABC -中,ABC V 是以AC 为底边的等腰直角三角形,DAC △是等边三角形,AC =,又BD 与平面ADCD ABC -外接球的表面积是( )A .8πB .12πC .14πD .16π4.(2023秋·湖南湘潭·高三校联考期末)点,M N 分别是棱长为2的正方体1111ABCD A B C D -中棱1,BC CC 的中点,动点P 在正方形11BCC B (包括边界)内运动.若1//PA 面AMN ,则1PA 的长度范围是( )A .⎡⎣B .C .⎤⎥⎦D .[]2,35.(2023春·湖南·高三统考阶段练习)正方体1111ABCD A B C D -的棱长为1,点P 在三棱锥1C BCD -的表面上运动,且1A P =P 轨迹的长度是( )A BC D 6.(2023·广东梅州·统考一模)《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面ABCD 为正方形,EF P 平面ABCD ,四边形ABFE ,CDEF 为两个全等的等腰梯形,122EF AB ==,且AE =则此刍甍的外接球的表面积为( )A .60πB .64πC .68πD .72π7.(2023·广东·校联考模拟预测)已知四棱锥P ABCD -的五个顶点都在球面O 上,底面ABCD 是边长为4的正方形,平面PAD ⊥平面ABCD ,且PA PD ==,则球面O 的表面积为( )A .39πB .40πC .41πD .42π8.(2023·广东深圳·深圳中学校联考模拟预测)在矩形ABCD 中,已知24AB AD ==,E 是AB 的中点,将ADE V 沿直线DE 翻折成1A DE △,连接1A C ,当二面角1A DE C --的平面角的大小为60︒时,则三棱锥1A CDE -外接球的表面积为( )A .56π3B .18πC .19πD .53π3二、多选题9.(2023·浙江温州·统考二模)蜜蜂是自然界的建筑大师,在18世纪初,法国数学家马拉尔迪指出,蜂巢是由许许多多类似正六棱柱形状的蜂房(如图)构成,其中每个蜂房的底部都是由三个全等的菱形构成,每个菱形钝角的余弦值是13-,则( )A .AB P 平面11EDD E B .AB EF⊥C .蜂房底部的三个菱形所在的平面两两垂直D .该几何体的体积与以六边形111111A B C DEF 为底面,以1BB 为高的正六棱柱的体积相等10.(2023春·江苏扬州·高三统考开学考试)在四面体ABCD 的四个面中,有公共棱AC的两个面全等,1AD =,CD =,90CDA ∠=︒,二面角B AC D --大小为θ,下列说法中正确的有( )A .四面体ABCD 外接球的表面积为3πB .四面体ABCDC .若AD AB =,AD AB ⊥,则120θ=°D .若AD BC =,120θ=°,则BD =11.(2023春·江苏南京·高三南京市第五高级中学校考阶段练习)已知正四棱台1111ABCD A B C D -的上下底面边长分别为4,6E 是11A B 的中点,则( )A .正四棱台1111ABCD ABCD -B .平面1BC D ⊥平面11AA C CC .AE ∥平面1BCD D .正四棱台1111ABCD A B C D -的外接球的表面积为104π12.(2023秋·辽宁葫芦岛·高三统考期末)在正方体1AC 中,M 为AB 中点,N 为BC 中点,P 为线段1CC 上一动点(不含C )过M ,N ,P 的正方体的截面记为α,则下列判断正确的是( )A .当P 为1CC 中点时,截面α为六边形B .当112CP CC <时,截面α为五边形C .当截面α为四边形时,它一定是等腰梯形D .设1DD 中点为Q ,三棱锥Q PMN -的体积为定值13.(2023春·江苏苏州·高三统考开学考试)六面体1111ABCD A B C D -中,底面ABCD 、1111D C B A 分别是边长为4和2的正方形,侧面11CDD C 、侧面11BCC B 均是直角梯形,且13CC =,1CC CD ⊥.若该六面体为台体,下列说法正确的是( )A .六面体1111ABCD ABCD -的体积为28B .异面直线1DD 与1BB 的夹角的余弦值为913C .二面角1B AB D --D .设P 为上底面上一点,且AP CP ⊥,则P 的轨迹为一个圆14.(2023·山东·沂水县第一中学校联考模拟预测)已知圆锥顶点为S ,高为1,底面圆O 的直径AB长为C 为底面圆周上不同于,A B 的任意一点,则下列说法中正确的是( )A .圆锥SO的侧面积为B .SAC V 面积的最大值为32C .圆锥SO 的外接球的表面积为9πD .若AC BC =,E 为线段AC 上的动点,则SE BE +15.(2023·湖北·校联考模拟预测)如图,在正四面体ABCD 中,棱AB 的中点为M,棱CD 的中点为N ,过MN 的平面交棱BC 于P ,交棱AD 于Q ,记多面体CAMPNQ 的体积为1V ,多面体BDMPNQ 的体积为2V ,则( )A .直线MQ 与PN 平行B .AQ BP AD BC =C .点C 与点D 到平面MPNQ 的距离相等D .12V V =16.(2023春·湖北武汉·高三华中师大一附中校考期中)已知异面直线a 与b 所成角为60 ,平面α与平面β的夹角为80 ,直线a 与平面α所成的角为20 ,点P 为平面α、β外一定点,则下列结论正确的是( )A .过点P 且与直线a 、b 所成角都是60 的直线有4条B .过点P 且与平面α、β所成角都是30 的直线有4条C .过点P 且与平面α、β所成角都是40 的直线有3条D .过点P 与平面α成60 角,且与直线a 成60 的直线有3条17.(2023春·湖南·某同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示,是由等高的半个圆柱和14个圆柱拼接而成,其中四边形ABCD 是边长为4的正方形,点G 是弧CD 上的动点,且,,,C E D G 四点共面.下列说法正确的有( )A .若点G 为弧CD 的中点,则平面BFD ⊥平面BCGB .存在点G ,使得BG DF∥C .存在点G ,使得直线CF 与平面BCG 所成的角为60D .当点G 到平面BDF 的距离最大时,三棱锥G BDF -外接球的半径R =18.(2023春·江苏南通·高三海安高级中学校考阶段练习)如图的六面体中,CA =CB =CD =1,AB =BD =AD =AE =BE =DE )A .CD ⊥平面ABCB .AC 与BE 所成角的大小为π3C .CE D .该六面体外接球的表面积为3π19.(2023·湖南岳阳·统考二模)在中国共产党第二十次全国代表大会召开期间,某学校组织了“喜庆二十大,永远跟党走,奋进新征程,书画作品比赛.如图①,本次比赛的冠军奖杯由一个铜球和一个托盘组成,若球的体积为4π3;如图②,托盘由边长为4的正三角形铜片沿各边中点的连线垂直向上折叠而成,则下列结论正确的是( )A .直线AD 与平面BEF 所成的角为π6B .经过三个顶点,,A BC 的球的截面圆的面积为π4C .异面直线AD 与CF 所成的角的余弦值为58D .球离球托底面DEF 120.(2023·广东·高三校联考阶段练习)如图,矩形ABCD 中,4AB =,2BC =,E 为边AB 的中点,沿DE 将ADE V 折起,点A 折至1A 处(1A ∉平面ABCD ),若M 为线段1A C 的中点,平面1A DE 与平面DEBC 所成锐二面角α,直线1A E 与平面DEBC 所成角为β,则在ADE V 折起过程中,下列说法正确的是( )A .存在某个位置,使得1BM A D⊥B .1A EC △面积的最大值为C .sin αβ=D .三棱锥1A EDC -体积最大时,三棱锥1A EDC -的外接球的表面积16π21.(2023·广东深圳·统考一模)如图,已知正三棱台111ABC A B C -的上、下底面边长分别为2和3,侧棱长为1,点P 在侧面11BCC B 内运动(包含边界),且AP 与平面11BCC B,则( )A .CP 1B .存在点P ,使得⊥AP BCC .存在点P ,存在点11Q B C ∈,使得1AP A Q∥D .所有满足条件的动线段AP 22.(2023·江苏南通·二模)如图,正三棱锥A -PBC 和正三棱锥D -PBC 的侧棱长均为BC = 2.若将正三棱锥A -PBC 绕BC 旋转,使得点A ,P 分别旋转至点A P '',处,且A ',B ,C ,D 四点共面,点A ',D 分别位于BC 两侧,则( )A .A D CP '⊥B .//PP '平面A 'BDCC .多面体PP A BDC ''的外接球的表面积为6πD .点A ,P 旋转运动的轨迹长相等23.(2023·广东江门·统考一模)勒洛Franz Reuleaux (1829~1905),德国机械工程专家,机构运动学的创始人.他所著的《理论运动学》对机械元件的运动过程进行了系统的分析,成为机械工程方面的名著.勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的相交部分围成的几何体.如图所示,设正四面体ABCD 的棱长为2,则下列说法正确的是( )A .勒洛四面体能够容纳的最大球的半径为2B .勒洛四面体被平面ABC 截得的截面面积是(2πC .勒洛四面体表面上交线AC 的长度为2π3D 224.(2023秋·浙江·高三浙江省永康市第一中学校联考期末)正方体1111ABCD A B C D -的棱长为1,中心为O ,以O 为球心的球与四面体11AB CD 的四个面相交所围成的曲线的总O 的半径为( )A B C D 三、填空题25.(2023·浙江金华·浙江金华第一中学校考模拟预测)已知矩形ABCD 在平面α的同一侧,顶点A 在平面上,4AB =,BC =且AB ,BC 与平面α所成的角的大小分别为30°,45°,则矩形ABCD 与平面α所成角的正切值为______.26.(2023春·江苏南通·高三校考开学考试)在直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,侧棱12AA =,M 为侧棱1BB 的中点,N 在侧面矩形11ADD A 内(异于点1D ),则三棱锥1N MCD -体积的最大值为____________.27.(2023秋·江苏南京·高三南京市第一中学校考期末)在三棱锥-P ABC 中,AC BC PC ==,且30APC BPC ACB ∠=∠=∠=︒,则直线PC 与平面ABC 所成角的余弦值为__________.28.(2023·山东聊城·统考一模)已知正四棱柱1111ABCD A B C D -的体积为16,E 是棱BC 的中点,P 是侧棱1AA 上的动点,直线1C P 交平面11EB D 于点P ',则动点P '的轨迹长度的最小值为______.29.(2023春·湖北武汉·高三华中师大一附中校考阶段练习)蹴鞠(如图所示),又名蹴球,蹴圆,筑球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似于今日的足球.2006年5月20日,蹴鞠作为非物质文化遗产经国务院批准已列入第一批国家非物质文化遗产名录.已知某鞠(球)的表面上有四个点A ,B ,C ,P ,且球心О在PC 上,4AC BC ==,AC BC ⊥,tan tan PAB PBA ∠=∠=__________.30.(2023春·湖南·高三校联考阶段练习)在正四棱锥S ABCD -中,M 为SC 的中点,过AM 作截面将该四棱锥分成上、下两部分,记上、下两部分的体积分别为12,V V ,则21V V 的最大值是___________.。
立体几何压轴小题含答案)

即R2=(4-R)2+(3 )2,解得:R= ,故选C.
考点:三视图,球与多面体的切接问题,空间想象能力
12.如右图,在长方体 中, =11, =7, =12,一质点从顶点A射向点 ,遇长方体的面反射(反射服从光的反射原理),将 次到第 次反射点之间的线段记为 , ,将线段 竖直放置在同一水平线上,则大致的图形是()
一、选择题
1.如图,已知正方体 的棱长为4,点 , 分别是线段 , 上的动点,点 是上底面 内一动点,且满足点 到点 的距离等于点 到平面 的距离,则当点 运动时, 的最小值是()
A. B. C. D.
【答案】D
【解析】
试题分析:因为点 是上底面 内一动点,且点 到点 的距离等于点 到平面 的距离,所以,点 在连接 中点的连线上.为使当点 运动时, 最小,须 所在平面平行于平面 , ,选
故选A
点评:本题是基础题,考查球的内接多面体的知识,能够正确推出四棱锥的一条侧棱垂直底面的一个顶点,最长的侧棱就是直径是本题的关键,考查逻辑推理能力,计算能力.
18.二面角 为60°,A、B是棱 上的两点,AC、BD分别在半平面 内, , ,且AB=AC= ,BD= ,则CD的长为()
A. B. C. D.
考点:棱柱的结构特征.
9.下列命题中,错误的是()
A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交
B.平行于同一平面的两条直线不一定平行
C.如果平面 不垂直于平面 ,那么平面 内一定不存在直线垂直于平面
D.若直线 不平行于平面 ,则在平面 内不存在与 平行的直线
【答案】B
【解析】
压轴题05 立体几何压轴题(原卷版)--2023年高考数学压轴题专项训练(全国通用-文)

压轴题05立体几何压轴题题型/考向一:点、线、面间的位置关系和空间几何体的体积、表面积题型/考向二:外接球、内切球等相关问题题型/考向三:平面关系、垂直关系、体积、表面积等综合问题一、空间几何体的体积、表面积热点一空间几何体的侧面积、表面积柱体、锥体、台体和球的表面积公式:(1)若圆柱的底面半径为r,母线长为l,则S侧=2πrl,S表=2πr(r+l).(2)若圆锥的底面半径为r,母线长为l,则S侧=πrl,S表=πr(r+l).(3)若圆台的上、下底面半径分别为r′,r,则S侧=π(r+r′)l,S表=π(r2+r′2+r′l +rl).(4)若球的半径为R,则它的表面积S=4πR2.热点二空间几何体的体积柱体、锥体、台体和球的体积公式:(1)V柱体=Sh(S为底面面积,h为高);Sh(S为底面面积,h为高);(2)V锥体=13(S上+S下+S上S下)h(S上、S下分别为上、下底面面积,h为高);(3)V台体=13(4)V球=4πR3.3二、外接球、内切球问题类型一外接球问题考向1墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a,b,c,外接球半径为R.则(2R)2=a2+b2+c2,即2R=a2+b2+c2.常见的有以下三种类型:考向2对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决,外接球的直径等于长方体的体对角线长,如图所示,(2R )2=a 2+b 2+c 2(长方体的长、宽高分别为a ,b ,c ),即R 2=18(x 2+y 2+z 2),如图.考向3汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型,模型如下,由对称性可知,球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2的连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=h 2,所以R 2=r 2+h 24.考向4垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球;如图所示,由对称性可知球心O 的位置是△CBD 的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O1的半径CO1=r,OO1=h2,则R=r2+h24.类型二内切球问题内切球问题的解法(以三棱锥为例)第一步:先求出四个表面的面积和整个锥体的体积;第二步:设内切球的半径为r,建立等式V P-ABC=V O-ABC+V O-P AB+V O-P AC+V O-PBC⇒V P-ABC=13S△ABC·r+13S△P AB·r+13S△P AC·r+13S PBC·r=13(S△ABC+S△P AB+S△P AC+S△PBC)r;第三步:解出r=3V P-ABCS△ABC+S△P AB+S△P AC+S△PBC.类型三球的截面问题解决球的截面问题抓住以下几个方面:(1)球心到截面圆的距离;(2)截面圆的半径;(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).三、平行关系和垂直关系的证明、二面角等热点一空间线、面位置关系的判定判断空间线、面位置关系的常用方法(1)根据空间线面平行、垂直的判定定理和性质定理逐项判断,解决问题.(2)利用直线的方向向量、平面的法向量判断.(3)必要时可以借助空间几何模型,如从长方体、四面体等模型中观察线、面的位置关系,并结合有关定理进行判断.热点二几何法证明平行、垂直1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面○热○点○题○型一点、线、面间的位置关系和空间几何体的体积、表面积一、单选题1.设l ,m 是两条不同的直线,α,β,γ是三个不同的平面,下列说法正确的是()A .若//l α,//m α,则//l mB .若//l α,//l β,则//αβC .若l α⊥,m α⊥,则//l mD .若αγ⊥,βγ⊥,则//αβ2.将半径为6的半圆卷成一个无底圆锥(钢接处不重合),则该无底圆锥的体积为()A .273πB .27πC .3πD .9π3.在正方体1111ABCD A B C D -中,直线m 、n 分别在平面ABCD 和11ABB A ,且m n ⊥,则下列命题中正确的是()A .若m 垂直于AB ,则n 垂直于AB B .若m 垂直于AB ,则n 不垂直于ABC .若m 不垂直于AB ,则n 垂直于ABD .若m 不垂直于AB ,则n 不垂直于AB4.如图是一款多功能粉碎机的实物图,它的进物仓可看作正四棱台,已知该四棱台的上底面边长为40cm ,下底面边长为10cm ,侧棱长为30cm ,则该款粉碎机进物仓的容积为()A .32cmB .386003cmC .3105002cmD .33cm5.已知在春分或秋分时节,太阳直射赤道附近.若赤道附近某地在此季节的日出时间为早上6点,日落时间为晚上18点,该地有一个底面半径为4m 的圆锥形的建筑物,且该建筑物在一天中恰好有四个小时在地面上没有影子,则该建筑物的体积为()A .643πB .π3C .16π3D .π36.攒尖是古代中国建筑中屋顶的一种结构形式,依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑.如故宫中和殿的屋顶为四角攒尖顶,它的主要部分的轮廓可近似看作一个正四棱锥,设正四棱锥的侧面等腰三角形的顶角为60°,则该正四棱锥的侧面积与底面积的比为()A .4B 3C D 7.在三棱锥A BCD -中,4AB AC BD CD BC =====,平面α经过AC 的中点E ,并且与BC 垂直,则α截此三棱锥所得的截面面积的最大值为()A B .34C 2D .328.已知圆台的母线长为4,上底面圆和下底面圆半径的比为1:3,其侧面展开图所在扇形的圆心角为π2,则圆台的高为()A .BC .4D .二、多选题9.已知平面α,β,直线l ,m ,则下列命题正确的是()A .若αβ⊥,,,m l m l αβα⋂=⊥⊂,则l β⊥B .若l αβα⊂∥,,m β⊂,则//l mC .若m α⊂,则“l α⊥”是“l m ⊥”的充分不必要条件D .若m α⊂,l α⊄,则“l α∥”是“l m ”的必要不充分条件10.下列说法正确的是()A .若直线a 不平行于平面α,a α⊄,则α内不存在与a 平行的直线B .若一个平面α内两条不平行的直线都平行于另一个平面β,则αβ∥C .设l ,m ,n 为直线,m ,n 在平面α内,则“l α⊥”是“l m ⊥且l n ⊥”的充要条件D .若平面α⊥平面1α,平面β⊥平面1β,则平面α与平面β所成的二面角和平面1α与平面1β所成的二面角相等或互补三、解答题11.已知直棱柱1111ABCD A B C D -的底面ABCD 为菱形,且2AB AD BD ===,1AA =,点E 为11B D 的中点.(1)证明://AE 平面1BDC ;(2)求三棱锥1E BDC -的体积.12.如图,在三棱柱111ABC A B C -中,ABC 为边长为2的正三角形,D 为BC 的中点,12AA =,且160CCB ∠= ,平面11BB C C ⊥平面ABC .(1)证明:1C D AB ⊥;(2)求三棱锥111B AA C -的体积.○热○点○题○型二外接球、内切球等相关问题一、单选题1.已知ABC 是边长为3的等边三角形,其顶点都在球O 的球面上,若球O 的体积为323π,则球心O 到平面ABC 的距离为()AB .32C .1D .22.已知三棱锥-P ABC 的底面ABC 是边长为1的正三角形,侧棱,,PA PB PC 两两垂直,若此三棱锥的四个顶点都在同一个球面上,则该球的表面积是()A .3πB .πC .3π4D .3π23.一个圆锥的底面圆和顶点都恰好在一个球面上,且这个球的半径为5,则这个圆锥的体积的最大值时,圆锥的底面半径为()A .103B .2C .3D 4.已知圆锥的侧面积为2π,母线与底面所成角的余弦值为12,则该圆锥的内切球的体积为()A .4π3B C D 5.如图,几何体Ω为一个圆柱和圆锥的组合体,圆锥的底面和圆柱的一个底面重合,圆锥的顶点为A ,圆柱的上、下底面的圆心分别为B 、C ,若该几何体Ω存在外接球(即圆锥的顶点与底面圆周在球面上,且圆柱的底面圆周也在球面上).已知24BC AB ==,则该组合体的体积等于()A .56πB .70π3C .48πD .64π6.已知矩形ABCD 的顶点都在球心为O 的球面上,3AB =,BC =,且四棱锥O ABCD-的体积为,则球O 的表面积为()A .76πB .112πCD 7.水平桌面上放置了4个半径为2的小球,4个小球的球心构成正方形,且相邻的两个小球相切.若用一个半球形的容器罩住四个小球,则半球形容器内壁的半径的最小值为()A .4B .2C .2D .68.已知三棱锥-P ABC 的四个顶点均在球O 的球面上,2PA BC ==,PB AC ==PC AB =Q 为球O 的球面上一动点,则点Q 到平面PAB 的最大距离为()A 2211B C 2211D 二、填空题9.在三棱锥-P ABC 中,PA ⊥平面ABC ,14AB AC PA AB AC ⊥=+=,,,当三棱锥的体积最大时,三棱锥-P ABC 外接球的体积为______.10.如图,在直三棱柱111ABC A B C -中,1AA AB BC ==.设D 为1AC 的中点,三棱锥D ABC -的体积为94,平面1A BC ⊥平面11ABB A ,则三棱柱111ABC A B C -外接球的表面积为______.11.如图,直三棱柱111ABC A B C -的六个顶点都在半径为1的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则直三棱柱111ABC A B C -的体积为___________.12.如图所示的由4个直角三角形组成的各边长均相等的六边形是某棱锥的侧面展开图,若该六边形的面积为12,则该棱锥的内切球半径为___.○热○点○题○型三平面关系、垂直关系、体积、表面积等综合问题1.已知直棱柱1111ABCD A B C D -的底面ABCD 为菱形,且2AB AD BD ===,1AA =,点E 为11B D 的中点.(1)证明://AE 平面1BDC ;(2)求三棱锥1E BDC -的体积.2.如图,在四棱锥P ABCD -中,PAD 是等边三角形,底面ABCD 是棱长为2的菱形,平面PAD ⊥平面ABCD ,O 是AD 的中点,π3DAB ∠=.(1)证明:OB ⊥平面PAD ;(2)求点O 到平面PAB 的距离.3.如图,在三棱柱111ABC A B C -中,ABC 为边长为2的正三角形,D 为BC 的中点,12AA =,且160CCB ∠= ,平面11BB C C ⊥平面ABC .(1)证明:1C D AB ⊥;(2)求三棱锥111B AAC -的体积.4.如图1,在直角梯形ABCD 中,90ADC ∠=︒,AB CD ,122AD CD AB ===,E 为AC 的中点,将ACD 沿AC 折起,使折起后的平面ACD 与平面ABC 垂直,如图2.在图2所示的几何体D ABC -中:(1)求证:BC ⊥平面ACD ;(2)点F 在棱CD 上,且满足AD EF ,求几何体F BCE -的体积.5.在如图所示的几何体中,四边形ABCD 为菱形,60BCD ∠=︒,4AB =,EF CD ∥,2EF =,4CF =,点F 在平面ABCD 内的射影恰为BC 的中点G .(1)求证:平面ACE 平面BED;(2)求该几何体的体积.。
立体几何压轴小题

立体几何压轴小题一、单选题1.已知一圆锥底面圆的直径为3,圆锥的高为2,在该圆锥内放置一个棱长为a 的正四面体,并且正四面体在该几何体内可以任意转动,则a 的最大值为( )A .3BC .92D .22.如图,在棱长为3的正方体1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足12DP PB +=,则直线1B P 与直线1AD 所成角的余弦值的取值范围为( )A .10,2⎡⎤⎢⎥⎣⎦B .10,3⎡⎤⎢⎥⎣⎦C .12⎡⎢⎣⎦D .12⎡⎢⎣⎦3.已知正六棱锥V ABCDEF -,P 是侧棱VC 上一点(不含端点),记直线PB 与直线DE 所成角为α,直线PB 与平面ABC 所成角为β,二面角P CD F --的平面角为γ,则( ) A .βγ<,αγ< B .βα<,βγ< C .βα<,γα<D .αβ<,γβ<4.斜三棱柱111ABC A B C -中,底面ABC 是正三角形,侧面11ABB A 是矩形,M 是线段AB 上的动点,记直线1A M 与直线AC 所成的角为α,直线1A M 与平面ABC 所成的角为β,二面角1A AC B --的平面角为γ,则( )A .αβ≤,≤βγB .≤βα,≤βγC .αβ≤,βγ≥D .≤βα,βγ≥5.如图,在正四棱台1111ABCD A B C D -中,上底面边长为4,下底面边长为8,高为5,点,M N 分别在1111,A B D C 上,且111A M D N ==.过点,M N 的平面α与此四棱台的下底面会相交,则平面α与四棱台的面的交线所围成图形的面积的最大值为A .B .C .D .6.如图,直三棱柱111ABC A B C -的底面是边长为6的等边三角形,侧棱长为2,E 是棱BC 上的动点,F 是棱11B C 上靠近1C 点的三分点,M 是棱1CC 上的动点,则二面角A FM E --的正切值不可能...是( )A .5B .5C D 7.在棱长为3的正方体1111ABCD A B C D -中,O 为棱DC 的中点,E 为线段AO 上的点,且2AE EO =,若点,F P 分别是线段1DC ,1BC 上的动点,则PEF 周长的最小值为( )A .B .2C D8.三棱锥P ABC -中,AB BC ⊥,△PAC 为等边三角形,二面角P AC B --的余弦值为棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( ) A .1B .2C .12D .139.已知矩形,4,2,ABCD A AD E B ==为AB 中点,沿直线DE 将ADE 翻折成PDE △,直线PB 与平面BCDE 所成角最大时,线段PB 长是( )A .743B .543C .742D .54210.已知四面体ABCD 的三组对棱的长分别相等,依次为3,4,x ,则x 的取值范围是( )A .B .)C .)D .()4,711.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则( ) A .,βγαγ<< B .,βαβγ<< C .,βαγα<<D .,αβγβ<<12.已知,,,A B C D 四点均在半径为R (R 为常数)的球O 的球面上运动,且AB AC =,AB AC ⊥,AD BC ⊥,若四面体ABCD 的体积的最大值为16,则球O 的表面积为( )A .32π B .2πC .94π D .83π 13.蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是10928'︒,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱ABCDEF A B C D E '''''﹣的三个顶点A ,C ,E 处分别用平面BFM ,平面BDO ,平面DFN 截掉三个相等的三棱锥M ABF -,O BCD -,N DEF -,平面BFM ,平面BDO ,平面DFN 交于点P ,就形成了蜂巢的结构.如图,设平面PBOD 与正六边形底面所成的二面角的大小为θ,则有:( )A.tan 5444θ'=︒ B.sin 5444θ'=︒ C.cos tan 54443θ'=︒ D .以上都不对14.如图,正方体1111ABCD A B C D -的棱长为,,a E F 分别是棱1AA ,1CC 的中点,过点,E F 的平面分别与棱1BB ,1DD 交于点,G H ,设,[0,]BG x x a =∈.给出以下四个命题: ①平面EGFH 与平面ABCD 所成角的最大值为45°; ②四边形EGFH 的面积的最小值为2a ;③四棱锥1C EGFH -的体积为36a ;④点1B 到平面EGFH的距离的最大值为3. 其中命题正确的序号为( )A .②③④B .②③C .①②④D .③④15.在三棱锥A BCD -中,60BAC BDC ∠=∠=︒,二面角A BC D --的余弦值为13-,当三棱锥A BCD -) A .5πB .6πC .7πD .8π16.在正方体1111ABCD A B C D -中,点E ∈平面11AA B B ,点F 是线段1AA 的中点,若1D E CF ⊥,则当EBC ∆的面积取得最小值时,=EBC ABCDS S ∆四边形( )A B .12C D 17.有一正三棱柱(底面为正三角形的直棱柱)木料111ABC A B C -,其各棱长都为2.已知12,O O 分别为上,下底面的中心,O 为线段12O O 的中点,过A B O ,,三点的截面把该木料截成两部分,则截面面积为( )AB C D .218.已知α,β为两个不重合的平面,m ,n 为两条不重合的直线,且m αβ=,n β⊂.记直线m 与直线n 的夹角和二面角m αβ--均为1θ,直线n 与平面α的夹角为2θ,则下列说法正确的是( ) A .若106πθ<<,则122θθ> B .若164ππθ<<,则12tan 2tan θθ> C .若143ππθ<<,则12sin sin θθ<D .若132ππθ<<,则123cos cos 4θθ>19.如图,在矩形ABCD 中,2AB =,1BC =,E 、N 分别为边AB 、BC 的中点,沿DE 将ADE ∆折起,点A 折至1A 处(1A 与A 不重合),若M 、K 分别为线段1A D 、1A C 的中点,则在ADE ∆折起过程中( )A .DE 可以与1A C 垂直B .不能同时做到//MN 平面1A BE 且//BK 平面1A DEC .当1MN AD ⊥时,MN ⊥平面1A DED .直线1AE 、BK 与平面BCDE 所成角分别为1θ、2θ,1θ、2θ能够同时取得最大值20.在四面体ABCD 中,若1AD DB AC CB ====,则当四面体ABCD 的体积最大时其外接球表面积为( ) A .53π B .43π C .πD .2π二.多选题21.(2020·蒙阴县实验中学高三期末)已知四棱锥P ABCD -,底面ABCD 为矩形,侧面PCD ⊥平面ABCD ,BC =CD PC PD ===.若点M 为PC 的中点,则下列说法正确的为( )A .BM ⊥平面PCDB .//PA 面MBDC .四棱锥M ABCD -外接球的表面积为36π D .四棱锥M ABCD -的体积为622.(2020·山东高一期末)如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立 C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为423.(2020·山东高三)如图,矩形ABCD 中,M 为BC 的中点,将ABM 沿直线AM 翻折成1AB M ,连结1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得CN AB ⊥ B .翻折过程中,CN 的长是定值C .若AB BM =,则1AM BD ⊥D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -的外接球的表面积是4π 24.(2020·全国高三(理))如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DPB .DPC .1AP PC +D .1AP PC +的最小值为525.(2020·山东高一期末)已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 为球为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( ) A .11//A D 平面EFGH B .1A C ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 二、填空题26.已知长方体1111ABCD A B C D -的棱12AA =,4,3AB AD ==,点E ,F 分别为棱BC ,1CC 上的动点.若四面体11A B EF 的四个面都是直角三角形,则下列命题正确的是__________.(写出所有正确命题的编号)①存在点E ,使得1EF A F ⊥; ②不存在点E ,使得11B E A F ⊥;③当点E 为BC 中点时,满足条件的点F 有3个; ④当点F 为1CC 中点时,满足条件的点E 有3个; ⑤四面体11A B EF 四个面所在平面,有4对相互垂直.27.在四棱锥P ABCD -中,PAB 是边长为ABCD 为矩形,2AD =,PC PD ==若四棱锥P ABCD -的顶点均在球O 的球面上,则球O 的表面积为_____.28.《九章算术》中记载:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱剖开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中,12,4,BB BC AB AC ====且有鳖臑C 1-ABB 1和鳖臑1C ABC -,现将鳖臑1C ABC -沿线BC 1翻折,使点C 与点B 1重合,则鳖臑1C ABC -经翻折后,与鳖臑11C ABB -拼接成的几何体的外接球的表面积是______.29.点M 为正方体1111ABCD A B C D -的内切球O 球面上的动点,点N 为11B C 上一点,112,NB NC DM BN =⊥,若球O 的体积为,则动点M 的轨迹的长度为__________.30.如图所示,某几何体由底面半径和高均为1的圆柱与半径为1的半球对接而成,在该封闭几何体内部放入一个小圆柱体,且小圆柱体的上下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为__________.31.如图,AB 是平面α的斜线段,A 为斜足,点C 满足()0BC AC λλ=>,且在平面α内运动,则有以下几个命题:①当1λ=时,点C 的轨迹是抛物线; ②当1λ=时,点C 的轨迹是一条直线; ③当2λ=时,点C 的轨迹是圆; ④当2λ=时,点C 的轨迹是椭圆; ⑤当2λ=时,点C 的轨迹是双曲线.其中正确的命题是__________.(将所有正确的命题序号填到横线上) .32.已知三棱锥D ABC -的所有顶点都在球O 的表面上,AD ⊥平面ABC ,AC =1BC =,cos ACB ACB ∠=∠,2AD =,则球O 的表面积为__________.33.如图所示,在边长为2的菱形ABCD 中,60BCD ∠=︒,现将ABD △沿对角线BD 折起,得到三棱锥P BCD -.则当二面角P BD C --的大小为23π时,三棱锥P BCD -的外接球的表面积为______.34.如图,在四面体ABCD 中,2AB CD ==,AC BD ==AD BC ==,E F 分别是,AD BC 的中点若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积的最大值为______.35.现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为221254y x += ,将此椭圆绕y 轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.36.已知四面体ABCD 的四个顶点均在球O 的表面上,AB 为球O 的直径,4,2AB AD BC ===,四面体ABCD 的体积最大值为____37.已知单位向量i j k ,,两两的夹角均为θ(0θπ<<,且2πθ≠),若空间向量a 满足a xi y j zk =++,(,,)x y z R ∈,则有序实数组(,,)x y z 称为向量a 在“仿射”坐标系O xyz -(O 为坐标原点)下的“仿射”坐标,记作(, , )a x y z θ=,有下列命题:①已知()111,,a x y z θ=,(4,0,2)b θ=,则a b =0; ②已知3(,,0)a x y π=,3(0,0,)b z π=,其中,,0x y z >,则当且仅当x y =时,向量,a b 的夹角取得最小值;③已知()111,,a x y z θ=,()222,,b x y z θ=,则()123232,,a b x x y y z z θ+=+++;④已知()31,0,0OA π=,3(0,1,0)OB π=,3(0,0,1)OC π=,则三棱锥O ABC -的表面积S =其中真命题为________(写出所有真命题的序号).38.如图,在边长为4的正三角形ABC 中,D ,E ,F 分别为各边的中点,G ,H 分别为DE ,AF 的中点,将ABC 沿DE ,EF ,DF 折成正四面体P DEF -,则在此正四面体中,下列说法正确的是______.①异面直线PG 与DH 所成的角的余弦值为23; DF PE ⊥②;GH ③与PD 所成的角为45;PG ④与EF 所成角为6039.已知P ,E ,G F ,都在球面C 上,且P 在EFG ∆所在平面外,PE EF ⊥,PE EG ⊥,224PE GF EG===,120EGF∠=,在球C内任取一点,则该点落在三棱锥P EFG-内的概率为__________.40.如图,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形的面积不改变;③棱始终与水面平行;④当时,是定值.其中正确说法是.41.(2017届高三第二次湖北八校文数试卷第16题)祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆22221(0)y xa ba b+=>>所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于______.42.斜线OA与平面α成15°角,斜足为O,A'为A在α内的射影,B为OA的中点,l是α内过点O的动直线,若l 上存在点1P ,2P 使1230APB AP B ︒∠=∠=,则12||P P AB 则的最大值是_______,此时二面角12A PP A '--平面角的正弦值是_______43.三棱锥P ABC -中,顶点P 在底面ABC 的投影恰好是ABC 的内心,三个侧面的面积分别为12,16,20,且底面的面积为24,则该三棱锥P ABC -的体积是________;它的外接球的表面积是________.立体几何压轴小题解析一、单选题1.已知一圆锥底面圆的直径为3,圆锥的高为2,在该圆锥内放置一个棱长为a 的正四面体,并且正四面体在该几何体内可以任意转动,则a 的最大值为( )A .3 BC .92 D 【答案】B【解析】【分析】根据题意,该四面体内接于圆锥的内切球,通过内切球即可得到a 的最大值.【详解】依题意,四面体可以在圆锥内任意转动,故该四面体内接于圆锥的内切球设球心为P ,球的半径为r ,下底面半径为R ,轴截面上球与圆锥母线的切点为Q ,圆锥的轴截面如图:则32OA OB ==,因为SO ,故可得:3SA SB ===;所以SAB 为等边三角形,故P 是SAB 的中心,连接BP ,则BP 平分SBA ∠,所以30PBO ∠=︒;所以tan 30r R︒=,即32r ==,即四面体的外接球的半径为r =另正四面体可以从正方体中截得,如图:从图中可以得到,当正四面体的棱长为a 时,截得它的正方体的棱长为2a , 而正四面体的四个顶点都在正方体上,故正四面体的外接球即为截得它的正方体的外接球,所以12r ===,所以a =即a .故选:B .【点睛】本题考查了正四面体的外接球,将正四面体的外接球转化为正方体的外接球,是一种比较好的方法,本题属于难题.2.如图,在棱长为3的正方体1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足12DP PB +=,则直线1B P 与直线1AD 所成角的余弦值的取值范围为( )A .10,2⎡⎤⎢⎥⎣⎦B .10,3⎡⎤⎢⎥⎣⎦C .122⎡⎢⎣⎦D .1,22⎡⎢⎣⎦【答案】A【解析】【分析】求得点P 的轨迹是平面11A BC 内以点O 为圆心,半径为1的圆,可得111////AD BC B M ,进而可得出题中所求角等于直线1B M 与直线1B P 的夹角,然后过点O 作OH ⊥平面ABCD 于点H ,过点H 作HN BC ⊥于点N ,连接ON ,找出使得1PB M ∠最大和最小时的位置,进而可求得所求角的余弦值的取值范围.【详解】连接1B D 交平面11A BC 于点O ,延长线段CB 至点M ,使得CB BM =,连接1B M 、OM 、PM ,如下图所示:已知在正方体1111ABCD A B C D -中,1DD ⊥底面1111D C B A ,11A C ⊂平面1111D C B A ,111DD A C ∴⊥, 又四边形1111D C B A 为正方形,所以,1111AC B D ⊥, 1111DD B D D ⋂=,11A C ∴⊥平面11B DD ,1B D ⊂平面11B DD ,111B D AC ∴⊥,同理11B D A B ⊥,1111AC A B A =,1B D ∴⊥平面11A BC ,三棱锥111B A B C -的体积为11131193322B A BC V -=⨯⨯=,(111242A B C S ==△,1111119322B A BC V B O O -=⨯==,可得1113B O B D ==, 所以,线段1B D 的长被平面11A BC 与平面1AD C 三等分,且与两平面分别垂直,而正方体1111ABCD A B C D -的棱长为3,所以1OB =OD =其中1PO B D ⊥,不妨设OP x =,由题意可12PB PD +=2=1x =,所以,点P 在平面11A BC 内以点O 为圆心,半径为1的圆上.因为111////AD BC B M ,所以,直线1B M 与直线1B P 的夹角即为直线1B P 与直线1AD 所成角.接下来要求出线段1B M 与PM 的长,然后在1B PM △中利用余弦定理求解.如图,过点O 作OH ⊥平面ABCD 于点H ,过点H 作HN BC ⊥于点N ,连接ON ,根据题意可知2OH =,1HN BN ==,且ON MN ⊥,所以,ON =OM ==如图所示,121OP OP ==,当点P 在1P 处时,1PB M ∠最大,当点P 在2P 处时,1PB M ∠最小.这两种情况下直线1B P 与直线1B M 夹角的余弦值最大,为111cos sin 2PB M PB O ∠=∠=; 当点P 在点O 处时,1PB M ∠为直角,此时余弦值最小为0.综上所述,直线1B P 与直线1AD 所成角的余弦值的取值范围是10,2⎡⎤⎢⎥⎣⎦. 故选:A.【点睛】本题考查异面直线所成角的取值范围的求解,解题的关键就是确定点P 的轨迹,考查推理能力与计算能力,属于难题.3.已知正六棱锥V ABCDEF -,P 是侧棱VC 上一点(不含端点),记直线PB 与直线DE 所成角为α,直线PB 与平面ABC 所成角为β,二面角P CD F --的平面角为γ,则( )A .βγ<,αγ<B .βα<,βγ<C .βα<,γα<D .αβ<,γβ<【答案】B【解析】【分析】通过明确异面直线所成的角、直线与平面所成的角、二面角,应用三角函数知识求解,而后比较大小.【详解】解:如图,设点V 在底面上的射影为O 点,连接OC ,PB ,作PG VO //,则PG ⊥平面ABC ,所以PB 与平面ABC 所成的角为PBG ∠,即PBG β=∠,根据线面角最小定理知βα<,作GM CD ⊥,则二面角P CD F --的平面角为PMG ∠,即PMG γ=∠,根据tan tan PG PG GM GBγβ=>=,所以γβ>. 故选B.【点睛】本题考查立体几何中异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算,考查空间想象能力,数形结合思想,分析问题能力,属于难题.4.斜三棱柱111ABC A B C -中,底面ABC 是正三角形,侧面11ABB A 是矩形,M 是线段AB 上的动点,记直线1A M 与直线AC 所成的角为α,直线1A M 与平面ABC 所成的角为β,二面角1A AC B --的平面角为γ,则( )A .αβ≤,≤βγB .≤βα,≤βγC .αβ≤,βγ≥D .≤βα,βγ≥【答案】B【解析】【分析】根据直线和平面的最小角定理,结合线面角和二面角的定义,即可得解.【详解】根据最小角定理,可得≤βα,当M 在线段AB 上的移动时,M 和A 重合时,1A M 与平面ABC 所成角最大,(因为ABB 1A 1为矩形)作1A P ⊥平面ABC 于P ,作PQ CA ⊥的延长线于Q ,连接1A Q 和PQ ,则1A MP β=∠,1=A QP γ∠,由于1A QA ∠ 为直角,所以11A M AQ ≥,可得βγ≤, 故选:B.【点睛】本题考查了线线角、线面角以及面面角的比较,考查了最小角定理,考查了线面角以及面面角的定义以及立体空间感,属于难题.5.如图,在正四棱台1111ABCD A B C D -中,上底面边长为4,下底面边长为8,高为5,点,M N 分别在1111,A B D C 上,且111A M D N ==.过点,M N 的平面α与此四棱台的下底面会相交,则平面α与四棱台的面的交线所围成图形的面积的最大值为A .B .C .D .【答案】B 【解析】 【分析】由题意可知,当平面α经过BCNM 时取得的截面面积最大,此时截面是等腰梯形;根据正四棱台的高及MN 中点在底面的投影求得等腰梯形的高,进而求得等腰梯形的面积. 【详解】当斜面α经过点BCNM 时与四棱台的面的交线围成的图形的面积最大,此时α为等腰梯形,上底为MN=4,下底为BC=8此时作正四棱台1111ABCD A B C D -俯视图如下:则MN 中点在底面的投影到BC 的距离为8-2-1=5因为正四棱台1111ABCD A B C D -的高为5=所以截面面积的最大值为()1482S =⨯+⨯= 所以选B 【点睛】本题考查了立体几何中过定点的截面面积问题,关键是分析出截面的位置,再根据条件求得各数据,需要很好的空间想象能力,属于难题.6.如图,直三棱柱111ABC A B C -的底面是边长为6的等边三角形,侧棱长为2,E 是棱BC 上的动点,F 是棱11B C 上靠近1C 点的三分点,M 是棱1CC 上的动点,则二面角A FM E --的正切值不可能...是( )A B C D 【答案】B 【解析】 【分析】建立空间直角坐标系,求得二面角A FM E --的余弦值,进而求得二面角A FM E --的正切值,求得正切值的最小值,由此判断出正确选项. 【详解】取BC 的中点O ,连接OA ,根据等边三角形的性质可知OA BC ⊥,根据直三棱柱的性质,以O 为原点建立如图所示的空间直角坐标系.则()(),1,0,2A F ,设()()3,0,02M t t ≤≤. 则()()1,33,2,2,0,2AF FM t =-=-. 设平面AMF 的一个法向量为(),,m x y z =,则()20220m AF x z m FM x t z ⎧⋅=-+=⎪⎨⋅=+-=⎪⎩,令1y =,得63m ⎛= ⎝⎭. 平面FME 的一个法向量是()0,1,0n =,所以cos ,6m n m n m n⋅===⋅⎛,所以2sin ,1cos ,m n m n =-120252t =+所以二面角A FME --的正切值为()sin ,27cos ,m n f t m n===因为02t ≤≤,所以111466t -≤≤--,216125405-=-⨯ 结合二次函数的性质可知 当1165t =--时,()f t= 当1166t =--时,()f t=, 所以()f t ∈⎣, 所以二面角A FM E --的正切值不可能是5. 故选:B. 【点睛】本小题主要考查二面角的求法,考查数形结合的数学思想方法,属于难题.7.在棱长为3的正方体1111ABCD A B C D -中,O 为棱DC 的中点,E 为线段AO 上的点,且2AE EO =,若点,F P 分别是线段1DC ,1BC 上的动点,则PEF 周长的最小值为( )A .BC D【答案】D 【解析】 【分析】连接BD ,易知E 为线段AO 与BD 的交点,即E 为线段DB 上靠近D 的三等分点,将PEF 周长的最小值问题转化到平面上几何知识连接两点间的线中线段最短与平面几何中对称问题处理,最后由余弦定理求得12E E 的长度即可. 【详解】连接BD ,易知E 为线段AO 与BD 的交点,即E 为线段DB 上的点,由勾股定理可知BD =2BE DE ==分别作点E 关于线段1DC ,1BC 的对称点1E ,2E ,且由对称关系有垂直关系且显然1BDC 为等边三角形,即12120E EE ∠=︒,由等边三角形对称问题可求得1EE =2EE =据余弦定理得12E E ==,由平面几何知识连接两点间的线中线段最短,得PEF .故选:D 【点睛】本题考查空间中三角形周长的最值,涉及空间中直线与对称点的算法,属于难题.8.三棱锥P ABC -中,AB BC ⊥,△PAC 为等边三角形,二面角P AC B --的余弦值为3-,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( ) A .1 B .2C .12D .13【答案】D 【解析】 【分析】由已知作出图象,找出二面角P AC B --的平面角,设出AB BC AC ,,的长,即可求出三棱锥P ABC -的高,然后利用基本不等式即可确定三棱锥体积的最大值(用含有AC 长度的字母表示),再设出球心O ,由球的表面积求得半径,根据球的几何性质,利用球心距,半径,底面半径之间的关系求得AC 的长度,则三棱锥体积的最大值可求. 【详解】如图所示,过点P 作PE ⊥面ABC ,垂足为E ,过点E 作ED AC ⊥交AC 于点D ,连接PD , 则PDE ∠为二面角PAC B -的平面角的补角,即有63cos PDE, 易知AC ⊥面PDE ,则AC PD ⊥,而△PAC 为等边三角形,∴D 为AC 中点, 设22ABa BCb ACa b c ,,,则PE PDsin PDE =∠=c 32c ⨯=, 故三棱锥P ABC -的体积为:1132V ab =⨯2231121212224c a b c abc c +⨯=≤⨯=,当且仅当2a b ==时,体积最大,此时B D E 、、共线. 设三棱锥P ABC -的外接球的球心为O ,半径为R ,由已知,248R ππ=,得R =.过点O 作OF PE ⊥于F ,则四边形ODEF 为矩形,则OD EF ==232ED OF PDcos PDE c ==∠=⨯=,2c PE =,在Rt △PFO 中222)(22c c =+-,解得2c = ∴三棱锥P ABC -的体积的最大值为:332124243c ==.故选:D. 【点睛】本题考查三棱锥体积最值的求法与三棱锥外接球的表面积的求法,涉及二面角的运用,基本不等式的应用,以及球的几何性质的应用,属于难题.9.已知矩形,4,2,ABCD A AD E B ==为AB 中点,沿直线DE 将ADE 翻折成PDE △,直线PB 与平面BCDE 所成角最大时,线段PB 长是( )A .743B .543C .742D .542【答案】C 【解析】 【分析】取CD 的中点F ,连接AF 交于DE 的中点O ,AF DE ⊥,进而有DE ⊥平面POF ,过点P 作PQ AF ⊥于点Q ,可证PQ ⊥平面BCDE ,连接BQ ,设直线PB 与平面BCDE 所成的角为α,平面PDE 与平面BCDE 所成的角为β,根据条件可知,AO DE PO DE ⊥⊥,PQ ⊥平面BCDE ,,PBQ POQ αβ∠=∠=,通过边长关系求出OQ β=,PQ β=,AQ AO OQ β=+=,以及利用余弦定理求出)228BQ β=+,从而得出)()22222tan 8PQBQ βαβ==+,根据同角三角函数关系和换元法令[]2cos 64,8t β+=∈,得出24tan 1328t tα=-++-,再根据基本不等式时得出当cos 3t β=⇒=时,2tan α取得最大值,从而可求出线段PB 长【详解】解:取CD 的中点F ,连接AF 交于DE 的中点O , 在矩形ABCD 中,4,2,AB AD E ==为AB 中点, 所以四边形AEFD 为正方形,AF DE ⊥, 所以,,PO DE OF DE POOF O ⊥⊥=,故DE ⊥平面POF ,在平面POF 内过点P 作PQ AF ⊥于点Q , 则,DE PQ DEAF O ⊥=,所以PQ ⊥平面BCDE ,连接BQ ,设直线PB 与平面BCDE 所成的角为α,即PBQ α∠= 设平面PDE 与平面BCDE 所成的角为β,,OF DE PO DE ⊥⊥,所以POQ β∠=,所以DE PO AO ===所以在Rt POQ △中,,PQ OQ ββ==,则AQ AO OQ β=+=,在ABQ △中,4,4AB BAQ π=∠=,则由余弦定理得出:)228BQ β=+,则有)()22222tan 8PQBQ βαβ==+222sin 822cos 4cos βββ=+++22sin cos 2cos 5βββ=++ 221cos cos 2cos 5βββ-=++22cos 61cos 2cos 5βββ+=-+++,令[]2cos 64,8t β+=∈,则6cos 2t β-=, 即:24tan 1328t tα=-++-, 当直线PB 与平面BCDE 所成角α最大时,2tan α最大, 即24tan 1328t tα=-++-取得最大值时,当且仅当32t t=,此时cos 3t β=⇒=,所以,))2228PB ββ=++72124cos 2β=+==,即742PB =.故选:C.【点睛】本题考查线面角和二面角的定义,还运用余弦定理和利用基本不等式求最值,还涉及同角三角函数关系和换元法,考查转化思想和化简运算能力.10.已知四面体ABCD 的三组对棱的长分别相等,依次为3,4,x ,则x 的取值范围是( )A .B .)C .)D .()4,7【答案】B 【解析】 【分析】作出图形,设3AB =,4AC =,四面体A ABC '-可以由ABC ∆和在同一平面的△A BC '沿着BC 为轴旋转构成,利用数形结合能求出x 的取值范围. 【详解】 解:如图所示,第一排 三个图讨论最短;第二排 三个图讨论最长,设3AB =,4AC =,四面体A ABC '-可以由ABC ∆和在同一平面的△A BC '沿着BC 为轴旋转构成, 第一排,三个图讨论最短:当90ABC ∠<︒向90︒趋近时,BC 逐渐减少,AA BC '<,可以构成x AA BC '==的四面体; 当90ABC ∠︒时构成的四面体AA BC '>,不满足题意;, 第二排,三个图讨论最长:当90BAC ∠<︒向90︒趋近时,BC 逐渐增大,AA BC '>,可以构成x AA BC '==的四面体; 当90ABC ∠︒时构成的四面体AA BC '<,不满足题意;5;综上,x ∈5). 故选B . 【点睛】本题考查了四面体中边长的取值范围问题,也考查了推理论证能力,属于难题.11.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则( ) A .,βγαγ<< B .,βαβγ<< C .,βαγα<< D .,αβγβ<<【答案】B 【解析】 【分析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半. 【详解】方法1:如图G 为AC 中点,V 在底面ABC 的投影为O ,则P 在底面投影D 在线段AO 上,过D 作DE 垂直AE ,易得//PE VG ,过P 作//PF AC 交VG 于F ,过D 作//DH AC ,交BG 于H ,则,,BPF PBD PED α=∠β=∠γ=∠,则cos cos PF EG DH BDPB PB PB PBα===<=β,即αβ>,tan tan PD PDED BDγ=>=β,即y >β,综上所述,答案为B.方法2:由最小角定理βα<,记V AB C --的平面角为γ'(显然γ'=γ) 由最大角定理β<γ'=γ,故选B.方法3:(特殊位置)取V ABC -为正四面体,P 为VA 中点,易得cos sin sin α=⇒α=β=γ=,故选B. 【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法. 12.已知,,,A B C D 四点均在半径为R (R 为常数)的球O 的球面上运动,且AB AC =,AB AC ⊥,AD BC ⊥,若四面体ABCD 的体积的最大值为16,则球O 的表面积为( )A .32π B .2πC .94π D .83π 【答案】C 【解析】 【分析】由题意要使四面体的体积最大,则D 在底面ABC 的投影恰好为底面三角形外接圆的圆心N ,则外接球的球心在DN 上,求出三棱锥的体积,由均值不等式可得R 的值,进而求出外接球的表面积. 【详解】因为,,AB AC AB AC AD BC =⊥⊥,作AN BC ⊥于N , 则N 为BC 的中点,且12AN BC =, 若四面体ABCD 的体积的最大值时,则DN ⊥面ABC ,则外接球的球心在DN 上,设为O , 设外接球的半径为R ,连接OA ,则OA OD R ==,()()2111123263D ABC V BC AN DN AN AN R ON AN R ON -=⋅⋅⋅⋅=⋅⋅⋅+=⋅+()2213()OA ON R ON =-+ ()()()13R ON R ON R ON =+-+ ()()()1226R ON R ON R ON =+-+ 331()(22)()146363R ON R ON R ON R ++-++⎛⎫⎛⎫≤=⋅ ⎪ ⎪⎝⎭⎝⎭当且仅当22R ON R ON -=+,即3R ON =时取等号, 因为三棱锥的最大体积为16, 所以3141636R ⎛⎫⋅= ⎪⎝⎭,可得34R =, 所以外接球的表面积为29944164S R πππ==⋅=, 故选:C . 【点睛】本题考查的是几何体的体积和表面积公式及利用基本不等式求最值,属于较难题.13.蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是10928'︒,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱ABCDEF A B C D E '''''﹣的三个顶点A ,C ,E 处分别用平面BFM ,平面BDO ,。
九年级几何模型压轴题单元练习(Word版 含答案)

九年级几何模型压轴题单元练习(Word版含答案)一、初三数学旋转易错题压轴题(难)1.我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.特例感知:(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;②如图3,当∠BAC=90°,BC=8时,则AD长为.猜想论证:(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.拓展应用(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=23,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.【答案】(1)①12;②4;(2)AD=12BC,证明见解析;(3)存在,证明见解析,39.【解析】【分析】(1)①首先证明△ADB′是含有30°是直角三角形,可得AD=12AB′即可解决问题;②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;(2)结论:AD=12BC.如图1中,延长AD到M,使得AD=DM,连接E′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;(3)存在.如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.连接DF交PC于O.想办法证明PA=PD,PB=PC,再证明∠APD+∠BPC=180°,即可;【详解】解:(1)①如图2中,∵△ABC是等边三角形,∴AB=BC=AB=AB′=AC′,∵DB′=DC′,∴AD⊥B′C′,∵∠BAC=60°,∠BAC+∠B′AC′=180°,∴∠B′AC′=120°,∴∠B′=∠C′=30°,∴AD=12AB′=12BC,故答案为12.②如图3中,∵∠BAC=90°,∠BAC+∠B′AC′=180°,∴∠B′AC′=∠BAC=90°,∵AB=AB′,AC=AC′,∴△BAC≌△B′AC′,∴BC=B′C′,∵B′D=DC′,∴AD=12B′C′=12BC=4,故答案为4.(2)结论:AD=12 BC.理由:如图1中,延长AD到M,使得AD=DM,连接E′M,C′M∵B′D=DC′,AD=DM,∴四边形AC′MB′是平行四边形,∴AC′=B′M=AC,∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠MB′A,∵AB=AB′,∴△BAC≌△AB′M,∴BC=AM,∴AD=1BC.2(3)存在.理由:如图4中,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作△PCD的中线PN.连接DF交PC于O.∵∠ADC=150°,∴∠MDC=30°,在Rt△DCM中,∵3,∠DCM=90°,∠MDC=30°,∴CM=2,DM=4,∠M=60°,在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,∴EM=1BM=7,2∴DE=EM﹣DM=3,∵AD=6,∴AE=DE,∵BE⊥AD,∴PA=PD,PB=PC,在Rt△CDF中,∵3CF=6,∴tan∠3∴∠CDF=60°=∠CPF,易证△FCP≌△CFD,∴CD=PF,∵CD∥PF,∴四边形CDPF是矩形,∴∠CDP=90°,∴∠ADP=∠ADC﹣∠CDP=60°,∴△ADP是等边三角形,∴∠ADP=60°,∵∠BPF=∠CPF=60°,∴∠BPC=120°,∴∠APD+∠BPC=180°,∴△PDC是△PAB的“旋补三角形”,在Rt△PDN中,∵∠PDN=90°,PD=AD=6,DN=3,∴PN=2222++=39.DN PD=(3)6【点睛】本题考查四边形综合题.2.综合与实践问题情境在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.观察发现(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是;(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;实践探究(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:在图2中,线段AB、DB、CB之间满足的数量关系是;在图3中,线段AB、DB、CB之间满足的数量关系是;提出问题(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.【答案】(1)AB+DB=CB;(2)见解析;(3)AB-DB=CB;DB-AB=CB;(4)23【解析】【分析】(1)根据图中数据直接猜想AB+DB=CB(2)在射线AM上一点E,使得∠ECB=60°,证明△ACE≌△DCB,推出EB=CB从而得出(1)中的结论;(3)利用旋转的性质和线段的和差关系以及全等三角形的性质得出线段关系;(4)过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.证明△ACE≌△DCB,得出BC=EC,结合△ECB为等边三角形,得出∠ECA=90°,在Rt△AEC中根据边长计算出AC的长度.【详解】综合与实践(1)AB+DB=CB(2)线段CE如图所示.证明:∵∠ECB=∠ACD=60º,∴∠2+∠ACB=∠1+∠ACB,∴∠2=∠1.∵∠ACD=∠DBN=60º, ∠ABD+∠DBN=180º,∴∠ABD+∠ACD=180º,∴在四边形ACDB中,∠CAB+∠3=180º.∵∠CAB+∠4=180º,∴∠4=∠3.又∵AC=DC,∴△ACE≌△DCB(ASA)∴EA=BD,EC=BC.又∵∠ECB=60°,∴△ECB为等边三角形,∴EB=CB.而EB=EA+AB=DB+AB,∴CB=DB+AB.(3) AB-DB=CB;DB-AB=CB;(4)证明:如图,过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.∵∠DCA=60º∴∠ECB+∠BCA=∠DCA+∠BCA即∠ECA=∠BCD∵∠DBN=120º∴∠DBA=60º又∵∠AFB=∠DFC∴∠EAF=∠BDC又∵AC=DC∴△ACE≌△DCB(ASA)∴BC=EC∴△ECB为等边三角形∴∠CEB=60º∵BC⊥CD∴∠ECA=∠BCD=90º∴在Rt△AEC中,∠CAE=30º∵BC=2,EC=BC∴AC=EC·tan60º= 23【点睛】本题考查了全等三角形的判定和性质,旋转的性质,根据题中条件适当添加辅助线构造全等三角形,利用全等的性质得出线段关系是本题的关键.3.请阅读下列材料:问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=3,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),从而得到∠BPC=∠AP′B=__________;,进而求出等边△ABC的边长为__________;问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=5,BP=2,PC=1.求∠BPC度数的大小和正方形ABCD的边长.【答案】(17;(25【解析】试题分析:(1)利用旋转的性质,得到全等三角形.(2)利用(1)中的解题思路,把△BPC,旋转,到△BP’A,连接PP’,BP’,容易证明△APP’是直角三角形,∠BP’E=45°,已知边BP’=BP2,BE=BP’=1,勾股定理可求得正方形边长.(17(2)将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.∴AP′=PC=1,BP=BP′=2;连接PP′,在Rt△BP′P中,∵BP=BP′=2,∠PBP′=90°,∴PP′=2,∠BP′P=45°;在△AP′P中,AP′=1,PP′=2,AP=5,∵222+=,即AP′2+PP′2=AP2;125∴△AP′P是直角三角形,即∠AP′P=90°,∴∠AP′B=135°,∴∠B PC=∠AP′B=135°.过点B作BE⊥AP′,交AP′的延长线于点E;则△BEP′是等腰直角三角形,∴∠EP′B=45°,∴EP′=BE=1,∴AE=2;∴在Rt△ABE中,由勾股定理,得AB=5;∴∠BPC=135°,正方形边长为5.点睛:本题利用题目中的原理迁移解决问题,解题利用了旋转的性质,一般利用正方形,等腰,等边三角形的隐含条件,构造全等三角形,把没办法利用的已知条件转移到方便利用的图形位置,从而求解.4.在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.【答案】(1)证明见解析;(2)成立,理由见解析【解析】试题分析:(1)①由旋转的性质得出OC=OC′,OD=OD′,∠AOC′=∠BOD′,证出OC′=OD′,由SAS证明△AOC′≌△BOD′,得出对应边相等即可;②由全等三角形的性质得出∠OAC′=∠OBD′,又由对顶角相等和三角形内角和定理得出∠BEA=90°,即可得出结论;(2)由旋转的性质得出OC=O C′,OD=OD′,∠AOC′=∠BOD′,由平行线得出比例式,得出,证明△AOC′∽△BOD′,得出∠OAC′=∠OBD′再由对顶角相等和三角形内角和定理即可得出∠AEB=θ.试题解析:(1)证明:①∵△OCD旋转到△OC′D′,∴OC=OC′,OD=OD′,∠AOC′=∠BOD′,∵OA=OB,C、D为OA、OB的中点,∴OC=OD,∴OC′=OD′,在△AOC′和△BOD′中,,∴△AOC′≌△BOD′(SAS),∴AC′=BD′;②延长AC′交BD′于E,交BO于F,如图1所示:∵△AOC′≌△BOD′,∴∠OAC′=∠OBD′,又∠AFO=∠BFE,∠OAC′+∠AFO=90°,∴∠OBD′+∠BFE=90°,∴∠BEA=90°,∴AC′⊥BD′;(2)解:∠AEB=θ成立,理由如下:如图2所示:∵△OCD旋转到△OC′D′,∴OC=OC′,OD=OD′,∠AOC′=∠BOD′,∵CD∥AB,∴,∴,∴,又∠AOC′=∠BOD′,∴△AOC′∽△BOD′,∴∠OAC′=∠OBD′,又∠AFO=∠BFE,∴∠AEB=∠AOB=θ.考点:相似三角形的判定与性质;全等三角形的判定与性质;旋转的性质.5.如图,在直角坐标系中,已知点A(-1,0)、B(0,2),将线段AB绕点A按逆时针方向旋转90°至AC.(1)点C的坐标为(,);(2)若二次函数的图象经过点C.①求二次函数的关系式;②当-1≤x≤4时,直接写出函数值y对应的取值范围;Z_X_X_K]③在此二次函数的图象上是否存在点P(点C除外),使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.【答案】(1) ∴点C的坐标为(-3,1) .(2)①∵二次函数的图象经过点C(-3,1),∴.解得∴二次函数的关系式为②当-1≤x≤4时,≤y≤8;③过点C作CD⊥x轴,垂足为D,i) 当A为直角顶点时,延长CA至点,使,则△是以AB为直角边的等腰直角三角形,过点作⊥轴,∵=,∠=∠,∠=∠=90°,∴△≌△,∴AE=AD=2,=CD=1,∴可求得的坐标为(1,-1),经检验点在二次函数的图象上;ii)当B点为直角顶点时,过点B作直线L⊥BA,在直线L上分别取,得到以AB为直角边的等腰直角△和等腰直角△,作⊥y轴,同理可证△≌△∴BF=OA=1,可得点的坐标为(2, 1),经检验点在二次函数的图象上.同理可得点的坐标为(-2, 3),经检验点不在二次函数的图象上综上:二次函数的图象上存在点(1,-1),(2,1)两点,使得△和△是以AB为直角边的等腰直角三角形.【解析】(1)根据旋转的性质得出C点坐标;(2)①把C点代入求得二次函数的解析式;②利用二次函数的图象得出y的取值范围;③分二种情况进行讨论.6.在平面直角坐标系中,O为原点,点A(8,0),点B(0,6),把△ABO绕点B逆时针旋转得△A′B′O′,点A、O旋转后的对应点为A′、O′,记旋转角为α.(1)如图1,若α=90°,则AB= ,并求AA′的长;(2)如图2,若α=120°,求点O′的坐标;(3)在(2)的条件下,边OA上的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,直接写出点P′的坐标.【答案】(1)10,102;(2)(33,9);(3)123545(,)【解析】试题分析:(1)、如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90°,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;(2)、作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120°,则∠HBO′=60°,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;(3)、由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y=x﹣3,从而得到P(,0),则O′P′=OP=,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D 和DO′的长,从而可得到P′点的坐标.试题解析:(1)、如图①,∵点A(4,0),点B(0,3),∴OA=4,OB=3,∴AB==5,∵△ABO绕点B逆时针旋转90°,得△A′BO′,∴BA=BA′,∠ABA′=90°,∴△ABA′为等腰直角三角形,∴AA′=BA=5;(2)、作O′H⊥y轴于H,如图②,∵△ABO绕点B逆时针旋转120°,得△A′BO′,∴BO=BO′=3,∠OBO′=120°,∴∠HBO′=60°,在Rt△BHO′中,∵∠BO′H=90°﹣∠HBO′=30°,∴BH=BO′=,O′H=BH=,∴OH=OB+BH=3+,∴O′点的坐标为();(3)∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′,∴BP=BP′,∴O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,∵点C与点B关于x轴对称,∴C(0,﹣3),设直线O′C的解析式为y=kx+b,把O′(),C (0,﹣3)代入得,解得,∴直线O′C 的解析式为y=x ﹣3, 当y=0时,x ﹣3=0,解得x=,则P(,0), ∴OP=, ∴O′P′=OP=, 作P′D ⊥O′H 于D ,∵∠BO′A=∠BOA=90°,∠BO′H=30°, ∴∠DP′O′=30°, ∴O′D=O′P′=,P′D=, ∴DH=O′H ﹣O′,∴P′点的坐标为(,).考点:几何变换综合题7.在矩形ABCD 中,2AB =,1BC =,以点A 为旋转中心,逆时针旋转矩形ABCD ,旋转角为(0180)αα<<,得到矩形AEFG ,点B 、点C 、点D 的对应点分别为点E 、点F 、点G .()1如图①,当点E 落在DC 边上时,直写出线段EC 的长度为______; ()2如图②,当点E 落在线段CF 上时,AE 与DC 相交于点H ,连接AC ,①求证:ACD ≌CAE ; ②直接写出线段DH 的长度为______.()3如图③设点P 为边FG 的中点,连接PB ,PE ,在矩形ABCD 旋转过程中,BEP 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.【答案】(1)23;(2)①见解析;34②;(3)存在,PBE 的面积的最大值为21,理由见解析 【解析】 【分析】()1如图①中,在Rt ADE 中,利用勾股定理即可解决问题; ()2①证明:如图②中,根据HL 即可证明ACD ≌CAE ;②如图②中,由ACD ≌CAE ,推出ACD CAE ∠∠=,推出AH HC =,设AH HC m ==,在Rt ADH 中,根据222AD DH AH +=,构建方程即可解决问题; ()3存在.如图③中,连接PA ,作BM PE ⊥交PE 的延长线于M.由题意:PF PC 1==,由AG EF 1==,G F 90∠∠==,推出PA PE 2==PBE12SPE BM 22=⋅⋅=,推出当BM 的值最大时,PBE 的面积最大,求出BM 的最大值即可解决问题; 【详解】()1四边形ABCD 是矩形,AB CD 2∴==,BC AD 1==,D 90∠=,矩形AEFG 是由矩形ABCD 旋转得到,AE AB 2∴==,在Rt ADE 中,22DE 213=-=CE 23∴=,故答案为23.()2①当点E 落在线段CF 上,AEC ADC 90∠∠∴==,在Rt ADC 和Rt AEC 中,{AC CACD AE ==,Rt ACD ∴≌()Rt CAE HL ;ACD ②≌CAE ,ACD CAE ∠∠∴=,AH HC ∴=,设AH HC m ==,在Rt ADH 中,222AD DH AH +=,2221(2m)m ∴+-=,5m 4∴=, 53DH 244∴=-=, 故答案为34; ()3存在.理由如下:如图③中,连接PA ,作BM PE ⊥交PE 的延长线于M ,由题意:PF PC 1==,AG EF 1==,G F 90∠∠==, PA PE 2∴==PBE12SPE BM BM 22∴=⋅⋅=, ∴当BM 的值最大时,PBE 的面积最大,BM PB ≤,PB AB PA ≤+,PB 22∴≤,BM 22∴≤BM ∴的最大值为22+ PBE ∴21.【点睛】本题是四边形综合题,考查了矩形的性质,旋转变换,全等三角形的判定和性质,勾股定理,三角形的面积,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.8.如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形,如图2.①在旋转过程中,当∠是直角时,求的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)②若正方形ABCD的边长为1,在旋转过程中,求长的最大值和此时的度数,直接写出结果不必说明理由.【答案】(1)DE⊥AG (2)①当∠为直角时,α=30°或150°.②315°【解析】分析:(1)延长ED交AG于点H,证明≌,根据等量代换证明结论;(2)根据题意和锐角正弦的概念以及特殊角的三角函数值得到,分两种情况求出的度数;(3)根据正方形的性质分别求出OA和OF的长,根据旋转变换的性质求出AF′长的最大值和此时的度数.详解:如图1,延长ED交AG于点H,点O是正方形ABCD两对角线的交点,,,在和中,,≌,,,,,即;在旋转过程中,成为直角有两种情况:Ⅰ由增大到过程中,当时,,在中,sin∠AGO=,,,,,即;Ⅱ由增大到过程中,当时,同理可求,.综上所述,当时,或.如图3,当旋转到A、O、在一条直线上时,的长最大,正方形ABCD 的边长为1,,,, ,,,此时.点睛:考查了正方形的性质,全等三角形的判定与性质,锐角三角形函数,旋转变换的性质的综合应用,有一定的综合性,注意分类讨论的思想.二、初三数学 圆易错题压轴题(难)9.在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、 AD 、BD .已知圆O 的半径长为5,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC=x ,ACO OBDS S=y ,求y 关于x 的函数解析式并写出定义域;(3)若四边形AOBD 是梯形,求AD 的长.【答案】(1)2;(2)2825x x x -+(0<x <8);(3)AD=145或6.【解析】 【分析】(1)根据垂径定理和勾股定理可求出OC 的长.(2)分别作OH ⊥AB ,DG ⊥AB ,用含x 的代数式表示△ACO 和△BOD 的面积,便可得出函数解析式.(3)分OB ∥AD 和OA ∥BD 两种情况讨论. 【详解】解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB=8, ∴OD ⊥AB ,AC=12AB=4, 在Rt △AOC 中,∵∠ACO=90°,AO=5,∴,∴OD=5, ∴CD=OD ﹣OC=2;(2)如图2,过点O 作OH ⊥AB ,垂足为点H , 则由(1)可得AH=4,OH=3, ∵AC=x , ∴CH=|x ﹣4|,在Rt △HOC 中,∵∠CHO=90°,AO=5,∴∴CD=OD ﹣OC=5过点DG ⊥AB 于G , ∵OH ⊥AB , ∴DG ∥OH , ∴△OCH ∽△DCG , ∴OH OCDG CD=, ∴DG=OH CD OC ⋅35, ∴S △ACO =12AC ×OH=12x ×3=32x , S △BOD =12BC (OH +DG )=12(8﹣x )×(335)=32(8﹣x )∴y=ACO OBDS S=()323582x x-=()58x -(0<x <8)(3)①当OB ∥AD 时,如图3,过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F , 则OF=AE , ∴S=12AB•OH=12OB•AE , AE=AB OH OB ⋅=245=OF , 在Rt △AOF 中,∠AFO=90°,AO=5,∴AF=22AO OF -=75∵OF 过圆心,OF ⊥AD ,∴AD=2AF=145. ②当OA ∥BD 时,如图4,过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G ,则由①的方法可得DG=BM=245, 在Rt △GOD 中,∠DGO=90°,DO=5,∴GO=22DO DG -=75,AG=AO ﹣GO=185, 在Rt △GAD 中,∠DGA=90°,∴AD=22AG DG +=6综上得AD=145或6.故答案为(1)2;(2)()2825x x x -+(0<x <8);(3)AD=145或6.【点睛】本题是考查圆、三角形、梯形相关知识,难度大,综合性很强.10.已知:四边形ABCD 内接于⊙O ,∠ADC =90°,DE ⊥AB ,垂足为点E ,DE 的锯长线交⊙O 于点F ,DC 的延长线与FB 的延长线交于点G . (1)如图1,求证:GD =GF ;(2)如图2,过点B 作BH ⊥AD ,垂足为点M ,B 交DF 于点P ,连接OG ,若点P 在线段OG 上,且PB =PH ,求∠ADF 的大小;(3)如图3,在(2)的条件下,点M 是PH 的中点,点K 在BC 上,连接DK ,PC ,D 交PC 点N ,连接MN ,若AB =2,HM +CN =MN ,求DK 的长.【答案】(1)见解析;(2)∠ADF =45°;(3)1810. 【解析】【分析】 (1)利用“同圆中,同弧所对的圆周角相等”可得∠A =∠GFD ,由“等角的余角相等”可得∠A =∠GDF ,等量代换得∠GDF =∠GFD ,根据“三角形中,等角对等边”得GD =GF ; (2)连接OD 、OF ,由△DPH ≌△FPB 可得:∠GBH =90°,由四边形内角和为360°可得:∠G =90°,即可得:∠ADF =45°;(3)由等腰直角三角形可得AH =BH =12,DF =AB =12,由四边形ABCD 内接于⊙O ,可得:∠BCG =45°=∠CBG ,GC =GB ,可证四边形CDHP 是矩形,令CN =m ,利用勾股定理可求得m =2,过点N 作NS ⊥DP 于S ,连接AF ,FK ,过点F 作FQ ⊥AD 于点Q ,过点F 作FR ⊥DK 交DK 的延长线于点R ,通过构造直角三角形,应用解直角三角形方法球得DK .【详解】解:(1)证明:∵DE ⊥AB∴∠BED =90°∴∠A +∠ADE =90°∵∠ADC =90°∴∠GDF +∠ADE =90°∴∠A =∠GDF∵BD BD =∴∠A =∠GFD∴∠GDF =∠GFD∴GD =GF(2)连接OD 、OF∵OD =OF ,GD =GF∴OG ⊥DF ,PD =PF在△DPH 和△FPB 中PD PF DPH FPB PH PB =⎧⎪∠=∠⎨⎪=⎩∴△DPH ≌△FPB (SAS )∴∠FBP =∠DHP =90°∴∠GBH =90°∴∠DGF =360°﹣90°﹣90°﹣90°=90°∴∠GDF =∠DFG =45°∴∠ADF =45°(3)在Rt △ABH 中,∵∠BAH =45°,AB =∴AH =BH =12∴PH =PB =6∵∠HDP =∠HPD =45°∴DH =PH =6∴AD =12+6=18,PN =HM =12PH =3,PD = ∵∠BFE =∠EBF =45°∴EF =BE∵∠DAE =∠ADE =45°∴DE =AE∴DF =AB =∵四边形ABCD 内接于⊙O∴∠DAB +∠BCD =180°∴∠BCD =135°∴∠BCG =45°=∠CBG∴GC =GB又∵∠CGP =∠BGP =45°,GP =GP∴△GCP ≌△GBP (SAS )∴∠PCG =∠PBG =90°∴∠PCD =∠CDH =∠DHP =90°∴四边形CDHP 是矩形∴CD =HP =6,PC =DH =6,∠CPH =90°令CN =m ,则PN =6﹣m ,MN =m +3在Rt △PMN 中,∵PM 2+PN 2=MN 2∴32+(6﹣m )2=(m +3)2,解得m =2∴PN =4过点N 作NS ⊥DP 于S ,在Rt △PSN 中,PS =SN =DS =﹣=SN 1tanDS 2SDN ∠=== 连接AF ,FK ,过点F 作FQ ⊥AD 于点Q ,过点F 作FR ⊥DK 交DK 的延长线于点R在Rt △DFQ 中,FQ =DQ =12 ∴AQ =18﹣12=6∴tan 1226FQ FAQ AQ ∠=== ∵四边形AFKD 内接于⊙O ,∴∠DAF +∠DKF =180°∴∠DAF =180°﹣∠DKF =∠FKR在Rt △DFR 中,∵DF =1122,tan 2FDR ∠= ∴12102410,FR DR == 在Rt △FKR 中,∵FR =1210 tan ∠FKR =2 ∴KR =6105∴DK =DR ﹣KR =24106101810555=-= .【点睛】本题是一道有关圆的几何综合题,难度较大,主要考查了圆内接四边形的性质,圆周角定理,全等三角形性质及判定,等腰直角三角形性质,解直角三角形等知识点;解题关键是添加辅助线构造直角三角形.11.已知:如图,梯形ABCD 中,AD//BC ,AD 2=,AB BC CD 6===,动点P 在射线BA 上,以BP 为半径的P 交边BC 于点E (点E 与点C 不重合),联结PE 、PC ,设x BP =,PC y =.(1)求证:PE //DC ; (2)求y 关于x 的函数解析式,并写出定义域;(3)联结PD ,当PDC B ∠=∠时,以D 为圆心半径为R 的D 与P 相交,求R 的取值范围.【答案】(1)证明见解析;(2)2436(09)y x x x =-+<<;(3)3605R << 【解析】【分析】 ()1根据梯形的性质得到B DCB ∠=∠,根据等腰三角形的性质得到B PEB ∠∠=,根据平行线的判定定理即可得到结论;()2分别过P 、A 、D 作BC 的垂线,垂足分别为点H 、F 、.G 推出四边形ADGF 是矩形,//PH AF ,求得2BF FG GC ===,根据勾股定理得到22226242AF AB BF =-=-=,根据平行线分线段成比例定理得到223PH x =,13BH x =,求得163CH x =-,根据勾股定理即可得到结论; ()3作//EM PD 交DC 于.M 推出四边形PDME 是平行四边形.得到PE DM x ==,即 6MC x =-,根据相似三角形的性质得到1218655PD EC ==-=,根据相切两圆的性质即可得到结论.【详解】 ()1证明:梯形ABCD ,AB CD =,B DCB ∠∠∴=,PB PE =,B PEB ∠∠∴=,DCB PEB ∠∠∴=,//PE CD ∴;()2解:分别过P 、A 、D 作BC 的垂线,垂足分别为点H 、F 、G .梯形ABCD 中,//AD BC ,,BC DG ⊥,BC PH ⊥,∴四边形ADGF 是矩形,//PH AF ,2AD =,6BC DC ==,2BF FG GC ∴===,在Rt ABF 中,AF ===,//PH AF ,PH BP BH AF AB BF∴==62x BH ==,PH ∴=,13BH x =, 163CH x ∴=-, 在Rt PHC中,PC =y ∴=9)y x =<<, ()3解:作//EM PD 交DC 于M .//PE DC ,∴四边形PDME 是平行四边形.PE DM x ∴==,即 6MC x =-,PD ME ∴=,PDC EMC ∠∠=,又PDC B ∠∠=,B DCB ∠=∠,DCB EMC PBE PEB ∠∠∠∠∴===.PBE ∴∽ECM ,PB BE EC MC ∴=,即232663x x xx =--, 解得:185x =, 即125BE =, 1218655PD EC ∴==-=, 当两圆外切时,PD r R =+,即0(R =舍去); 当两圆内切时,-PD r R =,即10(R =舍去),2365R =;即两圆相交时,365R<<.【点睛】本题属于圆综合题,梯形的性质,平行四边形的性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.12.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);①求此抛物线的函数解析式;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,c=-4,求证:无论b取何值,点D的坐标均不改变.【答案】(1)①y=x2-x-4;②△BDM的面积有最大值为36;(2)证明见解析.【解析】试题分析:(1)①只需运用待定系数法就可解决问题;②过点M作ME∥y轴,交BD于点E,连接BC,如图1.根据勾股定理的逆定理可得∠ACB=90°,从而可得AB为直径,根据垂径定理可得OD=OC,即可得到D(0,4),然后运用待定系数法可求得直线BD的解析式为y=-x+4,设M(x,x2-x-4),则E(x,-x+4),从而得到ME=-x2+x+8,运用割补法可得S△BDM=S△DEM+S△BEM=-(x-2)2+36,然后根据二次函数的最值性就可求出△BDM 的面积的最大值;(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,可得C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,根据根与系数的关系可得OA•OB=4.由A、D、B、C四点共圆可得∠ADC=∠ABC,∠DAB=∠DCB,从而可得△ADO∽∽△CBO,根据相似三角形的性质可得OC•OD=OA•OB=4,从而可得OD=1,即可得到D(0,1),因而无论b取何值,点D的坐标均不改变.试题解析:(1)①∵抛物线y=ax2+bx+c过点A(-2,0),B(8,0),C(0,-4),∴,解得.∴抛物线的解析式为y=x2-x-4;②过点M作ME∥y轴,交BD于点E,连接BC,如图1.∵A(-2,0),B(8,0),C(0,-4),∴OA=2,OB=8,OC=4,∴AB=10,AC=2,BC=4,∴AB2=AC2+BC2,∴∠ACB=90°,∴AB为直径.∵CD⊥AB,∴OD=OC,∴D(0,4).设直线BD的解析式为y=mx+n.∵B(8,0),D(0,4),∴,解得,∴直线BD的解析式为y=-x+4.设M(x,x2-x-4),则E(x,-x+4),∴ME=(-x+4)-(x2-x-4)=-x2+x+8,∴S△BDM=S△DEM+S△BEM=ME(x E-x D)+ME(x B-x E)=ME(x B-x D)=(-x2+x+8)×8=-x2+4x+32=-(x-2)2+36.∵0<x<8,∴当x=2时,△BDM的面积有最大值为36;(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,则C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,∴OA•OB=-x1•x2=-(-4)=4.∵A、D、B、C四点共圆,∴∠ADC=∠ABC,∠DAB=∠DCB,∴△ADO∽△CBO,∴,∴OC•OD=OA•OB=4,∴4OD=4,∴OD=1,∴D(0,1),∴无论b取何值,点D的坐标均不改变.考点:圆的综合题13.如图1,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=13,BC=8.(1)求证:CF是⊙O的切线;(2)求⊙O的半径OC;(3)如图2,⊙O的弦AH经过半径OC的中点F,连结BH交弦CD于点M,连结FM,试求出FM的长和△AOF的面积.【答案】(1)见解析;(2)32332232【解析】【分析】(1)由DF=2OD,得到OF=3OD=3OC,求得13OE OCOC OF==,推出△COE∽△FOE,根据相似三角形的性质得到∠OCF=∠DEC=90°,于是得到CF是⊙O的切线;(2)利用三角函数值,设OE=x,OC=3x,得到CE=3,根据勾股定理即可得到答案;(3)连接BD,根据圆周角定理得到角相等,然后证明△AOF∽△BDM,由相似三角形的性质,得到FM为中位线,即可求出FM的长度,由相似三角形的性质,以及中线分三角形的面积为两半,即可求出面积.【详解】解:(1)∵DF=2OD,∴OF=3OD=3OC,∴13 OE OCOC OF==,∵∠COE=∠FOC,∴△COE∽△FOE,∴∠OCF=∠DEC=90°,∴CF是⊙O的切线;(2)∵∠COD=∠BAC,∴cos∠BAC=cos∠COE=13 OEOC=,∴设OE=x,OC=3x,∵BC=8,∴CE=4,∵CE⊥AD,∴OE2+CE2=OC2,∴x2+42=9x2,∴x2(负值已舍去),∴OC =3x =32,∴⊙O 的半径OC 为32;(3)如图,连结BD ,由圆周角定理,则∠OAF=∠DBM ,2AOF ADC ∠=∠,∵BC ⊥AD ,∴AC AB =,∴∠ADC=∠ADB ,∴2AOF ADC BDM ∠=∠=∠,∴△AOF ∽△BDM ;∵点F 是OC 的中点,∴AO :OF=BD :DM=2,又∵BD=DC ,∴DM=CM ,∴FM 为中位线,∴322, ∴S △AOF : S △BDM =(326 2 34=; ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯= ∴S △AOF =3424=32 【点睛】本题考查了圆的综合问题,圆周角定理,切线的判定和性质,相似三角形的判定和性质,利用勾股定理求边长,以及三角形中线的性质,解题的关键是熟练掌握所学的定理和性质,运用属性结合的思想进行解题.14.已知:ABC 内接于O ,过点B 作O 的切线,交CA 的延长线于点D ,连接OB .(1)如图1,求证:DAB DBC ∠=∠;(2)如图2,过点D 作DM AB ⊥于点M ,连接AO ,交BC 于点N ,BM AM AD =+,求证:BN CN =;(3)如图3,在(2)的条件下,点E 为O 上一点,过点E 的切线交DB 的延长线于点P ,连接CE ,交AO 的延长线于点Q ,连接PQ ,PQ OQ ⊥,点F 为AN 上一点,连接CF ,若90DCF CDB ∠+∠=︒,tan 2ECF ∠=,12ON OQ =,10PQ OQ +=求CF 的长.【答案】(1)详见解析;(2)详见解析;(3)10=CF【解析】【分析】(1)延长BO 交O 于G ,连接CG ,根据切线的性质可得可证∠DBC +∠CBG=90°,然后根据直径所对的圆周角是直角可证∠CBG +∠G=90°,再根据圆的内接四边形的性质可得∠DAB=∠G ,从而证出结论;(2)在MB 上截取一点H ,使AM=MH ,连接DH ,根据垂直平分线性质可得DH=AD ,再根据等边对等角可得∠DHA=∠DAH ,然后根据等边对等角和三角形外角的性质证出∠ABC=∠C ,可得AB=AC ,再根据垂直平分线的判定可得AO 垂直平分BC ,从而证出结论;(3)延长CF 交BD 于M ,延长BO 交CQ 于G ,连接OE ,证出tan ∠BGE=tan ∠ECF=2,然后利用AAS 证出△CFN ≌△BON ,可设CF=BO=r ,ON=FN=a ,则OE=r ,根据锐角三角函数和相似三角形即可证出四边形OBPE 为正方形,利用r 和a 表示出各线段,最后根据10PQ OQ +=a 和CF .【详解】解:(1)延长BO 交O 于G ,连接CG∵BD 是O 的切线∴∠OBD=90°∴∠DBC +∠CBG=90°∵BG 为直径∴∠BCG=90°∴∠CBG +∠G=90°∴∠DBC=∠G∵四边形ABGC 为O 的内接四边形∴∠DAB=∠G∴∠DAB=∠DBC(2)在MB 上截取一点H ,使AM=MH ,连接DH∴DM 垂直平分AH∴DH=AD∴∠DHA=∠DAH∵BM AM AD =+,=+BM MH BH∴AD=BH∴DH=BH∴∠HDB=∠HBD∴∠DHA=∠HDB +∠HBD=2∠HBD由(1)知∠DAB=∠DBC∴∠DHA=∠DAB=∠DBC∴∠DBC =2∠HBD∵∠DBC =∠HBD +∠ABC∴∠HBD=∠ABC ,∠DBC=2∠ABC∴∠DAB=2∠ABC∵∠DAB=∠ABC +∠C∴∠ABC=∠C∴AB=AC∴点A 在BC 的垂直平分线上∵点O 也在BC 的垂直平分线上∴AO 垂直平分BC∴BN CN =(3)延长CF 交BD 于M ,延长BO 交CQ 于G ,连接OE ,∵90DCF CDB ∠+∠=︒∴∠DMC=90°∵∠OBD=90°∴∠DMC=∠OBD∴CF ∥OB∴∠BGE=∠ECF ,∠CFN=∠BON ,∴tan ∠BGE=tan ∠ECF=2由(2)知OA 垂直平分BC∴∠CNF=∠BNO=90°,BN=CN∴△CFN ≌△BON∴CF=BO ,ON=FN ,设CF=BO=r ,ON=FN=a ,则OE=r∵12ON OQ = ∴OQ=2a∵CF ∥OB∴△QGO ∽△QCF∴=OG QO CF QF 即2122==++OG a r a a a ∴OG=12r 过点O 作OE ′⊥BG ,交PE 于E ′∴OE ′=OG ·tan ∠BGE=r=OE∴点E ′与点E 重合∴∠EOG=90°∴∠BOE=90°∵PB 和PE 是圆O 的切线∴∠OBP=∠OEP=∠BOE=90°,OB=OE=r∴四边形OBPE 为正方形∴∠BOE=90°,PE=OB=r∴∠BCE=12∠BOE==45° ∴△NQC 为等腰直角三角形∴NC=NQ=3a ,∴BC=2NC=6a在Rt △CFN 中,=∵PQ OQ ⊥∴PQ ∥BC∴∠PQE=∠BCG∵PE ∥BG∴∠PEQ=∠BGC∴△PQE ∽△BCG ∴=PQ PE BC BG即126=+PQ r r a r 解得:PQ=4a∵PQ OQ +=∴4a +2a=解得:∴=10【点睛】此题考查的是圆的综合大题,难度较大,掌握圆的相关性质、相似三角形的判定及性质、锐角三角函数、勾股定理、全等三角形的判定及性质、等腰三角形的判定及性质、正方形的判定及性质是解决此题的关键.15.如图,PA ,PB 分别与O 相切于点A 和点B ,点C 为弧AB 上一点,连接PC 并延长交O 于点F ,D 为弧AF 上的一点,连接BD 交FC 于点E ,连接AD ,且2180APB PEB ∠+∠=︒.(1)如图1,求证://PF AD ; (2)如图2,连接AE ,若90APB ∠=︒,求证:PE 平分AEB ∠;(3)如图3,在(2)的条件下,连接AB 交PE 于点H ,连接OE ,8AD =,4sin 5ABD ∠=,求PH 的长. 【答案】(1)见解析;(2)见解析;(3)257【解析】【分析】 (1)连接OA 、OB ,由切线的性质可得90OAP OBP ∠=∠=︒,由四边形内角和是360︒,得180∠+∠=︒P AOB ,由同弧所对的圆心角是圆周角的一半,得到2AOB ADB ∠=∠,等量代换得到ADB PEB ∠=∠,由同位角相等两直线平行,得到//PF AD ;(2)过点P 做PK PF ⊥交EB 延长线于点K ,由90APB ∠=︒得290PEB ∠=︒,从而45PEB ∠=︒,由切线的性质,得PA PB =,由PK PE ⊥,45PEK ∠=︒,得PE PK =,从而90APE EPB ︒∠=-∠,进而APE BPK ∠=∠,即可证得APE BPK ∆∆≌由此45K AEP ∠=∠=︒,得到AEP PEB ∠=∠,即可证得PE 平分AEB ∠;(3)连接AO 并延长交圆O 于点M ,连接OB 、OH 、OP 、OD 、DM ,由45ADE ∠=︒,90AED ∠=︒,可得DE AE =,由OA 、OD 为半径,可得OA OD =,即可证出DEO AEO ∆∆≌,由直径所对的圆周角是直角,可得90ADM ∠=︒,在Rt ADM ∆中,由正弦定义可得10AM =,由此5OA OB ==,由OAPB 为正方形,对角线AB 垂直平分OP ,从而,OH PH =.在Rt OAP ∆中,252OP OA ==延长EO 交AD 于K ,在Rt OEP ∆中,由勾股定理得7PE =,在Rt OEH ∆中,由勾股定理得257PH =.【详解】(1)连接OA 、OB∵PA 、PB 与圆O 相切于点A 、B ,且OA 、OB 为半径,∴OA AP ⊥,OB BP ⊥,∴90OAP OBP ∠=∠=︒,∴在四边形AOBP 中,360180180P AOB ∠+∠=︒-︒=︒,∵AB AB =,∴2AOB ADB ∠=∠,∴2180P ADB ∠+∠=︒,∵2180P PEB ∠+∠=︒,∴ADB PEB ∠=∠,∴//PF AD(2)过点P 做PK PF ⊥交EB 延长线于点K∵90APB ∠=︒,∴21809090PEB ∠=︒-︒=︒,∴45PEB ∠=︒,∵PA 、PB 为圆O 的切线,∴PA PB =,∵PK PE ⊥,45PEK ∠=︒,∴PE PK = ,∵9090APE EPB KPB EPB ︒︒∠=-∠=∠=-∠,∴APE BPK ∠=∠,∴APE BPK ∆∆≌,∴45K AEP ∠=∠=︒,∴AEP PEB ∠=∠,∴PE 平分AEB ∠;(3)连接AO 并延长交圆O 于点M ,连接OB 、OH 、OP 、OD 、DM。
立体几何压轴题

1. 如图,四棱锥P-ABCD中,底面ABC[为矩形,AB=8 AD=4 3,侧面PAD为等边三角形,并且与底面ABCD所成二面角为60(1)求四棱锥P-ABCD勺体积(2)证明PAL BD2、如图,长方体框架ABCD- A,B,C,D,,三边AB、AD、AA,的长分别为6、&3.6,AE与底面的对角线B,D,垂直于E。
(1)证明A,E BD ;(2)求AE的长n(2)若直线AM 与平面VAC 所成角为-,求三棱锥B-ACM 的体积 43、如图,已知。
O 的直径AB=3点C 为。
0上异于A , B 的一点,VC 1平面ABC, 且VC=2点M 为线段VB 的中点。
(1)求证:BC 丄平面VAC;4、如图,在多面体ABCDE中,四边形ABCD是正方形,AB=2EF=2 EF// AB, EF 丄FB,CF丄FB, BF=CF G为BC的中点,(1)求证:FG//平面BDE⑵求平面BDE与平面BCF所成锐二面角的大小;⑶求四面体B-DEF的体积。
5、如图,三棱锥P-ABC中,PC丄平面ABC PC=AC=2AB=BC D是PB上的一点, 且CD L平面PAB(1)求证AB丄平面PCB(2)求二面角C-PA-B的大小的余弦值。
仁BE7、如图,直二面角D-AB-E 中,四边形ABCD 是边长为2的正方形,AE=EB,F 为 CE上的点,且BF 丄平面ACE(1)求证AE!平面BCE(2)求二面角B-AC-E 的正弦值;(3)求点D 到平面ACE 的距离。
1.如图,四棱锥 P-ABCD 中,底面ABCD 为矩形,AB=8, AD=4. 3,侧面PAD 为等边三角形, 并且与底面ABCD 所成二面角为60°(3 )求四棱锥P-ABCD 的体积(4)证明 PA ^ BD解;< I )如园L ,5UD 的中点E ,连接FE ,则PE 丄舶)・所以NFEO 为側面P2D 与底面所成的二面角的平面角*所以PO3也,四複锥P-ABCD 的体积^P-ABCO=y x 8^443«343=96 ・迭二:如图2,连接込 延卡;L O 交BD 于点F.通过计算可得£0二4 AE=2^J )又知和二4於,A0=S -得 EO-ADAE AB朋以5.t AAEGcoRt A BAD - 得 ZEAO=ZABD-所以 ZIAO+ZADF=90°所BUF 丄BD ・因为直线AF 为頁线菲在平面圧CDF1的身剧,所以醐丄前. 2、如图,长方体框架 ABCD - A 'BC 'D ',三边 与底面的对角线 B ,D ,垂直于E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球体毛坯体积的最小值应为(
)
A.64
B.32
C.8 6
D.32 6
二.填空题(共2小题)
7(.2018?台州一模)如图,在直角梯形ABCD中,AB / /CD,ABC 90,
1
,
AB
AC
CD DA
2,动点M在边DC上(不同于D点),P为边AB上任意一
点,沿AM将
ADM翻折成
AD M,当平面AD M垂直于平面ABC时,线
在梯形ACEF中,由AF
CE
EF,可得AG
1,
2
由三角形ABC为直角三角形,且AB
1,BC
3,可得
BAC 60,
则BG
12
(1)2
2 1
1 1
3.
2
2
2
AGB
90,即BG
AC,则AC
平面GFB,
BFG为二面角B EF
A的平面角,
同理可得
DEH为二面角D
EF
C的平面角,
AC平 面B G F,AC
平面DHE,则 二 面 角B
BCD与平面ABC在
异侧与平面BCD与平面ABC在
同侧两类求解得答案.
【解答】 解:如图,设正四面体ABCD的棱长为2,过A作AO
底面BCD,
连接DO并延长,交BC于E,连接AE,可知
AEO为二面角A
的等腰三角形,且AC
2,
点D是AB的中点.将ACD沿CD折起,使得AC
BC,则此时直线BC与
平 面
A
C所 成 角 的 正 弦 值 为(
)
A.
6
B.3
C.2
D.1
3
3
3
3
6.(2017?浙江模拟)利用一个球体毛坯切削后得到一个四棱锥
P ABCD,其中
底面四边形ABCD是边长为
2的正方形,PA 4,且PA
CDBC,
即有CD平面ABC,
D.不是平面图形
BD,连接AD,CD,
,即可得到所求轨迹.
可得CD
BH,
BH AC,
即有BH
平面ACD,
则BH
DH,
在直角三角形BDH中,可得OH OB OD
r,
即有H的轨迹为以O为圆心,r为半径的圆.
故选:A.
第5页(共13页)
【点评】本题考查线面垂直的判定定理和性质定理的运用,考查动点的轨迹问题,
立体几何压轴题
一.选择题(共6小题)
1.(2018?浙江三模)在平面内,已知ABBC,过直线AB,BC分别作平面
,,使锐二面角AB为,锐二面角BC为,则平面与
33
平面所成的锐二面角的余弦值为()
1
B.
3
1
D.
3
A.
4
C.
4
4
2
2.(2018?温州二模)已知线段
AB垂直于定圆所在的平面,
B,
C是圆上的两
BG,DH,可得
BFG为二面角B
EF A的平面角,
DEH为二面角
D
EF
C的平面角,由AC
平面BGF,AC平面DHE,可得二面角
B
EF
D的平面角为BFG
DEH,进一步求得
BFG
DEH 90得
答案.
【解答】 解:如图,
第6页(共13页)
在等腰梯形ACEF中,过F作FG
AC于G,作EH
AC于H,
连接BG,DH,
上的射影,当C运动,点H运动的轨迹()
第4页(共13页)
A.是圆B.是椭圆C.是抛物线
【分析】 设定圆圆心为O,半径为r,连接OH,设直径
运用线面垂直的判定定理和性质定理,可得BHDH
【解答】 解:设定圆圆心为O,半径为r,
连接OH,设直径BD,连接AD,CD,
由AB平面BCD,
可得ABCD,
由直径所对圆周角为直角,可得
等基础知识,训练了二面角的平面的求法,考查运算求解能力,是中档题.
4.已知正四面体ABCD和平面,BC,当平面ABC与平面所成的二面
角为60,则平面BCD与平面所成的锐二面角的余弦值为()
A.2 6
1
B.2 23
C.2 6 1或2 23
6
6
6
6
第7页(共13页)
D.2 6
1或2
2
3
6
6
【分析】首先求出正四面体侧面与底面所成角,然后分平面
考查推理能力和空间想象能力,属于中档题.
3.如图,设矩形ABCD所在平面与梯形ACEF所在平面相交于AC,若AB1,
BC3,AFFEEC1,则下列二面角的平面角大小为定值的是(
)
A.F AB C
B.B EF D
C.A BF C
D.B AF D
【分析】在等腰梯形
ACEF中,过F作FG
AC于G,作EH
AC于H,连接
第1页(共13页)
4.(2017?浙江模拟)已知正四面体ABCD和平面 ,BC
,当平面ABC与
平面 所成的二面角为60,则平面BCD与平面
所成的锐二面角的余弦值
为(
)
A.2 6 1
B.2 2
3
C.2 6 1或2 2
3
6
6
6
6
D.2 6
1或2
23
6
6
5.(2017?浙江模拟)如图,已知ABC是顶角为C 120
点,H是点B在AC上的射影,当C运动,点H运动的轨迹(
)
A.是圆B.是椭圆C.是抛物线D.不是平面图形
3.(2018?浙江模拟)如图,设矩形ABCD所在平面与梯形ACEF所在平面相交
于AC,若AB1,BC3,AFFEEC1,则下列二面角的平面角大
小为定值的是()
A.FABCB.BEFDC.ABFCD.BAFD
段PD长度的最小值为.
第2页(共13页)
8.(2016?太原三模)在正方体ABCDA BC D中,E是棱CC的中点,F是侧
11111
面BCC1B1内的动点, 且A1F / /平面D1AE,则A1F与平面BCC1B1所成角的正
切值的取值范围是.
第3页(共13页)
立体几何压轴题
参考答案与试题解析
一.选择题(共
6小题)
1.在平面内,已知AB
BC,过直线AB,BC分别作平面
, ,使锐二面
角AB
为
,锐二面角
BC为
,则平面
与平面
所成的锐二
3
3
面角的余弦值为(
)
1
B.
3
1
D.
3
A.
4
C.
4
4
2
【 分 析 】 推 导 出 平 面与 平 面所 成 的 锐 二 面 角的 余 弦 值 为 :
cos
cos
cos
3
1.
3
4
【解答】 解:
在平面
内,AB
BC,过直线AB,BC分别作平面
,
,
使锐二面角
AB
为
,锐二面角BC
为
,
3
3
平面
与平面
所成的锐二面角
的余弦值为:
cos
coscos
1.
3
3
4
故选:A.
【点评】本题考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位
置关系,考查运算求解能力,考查函数与方程思想,是中档题.
2.已知线段AB垂直于定圆所在的平面,B,C是圆上的两点,H是点B在AC
EF
D的 平 面 角 为
B F G
D E.H
BGF与DHE均为等腰三角形,
BFG
180
BGF,DEH
180
DHE,
2
2
FG / / EH,GB / /HD,
BGF
DHE
180
,
BFG
DEH
360
(
BGF
DHE )
360
180
90
.
2
2
二面角BEFD为定值.
故选:B.
【点评】本题考查面面垂直的证明,考查空间中线线、线面、面面间的位置关系
