激光原理平行平面腔
激光原理与技术:第二章

➢光学谐振腔的种类:
谐振腔的开放程度: 闭腔、开腔、波导腔 开腔通常可以分为: 稳定腔、非稳定腔、临界腔 反射镜形状: 球面腔与非球面腔,端面反射腔与分
布反馈腔 反射镜的多少: 两镜腔与多镜腔(折叠腔、环形
r00
T
r00
共轴球面镜腔 往返传输矩阵:
L A 1
f2
C
1 f1
1 f2
1
L f1
B L 2
L f2
D
L f1
1
L f1
1
L f2
•往返矩阵T与光线的初始坐标参数r0和
轴光线在腔内往返传播的行为
0
无关,因而它可以描述任意近
例:
L 3 R2 4
g1
1
L R1
1;
g2
1
L R2
1 4
§2.1.3. 光学谐振腔的损耗,Q值及线宽
损耗的大小是评价谐振腔的一个重要指标,在激光振荡中, 光腔的损耗决定了振荡的阈值和激光的输出能量,也是腔 模理论的重要研究课题
➢光腔的损耗:
1. 几何损耗
选择性损耗、对不同模式,损耗不同
2. 衍射损耗 3. 腔镜反射不完全引起的损耗
非选择性损耗
4. 腔内介质不均匀引起的损耗
Q 2v R
Q
2v
R
2v
L'
C
❖腔的品质因数Q值是衡量腔质量的一个重要的物理量,它
表征腔的储能及损耗特征。
总之,腔平均单程损耗因子、光子寿命、与腔的品质因数三个 物理量之间是关联的,腔平均单程损耗因子越小,光子寿命越 长,腔的品质因数越高。
激光原理第二讲2012
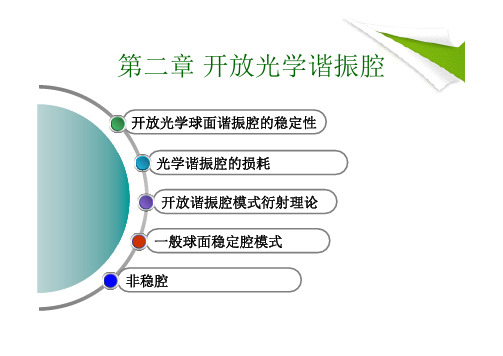
6.ABCD矩阵的应用-球面镜腔的往返矩阵 球面镜腔中往返一周的光线矩阵(简称往返矩阵)
⎛ r5 ⎞ ⎛ r1 ⎞ ⎜ ⎟ = T R1 T L T R 2 T L ⎜ ⎟ ⎝θ1 ⎠ ⎝θ5 ⎠ ⎛ r0 ⎞ ⎛ A B ⎞ ⎛ r0 ⎞ =T ⎜ ⎟ = ⎜ ⎟ ⎜θ ⎟ θ C D ⎠⎝ 0 ⎠ ⎝ 0⎠ ⎝
⎛A T =⎜ ⎝C
B⎞ ⎛ 1 ⎟ = ⎜− 2 D⎠ ⎜ R1 ⎝
0⎞⎛1 ⎟⎜ 1⎟⎝0 ⎠
L⎞⎛ 1 ⎟⎜− 2 1 ⎠⎜ R2 ⎝
0⎞⎛1 ⎟⎜ 1⎟⎝0 ⎠
L⎞ ⎟ 1⎠
A = 1−
2L R2 ⎞⎤ ⎟ ⎟⎥ ⎠⎦
⎛ L ⎞ ⎟ B = 2L⎜ 1 − ⎜ ⎟ R ⎝ 2 ⎠ ⎡2L ⎛ 2L D = −⎢ −⎜ 1 − ⎜ R R1 ⎝ 1 ⎣ ⎞⎛ 2L ⎟ ⎜ 1 − ⎟⎜ R2 ⎠⎝ ⎞⎤ ⎟ ⎟⎥ ⎠⎦
0
谐振腔损耗越小,腔内光子的平均寿命越长。
2.3.3 谐振腔的品质因数Q
谐振腔品质因数的定义:
ε Q = 2πν P ε为腔内储存的总能量,P为单位时间损耗的能量
设V为谐振腔的体积
ε = N (t )hν V dN ( t ) hν VN (t ) dε = − hν V = 单位时间消耗的能量 P = − dt dt τR L′ ⇒ Q = ωτ R = 2πν δc
1 讨论: φ = arccos ( A + D ) 2 1 ( A + D) 对于一定几何结构的球面腔是一个不变量,与光线 2 的初始坐标、出发位置及往返一次的顺序都无关
(1)
1 (A + D ) < 1 ⇒ φ 实数(≠kπ),An, Bn, Cn, Dn有界⇒ 稳定腔 2
激光原理第二章
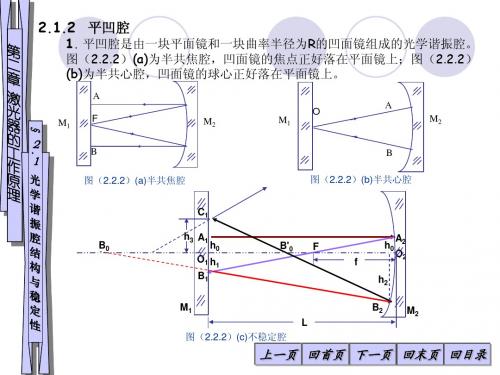
第 2.利用稳定条件可将球面腔分类如下: 二 章 (1) 稳定腔 激 双凹稳定腔,由两个凹面镜组成,对应图中l、2、3和4区 光 器 平凹稳定腔,由一个平面镜和一个凹面镜组成,对应图中AC、AD段 的 2 凹凸稳定腔,由一个凹面镜和一个凸面镜组成,对应图中5区和6区。 工 共焦腔,R1=R2=L,因而,g1=0,g2=0,对应图中的坐标原点。 作 1 原 光 半共焦腔,由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点。 理 学
(一)对称腔
1 2 第 而坐标原点O则代表R1=R2=L,即共焦腔;A点代表R1=R2→∞,即平行平面腔;B 二 代表R1=R2=L/2,即共心腔。 章 激 (二)长焦距非对称腔 光 在坐标系上 0 g1 1 和 0 g 2 1 的区域,这是第二类腔,即图中的第Ⅱ部分, 器 的 2 代表曲率半径大于腔长的非对称腔。其特点:R1≠R2;R1>L,R2>L 工 g2 1 作 (三)短焦距非对称腔 原 光 在坐标系上除去OB的整个 g 0 和 g 0 1 2 理 学
在坐标系上,直线线段BOA代表第一类腔(Ⅰ)---对称腔。其特点是:R =R =R。
谐 振 代表曲率半径小于腔长的非对称腔。其特点: R ≠R2;0<R1<L,0<R2<L,但必须满足 腔 1 结 R1+R2>L 构 (四)凹凸腔 与 坐标系上 g1 1、0 g 2 1 和 g 2 1、0 g1 1 稳 的区域代表第四类腔,即图中的第Ⅳ部分,它是 定 由一块R<0的凸面镜和一块R>L的凹面镜构成, 性
2.1.2 平凹腔 第 二 章 激 光 器 的 2 工 作 1 原 光 理 学
谐 振 腔 结 构 与 稳 定 性
1. 平凹腔是由一块平面镜和一块曲率半径为R的凹面镜组成的光学谐振腔。 图(2.2.2)(a)为半共焦腔,凹面镜的焦点正好落在平面镜上;图(2.2.2) (b)为半共心腔,凹面镜的球心正好落在平面镜上。
第二讲激光原理与选模

选频--- 反射镜镀上多层膜,膜厚度λ/4, 使反射最强,形成稳定振荡并不断加强,
得到单色性好的激光
第23页,此课件共41页哦
典型的激光器镜面的安装
谐振腔的种类:
平行平面腔 同心球面腔 共焦谐振腔 长半径球面腔 半球型谐振腔 平凹稳定腔 非稳定腔
原子在激发态的平均停留时间称之为激发态的寿命。
E3
E2
hv
E1
图1-2 自发辐射示意图
第10页,此课件共41页哦
自发辐射的特点: 这种过程与外界作用无关。各原子的辐射都是独立地进行。因
而所发光子的频率、初相、偏振态、传播方向等都不同。不同光波 列是不相干的。例如霓虹灯管内充有低压惰性气体,在管两端加上 高电压来激发气体原子,当它们从激发态跃迁返回基态时,便放出 五颜六色的光彩。其频率成分极为复杂,发光方向各向都有,初位 相也各不相同。这正是普通光源的自发辐射。
E1
第8页,此课件共41页哦
原子吸收 E3
E3
E2
E2
hv
E1
E1
图1-1 原子吸收示意图
如图1-1所示,有一个原子开始时处于基态E1,若不存在任何外来影响
,它将保持状态不变。如果有一个外来光子,能量为hv,与该原子发生相
互态作—用—。激且发态。则原子就有可,能其吸中收:h 这E2为一v 原光E 子子2 的, 某而E 一被1 较激高发的到能高量能状态
第5页,此课件共41页哦
该领域的有关诺贝尔奖
❖ 1964: Townes, Basov, 微波激射器和激光器的发明 ❖ 1971: Dennis Gabor, 激光全息术
❖ 1981: 洛.布隆姆贝根, 激光光谱学 ❖ 1997: 朱隶文等三人, 激光冷却和陷俘原子
激光产生基本原理

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载激光产生基本原理地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容激光基本原理一、激光产生原理1、普通光源的发光——受激吸收和自发辐射普通常见光源的发光(如电灯、火焰、太阳等地发光)是由于物质在受到外来能量(如光能、电能、热能等)作用时,原子中的电子就会吸收外来能量而从低能级跃迁到高能级,即原子被激发。
激发的过程是一个“受激吸收”过程。
处在高能级(E2)的电子寿命很短(一般为10-8~10-9秒),在没有外界作用下会自发地向低能级(E1)跃迁,跃迁时将产生光(电磁波)辐射。
辐射光子能量为hυ=E2-E1这种辐射称为自发辐射。
原子的自发辐射过程完全是一种随机过程,各发光原子的发光过程各自独立,互不关联,即所辐射的光在发射方向上是无规则的射向四面八方,另外未位相、偏振状态也各不相同。
由于激发能级有一个宽度,所以发射光的频率也不是单一的,而有一个范围。
在通常热平衡条件下,处于高能级E2上的原子数密度N2,远比处于低能级的原子数密度低,这是因为处于能级E的原子数密度N的大小时随能级E的增加而指数减小,即N∝exp(-E/kT),这是著名的波耳兹曼分布规律。
于是在上、下两个能级上的原子数密度比为N2/N1∝exp{-(E2-E1)/kT}式中k为波耳兹曼常量,T为绝对温度。
因为E2>E1,所以N2《N1。
例如,已知氢原子基态能量为E1=-13.6eV,第一激发态能量为E2=-3.4eV,在20℃时,kT≈0.025eV,则N2/N1∝exp(-400)≈0可见,在20℃时,全部氢原子几乎都处于基态,要使原子发光,必须外界提供能量使原子到达激发态,所以普通广义的发光是包含了受激吸收和自发辐射两个过程。
激光原理第二章 激光器的工作原理
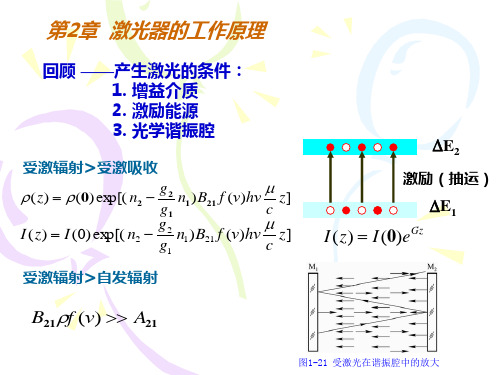
可以证明,在对称共焦腔内,任意傍轴光线可往返多次
而不横向逸出,而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上,因此,对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞,g1=g2=1, g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔,由一个凹面镜和一个凸面镜组成,对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔,R1=R2=L,因而,g1=0,g2=0,对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔,由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1,g2=1/2
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转? 粒子数反转和什么因素有关?
速率方程方法: 量子理论的一种简化形式
——速率方程理论:把光频电磁场看成量子化的光子,把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且:
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性,并粗略描 述烧孔、兰姆凹陷、多模竞争等效应
激光原理教学大纲

《激光原理》课程教学大纲课程代码:090631009课程英文名称:PrinciplesofLaser课程总学时:48讲课:48实验:0上机:适用专业:■■■■■■■■■大纲编写(修订)时间:2017.10一、大纲使用说明(一)课程的地位及教学目标本课程是光电信息科学与工程专业的必修主干专业基础课程,主要讲授有关激光的基本知识和基本理论,在光电信息科学与工程专业培养计划中,它起到由专业基础理论课向专业课过渡的承上启下的作用。
本课程在教学内容方面除基本知识、基本理论的教学外,还通过课程设计培养学生的理论分析及其实际应用能力。
通过本课程的学习,可以使学生:1.掌握激光的概念及产生原理、光学谐振腔理论、速率方程理论、激光器的特性及其控制和改善的原理。
了解激光技术新的发展和应用;2.具有综合运用数学、物理等学科知识对实际与激光有关的问题进行理论分析的能力;3.获得初步的激光器件设计技能,为后续课程的学习以及相关课程设计、毕业设计等奠定重要的基础。
(二)知识、能力及技能方面的基本要求1.知识方面的基本要求通过本科程的学习,使学生掌握:激光的概念、特性及产生原理;激光器的构成及工作原理;光学谐振腔与高斯光束知识;光与物质的共振相互作用的速率方程理论;激光的振荡特性、放大特性及其特性的控制和改善知识。
2.能力方面的基本要求通过本科程的学习,培养学生:光学谐振腔分析能力及其初步设计能力;激光器的振荡特性、放大特性的分析能力;激光器特性的控制与改善的初步设计能力。
3.技能方面的基本要求通过本课程的学习,使学生获得:光学谐振腔设计的初步技能;激光器特性的控制与改善的初步的理论设计能力。
(三)实施说明1.教学方法:课堂中要重点突出对基本概念和基本原理的讲解;采用启发式教学,培养学生思考问题、分析问题和解决问题的能力;引导学生主动思考,提高学生的自学能力;鼓励学生参与讨论和课堂发言,调动学生学习的积极性;教学中注意理论联系实际,培养学生的工程意识(创新、实践、安全、标准、竞争、法律和管理等意识)和工程能力(思维、自学、研究、操作和创造能力等)。
激光原理第6章平行平面腔

平行平面腔是历史上最早被采用的,如世界上第一台 红宝石激光器就是用的平行平面腔,平行平面腔的优点是, 光束方向性好,模体积大,容易获得单横模振荡。缺点是 调整精度要求很高,属于非稳腔,衍射损耗、几何损耗都 比较大。因此,小增益激光器不适用平行平面腔,目前, 平行平面腔在中等以上功率的激光器中仍有普遍应用。平 行平面腔的自再现模积分方程至今尚未得到精确的解析解, 可用迭代法对积分方程做数值计算,其结果用图表反映。 本章介绍条形、方形、圆形镜面的平行平面腔的积分方程 解法以及模式特征。
umn (x, y)e 2L e 2L dxdy 3
2、变量分离 mn=mn umn(x,y)=um(x)un(y)
mum
(x)
nun (y)
ieikL
L
a
ik (xx)2
a um (x)e 2L dx
ieikL
L
a
ik (y y)2
a un (y)e 2L dy
二、求解方法——迭代法(为了简化,考虑一维条形腔)
程衍射损耗率应由下式计算
F F F
mn
m
n
m(F)与n(F)分别为菲涅尔数为F的条形
腔的m和n阶模的单程衍射损耗。
10
§2 圆形镜平行平面腔
一、积分方程的简化形式
1、变量未分离
(r cos r cos )2 (r sin r sin )2 L2
r 2 r2 2rr(cos cos sin sin ) L2
x
(x x)2 (y y)2 L2
x
z (x,y)
L[1
x
x
2
y
y
2
1
]2
L
L L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c q 2L
(横模参数的影响可忽略)
§2 圆形镜平行平面腔
一、积分方程的简化形式
1、变量未分离
(r cos r cos ) 2 (r sin r sin ) 2 L2
r 2 r2 2rr(cos cos sin sin ) L2
第六章 平行平面腔 §1 方形镜平行平面腔 一、积分方程的简化形式 y 1、变量未分离
( x x) 2 ( y y) 2 L2
2 2
(x,y)
x
y
x z (x,y)
x x y y 1 L[1 ]2 L L
e
( y y ) 2 ik 2L
dxdy
2、变量分离
mn=mn
ikL
umn(x,y)=um(x)un(y)
( x x) 2 ik 2L
ie m u m (x) L ie n u n ( y) L
a
a a
u m ( x)e u n ( y)e
dx
ikL
( y y ) 2 ik 2L
a
dy
二、求解方法——迭代法 1、步骤
(1)选取初始场u1(x) (2)计算u2(x), 并进行归一化,即令|u2(x)|max=1 (3)依次计算u3(x)、u4(x)…,直至达到稳态分布
2、初始场分布函数的选取
(1)基模TEM0
u0(x)= +1 0 +1 -1 0 -a<x<a 其它 0<x<a -a<x<0 其它 F为奇数
2、场相位分布
(1)镜面中心处近似为等相位面,F越大近似性越好
(2)边缘处相位比中心处滞后 (3)相位分布曲线有起伏,F越大起伏越多
3、单程衍射损耗率
(1)同一横模,菲涅耳数F越大,损耗率越小 (2)菲涅耳数F相同时,模的阶次越高,损耗率越大
1 0.1 0.01 TEM1 TEM0 0 1 10 100
a
1
x
0 -a 1 x a
(2)一阶模TEM1 u1(x)=
三、自再现模特征 1、场振幅分布
(1)从镜面中心到边缘,振 幅逐渐减小,腔菲涅耳数 F越大,边缘处相对振幅 越小(F大,镜面尺寸大,光 场分布的均匀性差)
0 -a -1
u(x)
F为偶数 x
0
(2)相对振幅对场点坐 标x的变化呈偶对称
(3)振幅曲线有起伏,菲涅耳数F越大,起伏越多(从 镜面中心到边缘,F数的奇偶性交替变化) (4)菲涅耳数F为偶数时,镜面中心振幅为极小值,反 之为极大值(镜面中心的F为偶数时,光场互相抵消)
2
r r2 2rr cos ( ) 1 2 L[1 ] L2 r 2 r2 2rr cos ( ) L 2L
(r,)
(r,)
L
r 2 r2 rr cos ( ) ik[ ] 2L L
z
ie mn u mn (r ,) L
ikL
a
2
0 0
u mn (r,)e
rdrd
2、变量分离方法 二、自再现模特征
umn(r,)=Rmn(r)e-im
同方形镜
2 2
L
1 x x 1 y y ( x x ) 2 ( y y) 2 L[1 ] L 2 L 2 L 2L 2L
ie mn u mn ( x , y) L
ikL
u
mn
( x, y)e
( x x) 2 ik 2L
