费米-狄拉克分布和玻色-爱因斯坦分布的简单推导
费米狄拉克分布函数解析图像和应用

费米狄拉克分布函数解析图像和应用文件管理序列号:[K8UY-K9IO69-O6M243-OL889-F88688]各能级被电子占据的数目服从特定的统计规律这个规律就是费米-狄拉克分布规律。
一般而言,电子占据各个能级的几率是不等的。
占据低能级的电子多而占据高能级的电子少。
统计物理学指出,电子占据能级的几率遵循费米的统计规律:在热平衡...状态下,能量为E 的能级被一个电子占据的几率为: f(E)称为电子的费米(费米-狄拉克)分布函数,k 、TE fermi 称为费米能级,它与物质的特性有关。
只要知道了费米能级E fermi 的数值,在一定温度下,电子在各量子态上的统计分布就完全确定了。
费米分布函数的一些特性:【根据f(E)公式来理解】第一,费米能级E fermi 是一种用来描述电子的能级填充水平的假想能级....,E f 越大,表示处于高能级的电子越多;E f 越小,则表示高能级的电子越少。
(E f 反映了整体平均水平)第二,假定费米能级E f 为已知,则f(E)f(E)式可画出f(E)的曲线如图所示,但要注意因变量f(E)不像普通习惯画在纵轴,而是破天荒的画在横轴。
的能级都空着。
因而费米能级E f 是在绝对零度时电子所具有的最大能量,是能级在绝对零度时能否被占据的一个界限,因而它是一个很重要的参数。
费米分布函数变化曲线T 3>T 2>T 1>T 0第五,在T≠0K时即不处于绝对零度的前提下,若E-E f>5kT,则f(E)<0.007;在T≠0K 前提下,若E-E f<-5kT,则f(E)>0.993。
(k、T分别为波耳兹曼常数和绝对温度)可见,温度T高于绝对零度的前提下,能量比E f高5kT的能态被电子占据的几率只有0.7%,几率很小,能级几乎是空的;而能级比E f低5kT的能态被电子占据的几率是99.3%,几率很大,该能级范围几乎总有电子。
一般可以认为,在T不为绝对零度但也不很高时,能量小于E f的能态基本上为电子所占据,能量大于E f的能态基本上没有被电子占据;而电子占据费米能级E f这个能级的概率是(不论任何温度下)都是1/2。
量子力学 公式

量子力学公式
量子力学中的一些常见公式包括:
1. 薛定谔方程式:描述了量子物理学的宏观世界,即微观粒子如何随着时间的推移而演变。
其一般形式为:iℏ∂Ψ/∂t=HΨ,其中i是虚数单位,ℏ是普
朗克常数的约化常数,Ψ是波函数,H是哈密顿算符。
2. 波粒二象性:描述了物质粒子的波动性质和粒子性质之间的相互作用关系。
其表达式为λ=h/p,其中λ是波长,h是普朗克常数,p是粒子的动量。
3. 测量理论:物理量的测量和观测结果有一定的概率性和不确定性。
测量理论采用概率统计的方法来描述这种不确定性。
最常见的公式是海森堡不确定性原理:ΔxΔp≥h/4π,其中Δx和Δp分别表示位置和动量的不确定度,h 是普朗克常数。
4. 费米-狄拉克统计和玻色-爱因斯坦统计:描述了物质粒子的统计行为。
费米-狄拉克统计用于描述费米子(如电子、质子等)的行为,玻色-爱因斯坦统计用于描述玻色子(如光子、声子等)的行为。
5. 波函数的复共轭:Ψ^(r,t)。
6. 归一化条件:∫Ψ(r,t)^2d3r=1。
7. 位置算符:x。
8. 动量算符:-iℏ∇。
9. 能量算符:iℏ∂/∂t。
10. 完备性条件:∫ψn^(r)ψm(r)d3r=δnm。
以上公式仅供参考,如需更准确的信息,建议查阅量子力学相关的书籍或咨询专业人士。
玻色统计和费米统计+ppt

f (ε) =
称为费米函数。在固体物理学中,化学势称为费 称为费 称为费米函数。在固体物理学中, 费米函数 米能级, 表示。 米能级,用ε F表示。 ),此时 当T→0 K时(费米能级ε F(0)),此时 → 时 ),此时1/kT→∞ , →∞ 由上式得到
ωl
al
=
1 e
(ε -) kT
+1
f (ε ) = 1 , 当 ε ≤ ε F (0) 时; f (ε ) = 0 , 当 ε > ε F (0) 时.
U (ν , T ) 8πhν dν ρ ν ( T ) dν = dν = V c 3 e hν / kT 1
3
6
利用λν = c 和 dν = 上式化为
cdλ
λ
2
并考虑 ρν dν = ρλ dλ
ρ λ (T ) =
8 πhc
λ
5
(
1 e
hc / λ kT
1
)
将上式代入单色辐出度Mλ (T ) ,将Mλ (T) 改为 将上式代入单色辐出度 Mλ 0 (T),得到 ,
f 1 1/2 /
o
2
εF(0)
3 5π kT 2 U(T) = Nε F (0)[1 + ( ) ] 5 12 ε F (0)
19
N是系统内自由电子总数。 是系统内自由电子总数。 是系统内自由电子总数
18
处于ε F(0) 附近能态的电子和低能态的电子情 附近、 况不同 ,只有在εF(0)附近、数量级为 能量范 附近 数量级为kT 围内的能态占据情况才会发生变化 , 其余绝大 多数能态的占据实际上并不改变,如图所示。 多数能态的占据实际上并不改变,如图所示。 对自由电子热容有贡献 的也是处于εF(0)附近能态 附近能态 的电子。 的电子。 自由电子气体系统的内 能用εF (0)可表示为 可表示为
费米统计和玻色统计
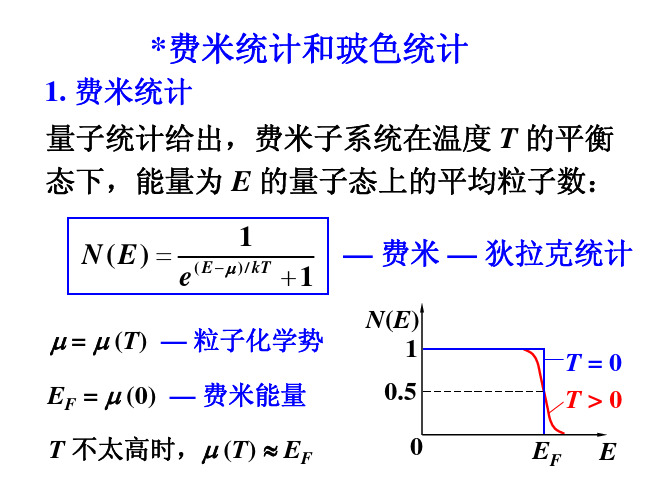
1. 费米统计 量子统计给出,费米子系统在温度 T 的平衡 态下,能量为 E 的量子态上的平均粒子数:
N (E) = 1 e
( E − μ ) / kT
+1
— 费米 — 狄拉克统计
N(E) 1 0.5 0 EF
μ = μ (T) — 粒子化学势
EF = μ (0) — 费米能量 T 不太高时,μ (T) ≈ EF
±1
≈e
− ( E − μ ) / kT
=e
μ / kT
⋅e
− E / kT
= A(T )e − E / kT
— 麦克斯韦 — 玻耳兹曼统计 所以高能态时,量子统计就过渡到经典的 麦克斯韦 — 玻耳兹曼统计。
Hale Waihona Puke 2. 玻色统计 量子统计给出,玻色子系统在温度 T 的平衡 态下,能量为 E 的量子态上的平均粒子数:
N (E) = 1 e ( E − μ ) / kT − 1
— 玻色 — 爱因斯坦统计 对所有温度 T ,N(E) 应满足 0 ≤ N(E) < ∞ , 由此可引出玻色 — 爱因斯坦凝聚的概念。
设最低能级(基态)为能量零点:E0 = 0, 1 N 0 = N ( E 0 ) = − μ / kT e −1 T → 0K 时,要求 0 ≤ N0 < ∞ , 则有 μ < 0 。
原子速度分布逐渐达到BEC的三维示意图 1995年实现了超冷原子的BEC,达到了宏观数量的 原子处于同一量子态(2001 Nobel)。 BEC实现了 原子相干,可做成原子干涉仪和量子频标等。
3. 量子统计到经典统计的过渡 当 E 很高时,(E−μ) >> kT
N (E) = 1 e
说明玻尔兹曼系统玻色子系统费米子系统的区别

说明玻尔兹曼系统玻色子系统费米子系统的区别玻尔兹曼系统和玻色子系统以及费米子系统是统计力学中的三种重要模型。
它们描述了微观粒子在宏观尺度上的行为。
本文将逐步阐述玻尔兹曼系统、玻色子系统和费米子系统的区别。
1.玻尔兹曼系统:玻尔兹曼系统是一种描述粒子统计行为的模型。
在玻尔兹曼系统中,粒子可以以任意数量存在于相同的量子态。
这意味着多个粒子可以处于相同的能量状态,也就是说,它们之间没有排斥效应。
玻尔兹曼系统中的粒子是无标识的,它们之间是可以交换的。
2.玻色子系统:玻色子系统描述了玻色子的统计行为。
玻色子是一类具有整数自旋的粒子,例如光子、声子等。
玻色子系统中,多个粒子可以同时处于相同的能量状态,它们之间没有排斥效应。
这种行为被称为玻色-爱因斯坦统计。
玻色子系统的一个重要特点是它们会聚集到基态,即粒子会尽可能地集中在能量最低的状态。
3.费米子系统:费米子系统描述了费米子的统计行为。
费米子是一类具有半整数自旋的粒子,例如电子、质子等。
费米子系统中,根据泡利不相容原理,每个能级只能有一个粒子占据,它们之间存在排斥效应。
这种行为被称为费米-狄拉克统计。
费米子系统的一个重要特点是它们填充能级从低到高,直到达到所谓的费米能级。
根据以上的描述,可以总结出玻尔兹曼系统、玻色子系统和费米子系统的区别:1.统计行为:玻尔兹曼系统中粒子之间无排斥效应,玻色子系统中多个粒子可以处于相同的能级,费米子系统中每个能级只能有一个粒子占据。
2.粒子类型:玻尔兹曼系统中的粒子是无标识的,玻色子系统中的粒子具有整数自旋,费米子系统中的粒子具有半整数自旋。
3.基态分布:玻色子系统会聚集到能量最低的状态,费米子系统填充能级从低到高。
4.波尔茨曼系统、玻色子系统和费米子系统在实际应用中有着不同的物理特性和行为模式。
综上所述,玻尔兹曼系统、玻色子系统和费米子系统在统计行为、粒子类型、基态分布等方面存在着明显的区别。
这些模型在研究微观粒子的统计性质和宏观行为时提供了重要的理论基础和工具,对于理解物质的性质和行为具有重要意义。
热力学与统计物理学第七章 量子统计

2
§7.1 玻色子和费米子
自然界中的所有粒子,按照交换全同粒子时它们波 函数的行为,能被分类为以下两组中的一个。
玻色自 子旋 :为(n整 0数 ,1,2,),波函数具有对称性 费米自 子旋 :为半 (n整 1数 ,3,),波函数具有反对
第七章:量子统计
动机和目标 一、 玻色子和费米子 二、量子分布律 三、理想费米气体 四、理想玻色气体
小结和习题课
1
经典统计的不足: 1)同种物质的粒子可以编号加以区别,从而 带来了体系微观状态数增多的弊端; 2)相格的大小是人为引入的; 3)粒子能量是连续的,在计算双原子分子气 体热容量在低温与实验不符。
5.0
4.5
4.0
3.5
3.0
2.5 2.0 Maxwell-Boltzmann
Bose-Einstein
1.5
1.0
0.5 Fermi-Dirac
0.0
-3
-2
-1
0
1
2
3
16
()/k T B
N0 /g jj
7.2.3 量子统计向经典统计过渡的条件
当满足稀薄气体条件:
N
0 i
gi,
即在量子统计分布中
小结和习题课
8
§7. 2 费米-狄拉克分布和玻色-爱因斯坦分布
一、量子统计的出发点
设一个系统i(的 i0能 ,1,2, 级 ),为 能i上 级有 gi个 量子态, N个现 粒有 子按单0粒 ,1,子 2, 的 能级
一种{分 Ni}配 {N0,N1,N2, }
二、量子系统的微观态数 1)费米系统的微观态数
天津市考研物理学复习资料统计物理基础知识梳理

天津市考研物理学复习资料统计物理基础知识梳理统计物理学是物理学中的一个重要分支,研究的对象是物质的宏观统计性质以及宏观物理量的统计规律。
在天津市考研中,统计物理学作为物理学的一门必修课程,对于学生们来说是一个重要的复习内容。
本文将为大家梳理天津市考研物理学复习资料中的统计物理学的一些基础知识,希望对大家复习有所帮助。
一、热力学基础概念1. 系统和环境在热力学中,我们将要研究的对象称为系统,而与系统有能量和物质交换的外部部分则称为环境。
2. 状态量和过程量热力学中,状态量是指与系统的状态有关的物理量,如温度、压力等;而过程量则是指与系统的状态变化有关的物理量,如热量、功等。
3. 平衡态和非平衡态平衡态是指系统处于稳定状态,各个宏观性质保持不变;非平衡态则是指系统处于不稳定状态,各个宏观性质处于变化过程中。
二、统计物理学基本框架统计物理学的基本框架是建立在微观粒子的运动规律上的。
通过统计物理学的方法,我们可以将宏观物理量与微观粒子的动力学联系起来。
1. 经典统计物理学经典统计物理学适用于宏观物理系统,其中的粒子之间的相互作用是经典力学描述的。
通过经典统计物理学,我们可以计算出宏观物理量的统计规律,如分子平均速度、能量分布等。
2. 量子统计物理学量子统计物理学适用于微观粒子系统,其中的粒子之间的相互作用是量子力学描述的。
通过量子统计物理学,我们可以计算出微观粒子系统的物理量统计规律,如费米子和玻色子的分布等。
三、热力学基本定律热力学是研究能量转化和宏观性质变化的学科,其基本定律为热力学第一定律和热力学第二定律。
1. 热力学第一定律热力学第一定律也称为能量守恒定律,它指出能量的变化等于系统对外界做功和从外界吸收的热量之和。
2. 热力学第二定律热力学第二定律也称为熵增定律,它指出孤立系统的熵总是不会减小,而在实际过程中总是增大或保持不变。
四、统计物理学中的分布律统计物理学中有几个重要的分布律,它们可以用于描述微观粒子在宏观物理系统中的分布情况。
热力学中统计力学的数学基础

热力学中统计力学的数学基础统计力学是连接微观世界与宏观现象之间的重要桥梁。
通过统计方法,统计力学能够从大量粒子的行为中推导出热力学的基本定律和性质。
本文将重点讨论热力学中统计力学的数学基础,包括主要概念、相关数学工具及其在热力学中的应用。
一、统计力学的基本概念1.1 微观状态与宏观状态在统计力学中,物质的微观状态是描述该系统中粒子位置和动量的详细信息。
每一个微观状态都可以看作是系统的一种可能的排列组合,系统可以通过不同方式达到这些排列。
而宏观状态则是指一组微观状态所对应的宏观性质,如温度、压强和体积等。
这两个层面之间的关系是统计力学研究的核心。
1.2 配分函数配分函数是统计力学中的重要工具,用于计算系统的热力学性质。
对于一个包含粒子数量为N的系统,配分函数Z定义为所有可能微观状态能量E_i的指数形式:[ Z = _{i} e^{-E_i/(kT)} ]其中 ( k ) 是玻尔兹曼常数,( T ) 是绝对温度。
配分函数不仅可以帮助我们获得内能、熵等热力学量,还能反映出系统的概率分布特征。
二、概率论与统计分布2.1 概率分布在统计力学中,研究系统时常涉及概率分布。
最常用的几种分布包括:麦克斯韦-玻尔兹曼分布:用于描述气体分子的速度分布,适用于经典气体。
费米-狄拉克分布:适用于费米子,如电子和质子。
玻色-爱因斯坦分布:用于描述玻色子,如光子和声子。
这些概率分布为我们提供了理解不同微观粒子行为的重要框架。
2.2 大数法则与中心极限定理大数法则说明当样本容量趋向于无穷大时,样本均值趋近于总体均值。
中心极限定理则指出,不论原始数据的分布形式如何,只要样本数量足够大,样本均值会呈现正态分布。
这些理论在统计力学中非常重要,因为它们使我们能够基于有限数量粒子的行为推测整个系统的性质。
三、热力学中的重要量3.1 内能与亥姆霍兹自由能内能 ( U ) 是描述系统微观粒子总能量的重要量。
在配分函数的帮助下,我们可以通过以下公式计算内能:[ U = - ]其中 ( = )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
万方数据
万方数据
万方数据
费米-狄拉克分布和玻色-爱因斯坦分布的简单推导
作者:佘守宪, 唐莹, She Shouxian, Tang Ying
作者单位:北方交通大学,物理系,北京,100044
刊名:
物理与工程
英文刊名:PHYSICS AND ENGINEERING
年,卷(期):2001,11(2)
被引用次数:2次
1.陈仁烈统计物理引论 1979
2.马本堃热力学与统计物理 1983
1.陶冶费米面系统热力学性质的±5kT能级宽度修正[期刊论文]-重庆文理学院学报(自然科学版) 2009(4)
2.张连水.刘凤良.党伟.王百荣脉冲放电等离子体电子激发温度发射光谱诊断[期刊论文]-河北大学学报(自然科学版) 2009(3)
本文链接:/Periodical_wlygc200102004.aspx。
