热力学习题课
合集下载
2016第十章 热力学习题课

第 九 章 气 体 动 理 论
m i 3 E RT 10 8.311 124.7( J ) M 2 2
Q E W 124.7 209 84.3(J )
31
普 通 物 理 教 程
第十章 热力学习题
6. 一定量的某种理想气体在等压过程中对外作 功为 200 J.若此种气体为单原子分子气体 ,则该过程中需吸热___________ J;若为 双原子分子气体,则需吸热___________ J. 【分析与解答】
第 九 章 气 体 动 理 论
1
普 通 物 理 教 程
第十章 热力学习题
【分析与解答】 m i 因为 QV R T
M 2
第 九 章 气 体 动 理 论
m pV = RT M
氧气和水蒸气的自由度不同,吸收热量相等 则温度升高不同,压强增加亦不同。 正确答案是B。
,
2
普 通 物 理 教 程
第十章 热力学习题
WN2 WHe
p(V2 V1 ) TN2 5 p(V2 V1 ) THe 7
正确答案是B。
10
普 通 物 理 教 程
第十章 热力学习题
6. 一定量的理想气体,由初态a经历a c b过程到达终态b(如 图10-19示),已知a、b两状态处于同一条绝热线上,则 ______. (A)内能增量为正,对外作功为正,系统吸热为正。 (B)内能增量为负,对外作功为正,系统吸热为正。 (C)内能增量为负,对外作功为正,系统吸热为负。 (D)不能判断。
内能增加了ΔE = | W2 |
E = ;
Q=
第 九 章 气 体 动 理 论
29
普 通 物 理 教 程
第十章 热力学习题
热力学习题课

A.< ', Q< Q ' ; √B.< ', Q> Q ' ; C.>', Q< Q ' ; D.>', Q>Q ' ;
27
例20. 双原子分子气体 1 mol 作图示曲 线 1231 的循环过程。其中1-2 为直线过程, 2-3 对应的过程方程为 PV1/2=常数, 3-1 对应的是等压过程。
九、卡诺循环:
P
T1 1 T2 P T1
T1
1 e T1 1
T2
T2
V
十、热力学第二定律:
文字表述:
开氏表述:功 热转化不可逆
克氏表述:热 传导不可逆
T2
V
等价。
7
数学表述:S kn (玻氏熵公式)
热力学第二定律的实质:一切与热现象有 关的实际宏观过程都是不可逆的。
无摩擦的准静态过程才是可逆的
例9.一定量的理想气体,其状态改变在P-T图 上沿着一条直线从平衡态a到b。这是一个()
P
A.绝热压缩过程
P2
b
B.等体吸热过程
P1
a
C.吸热压缩过程
T1
T2
T √D.吸热膨胀过程 19
例10:判断下列图1-2-3 -1各过程中交换 的热量, 内能的变化,作功的正负? 并画 出在 p - V 图上对应的循环过程曲线。
Mi
E
RT
Mmol 2
Mi
E
RT
Mmol 2
1
四、准静态过程,系统对外做的功:
dW PdV W V2 PdV V1
P
P
W0
0 V1
V2
W0
27
例20. 双原子分子气体 1 mol 作图示曲 线 1231 的循环过程。其中1-2 为直线过程, 2-3 对应的过程方程为 PV1/2=常数, 3-1 对应的是等压过程。
九、卡诺循环:
P
T1 1 T2 P T1
T1
1 e T1 1
T2
T2
V
十、热力学第二定律:
文字表述:
开氏表述:功 热转化不可逆
克氏表述:热 传导不可逆
T2
V
等价。
7
数学表述:S kn (玻氏熵公式)
热力学第二定律的实质:一切与热现象有 关的实际宏观过程都是不可逆的。
无摩擦的准静态过程才是可逆的
例9.一定量的理想气体,其状态改变在P-T图 上沿着一条直线从平衡态a到b。这是一个()
P
A.绝热压缩过程
P2
b
B.等体吸热过程
P1
a
C.吸热压缩过程
T1
T2
T √D.吸热膨胀过程 19
例10:判断下列图1-2-3 -1各过程中交换 的热量, 内能的变化,作功的正负? 并画 出在 p - V 图上对应的循环过程曲线。
Mi
E
RT
Mmol 2
Mi
E
RT
Mmol 2
1
四、准静态过程,系统对外做的功:
dW PdV W V2 PdV V1
P
P
W0
0 V1
V2
W0
热力学习题课
解:状态函数变化与过程无关,三个过程有相同答案。 状态函数变化与过程无关,三个过程有相同答案。
∆U = 0
∆H = 0
p2 p1
∆S =− nR ∫ (dp / p ) = − nR ln( p2 / p1 )
= [−2 × 8.3145 × ln( 0.1 / 1)]J ⋅ K −1 = 38.29J ⋅ K −1
∆S − ∫ δQ/ T = 0
(b)
∆U = W
o nCV ,m (T2 − T1 ) = − p外 (V2 − V1 )
n( 3 R / 2)(T2 − T1 ) = − p外 nR(T2 / p2 − T1 / p1 )
3(T2 − T1 ) / 2 = − (T2 − T1 / 10),T1 = 273.2K
∆S = ∆S (O 2 ) + ∆S ( N 2 ) = 4.160J ⋅ K −1
∆A = ∆G = −T ∆S = ( −273.2 × 4.160 ) J = −1136.7J < 0
1 1
V2
V2
= [2 × 8.3145 × 300 ln(1/ 0.1) ] J = 11.49 ×103 J
∆S − Q / T = ( 38.29 − 11.49 × 10 3 / 300)J ⋅ K −1 = 0
的单原子分子理想气体, 例3 0℃、1MPa、10dm3的单原子分子理想气体, ℃ 、 绝热膨胀至0.1MPa, 计算 、 W、 ∆U、 ∆H、 ∆S, 绝热膨胀至 , 计算Q、 、 、 、 , 并判断可逆性。 并判断可逆性。(a) p外=p,(b) p外=0.1MPa,(c) p外 , , =0 。 解:三个过程终态不同。 三个过程终态不同。 (a) V2 = ( p1 / p2 )1 / γ V1 = [(1 / 0.1) 3 / 5 × 10]dm 3 = 39.81dm 3
∆U = 0
∆H = 0
p2 p1
∆S =− nR ∫ (dp / p ) = − nR ln( p2 / p1 )
= [−2 × 8.3145 × ln( 0.1 / 1)]J ⋅ K −1 = 38.29J ⋅ K −1
∆S − ∫ δQ/ T = 0
(b)
∆U = W
o nCV ,m (T2 − T1 ) = − p外 (V2 − V1 )
n( 3 R / 2)(T2 − T1 ) = − p外 nR(T2 / p2 − T1 / p1 )
3(T2 − T1 ) / 2 = − (T2 − T1 / 10),T1 = 273.2K
∆S = ∆S (O 2 ) + ∆S ( N 2 ) = 4.160J ⋅ K −1
∆A = ∆G = −T ∆S = ( −273.2 × 4.160 ) J = −1136.7J < 0
1 1
V2
V2
= [2 × 8.3145 × 300 ln(1/ 0.1) ] J = 11.49 ×103 J
∆S − Q / T = ( 38.29 − 11.49 × 10 3 / 300)J ⋅ K −1 = 0
的单原子分子理想气体, 例3 0℃、1MPa、10dm3的单原子分子理想气体, ℃ 、 绝热膨胀至0.1MPa, 计算 、 W、 ∆U、 ∆H、 ∆S, 绝热膨胀至 , 计算Q、 、 、 、 , 并判断可逆性。 并判断可逆性。(a) p外=p,(b) p外=0.1MPa,(c) p外 , , =0 。 解:三个过程终态不同。 三个过程终态不同。 (a) V2 = ( p1 / p2 )1 / γ V1 = [(1 / 0.1) 3 / 5 × 10]dm 3 = 39.81dm 3
第2章_热力学第二定律-习题课

G
s l
不可逆相变
1mol H2O(s) 263.15K 101.325Pa
G1
等温 可逆
G5
等温 可逆
1mol H2O(l) 263.15K 611Pa
1mol H2O(s) 263.15K 552Pa
G2
g l
等温等压 可逆相变
s g
等温等压 G4 可逆相变
1mol H2O(g) 263.15K 611Pa
上一页 下一页
第二定律习题课
选择题: 1、分别在一定压力和一定体积下,将1mol理想气 体从300K加热到600K时,对应的熵变为△S1和△S2 则 A、△S1<△S2 B、△S1 >△S2
C、△S1=△S2
D、无法确定
上一页
下一页
第二定律习题课
2、25℃,1标准大气压下,NaCl在水中溶解度为 6mol.L-1,如将1molNaCl溶解于1L水中,此溶解过 程体系的△S和△G变化为 A、△S<0,△G>0 C、△S>0,△G<0 B、△S>0,△G>0 D、△S>0,△G=0
b、等温、等压可逆相变
G 0
不可逆相变,设计一个可逆过程。 c、 G
H TS
(等温)
G2 G1 1 1 d、 H ( ) T2 T1 T2 T1
上一页 下一页
(变温)
第二定律习题课
(3)自由能判据
G W
'
()T,P可逆过程中,一个密闭体系所做的最大 非膨胀功(有效功)等于其自由能的减少,等 温不可逆,则所做的非膨胀功小于体系自由能 的减少。 判据 等温等压不做其他功的条件下 <0 自发 =0 平衡 >0 不能自发
大学物理热学习题课

dN m 32 4 ( ) e Ndv 2kT
v2
对于刚性分子自由度 单原子 双原子 多原子
i tr
(1)最概然速率
2kT 2 RT RT vp 1.41 m
(2)平均速率
i=t=3 i = t+r = 3+2 = 5 i = t+r = 3+3 =6
6、能均分定理
8kT 8 RT RT v 1.60 m
M V RT ln 2 M mol V1
QA
绝热过程
PV 常量
M E CV T M mol
(2)由两条等温线和两条绝热线 组成的循环叫做 卡诺循环。 •卡诺热机的效率
Q0
Q2 T2 卡诺 1 1 Q1 T1
M P1V1 P2V2 A CV T M mol 1
E 0
•热机效率
A Q1 Q2
M E CV T M mol M Q C P T M mol
A Q1 Q2 Q2 1 Q1 Q1 Q1
A=P(V2-V1) 等温过程
A
E 0
Q1 Q2 •致冷系数 e W Q1 Q2
热机效率总是小于1的, 而致冷系数e可以大于1。
定压摩尔热容
比热容比
CP ( dQ )P dT i2 i
8、平均碰撞次数 平均自由程
z
2d v n
2
CV •对于理想气体:
Cp
v z
1.热力学第一定律
1 2 2d n
二、热 力 学 基 础
Q ( E2 E1 ) A dQ dE dA
准静态过程的情况下
4. 摩尔数相同的两种理想气体 一种是氦气,一种是氢气,都从 相同的初态开始经等压膨胀为原 来体积的2倍,则两种气体( A ) (A) 对外做功相同,吸收的热量 不同. (B) 对外做功不同,吸收的热量 相同. (C) 对外做功和吸收的热量都不 同. (D) 对外做功和吸收的热量都相 同. A=P(V2-V1)
热力学第一定律习题课 (1)全

= 1.3%
(5)
P
qm ws
220 t/h103 kg/t 3600 s/h
1.1361 03
kJ/kg
=
6.94 104
kW
讨论
(1)本题的数据有实际意义,从计算中可以看到,忽略进出 口的动、位能差,对输轴功影响很小,均不超过3%,因此在实 际计算中可以忽略。 (2)蒸汽轮机散热损失相对于其他项很小,因此可以认为一 般叶轮机械是绝热系统。
m2u2 m1u1 m2 m1 h 0
u2
m2
m1 h
m2
m1u1
方法三 取充入气罐的m2-m1空气为闭口系
Q U W
Q 0 ? W ? U ?
U m2 m1 u2 u
W W1 W2 m2 m1 pv W2
2
则 Q23 U23 W23 U3 U2 87.5 kJ175 kJ 87.5 kJ
U1 U3 U123 87.5 kJ (77.5 kJ) 165 kJ
讨论
热力学能是状态参数,其变化只决定于初 终状态,于变化所经历的途径无关。
而热与功则不同,它们都是过程量,其变 化不仅与初终态有关,而且还决定于变化所 经历的途径。
1 2
(cf23
c22 )
ws
因为w3 0,所以
燃烧室 压 气 机
cf 3' 2 q (h3' h2 ) cf22
2 670103 J/kg- (800 - 580) 103 J/kg + (20 m/s)2 = 949 m/s
( 4 ) 燃气轮机的效率
取燃气轮机作为热力系,因为燃气在
( 5 ) 燃气轮机装置的总功率 装置的总功率=燃气轮机产生的功率-压气机消耗的功率
热力学第一、第二定律习题课
5.理想气体在下列过程中,系统与环境的总熵变是多少?
恒温下向真空中膨胀(始态P1、V1、T1末态P2、V2、T2)。 恒温可逆膨胀。
6.一切绝热过程的熵变都等于零,这样理解是否正确?为什么?
7. 进行下述过程时,系统的ΔU、ΔH、ΔS和ΔG何者为零?
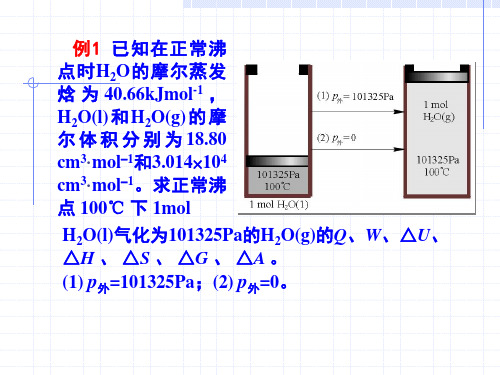
(1)非理想气体的卡诺循环;(2)在100℃,101325Pa下1mol水蒸发
(A )
A. 等于2.5mol B. 等于-2.5mol C. 对不同反应物计算结果不一样 D. 反应物没反应完而无法计算
已知某温度下,∆fHmΘ(CO2)=-393.3kJ/mol,∆cHmΘ(CO)=- 282.8kJ/mol,则∆fHmΘ(CO)为 (C)-676.1 kJ/mol; (A ) (A)-110.5 kJ/mol ; (B)110.5 kJ/mol ; (D)-172.3 kJ/mol
(B)
在300K时,2mol某理想气体的吉布斯函数G与赫姆霍
兹函数A的差值为 ( C )
A. G-A=1.247kJ; C. G-A = 4.988kJ; B. G-A= 2.494kJ; D. G-A = 9.977kJ
当10mol N2和20mol H2混合通过合成氨塔,反应一段时间后有5mol NH3生成。对反应式N2+3H2=2NH3,反应进度
ΔrSm,隔离 = ΔrSm,体+ ΔSm,环= 147.6 J· K-1· mol-1
(3) ΔrGm = ΔrHm- TΔrSm= QR' - QR= - 4.400 kJ
Wf = -ΔrGm= 44.000 kJ
2. 2mol单原子理想气体始态为298K,3039.75kPa,经绝热膨胀压 力突然降到1013.25kPa,做了2095 J的功,求该体系的熵变值。 [答 ] 因为是绝热过程,所以Q=0,所以有:
热学习题课
绝热
Qo
dQ o
CV ,m T
1 p1V 1 p2V2 1
0
p 1T c3
pV c1 TV 1 c2
dp p dV V
5、循环过程
A Q1
T2 1 T1
Q2 A Q1 Q2 1 Q1 Q1 Q1
解:
TV1 1
1
T2V2
1
T1 V2 T2 V1
1
v
8RT
v2 T2 V1 v1 T1 V2
1
2
2
1
2
5. 图为一理想气体几种状态变化过程的 p-V 图,其中 MT 为等温线,MQ 为绝热线,在 AM, BM, CM 三种准静态过程中: (1) 温度升高的是 BM, CM CM (2) 气体吸热的是 过程; 过程。
最概然速率 三种速率
vp 2kT m
3/ 2
ve
2 RT RT 1.41 M M
平均速率
方均根速率
v
vrms
8kT m
3kT m
8RT RT 1.59 M M
3RT RT 1.73 M M
7、玻耳兹曼分布律 在温度为T 的平衡态,系统的微观粒子按状态的分布与粒子的 能量 E 有关,且与成
S k ln
dQ dS T S S B S A
B A
dQ T
对孤立系统的自然过程,总有
S 0
绝 V 1T 常量 热 pV 常量 方 1 程 p T 常量
熵 的计算
dQ S 2 S1 (1) T R
( 2)
热力学第一定律习题课
H2(g)+1/2 O2(g)= H2O(g) H2O(g)+9.5O2(g) 298K升温到T U(1) U(2)
U(1) = H(1) –RTn(g) = 241.5 kJ (n = –1.5)
15
概念
1
2
3
4
5
6
7
8
9
第二章 热力学第一定律(10学时)
例题讲解
说明下列公式的适用条件
(1) U p (V 2 V 1 ) ( 2 )W R T ln (3) d H C p d T (4)H U pV (5 ) p V
16
V1 V2
K
1 2 3 4 5 6 7
Q = 10.1kJ
U(总)= Q = 10.1kJ
H(总) = U(总)= 14.2kJ
27
概念
1
2
3
4
5
6
7
8
9
例4 25℃时,将1molH2(g),10molO2(g)放入定容容器 中充分燃烧,生成水。已知: 298K时fHm (H2O, g) = 242.7 kJmol-1 vapHm (H2O) = 44.0 kJmol-1 H2(g) Cp,m/ JK-1 mol-1 27.2 O2(g) 27.2 H2O( g) 31.4
U = W = (p2V2 p1V1)/( 1 ) =1.14kJ n = p1V1/RT1 = 0.818mol U= nCV,m(T2 T1)=1.14kJ H = U = 1.56kJ
25
概念
1
2
3
4
5
6
7
8
9
(2) 以左室气体为系统
U(1) = H(1) –RTn(g) = 241.5 kJ (n = –1.5)
15
概念
1
2
3
4
5
6
7
8
9
第二章 热力学第一定律(10学时)
例题讲解
说明下列公式的适用条件
(1) U p (V 2 V 1 ) ( 2 )W R T ln (3) d H C p d T (4)H U pV (5 ) p V
16
V1 V2
K
1 2 3 4 5 6 7
Q = 10.1kJ
U(总)= Q = 10.1kJ
H(总) = U(总)= 14.2kJ
27
概念
1
2
3
4
5
6
7
8
9
例4 25℃时,将1molH2(g),10molO2(g)放入定容容器 中充分燃烧,生成水。已知: 298K时fHm (H2O, g) = 242.7 kJmol-1 vapHm (H2O) = 44.0 kJmol-1 H2(g) Cp,m/ JK-1 mol-1 27.2 O2(g) 27.2 H2O( g) 31.4
U = W = (p2V2 p1V1)/( 1 ) =1.14kJ n = p1V1/RT1 = 0.818mol U= nCV,m(T2 T1)=1.14kJ H = U = 1.56kJ
25
概念
1
2
3
4
5
6
7
8
9
(2) 以左室气体为系统
热学习题课
Ω2 熵增加原理: 熵增加原理:在一个孤 ∆S = k ln ≥0 立系统(或绝热系统)可 立系统(或绝热系统) Ω1 能发生的过程是熵增加或保持不变的过程。 能发生的过程是熵增加或保持不变的过程。
孤立系统内进行的过程总是由微观状态数 小的状态向微观状态数大的宏观状态进行。 小的状态向微观状态数大的宏观状态进行。
B
i E = vRT ∝ V , pV = vRT 2 ⇒ p = constant
E V
8/8
例2:对于氢气(刚性双原子分子气体)和氦气, 对于氢气(刚性双原子分子气体)和氦气, 压强、体积和温度都相等时, 1.压强、体积和温度都相等时,它们的质量比 M(He)=______,内能比E(H ______; M(H2)⁄ M(He)=______,内能比E(H2)⁄ E(He)= ______; 压强和温度相同,(a)各为单位体积时的内能之 2.压强和温度相同,(a)各为单位体积时的内能之 =______,(b)各为单位质量时的内能之比 比 =______,(b)各为单位质量时的内能之比 = ______。 ______。
适用范围:可逆过程, 适用范围:可逆过程,只存在体积功
7/8
例1:一定质量的理想气体的内能E 随体积V 的变化 关系为一直线, 关系为一直线,则此直线表示的过程为 [ ] (A)等温过程 等温过程。 等压过程。(C)等容过程 (D)绝 等容过程。 (A)等温过程。(B)等压过程。(C)等容过程。(D)绝 热过程。 热过程。
解:(1) :( )
1
dS = δ Q / T
T
Hale Waihona Puke T = const.Q = const.
3 2
1
dT = 0
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、体积功的计算 1、定义式:δW=-PedV 2、理想气体各过程W的计算 3、凝聚系统功的计算 如P变化不大,W=- V V pdV =0。 若恒压,W=-peΔV, 4、相变过程:始-终的Wf=0,对于S-g、l-g过 程,W=-p(Vg-Vs,l)=-pVg=-nRT。 5、化学反应 液相(无气体)反应,W=0。 n RT n RT 产 反 气体反应:W=-p(V产-V反)=-P P P
8.关于焓的性质, 下列说法中正确的是 (A) 焓是系统内含的热能, 所以常称它为热焓 (B) 焓是能量, 它遵守热力学第一定律 (C) 系统的焓值等于内能加体积功 (D) 焓的增量只与系统的始末态有关 9.关于热力学第二定律下列哪种说法是错误的 (A) 热不能自动从低温流向高温 (B) 不可能从单一热源吸热做功而无其它变化 (C) 第二类永动机是造不成的 (D) 热不可能全部转化为功 10. 热力学第三定律可以表示为: (A)在0K时,任何晶体的熵等于零 (B)在0K时,任何完整晶体的熵等于零 (C)在0℃时,任何晶体的熵等于零 (D)在0℃时,任何完整晶体的熵等于零
T2 T1 Q2 Q1 T2 Q2
4、热二律(两种典型说法) 5、熵增原理
S iso 0
dS
Q 0 T
§2 基本公式 一、基本过程的特征 1、简单pVT变化(无相变,化变) (1)等温过程:T1=T2=T环,dT=0 (2)变温过程:T1≠T2(=T环),dT≠0 (3)等压过程:P1=P2=P环,dP=0, 恒外压过程:P1≠P2=P环, 向真空膨胀:Pe=0,但P1、P2≠0。 (4)等容过程:V1=V2, dV=0 (5)绝热过程:Q=0 2、相变:可逆、不可逆。 3、可逆、不可逆。
热力学
§1 基础概念与术语
பைடு நூலகம்
热力学及 其应用小结
一、基本概念 1、系统与环境 2、广度性质、强度性质 3、状态函数 4、热力学平衡态,满足四大平衡。 5、热、功(体积功,有用功) 6、过程与途径 7、可逆过程 8、自发过程 9、卡诺循环
二、热力学函数 U、H、S、A、G 三、基本原理: 1、热一律 2、盖斯定律 3、卡诺定律
§3 热力学基本关系式 一、定义式及4个基本关系(及4个特征函数) §4热力学判据 > 0 不可逆,自发过程 熵判据 (dS )U .V 0 = 0 可逆,达到平衡 Helmholtz (dA) T ,V ,Wf 0 0 自由能 Gibbs 自由能 Wf ≠ 0 电池中
< 0 不可逆,自发过程 = 0 可逆,达到平衡
2、各过过程△S计算 理气 P1V1T1→P2V2T2 △S=nCV,mlnT2/T1+nRlnV2/V1 =nCP,mlnT2/T1+nRlnP1/P2 =nCV,mlnP2/P1+nCP,mlnV2/V1
又如,可逆相变,可逆化变(Wf=0)
S H 相 T相
S R
QP , R T
S sur
二、计算题 1.苯的正常沸点为353K,摩尔汽化焓为 30.77kJ•mol-,现将353K,标准压力下的1 摩尔液态苯向真空等温蒸发为同温同压的苯 蒸汽(设为理想气体)。 A.计算该过程苯吸收的热量和做的功; B.求过程的△G和△S; C.求环境的熵变; D.可以使用何中判据判断过程的性质。
2
(dG )T , p ,Wf 0 0
-dGT,p≥-Wf -dGT,p≥nEF
一、选择题
1.在101.325KPa,25℃下,下列反应分别经途径Ⅰ(在烧杯中进 行)和途径Ⅱ(在电池中进行)Zn+CuSO4(1mol.Kg-1) →Cu+ ZnSO4(1mol.Kg-1) 问下列各式成立的是____; A.△HⅠ=△HⅡB.QⅠ= QⅡC.△HⅠ= QⅠ D.△HⅡ= QⅡ 2.第一类永动机不能制造成功的原因是 A.能量不能创造也不能消灭 C.能量传递的形式只有热和功 B. 实际过程中功的损失无法避免 D. 热不能全部转换成功 3.在系统温度恒定的变化中,系统与环境之间_ _ 。 A.一定产生热交换 B.一定不产生热交换 C. 不一定产生热交换 D.温度恒定与热交换无关 4.在一定温度下,发生变化的孤立体系,其总熵 A.不变 B.可能增大或减小 C.总是减小 D.总是增大 5.内燃机车头牵引相同的一列车厢,在下列____环境下,消耗 燃料最多。 A.北方冬天 B.北方夏天 C.南方冬天 D.南方夏天 6.已知反应B→A,B → C的等压反应热分别为∆H1与∆H2,那 么A → C的∆H3与它们的关系是:( ) (A) ∆H3 = ∆H1 + ∆H2 ; (B) ∆H3 = ∆H1 - ∆H2 ; (C) ∆H3 = ∆H2 - ∆H1 ; (D) ∆H3 = 2∆H1 - ∆H2 。 7. 理想气体模型的基本特征是 (A) 分子不断地作无规则运动、它们均匀分布在整个容器中 (B) 各种分子间的作用相等,各种分子的体积大小相等 (C) 所有分子都可看作一个质点, 并且它们具有相等的能量 (D) 分子间无作用力, 分子本身无体积
Q系 T环
1
七、△G 1、定义式△G=△H-△(TS),dG=-SdT+VdP 2、各种体系与过程△G的计算。 八、计算要决: 1、掌握定义式及基本关系式 2、明确体系的类型 (1)气态:理气 (2)凝聚态:纯物质及蒸气 (3)混合聚集态:均相还是多相 3、认准过程特征 4、不可逆相变要设计一条可逆途径代替 (具有相同的始终态),符合题给条件,并有相应公式。 5、检验结果正确性。
2 1
三、热 1、定义式δQ=CdT; 2、理气各过程Q的计算 3、凝聚系统Q的计算 δQv=CvdT 、δQp=CpdT 4、相变过程:等压Wf=0,Qp=△H相 5、化变:Qv=△U Qp=△rH (Wf=0)
=-∑ngRT。
四、 △ U 1、定义式: (1)△U=Q+W (2)dU=TdS-pdV(Wf=0) (3) dU=nCV,mdT 2、各种过程△U的计算 五、△H 1、定义式: dH=dU+d(PV)、 dH=TdS+VdP、 dH=nCP,mdT 2、各种过程△H的计算 等压,Wf=0、△H=QP
U、H与Q、W的区别及联系 1) U、H是状态函数,与始末状态有关,与 过程无关; Q、W是能量传递的形式,与过程 有关 2)在某些特定的条件下,系统的⊿U、 ⊿H 在数值上与Q、W相等
六、△S 1、定义式:
dS
QR
T
S S 2 S1
dU WR T
△H=QP (封闭系统,等压过程,Wf=0) △U=Qv (封闭系统,等容过程,Wf=0) △U=W (封闭系统,绝热过程)
