结构化学第一章-北京师范大学出版社
合集下载
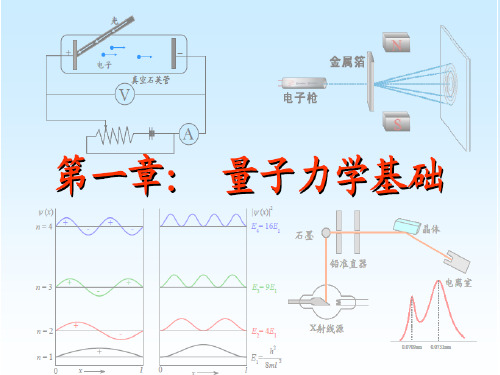
结构化学第一章
E = hν p = h /λ
这就是著名的德布罗意关系式 大胆想象
波和粒子的统一
实物微粒的波动性和粒子性的内在联系可由如 下两个公式反映出来:
E = hν
p = h /λ
左边的能量 E 和动量 p 是表征微粒性的物理量。 右边的频率ν和波长λ是表征波动性的物理量,这两 套物理量通过普朗克常数 h 定量地联系起来。
发生衍射
对处在同一状态下的大量粒子而言,(x,y,z)2代表 了空间某点(x,y,z)的电子密度,即空间某点(x,y,z)处 附近的电子密度与波函数模的平方成正比。
六、化学中的电子波动性
化学反应的本质:旧键断裂 和新键生成(电子得失)
电子具有波动性:电子云
原子轨道
分子轨道
不同分子轨道互相接近, 决定了不同的化学反应
§1.1.3 实物微粒的波粒二象性
小 结一
宏观粒子
实物微粒
粒子性
服从牛顿力
学,有可预测的运动轨 道
不服从牛顿 力学,无法预 测运动规律
波动性
无波动性
有波动性, 其分布具有几 率性
小结二:
德波罗意关系式:
p h
E h
小结三:
物质波的几率解释:波的强度(即振幅绝对值的平方 )和粒子出现的几率成正比,物质波又被称为几率波。
波性:光的强度 I ∝||2 粒子性:光的强度与单位体积内的光子数目成正比
I ∝ ρ=ΔN/Δτ 二者结合: ρ∝||2 (2)光的波粒二象性
光在传播过程中显示波性, 与实物微粒相互作用时显示微粒性。
光具有微粒和波动的双重性质,这种性质称为波粒二象性。
二、 德波罗意假设(De Broglie’s Hypothesis)
一、 光的波粒二象性
这就是著名的德布罗意关系式 大胆想象
波和粒子的统一
实物微粒的波动性和粒子性的内在联系可由如 下两个公式反映出来:
E = hν
p = h /λ
左边的能量 E 和动量 p 是表征微粒性的物理量。 右边的频率ν和波长λ是表征波动性的物理量,这两 套物理量通过普朗克常数 h 定量地联系起来。
发生衍射
对处在同一状态下的大量粒子而言,(x,y,z)2代表 了空间某点(x,y,z)的电子密度,即空间某点(x,y,z)处 附近的电子密度与波函数模的平方成正比。
六、化学中的电子波动性
化学反应的本质:旧键断裂 和新键生成(电子得失)
电子具有波动性:电子云
原子轨道
分子轨道
不同分子轨道互相接近, 决定了不同的化学反应
§1.1.3 实物微粒的波粒二象性
小 结一
宏观粒子
实物微粒
粒子性
服从牛顿力
学,有可预测的运动轨 道
不服从牛顿 力学,无法预 测运动规律
波动性
无波动性
有波动性, 其分布具有几 率性
小结二:
德波罗意关系式:
p h
E h
小结三:
物质波的几率解释:波的强度(即振幅绝对值的平方 )和粒子出现的几率成正比,物质波又被称为几率波。
波性:光的强度 I ∝||2 粒子性:光的强度与单位体积内的光子数目成正比
I ∝ ρ=ΔN/Δτ 二者结合: ρ∝||2 (2)光的波粒二象性
光在传播过程中显示波性, 与实物微粒相互作用时显示微粒性。
光具有微粒和波动的双重性质,这种性质称为波粒二象性。
二、 德波罗意假设(De Broglie’s Hypothesis)
一、 光的波粒二象性
第一章结构化学

氢原子核电荷z=1,能量可写成
1 2 e e e E mv 2 4 0 r 8 0 r 4 0 r
m e4 1 1 2 2 2 R 2 8 0 r 8 0 h n n e2
2
2
2
m e4 其中, R 2 2 13.6eV 8 0 h 当n=1时,E= -13.6 eV,称为氢原子基态的能量。
(2)玻尔假定:
1913年丹麦物理学家玻尔把量子论 的基本观点应用于原子核外电子的运 动,从而创立了玻尔理论。其基本论 点可归纳为:
(A)原子存在于具有确定能量的稳 定态(简称定态),定态中的原子不辐
Nobel 1922
射能量。
h h M (C)玻尔量子化规则: n n, n 1,2,3... ,n为量子数 2
1 1 RH ( 2 2 ) n1 n2
~
1
氢原子光谱——玻尔提出原子结构理论,主 张原子能量具有不连续性。
(1)巴耳麦公式:
白光本来是由波长不同的各种颜色的光线组成,当它通过三棱镜 或者光栅后便分解为红、橙、黄、绿、青、蓝、紫的连续谱带,称 为连续光谱。
含有低压氢气的放电管所发生的光通过三棱镜或光栅后不是形成 连续的谱带,而是形成一条一条孤立的谱线,由这些谱线构成谱图, 这种光谱称为不连续光谱或线状光谱。
1.1.1 黑体辐射与能量量子化
黑体:能全部吸收外来电磁波的物体。黑色物体或开一小孔 的空心金属球近似于黑体。 黑体辐射:加热时,黑体能辐射出各种波长电磁波的现象。 黑体辐射能量密度与波长的关系是19世纪末物理学家 关心的重要问题之一.经典物理学在此遭遇严重困难: 维恩公式只适用于短波部分;
由能量均分定理导出的瑞利-金斯公式则只适用于长波
结构化学《结构化学》第1章 第2讲(1.2)1.2 《结构化学》第1章第2讲

6. 量子力学中最重要的算符
是哈密顿(能量)算符:
Hˆ h2 2 Vˆ
8 2m
这里
2
2 x2
2 y2
2 z 2
称为Laplace算符。
6
1.2.3 本征态、本征值和Schrödinger方程
1. 量子力学基本假设III的主要内容
若某一物理量A的算符Â作用于某一状态函数ψ, 等于某一常数a乘以ψ,即
将能量算符作用于描述该状态的波函数ψ,求出
能量算符的本征值, 该本征值应与实验测量的该状态的能量相一致。
8
4. 自轭算符的重要性质之一 自轭算符的本征值一定为实数。
5. 能量算符的本征方程为:
Hˆψ Eψ
h2
8 2m
2
Vˆ
ψ
Eψ
2
2m
2
Vˆ
ψ
1.2 量子力学基本假设
1. 对量子力学基本假设的几点说明 1)这些假设类似于公理,人们都认为是正确的, 但却无法证明; 2)从这些基本假设出发,可以推导出一些重要 的结论,这些结论与已有的实验事实相符; 3)从这些基本假设出发,可以从理论上预测一 些实验现象,这些理论预测结果后来与实验测定结 果相符合。
1
1.2.1 波函数和微观粒子的状态 1. 量子力学基本假设I的主要内容 一个微观体系的状态和由该状态所决定的各种物
理性质,可用波函数(x, y, z, t)表示。是体系的
状态函数,是体系中所有粒子坐标和时间的函数。 2. 定态波函数
不含时间的波函数ψ(x, y, z)称为定态波函数,也
就是体系的性质不随时间的改变而改变。 本课程主要讨论定态波函数,而不是含时波函数。
结构化学第一章

V
E
E=hv
实物粒子
V
E
E=hv
光子
注意光子实物粒子的 P与E的关系
实物粒子的运动速递与传播速度(又称之为相 速度)的关系
海森堡与他的测不准:上帝的色子
例题: 利用不确定关系说明使用光学光栅(周期10-6m),观察 不到点子衍射(10000V加速)的原因
沃纳·海森堡 德国人 二战期间希特勒手下的王牌 核物理学家之一,第三帝国的支持者。
8 abc
1
2
sin(
nx
a
x
)
sin(
ny
b
y
)
sin(
nz
a
z
)
能量
Eபைடு நூலகம்
h2 8m
nx2 a2
ny2 b2
nz2 c2
简并态,简并度,简并能级
叠加原理
参考宏观下波的叠加
薛定谔的方程
薛定谔的方程与运动状态的解析
一维与多维量子学势阱(重点之一) 与经典力学的差别 1、能量量子化,分立的,不连续的。E=n2h2/(8π2m) 2、E最小时,仍然大于0,为基态,称之为零点能。 3、在一维势箱之中,分布并不是处处相同 4、波函数为正或者负、0皆有可能。 5、n(能级)不同,则波函数[(2/L)0.5sin(nπ/L)]不同,微观粒子的分布不同 手动画图,画出波函数,概率的分布 什么事简并度?
2、德布罗意波之中的波 速度与微观粒子的速度两 个速度的定义差别
实验设计: 如何利用光电效应,求出量子常数?要求:简单
该实验之中,变量 :入射光的频率 光度,对实验 结果有什么影响? 两个变量的改变会影响到什么?
结构化学第一章课后习题答案

T=
1 mυ 2 = hv − hv0 2 p = mυ = 2mT = 2mh(v − v0 ) 3.0 ×108 − 5.464 × 1014 ) 300 ×10−9
= 2 × 9.109 × 10−31 × 6.626 × 10−34 × ( = 7.40 × 10−25 J S m −1
λ= h
d2 2 14. 下列函数,哪个是算符 dx 的本征函数?若是,求出相应的本征值。 eimx
sin x
x2 + y 2
( a − x )e − x
解:
d 2 imx d e = imeimx = − m 2eimx dx 2 dx 2 d d sin x = cos x = − sin x 2 dx dx 2 d d2 2 d2 2 d2 2 2 2 + = + = + ( ) 2 x y x y y dx 2 dx 2 dx 2 dx 2 d2 a − x ) e− x = ( a − x + 2 ) e− x 2 ( dx
b
解: (1)
nxπ x ⎞ ⎛ a 1 − cos 2 8 ⎜ a ⎟dx = ⎜ ⎟ ∫ abc 0 ⎜ 2 ⎟ ⎝ ⎠ 8 a b c = × × × =1 abc 2 2 2
nxπ z ⎞ ⎛ ⎜ 1 − cos 2 a ⎟ ⎜ ⎟dz ∫ 2 0⎜ ⎟ ⎝ ⎠
c
(2) a=b=c 此时,方程变为ψ nx ny nz ( x, y, z ) =
∫ ∫ ∫ψ
0 0 0
a b c
nx n y n z
( x, y , z ) ψ nx ny nz * ( x, y, z )dτ
= ∫∫∫
0 0 0
a b c
1 mυ 2 = hv − hv0 2 p = mυ = 2mT = 2mh(v − v0 ) 3.0 ×108 − 5.464 × 1014 ) 300 ×10−9
= 2 × 9.109 × 10−31 × 6.626 × 10−34 × ( = 7.40 × 10−25 J S m −1
λ= h
d2 2 14. 下列函数,哪个是算符 dx 的本征函数?若是,求出相应的本征值。 eimx
sin x
x2 + y 2
( a − x )e − x
解:
d 2 imx d e = imeimx = − m 2eimx dx 2 dx 2 d d sin x = cos x = − sin x 2 dx dx 2 d d2 2 d2 2 d2 2 2 2 + = + = + ( ) 2 x y x y y dx 2 dx 2 dx 2 dx 2 d2 a − x ) e− x = ( a − x + 2 ) e− x 2 ( dx
b
解: (1)
nxπ x ⎞ ⎛ a 1 − cos 2 8 ⎜ a ⎟dx = ⎜ ⎟ ∫ abc 0 ⎜ 2 ⎟ ⎝ ⎠ 8 a b c = × × × =1 abc 2 2 2
nxπ z ⎞ ⎛ ⎜ 1 − cos 2 a ⎟ ⎜ ⎟dz ∫ 2 0⎜ ⎟ ⎝ ⎠
c
(2) a=b=c 此时,方程变为ψ nx ny nz ( x, y, z ) =
∫ ∫ ∫ψ
0 0 0
a b c
nx n y n z
( x, y , z ) ψ nx ny nz * ( x, y, z )dτ
= ∫∫∫
0 0 0
a b c
结构化学-第1章讲义
2020/8/1
4
二 课程内容 对象 主要理论工具
章节
原子 量子力学
分子 点群理论 共价键理论
第一章 量子力学 第二章 原子结构
第三章 分子对称性 第四章 双原子分子 第五章 多原子分子
2020/8/1
21
对象 主要理论工具
章节
络合物 配位场理论 第六章 配位化合物
晶体 点阵结构理论 第七章 晶体结构 密堆积原理 第八章 晶体材料
献有发明了微积分,发现了万有引力定律和经典力学等等,被誉为人类历
史上最伟大,最有影响力的科学家。为了纪念牛顿在经典力学方面的杰出
成就,“牛顿”后来成为衡量力的大小的物理单位。
2020/8/1
27
2. Maxwell电磁场理论
波函数描述运动状态:
单色平面波 (x,t) Acos(x t)
(λ为波长,ν为频率)
这些振子的能量只能取某些基本能量单位的 整数倍,基本能量单位和频率成正比——
h E n n h (n=1, 2, 3…)
Planck 常数:h=6.626× 10-34 J·s
2020/8/1
35
振子在吸收或者发射电磁波时,只能从某一个特 定状态过渡到另一个特定状态,
E(v,T
)dv
8v2k
维恩公式只适用于短波部分;
瑞利-金斯公式则只适用于长波部分,它在短 波部分引出了 “紫外灾变”,即波长变短时辐 射的能量密度趋于无穷大,而不象实验结果那样 趋于零。
2020/8/1
34
Planck 量子论
1900年12月14日,普朗克公布了他对黑体 辐射的研究成果。
提出假设:黑体辐射的是带电的谐振子。
结构化学
结构化学第一章 量子力学基础chap1
综
述
›››
• • • • •
三种理论和三种结构
量子理论 原子结构 H 化学键理论 分子结构 化学键 点阵群理论 晶体结构
多电子原子
分子轨道理论 价键理论 配位场理论
两条主线: 电子构型和几何构型
一条渠道: 结构 - 性能 - 应用
第一章
量子力学基础
Chapter 1. Introduction to Quantum Mechanics
λ= 2dsinθ
1.1.3 不确定关系
Bohr, Heisenberg, Pauli(从左到右)
直认为是实物粒子的电子等物质, 也看作是波.
de Broglie关系式为:
ν= E / h
λ= h / p
1.1.2.1 德布罗依假说
1924年, de Broglie提出实物微粒也有波性的假设 区别:实物微粒的静止质量不为0 E=hν α粒子,电子,质子,中子,原子,分子 p=h /λ λ= h /p=h/(mv) 实物微粒在以大小p=mv 的动量 运动时,伴随有波长为λ的波
1.2
1.2.1
量子力学的建立
实物粒子的波粒二象性
L.V.de Broglie(德布罗意)认为辐射的波粒二象性 (wave-particle duality )同样适用于物质. 波以某种方式伴随 电子和其他粒子, 正如波伴随着光子一样. 这就是说, 一度被 视为波的光已被证明也有粒子性, 现在需要“反过来”把一
例1 家中烹调使用的微波炉发射一定的电磁波,其波长λ为 122mm,计算该电磁波的能量。
ν= c/ λ =3.0 ×108m•s-1/(122 ×10-3)m
= 2.46 ×1010 s-1 E= hν = 6.624×10-34J. s × 2.46 ×1010 s-1 = 1.63×10-23J
结构化学第一章 量子力学基础

~= 1 =R 1 − 1 ν H 2 2 λ n1 n2
1913年为解释氢原子光谱的实验事实, Bohr综合 1913年为解释氢原子光谱的实验事实, Bohr综合 年为解释氢原子光谱的实验事实 了Planck的量子论、Einstein的光子说以及卢瑟福的原 Planck的量子论、Einstein的光子说以及卢瑟福的原 的量子论 子有核模型,提出: 子有核模型,提出:
氢原子线状光谱
1885年巴耳麦(Balmer)和随后的里德堡(Rydberg) 1885年巴耳麦(Balmer)和随后的里德堡(Rydberg) 建立了 年巴耳麦 对映氢原子光谱的可见光区14条谱线的巴尔麦公式。20世纪 14条谱线的巴尔麦公式 对映氢原子光谱的可见光区14条谱线的巴尔麦公式。20世纪 初又在紫外和红外区发现了许多新的氢谱线,公式推广为: 初又在紫外和红外区发现了许多新的氢谱线,公式推广为:
一、 经典物理学的困难与旧量子论的诞生 1.黑体辐射实验与普朗克的量子论 黑体辐射是最早发现与经 典物理学相矛盾的实验现象之 一。 所谓黑体是指能全部吸 收各种波长入射光线辐射的物 体。带有一个微孔的空心的金 属球,非常接近于黑体,进入 金属小孔的辐射,经过多次吸 收、反射,使射入的辐射完全 被吸收,当空腔受热时,又能 发射出各种波长的电磁波。 黑体辐射:加热时,黑体能辐射出各种波长电磁波的现象。 黑体辐射:加热时,黑体能辐射出各种波长电磁波的现象。
1 2 hν = W + EK = hν 0 + mv 2
是电子逸出金属所需要的最小能量,称为逸出功, 式中W是电子逸出金属所需要的最小能量,称为逸出功, 它等于hν0;EK是电子的动能, 是电子的动能,
1 2 解释了光电效应实验的全部结果: 上式解释了光电效应实验的全部结果: 光子没有足够的能量使电子逸出金属, hν< 当hν<W 时,光子没有足够的能量使电子逸出金属,不发生 光电效应; 光电效应; 这时的频率是产生光电效应的临阈频率( 当hν=W 时,这时的频率是产生光电效应的临阈频率(ν0) ; 从金属中发射的电子具有一定的动能, hν> 当hν>W 时,从金属中发射的电子具有一定的动能,它随ν 的增加而增加( 与光强无关。 的增加而增加(T=hν-hν0),与光强无关。但 增加光的强度可增加光束中单位体积内的光子 因此增加发射电子的数目。 数,因此增加发射电子的数目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
薄膜、狭缝
荧光屏
一个电子对应屏上一个亮点。—— 粒子性
时间 统计结果——波动性
(M. Born玻恩统计解释) 大量电子:(1)衍射强度大的地方出现的电子多
(2)衍射强度小的地方出现的电子少 单个电子:(1)衍射强度大的地方电子出现的机会多
(2)衍射强度小的地方电子出现的机会少
物质波是几率波。
物质波的叠加性
Aˆu v
则表示这种运算的符号
Aˆ 就称为算符。
如
:
d, dx
d2, dx2
lo, gsin,,
量子力学中的算符只对它后面的东西进行运算。
二、线性算符
算符满足下列条件:
AˆA 1ˆc121Acˆ1Aˆ11Aˆ2
A ˆ c 11 c 22 c 1 A ˆ1 c 2 A ˆ2
二、光电效应不能用电磁场理论解释
光电效应是19世纪末人们发现的新的物 理现象:当光照射到纯净金属表面时有电子 (称光电子)逸出。
实验现象: (1)光电子的动能Ek与光的强度无 关,与入射光的频率有关。 (2) 对于一定金属,存在临阈频率。 (3)加反向电压,抑制光电流发生。
按照电磁波理论,光电子的动能Ek与光的强度 有关,与入射光的频率无关。
=7.08×10-9 (cm)
四、实物微粒波的实验证实
1927年,戴维逊(dawison)-革末( Germer )用 单晶体电子衍射实验,汤姆逊(G. P. Thomson)用 多晶体电子衍射实验,发现电子入射到金属晶体 上产生与光入射到晶体上同样产生衍射条纹,证 实了德布罗意假说。
后来采用中子、质子、氢原子和氦原子等微 粒流,也同样观察到衍射现象,充分证明了实物 微粒也具有波动性,而不仅限于电子。
hν= eVs + W0 = 1/2mev2 + hν0 当光照射到金属表面后,一个光子被一
个电子吸收,光子的能量一部分用来克服金 属对表面电子的束缚能W0(又称逸出功), 另一部分转化为光电子动能。
光电方程hν= eVs + W0 = 1/2mev2 + hν0在 1916年被罗伯特·安德罗·密里根精确实验证实 具有普适性。
后者为算符 Aˆ 的本征方程 f(x) —— 算符 Aˆ 的本征函数(本征态) a—— 算符 Aˆ 的本征函数f(x)的本征值
算符本征方程的物理意义:本征算符作用后的结 果导致本征函数平移,本质没有改变。
A ˆfxafx
a i 可以很多 a i 的集合叫本征值谱
ai(i1,2,...)
Einstein 光子学说
1905 年 爱 因 斯 坦运用量子概念成 功解释光电效应。
爱因斯坦获1921年诺贝尔物理学奖
(1)光是一种粒子流,能量量子化,最小 单位称光量子。光的辐射场是由光量子(简 称光子)组成的。 (2)光速为c =2.99792×108 m·s-1
(3)每个光子的能量=hν=mc2
微分算符不是厄米算符
如果一个算符既是线性算符又是厄米算 符,称该算符为线性厄米算符。
微观体系的每一个可观测的物理量,都 对应于一线性厄米算符。
可观测物理量: 如坐标、动量、能量等 某些化学概念并不是可观测物理量,比 如化学键的键级、原子的电负性等。
量子力学中每个可观测物理量对应的 算符为线性厄米算符,从而保证了可观测 的物理量为实数。
归一化公式,取正值
四、物质波的统计解释(1926,M. Born)
机械波:介质质点振动,不能在真空传播。
实物微粒波可以在真空传播——不是机械波 电磁波:电场和磁场的振动在空间传播,不依
赖于介质,能在真空传播。 实物微粒波产生于所有带电或不带电物体的
运动——不是电磁波
电子单缝衍射逻辑实验 入 射 光
1A ˆ1dexixp id d x exixp dx
exixp iddxexpix dx ei x x p iex ix p id x
x
这个波长相当于分子大小的数量级,说明分子 和原子中电子运动的波动性是显著的。
例3:计算动能为300 eV的电子的de Broglie波长。
T p2 2m
p 2mT
h h
p 2mT
6.62160 3J4s
29.11100 3k 1 g 1.60120 1C 9 30V0
1923年,德布罗意试图把粒子性 和波动性统一起来。1924年,在博士 论文《关于量子理论的研究》中提出 德布罗意波,同时提出用电子在晶体 上做衍射实验的想法。
法国物理学家,1929年
爱因斯坦觉察到德布罗意物质波
ห้องสมุดไป่ตู้
诺贝尔物理学奖获得者,思想的重大意义,评价说“我相信这
波动力学的创始人,量 是揭开我们物理学最困难谜题的第一
(x,y,z)eit
(x, y,z)
解:
2 ( x ,y ,z )2 e ite it( x ,y ,z )2 e 0( x ,y ,z )2
2 (x,y,z)2
2 (x,y,z)2
粒子在空间某点出现的概率密度不随 时间改变,称为定态。
定态波函数并不意味着粒子不运动, 而表明体系的状态不随时间改变。
二、合格波函数
1)单值 (几率密度要求) 2)连续,且二阶导数存在
( Schrödinger 方程要求) 3)平方可积,收敛有限 (w=∫v│ψ (x,y,z)│2 dτ要求)
若c为常数, ψ(x,y,z)和cψ(x,y,z)描述同一态 。
│ψ(x1,y1,z1)│2 :│ψ(x2,y2,z2)│2 = │cψ(x1,y1,z1)│2 :│cψ(x2,y2,z2)│2
主编 李奇 黄元河 陈光巨
第一章 量子理论基础
第七章 计算化学简介
第二章 原子的结构与性质
第八章 分子间作用力与超分子化学
第三章 双原子分子结构与分子光谱 第九章 晶体结构
第四章 分子对称性和群论
第十章 固体结构基础理论简介
第五章 多原子分子的结构和性质
第十一章 结构与材料
第六章 配位化合物的结构和性质
• 1.1量子力学基础 • 1.2量子力学在简单体系中的应用 • 1.3量子力学若干基本概念
一 . 黑体辐射能量密度 分布不服从经典统计规律
黑体辐射所研究的 问题是黑体腔内热辐射
能量密度ρ随波长λ
(或频率)的变化规律。
1911年诺贝尔物理学奖 维恩
维 恩 位 移 定 律 不 能 解 释
Planck 量子论
例: 请指出下列算符中的线性算符和线性厄米算符。
x ˆ, d, d x
d d x 2 2,
lo , gsin,,
id d x
线性算符:
xˆ,
d, dx
i d, dx
d2 dx2
线性厄米算符:
xˆ,
id, dx
d2 dx2
四、算符方程
Aˆ f x g x , Aˆ f x af x
(4)动量为p=h/λ, ρ=dN/dτ 光具有波粒二 象性 。
(5)光子存在动质量m,静止质量m0为0, 碰撞时动量和能量守恒。
粒子性
Eh
p h
波动性
h m c2
可见,光具有波粒二象性,通过h联系起来。
传播时——呈波动性
与物质作用时——呈粒子性
Einstein 光电方程
jdx
i
i
d
j
i
i
j
jd
i
i
j
d
i
j
i
d
dx
i
dx
得证。
u 1 *d d u x 2d x u 1 * u 2| u 2d d u x 1 *d x u 2(d d x)* u 1 * d x
密里根
荣获1923年 度诺贝尔物 理学奖
爱因斯坦关系式 p=h/λ在1923年被阿 瑟·荷里·康普顿的X射 线与电子碰撞的散射 实验证实。
康普顿
三、微观粒子的波粒二象性
实物微粒是指静止质量不为零的微观 粒子(m0≠0)。如电子、质子、中子、原 子、分子等。
1924年,德布罗意(de Broglie)受到 光的波粒二象性的启示,提出实物粒子也 具有波粒二象性。
1900年12月14日,普朗克公布了他对 黑体辐射的研究成果。
提出假设:黑体腔内辐射能的吸收或 释放不能连续进行,只能以某一个最小单 位做跳跃式改变,而且大小与辐射波频率 有关。
ε= hν , E= nε=nhν(n=1,2,3,…) Planck常数:h=6.6260755×10-34 J·s
普朗克
例如:
d 是线性算符; dx log, sin, 等不是线性算符。
三、线性厄米算符
若线性算符 Aˆ 和它的复共轭算符 Aˆ *
满足 u 1*A ˆu2d xu2A ˆ*u 1*d x
则 Aˆ 为厄米算符
厄米算符完整的证明如下:
i
Aˆ
jd
i
i
d dx
子力学的奠基人之一。 道微弱的希望之光”。
例1: 求m = 1.0×10-3 kg的宏观粒子以1.0×10-2 m·s-1 的速度运动时,粒子的de Broglie波长。
m h 1 v 16 3 .6 0 k 2 g 1 .0 1 6 1 3 0 J 4 2 2 0 m ss 1 6 .62 16 2 0 m 9 2
a
b
c
a. X射线通过铝箔所得到的衍射环
