基于Hopfield神经网络的数据分类
HopfieldNetwork霍普菲尔德网络入门

HopfieldNetwork霍普菲尔德⽹络⼊门简介Hopfield Network (霍普菲尔德⽹络),是 Hopfield 在1982年提出的⼀种基于能量的模型,发表的⽂章是 Neural networks and physical systems with emergent collective computational abilities。
基本结构如下图所⽰:⾸先我们来看Hopfield Network的⼀句话定义:Hopfield Network is a model that can reconstruct data after being fed with corrupt versions of the same data.也就是说利⽤Hopfield Network的过程是:some data→Hopfield Network→full data可以看到Hopfield Network的⼏个基本特点:只有单层神经元节点之间是全连接的只有输⼊,没有输出主要功能是:联想记忆 associatIve memory,例如重新构建图形。
假设我们在⽹络中存储了右侧的三张图⽚,如果我们只输⼊⼀部分图⽚,例如左侧的六张图⽚,⽹络可以从记忆中取出完整的图像。
Energy Function能量函数:Energy Function,可以看作⼀种代价函数。
这个概念最先在热⼒学中被提出,⽤来描述系统的能量值。
当能量函数求得的能量值达到最⼩值的时候,整个热⼒学系统达到稳定状态。
在深度学习之中,引⼊这个概念也是为了使模型达到稳定的状态。
Energy Based Models利⽤了能量函数的模型被称为Energy Based Models,EBM。
Energy Function for Images对于有d个像素的⿊⽩图像,假设每⼀个图像都有参数x={x j}1≤j≤d,那么我们可以建⽴如下形式的能量函数:如果我们有p个图像,我们就能得到基于E(x)的p个极⼩值。
基于Hopfield神经网络的数据分类

n t r v r o e d me t f o p t r a a i t .I d i o ,ame s r —r i t o s p t o w r od c e et e ewok t o e c me t e r w at n c p bl y n a d t n a u e tan me h d wa u r a d t e r a h O h i ol e i i f s
ic u e h e r i g ag r h n l d s t e l an n lo t m, h c a r p s d b lt a d Ve gn t r i h e rl n t o k e a  ̄ g t e n u a i w ih w s p o o e y B a t n r i , o t n t e n u a ew r , n b n h e r a l
中 图分 类 号 : P 1 .3 T 3 1 1 文 献 标 志码 : A
Da a ea sfc to ba e n Ho fed ne r lnewo k t ls i a in s d o p l u a t r i i
WANG e h a Zh n. u (colfMa a e et n cnm , Sh o o n gm n dEoo y a nU iri,Taj 0 0 2 hn) n esy ini 3 0 7 ,C ia v t n
基 于 H pe of l 经 网络 的数 据 分 类 i d神
王振 华
( 天津大学 管理与经济学部 , 天津 3 o 7 ) O o 2
( aghnu . al m i tm) w nze ha m i @g al o .
摘
要: 针对 H p e of l 经网络 的 自联 想特 性 , 出一种 新的 带有粒 子群优 化 过程 的 H p e i d神 提 of l 类算 法 ( S . i d分 P O
hopfield神经网络及其应用教学课件PPT

02
Hopfield神经网络的数学基础
向量运算和矩阵运算
向量加法
对应元素相加,得到一个新的向量。
向量数乘
一个标量与一个向量相乘,得到一个新的向量。
向量点乘
两个向量的对应元素相乘后求和,得到一个标量。
向量运算和矩阵运算
01
020304 Nhomakorabea向量叉乘
两个向量按照顺序相乘,得到 一个新的向量。
矩阵加法
对应位置的元素相加,得到一 个新的矩阵。
适用场景
旅行商问题、背包问题、图着色问题等组合优化问题,以 及各种工程优化问题。
05
Hopfield神经网络的未来发展
Hopfield神经网络与其他神经网络的结合
与卷积神经网络结合
利用Hopfield神经网络的记忆特性,与卷积神经网络共同处理图 像识别等任务,提高识别精度和稳定性。
与循环神经网络结合
训练方法
通过特定的训练算法,对 Hopfield神经网络进行训练,使 其能够记忆和识别特定的模式或 状态。
优化算法
采用优化算法(如梯度下降法、 遗传算法等),对Hopfield神经 网络的参数进行调整和优化,以 提高其性能和稳定性。
性能评估
通过测试和评估,对训练和优化 后的Hopfield神经网络进行性能 评估,包括准确率、稳定性、实 时性等方面的评估。
Hopfield神经网络及其应用教 学课件
目
CONTENCT
录
• Hopfield神经网络简介 • Hopfield神经网络的数学基础 • Hopfield神经网络的实现 • Hopfield神经网络的应用案例 • Hopfield神经网络的未来发展
01
Hopfield神经网络简介
霍普菲尔德Hopfield神经网络

故对任意的神经元k有E 0。另外能量函数是有界的,
所以它总能收敛到它的一个局部极小点。
全并行方式下也有同样的结论。
DHNN网络设计
用 DHNN实现联想记忆需要考虑两个重要的 问题:
①怎样按记忆确定网络的W和;②网络给定之 后如何分析它的记忆容量。下面将分别讨论。
1、权值设计的方法 2、记忆容量分析 3、权值修正的其它方法
图2.8.2
两种工作方式
DHNN主要有以下两种工作方式: 〔1〕串行工作方式 在某一时刻只有一个神经 元按照上式改变状态,而其它神经元的输出不 变。这一变化的神经元可以按照随机的方式或 预定的顺序来选择。 〔2〕并行工作方式 在某一时刻有N个神经元 按照上式改变状态,而其它的神经元的输出不变。 变化的这一组神经元可以按照随机方式或某种规 那么来选择。当N=n时,称为全并行方式。
dE 0,当且仅当 dv i 0时,dE 0, i 1,2, , n
dt
dt
dt
证明: dE n E dv i
dt i1 vi dt
E
vi
1 2
n
w ij v j
j 1
1 2
n
w ji v j
j 1
Ii
ui Ri
n
w ij v j
j 1
Ii
ui Ri
ci
du i dt
ci
1 i
穿插干扰
网络在学习多个样本后,在回忆阶段即验证该记忆样 本时,所产生的干扰,称为穿插干扰。
对外积型设计而言,如果输入样本是彼此正交的,n个 神经元的网络其记忆容量的上界为n。但是在大多数情况 下,学习样本不可能是正交的,因而网络的记忆容量要 比n小得多,一般为(0.13~0.15)n,n为神经元数。
五.反馈(Hopfield)神经网络

五.反馈(Hopfield)神经⽹络 前馈⽹络⼀般指前馈神经⽹络或前馈型神经⽹络。
它是⼀种最简单的神经⽹络,各神经元分层排列。
每个神经元只与前⼀层的神经元相连。
接收前⼀层的输出,并输出给下⼀层,数据正想流动,输出仅由当前的输⼊和⽹络权值决定,各层间没有反馈。
包括:单层感知器,线性神经⽹络,BP神经⽹络、RBF神经⽹络等。
递归神经⽹络(RNN)是两种⼈⼯神经⽹络的总称。
⼀种是时间递归神经⽹络(recurrent neural network),⼜名循环神经⽹络,包括RNN、LSTM、GRU等;另⼀种是结构递归神经⽹络(recursive neural network)。
反馈⽹络(Recurrent Network),⼜称⾃联想记忆⽹络,输出不仅与当前输⼊和⽹络权值有关,还和⽹络之前输⼊有关。
其⽬的是为了设计⼀个⽹络,储存⼀组平衡点,使得当给⽹络⼀组初始值时,⽹络通过⾃⾏运⾏⽽最终收敛到这个设计的平衡点上。
包括Hopfield,Elman,CG,BSB,CHNN、DHNN等。
反馈⽹络具有很强的联想记忆和优化计算能⼒,最重要研究是反馈⽹络的稳定性(即其吸引⼦)离散Hopfield神经⽹络Hopfield神经⽹络是⼀种单层反馈,循环的从输⼊到输出有反馈的联想记忆⽹络。
离散型为DHNN(Discrete Hopfield Neural Network)和连续型CHNN(Continues Hopfield Neural Network)。
Hopfield最早提出的⽹络是⼆值神经⽹络,各神经元的激励函数为阶跃函数或双极值函数,神经元的输⼊、输出只取{0,1}或者{ -1,1},所以也称为离散型Hopfield神经⽹络DHNN(Discrete Hopfiled Neural Network)。
在DHNN中,所采⽤的神经元是⼆值神经元;因此,所输出的离散值1和0或者1和-1分别表⽰神经元处于激活状态和抑制状态。
霍普菲尔德(Hopfield)神经网络概述

Hopfield网络的应用
组合优化 (TSP问题) 组合优化问题,就是在给定约束条件下, 求出使目标函数极小(或极大)的变量组 合问题。 将Hopfield网络应用于求解组合优化问题, 就是把目标函数转化为网络的能量函数, 把问题的变量对应于网络的状态。这样当 网络的能量函数收敛于极小值时,问题的 最优解也随之求出。
Hopfield网络的特点
单层反馈式网络
x1 o1 W x2 o2 … … xn
on
Hopfield网络的特点
灌输式学习方式 灌输式学习中网络权值不是通过训练逐渐 形成的,而是通过某种设计方法得到的。 权值一旦设计好就一次灌输给网络,不再 变动, 这种学习是死记硬背式的,而不是训练式 的。
Hopfield网络的特点
各神经元的状态在运行中不断更新
x1 o1 W x2 o2 … … xn
on
Hopfield网络的特点
首次引入能量函数
考虑了输入与输出的延迟因素
Hopfield网络的分类
根据激活函数的不同,可以分为: 离散型 Hopfield神经网络(DHNN) 1 netj ≥ 0 f(netj ) = sgn(netj ) = − 1 netj < 0 连续型 Hopfield神经网络(CHNN)
霍普菲尔德(Hopfield Hopfield) Hopfield 神经网络概述
旅行商问题(TSP)
旅行商问题(Traveling Saleman Problem, TSP)又译为旅行推销员问题、货郎担问题, 简称为TSP问题,是最基Байду номын сангаас的路线问题。
是指一名推销员要拜访多个地点时,如何 找到在拜访每个地 TSP问题点一次后再回 到起点的最短路径。
人工神经网络-连续型Hopfield神经网络
两点说明:
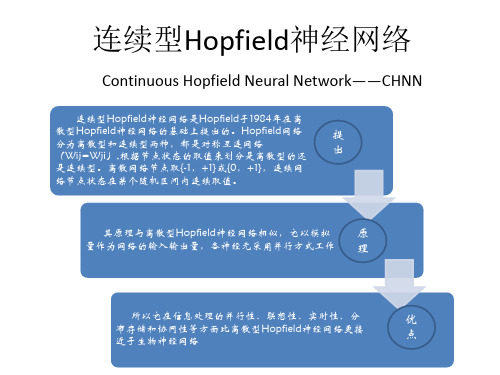
1)能量函数为反馈网络的重要概念。 根据能量函数可以方便的判断系统的稳定 性; 2)Hopfield选择的能量函数,只是保 证系统稳定和渐进稳定的充分条件,而不 是必要条件,其能量函数也不是唯一的。
* CHNN的几点结论
1)具有良好的收敛性; 2)具有有限个平衡点; 3)如果平衡点是稳定的,那么它也一定是渐进稳 定的; 4)渐进稳定平衡点为其能量函数的局部极小点; 5)能将任意一组希望存储的正交化矢量综合为网 络的渐进平衡点; 6)网络的存储信息表现为神经元之间互连的分布 式动态存储; 7)网络以大规模、非线性、连续时间并行方式处 理信息,其计算时间就是网络趋于平衡点的时间。
E 1 WijVj I i Ui Vi Ri j
由连续Hopfield运行方程可得
dVi d E dU i dU i C i C i C i f 1 i V dt dV Vi dt dVi i
将上式代入原式可得:
dV i dE C i dt dt j 1 f i V
WijViVj
i 1 j 1
n
n
ViIi
i 1
n
R i i
1
n
1
Vi
0
f 1 dV V
求取 其中:
dE
dt
dE dt
i
E dV i Vi dt
E 1 Vi 2
1 WijVj 2 j
W jiVj j
Ii
1
Ri
Ui
• 由于Wij=Wji 则有:
提 出
其原理与离散型Hopfield神经网络相似,它以模拟 量作为网络的输入输出量,各神经元采用并行方式工作
第五章霍普菲尔德(Hopfield)神经网络

反馈网络(Recurrent Network),又称自联 想记忆网络,如下图所示:
x1
x2
x3
y1
y2
y3
图 3 离散 Hopfield 网络
考虑DHNN的节点状态,用yj(t)表示第j个神经元,即节点j在时 刻t的状态,则节点的下一个时刻t+1的状态可以求出如下:
1, u j (t) 0 y j (t 1) f[u j (t)] 0, u j (t) 0 u j (t) w i, j y i (t) x j θ j
在不考虑外部输入时,则有
j 1,2,..., n
n y j (t 1) f w i, j yi (t) θ j i 1
•通常网络从某一初始状态开始经过多次更新后才可 能达到某一稳态。使用异步状态更新策略有以下优点: (1)算法实现容易,每个神经元节点有自己的状态 更新时刻.不需要同步机制; (2)以串行方式更新网络的状态可以限制网络的输 出状态,避免不同稳态以等概率出现。 一旦给出HNN的权值和神经元的阈值,网络的状态转 移序列就确定了。
5.2 离散Hopfield网络
• Hopfield最早提出的网络是神经元的输出为 0-1二值的NN,所以,也称离散的HNN (简称为 DHNN).
–下面分别讨论DHNN的
• • • • 结构 动力学稳定性(网络收敛性) 联想存储中的应用 记忆容量问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
J l = J l -1 + 并且: ( Δ(ml) )
( l) ij
∑Δ
m =1 m -1
( l) m
( 6)
=
( k N )( ξ
( l -1 ) ij
l i
- h i ) ( ξ lj - h j )
( 7)
其中 Δm 是突触矩阵在 m 次呈现之后的改变值, 并且局部值 h 是在突触矩阵第 m - 1 次改动后才计算: hi =
0
引言
分类算法作为数据挖掘的一个重要分支, 是指从数据中
接。每个神经元都通过连接权重接受所有其他神经元输出反 [4 ] 其目是为了让每个神经元的输出能够接受所 馈来的信息 , 有其他神经元输出的控制, 从而使各神经元能够相互制约 。 Hopfield 分为离散型 Hopfield 神经网络和连续型 Hopfield 神经网络。连续型 Hopfield 神经网络主要用于优化, 而离散 离散 Hopfield 网络的 型 Hopfield 主要用于联想记忆。 其中, 神经元变化函数为符号函数, 网络的节点状态仅取两值 + 1 和 - 1 ( 或 0 和 + 1 ) 。离散型 Hopfield 神经网络结构如图 1 所 示。由于离散型 Hopfield 的结构特点, 其输出的数据与其输 入的模式大小以及维度相等 。 对于离散型 Hopfield 神经网络, 其神经元可取二值 ( 1 , - 1 ) 或( 1 , 0 ) 。其中神经元 i 与神经元 j 之间的突触权值为 w ij , 因此对于一个有 N 个神经元的 Hopfield 神经网络, 其权 重的矩阵大小为 N × N 。而其独有的联想记忆过程则是通过 一系列的迭代过程, 直至系统稳定。 具体为: 假设某一时间 Hopfield 神经网络的状态为: S =[ S1 , S2 , …, Si , …, SN ] 该神经元的局部域( local field) h i 为: ( 1) 其中: S i 代表第 i 个神经元的当前状态, 即可为 + 1 或 - 1 , 则
选出已经分好类的训练集, 再在该训练集上运用数据挖掘分 类的技术, 建立分类模型, 并对没有分类的数据进行分类 。 这 并可以进一步衍生出预 测 算 类算法具有广泛的应用领域, 法
[1 ]
。分类技术主要分为训练和分类两个步骤 。 在训练过
程中, 算法会对有类标号的训练集进行特征选择, 然后进行训 。 练生成分类器 而在分类过程, 分类器会先对无类标号的样 本进行特在选择, 然后分类, 判定其类别。目前主要的分类算 法分为监督学习和半监督学习
j
( 2)
其中 w ij 为 j 神经元到 i 神经元的连接权重, 则该神经元接下 来的状态 S' 则根据其局部域和原状态通过一个函数得出: Si ' =
Marcelo G. Blatt 和 Eduardo G. Vergini 提出 容量过低的缺点, [8 ] 了一种新的局部学习规则 ( 后文简称 BV 算法) 。这种学习 规则对训练集没有任何要求, 只需要通过对训练集有限次的 呈现, 从而确保所训练的模式的稳定性 。 假设神经网络需要 l l -1 并且假设 J 是已经存储了 l - 1 个ion based on Hopfield neural network
WANG Zhenhua
( School of Management and Economy, Tianjin University, Tianjin 300072 , China)
Abstract: According to Hopfield neural network's autoassociate property, a new Hopfield classification algorithm ( PSOHOP for short) was proposed, which includes the discrete particle swarm optimization. This new classification algorithm includes the learning algorithm, which was proposed by Blatt and Vergin, to train the neural network, enabling the neural network to overcome the demerit of low pattern capability. In addition, a measuretrain method was put forward to decrease the time complexity, making the classification more efficient. To better deal with the noise data such as missing value, the algorithm takes the advantage of the autoassociate property of the discrete Hopfield neural network, and applies it in the expression of the attribute and class. The PSOHOP algorithm also contains a discrete particle swarm optimization to optimize the structure of the neural network. By distributing the redundant neurons to the attributes,the weight of the attributes can be changed, resulting in the increase of the precision and reflecting the significance of different attributes. The PSOHOP algorithm is a new approach to classify the data and its validity is substantiated by abundant experiment results Key words: Hopfield neural network; Particle Swarm Optimization ( PSO) ; autoassociate; classification
N m m vμ μ j
。
2
粒子群优化算法
PSO ) 由 粒 子 群 优 化 算 法 ( Particle Swarm Optimizer, Kenney 和 Eberhart 于 1995 年提出, 它源于对鸟类捕食行为的 [14 ] 研究, 其最初提出是针对连续空间的优化问题 。 PSO 算法 中每个粒子即解空间中的一个解, 它根据自己的移动经验和 同伴的移动经验来调整自己的移动 。每个粒子在移动过程所 经历过的最好位置, 就是粒子本身找到的最优解 。 整个群体 所经历过的最好位置, 就是整个群体目前找到的最优解 。 前 者叫作个体极值( p best ) , 后者叫作全局极值( g best ) 。 每个粒 子都通过上述两个极值不断更新自己, 从而产生新一代群体。 实际操作中通过由优化问题所决定的适应度函数值来评价粒 [15 ] 子的优劣程度 。显然, 每个粒子的行为就是种追随着当前 的最优粒子在解空间中搜索 。 类似于遗传算法, 粒子群算法 也是使用群体演化的策略来不断改进问题的候选解 。其标准 版本可用如下的迭代式表达: v i = w × v i + c1 × rand( ) × ( p ibest - x i ) + c2 × rand( ) × ( g ibest - x i ) x = xi + vi
收稿日期: 2011 - 10 - 05 ; 修回日期: 2011 - 11 - 15 。 作者简介: 王振华( 1989 - ) , 男, 四川成都人, 硕士研究生, 主要研究方向: 数据挖掘、 神经网络。
增刊 2 hi =
王振华: 基于 Hopfield 神经网络的数据分类
93
∑w S
ij j≠ i
目前 Hopfield 神 经 网 络 的 训 练 算 法 主 要 分 为 三 类, 即 Hebb 学习算法、 伪逆矩阵学习算法以及感知器方式的学习算 法。 第一类为传统的 Hebb 算法, 其学习方法的绝对容量有 [4 ] 。 为此 Storkey 在原有 Hebb 学习算 限, 仅为 N / ( 0 . 5ln N) [5 ] 法的基础上进行改进, 提出了一些新的训练方式 。 第二类训练方法为伪逆方法, 这一类算法都是希望通过 伪逆算法来得出 Hopfield 神经网络的权重矩阵, 其中最传统 的方式为: wv ij = Q = 1 ∑ξvi ( Q -1 ) N∑ v =1 μ =1 1 v ξk ξμ k N∑ k =1
∑{J
j =1
N
m -1
+
∑( Δ
k =1
( l) k
)
ij
}ξlj
( 8)
k 越大则存储模式所需要的步骤就 其中: k 是一个记忆系数, 如果: 越少。该算法另外一个重要的特点是当 0 ≤ T < 1 时, n μ ≥ log k 那么: hi ξμ i ≥ T;
[ ( 1 -N T) ]
2
( 9)
图1
离散型 Hopfield 神经网络结构示意图
i = 1, …, N
( 10 )
该算法通过伪逆矩阵的近似计算, 并且除去所有的自连 接权重, 大大地提高了 Hopfield 神经网络的存储容量, 同时保 留了 Hebb 算法中样本可以递增学习的优点, 避免了对已训 练模式的干扰
