圆轴扭转时的应力(材料力学)
材料力学(第五版)扭转切应力
p
q
a’ b’
φ 圆轴两端面的
相对扭转角
M
d’
e
M
φ q R
e
c’
qq平面相对于pp的相对扭转 角为： d 圆轴表面的切应变γ 为：
p p
q
d c
p
a a
Rd a a d R ad dx dx
ρ
b
q
d R (a ) dx
b
现研究圆轴内部的切应变
圆轴内部的切应变
作 业
3-1
3-2
3-7
3-8
d G (c ) dx
0
0
d maxGR dx
R
三、静力关系
M
e
T dA ) (
A
T
代入: 得:
d G ( c ) dx
d 2 T G dA dx A
dA
令: 得:
IP dA
D
1
max
D2
扭转时切应力沿半径线性分布，圆心部分的 材料未能充分发挥作用。
例题
已知： P1=14kW,
P2= P3= P1/2=7 kW
n1= n2= 120r/min, z1=36, z3=12; d1=70mm, d 2 =50mm, d3=35mm
求:各轴横截面上的最大切应力。
P1=14kW， P2= P3=7 kW n1= n2= 120r/min
p
q
a’ b’
M
d’
e
M
e
c’
p
q
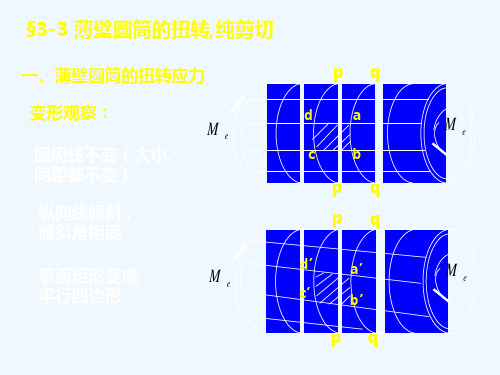
因为各圆周线大小、形状、间距都不变
2、沿同一圆周线上的切应力 大小相等
材料力学-第4章圆轴扭转时的强度与刚度计算
I
C
A
II
D
III
I
II
III
M
x
0
确定各段圆轴内的扭 矩。
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
3 ． 建立 Mx － x 坐 标系，画出扭矩图 建 立 Mx － x 坐 标 系，其中x轴平行于 圆轴的轴线，Mx轴垂 直于圆轴的轴线。将 所求得的各段的扭矩 值，标在 Mx － x 坐标 系中，得到相应的点 ，过这些点作x轴的 平行线，即得到所需 要的扭矩图。
P M e 9549 [N m] n
其中P为功率，单位为千瓦（kW）；n为轴的转速，单位为转/ 分（r/min）。 如果功率P的单位用马力（1马力=735.5 N•m/s），则
P[马力] M e 7024 [N m] n[r / min]
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律
圆轴扭转时横截面上的剪应力分析 与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
绘出扭矩图：
第4章 圆轴扭转时的强度与刚度计算
B C
I
外加扭力矩、扭矩与扭矩图 A III D II
I 扭矩Mn-图
II
III
159.2
（+）
（-）
63.7 159.2
M n,max 159.2( N m)
（在CA段和AD段）
《工程力学：第七章+圆轴扭转时的应力变形分析与强度和刚度设计》
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
背 景
材
料
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
背 景
材
料
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 一、扭转的概念 复习 Me
mA
阻抗力 偶
主动力 偶
me
受力特点：杆两端作用着大小相等、方向相反的力偶，且力 偶作用面垂直于杆的轴线。 变形特点：杆任意两截面绕轴线发生相对转动。 主要发生扭转变形的杆——轴。
Mx 16M x 16 1.5kN m 103 max＝ ＝ 3 ＝ ＝50.9MPa 3 4 -3 4 WP πD 1 π 90mm 10 1 0.9传动轴的强度是安全的。
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 2．确定实心轴的直径 根据实心轴与空心轴具有同样数值的最大剪应力的要求， 实心轴横截面上的最大剪应力也必须等于 50.9MPa 。若设实 心轴直径为d1，则有
b b
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 T 一、 扭转强度计算 变截面圆轴: max W [ ] 1、强度条件： p
max
max
对脆性材料 [ ] 对韧性材料 [ ]
b
nb
材料力学 圆轴扭转内力、应力
T
IP
27
§ 3.4 圆轴扭转时横截面上的应力
Mechanic of Materials
T
Ip
—横截面上距圆心为处任一点切应力计算公式。
4. 公式讨论：
① 仅适用于各向同性、线 弹性材料，在小变形时的 等圆截面直杆。
τ
O
② 式中： —该点到圆心的距离。
T—横截面上的扭矩，由截面法通过外力偶矩求得。 IP—极惯性矩，纯几何量，无物理意义。
重点：扭转内力、应力。 难点：切应力互等定理的证明。 学时安排：2
Mechanic of Materials
第八讲内容目录 第三章 扭 转
§ 3.1 扭转的概念和实例和实例 § 3.2 外力偶的计算 扭矩与扭矩图 § 3.3 纯剪切 § 3.4 圆轴扭转时横截面上的应力
目录
§ 3.1 扭转的概念和实例
§3-4 圆轴扭转时横截面上的应力
约为80GPa。
剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三
个常数。对各向同性材料，这三个弹性常数之间存在下列关系：
G
E 2(1
)
22
Mechanic of Materials
§ 3.4 圆轴扭转时横截面上的应力
一、圆轴扭转时横截面上的应力公式推导思路 （一）几何方面：
扭转时，圆轴的表面 变形和薄壁圆筒表面变形 相似。实验现象：
M
A
9549
36 300
1146N.m
MB
MC
9549
11 300
350N.m
MD
9549
第9章圆轴扭转时的应力变形分析与强度刚度设计
n1=n2= 120r/min
转速与齿数成反比，所以有
1
36
3 ＝1 × ＝ 120 ×
r/min＝360r/min
3
12
2. 根据 = 9549
N ⋅ m 计算各轴的扭矩
3
Mx1=T1=1114 N.m
Mx2=T2=557 N.m
Mx3=T3=185.7 N.m
大连大学
10
9.1 工程上传递功率的圆轴及其扭转变形
A
B
D ▪ 不难看出，圆轴受扭后，将
产生扭转变形（twist
deformation），圆轴上的每
个微元的直角均发生变化，
这种直角的改变量即为切应
C'
变。这表明，圆轴横截面和
纵截面上都将出现切应力分
τ
别用 和 表示。
D'
A'
B'
大连大学
横截面上的切应力分布有着很大的差异。本章主要介绍圆轴扭转时的
应力变形分析以及强度设计和刚度设计。
▪ 分析圆轴扭转时的应力和变形的方法与分析梁的应力和变形的方法基
本相同。依然借助于平衡、变形协调与物性关系。
第9章 圆轴扭转时的应力变形分析与强度刚度设计
▪ 9.1 工程上传递功率的圆轴及其扭转变形
▪ 9.2 切应力互等定理
3. 设计螺栓等间距分布时的直径d
利用1中所得的结果，应用剪切假定计算的强度条件，有
2
=
=
≤
2
8××
4×
×
4
螺栓直径 ≥
大连大学
= 35.2mm
圆轴扭转时的强度条件
圆轴扭转时的强度条件
圆轴扭转时的强度条件可以通过研究轴材料的变形和破坏来确定。
以下是圆轴扭转时的强度条件：
1. 扭转强度：圆轴在扭转时会受到扭矩的作用，扭矩会产生剪应力。
扭转强度是指材料在扭转作用下能够承受的最大剪应力。
扭转强度与材料弹性模量、截面形状和尺寸有关。
2. 疲劳强度：圆轴在长时间的扭转作用下可能会发生疲劳破坏。
疲劳强度是指材料在循环载荷作用下能够承受的最大应力范围，它与材料的疲劳寿命有关。
3. 断裂强度：圆轴在扭转超过其承受能力时可能会发生断裂破坏。
断裂强度是指材料在正常使用条件下能够承受的最大应力，它与材料的断裂特性有关。
为了满足圆轴的强度条件，一般采取以下措施：
1. 选择合适的轴材料，保证其扭转强度和断裂强度满足工程要求。
2. 根据应力分布的特点，设计合理的截面形状和尺寸，以提高扭转强度和疲劳强度。
3. 对于长期扭转作用下的轴，可以采取热处理等工艺措施来提高其强度和耐疲劳性能。
需要注意的是，圆轴的强度条件与其几何形状、材料特性、工作条件等因素密切相关，因此在具体设计时需要进行详细的力学计算和强度分析。
13-1应力状态理论-材料力学
• (3)式中两式相减与(4)式比较:
max min
max
22
my in
maxx2
y
2
2 xy
• (3)式中两式相加:
mmmmianiaxnx
maxx2mx yi2nyx2
x
2
2. 应力圆作法
y
yx
B
xy
A x
x y
2
a (x ,xy)
fc
o
Re
b (y ,yx)
•在- 坐标中，取对应于单元体A、B面的点a、b； • a、b两点连线交轴于c点； •以c为圆心ac为半径作圆。
x y
2
a (x ,xy)
fc
o
Re
b (y ,yx)
9、单向应力状态：三个主应力中只有一个主应力不等于零的 应力状态叫单向应力状态。例如：拉压杆 叫单向应力状态，纯弯曲状态。
■原始单元体的画法（各侧面应力已知的单元体）
P
P
1、截取无限小六面体作为单元体；
1）截取横截面； 2）在横截面上平行于边缘截取小矩形； 3）从横截面开始沿边缘截取小立方体；
2、分析单元体各个面的含义，分清哪个面是横截面；
杆
轴
I p梁
M y
Iz
x
x
QS
z
Izb
z
z
zx zy
xz yz
y
xy
yx
y
3、原始单元体：各侧面应力已知的单元体
M y
Iz
QSz
梁
Izb
材料力学 第7章 扭转
T Me
m
m Me
xn
2. 扭矩的符号规定
Me
T
T矢量的方向与截面外法线方 向相同时为正，反之为负。
n
x
T Me
7.2 扭矩和扭矩图
3. 扭矩图 (1) 定义：扭矩随杆轴线变化规律的图线称为扭矩图。 (2) 扭矩图的绘制步骤： ① 确定扭矩随截面位置的变化规律， ② 建立扭矩坐标系， ③ 画扭矩图。
7.2 扭矩和扭矩图
例7-1 已知一传动轴， n =300r/min，主动轮输入 PA=36kW， 从动轮输出 PB=PC=11kW，PD=14kW，求指定截面的扭矩。
解： 1. 计算外力偶矩
MB
B
MA
9549
PA n
1146(N m)
MC
1
2n
C
A
1
2 MA
MD
3
D
3
M B MC 350N m
7.3 圆轴扭转时的应力分析和强度计算
钻杆
7.3 圆轴扭转时的应力分析和强度计算
传动轴
第七章 扭转
7.1 引言 7.2 扭矩和扭矩图 7.3 圆轴扭转时的应力分析和强度计算 7.4 圆轴扭转时的变形计算和刚度设计
7.4 圆轴扭转时的变形计算和刚度设计
一、圆轴扭转时的变形
dφ T dx GIP dφ T dx
WP
πD13 16
D1
3 16Tmax 3 16 1.5 106
π[ τ ]
π 60
50mm
D1
(2) 空心轴
τ max
Tmax WP
[τ]
WP
πD23 (1 16
α4 )
d2
D2
讨论圆轴扭转时的应力状态
130一、讨论圆轴扭转时的应力状态，并分析铸铁试件受扭时的破坏现象。
解 根据第十九章讨论，圆轴扭转时，在横截面的边缘处剪应力最大，其数值为:n n W M=τ (e )在圆轴的最外层，按图22-5(a )，所示方式取出单元体ABCD ，单元体各面上的应力如图22-5(b )所示。
在这种情况下，ττσσ===xy y x ，0 （f ）单元体侧面上只有剪应力作用，而无正应力作用的这种应力状态称为纯剪切应力状态。
把(f )式代入公式(22-6)得:min maxσσ ττσσσσ±=+-±+=22)2(2xy y x y x 由公式（22-5）：yx xytg σστα--=220 →∞-所以 2709020--=或α450-=α 或 1350-=α以上结果表明，从x 轴量起，由 450-=α(顺时针方向)所确定的主平面上的主应力为max σ；而由 1350-=α所确定的主平面上的主应力为min σ。
按照主应力的记号规定：τσσστσσ-=====min 32max 10所以，纯剪切是二向应力状态，两个主应力的绝对值相等，都等于剪应力τ，但一个为拉应力，一个为压应力。
圆截面铸铁试件扭转时，表面各点max σ所在的主平面联成倾角为︒45的螺旋面[图22-5（a ）]。
由于铸铁抗拉强度较低，试件将沿这一螺旋面因拉伸而发生断裂破坏，如(a )(c ) 图22-5131图22-5（c ）所示。
二、 图22-6（a ）所示为一横力弯曲下的梁，求得截面m －n 上的弯矩M 及剪力Q 后，算出截面上一点A 处弯曲正应力和剪应力分别为：MPa MPa 50,70=-=τσ[图22-6（b ）]试确定A 点处的主应力及主平面的方位，并讨论同一横截面上其它点处的应力状态。
解 把从A 点处截取的单元体放大如图22-6（c ）所示。
选定x 轴的方向垂直向上，则0=x σ MPa y 70-=σ MPa xy 50-=τ由公式（22-5）得： 429.1)70(0)50(2220=----=--=yx xytg σστα︒=5520α或︒235 ︒=5.270α或︒5.117从x 轴量起，按逆时针方向量取的角度︒5.27，确定max σ所在主平面，以同一方向量取的角度,5.117︒确定min σ所在的另一主平面。
材料力学教案 第3章 扭转
第3章扭转教学目的：理解圆轴扭转的受力和变形特点，剪应力互等定理；掌握圆轴受扭时的内力、应力、变形的计算；熟练掌握圆轴受扭时的强度、刚度计算。
教学重点：外力偶矩的计算、扭矩图的画法；纯剪切的切应力；圆杆扭转时应力和变形；扭转的应变能。
教学难点：圆杆扭转时截面上切应力的分布规律；切应力互等定理，横截面上切应力公式的推导，扭转变形与剪切变形的区别；掌握扭转时的强度条件和刚度条件，能熟练运用强度和刚度计算。
教具：多媒体。
通过工程实例建立扭转概念，利用幻灯片演示和实物演示表示扭转时的变形。
教学方法：采用启发式教学，通过提问，引导学生思考，让学生回答问题。
通过例题、练习和作业熟练掌握强度和刚度计算。
本章中给出了具体情形下具体量的计算公式，记住并会使用这些公式，强调单位的统一，要求学生在学习和作业中体会。
教学内容：扭转的概念；扭转杆件的内力（扭矩）计算和画扭矩图；切应力互等定理及其应用，剪切胡克定律与剪切弹性模量；扭转时的切应力和变形，圆杆扭转时截面上切应力的分布规律；扭转杆件横截面上的切应力计算方法和扭转强度计算方法；扭转杆件变形（扭转角）计算方法和扭转刚度计算方法。
教学学时：6学时。
教学提纲：3.1 扭转的概念和实例工程实际中，有很多构件，如车床的光杆、搅拌机轴、汽车传动轴等，都是受扭构件。
还有一些轴类零件，如电动机主轴、水轮机主轴、机床传动轴等，除扭转变形外还有弯曲变形，属于组合变形。
例如，汽车方向盘下的转向轴，攻螺纹用丝锥的锥杆（图3-1）等，其受力特点是：在杆件两端作用大小相等、方向相反、且作用面垂直于杆件轴线的力偶。
在这样一对力偶的作用下，杆件的变形特点是：杆件的任意两个横截面围绕其轴线作相对转动，杆件的这种变形形式称为扭转。
扭转时杆件两个横截面相对转动的角度，称为扭转角，一般用φ表示（图3-2）。
以扭转变形为主的杆件通常称为轴。
截面形状为圆形的轴称为圆轴，圆轴在工程上是常见的一种受扭转的杆件。
材料力学 (扭转)(四章 圆轴扭转时的强度与刚度计算)
Mx 0: T1 MA 0
C
T1 MA 7.03KN.m
22
Mx 0: -T2 MC 0
T2 MC 2.32KN.m
X
(4)讨论现在的设计是否合理。
若将A轮与B轮调换， X 则扭矩图如下：
可见轴内的最大扭矩值减小了。10
T(KN.M)
§3.2 薄壁圆筒扭转
在圆筒表面画 上许多纵向线 与圆周线,形成 许多小方格.
G
剪切胡克定律
Ｇ－剪切弹性模量
G E
2(1 )
2021/8/19
17
圆轴扭转时的应力和变形
根据观察到的现象， 经过推理，得出关于圆 轴扭转的基本假设。
m
m
圆轴扭转变形前的横截面，变形后仍保持为平面，
形状和大小不变。且相邻两截面间的距离不变。这就 是圆轴扭转的平面假设。
2021/8/19
18
二. 应力在横截面上的分布
2
而象电动机的主轴，水轮 机的主轴也承受扭转作用， 但这些零件除扭转变形外， 还伴随有其它形式的变形， 属于组合变形。
• 以扭转变形为主要变形形式的构件通常称为轴。 • 工程上应用最广的多为圆截面轴，即圆轴。
2021/8/19
3
• 扭转受力的特点是：
• 在构件的两端作用两个大小相等、方向相反且作 用面垂直于构件轴线的力偶矩。致使构件的任意 两个截面都发生绕构件轴线的相对转动，这种形 式的变形即为扭转变形。
在转矩m作用下，发现圆 周线相对地旋转了一个角 度，但大小、形状和相邻 两圆周线的距离不变。
表明，在圆筒的横截面上没有正应力和径向剪应力。
2021/8/19
11
设圆筒平均半径为r，筒壁厚度为t
因圆筒壁厚很小，可认为剪应力沿
材料力学第3章-扭转
第3章 扭转1、扭转的概念：杆件的两端个作用一个力偶，其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线，致使杆件的任意两个横截面都发生绕轴线的相对转动，即为扭转变形。
2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中，e M 为外力偶矩。
又由截面法：e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。
规定：若按右手螺旋法则把T 表示为矢量，当矢量方向与研究部分中截面的外法线的方向一致时，T 为正；反之为负。
3、纯剪切（1）薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=（2）切应力互等定理：在单元体相互垂直的两个平面上，切应力必然成对存在，且数值相等；两者都垂直于平面的交线，方向则共同指向或背离这一交线。
（3）切应变 剪切胡克定律：当切应力不超过材料的剪切比例极限时，切应变γ与切应力τ成正比。
γτG = G 为比例常数，称为材料的切变模量。
弹性模量E 、泊松比μ和切变模量G 存在关系：)1(2μ+=EG 4、圆轴扭转时的应力（1）变形几何关系：距圆心为ρ处的切应变为dxd ϕργρ=（2）物理关系：ρτ为横截面上距圆心为ρ处的切应力。
dxd G G ϕρτγτρρρ=⇒= （3）静力关系：内力系对圆心的力矩就是横截面的扭矩：dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式：dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩（截面二次极矩）横截面上距圆心为ρ的任意点的切应力：pI T ρτρ=ρ最大时为R ，得最大切应力：pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。
则tW T =max τp I 和t W 的计算（1）实心轴：3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===（2）空心轴：)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角，l 为两横截面间的距离。
圆轴扭转时的强度与刚度计算材料力学
•
度条件为
max
Mn Wp
maxG MnIp •180
返回 下一张 上一张 小结
精品课件！
精品课件！
• （五）用强度，刚度条件解决实际部题的步骤
•
1）求出轴上外力偶矩；
•
2）计算扭矩和作出扭矩图；
•
3）分析危险截面；
•
4）列出危险截面的强度、刚度条件并进行计算。
返回 下一张 上一张 小结
返回 下一张 上一张 小结
• 二 剪应力计算：
• 1 几何关系： • • 2 物理关系：
P G
• • 3 静力关系：
Mnl d
G Ip
Mn d GIp d
• 扭转剪应力公式：
p
M n Ip
max
Mn Wp
返回 下一张 上一张 小结
•三
• •
截面极惯性矩 ；抗扭截面模量
ax
•
故求得直径为
4010
D3
16Mnmax3
1
6
628.467
0 .03 m 332 .2 3 mm
返回 下一张 上一张 小结
• （4）由刚度条件，得
maxM G nm pIax180G M nm D a4x 18 G n m 2a•x 18038 2 0 216 80 . 46 7 21 180
m ax0 .5 WM Pn 0 .6
0 .8 1 .0
• 2 强度计算的三个方面：
•
a 强度校核
•
b 截面选择
•
c 许可荷载确定
返回 下一张 上一张 小结
• 例1 如图为一钢圆轴，两端受外力偶m的作用，已知m=2.5
• KN.m,直径d=60m，许用应力为60MPa。试校核该轴的强度。
材料力学(第五版)扭转切应力 PPT课件
pq
da
Me
cb
pq
pq
d’ a’
Me
c’
b’
pq
切应力互等定理
切应力互等定理
d
a
d
a
c
b
c
b
在相互垂直的两个截面上，切应力 必然成对出现，且大小相等，方向为共 同指向或共同背离两个截面的交线。
二、剪切胡克定律
d
a
Me
c
b
d’
γ
a’
pq
da
Me
cb
pq pq
T3 158.7 N m
Wp1
d13 16
703 109 16
67.34 106 m3
Wp 2
d32 16
503 109 16
24.54 106 m3
Wp3
d33 16
353 109 16
8.418106 m3
(max )E
D4 d 4 32
D
I p
πD4
1 α4 32
d
O
式中: d
D
D
圆轴扭转最大切应力
max
|R
TR IP
令:
Wp
IP R
抗扭截面系数
圆轴扭转最大切应力为:
max
T Wp
实心圆轴的抗扭截面系数为:
D3 Wp 16
空心圆轴的抗扭截面系数为:
Wp
A1
4
d12
A2
4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dA T
dA
(扭矩定义)
横截面上的扭矩应与截面一侧的外力偶矩相平衡
d d 2 T dA G dA G dA A A A dx dx
Ip
A
2 dA
Ip
横截面对形心的极惯性矩
(截面二次极矩，单位为m4)
d T GI p dx
圆轴扭转时的应力
材料力学（第五版） 刘鸿文 主编
1、变形几何关系
Me
p q
Me
圆周线长度形状不变，各圆周线 间距离不变，只是绕轴线转了一个 微小角度；纵向平行线仍然保持为 直线且相互平行，只是倾斜了一个 微小角度。
x
p
q
Me
圆轴扭转的平面假设：
p q
Me
p
x
q
圆轴扭转变形前原为平 面的横截面，变形后仍 保持为平面，形状和大 小不变，半径仍保持为 直线；且相邻两截面间 的距离不变。
I p 2dA
A
其中D为圆截面直径
2
0
R
0
3dd
R 4
2
D 4
32
Wt
Ip R
R3
2
D3
16
在空心轴的情况下：
I p dA
2 A
2
0
D
2dBiblioteka dd34 4
2
D 32
D
3
4
d
4
D
1 32
d 0.945 D Wt 0.2 D3 (1 4 ) 0.2 8.93 (1 0.9454 ) 29 cm3
（2） 强度校核
max
T 1930 6 66.7 10 Pa 6 Wt 29 10 66.7MPa [ ] 70MPa
d D
Wt
扭转强度条件： max
1 16
4
Tmax Wt
例3.2 由无缝钢管制成的汽车传动 轴，外径 D=89mm、壁厚 =2.5 mm， 材料为20号钢，使用时的最大扭矩 T=1930N·m,[ ]=70 MPa. 校核此轴 的强度。
解：（1）计算抗扭截面模量
满足强度要求
d G dx
T Ip
R
TR max Ip
在圆截面边缘上有最大切应力：
TR T max Ip Ip R
令
Wt
Ip R
抗扭截面系数
max
T Wt
(单位：m3)
公式适用条件：
1）圆杆
2）
max p
I p与 Wt 的计算
在实心轴的情况下：
( sin tan )
2、物理关系
根据剪切胡克定律
G
d G G dx
距圆心为 处的切应力：
d dx
尚未求出
3、静力关系
Me
dA
微分面积：
dA dd
dA上的微内力对圆心的力矩： 对上式进行积分：
p d c p
q a
p d
q a e
d
O
d
a' b
b′
c
R
q
O a ' e′ b
p
b′
R
q
dx
边缘上a点的错动距离：
dx
距圆心为处的切应变：
aa Rd
则a点的切应变：
d dx
d dx
—扭转角
aa Rd d R ad dx dx
沿x轴的变化率。