电场强度与电势的关系
电势能与电场强度的关系与计算

电势能与电场强度的关系与计算电势能和电场强度是电学中的两个重要概念,它们之间存在着密切的关系。
本文将介绍电势能与电场强度的概念,阐述它们的关系,并详细说明如何计算电势能和电场强度。
一、电势能的概念电势能是指电荷在电场中由于位置而具有的能量。
当一个电荷在电场中从一个位置移动到另一个位置时,其电势能会发生变化。
电势能的大小与电荷的大小、电荷所处位置以及电场强度有关。
二、电场强度的概念电场强度是指单位正电荷在电场中所受到的力的大小。
它描述了电场的强弱和方向。
电场强度的大小与电荷的大小及所处位置有关。
三、电势能与电场强度的关系电场强度与电势能之间具有如下关系:电场强度的负梯度等于电势能的改变率。
换言之,电场强度的方向是电势能下降最快的方向。
这一关系可以用如下的公式表示:E = -∇V其中,E代表电场强度,V代表电势能,∇表示导数算符。
四、电势能的计算方法根据电势能与电场强度的关系,可以通过计算电场强度的负梯度来获得电势能的数值。
如果电场强度是已知的,可以使用积分计算电势能的数值。
具体计算方法如下:1. 根据电场强度的定义,可以通过求解库仑定律来获得电场强度的表达式。
库仑定律可以表示为:F = qE其中,F代表电荷所受到的力,q代表电荷的大小,E代表电场强度。
2. 如果已知电场强度E的表达式,可以使用积分计算电势能。
电势能的表达式为:V = -∫E·dl其中,V代表电势能,E代表电场强度,dl代表路径元素。
3. 根据具体情况,选择合适的路径进行积分计算。
路径可以是直线、曲线或者任意形状。
五、电场强度的计算方法电场强度可以通过电势能的梯度计算得到。
根据电场强度与电势能的关系,可以使用偏导数计算电场强度的大小和方向。
具体计算方法如下:1. 根据电势能的定义,可以通过计算电势能的偏导数来获得电场强度的表达式。
电场强度的表达式为:E = -∂V/∂x其中,E代表电场强度,V代表电势能,∂V/∂x代表电势能对位置坐标x的偏导数。
电场强度和电势

第4课时 电场强度与电势的关系 电场中的功能关系要点一 电场强度与电势的关系 【自学再现】1、电场强度是反映电场 的性质的物理量,而电势则是反映电场 的性质的物理量。
二者与试探电荷 。
2、电势跟零电势点的选取有关,而电势差与零电势点的选取是无关的!3、电场强度的方向是电势降低最快的方向。
4、匀强电场中,场强E 与电势差U 的关系为 。
5、匀强电场中,由U=Ed 可知,沿任何方向(除等势面)电势的变化都是均匀的,即电势差U 与距离成正比关系。
【规律方法】1、 电场强度和电势比较(1) 电势与电场强度的大小没有必然联系,某点的电势为零,而电场强度不一定是零,反之亦然。
(2) 电势和电场强度都是由电场本身的因素决定,与该点的试探电荷无关。
(3) 沿着电场线的方向电势越来越低,电场线的方向是电势降落最快的方向,电场线总是由电势高的等势面指向电势低的等势面,且电场线永远垂直于等势面。
、2、关系式:U=Ed 只适用于匀强电场,同时要注意d 是沿场强方向的距离!即学即用1.如图1所示,ABCD 是匀强电场中一正方形的四个顶点,已知A 、B 、C 三点的电势分别为ϕA =15 V, ϕB =3 V, ϕC =-3 V,由此可得D 点电势ϕD = .图12、如图2所示,在沿x 轴正方向的匀强电场E 中,有一质点A 以O 为圆心、以r 为半径逆时针转动,当质点A 转动至其与O 点的连线与x 轴正方向间夹角为θ时,则O 、A 两点间的电势差为( ) A.Er U A =0 B.θsin 0Er U A = C.θcos 0Er U A= D.θcos 0r EU A =3、如图1-6-18中A 、B 、C 三点都在匀强电场中,已知AC ⊥BC ,∠ABC =60°,BC =20 cm ,把一个电荷量q =10-5C 的正电荷从A 移到B ,静电力做功为零,从B 移到C ,静电力做功为-1.73×10-3J ,则该匀强电场的场强大小和方向是( )A .865 V/m ,垂直AC 向左B .865 V/m ,垂直AC 向右 C .1000 V/m ,垂直AB 斜向上D .1000 V/m ,垂直AB 斜向下图1-6-18图21.如右图,a 、b 、c 、d 是匀强电场中的四个点,它们正好是一个梯形的四个顶点.电场线与梯形所在的平面平行.ab 平行cd ,且ab 边长为cd 边长的一半,已知a 点的电势是3 V ,b 点的电势是5 V ,c 点的电势是7 V .由此可知,d 点的电势为( C )A .1VB .2VC .3VD .4V2. (2011年湖北黄冈质检)如图1-6-16所示,图中五点均在匀强电场中,它们刚好是一个圆的四个等分点和圆心.已知电场线与圆所在平面平行.下列有关圆心O 和等分点a 的电势、电场强度的相关描述正确的是( )A .a 点的电势为6 VB .a 点的电势为-2 VC .O 点的场强方向指向a 点D .O 点的场强方向指向电势为2 V 的点图1-6-162.(2008·海南·6)如图所示,匀强电场中有a 、b 、c 三点,在以它们为顶点的三角形中,∠a = 30°,∠c =90°.电场方向与三角形所在平面平行.已知a 、b 和c 点的电势分别为(2-3) V 、(2+3) V 和2 V.该三角形的外接圆上最低、最高电势分别为 ( ) A.(2-3) V 、(2+3) V B.0 V 、4 VC.(2-334)V 、(2+334)V D.0 V 、23 V 1、如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径成等差数列。
电势差与电场强度的关系

1.如图所示,在电场中任意取一条电场线,电场线
上的a、 b两点相距为d,则:
·a ·bBDFra bibliotekA.a点的场强一定大于b点的场强
B.a点的电势一定高于b点的电势
C.a、b两点间的电势差一定等于Ed(E为a点场强)
D.a、b两点间的电势差等于单位正电荷由a点沿任意 路径移到b点的过程中电场力所做的功.
1.如图所示,在电场中任意取一条电场线,电场线
.O
.O
对O点:E=0,φ ≠0
对O点:φ =0,E ≠0
结论2:E为零处,φ不一定为零;φ为零处E不一定为零.
结论:电场强度E与电势φ无直接关系。
二、电势差与电场强度的关系
.B
问题1:A到B、从A到C 、从 A到D电势都是降低的,沿哪 个方向电势降低最快?
s
. . A
)α
d
C
E
·D
结论1:在电场中场强方向是电势降低最快的方向。
A.在0—x1之间不存在沿x方向的电场 B.在0—x1之间存在着沿x方向的匀强电场 C.在x1—x2之间存在着沿x方向的匀强电场 D.在x1—x2之间存在着沿x方向的非匀强电场
AC
在0-----x1之间任意两点的电势 差为零,说明0----x1之间为等势 面(体).
U U0
在x1-----x2之间电势线性减小
1.如图所示,在电场中任意取一条电场线,电场线
上的a、 b两点相距为d,则:
·a ·b
BD
A.a点的场强一定大于b点的场强 全面分析问题(六种常见电场)
B.a点的电势一定高于b点的电势
沿着电场线方向电势越来越低.
C.a、b两点间的电势差一定等于Ed(E为a点场强)
电场与电势的电场强度计算

电场与电势的电场强度计算电场强度是描述电场强弱的物理量,是电力学的基本概念之一。
在电场中,带电粒子会受到电场力的作用,而电场强度则是描述这种力的大小和方向。
电场强度的计算涉及到库仑定律、电势、电场线等基本概念和公式。
本文将介绍如何计算电场强度,并给出一些相关的例题。
一、库仑定律库仑定律是描述点电荷之间相互作用的基本规律,它表明电场强度与距离的平方成反比。
库仑定律的数学表达式为:\[F = \frac{{k \cdot q_1 \cdot q_2}}{{r^2}}\]其中,F是电场力的大小,k是一个常数,q1和q2分别是两个电荷的大小,r是两个电荷之间的距离。
根据库仑定律,我们可以通过已知电场力的大小和两个电荷的大小来计算电场强度。
假设已知两个点电荷分别为q1和q2,它们之间的距离为r,且受到的电场力的大小为F。
那么我们可以得到以下关系:\[E = \frac{F}{q_0}\]其中,E是电场强度,q0是测试电荷的大小。
根据库仑定律的公式,我们可以将F代入上式中,得到电场强度的计算公式:\[E = \frac{{k \cdot q_1 \cdot q_2}}{{r^2 \cdot q_0}}\]这个公式描述了点电荷之间的电场强度。
二、电势和电场强度的关系电势是描述电场中某一点的势能大小的物理量,是电场力做功的势能单位。
电势的计算公式为:\[V = \frac{{k \cdot q}}{{r}}\]其中,V是电势,k是常数,q是电荷大小,r是与电荷产生电场力的地点之间的距离。
电场强度与电势之间有一定的关系。
根据电场力和势能之间的关系,我们可以得到以下公式:\[E = \dfrac{-dV}{dr}\]根据这个公式,我们可以通过求解电势函数的导数来计算给定位置处的电场强度。
这个方法在计算连续分布的电荷的电场强度时尤为有用。
三、电场强度的计算实例例1:求解均匀带电长直线的电场强度假设有一根长度为L、线密度为λ的均匀带电长直线。
学习电场中电势与电场强度的计算

学习电场中电势与电场强度的计算电场是物理学中的一个重要概念,它描述了电荷受到的力和电势的分布情况。
在学习电场的过程中,我们需要掌握电势和电场强度的计算方法。
一、电势的计算电势是描述电荷周围电场状态的物理量,它是用来衡量电荷所具有的能量。
在电场中,电势的计算可以通过以下公式进行:V = k * Q / r其中,V表示电势,k表示库仑常数,Q表示电荷大小,r表示距离。
通过这个公式,我们可以计算出电荷点周围的电势大小。
需要注意的是,电势是一个标量量,它没有方向性。
因此,我们可以简单地将电势看作是一个点的属性,而不需要考虑具体的方向。
二、电场强度的计算电场强度是描述电荷周围电场状态的物理量,它是用来衡量电荷对其他电荷施加的力的大小。
在电场中,电场强度的计算可以通过以下公式进行:E = k * Q / r^2其中,E表示电场强度,k表示库仑常数,Q表示电荷大小,r表示距离。
通过这个公式,我们可以计算出电荷点周围的电场强度大小。
需要注意的是,电场强度是一个矢量量,它具有方向性。
因此,在计算电场强度时,我们需要考虑具体的方向。
三、电势与电场强度的关系电势和电场强度之间存在着一定的关系。
根据电场的定义,电场强度是电势在空间上的梯度。
也就是说,电场强度的方向是电势下降最快的方向。
具体来说,电场强度的方向是从高电势指向低电势的。
这是因为电势表示了单位正电荷在电场中所具有的能量,而电场强度表示了单位正电荷所受到的力。
因此,电势越高,电场强度越大。
在计算电场强度时,我们可以利用电势的概念。
根据电场强度的定义,我们可以将电场强度表示为电势的负梯度。
也就是说,电场强度的大小可以通过电势的变化率来计算。
四、电势与电场强度的应用电势和电场强度的计算方法在物理学中有着广泛的应用。
它们可以用来描述电荷之间的相互作用,解释电场中的运动规律,以及计算电场中的能量分布等。
例如,在电场中,电荷受到的力可以通过电场强度进行计算。
根据库仑定律,电荷之间的力与电场强度成正比。
电场强度与电势关系

电场强度与电势关系嘿,朋友们!咱今天来聊聊电场强度和电势这俩玩意儿,这可真是电学里特别有意思的一对“好兄弟”呀!你说电场强度,那它就像是电场的“力气”大小。
想象一下,电场就好比是一片海洋,电场强度就是这海洋里波涛的汹涌程度。
有的地方波涛汹涌,那电场强度就大;有的地方风平浪静,那电场强度就小。
它能告诉我们电场在各个点上有多“厉害”。
那电势呢?这就好比是电场这片海洋里的“水位”高低。
高电势就像高处的水位,低电势就像低处的水位。
电荷在电场里移动,就像是小球在高低不同的水位之间滚动。
咱再打个比方,电场强度就像是道路的坡度,坡越陡,走起来越费劲,就相当于电场强度越大;而电势呢,就像是你站在不同高度的山坡上,位置高的电势就高呀。
那它们之间有啥关系呢?这可太重要啦!电场强度的方向总是指向电势降低最快的方向。
这就好像水流总是往低处流一样自然。
如果电场强度是个指引方向的箭头,那电势就是它要努力奔向的目标。
比如说,在一个电场里,你能感觉到电场强度在推动着电荷往前走,而电荷会朝着电势降低的方向跑。
就好像有一股力量在拉着电荷,让它去寻找更低的电势。
而且呀,这两者结合起来能告诉我们好多事情呢!比如说,我们可以通过电场强度和电势的关系来计算电荷在电场里的能量变化。
这就像我们知道了道路的坡度和位置的高低,就能算出小球滚动时能量的变化一样。
你们说神奇不神奇?这电场强度和电势就像是一对默契十足的搭档,一个负责出力,一个负责指引方向,共同构成了电场这个奇妙的世界。
所以啊,可别小看了这电场强度和电势的关系,它们在电学里的作用可大着呢!它们能让我们更好地理解电的世界,让我们知道电荷是怎么运动的,能量是怎么变化的。
总之呢,电场强度和电势这俩家伙,真是电学里不可或缺的存在呀!它们让我们的电世界变得丰富多彩,充满了奥秘和惊喜!大家可得好好琢磨琢磨它们呀!。
电势与电场强度的微分关系.
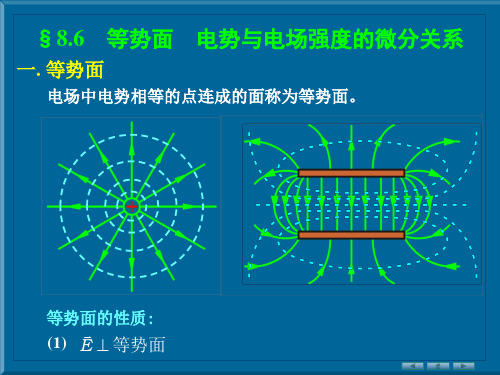
一. 等势面
电场中电势相等的点连成的面称为等势面。
等势面的性质:
(1)
E 等势面
证明: 设等势面上P点的电场强度与等势面夹角为 ,
把q0
在等势面上移动
dl ,电场力作功为
dA q0E dl q0E cosdl
q0 (up uQ ) up uQ
E
p
dl
q0E cosdl 0
Q
cos 0
2
(2) 规定相邻两等势面 间的电势差都相同
等势面密
E大
等势面疏
E小
(3) 电场强度的方向总是指向电势降落的方向
二.
电势与电场强度的微分关系
取两个相邻的等势面,等势面法线方向为
n
,设
E
的方向与
n 相同,把点 电荷从P移到Q,电场力作功为:
dA qE ddl
电场强度在 l 方向的投影等于电势沿该方向变化率的负值
dl dn
du du dl dn
电势沿等势面法线方向的变化率最大
在直角坐标系中
Ex
u x
Ey
u y
Ez
u z
E
(u
i
u
j
u
k)
grad(u)
x y z
某点的电场强度等于该点电势梯度的负值,这就是电势与
电场强度的微分关系。
u+du
qEdn
dn
n E
Q
dA q[u (u du)] qdu
E cosdl Edn du
u dl
P
E du dn
任意一场点P处电场强度的大小等于沿过该点等势面法线方
电场强度和电势差的关系和计算

电场强度和电势差的关系和计算一、电场强度和电势差的定义电场强度(E):描述电场力对单位正电荷的作用力大小,单位为牛顿/库仑(N/C)。
电势差(U):描述电场力对电荷做功的势能差,单位为伏特(V)。
二、电场强度和电势差的关系1.电场力做功与电势差的关系:电场力做的功(W)等于电荷(q)在电场中从一点移动到另一点时电势差(U)与电荷量(q)的乘积,即 W = qU。
2.电场强度与电势差的关系:在电场中,电势差(U)等于电场强度(E)与电荷量(q)的乘积,即 U = Eq。
三、电场强度的计算1.静电场中电场强度的计算:对于一个点电荷产生的静电场,电场强度(E)等于库仑常数(k)与点电荷量(Q)的比值,再除以距离的平方(r^2),即 E = kQ / r^2。
2.均匀电场中电场强度的计算:在均匀电场中,电场强度(E)等于电场力(F)与电荷量(q)的比值,即 E = F / q。
四、电势差的计算1.两点间的电势差计算:两点间的电势差(U)等于两点电势(φ)之差,即U = φA - φB。
2.沿电场线的电势差计算:沿电场线方向,电势差(U)等于电场强度(E)与沿电场线方向上的距离(d)的乘积,即 U = Ed。
五、电场强度和电势差的物理意义1.电场强度反映了电场力对电荷的作用力大小,电势差反映了电场力对电荷做功的势能差。
2.电场强度和电势差的关系表明了电场力做功与势能变化的关系,以及在电场中移动电荷时能量的转换。
六、注意事项1.在计算电场强度和电势差时,要区分清楚各物理量的单位,确保计算正确。
2.在应用公式时,要注意各物理量的符号,避免出现计算错误。
3.理解电场强度和电势差的物理意义,能更好地应用于解决实际问题。
习题及方法:一个点电荷量为+2μC,距离该点电荷10cm(即0.1m)处的电场强度是多少?已知库仑常数k=9×10^9 N·m2/C2。
使用点电荷产生的静电场电场强度公式:E = kQ / r^2将已知数值代入公式:E = (9×10^9 N·m2/C2) × (2×10^-6 C) / (0.1 m)^2E = 1.8×10^4 N/C一个电荷量为+5μC的点电荷置于电场中,受到的电场力是2.5N,求该点电荷所在位置的电场强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电场有两个宏观性质
1.对引入其中的电荷有力的作用; 2.对运动电荷做功。
场强 高斯定理 静电场是有通量源场
功与路径无关(环流定理) 静电场是保守场(有势场)
一、等势面 电势相等的空间各点所组成的面
1)沿等势面移动电荷,电场力不作功
A12 qV1 V2 0
2)等势面处处与电场线正交
结论:电场线指向电势降落的方向
二、场强与电势的微分关系
V1 V2 dV E dl Edl cos
E cos dV
dl
E
dl
1
2
V1 V2 V1 du
dV dl
为电势函数沿
dl
方向经单位长度时的变化,即
电势沿 dl 方向的空间变化率。
电场中某点场强沿某一方向的分量等于电势沿此方向的 空间变化率的负值。
4 0 R 2 x 2
利用电场强度与电势梯度的关系
E V
V
Q
4 o R2 x2
dQ
r
R
0
xP
x
Ex
V x
4 0
xQ x2 R2
3 2
有对称性可得: E y Ez 0
E Ex i Ey j Ez k
4 0
xQ x2 R2
3 2
i
2)方法二(场强叠加原理)
dQ
E
4 0
x2 R2
3 2
Q
4 0 R 2 x 2
பைடு நூலகம்
例 设有一均匀带电直线段长度为L,总电荷量为q,求其延
长线上一点P电势和电场强度。
P
a
P’
dE
x’
dx’
r
x
不能用定点 p 电势求场强,求 p(x) 点电势。
V (x)
dU
dq
4 0 r
L
0
dx 40 ( x
x)
4 0
ln
x
x
L
E
21
电势梯度是一矢量,它沿该点电势升高最快的方向。
E dV dn
电场中任一点的场强等于该点电势梯度的负值。负号反映了场 强的方向与电势梯度的方向相反,即场强沿电势降落的方向
在直角坐标系中 V V ( x,y,z)
E
V x
i
V
y
j
V
z
k
x
i
y
j
z
k
V
V
gradV
i
j
k
x y z
V E x x
Ey
V y
Ez
V z
例 已知:总电量Q ;半径R 。求: 均匀带电圆环轴
线上的电势和场强的分布。
解: 轴线上P点的电势
dQ
1)方法一(电势叠加原理) R
r
dV dQ
4 0r
0
x
Px
V
dQ
Q 4 0r
1
4 0r
dQ
Q
4 0r
r R2 x2
Q V
Qdl
2R
dQ
dE 40r 2
dE dE// dE
R
r
dE
dE //
x
dE
E E // E
E L dE 0
E//
L dE//
xQ
4 0r 3
E
E//
xQ
4 0 x2
i R2
3 2
ox
E
X
R
V x E d l
Qx dx
x
4 0
R2 x2
3 2
xQ i
dA qE dl qEdl cos , q 0 E 0 d l 0 ,
E dl 3)等势面稠密处 —— 电场强度大
规定相邻两等势面的 电势差为定值
等势面越密电势 变化越快
电场强度大
点电荷的电场线与等势面
-
一对等量异号点电荷的电场线和等势面
-
+
两平行带电平板的电场线和等势面
++++++++++++
说明:
E cos dV
dl
1). 不同,E cos E1 不同
过电场中任一点,沿 不同方向电势随空间的变化率是不一样的。
2) 0 dl 与 E 方向相同, dV 有最大值
dl
设此时 dl dn
dV 称为该点的电势梯度(gradient)
dn
gradV dV nˆ V
dl
nˆ
dn
dn
dU
i
(1
1
)i
dx 4 0 x L x
V (x a L) ln a ln a L 40 a L 40 a
Ep
E(x
a
L)
4 0
(1 a
a
1
)i L
