2016-2017年宁夏石嘴山三中高二上学期数学期中试卷带答案(文科)
宁夏石嘴山市第三中学2016届高三三模数学(文)试题

宁夏石嘴山市第三中学2016届高三三模数学(文)试题学校:___________姓名:___________班级:___________考号:___________+A.202πA ..C ..10.公元263年左右,我国数学刘徽发现当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了割圆术.利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名是徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n 为()(参考数据:3 1.732,sin150.2588,sin 7.50.1305︒≈≈)A .12B .2411.已知双曲线22221(0,0)x y a b a b -=>>一象限三等分,则双曲线22221x y a b-=A .6或233C .2或312.设函数()e (sin cos )x f x x x =-(0A .220162)e (1e 1e πππ---C .210082)e (1e 1e πππ---二、填空题13.已知α是锐角,3,sin ,4a b α⎛⎫= ⎪⎝⎭14.已知各项均为正数的等比数列{a ________.15.下列命题:①已知m ,n 表示两条不同的直线,n β⊂,则“αβ⊥”是“//m n ”的必要不充分条件;②不存在23log log x x <成立;③“若22am bm <()sin(2)f x x θ=+都不是偶函数.正确的命题序号是16.在球O 的内接四面体A BCD -中,(1)求a的值;(2)用分层抽样的方法在A,B类轿车中抽取一个容量为总体,从中任取2辆,求至少有1辆A(3)用随机抽样的方法从A,B两类轿车中各抽取.设,函数(Ⅱ)已知(是自然对数的底数)和。
宁夏石嘴山市高二上学期期中数学试卷

宁夏石嘴山市高二上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2017高一下·承德期末) 在△ABC中,角A,B,C的对边分别是a,b,c,若C=45°,c= a,则A等于()A . 120°B . 60°C . 150°D . 30°2. (2分)在△ABC中,a,b,c分别是角A,B,C的对边,若a,b,c成等比数列,A=600 ,则=()A .B .C .D .3. (2分) (2017高二上·江门月考) 在等比数列中,若,则的前项和等于()A .B .C .D .4. (2分)已知等差数列的前n项和为,,,为等比数列,且,则的值为()A . 64B . 128C . -64D . -1285. (2分) (2017高一下·卢龙期末) 不等式(x﹣2)(3﹣x)>0的解集是()A . {x|x<2或x>3}B . {x|2<x<3}C . {x|x<2}D . {x|x>3}6. (2分)随着市场的变化与生产成本的降低,每隔年计算机的价格降低,则年价格为元的计算机到年价格应为()A . 元B . 元C . 元D . 元7. (2分)在中,,则b等于()A .B .C .D .8. (2分)设是等差数列的前n项和,若,则=()A . 1B . -1C . 2D .9. (2分)下列命题中,正确的是()A . 若a>b,c>d,则a>cB . 若ac>bc,则a>bC . 若,则a<bD . 若a>b,c>d,则ac>bd10. (2分)若实数x,y满足约束条件,且目标函数z=x+y的最大值等于()A . 2B . 3C . 4D . 111. (2分)在由正数组成的等比数列}中,若()A .B .C . 2D .12. (2分) (2018高一下·鹤岗期中) 已知等差数列的通项为,则这个数列共有正数项()A . 44项B . 45项C . 90项D . 无穷多项二、填空题 (共4题;共4分)13. (1分)如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为________ km.14. (1分)(2018·上海) 设等比数列{ }的通项公式为an=qn-1(n∈N*),前n项和为Sn。
数学---宁夏石嘴山市第三中学2017届高三上学期期中考试(文)
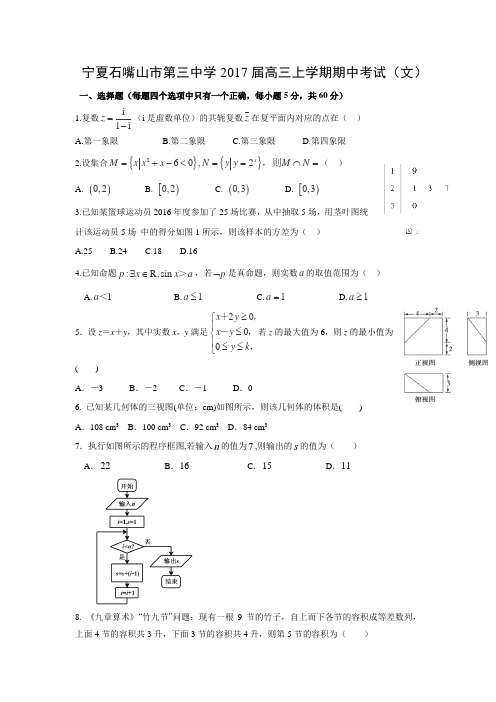
宁夏石嘴山市第三中学2017届高三上学期期中考试(文)一、选择题(每题四个选项中只有一个正确,每小题5分,共60分) 1.复数i1iz =-(i 是虚数单位)的共轭复数z 在复平面内对应的点在( ) A.第一象限B.第二象限C.第三象限D.第四象限2.设集合{}{}260,2x M x x x N y y M N =+-<==⋂=,则( ) A. ()0,2B. [)0,2C. ()0,3D. [)0,33.已知某篮球运动员2016年度参加了25场比赛,从中抽取5场,用茎叶图统计该运动员5场 中的得分如图1所示,则该样本的方差为( ) A.25B.24C.18D.164.已知命题:R,sin p x x a ∃∈>,若p ⌝是真命题,则实数a 的取值范围为( ) A.1<a B.1≤a C.1=a D.1≥a5.设z =x +y ,其中实数x ,y 满足20 00x y x y y k ≥⎧⎪≤⎨⎪≤≤⎩+,-,,若z 的最大值为6,则z 的最小值为( )A .-3B .-2C .-1D .06. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( ) A .108 cm 3 B .100 cm 3 C .92 cm 3 D .84 cm 37.执行如图所示的程序框图,若输入n 的值为7,则输出的s 的值为( ) A .22 B .16 C .15 D .118. 《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )A.1升B.升C.升D.升9.直线()0,0022>>=+-b a by ax ,被圆014222=+-++y x y x 截得的弦长为4,则ba 11+的最小值为( ) A .41 B .2 C .21D .410.已知点,,在圆上运动,且,若点的坐标为,则的最大值为( )A.6B.7C.8D.911.双曲线C 的左右焦点分别为12,F F ,且2F 恰为抛物线24y x =的焦点,设双曲线C 与该抛物线的一个交点为A ,若12AF F ∆是以1AF 为底边的等腰三角形,则双曲线C 的离心率为( )B.1C.1D.2+12. 函数(){}2,min-=x x x f ,其中,若动直线与函数的图像有三个不同的交点,它们的横坐标分别为、、,则的取值范围是 ( )A .()32,B .()43,C .()54,D .()65,二、填空题:(每题5分,共20分)13.已知,lg ,24a x a==则x =________.14.等比数列的各项均为正数,且,则________.15.抛物线C :y 2=2px (p >0)的焦点为F ,M 是抛物线C 上的点,若△OFM 的外接圆与抛 物线C 的准线相切,且该圆面积为36π,则p = .16.在四面体S ﹣ABC 中,SA ⊥平面ABC ,∠BAC =120°,SA =AC =2,AB =1,则该四面体的外 接球的表面积为 . 三、解答题:(共6道题,满分70分)A B C 221x y +=AB BC ⊥P (2,0)PA PB PC ++{}n a 154a a =2122232425log +log +log +log +log =a a a a a17.(本小题满分12分)如图△ABC 中,已知点D 在BC 边上,且(1)求AD 的长, (2)求cos C .18.如图,四面体中,、分别的中点,,.(1)求证:平面; (2)求点到平面的距离.19.为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:0,sin 3AD AC BAC ⋅=∠=AB BD ==ABCD O E BD BC 2CA BC CD BD ====AB AD ==AO ⊥BCD E ACD(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;(2)用简单随机抽样方法从这条道路中抽取条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过的概率.20.如图,DP⊥x轴,点M在DP的延长线上,且|DM|=2|DP|.当点P在圆x2+y2=1上运动时.(1)求点M的轨迹C的方程;(2)过点T(0,t)作圆x2+y2=1的切线交曲线C于A,B两点,求△AOB面积S的最大值和相应的点T的坐标.21.(本小题满分12分)已知函数2()ln(1)1f x p x p x=+-+.625.0(1)讨论函数的单调性;(2)当时,()f x kx ≤恒成立,求实数的取值范围;(3111请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一部分,做答时请写清题号.22.如图,已知AD ,BE ,CF 分别是△ABC 三边的高,H 是垂心,AD 的延长线交△ABC 的外接圆于点G .求证:DH =DG .23.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :ρsin 2θ=2cos θ,过点P (-2,-4)的直线l :⎩⎨⎧x =-2+22ty =-4+22t(t 为参数)与曲线C 相交于M ,N两点.(1)求曲线C 的直角坐标方程和直线l 的普通方程; (2)证明|PM |,|MN |,|PN |成等比数列.选修4—5:不等式选讲24、设函数1()11()2f x x x x R =++-∈的最小值为a . (1)求a ;(2)已知两个正数,m n 满足22,m n a +=求11m n+的最小值. 参考答案一、选择题二、填空题 13.1014.5 15.8 16.三、解答题 17.(1)3(2)36 18.(1)证明:连结.∵,,∴. ∵,,∴.在中,由已知可得,,而,∴,∴,即.,∴平面.(2)解:设点到平面的距离为. ∵,∴, 在△ACD 中,CA =CD =2,AD =,∴, 而,,∴,∴点E 到平面ACD 的距离为.19.解:(1)6条道路的平均得分为∴该市的总体交通状况等级为合格.(2)设表示事件“样本平均数与总体平均数之差的绝对值不超过”OC BO DO =AB AD =AO BD ⊥BO DO =BC CD=CO BD ⊥AOC ∆1AO=CO =2AC =222AO CO AC +=90AOC ∠=AO OC ⊥BD OC O = AO ⊥BCD E ACD h A ACD A CDE V V --=1133ACD CDES h S AO ∆∆⋅=⋅212ACDS ∆==1AO =2122CDE S ∆==17CDE ACDAO S h S ∆∆⋅===7215.7)1098765(61=+++++A 5.0从条道路中抽取条的得分组成的所有基本事件为:,,,,,,,,,,,,,,共个基本事件事件包括,,,,,,共个基本事件.…10分 ∴. 答:该样本平均数与总体平均数之差的绝对值不超过的概率为. 20.解:(1)设点M 的坐标为(x ,y ),点P 的坐标为(x 0,y 0), 则x =x 0,y =2y 0,所以x 0=x ,y 0=,①因为P (x 0,y 0)在圆x 2+y 2=1上,所以x 02+y 02=1②,将①代入②,得点M 的轨迹方程C 的方程为x 2+=1;…(2)由题意知,|t |≥1,设切线l 的方程为y =kx +t ,k ∈R ,由,得(4+k 2)x 2+2ktx +t 2﹣4=0③,设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2), 由③得:x 1+x 2=﹣,x 1x 2=,又直线l 与圆x 2+y 2=1相切,得=1,即t 2=k 2+1,∴|AB |===,又|AB |==≤2,且当t =±时,|AB |=2,综上,|AB |的最大值为2,62)6,5()7,5()8,5()9,5()10,5()7,6()8,6()9,6()10,6()8,7()9,7()10,7()9,8()10,8()10,9(15A )9,5()10,5()8,6()9,6()10,6()8,7()9,7(7157)(A P 5.0157依题意,圆心O到直线AB的距离为圆x2+y2=1的半径,∴△AOB面积S=|AB|×1≤1,当且仅当t=±时,△AOB面积S的最大值为1,相应的T的坐标为(0,﹣)或(0,).21.(本小题满分12分)解:(1)的定义域为(0,+∞),p 时,>0,故在(0,+∞)单调递增;当1当时,<0,故在(0,+∞)单调递减;当0<<1时,令=0,解得.则当时,>0;时,<0.故在单调递增,在单调递减(2)因为,所以p=时,恒成立当1令,则,因为,由得,且当时,;当时,.所以在上递增,在上递减.所以,故(3)由(2)知当时,有,当时,即,令,则,即所以,,…,,相加得而所以,22、解:连结CG ,∵AD ⊥BC ,∴∠ABC +∠GAB =90°同理可得∠ABC +∠FCB =90°,从而得到∠GAB =∠FCB =90°﹣∠ABC 又∵∠GAB 与∠GCB 同对弧BG , ∴∠GAB =∠GCB ,可得∠GCB =∠FCB , ∵CD ⊥GH ,即CD 是△GCH 的高线∴△CHG 是以HG 为底边的等腰三角形,可得DH =DG .23.解:(1)把⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ代入ρsin 2θ=2cos θ,得y 2=2x由⎩⎨⎧x =-2+22ty =-4+22t(t 为参数),消去t 得x -y -2=0∴曲线C 的直角坐标方程和直线l 的普通方程分别是y 2=2x ,x -y -2=0.(2)证明将⎩⎨⎧x =-2+22ty =-4+22t (t 为参数)代入y 2=2x ,整理得t 2-102t +40=0. 设t 1,t 2是该方程的两根,则t1+t2=102,t1·t2=40,∵|MN|2=(t1-t2)2=(t1+t2)2-4t1·t2=40 |PM|·|PN|= t1·t2=40,∴|MN|2==PM|·|PN| ∴|PM|,|MN|,|PN|成等比数列……10分24、解:(1)函数3-,2211()11=2,21 223,12x xf x x x x xx x⎧≤-⎪⎪⎪=++--+-<<⎨⎪⎪≥⎪⎩,当x∈(﹣∞,1]时,f(x)单调递减当x∈[1,+∞)时,f(x)单调递增,所以当x=1时,f(x)的最小值a=32.(2)由(1)知m2+n2=32,由m2+n2≥2mn,得mn≤34,∴≥43故有+≥2≥43,当且仅当m=n=3时取等号.所以+的最小值为43.。
宁夏石嘴山市第三中学高二数学上学期期中试题 文

2015-2016第一学期期中高二数学文科试卷注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将答题卡交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
第I 卷(选择题) 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是( )A .系统抽样B .分层抽样C .抽签抽样D .随机抽样 2.双曲线244x 2-y =的离心率为A .6B .5C .6D .53.将二进制数)2(11100转化为四进制数,正确的是( )A .)4(120B .)4(130C .)4(200D .)4(202 4.下列说法错误的是( )A .若p :∃x ∈R ,x 2-x +1=0,则¬p :∀x ∈R ,x 2-x +1≠0 B .“sin θ=12”是“θ=30°”的充分不必要条件C .命题“若a =0,则ab =0”的否命题是“若a ≠0,则ab ≠0”D .已知p :∃x ∈R ,cosx =1,q :∀x ∈R ,x 2-x +1>0,则“p ∧(¬q )”为假命题 5.如图是在一次全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( ) A .84,4.84 B .84,1.6 C .85,1.6 D .85,47 78 4 4 6 4 7 9 36.运行如图所示的程序框图,则输出的所有实数对(,)x y 所对应的点都在函数( )A 、2()log (1)f x x =+的图像上 B 、2()22f x x x =-+的图像上C 、4()3f x x =的图像上 D 、1()2x f x -=的图像上7.若样本的频率分布直方图中一共有n 个小矩形,中间一个小矩形的面积等于其余1n -个小矩形面积和的14,且样本容量为160,则中间一组的频数是( )A .32B .20C .40D .258.已知m R ∈,“函数21x y m =+-有零点”是“函数log m y x =在0+∞(,)上为减函数”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 9.过椭圆()的左焦点作轴的垂线交椭圆于点,为右焦点,若,则椭圆的离心率为( )A.B.C.D.10.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为A .2214536x y +=B .2213627x y +=C .2212718x y += D .221189x y +=11.下列四个命题:①样本方差反映的是所有样本数据与样本平均值的偏离程度;②某只股票经历了l0个跌停(每次跌停,即下跌l0%)后需再经过10个涨停(每次涨停,即上涨10%)就可以回到原来的净值;③某校高三一级部和二级部的人数分别是m 、n ,本次期末考试两级部;数学平均分分别是a 、b ,则这两个级部的数学平均分为na mb mn+④某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l ~016中随机抽到的学生编号是007. 其中真命题的个数是A .0个B .1个C .2个D .3个12.若双曲线22221(0,0)x y a b a b-=>>的一条渐近线与圆22(3)1x y -+=有公共点,则双曲线的离心率的取值范围是( )A.]26,1( B.),26[+∞ C.),36[+∞ D.)1,36[二、填空题:本大题共4小题,每小题5分. 13.运行如图所示的程序,其输出的结果为 .14.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据: 单价x (元) 8 8.2 8.4 8.6 8.8 9 销量y (件)908483807568由表中数据,求得线性回归方程为ˆˆ20y x a =-+.若在这些样本点中任取一点,则它在n=5s=0WHILE s <14 s=s+n n=n-1 WEND PRINT n END回归直线左下方的概率为_______.15.以椭圆22185x y +=的焦点为顶点,顶点为焦点的双曲线方程为 .16.若r(x):m x x >+cos sin ,s(x):x 2+mx +1>0,如果对∀x ∈R ,r(x)为假命题,s(x)为真命题,则m 的取值范围 。
宁夏石嘴山市第三中学2016-2017学年高二上学期期中考试数学(文)试题 含答案

石嘴山三中高二文科数学(上)期中考试题卷命题人:哈红军 考试时间:120分钟 满分:150分请考生注意:本试卷分试题卷和答题卷。
请将答案写在答题卷上.答案写在试题卷上无法给分。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1。
已知数列{}na 是等比数列,且141,18aa ==-,则{}n a 的公比q 为( )A. 2-B. 2C 。
12D 。
12-2. 已知实数m 和2n 的等差中项是4,实数2m 和n 的等差中项是5,则m 和n 的等差中项是( )A .2B .3C .6D .9 3.在△ABC 中,已知222ab bc c =++,则角A 为( )A . 3π B .6π C .23π D .233ππ或4.在△ABC 中,若∠A=60°,∠B=45°,BC=32则AC=( ) A .43 B .23 C 3 D 35.下列命题正确的是( ) A .若a >b,则22acbc > B .若a >﹣b ,则﹣a >bC .若ac >bc,则a >bD .若a >b ,则a ﹣c >b ﹣c 6.已知等比数列{}na ,3103,384aa ==,则该数列的通项na =( )A. 332n -B 。
132n -C 。
32n D 。
323n -•7.已知{}na 是等差数列,1010a=,其前10项和1070s =,则其公差d =( )A .-错误!B .-错误! C.错误! D 。
错误! 8。
已知,a b 为非零实数,且a b >,则下列不等式成立的是( ) A .22a b >B .11ab< C .22ab > D .a b >9。
不等式3102x x-≥-的解集是( )A .{x|34≤x<2} B .{x|123x ≤<}C .{x |x >2或13x <} D .{x|x <2}10。
宁夏回族自治区石嘴山市光明中学2016-2017学年高二上学期期末考试数学文试题Word版含答案

宁夏回族自治区石嘴山市光明中学2016~2017学年高二第一学期期终考试数学试题(文科)考试寄语:考试没有什么大不了的,我能做得出的题目别人不一定能做出来,我做不出的题目别人同样做不出,我所做的就是对的,我就是最棒的!预祝同学们考试取得好成绩............!!! 一、选择题(每题5分,共12题,满分60分) 1.全称命题“2,54x R x x ∀∈+=”的否定是( )A .2000,54x R x x ∃∈+= B .2,54x R x x ∀∈+≠ C .2000,54x R x x ∃∈+≠D .以上都不正确2.下列事件中,随机事件的个数为( )①在学校明年召开的田径运动会上,学生张三获得100米短跑冠军; ②在体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李四; ③王麻子从标有1,2,3,4的4张号签中任取一张,恰为1号签。
A .0 B .1 C .2 D .3 3.下列命题中的假命题是( ) A .R x ∈∃0,1lg 0<x B. R x ∈∃0,2tan 0=xC .x R ∀∈,021>-xD. *x N ∀∈,()012>-x4.函数32()31f x x x =-+是减函数的区间为( )A .(2,)+∞B. (,2)-∞C .(,0)-∞D. (0,2)5.对于实数,,a b c ,“a b >”是“22ac bc >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.抛掷一枚骰子,得到奇数点的概率是( )A .61 B .41C .31D .217.已知1F ,2F 是椭圆192522=+y x 的两个焦点,过焦点1F 的直线交椭圆于A ,B 两点, 若||8AB =,则22||||AF BF += ( ) A .12B. 14C. 16D. 108.与曲线2212449x y +=共焦点,而与曲线2213664x y -=共渐近线的双曲线方程为( ) A .191622=-y x B .191622=-x y C .116922=-x y D .116922=-y x 9.函数)(x f 的定义域为开区间),(b a , 导函数)(x f '在),(b a 内的图象如图 所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个D .4个10的一条渐近线与直线012=++y x 垂直,则双曲线的离心率为( )11.函数)(x f ,)(x g 分别是定义在R 上的奇函数和偶函数,当0<x 时,0)(')()()('>+x g x f x g x f ,且0)3(=-g ,则不等式0)()(<x g x f 的解集是( )A .(-3,0)∪(3,+∞)B .(-3,0)∪(0,3)C .(-∞,-3)∪(3,+∞)D .(-∞,-3)∪(0,3)12.直线2+=x y 与曲线1222=-x x y 的交点个数为( ) A .0 B .1 C .2 D .3 二、填空题(每题5分,共4题,满分20分)13.抛物线24y x =的准线方程是 。
宁夏2016-2017学年高二上学期期中考试数学(文)试题 Word版含答案

宁夏育才中学2016~2017学年第一学期高二年级期中试卷数学(文科)(试卷满分 150 分,考试时间为 120 分钟) 命题人:一.选择题(共12小题,每小题5分,共60分,每小题只有一个正确选项)1.不等式0623≥-+y x 表示的平面区域是 ( )A B C D 2.在ABC ∆中,三边长7AB =,5BC =,6AC =,则B cos 的值等于 ( )A . 3519B . 3514-C .3518-D . 3519- 3.设10<<<b a ,则下列不等式成立的( )A .22b a > B.ba 11< C . 1>b a D .0)lg(<-a b 4.设集合{}062≤-+=x x x A ,集合B 为函数11-=x y 的定义域,则B A 等于( ) A .(1,2) B .[1,2] C.(1,2] D .[1,2)5.对任意等比数列{}n a ,下列说法一定正确的是( )A .931,,a a a 成等比数列B .632,,a a a 成等比数列C .842,,a a a 成等比数列D .963,,a a a 成等比数列6.设等比数列{}n a 中,公比2=q ,前n 项和为n S ,则34S a 的值( ) A.154 B.152 C.74 D.727.等差数列{}n a 中, 1664=+a a ,则数列前9项和9S 的值为 ( )A .144B .54C .60D .728.设x ,y 满足约束条件⎩⎨⎧x -y +1≥0,x +y -1≥0,x ≤3,则z =2x -3y 的最小值是() A .-7 B .-6 C .-5 D .-39.在ABC ∆中,bc c b a 3222-+=,则角A 等于 ( )A. 30B. 45C. 60D. 12010.等比数列{}n a 的各项均为正数,且187465=+a a a a ,则=+++1032313log log log a a a ( )A 12B 10C 5D 5log 23+11.已知{}n a 是等差数列,55,1554==S a ,则过点)(3,3P a ,),(44Q a 的直线的斜率为( )A .4 B.14 C .-4 D .-1412.若直线1=+by a x )0,0(>>b a 过点(2,2),则b a +的最小值等于( ) A .2 B .3 C .4 D .8二.填空题(共4小题,每小题5分,共20分)13.等差数列{}n a 中, ,33,952==a a 则数列{}n a 的公差为 。
宁夏石嘴山三中2017届高三上学期第一次月考数学试卷(文科) 含解析

2016-2017学年宁夏石嘴山三中高三(上)第一次月考数学试卷(文科)一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x(x﹣2)≤0},B={﹣2,﹣1,0,1,2},则A∩B=()A.{﹣2,﹣1}B.{1,2}C.{﹣1,0,1,2} D.{0,1,2}2.命题“∀x∈R,x2+2x﹣1>0”的否定是()A.∀x∈R,x2+2x﹣1≤0 B.∃x∈R,x2+2x﹣1≤0C.∃x∈R,x2+2x﹣1<0 D.∃x∈R,x2+2x﹣1>03.已知向量=(1,2),=(a,﹣1),若(+)⊥,则实数a的值为()A.﹣3 B.﹣C.D.24.设i是虚数单位,复数z=,则|z|=()A.1 B.C.D.25.某三棱锥的三视图如图所示,该三棱锥的体积为()A.80 B.40 C.D.6.已知a n是由正数组成的等比数列,S n表示a n的前n项的和.若a1=3,a2a4=144,则S10的值是()A.511 B.1023 C.1533 D.30697.已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:①若m⊥α,m⊂β,则α⊥β;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;③m⊂α,n⊂α,m、n是异面直线,那么n与α相交;④若α∩β=m,n∥m,且n⊄α,n⊄β,则n∥α且n∥β.其中正确的命题是()A.①②B.②③C.③④D.①④8.设等差数列{a n}的前n项和为S n,已知2a1+a13=﹣9,则S9=()A.﹣27 B.27 C.﹣54 D.549.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π10.已知<β<απ,cos(α﹣β)=,sin(α+β)=﹣,则sin2α的值为()A.B.C.D.11.已知y=f(x)是定义在R上的奇函数,且f(x)=,则函数y=f(x﹣1)﹣(x﹣1)的零点个数为()A.2 B.3 C.4 D.512.若点P(a,b)在函数y=﹣x2+3lnx的图象上,点Q(c,d)在函数y=x+2的图象上,则(a ﹣c)2+(b﹣d)2的最小值为()A.B.2 C.2D.8二、填空题:本大题共4小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年宁夏石嘴山三中高二(上)期中数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知数列{a n}是等比数列,且a1=,a4=﹣1,则{a n}的公比q为()A.2 B.﹣ C.﹣2 D.2.(5分)已知实数m和2n的等差中项是4,实数2m和n的等差中项是5,则m和n的等差中项是()A.2 B.3 C.6 D.93.(5分)在△ABC中,已知a2=b2+c2+bc,则A=()A.B.C. D.或4.(5分)在△ABC中,若∠A=60°,∠B=45°,BC=3,则AC=()A.B.C.D.5.(5分)下列命题正确的是()A.若a>b,则ac2>bc2B.若a>﹣b,则﹣a>bC.若ac>bc,则a>b D.若a>b,则a﹣c>b﹣c6.(5分)已知等比数列{a n}中,a3=3,a10=384,则该数列的通项a n=()A.3•2n﹣4B.3•2n﹣3C.3•2n﹣2D.3•2n﹣17.(5分)已知{a n}是等差数列,a10=10,其前10项和S10=70,则其公差d=()A.B.C.D.8.(5分)已知a,b为非零实数,且a>b,则下列不等式成立的是()A.a2>b2B.C.|a|>|b|D.2a>2b9.(5分)不等式≥0的解集是()A.{x|≤x<2}B.{x|}C.{x|x>2或}D.{x|x<2} 10.(5分)(文)已知数列{a n}的前n项和S n=2n(n+1)则a5的值为()A.80 B.40 C.20 D.1011.(5分)设x、y满足约束条件,则z=2x﹣3y的最小值是()A.﹣7 B.﹣6 C.﹣5 D.﹣312.(5分)函数的值域是()A.[﹣,]B.[﹣,]C.[]D.[]二、填空题:本大题共4小题,每小题5分,共30分.把答案填在题中横线上.13.(5分)关于x的不等式ax2+bx+2>0的解集是{x|﹣<x<},则a+b=.14.(5分)若0<α<<β<π,且cos β=﹣,sin(α+β)=,则cos α=.15.(5分)已知x>3,则函数y=+x的最小值为.16.(5分)已知数列{a n}的前n项和S n=3+2n,则数列{a n}的通项公式为.三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(10分)等差数列{a n}的前n项和记为S n.已知a10=30,a20=50.(Ⅰ)求通项a n;(Ⅱ)若S n=242,求n.18.(12分)若不等式:kx2﹣2x+6k<0(k≠0)①若不等式解集是{x|x<﹣3或x>﹣2},试求k的值;②若不等式解集是R,求k的取值范围.19.(12分)已知函数f(x)=(sinx+cosx)2+2cos2x.(Ⅰ)求f(x)最小正周期;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.20.(12分)在△ABC中,已知2sinBcosA=sin(A+C).(1)求角A;(2)若BC=2,△ABC的面积是,求AB.21.(12分)某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?22.(12分)已知数列{a n}中,S n是它的前n项和,并且S n+1=4a n+2(n=1,2,…),a 1=1(1)设b n=a n+1﹣2a n(n=1,2,…),求证{b n}是等比数列;(2)设c n=(n=1,2,…),求证{c n}时等差数列;(3)求数列{a n}的通项公式及前n项和公式.2016-2017学年宁夏石嘴山三中高二(上)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知数列{a n}是等比数列,且a1=,a4=﹣1,则{a n}的公比q为()A.2 B.﹣ C.﹣2 D.【解答】由,故选:C.2.(5分)已知实数m和2n的等差中项是4,实数2m和n的等差中项是5,则m和n的等差中项是()A.2 B.3 C.6 D.9【解答】解:由题意,m+2n=8,2m+n=10,两式作和得:3m+3n=18,即m+n=6,∴m和n的等差中项是3.故选:B.3.(5分)在△ABC中,已知a2=b2+c2+bc,则A=()A.B.C. D.或【解答】解:∵在△ABC中,a2=b2+bc+c2,即b2+c2﹣a2=﹣bc,∴cosA==﹣,则A=,故选:C.4.(5分)在△ABC中,若∠A=60°,∠B=45°,BC=3,则AC=()A.B.C.D.【解答】解:根据正弦定理,,则故选:B.5.(5分)下列命题正确的是()A.若a>b,则ac2>bc2B.若a>﹣b,则﹣a>bC.若ac>bc,则a>b D.若a>b,则a﹣c>b﹣c【解答】解:当c=0时,若a>b,则ac2=bc2,故A错误;若a>﹣b,则﹣a<b,故B错误;若ac>bc,当c>0时,则a>b;当c<0时,则a<b,故C错误;若a>b,则a﹣c>b﹣c,故D正确故选:D.6.(5分)已知等比数列{a n}中,a3=3,a10=384,则该数列的通项a n=()A.3•2n﹣4B.3•2n﹣3C.3•2n﹣2D.3•2n﹣1【解答】解:在等比数列{a n}中,由a3=3,a10=384,得,∴q=2.则,∴.故选:B.7.(5分)已知{a n}是等差数列,a10=10,其前10项和S10=70,则其公差d=()A.B.C.D.【解答】解:设{a n}的公差为d,首项为a1,由题意得,解得,故选:D.8.(5分)已知a,b为非零实数,且a>b,则下列不等式成立的是()A.a2>b2B.C.|a|>|b|D.2a>2b【解答】解:A选项不正确,当a=1,b=﹣2时,不等式就不成立;B选项不正确,因为a=1,b=﹣2时,不等式就不成立;C选项不正确,因为a=1,b=﹣2时,不等式就不成立;D选项正确,因为y=2x是一个增函数,故当a>b时一定有2a>2b,故选:D.9.(5分)不等式≥0的解集是()A.{x|≤x<2}B.{x|}C.{x|x>2或}D.{x|x<2}【解答】解:不等式≥0,等价为(3x﹣1)(2﹣x)≥0,且2﹣x≠0,解得≤x<2.即解集为{x|}.故选:B.10.(5分)(文)已知数列{a n}的前n项和S n=2n(n+1)则a5的值为()A.80 B.40 C.20 D.10【解答】解:由题意可得:a5=S5﹣S4,因为S n=2n(n+1),所以S5=10(5+1)=60,S4=8(4+1)=40,所以a5=20.故选:C.11.(5分)设x、y满足约束条件,则z=2x﹣3y的最小值是()A.﹣7 B.﹣6 C.﹣5 D.﹣3【解答】解:由z=2x﹣3y得y=,作出不等式组对应的平面区域如图(阴影部分ABC):平移直线y=,由图象可知当直线y=,过点A时,直线y=截距最大,此时z最小,由得,即A(3,4),代入目标函数z=2x﹣3y,得z=2×3﹣3×4=6﹣12=﹣6.∴目标函数z=2x﹣3y的最小值是﹣6.故选:B.12.(5分)函数的值域是()A.[﹣,]B.[﹣,]C.[]D.[]【解答】解:,故选:C.二、填空题:本大题共4小题,每小题5分,共30分.把答案填在题中横线上.13.(5分)关于x的不等式ax2+bx+2>0的解集是{x|﹣<x<},则a+b=﹣14.【解答】解:∵不等式ax2+bx+2>0的解集为{x|﹣},∴﹣和为方程ax2+bx+2=0的两个实根,且a<0,由韦达定理可得,解得a=﹣12,b=﹣2,∴a+b=﹣14.故答案为:﹣14.14.(5分)若0<α<<β<π,且cos β=﹣,sin(α+β)=,则cos α=.【解答】解:0<α<<β<π,cos β=﹣,可得sinβ===,sin(α+β)=,且<α+β<,可得cos(α+β)=﹣=﹣=﹣,则cosα=cos[(α+β)﹣β]=cos(α+β)cosβ+sin(α+β)sinβ=﹣×(﹣)+×=.故答案为:.15.(5分)已知x>3,则函数y=+x的最小值为5.【解答】解:x>3,则函数y=+x=+x﹣3+3≥2+3=2+3=5,当且仅当x=4时取等号,故函数y=+x的最小值为5,故答案为:5.16.(5分)已知数列{a n}的前n项和S n=3+2n,则数列{a n}的通项公式为.【解答】解:由S n=3+2n,当n=1时,a1=S1=5.当n≥2时,.所以.故答案为.三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(10分)等差数列{a n}的前n项和记为S n.已知a10=30,a20=50.(Ⅰ)求通项a n;(Ⅱ)若S n=242,求n.【解答】解:(Ⅰ)由a n=a1+(n﹣1)d,a10=30,a20=50,得方程组解得a1=12,d=2.所以a n=2n+10.(Ⅱ)由得方程.解得n=11或n=﹣22(舍去).18.(12分)若不等式:kx2﹣2x+6k<0(k≠0)①若不等式解集是{x|x<﹣3或x>﹣2},试求k的值;②若不等式解集是R,求k的取值范围.【解答】解:①∵不等式kx2﹣2x+6k<0的解集是{x|x<﹣3或x>﹣2}∴方程kx2﹣2x+6k=0的两个根为﹣3,﹣2∴=﹣3+(﹣2)=﹣5,∴k=﹣②:①∵不等式kx2﹣2x+6k<0的解集是R∴解得k<﹣19.(12分)已知函数f(x)=(sinx+cosx)2+2cos2x.(Ⅰ)求f(x)最小正周期;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.【解答】解:(Ⅰ)f(x)=(sinx+cosx)2+2cos2x=sin2x+2sinxcosx+cos2x+2cos2x=1+sin2x+1+cos2x=sin(2x+)+2,…(4分)所以f(x)的最小正周期为T=π;…(6分)(Ⅱ)由0≤x≤得,0≤2x≤π,所以≤2 x+≤;…(8分)根据正弦函数y=sinx的图象可知当时,f(x)有最大值为2+,…(11分)当时,f(x)有最小值为1.…(13分)20.(12分)在△ABC中,已知2sinBcosA=sin(A+C).(1)求角A;(2)若BC=2,△ABC的面积是,求AB.【解答】解:(1)由A+B+C=π,得sin(A+C)=sinB;所以2sinBcosA=sin(A+C)=sinB,解得cosA=,又因为A∈(0,π),所以;(2)由余弦定理,得BC2=AB2+AC2﹣2AB•ACcosA=22,①因为△ABC的面积为S △ABC=,所以AB•AC=4,②由①、②组成方程组,解得AB=BC=2.21.(12分)某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?【解答】解:设每天生产A型桌子x张,B型桌子y张,利润总额为z千元,则目标函数为:z=2x+3y作出可行域:把直线l:2x+3y=0向右上方平移至l'的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值,解方程得M的坐标为(2,3).答:每天应生产A型桌子2张,B型桌子3张才能获得最大利润.22.(12分)已知数列{a n}中,S n是它的前n项和,并且S n+1=4a n+2(n=1,2,…),a1=1(1)设b n=a n+1﹣2a n(n=1,2,…),求证{b n}是等比数列;(2)设c n=(n=1,2,…),求证{c n}时等差数列;(3)求数列{a n}的通项公式及前n项和公式.=4a n+2,【解答】证明:(1)由题意得,S n+1所以当n≥2时,S n=4a n﹣1+2,=4a n﹣4a n﹣1,两式相减得,a n+1又b n=a n+1﹣2a n,所以===2,由a1=1,S2=4a1+2得,a2=5,所以b1=a2﹣2a1=3,则{b n}是公比为2、首项为3的等比数列;(2)由(1)得,,﹣2a n=3•2n﹣1,两边同除以2n+1,得=,所以a n+1又c n=,则c1==,所以{c n}是公差为、首项为的等差数列;解:(3)由(2)得,c n==,因为c n=,所以=(3n ﹣1)•2n ﹣2,因为S n +1=4a n +2,所以当n ≥2时S n =4a n ﹣1+2, 则S n =(3n ﹣4)•2n ﹣1+2,当n=1时,S 1=1也适合上式,故S n =(3n ﹣4)•2n ﹣1+2.赠送初中数学几何模型【模型二】半角型:图形特征:45°4321DA1FDAB正方形ABCD 中,∠EAF =45° ∠1=12∠BAD 推导说明:1.1在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠FAE =45°,求证:EF =BE +DF45°DEa +b-a45°A1.2在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且EF =BE +DF ,求证:∠FAE =45°E-aaBE挖掘图形特征:a+bx-aa 45°DBa +b-a45°A运用举例:1.正方形ABCD 的边长为3,E 、F 分别是AB 、BC 边上的点,且∠EDF =45°.将△DAE 绕点D 逆时针旋转90°,得到△DCM . (1)求证:EF =FM(2)当AE =1时,求EF 的长.E3.如图,梯形ABCD中,AD∥BC,∠C=90°,BC=CD=2AD=4,E为线段CD上一点,∠ABE=45°.(1)求线段AB的长;(2)动点P从B出发,沿射线..BE运动,速度为1单位/秒,设运动时间为t,则t为何值时,△ABP为等腰三角形;(3)求AE-CE的值.变式及结论:4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图1),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图2),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图3),请你直接写出线段EF,BE,DF之间的数量关系.DABFEDCF。
