1网孔分析回路分析结点分析3_4
合集下载
电路分析网孔分析法和节点分析
等效单口网络：当两个单口网络的VCR关系完全 相同时，称这两个单口是互相等效的。
将电路中的某些单口用其等效电路代替，可以简化 电路的分析和计算。
一、线性电阻的串联和并联
1．线性电阻的串联（见第一章）
2．线性电阻的并联（见第一章）
3．线性电阻的串并联 由若干个线性电阻的串联和并联所形成的单口网
络，就端口特性而言，等效于一个线性二端电阻。
i5 R2 i＋2 R5 ib uS－2
支路电流： i1,i2,i3,i4,i5,i6 网孔电流：
假想沿网孔边沿流动的电流，
i4
R4 ic R6 i6
如图中ia,ib,ic
R3 ＋uS3－i3 参考方向可以任意选取。
若以网孔电流为求解变量， 所需方程数将大大减少。（重点）
一、网孔电流
设想电流i1、i2和i3沿每个
图中 节点1与公共点O间电阻称为R1 节点2与公共点O间电阻称为R2 节点3与公共点O间电阻称为R3
二、Δ形联接
当三个电阻依次联成一个 闭合电路，且三个联接点再 分别与外电路相联，叫Δ形 联接。
图中：
节点1与2间电阻称为R12 节点2与3间电阻称为R23 节点3与1间电阻称为R31
方法： Y-变换
R2
R12
R23 R12 R 23 R31
特例：当三电阻相等时，则
R 3RY
或
RY
1 3
R
历年考题：
9、图示电路，求u 。(2V)
10、图示电路，求i 。(9/13A)
3Ω
6Ω
i
+ 18V
+u–
1A
3Ω 2A 2Ω 4Ω
–
2Ω
6Ω
3Ω
第三章网孔分析法和结点分析法
将电路中的某些单口用其等效电路代替，可以简化 电路的分析和计算。
一、线性电阻的串联和并联
1．线性电阻的串联（见第一章）
2．线性电阻的并联（见第一章）
3．线性电阻的串并联 由若干个线性电阻的串联和并联所形成的单口网
络，就端口特性而言，等效于一个线性二端电阻。
i5 R2 i＋2 R5 ib uS－2
支路电流： i1,i2,i3,i4,i5,i6 网孔电流：
假想沿网孔边沿流动的电流，
i4
R4 ic R6 i6
如图中ia,ib,ic
R3 ＋uS3－i3 参考方向可以任意选取。
若以网孔电流为求解变量， 所需方程数将大大减少。（重点）
一、网孔电流
设想电流i1、i2和i3沿每个
图中 节点1与公共点O间电阻称为R1 节点2与公共点O间电阻称为R2 节点3与公共点O间电阻称为R3
二、Δ形联接
当三个电阻依次联成一个 闭合电路，且三个联接点再 分别与外电路相联，叫Δ形 联接。
图中：
节点1与2间电阻称为R12 节点2与3间电阻称为R23 节点3与1间电阻称为R31
方法： Y-变换
R2
R12
R23 R12 R 23 R31
特例：当三电阻相等时，则
R 3RY
或
RY
1 3
R
历年考题：
9、图示电路，求u 。(2V)
10、图示电路，求i 。(9/13A)
3Ω
6Ω
i
+ 18V
+u–
1A
3Ω 2A 2Ω 4Ω
–
2Ω
6Ω
3Ω
第三章网孔分析法和结点分析法
复杂电阻电阻电路的分析
3
i1
2 i4
R5 i5
i1+i2=iS1+iS2 -i2+i4+i3=0
R1 R4
+
u_S
-i3+i5=－iS2
iS2
i1+i2=iS1+iS2
1 i2 R2
i3 R3
3
-i2+i4+i3=0
-i3+i5=-iS2
iS1 i1
2 i4
R1 R4
R5 i5 +
把支路电流用节点电压表示：
u_S
un1 R1
回路2 u4 u5 u3 0 回路3 u1 u5 u6 0
R2 i2
11
2
R4
回路1
i3
i4 回路2
R32
3 回路3
u2 u3 u1 0 u4 u5 u3 0 u1 u5 u6 0
R1 i1 34
R5 i5
应用欧姆定律消去支路电压得：
i6
R2i2 R3i3 R1i1 0
1 R3
un2
1 R3
1 R5
un3
iS2
uS R5
令
Gk=1/Rk，k=1,
G11un1+G12un2
2, 3, 4, 5 上式简记为：
＋G13un3 = iSn1
等效电流源
G21un1+G22un2 ＋G23un3 = iSn2 G31un1+G32un2 ＋G33un3 = iSn3
i2 1
2
R2 i3
R4 i4
1
R32
R1 i1
R5 i5
有6个支路电流，需列写6个方 程。KCL方程:
大学物理电路分析精品课程 第三章 电路的一般分析方法
I S I4 I1 0
I
1
I3
I2
0
I
4
I3
I5
0
U 4 U S1 U 3 U1 0 U1 U 2 U 0 U 3 U S1 U 5 U S 2 U 2 0
I1R1 U1
I I
2 3
R2 R3
U2 U3
I
4
R4
U4
I 5 R5 U 5
支路电流法（1B法）
1) U 2
2
添加以下方程：
2U 23 2(U 2 U 3 ) 4U 43 4(U 4 U 3 ) U1 U 4
例题3——割集分析法
5 + 19V - 2
I1 +
30V _
4A 1.5I1
4
+ 25V
_
选树如图所示，则只需要对2、4支路 （树支）所决定的基本割集列写方程即可
(5 2 4) I1 (2 4) 4 4 1.5I1 30 25 19
I S
U4 R4
U1 R1
0
UR11
U3 R3
U2 R2
0
U
4
U3
U5
0
R4 R3 R5
3-3 节点法与割集法
一、节点法
1 .方法
任选电路中某一节点为参考节点， 其他节点与此参考节点间的电压称为 “节点电压”。节点法是以节点电压作 为独立变量，对各个独立节点列写KCL 电流方程，得到含(n-1)个变量的(n-1)个 独立电流方程，从而求解电路中待求量。
第三章 电路的一般分析方法
❖重点 1、支路法 2、节点法 3、网孔法
❖难点 1、改 拓扑术语
支路 节点 回路 网孔 基本回路 割集 基本割集
电路分析第3、4章习题课
图5
6. 图6 所示线性网络N只含电阻，若IS1=8A， IS2=12A，Ux为80V，若IS1=8A，IS2=4A，Ux为0.求： IS1=IS2=10A时，Ux是多少？
图6
7. 用戴维南定理求图7 电路中流过 20 kΩ电阻的电 流及 a 点电压 Ua.
图7
8. 图8（a）所示电路，输入电压为20V，U2=12.5V， 若将网络N短路，如图(b)所示，短路电流I为10mA， 试求网络N在AB端的戴维南等效电路
+
2U1
- 2V
(a)
-
(b )
图11
12. 如图12所示，RL为何值时能获得最大功率，并 求最大功率。 10 + a ＋ Uoc
2A
UR 20
UR 20 – + － 20V – b
图12
练习
1. 列出图1-1所示电路的网孔方程、节点方程。
+ uS 6 -
R6 2
uS2 +
1 R1
uS1 +
电路分析习题课（3—4章）
1. 电路如图1 所示 用网孔分析法求 I A 并求受控源 提供的功率 PK .
图1
2. 电路如图所示，用网孔分析法求4Ω电阻的功率。
图2
3. 试用结点分析法求解图3中的 U1及受控源的功率。
图3
4. 试列出为求解图4 所示电路中 Uo所需的结点方程。
图4
5. 电路如图5 所示，用叠加定理求Ix
图8
9. 求图9 所示电路的戴维南等效电路。
图9
10. 用戴维南定理求图10所示电路中2A电流源上的电 压U 。
15Ω 5Ω I
15Ω
5I
+
节点分析法
（2-7）
电路分析基础——第一部分：2-2
7/23
进一步整理后得： G11un1+G12un2+G13un3= is11 G21un1+G22un2+G23un3= is22 G31un1+G32un2+G33un3= is33
（2-8）
自电导：G11、G22、G33。它们分别是各个节点上所 有电导之和，如： G22= G1+G2+G3 ；
= 0.175
– 0.1 = 0.0306 – 0.01 = 0.0206
– 0.1 0.175
6 – 0.1 1 = – 6 0.175 = 1.050 – 0.6 = 0.45
电路分析基础——第一部分：2-2
0.175 6 2 = – 0.1 – 6 = – 1.050 + 0.6 = – 0.45
电路分析基础——第二部分：第二章 目录
第二章 运用独立电流电压变量 的分析方法
1 网孔分析法 2 节点分析法 3 含运算放大器
的电阻电路 4 树的概念
5 割集分析法
6 回路分析法
7 线性电阻电路解答的 存在性和唯一性定理
电路分析基础——第一部分：2-2
1/23
2-2 节点分析法
内容回顾：如何选用完备独立的变量作为第一步求解
方程，因此与该节点有关的所有
电流都必须计算在内。
+
G1
Is33可一理般解在为此流种入情节况点下的，所I有s11已、知Is2的2、–
2 Us
电流源电流和未知的电压源电流的
G4
代数和。节点分析法都是如此处理
非接地电压源的！
1
G2
G3
网孔分析法
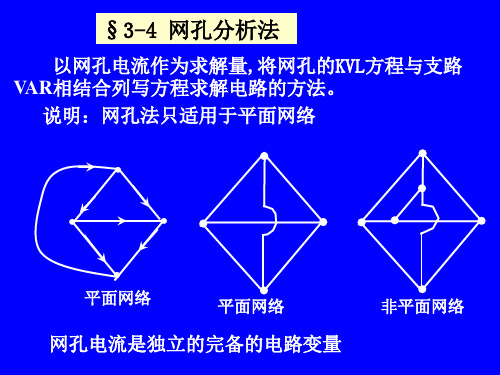
im1
im2 6
b)电路含受控电流源 b)电路含受控电流源 1、受控电流源在边沿支路上 例5、用网孔法求图中流过4V电压源的电流。 用网孔法求图中流过4 电压源的电流。 i1 2 4V i 1 3i1
10V
im1
im2 1
2、受控电流源为两个网孔公有 例6、列出图示电路的网孔方程。 列出图示电路的网孔方程。 6V
三）含理想电压源、受控源电路的节点分析法 含理想电压源、 (1) 电路含有理想电压源时
a)含有一个理想电压源支路时 a)含有一个理想电压源支路时 例2：用节点法求图示电路中的u1 ，u2 。 用节点法求图示电路中的u
is1
①
R1
②
us2 is2
③
u1
R2
u2
R3
④
b)含有两个 含两个 以上理想电压源支路时 含有两个(含两个 含有两个 含两个)以上理想电压源支路时 例3：用节点法求图示电路中的u 。 用节点法求图示电路中的u
例1：用割集法求 i1 ：
1
① 2A ② 12V ③
C2
5 3
③
5i2
6V
i2
20
④
i1
8
①
4 2
②
6
④
C1
C3
说明：用割集法时尽可把电压源支路选为树支， 说明：用割集法时尽可把电压源支路选为树支， 使之未知的独立变量减少。 使之未知的独立变量减少。
§3-7 回路分析法 以连支电流作为求解量, 以连支电流作为求解量,对每一基本回 路列写支路电压以连支电流和电阻表示的 KVL方程求解电路的方法。 方程求解电路的方法 方程求解电路的方法。
i5 i3
G3
i1
电路分析网孔法及应用
第三章网孔分析法和节点分析科学家研究世界工程师创造崭新世界西奥多•冯•卡曼(Theodore von Karman)美籍匈牙利力学家,近代力学奠基人之一。
第三章网孔分析法和结点分析法3－1 网孔分析法(重点）3－2 结点分析法（重点）3－3 含受控源的电路分析（重点）3－4 回路分析法和割集分析法3－5 计算机分析电路实例3－6 树支电压与连支电流法§3－1 网孔分析法(重点)本章介绍利用独立电流或独立电压作变量来建立电路方程的分析方法，可以减少联立求解方程的数目，适合于求解稍微复杂一点的线性电阻电路，是求解线性电阻电路最常用的分析方法。
网孔方程：用网孔电流作变量建立的电路方程。
求解网孔方程得到网孔电流后，用KCL 方程可求出全部支路电流，再用VCR 方程可求出全部支路电压。
一、网孔电流设想电流i 1、i 2和i 3沿每个网孔边界闭合流动而形成，如图中箭头所示。
这种在网孔内闭合流动的电流，称为网孔电流。
为何提出网孔电流作为求解变量？是因为网孔电流具有如下令人感兴趣的特点：（1）完备性——网孔电流一旦求出，各支路电流就被唯一确定。
（2）独立性——网孔电流自动满足KCL 。
这一特点的意义在于：求解i 1、i 2、i 3时，不必再列写KCL 方程，只需列出三个网孔的KVL 方程。
因而可用较少的方程求出网孔电流。
二﹑网孔方程⎪⎭⎪⎬⎫=++−=−++=−++0003S 4466332S 6655221S 445511u i R i R i R u i R i R i R u i R i R i R 将以下各式代入上式，消去i 4、i 5和i 6后可以得到：326215314 i i i i i i i i i −=+=+=网孔方程⎪⎭⎪⎬⎫++−−+++=+++3S 314326332S 326215221S 31421511)()()()()()(i i R i i i i R i i R u i i i i R i R 1S 34251541)(u i R i R i R R R =++++S236265215)(u i R i R R R i R =−+++3S 36432614)(u i R R R i R i R −=+++−以图示网孔电流方向为绕行方向，写出三个网孔的KVL 方程分别为：﹑将网孔方程写成一般形式：⎪⎭⎪⎬⎫=++=++=++S3333323213122S 32322212111S 313212111u i R i R i R u i R i R i R u i R i R i R 其中R 11,R 22和R 33称为网孔自电阻，它们分别是各网孔内全部电阻的总和。
运用节点法和网孔法进行电路分析
确定了节点电压，支路电流的计算可从欧姆定律的简单应用得出。 例子4.1 含超节点的节点分析
(4.25)
(4.26)
图7所示电路包含两个电压源，而且经我们指定参考节点，电压源 V 2 是一个浮动电压源。 如图中所示，超节点包括电压源和与它并联的电阻元件 R 4 。
图7 另一个超节点例子
首先，我们注意到通过电阻 R 4 的电流 I 4 由公式(4.27)给出：
R R1 R3
这种形式。如
果对角线上的某个元素由正、负两部分组成，那么一定有一个符号是错误的。 · 所有的对角线上的元素都是正的，其它元素都是负的，而且矩阵是对称的 Aij = A ji 。如果矩 阵不具有这个特性，那一定存在错误。 用上面的形式列写电路方程式，一定存在一组由真实电流值构成的解。 一旦我们把方程式变为矩阵形式，对结果进行逐条的检验。如果 det A = 0 ，那么就能得出 一组解。 未知电压 VK 为：
运用节点法和网孔法进行电路分析运用节点法和网孔法进行电路分析众所周知运用基尔霍夫定律和欧姆定律我们可以对任何一个电路进行分析以确定其运行条件电流和电压值
运用节点法和网孔法进行电路分析
众所周知，运用基尔霍夫定律和欧姆定律，我们可以对任何一个电路进行分析，以确定其 运行条件（电流和电压值）。一般电路分析的难点在于用最少的联立方程描述电路的运行特性。 在这一讲里，我们将介绍两种非常有效的可用于对任意电路进行分析的方法：节点法和网 孔法。这些方法是建立在对基尔霍夫定律的系统应用基础上的，我们将通过图1的例子电路来说 明求解的步骤。
图10 标注网孔电流方向 现在，让我们把注意力转移到标记各个支路上的元件电压。 电阻上电压极性与指定的网孔电流的方向一致。万一某一处支路被两个网孔共用，就像例 子中含有电阻 R 2 的支路，电压的极性与各自网孔中指定的网孔电流的方向一致。 在这个电路中，我们进行网孔分析的第一步是单独分析每个网孔，根据定义的网孔电流方 向在回路上应用KVL定律。 考虑网孔1 为了分析更方便，我们把网孔1从图11所示的电路中分离出来。这么做的时候，必须注意要 包括共享支路的所有信息。在这里，我们给出了网孔电流 I 2 在共享支路上的方向。
(4.25)
(4.26)
图7所示电路包含两个电压源，而且经我们指定参考节点，电压源 V 2 是一个浮动电压源。 如图中所示，超节点包括电压源和与它并联的电阻元件 R 4 。
图7 另一个超节点例子
首先，我们注意到通过电阻 R 4 的电流 I 4 由公式(4.27)给出：
R R1 R3
这种形式。如
果对角线上的某个元素由正、负两部分组成，那么一定有一个符号是错误的。 · 所有的对角线上的元素都是正的，其它元素都是负的，而且矩阵是对称的 Aij = A ji 。如果矩 阵不具有这个特性，那一定存在错误。 用上面的形式列写电路方程式，一定存在一组由真实电流值构成的解。 一旦我们把方程式变为矩阵形式，对结果进行逐条的检验。如果 det A = 0 ，那么就能得出 一组解。 未知电压 VK 为：
运用节点法和网孔法进行电路分析运用节点法和网孔法进行电路分析众所周知运用基尔霍夫定律和欧姆定律我们可以对任何一个电路进行分析以确定其运行条件电流和电压值
运用节点法和网孔法进行电路分析
众所周知，运用基尔霍夫定律和欧姆定律，我们可以对任何一个电路进行分析，以确定其 运行条件（电流和电压值）。一般电路分析的难点在于用最少的联立方程描述电路的运行特性。 在这一讲里，我们将介绍两种非常有效的可用于对任意电路进行分析的方法：节点法和网 孔法。这些方法是建立在对基尔霍夫定律的系统应用基础上的，我们将通过图1的例子电路来说 明求解的步骤。
图10 标注网孔电流方向 现在，让我们把注意力转移到标记各个支路上的元件电压。 电阻上电压极性与指定的网孔电流的方向一致。万一某一处支路被两个网孔共用，就像例 子中含有电阻 R 2 的支路，电压的极性与各自网孔中指定的网孔电流的方向一致。 在这个电路中，我们进行网孔分析的第一步是单独分析每个网孔，根据定义的网孔电流方 向在回路上应用KVL定律。 考虑网孔1 为了分析更方便，我们把网孔1从图11所示的电路中分离出来。这么做的时候，必须注意要 包括共享支路的所有信息。在这里，我们给出了网孔电流 I 2 在共享支路上的方向。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
－
b
－
m个网孔 的电路：
R11 I l1＋R12 I l 2＋„＋R1m I m U S11 R I R I ＋„＋R I U 21 l1 22 l 2 2m 2m S 22 „ „ „ „ „ Rm1 I l1 Rm 2 I l 2＋„＋Rmm I 2 m U Smm
I 1 I 2 2 10 3 I 3 10 10 3 I3 0.4347 mA 2501I 1 2751I 2 50.002 I 3 0 U o RLd I 3 2500 I 2550 I 60 I 0 1 2 3 4.347 V
结点KCL
① G2 G1 G3 I1 I3 I2
②
n1 : I1 I 2 I S1 n2 : I 2 I 3 I S2
IS1
IS2
G1U1 G2 (U1 U 2 ) I S1 G2 (U1 U 2 ) G3U 2 I S2
(G1＋G2 )U1－G2U 2＝I S1 －G2U1＋(G2＋G3 )U 2＝－I S2
a Rf
Ib
b
Ic
Re R Ld
Rb I 1 Rb I 2 U i RLd I 3 U i
I1
Rb I2
I b
I 3
Uo
RLd I c
Re I b
a Rf
b
Ic
Re R Ld
Rb I 1 Rb I 2 U i RLd I 3
Ui
§1-4 结点分析法（补充）
一. 结点电压 ●结点电压──结点与零电位参考点间的电压。 数目： (n-1)个。 支路电压＝两结点电压之差 如图 n＝3
① G2
G1 G3 I1 I3 I2
②
UG1 U1
U G 2 U1 U 2 UG3 U 2
IS1
IS2
UG1 U1 U G 2 U1 U 2
例：列出图示电路的网孔方程。 解：增设 U I
+ 7V 1
I 2 2
3
2 1
I1
UI
3I1 I 2 2 I 3 7 U I I 6 I 3 I 0 1 2 3 2 I 1 3 I 2 6 I 3 U I I1 I 3 7
解： I1 2U n2
Uo
① 10 I1 3S 5V
② 3A
U n1 5V
I1 2S
3Un1 (2 3)Un2 3 10I1
G
G1
G2
弥尔曼定理
特例2：含独立无伴电压源US
法1：尽量以无伴电压源的某一极作为参考点 .
法2： ①增设US上电流IUs为变量，代入相应结 点的KCL方程（好比电流源IUs）；
②补充该US与两端结点电压的关系式 。
例：求右图的Un2 、 Un3 及I 。 解：对7V电压源可用 法一， 而对而对4V电 压源则要用法二。
三. 结点法的特例情况
特例1：结点数 n=2 （独立结点数 n-1=1）
+ US1
-
① + US2
-
+ US3
-
(G1 G2 G3 G4 )U n1 G1US1 G2US2 G3US3
R1
R2
R3
R4
U n1＝
（GUS ） G1US1 G2U S2
①
G3U S3
G3 G4
R3 3
US3 + -
I l 2 1A I l 3 2A I1＝I l1 3A
R1 3
R2 2
I 2＝I l 2 － 1A
I3＝I l 3 2A
I 4＝I l1－I l 3 1A
I5＝I l 2－I l 3 3A I 6＝I l1－I l 2 4A
Ib
I1
Rb I2
I b
I 3
Re I 3 μRLd I 3 αRe(I1 I 2 )
RLd I c
Re I b
Re I 2 ( Re RLd ) I 3 Re ( I1 I 2 )
※网孔分析法特例
特例1：含电流源IS
1）为有伴电流源时 ，将其等效成有伴电压源， 再按基本步骤列写回路法方程。
2）增设IS上电压 UIS为变量，代入相应网孔的 KVL方程；
补充该IS与有关网孔电流的关系式 (多一变量、多一方程)。
特例2：含受控电源的处理方法
①先将控制量用独立变量(网孔电流)表示； ②将受控源看着独立电源，按上述方法列写 网孔法方程 ； ③将①中的表示式代入②中的方程，移项整 理后即得独立变量(网孔电流)的方程组。
2Ω ① + 7V 2Ω 1Ω ② I + 4V 1.5A 1Ω ③
特例3：含受控源 ① 先将控制量用独立变量(结点电压)表示；
② 将受控源看成独立电源，按上述方法列写 结点法方程 ； ③ 将①中的表示式代入②中的方程，移项整 理后即得独立变量(结点电压)的方程组。
例：列出图示电路的结点电压方程。
1)G kk ──结点k的所有电导之和，自电导0 。
2)Gki (k≠i) ──结点k、i 的公有电导之和的负值， 互电导0
3) I Skk──注入结点k的所有电流源之代数和。 若电路中存在有伴电压源，先转为有伴电流源。
列写步骤：
1. 选定参考结点，并标出其余(n-1)个结点的序号； 2. 直接按“自电导”、“互电导”、注入某结点 “电流源代数和”的概念列写结点方程 (有伴电压源有伴电流源) ； 3. 求解结点电压，进而解出其它待求量。
？系数规律 1) R11 、 R22 、…、 Rmm ——网孔1、2、…、m的 自电阻(“＋”)； 2) Rki (k i ) ──网孔k、i的公有电阻，为互电阻。 3)US11、 US22、 、USmm ──网孔1、2、…、m沿 Il1、 Il2、 …、 Ilm方向的电压源的电位升的 代数和。
(1)
(2)
( R1 R2 ) I l1 R2 I l 2 U S1 U S2 －R2 I l1 ( R2 R3 ) I l 2 U S2 U S3
R11 I l1＋R12 I l 2 U S11 R21 I l1 R22 I l 2 U S22
R1 3
－
R2 2
I l1 : ( R1 R4 R6 ) I l1 R6 I l 2 R4 I l 3 US1 US4
I l 2 : R6 I l1 ( R2 R5 R6 ) I l 2 R5 I l 3＝US5 US2 Il 3 : R4 Il1 R5 Il 2 (R3 R4 R5 )Il 3 US3 US5 US4
例：列出图示电路结点方程 ① 解：
+
IS
R6
R1 US
R2
② R4 R3 R5
③
－
1 US 1 1 1 1 ＋ ＋ U1－ U 2－ U 3 IS R R2 R6 R1 1 R2 R6 1 1 1 1 1 ＋ ＋ U 2－ U 3 0 － U1 R4 R 2 R3 R4 R2 1 1 1 1 1 － U1－ U 2 ＋ ＋ U 3 I S R R R R R 6 4 5 6 4
G11U1 G12U 2 I S11 G21U1 G22U 2 I S22
结点 方程 一般 形式
G11U1 G12U 2＋„＋G1nU n I S11 G U G U ＋„G U I 21 1 22 2 2n n S 22 „ „ „ „ „ „ G( n1)1U1 G( n1) 2U 2＋„＋G( n1)( n1)U ( n1) I S( n1)( n1)
例：图示电路，已知
I3
R3 3
US1 21V , US2 14V, US3 6V , US4 2V, US5 2V .
求各支路电流。 解：
US3 + -
US5 US4 Il3 I4 I - + 5 + I1 R4 6 I R5 2 I2 + 6 + US1 I US2 I l1 R6 1 l2 －
2. 网孔方程的规律
I1
a
I3 R2 + US2 Il2
R1
+ US1 Il1
－
I2
R3
+ US3
－
KVL
b
－
R1 I l1 R2 I l1 R2 I l 2 U S1 U S2 R2 I l 2 R3 I l 2 R2 I l1 U S2 U S3
( R1 R2 ) I l1 R2 I l 2 U S1 U S2 －R2 I l1 ( R2 R3 ) I l 2 U S2 U S3
UG3 U 2
其完备性──所有支路电压 均可由结点电压线性表示。 IS1
① G2
②
G1 G3 I1 I3
I2
IS2
I1 G1U1 I 2 G2 (U1 U 2 )
I 3 G3U 2
其独立性──从某一节点到参考节点的路径不同于 其它节点到参考节点的路径，
二. 结点方程的规律与列写步骤
7A
I3
例：右图为晶体管低频小信 号放大的电路模型。已知：
a Rf
Ib
Rb U o
b
Ic
Rb 1k， Re 50k， U i Rf 200k，RLd 10k， 2 104， 50 设 U i 10mV， 求 Uo