第3章 网孔分析法和节点分析法
网孔电流法和节点电压法例题分析

课题8:支路电流法、网孔电流法和节点电压法课型:讲授教学目的:(1)利用支路电流法求解复杂直流电路(2)利用网孔电流法求解支路数目较多的电路。
(3)利用节点电压法求解节点较少而网孔较多的电路重点、难点:重点:支路电流法、网孔电流法、节点电压法求解复杂直流电路难点:列方程过程中电压、电流参考方向及符号的确定。
教学分析:本节主要还是在巩固基尔霍夫定律的基础上,利用实例分析支路电流法、网孔电流法、节点电压法并将其用于实践案例中。
复习、提问:(1)节点的概念和判别?(2)网孔的概念和判别?教学过程:导入:求解复杂电路的方法有多种,我们可以根据不同电路特点,选用不同的方法去求解。
其中最基本、最直观、手工求解最常用的就是支路电流法。
一、支路电流法利用支路电流法解题的步骤:(1)任意标定各支路电流的参考方向和网孔绕行方向。
(2)用基尔霍夫电流定律列出节点电流方程。
有n个节点,就可以列出n-1个独立电流方程。
(3)用基尔霍夫电压定律列出L=b-(n-1)个网孔方程。
说明:L指的是网孔数,b指是支路数,n指的是节点数。
(4)代入已知数据求解方程组,确定各支路电流及方向。
例1试用支路电流法求图1中的两台直流发电机并联电路中的负载电流I及每台发电机的输出电流I1、和I2。
已知:R1=1Ω,R2=0.6Ω,R=24Ω,E1=130V,E2=117V。
解:(1)假设各支路电流的参考方向和网孔绕行方向如图示。
图1(2)根据KCL,列节点电流方程该电路有A、B两个节点,故只能列一个节点电流方程。
对于节点A有:I1+I2=I ①(3)列网孔电压方程该电路中共有二个网孔,分别对左、右两个网孔列电压方程:I1R1-I2R2+E2-E1=0 ②(沿回路循行方向的电压降之和为零,如果在I R+I2R2-E2=0 ③该循行方向上电压升高则取负号)(4)联立方程①②③,代入已知条件,可得:-I1-I2+I=0I1-0.6I2=130-1170.6I2+24I=117解得各支路电流为:I1=10A I2=-5A I=5A从计算结果,可以看出发电机E1输出10A的电流,发电机E2输出-5A的电流,负载电流为5A。
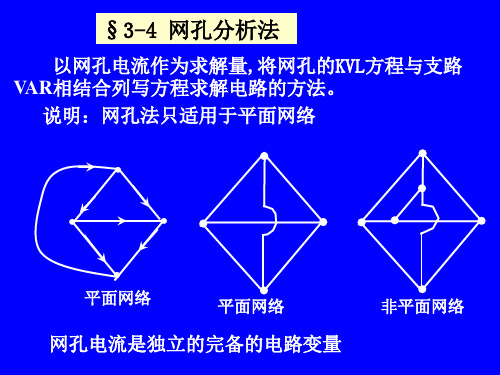
网孔分析法
im1
im2 6
b)电路含受控电流源 b)电路含受控电流源 1、受控电流源在边沿支路上 例5、用网孔法求图中流过4V电压源的电流。 用网孔法求图中流过4 电压源的电流。 i1 2 4V i 1 3i1
10V
im1
im2 1
2、受控电流源为两个网孔公有 例6、列出图示电路的网孔方程。 列出图示电路的网孔方程。 6V
三)含理想电压源、受控源电路的节点分析法 含理想电压源、 (1) 电路含有理想电压源时
a)含有一个理想电压源支路时 a)含有一个理想电压源支路时 例2:用节点法求图示电路中的u1 ,u2 。 用节点法求图示电路中的u
is1
①
R1
②
us2 is2
③
u1
R2
u2
R3
④
b)含有两个 含两个 以上理想电压源支路时 含有两个(含两个 含有两个 含两个)以上理想电压源支路时 例3:用节点法求图示电路中的u 。 用节点法求图示电路中的u
例1:用割集法求 i1 :
1
① 2A ② 12V ③
C2
5 3
③
5i2
6V
i2
20
④
i1
8
①
4 2
②
6
④
C1
C3
说明:用割集法时尽可把电压源支路选为树支, 说明:用割集法时尽可把电压源支路选为树支, 使之未知的独立变量减少。 使之未知的独立变量减少。
§3-7 回路分析法 以连支电流作为求解量, 以连支电流作为求解量,对每一基本回 路列写支路电压以连支电流和电阻表示的 KVL方程求解电路的方法。 方程求解电路的方法 方程求解电路的方法。
i5 i3
G3
i1
回路法、网孔法、节点法

U2=3(Ib-Ia)
②
4Ia -3Ib = 2 ③ -12Ia+15Ib-Ic = 0
9Ia -10Ib+3Ic= 0
各支路电流为:
解得
Ia=1.19A
Ib=0.92A Ic=-0.51A
I1= Ia=1.19A , I2= Ia- Ib=0.27A , I3= Ib=0.92A
I4= Ib- Ic=1.43A , I5= Ic=-0.52A
结点电压法
结点电压法:以结点电压为未知变量列写电路方程分析电路的方法。
iS6
R6
①i6 iS1 i1 i4
R1
R4 ② R5
③
i2 R2 i5 i3 R3
+
一、结点电压:
o
-- uS3
1、定义:设定某一个结点为参考结点后,其它结点与参考结点之间的电压称之
结点电压。
2、完备性:如果结点电压已经求出,则电路中各支路电压可以为某一个结点电
2021/4/7
5
例2 用回路法求含有受控电压源电路的各支路电流。
1
2
① 将看VCVS作独立源建立方程;
I1+ 2V
_
I2 I3
Ia 3
U2 +
Ib
将②代入①,得
I4 1
+ –3U2
Ic
I5
4Ia-3Ib=2 -3Ia+6Ib-Ic=-3U2
①
2
-Ib+3Ic=3U2
② 找出控制量和回路电流关系。
un 1 R1
is
2u1
i
1 (
R3
1 R4
)un 2
2u1
i 2iR3 R4
运用节点法和网孔法进行电路分析

(4.25)
(4.26)
图7所示电路包含两个电压源,而且经我们指定参考节点,电压源 V 2 是一个浮动电压源。 如图中所示,超节点包括电压源和与它并联的电阻元件 R 4 。
图7 另一个超节点例子
首先,我们注意到通过电阻 R 4 的电流 I 4 由公式(4.27)给出:
R R1 R3
这种形式。如
果对角线上的某个元素由正、负两部分组成,那么一定有一个符号是错误的。 · 所有的对角线上的元素都是正的,其它元素都是负的,而且矩阵是对称的 Aij = A ji 。如果矩 阵不具有这个特性,那一定存在错误。 用上面的形式列写电路方程式,一定存在一组由真实电流值构成的解。 一旦我们把方程式变为矩阵形式,对结果进行逐条的检验。如果 det A = 0 ,那么就能得出 一组解。 未知电压 VK 为:
运用节点法和网孔法进行电路分析运用节点法和网孔法进行电路分析众所周知运用基尔霍夫定律和欧姆定律我们可以对任何一个电路进行分析以确定其运行条件电流和电压值
运用节点法和网孔法进行电路分析
众所周知,运用基尔霍夫定律和欧姆定律,我们可以对任何一个电路进行分析,以确定其 运行条件(电流和电压值)。一般电路分析的难点在于用最少的联立方程描述电路的运行特性。 在这一讲里,我们将介绍两种非常有效的可用于对任意电路进行分析的方法:节点法和网 孔法。这些方法是建立在对基尔霍夫定律的系统应用基础上的,我们将通过图1的例子电路来说 明求解的步骤。
图10 标注网孔电流方向 现在,让我们把注意力转移到标记各个支路上的元件电压。 电阻上电压极性与指定的网孔电流的方向一致。万一某一处支路被两个网孔共用,就像例 子中含有电阻 R 2 的支路,电压的极性与各自网孔中指定的网孔电流的方向一致。 在这个电路中,我们进行网孔分析的第一步是单独分析每个网孔,根据定义的网孔电流方 向在回路上应用KVL定律。 考虑网孔1 为了分析更方便,我们把网孔1从图11所示的电路中分离出来。这么做的时候,必须注意要 包括共享支路的所有信息。在这里,我们给出了网孔电流 I 2 在共享支路上的方向。
网孔分析和节点分析47页PPT

理
R 4 i m 1 R 6 i m 2 ( R 3 R 4 R 5 ) i m 3 u S 3 u S 4
27.10.2019
电路分析基础
5
§2-1 网孔分析
2. 网孔方程一般形式:
R 1im 1 1 R 1im 2 2 R 1im 3 3 u S 1 1 R 2im 1 1 R 2im 2 2 R 2im 3 3 u S 22 R 3im 1 1 R 3im 2 2 R 3im 3 3 u S 33
27.10.2019
电路分析基础
16
§2-1 网孔分析
4. 含受控源网络的网孔方程 (1)受控源按独立源处理,列网孔方程; (2)辅助方程:控制量用网孔电流表示。
27.10.2019
电路分析基础
17
§2-1 网孔分析
例3:求网孔电流?
2Ω 6Ω
(1)设网孔电流方 +
向i1 ,i2
12V
(2)列网孔方程: -
(1)有伴时,化为戴维南模型; (2)无伴时:
(a) 电路最外边,为一网孔独有;
(b) 增加电流源电压u作变量来建立这些网孔
的网孔方程;同时,补充电流源电流与网孔电流关 系的方程。
27.10.2019
电路分析基础
14
§2-1 网孔分析
例2. 用网孔分析法求解图示 电路的网孔电流?
解:当电流源出现在电路外围边界上时,该网孔电流等于 电流源电流,成为已知量,此例中为i3=2A。此时不必 列出此网孔的网孔方程。
第2章 网孔分析和节点分析
本章主要介绍电路的另外两种基本分析方法:
网孔分析法和节点分析法
支路法优点:直接求解支路电流(电压)。
【推荐】电路原理基础:第三章 节点分析法

R4 i4
uo -
②式解出ub,因虚短 ua = ub代入①式得
uo
R2 R1
u1
R2 R1
R2 R1
1 u2
R3 R4
1
由题中条件得:
uo
R2 R1
(u2
u1)
差动运算电路
输出与两输入之差成正比, 被称作差动运算电路。
二、含理想运放的节点法
3
i1 =G1 un1,i2 =G2 (un1 - un2 ),i3 =G3 (un2 – uS3 ) (*)
节点: 列写KCL方程:
n1 : n2 :
i1 i2 iS1 i2 i3 iS2
将(*)式代入
① + u2 -②
+
i2 G2 +
+
uS3
iS1
u1 G1 i1
u3
un3 R2
uo R3
ui R1
R3
(1 R4
1 R5
)
1 R5
uo
0
节点③和④:不列写!
由虚短得 un1 0
R2
R1
+ ui
① -∞
+
③
+ -
∞
②
-
R4
R5
④ + uo
un2 un3
-
可得: uo R2R3 (R4 R5 ) ui R1(R3R4 R2R4 R2R5 )
例(解节.:点求节电u点压A③)、的、方iB④程.的组电。位有分受别控为源时,G12
第03章线性网络的一般分析方法

6
2. 电路元件与电路符号
• 经多年的设计、改进与演变,人们创造了一套图 形符号以表达标准元件。
• 所谓标准元件,
– 标准化了,被全面接受;
– 最基本的单元,其性能通常由一条定律确定, 例如,电阻元件由欧姆定律OL确定,PN结二 极管由其指数律方程(exponential function) 确定;
i6
R6 + uS –
(2) 对节点,根据KCL列方程
(设流出节点为正,
节点 1:i1 + i2 – i6 =0
流入节点为负)
节点 2:– i2 + i3 + i4 =0 (2) 节点 3:– i4 – i5 + i6 =0
独立KCL方程数为n–1=4–1=3个 节点 4:– i1 – i3 + i5 =0
13
电路理论相关的图论知识:路径与连 通图
2)路径:从图G的一个结点出发沿着一些支路连续
移动到达另一结点所经过的支路构成路径 (path)。 3)连通图:图G的任意两结点间至少有一条路径时 称为连通图(connected graph),非连通图至少 存在两个分离部分。 如下图,图的两部分有线相连称为连通图。
例1. US1=130V, US2=117V, R1=1, R2=0.6, R3=24.
a
I1
I2
R1
R2
+ 1+ 2
US1
US2
–
–
I3 求各支路电流。 R3
b
解 (1) n–1=1个独立KCL方程:
节点a:–I1–I2+I3=0 (2) b–( n–1)=2个独立KVL方程: UR降=US升
第三章电阻电路的一般分析

第三章电阻电路的一般分析本章内容:1.电路的图及KCL和KVL独立方程数 2.支路分析法3.网孔分析法4.回路电流法5.结点分析法本章重点:主要学习电阻电路的方程建立及一般分析方法(支路分析法、网孔分析法、节点分析法、回路分析法。
其中,支路分析法是最基本的方法)。
本章难点:独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识,学习应用图的方法选择电路方程的独立变量一、电路的图(G)数学上的图:是边(支路)和顶点(结点)的集合,每一条边都连到相应的顶点上,边是抽象的线段,当移去边时,顶点保留,当移去顶点时,应将顶点所连的支路移走。
1.电路的图(连通图G):是将支路画成的抽象线段形成的节点和支路的集合,结点相对于数学图的顶点,支路相当于数学图中的边。
支路是实体。
KVL和KCL 与元件的性质无关,故可用图讨论其方程。
2.无向图:画出的没有方向的图为无向图3.有向图:画出的有方向的图为有向图4.连通图:任意两个结点之间至少有一条支路或路径时的图为连通图。
二、电路的图的画法(有几种,其中简便的画法)1.一般将电阻和电压源串联的组合,电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。
如(b)2.指定电流和电压的参考方向,一般选关联参考方向。
如图(c)(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数(n个结点电路,KCL的独立方程是n-1个)将电路的有向图,结点和支路加以编号,如下图,对结点①②③④列写KCL 方程有由于每条支路与两个结点相联,其电流从一个节点流出,从另一个结点流入,一正,一负(从表达式可见),将上面4个方程相加,等式两边为0,说明4个方程不是独立的;将上面3个方程相加,等式两边不为0,说明3个方程是独立的。
可见,n个结点电路,n-1个结点的KCL方程是独立的一、KVL的独立方程数(b条支路,n个结点,KVL为b-(n-1)个)KVL的独立方程数等于独立回路数独立回路数等于基本回路数,回路与支路的方向无关,以无向图讨论。
