2018年安庆市高三模拟考试(二模)

合集下载

2018安庆二模word含答案安徽省安庆市2018届高三第二次模拟考试英语试题

安徽省安庆市2018届高三第二次模拟考试英语试题本试题卷共8页。

全卷满分150分。

考试用时120分钟。

第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。

录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。

听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例: How much is the shirt?A.￡19.15.B.￡9.18.C.￡9.15.答案是C。

1. Which shirt does the woman think is better?A. The green one.B. The blue one.C. The black one.2. What is Mike good at?A. Soccer.B. Volleyball.C. Basketball.3. What is the woman going to do?A. Go to see a doctor.B. Talk with her neighbor.C. Move to a different house.4. Where does the conversation probably take place?A. In a meeting room.B. On the highway.C. In a parking lot.5. What is the man doing?A. Eating dessert.B. Reading a book.C. Taking out the rubbish.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。

安徽省安庆市2024届高三模拟考试(二模)数学试题含答案

2024年安庆市高三模拟考试（二模）数学试题（答案在最后）命题：安庆市高考命题研究课题组考试时间120分钟，满分150分一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，有且只有一项符合题目要求．1.设集合{}213A x x =-≤，集合101x B x x ⎧⎫+=>⎨⎬-⎩⎭，则A B = （）A.(1,2]B.[1,2]C.(1,1)- D.(1,2)-【答案】A 【解析】【分析】计算出集合A 、B 后借助交集定义即可得.【详解】由213x -≤，可得12x -≤≤，故{}12A x x =-≤≤，由101x x +>-，可得()()110x x +->，即1x >或1x <-，故{1B x x =>或}1x <-，则{}12A B x x ⋂=<≤.故选：A.2.已知复数2z =，z 是z 的共轭复数，则z z ⋅=（）A.14B.1C.2D.4【答案】B 【解析】【分析】首先分析题意，对给定复数化简，再利用共轭复数知识求解即可.【详解】221=+i 422z -+-，而1i 22z =--，可得1113(+i)(1222244z z ⋅=---=+=.故选：B.3.设F 是椭圆22:1259x y C +=的一个焦点，过椭圆C 中心的直线交椭圆于P ，Q 两点，则PQF △的周长的最小值为（）A.12B.14C.16D.18【答案】C 【解析】【分析】根据椭圆的定义求出10PF QF +=，再由min 26PQ b ==，即可求解.【详解】由椭圆的对称性可知P ，Q 两点关于原点对称，设椭圆的另一个焦点为1F ，则四边形1PFQF 为平行四边形，由椭圆定义可知：11420PF PF QF QF a +++==，又1PF QF =，1PF QF =，所以10PF QF +=，又PQ 过原点，所以min 26PQ b ==，所以PQF △的周长的最小值为：10616+=.故选：C4.在一次学科核心素养能力测试活动中，随机抽取了100名同学的成绩（评分满分为100分），将所有数据按[40,50]，(50,60]，(60,70]，(70,80]，(80,90]，(90,100]进行分组，整理得到频率分布直方图如图所示，则估计这次调查数据的第64百分位数为（）A.80B.78C.76D.74【答案】B 【解析】【分析】借助百分位数的定义计算即可得.【详解】由0.005100.015100.020100.4⨯+⨯+⨯=，0.005100.015100.020100.030100.7⨯+⨯+⨯+⨯=，故这次调查数据的第64百分位数位于(70,80]之间，设这次调查数据的第64百分位数为x ，则有700.640.4100.70.4x --=-，解得78x =.故选：B .5.设{}n a 是公比不为1的无穷正项等比数列，则“{}n a 为递减数列”是“存在正整数0n ，对任意的正整数0n n >，1n a <”的（）A.充分不必要条件B.必要不充分条件C .充要条件D.既不充分也不必要条件【答案】C 【解析】【分析】由等比数列基本量的计算以及正项等比数列的单调性、充要条件的定义即可得解.【详解】{}n a 是公比不为1的无穷正项等比数列，所以()*0,N n a n >∈，一方面：“{}n a 为递减数列”，等价于101n na q a +<=<，要使得()111,0nn a a q a =<>，只需11nq a <，即1lg lg n q a <-，从而1lg lg a n q>-，所以取10lg max 1,1lg n q a ⎧⎫⎡⎤=-+⎨⎬⎢⎣⎦⎩⎭，其中[]x 是指不超过x 的最大整数，则当0n n >时，有1n a <，另一方面：我们假设1q >，且“存在正整数0n ，对任意的正整数0n n >，1n a <”，则当n 越来越大时，同理可得()111,0nn a a q a =>>，但这与“存在正整数0n ，对任意的正整数0n n >，1n a <”矛盾，综上所述，“{}n a 为递减数列”是“存在正整数0n ，对任意的正整数0n n >，1n a <”的充要条件.故选：C.6.已知点(1,0)P，(C ，O 是坐标原点，点B 满足1BC = ，则OP 与PB夹角的最大值为（）A.56π B.23π C.2π D.3π【答案】A 【解析】【分析】根据题意，求得点B的轨迹是以C 为圆心，半径1r =的圆，结合直线与圆相切，求得切线的倾斜角，即可求解.【详解】设点(,)B x y，可得()BC x y =--，因为1BC =，可得22(1x y +-=，即点B的轨迹是以C 为圆心，半径1r =的圆，如图所示，设过点P 与圆C 相切的直线PB 的方程为(1)y k x =-，即kx y k 0--=，1=，解得3k =-，设切线的倾斜角为(0π)αα≤<，则tan 3α=-，可得5π6α=，即OP 与PB 夹角的最大值为5π6.故选：A.7.已知函数2()2cos sin 21(0)f x x x ωωω=+->的图象关于点π,04⎛⎫ ⎪⎝⎭对称，且()f x 在π0,3⎛⎫⎪⎝⎭上没有最小值，则ω的值为（）A.12B.32C.52D.72【答案】B 【解析】【分析】先化简解析式，根据对称性可得12,2k k ω=-∈Z ，再结合最小值点即可求解.【详解】2π()2cos sin 21cos 2sin 224f x x x x x x ωωωωω⎛⎫=+-=+=+ ⎪⎝⎭，因为()f x 的图象关于点π,04⎛⎫⎪⎝⎭对称，所以πππ0424f ω⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，故πππ,24k k ω+=∈Z ，即12,2k k ω=-∈Z ，当ππ22π42x k ω+=-+，即3ππ,8k x k ωω=-+∈Z 时，函数()f x 取得最小值，因为()f x 在π0,3⎛⎫⎪⎝⎭上没有最小值，所以5ππ83ω≥，即158ω≤，由115228k ω=-≤解得1918k ≤，故1k =，得32ω=.故选：B8.如图，在长方体1111ABCD A B C D -中，122AB AD AA ==，点E 是棱AB 上任意一点（端点除外），则（）A.不存在点E ，使得1EC D E⊥B.空间中与三条直线11A D ，EC ，1BB 都相交的直线有且只有1条C.过点E 与平面1D AE 和平面DAEC 所成角都等于π8的直线有且只有1条D.过点E 与三条棱AB ，AD ，1AA 所成的角都相等的直线有且只有4条【答案】D 【解析】【分析】当E 为AB 的中点时判断A ；作图判断B ；利用角平分面的特征判断C ；建立空间直角坐标系，分析判断D.【详解】在长方体1111ABCD A B C D -中，122AB AD AA ==，对于A ，当E 为AB 的中点时，连接DE ，则45AED BEC ∠=∠= ，即有EC DE ⊥，而1DD ⊥平面ABCD ，EC ⊂平面ABCD ，则1EC DD ⊥，又11,,DE DD D DE DD ⋂=⊂平面1DD E ，因此EC ⊥平面1DD E ，而1D E ⊂平面1DD E ，则1EC D E ⊥，A 错误；对于B ，连接11,BD B D ，设BD EC K ⋂=，111////BB CC DD ，则平面11BDD B 与直线EC 交于K ，点K 在线段BD 上，不含端点，则直线1D K 与直线1BB 相交，同理直线1A E 与直线1BB 相交,因此直线1D K 、1A E 分别与三条直线11A D ，EC ，1BB 都相交，B 错误；对于C ，AB ⊥平面11ADD A ，而1AD ⊂平面11ADD A ，则1AB AD ⊥，又AB AD ⊥，于是1DAD ∠是二面角1D AE D --的平面角，且1π4DAD ∠=，显然1DAD ∠的平分线与平面1D AE 和平面DAEC 所成角都等于π8，过点E 与此直线平行的直线符合要求，这样的直线只有1条；半平面1D AE 与半平面DAEC 的反向延长面所成二面角的角平分面与平面1D AE 和平面DAEC 所成角都等于3π8，在此角平分面内过点E 与平面1D AE 和平面DAEC 所成角都等于π8的直线有2条，因此过点E 与平面1D AE 和平面DAEC 所成角都等于π8的直线有3条，C 错误；对于D ，建立如图所示的空间直角坐标系，直线1,,AB AD AA 的方向向量分别为(1,0,0),(0,1,0),(0,0,1)，设过点E 的直线l 方向向量为(,,)a x y z =，由直线l 分别与直线1,,AB AD AA 所成角都相等，==||||||x y z ==，不妨令||1x =，有(1,1,1)a =r 或(1,1,1)a =- 或(1,1,1)a =- 或(1,1,1)a =- ，显然使得||||||1x y z ===成立的向量a有8个，其余4个分别与上述4个向量共线，所以过点E 与三条棱AB ，AD ，1AA 所成的角都相等的直线有且只有4条，D 正确.故选：D【点睛】关键点睛：建立空间直角坐标系，利用线线夹角的求法是求解选项D 的关键.二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.已知定义在R 上的函数()f x ，满足对任意的实数x ，y ，均有()()()1f x y f x f y +=+-，且当0x >时，()1f x <，则（）A.(0)1f = B.(1)(1)1f f +-=C.函数()f x 为减函数 D.函数()y f x =的图象关于点()0,1对称【答案】ACD 【解析】【分析】对A ：借助赋值法令0x y ==计算即可得；对B ：借助赋值法令1x =，1y =-计算即可得；对C ：结合函数单调性的定义及赋值法令0y >计算即可得；对D ：结合函数对称性及赋值法令y x =-计算即可得.【详解】对A ：令0x y ==，则有()()()0001f f f =+-，故(0)1f =，故A 正确；对B ：令1x =，1y =-，则有()()()0111f f f =+--，故()()112f f +-=，故B 错误；对C ：令0y >，则有()()()1f x y f x f y +-=-，其中x y x +>，()10f y -<，令1x x y =+，2x x =，即有对1x ∀、2x ∈R ，当12x x >时，12())0(f x f x -<恒成立，即函数()f x 为减函数，故C 正确；对D ：令y x =-，则有()()()1f x x f x f x -=+--，又(0)1f =，故()()2f x f x +-=，故函数()y f x =的图象关于点()0,1对称，故D 正确.故选：ACD.10.抛物线2:2(0)C x py p =>的焦点为(0,1)F ，经过点F 且倾斜角为α的直线l 与抛物线C 交于A ，B 两点，分别过点A 、点B 作抛物线C 的切线，两切线相交于点E ，则（）A.当16AB =时，π3α=B.AOB 面积的最大值为2C.点E 在一条定直线上D.设直线EF 倾斜角为β，αβ-为定值【答案】CD 【解析】【分析】由焦点为(0,1)F 可得抛物线方程，联立直线与曲线方程，可得关于x 的一元二次方程，即可得与x 有关韦达定理，对A ：利用韦达定理与弦长公式计算即可得；对B ：利用韦达定理与弦长公式及面积公式计算即可得；对C ：借助导数的几何意义可得AE l 与BE l 的方程，即可得点E 坐标，即可得解；对D ：由tan tan 1αβ⋅=-，故可得2παβ-=.【详解】由抛物线的焦点为(0,1)F ，故2p =，即2:4C x y =，由题意可知，直线l 斜率存在，设():1tan AB l y kx k α=+=，()11,A x y ，()22,B x y ，联立241x y y kx ⎧=⎨=+⎩，有2440x kx --=，216160k ∆=+>，124x x k +=，124x x =-，对A：()241AB k ===+，当16AB =时，即有()24116k +=，故k =，即tan α=，即π3α=或2π3α=，故A 错误；对B：()2114122AOB S d AB k =⨯=+= ，故2AOB S ≥ ，故B 错误；对C ：由()11,A x y ，2:4C x y =，即24x y =，有2x y '=，故()111:2AE x l y x x y =-+，又2114x y =，故211:24AE x x l y x =-，同理可得222:24BE x x l y x =-，设点(),E m n ，则有2112222424x x n m x xn m ⎧=-⎪⎪⎨⎪=-⎪⎩，有22121212242x x x x m x x -+=⨯=-，21121122244x x x x x x n +=⨯-=，由124x x k +=，124x x =-，故2m k =，1n =-，故点E 在一条定直线上且该直线为1y =-，故C 正确；对D ：由()2,1E k -，(0,1)F ，则111tan 2k kβ+==--，故有1tan tan 1k k αβ⎛⎫⋅=⋅-=- ⎪⎝⎭，即π2αβ-=，故αβ-为定值且该定值为π2，故D 正确.故选：CD.【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：（1）设直线方程，设交点坐标为()()1122,,,x y x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，注意∆的判断；（3）列出韦达定理；（4）将所求问题或题中的关系转化为12x x +、12x x （或12y y +、12y y ）的形式；（5）代入韦达定理求解.11.满足12a =，21a =，()*21n n n a a a n ++=+∈N 的数列{}na 称为卢卡斯数列，则（）A.存在非零实数t ，使得{}()*1n n a ta n ++∈N 为等差数列B.存在非零实数t ，使得{}()*1n n a ta n ++∈N 为等比数列C.()*243n n n a a a n ++=+∈ND.()20242023113ii i a a =-=-∑【答案】BCD 【解析】【分析】对A 、B ：借助等差数列与等比数列定义计算即可得；对C ：借助21n n n a a a ++=+代入即可得；对D ：由()*21n n n a a a n ++=+∈N ，得到()()()2121111n n nn n n a a a ++++-=--+-，从而将()202411ii i a =-∑展开后借助该式裂项相消即可得.【详解】对A ：若数列{}()*1n n a ta n ++∈N为等差数列，则有211n n n n ad ta a ta +++-+=-，即()211n n n a t a ta d ++=-++，由()*21n n n a a a n ++=+∈N，故有()111n n n n a a t a ta d +++=-++恒成立，即有1110t t d -=⎧⎪=⎨⎪=⎩，无解，故不存在这样的实数t ，故A 错误；对B ：若数列{}()*1n n a ta n ++∈N为等比数列，则有211n n n na q ta a ta ++++=+，即()21n n n a q t a qta ++=-+，由()*21n n n a a a n ++=+∈N，故有()11n n n n a a q t a qta +++=-+恒成立，即有11q t qt -=⎧⎨=⎩，即210t t +-=，解得12t -±=，此时21110a ta +=-=≠，故存在非零实数t ，使得{}()*1n n a ta n ++∈N 为等比数列，故B 正确；对C ：由()*21n n n a a a n ++=+∈N，则32214223n n n n n n n n n n a a a a a a a a a a ++++++++=++=+++=，即有()*243n n n a a a n ++=+∈N，故C 正确；对D ：由()*21n n n a a a n ++=+∈N ，故()()()()()222121111111n n n n nn n n n n a a a a a +++++++-=-+-=--+-，故()()()()()20242320241232024111111ii i a a a a a =-=-+-+-+-=∑ ()()()()()()()()()()2232432023202221324320232022121111111111a a a a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤-⨯+-⨯+--+-+--+-+--+-++--+-⎣⎦⎣⎦⎣⎦⎣⎦()()202312023202321113a a a ⎡⎤=-++---=-⎣⎦，故D 正确.故选：BCD.【点睛】关键点点睛：D 选项中关键点在于由()*21n n n a a a n ++=+∈N，得到()()()2121111n n nn n n a a a ++++-=--+-，从而将()202411ii i a =-∑展开后可借助该式裂项相消.三、填空题：本大题共3小题，每小题5分，共15分．12.在二项式10的展开式中，常数项为__________．【答案】210【解析】【分析】借助二项式展开式的通项公式计算即可得.【详解】对10，有10151536211010C C kkk k k k T x x x ---+⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，令5506k -=，则6k =，则有655671010C C 210T x -===.故答案为：210.13.已知圆锥的顶点为P ，底面圆心为M ，底面直径2AB =．圆锥的内切球和外接球的球心重合于一点O ，则该圆锥的全面积为__________．【答案】3π【解析】【分析】画出圆锥的截面PAB ，由圆锥的内切球和外接球的球心重合于一点O ，可得PAB 为等边三角形，借助圆锥的表面积公式计算即可得.【详解】画出圆锥的轴截面如图所示，由O 为圆锥的内切球球心，则有BO 为PBA ∠的角平分线，由O 为圆锥的外接球球心，则OB OP =，故PBO OPB ∠=∠，故APB PBA ∠=∠，又PA PB =，故PAB 为等边三角形，故PM =，2PB =，则22πππ1π123πS r rl =+=⨯+⨯⨯=全.故答案为：3π.14.剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的中国民间艺术．其传承赓续的视觉形象和造型格式，蕴涵了丰富的文化历史信息，表达了广大民众的社会认知、道德观念、实践经验、生活理想和审美情趣，具有认知、教化、表意、抒情、娱乐、交往等多重社会价值．现有如图所示剪纸图案，其花纹中就隐含方程为222333(0)x y a a +=>的曲线C （称为星形线），则曲线C 的内切圆半径为__________；以曲线C 上点(,)(0)m n mn ≠为切点的直线被坐标轴截得的线段长等于__________．【答案】①.2a②.a【解析】【分析】由曲线C 的方程可得，该曲线关于x 轴、原点对称，故只需研究第一象限即可，求出第一象限上的点到曲线C 的最短距离即可得其内切圆半径；当0x >，0y >时，曲线可为函数322233y a x ⎛⎫=- ⎪⎝⎭的图象，结合导数的几何意义可得曲线上的点()00,x y 的切线方程，即可得该直线被坐标轴截得的线段长.【详解】设点(),P x y 在曲线222333(0)x y a a +=>上，则(),x y -、(),x y -、(),x y --亦在曲线222333(0)x y a a +=>上，故曲线222333(0)x y a a +=>关于x 轴、y 轴、原点对称，故只需研究第一象限内部分，当0x >，0y >时，由(),P x y 曲线222333(0)x y a a +=>上，故有222333x y a +=，即有2211331x y a a ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥⎢⎥+= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦，则可设13cos x a α⎛⎫= ⎪⎝⎭，13sin y a α⎛⎫= ⎪⎝⎭，π0,2α⎛⎫∈ ⎪⎝⎭，即3cos x a α=，3sin y a α=，则OP ======，由π0,2α⎛⎫∈ ⎪⎝⎭，则(]2sin 20,1α∈，则min2a OP ==，即曲线C 的内切圆半径为2a ；当0x >，0y >时，222333(0)x y a a +=>可化为322233y a x ⎛⎫=- ⎪⎝⎭，11221122223333333223y a x x x a x --⎛⎫⎛⎫⎛⎫=-⨯-='-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则曲线上的点()00,x y 的切线方程为：()3122122223333300y a x xa x x x -⎛⎫⎛⎫--=--- ⎪ ⎪⎝⎭⎝⎭，令0x =，则有()13122222233333000y xa x x a x -⎛⎫⎛⎫=---+- ⎪ ⎪⎝⎭⎝⎭11222222222122333333333300a x x a x a a x a y ⎡⎤⎛⎫⎛⎫⎛⎫=-+-=-=⎢⎥ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，令0y =，则有1222133333000x x a x x a x ⎛⎫=-+= ⎪⎝⎭，则AB a ====.即曲线C 上点(,)(0)m n mn ≠为切点的直线被坐标轴截得的线段长等于a .故答案为：2a；a .【点睛】关键点点睛：本题关键点在于借助曲线的对称性，得出只需研究第一象限部分，若点(),P x y 曲线222333(0)x y a a +=>上，可设13cos x a α⎛⎫= ⎪⎝⎭，13sin y a α⎛⎫= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，从而计算出点P 到曲线的最短距离即可得曲线C 的内切圆半径，当0x >，0y >时，曲线可为函数322233y a x ⎛⎫=- ⎪⎝⎭的图象，结合导数的几何意义可得曲线上的点()00,x y 的切线方程，即可计算得该直线被坐标轴截得的线段长.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.如图，在平面凸四边形ABCD 中，2sin tan tan cos BADABD ADB ABD∠∠+∠=∠.（1）求ADB ∠；（2）若4AD BD ==，6ACB BDC π∠=∠=，求CD .【答案】（1）3π（2）4【解析】【分析】（1）借助三角恒等变换将所给式子化简计算即可得；（2）结合题意，借助正弦定理与余弦定理计算即可得.【小问1详解】由已知得：sin sin 2sin cos cos cos ABD ADB BADABD ADB ABD∠∠∠+=∠∠∠，故sin cos cos sin 2sin cos cos cos ABD ADB ABD ADB BADABD ADB ABD∠∠+∠∠∠=∠∠∠，所以sin()2sin cos cos cos ABD ADB BADABD ADB ABD∠+∠∠=∠∠∠．因为()()sin sin πsin 0ABD ADB BAD BAD ∠+∠=-∠=∠≠，故1cos 2ADB ∠=，由三角形内角范围知π3ADB ∠=；【小问2详解】由4AD BD ==，π3ADB ∠=，故ABD △为边长为4的等边三角形，在ABC 中，π6ACB ∠=，由正弦定理得sin sin BC AB BAC ACB=∠∠，故sin 8sin sin AB BACBC BAC ACB∠==∠∠，由于πBAC BCA ABD CBD ∠+∠+∠+∠=，所以π2BAC CBD ∠+∠=，故8cos BC CBD =∠，在BCD △中，由余弦定理得2222cos CD BD BC BD BC CBD =+-⨯⨯∠，即22248cos 16CD BC BC CBD =+-⨯⨯∠=，得4CD =.16.已知函数()2ln ()mf x x x m x=-+∈R ．（1）当3m =-时，求函数()f x 的单调区间；（2）若不等式()0f x ≤对任意的[1,)x ∈+∞恒成立，求实数m 的取值范围．【答案】（1）递增区间为(0,3)，递减区间为(3,)+∞（2）(,1]-∞【解析】【分析】（1）求出导函数后借助导函数的正负即可得原函数的单调性；（2）可借助(1)0f ≤，得到1m £，在1m £的情况下，借助1()2ln 2ln m f x x x x x x x=-+≤-+，从而构造函数1()2ln g x x x x=-+，结合该函数的单调性及最值即可得解；亦可通过参变分离，得到22ln m x x x ≤-对任意的[1,)x ∈+∞恒成立，通过研究2()2ln h x x x x =-得解.【小问1详解】当3m =-时，3()2ln f x x x x=--，其定义域为(0,)+∞，()()2222312323()1x x x x f x x x x x--+-++='=-+=，令()0f x '=，得3x =（=1x -舍去），当03x <<时，()0f x '>，函数()f x 单调递增；当3x >时，()0f x '<，函数()f x 单调递减．所以函数()f x 的单调递增区间为(0,3)，单调递减区间为(3,)+∞；【小问2详解】方法1：由条件可知(1)0f ≤，于是10m -≤，解得1m £．当1m £时，1()2ln 2ln m f x x x x x x x=-+≤-+，构造函数1()2ln g x x x x=-+，1x ≥，()222121()10x g x x x x-=---'=≤，所以函数()g x 在[1,)+∞上单调递减，于是()(1)0g x g ≤=，因此实数m 的取值范围是(,1]-∞．方法2：由条件可知22ln m x x x ≤-对任意的[1,)x ∈+∞恒成立，令2()2ln h x x x x =-，1x ≥，只需min [()]m h x ≤即可．()()()22ln 12ln 1h x x x x x =-+=--'，令()ln 1x x x μ=--，则()10x x xμ-'=≥，所以函数()h x '在[1,)+∞上单调递增，于是()()10h x h ''≥=，所以函数()h x 在[1,)+∞上单调递增，所以()()min 11h x h ⎡⎤==⎣⎦，于是1m £，因此实数m 的取值范围是(,1]-∞．17.如图，将边长为2的菱形ABDC 沿其对角线BC 对折，使得点A 、D 分别位于边长为2的等边PBC 所在平面的两侧，且PA PD =．设E 是PA 的中点．（1）证明：平面PBC ⊥平面ABC ；（2）求平面EBD 与平面ABC 夹角的正弦值．【答案】（1）证明见解析（2）217【解析】【分析】（1）取BC 的中点O ，根据题意，分别证得OP BC ⊥和OP OA ⊥，利用线面垂直的判定定理，证得OP ⊥平面ABC ，进而证得平面PBC⊥平面ABC ．（2）以O 为原点，建立空间直角坐标系，根据题意，分别求得平面ABC 和EBD 得到法向量(0,0,1)m =和()3,2n =，结合向量的夹角公式，即可求解.【小问1详解】证明：取BC 的中点O ，连接OA 、OP ，如图所示．因为四边形ABDC 是边长为2的菱形，PBC 是边长为2的等边三角形，所以ABC 也是边长为2的等边三角形，在等边PBC 中，O 是BC 的中点，可得OP BC ⊥且3OA OP ==又因为6PA =222PA OA OP =+，所以OP OA ⊥，因为⋂=OA BC O ，且,OA BC ⊂平面ABC ，所以OP ⊥平面ABC ；又因为OP ⊂平面PBC ，故平面PBC ⊥平面ABC ．【小问2详解】解：由（1）知，OP BC ⊥，OP OA ⊥．因为O 是等边ABC 的BC 边中点，可得OA BC ⊥．所以，以O 为原点，分别以,,OA OB OP 所在直线为x 、y 、z 轴，建立空间直角坐标系，如图所示，则3,0,0),,(0,1,0)(0,1,0)3),A B C -，可得33,0,22E ⎛⎫⎪⎪⎝⎭，因为DBC △是边长为2的等边三角形，故OD OP PD ===，所以60POD ∠=︒，且OD BC ⊥，又因为OP BC ⊥，OD OP O ⋂=，故BC ⊥平面DOP ，则D 在平面xOz 内，可得3,0,22D ⎛⎫- ⎪ ⎪⎝⎭，所以,1,22BE ⎛⎫=- ⎪ ⎪⎝⎭，3,1,22BD ⎛⎫=-- ⎪ ⎪⎝⎭，设平面ABC 的法向量为(,,)m a b c = ，显然可令(0,0,1)m =；设平面EBD 的法向量为(,,)n x y z =，则0223022n BE x y z n BE x y z ⎧⋅=-+=⎪⎪⎨⎪⋅=--+=⎪⎩，令2z =，则0x =，y =()2n =，所以cos ,7m mm n m n ⋅===，设平面EBD 与平面ABC 的夹角为θ，则sin 7θ==，故平面EBD 与平面ABC 的夹角的正弦值为217．18.树人高中拟组织学生到某航天基地开展天宫模拟飞行器体验活动，该项活动对学生身体体能指标和航天知识素养有明确要求．学校所有3000名学生参加了遴选活动，遴选活动分以下两个环节，当两个环节均测试合格可以参加体验活动．第一环节：对学生身体体能指标进行测试，当测试值12.2ξ≥时体能指标合格；第二环节：对身体体能指标符合要求的学生进行航天知识素养测试，测试方案为对A ，B 两类试题依次作答，均测试合格才能符合遴选要求．每类试题均在题库中随机产生，有两次测试机会，在任一类试题测试中，若第一次测试合格，不再进行第二次测试．若第一次测试不合格，则进行第二次测试，若第二次测试合格，则该类试题测试合格，若第二次测试不合格，则该类试题测试不合格，测试结束．经过统计，该校学生身体体能指标ξ服从正态分布(9,2.56)N ．参考数值：()0.6827P X μσμσ-<<+=，(22)0.9545P X μσμσ-<<+=，(33)0.9973P X μσμσ-<<+=．（1）请估计树人高中遴选学生符合身体体能指标的人数（结果取整数）；（2）学生小华通过身体体能指标遴选，进入航天知识素养测试，作答A 类试题，每次测试合格的概率为13，作答B 类试题，每次测试合格的概率为14，且每次测试相互独立．①在解答A 类试题第一次测试合格的条件下，求测试共进行3次的概率．②若解答A 、B 两类试题测试合格的类数为X ，求X 的分布列和数学期望．【答案】（1）68（2）①34；②分布列见解析，115()144E X =.【解析】【分析】（1）首先分析题意，利用正态分布的性质求解即可.（2）进行分类讨论，求解出分布列，再求出期望即可.【小问1详解】10.9545(12.2)(2)0.022752P P ξξμσ-≥=≥+==．所以符合该项指标的学生人数为：30000.0227568.2568⨯=≈人．【小问2详解】①记1A 表示解答A 类试题第一次测试合格，1B ，2B 分别表示解答B 类试题第一次和第二次测试合格，测试共进行3次记为事件M ，则()113P A =，()()()1121213113313443444P A M P AB B P AB B =+=⨯⨯+⨯⨯=．()()()()()112112111134().143P A B B P A B B P A M P M A P A P A +====∣②设X 的取值为0，1，2，224(0)339P x ==⨯=，13321335(1)344334416P x ==⨯⨯+⨯⨯⨯=，35(2)1(0)(1)144P x P x P x ==-=-==，所以X 的分布列为X12P4951635144数学期望4535115()012916144144E X =⨯+⨯+⨯=．19.取整函数被广泛应用于数论、函数绘图和计算机领域，其定义如下：设x ∈R ，不超过x 的最大整数称为x 的整数部分，记作[]x ，函数[]y x =称为取整函数．另外也称[]x 是x 的整数部分，称{}[]x x x =-为x 的小数部分．（1）直接写出[]ln π和34⎧⎫-⎨⎬⎩⎭的值；（2）设a ，*b ∈N ，证明：a a a b b b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，且01a b b b ⎧⎫≤≤-⎨⎬⎩⎭，并求在b 的倍数中不大于a 的正整数的个数；（3）对于任意一个大于1的整数a ，a 能唯一写为1212k aaak a p p p =⨯⨯⨯ ，其中i p 为质数，i a 为整数，且对任意的i j <，i j p p <，i ，{1,2,3,,}j k ∈⋯，称该式为a 的标准分解式，例如100的标准分解式为2210025=⨯．证明：在!n 的标准分解式中，质因数i p （i p n ≤，1n >，*n ∈N ）的指数231i r r i i i i n n n n a p p p p ∞=⎡⎤⎡⎤⎡⎤⎡⎤=+++=⎢⎥⎢⎢⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦∑ ．【答案】（1）1，0.25（2）证明见解析，a b ⎡⎤⎢⎥⎣⎦个（3）证明见解析【解析】【分析】（1）结合定义计算即可得；（2）由题意可得a a ab b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，等式两边同时乘b ，即可得证a a a b b b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，由a ，b 都为整数，结合定义可证得0a b b b ⎧⎫≤<⎨⎬⎩⎭，即可得证01a b b b ⎧⎫≤≤-⎨⎬⎩⎭，假设b ，2b ，…，nb 都小于等于a ，可得a a nb a b b b b ⎡⎤⎧⎫≤=+⎨⎬⎢⎥⎣⎦⎩⎭，即有a a n b b ⎡⎤⎧⎫≤+⎨⎬⎢⎥⎣⎦⎩⎭，又01a b ⎧⎫≤<⎨⎬⎩⎭，即可得a n b ⎡⎤≤⎢⎥⎣⎦，即可得解；（3）利用（2）中结论可得i p 的倍数中不大于n 的正整数的个数为i n p ⎡⎤⎢⎥⎣⎦，2i p 的倍数中不大于n 的正整数的个数为2i n p ⎡⎤⎢⎥⎣⎦，3i p 的倍数中不大于n 的正整数的个数为3i n p ⎡⎤⎢⎥⎣⎦，依次进行下去，可得123r i r i i i i n n n n a p p p p ∞=⎡⎤⎡⎤⎡⎤⎡⎤=+++=∑⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦，即得证.【小问1详解】由e π2e <<，故12ln π<<，故[]1ln π=，()3333110.2544444⎧⎫⎡⎤-=---=---==⎨⎬⎢⎥⎩⎭⎣⎦；【小问2详解】因为a a a b b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，等式两边同时乘b ，得a a a b b b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，因为a ，b 都为整数，所以a a b a b b b⎧⎫⎡⎤=-⎨⎬⎢⎥⎩⎭⎣⎦也为整数，又01a b ⎧⎫≤<⎨⎬⎩⎭，所以0a b b b ⎧⎫≤<⎨⎬⎩⎭，所以01a b b b ⎧⎫≤≤-⎨⎬⎩⎭，即得证，假设b ，2b ，…，nb 都小于等于a ，*n ∈N ，因为a a a b b b b ⎡⎤⎧⎫=+⎨⎬⎢⎥⎣⎦⎩⎭，所以a a nb a b b b b ⎡⎤⎧⎫≤=+⎨⎬⎢⎥⎣⎦⎩⎭，所以a a n b b⎡⎤⎧⎫≤+⎨⎬⎢⎥⎣⎦⎩⎭，因为01a b ⎧⎫≤<⎨⎬⎩⎭，所以a n b ⎡⎤≤⎢⎥⎣⎦，所以b 的倍数中不大于a 的正整数的个数为a b⎡⎤⎢⎥⎣⎦个；【小问3详解】!123n n =⨯⨯⨯⨯ ，将2，3，…，n 每一个数都分解为质因数的乘积．对于质因数i p ，利用（2）中结论，i p 的倍数中不大于n 的正整数的个数为i n p ⎡⎤⎢⎥⎣⎦，记为1n ，将这些数都提取i p 出来，此时p 的倍数中还有可以提取出i p 的数，注意到2i p 的倍数中不大于n 的正整数的个数为2i n p ⎡⎤⎢⎥⎣⎦，记为2n ，将这些数提取i p 出来；同理，3i p 的倍数中不大于n 的正整数的个数为3i n p ⎡⎤⎢⎥⎣⎦，记为3n ，依此这样进行下去，则质因数i p的指数112323ri ri i i in n n na n n np p p p∞=⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=∑⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦，即得证．。

不等式综合练习题

不等式专题练习题一、知识内容不等式是高中数学的重要内容之一，不等式的性质是解证不等式的基础；两个正数的算术平均数不小于它们的几何平均数的定理（教材中称为基本不等式，通常称均值不等式）及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用；线性规划是运筹学的一个重要分支，在实际生活中有着广泛的应用．二、核心思想方法解不等式是研究方程和函数的重要工具，不等式的概念、性质涉及到求函数最大（小）值，实数大小比较，求参数的取值范围等；不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复习的难点；均值不等式的证明最终是利用了配方法，使用该不等式的核心方法则是整体思想方法，就是对哪两个正数使用定理，例如下面练习题的第5题是对2,a b使用不等式，而不是对,a b使用不等式；线性规划的核心方法是数形结合和转化的思想方法，在具体转化上涉及到面积、截距（目标函数为二元一次多项式）、距离（目标函数含二元二次多项式）、斜率（目标函数为分式）等几何意义，分别如下面练习题的第9、22、23、24题．三、高考命题趋势本专题的高考命题热点可从以下两个方面去把握：1．以客观题形式命题：不等式的性质和解不等式问题多以一个选择题的形式出现，且多与集合、简易逻辑、函数知识相结合，难度较低；均值不等式是历年高考的重点考查内容，考查方式多变，在客观题中出现，一般只有一个选择或填空，考查直接，难度较低；线性规划问题是近几年高考的一个新热点，在考题中主要以选择、填空形式出现，且设问也是灵活多变，每年高考必有一题．四个注意问题：（1）命题者有时把线性规划问题和均值不等式结合在一起，提高了难度，例如下面练习题的第8、28题．（2）线性规划的约束条件中含有参数的，例如下面练习题的第7、9题．（3）均值不等式的凑定值技巧，一是关注消元，而是关注整体代入思想方法，分别如下面练习题的第17、18题．（4）克服思维定势，有些题目很象是利用基本不等式的，其实只是解出未知数代入化简的，如下面练习题的第20题．2．以解答题形式命题：不等式证明与解法是高考的一个重点内容，且多以解答题的一个分支出现，常与函数、导数、数列、解析几何等知识结合，题目往往非常灵活，难度高．均值不等式在解答题中出现，其应用范围几乎涉及高中数学的所有章节，且常考常新，难度较高．线性规划问题也可以用实际问题进行考查，考查优化思想在解决问题的广泛应用，体现数学的应用价值，从而形成解决简单实际问题的能力，进一步考查了考生的数学应用意识．但是，考虑到线性规划应用题毕竟知识较为单一，所以在高考中出现的频率不高．考虑到不等式与函数、导数、解析几何的综合题中，不等式仅是其中的一个工具，所以本专题的选的解答题主要侧重于不等式的证明与解法．练习题1．（山东省临沂市高三教学质量检测考试）集合{}220A x x x =--≤，{}1B x x =<，则()R A C B ⋂=（）（A ）{}1x x > （B ）{}12x x ≤≤ （C ）{}12x x <≤ （D ）{}1x ≥2．（安徽省安庆市高三3月模拟考试（二模））下列命题中错误的是（）A ．命题“若2560x x -+=，则2x =”的逆否命题是“若2x ≠，则2560x x -+≠”B ．若,x y R ∈，则“x y =”是22x y xy +⎛⎫≥ ⎪⎝⎭成立的充要条件 C ．已知命题p 和q ，若p ∨q 为假命题，则例题p 与q 中必一真一假D ．对命题p ：x R ∃∈，使得210x x ++<，则:,p x R ⌝∀∈则210x x ++…3．（广东省深圳市松岗中学高三模拟试卷）设条件p ：102x x -≥+，条件:q (1)(2)0x x -+≥，则条件p 是条件q 的（） A ．充要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件4．（湖南省长、望、浏、宁高三3月一模联考）设,x y R ∈，则“22x y ≥≥且”是“224x y +≥”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．（山东省青岛市3月高三统一质量检测）已知0,0a b >>,且24a b +=,则1ab的最小值为（）A ．14B ．4C ．12D ．2 6．（广东省六校高三第二次联考试题）若函数1(),(2)2f x x x x =+>- 在x n =处有最小值，则n =( ) A．1．1 C ．4 D ．37．（山东省临沂市高三教学质量检测考试）实数,x y 满足1,(1),0,x y a a x y ≥⎧⎪≤>⎨⎪-≤⎩若目标函数z x y =+取得最大值4，则实数a 的值为（）（A ）4 （B ）3 （C ）2 （D ）328．（广东省深圳市松岗中学高三模拟试卷）设实数,x y 满足 2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩，则22x y u xy +=的取值范围是（） .A ．5[2,]2 .B ．10[2,]3 C ．510[,]23 D ．1[,4]4 9．（广州市普通高中毕业班综合测试）在平面直角坐标系中，若不等式组2020x y x y x t +-≥⎧⎪-+≥⎨⎪≤⎩表示的平面区域的面积为4，则实数t 的值为（）A ．1B ．2C ．3D ．410．（安徽省安庆市高三3月模拟考试）已知,x y 满足不等式组22y x x y x ≤⎧⎪+≥⎨⎪≤⎩，则2z x y =+的最大值与最小值的比值为（）A ． 12B ．2C ．32D ．4311．（江苏省南京市高三“市二模”模拟考试数学试卷）下面四个条件中，使a b >成立的充分而不必要的条件是（填写序号）． ①1a b >- ②1a b >+ ③22a b > ④33a b >12．（山东青岛高三期末检测）已知点(,)A m n 在直线220x y +-=上，则24m n +的最小值为．13． (江苏省泰州市高三年级第一次模拟)已知正实数,,x y z 满足112()x x yz y z ++=，则11()()x x y z++的最小值为_____．14．（湖南省长、望、浏、宁高三3月一模联考）若实数,,a b c 满足111111,122222a b a b b c a c ++++=++=，则c 的最大值是．15． (江苏省南京市高三第一次模拟考试)已知2()log (2)f x x =-，若实数,m n 满足()(2)3f m f n +=，则m n +的最小值是．16．（山东省胜利油田一中高三下学期第一次调研考试）已知0,0,lg 2lg8lg 2x y x y >>+=，则113x y+的最小值为．17．（江苏省启东中学高三第一次模拟考试）若正实数,,a b c 满足：320a b c -+=的最大值为． 18．（浙江省宁波市高三“十校”联考）设220,0,4x y x y x y >>+-=，则11x y+最小值为． 19．（上海华师大一附中高三联合调研考试数学试卷）若21316log 1a a M a -+=-,[4,17]a ∈,则M 的取值范围是_____．20．（安徽省安庆市高三3月模拟考试）已知4510x y ==，则12x y+= ． 21．（苏北四市高三年级二轮模拟考试）知ABC ∆的三边长a,b,c 成等差数列,且22284a b c ++=,则实数b 的取值范围是__________．22．（江苏省启东中学高三第一次模拟考试）实数,x y 满足，0,1,21x y x y x y -≥+≤+≥，则63z x y =+的最小值为．23．(湖北省黄冈中学模拟考试)若实数x ，y 满足430,14,7.x y x y x y +=⎧⎪-≥⎨⎪-≤⎩_____．24．（山东省青岛市3月高三统一质量检测）设变量,x y 满足约束条件3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,则目标函数1y z x +=的最小值为．25．（广东省六校高三第二次联考试题）已知,0,0x y xy x y +=>>则x y +的最小值是．26．（浙江省名校新高考研究联盟第一次联考）若不等式222(2)2a x y x xy +≥+对任意非零实数,x y 恒成立，则实数a 的最小值为．27．（北京朝阳区高三期末考试）某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润y （万元）与机器运转时间x （年数，x *∈N ）的关系为21825y x x =-+-．则当每台机器运转年时，年平均利润最大，最大值是万元．28．（广东省六校高三第二次联考试题数学理题）如果直线12:220,:840l x y l x y -+=--=与x 轴正半轴，y 轴正半轴围成的四边形封闭区域（含边界）中的点，使函数()0,0z abx y a b =+>>的最大值为8，求a b +的最小值．29．（江苏省启东中学高三第二次模拟考试）已知222:6160,:440(0)p x x q x x m m -++≥-+-≤>．（1）若p 为真命题，求实数x 的取值范围；（2）若p 为q 成立的充分不必要条件，求实数m 的取值范围．30．（江苏省南京市高三第二次模拟考试）已知0,0,1a b a b >>+=，求证：14921214a b +++…． 31．（江苏省南京市高三“市二模”模拟考试数学试卷）设命题p ：方程22167x y a a +=+-表示双曲线，命题q ：圆22(1)9x y +-=与圆22()(1)16x a y -++=相交．若“p ⌝且q ”为真命题，求实数a 的取值范围．32．（山东省青岛市高三期末检测数学理科）已知函数y 的定义域为R ，解关于x 的不等式220x x a a --+>．33．（江苏盐城市高三年级第二次模拟考试数学试题）设1a ，2a ，3a 均为正数，且123a a a m ++=．求证：1223311119.2a a a a a a m++≥+++ 34（山东省聊城市水城中学高三下学期第二次模拟考试）已知函数2()log (|1||2|f x x x a =-++-）．（Ⅰ）当7a =时，求函数()f x 的定义域；（Ⅱ）若关于x 的不等式()3f x ≥的解集是R ，求a 的取值范围．练习题答案：1．B 2．C 3．B4．A 5．C 6．D 7．C 8．B 9．B 10．B 11．② 12．4 13．22log 3-15． 7 16．4 1718．4 19． 3[2log 2,2]--- (或3[log 18,2]--等 20．2 21． 22．3 23．[0,10] 24．1 25．4 26．1 27．5，828．解：设(),P x y 为封闭区域中的任意点，(),P x y 满足约束条件2208400 , 0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩，作出可行域可知目标函数的最优解为(1,4)B ．把(1,4)B 代入(0,0)Z abx y a b =+>>得最大值8，解得 4ab =．由基本不等式得：4a b +≥=（当且仅当2a b ==时，等号成立），故a b +的最小值为4．29．解：（1）由26160x x -++…得，28x -剟，所以p 为真命题时，x 的取值范围是[2,8]-．(2):[2,2]q x m m ∈-+,若p 为q 成立的充分不必要条件，则[2,8]-是[2,2]m m -+的真子集，所以0,22,28.m m m >⎧⎪--⎨⎪+⎩……解得6m … 30．证明：因为0,0,1a b a b >>+=，所以(21)(21)4a b +++=，而14214(21)()(21)(21)1421212121b a a b a b a b ++++++=+++++++59+=…，所以结论成立． 31．解：若p 真，即方程22167x y a a +=+-表示双曲线，则(6)(7)0a a +-<，解得67a -<<．若q 真，即圆()2219x y +-=与圆()()22116x a y -++=相交，则17,解得a -<若“p ⌝且q ”为真命题，则p 假q 真，则67a a a ≤-≥⎧⎪⎨-<⎪⎩或6a -<≤-，所以符合条件的实数a的取值范围是6a -≤-．32．解：因为函数y 义域为R ，所以2210ax ax ++≥恒成立()*当0a =时，10≥恒成立,满足题意，当0a ≠时，为满足()* 必有0a >且2440a a ∆=-≤，解得01a <≤．综上可知：a 的取值范围是01a ≤≤．原不等式可化为()()10x a x a -⎡--⎤>⎣⎦．当102a ≤<时，不等式的解集为{x x a <或1}x a >-；当12a =时，不等式的解集为1{}2x x ≠；当112a <≤时，不等式的解集为{1x x a <-或}x a >． 33．证明：122331122331111()()()()a a a a a a a a a a a a ++++++++++ 3123()(9a a a a a a +++…，又123a a a m ++=，所以原不等式成立． 34．解：（Ⅰ）由题设知：127x x -++>，不等式的解集是以下不等式组解集的并集：1127x x x ≥⎧⎨-++>⎩，或21127x x x -<<⎧⎨-+++>⎩，或2127x x x ≤-⎧⎨-+-->⎩ 解得函数()f x 的定义域为(,4)(3,)-∞-+∞．（Ⅱ）不等式()3f x ≥即128x x a -++≥+，x R ∈时，恒有12(1)(2)3x x x x -++≥--+=，不等式128x x a -++≥+解集是R ，83,a +≤∴5,a ≤-∴a ∴的取值范围是(,-5]-∞．。

抛物线总结

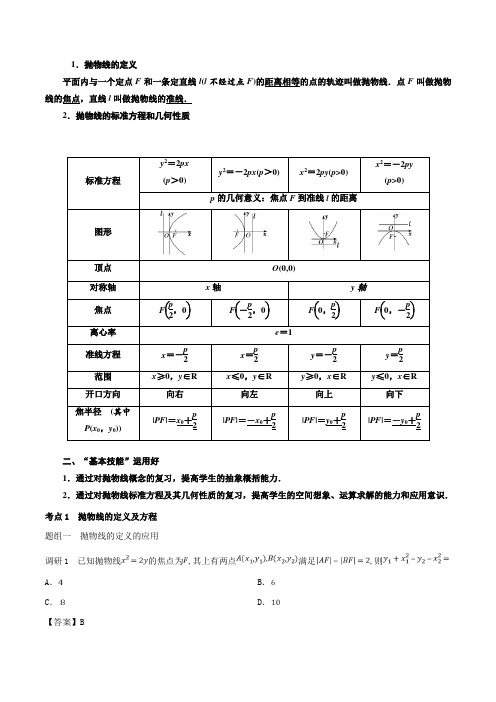
1．抛物线的定义平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．2．抛物线的标准方程和几何性质标准方程y 2＝2px(p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p >0)x 2＝－2py (p >0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 x 轴y 轴焦点 F ⎝⎛⎭⎫p2，0 F ⎝⎛⎭⎫－p2，0 F ⎝⎛⎭⎫0，p 2 F ⎝⎛⎭⎫0，－p2 离心率 e ＝1准线方程 x ＝－p2x ＝p 2y ＝－p2y ＝p 2 范围 x ≥0，y ∈Rx ≤0，y ∈Ry ≥0，x ∈Ry ≤0，x ∈R开口方向向右向左向上向下焦半径 (其中P (x 0，y 0)) |PF |＝x 0＋p2|PF |＝－x 0＋p2|PF |＝y 0＋p2|PF |＝－y 0＋p2二、“基本技能”运用好1．通过对抛物线概念的复习，提高学生的抽象概括能力．2．通过对抛物线标准方程及其几何性质的复习，提高学生的空间想象、运算求解的能力和应用意识．考点1 抛物线的定义及方程题组一抛物线的定义的应用调研1 已知抛物线的焦点为,其上有两点满足,则A ．B ．C ．D ．【答案】B【解析】由抛物线的定义可知()221212122AF BF y y x x -=-=-=,则,所以==.☆技巧点拨☆抛物线的离心率e ＝1，体现了抛物线上的点到焦点的距离等于到准线的距离，因此，涉及抛物线的焦半径、焦点弦的问题，可以优先考虑利用抛物线的定义将点到焦点的距离转化为点到准线的距离，即2PF px =+或2PF py =+，使问题简化．抛物线的定义常在高考中作为转为问题的工具，需熟练掌握.题组二求抛物线的方程调研 2 已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离与椭圆22194x y +=的长轴长相等,则抛物线的标准方程为__________. 【答案】212y x =【解析】在椭圆22194x y +=中，3a =，2b =，故长轴长为6，由抛物线的焦点F 到准线的距离与椭圆的长轴长相等可得6p =，故抛物线的标准方程为212y x =.调研3 已知抛物线的顶点在原点，它的准线过双曲线22221x y a b -=的一个焦点，抛物线与双曲线的交点为362P ⎛ ⎝，求抛物线方程和双曲线方程. 【解析】依题意设抛物线方程为()220y px p =>，∵点362P ⎛⎝在抛物线上，∴3622p =⨯，解得2p =，∴所求抛物线方程为24y x =. 故抛物线的准线方程为1x =-，∵双曲线的左焦点在抛物线的准线上，∴1c =，故221a b +=，又点3,62⎛⎫⎪⎝⎭在双曲线上，∴229614a b -=，由222219614a b a b⎧+=⎪⎨-=⎪⎩解得2213,44a b ==. ∴所求双曲线方程为224413x y -=.☆技巧点拨☆高考中常求抛物线的方程，一般会与其他知识相结合，求抛物线方程的常用方法是待定系数法，其关键是判断焦点的位置、开口方向，在方程的类型已经确定的前提下，由于标准方程只有一个参数p ，只需一个条件就可以确定抛物线的标准方程.考点2 抛物线的性质题组一焦点弦问题调研1 过抛物线y 2＝4x 的焦点F 作倾斜角为45°的直线交抛物线于A ，B 两点，则弦长|AB |为________．【答案】8【解析】设A (x 1，y 1)，B (x 2，y 2)，易得抛物线的焦点是F (1,0)，所以直线AB 的方程是y ＝x －1，联立⎩⎪⎨⎪⎧y 2＝4x ，y ＝x －1，消去y 得x 2－6x ＋1＝0，所以x 1＋x 2＝6，所以|AB |＝x 1＋x 2＋p ＝6＋2＝8.题组二最值问题调研 2 已知抛物线的焦点为,准线为,且过点在抛物线上,若点,则的最小值为A ．2B ．3C ．4D ．5【答案】B 【解析】由题可得,.由抛物线的定义可知,,所以=.故选B ．调研3 已知定点()3,4A ，点P 是抛物线24y x =上一动点，点P 到直线1x =-的距离为d ，则PA d +的最小值是_______ . 【答案】25【解析】点A 是抛物线24y x =外一点，所以PA d +()2231425PF PA AF =+≥=-+=，当且仅当点P 为线段AF 与抛物线的交点时取等号，故PA d +的最小值是25.☆技巧点拨☆有关抛物线上一点M 到抛物线焦点F 和到已知点E （E 在抛物线内）的距离之和的最小值问题，可依据抛物线的图形，过点E 作准线l 的垂线，其与抛物线的交点到抛物线焦点F 和到已知点E 的距离之和是最小值.1．（2017-2018学年重庆市九校联盟高三上学期第一次联合考试）已知抛物线=经过点,则该抛物线的焦点到准线的距离等于 A ． B ． C ．D ．1【答案】B 【解析】∵抛物线=经过点∴=∴=∴抛物线的焦点到准线的距离等于2．（北京市丰台区2018年高三年级一模数学）已知抛物线C 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则C 的标准方程为 A ．28y x =B ．28x y =-C ．22y x =D ．22x =【答案】B3．（吉林省吉林市2018届高三第三次调研考试数学）以抛物线28y x =上的任意一点为圆心作圆与直线2x =-相切，这些圆必过一定点，则这一定点的坐标是A ．()0,2B ．()2,0C ．()4,0D ．()0,4【答案】B【解析】由题意得抛物线28y x =的准线方程为2x =-，因为动圆的圆心在抛物线28y x =上，且与抛物线的准线相切，所以动圆的圆心必过抛物线的焦点，即过点()2,0．选B ．4．(2017河南八市联考)已知点M (－3,2)是坐标平面内一定点，若抛物线y 2＝2x 的焦点为F ，点Q 是该抛物线上的一动点，则|MQ |－|QF |的最小值是 A ．72 B ．3 C ．52 D ．2【答案】C5．（2018届河北省武邑中学高三上学期第五次调研考试）已知抛物线的焦点为,其准线与双曲线223=1y x -相交于两点,若MNF △为直角三角形,其中为直角顶点,则A ．B ．C ．D ．6【答案】A【解析】由题可得，抛物线的焦点为, 准线x =-.所以其准线与双曲线223=1 yx-相交于2233,3,,32424p p p pM N⎛⎫⎛⎫-+--+⎪ ⎪⎪ ⎪⎝⎭⎝⎭.因为MNF△为直角三角形,其中为直角顶点，所以2334pp=+，解得.故选A．6．（2017-2018学年湖南省长沙市第一中学高三高考模拟卷）已知抛物线的焦点为,准线与轴的交点为,点在抛物线上,且,则AFK△的面积为A．4 B．6C．8 D．12【答案】C【解析】抛物线的焦点为,准线与轴的交点为,点在抛物线上,且,过点A作准线的垂线,垂足为M,则,所以可知,所以可知AMK△为等腰直角三角形,所以AFK△也为等腰直角三角形,且腰长为,所以该三角形的面积为14482S=⨯⨯=.故选C．7．（上海市普陀区2018届高三下学期质量调研（二模）数学）抛物线212x y=的准线方程为__________.【答案】3y=-【解析】2212,32px py y==∴=，∴抛物线212x y=的准线方程为32py=-=-，故答案为3y=-.8．（河北省保定市2018届高三第一次模拟考试数学）抛物线的顶点在原点，焦点在x轴上，抛物线上的点()2,P a-到焦点的距离为3，则a=__________．【答案】22±9．（河南省2018届普通高中毕业班4月高考适应性考试数学）已知点是抛物线的焦点，，是该抛物线上两点，，则线段的中点的横坐标为__________．【答案】210．（2018届安徽省安庆市高三二模考试）设抛物线的焦点为点在抛物线上,且满足若32AF =，则的值为__________. 【答案】12【解析】由题意得.因为为抛物线的焦点弦,所以1121AF BF p+==.而,解得3BF =.又因为,所以31232AF BFλ===.11．（云南省保山市2018届普通高中毕业生第二次市级统测）已知F 是抛物线C ：28y x =的焦点，点A 的坐标为()2,6，点P 是C 上的任意一点，当P 在点1P 时，PF PA -取得最大值；当P 在点2P 时，PF PA -取得最小值，则1P ，2P 两点间的距离为__________．51712．（2017-2018学年福建省高三毕业班第三次质量检查）已知抛物线上的点到点距离的最小值为.(1)求抛物线的方程;△面(2)若,圆,过作圆的两条切线分别交轴于两点,求MAB积的最小值.【解析】(1),,==.,∴当即时,,不符合题意,舍去;则，即时,,(舍去),.1．（2016新课标全国I理科）以抛物线C的顶点为圆心的圆交C于A，B两点，交C的准线于D，E两点.已知|AB|=42|DE|=25C的焦点到准线的距离为A．2 B．4C．6 D．8【答案】B2．（2015上海理科）抛物线22y px =（0p >）上的动点Q 到焦点的距离的最小值为1，则p = ．【答案】2【解析】因为抛物线上动点到焦点的距离为动点到准线的距离，因此抛物线上动点到焦点的最短距离为顶点到准线的距离，即1, 2.2pp == 3．（2017新课标全国II 理科）已知F 是抛物线:C 28y x =的焦点，M 是C 上一点，FM 的延长线交y 轴于点N ．若M 为FN 的中点，则FN =_______________．【答案】6【解析】如图所示，不妨设点M 位于第一象限，设抛物线的准线与x 轴交于点F'，作MB l ⊥于点B ，NA l ⊥于点A ，由抛物线的解析式可得准线方程为2x =-，则||2,||4AN FF'==，在直角梯形ANFF'中，中位线||||||32AN FF'BM +==，由抛物线的定义有：||||3MF MB ==，结合题意，有||||3MN MF ==，故336FN FM NM =+=+=．【名师点睛】抛物线的定义是解决抛物线问题的基础，它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化．如果问题中涉及抛物线的焦点和准线，又能与距离联系起来，那么用抛物线定义就能解决问题．因此，涉及抛物线的焦半径、焦点弦问题，可以优先考虑利用抛物线的定义转化为点到准线的距离，这样就可以使问题简单化．。

2018安庆二模含答案。安徽省安庆市2018届高三二模考试数学(理)试题

2018安庆二模含答案。

安徽省安庆市2018届高三二模考试数学(理)试题2018年安庆市高三模拟考试（二模）数学试题（理）参考答案一、选择题1.【解析】因为B={x|x<1}，所以A∩B={x|x<1}，故选D。

2.【解析】(2+i)z=1-i，所以z的共轭复数为2-i。

故选B。

3.【解析】根据二倍角公式、正弦定理可得cos2A>cos2B ⟺ 1-2sinA>1-2sinB ⟺ sin2A>sin2B ⟺ sinA>sinB ⟺ a>b。

故选C。

4.【解析】根据条件可知，E={(x,y)|0<x<2,0<y<1/x}，所以阴影部分的面积为∫1/2 1 (2-x)dx = 3-2ln2.所以，豆子落在阴影部分的概率为3-2ln2.故选A。

5.【解析】x=2^t-k，所以k=log2(x+1)。

当x=1时，k=0；当x=2时，k=8；当x=16时，k=6.故选B。

6.【解析】该几何体的直观图如图所示，其体积为2×2×2+2×(1/2)×2×2×2=16（cm³）。

故选B。

7.【解析】f(x)=loga|x|={-loga(-x)。

x0}，故选C。

8.【解析】由函数y=f(x)图象相邻两条对称轴之间的距离为π可知其周期为π，所以ω=π/2.又f(x)=sin(2x+φ)，将函数y=f(x)的图象向左平移一个单位后，得到函数y=sin(2x-π/6)的图象。

因为得到的图象关于y轴对称，所以2(π/2)-φ=kπ，k∈Z，即φ=-π/3.又φ<π，所以φ=-π/3.故选A。

9.【解析】因为点D在边BC上，所以存在t∈R，使得BD=tBC=tAC-AB。

因为M是线段AD的中点，所以BD=1/2AC。

所以1/2AC=tAC-AB，即AB=AC/2t-1.故选D。

10.【解析】设三角形的三个内角分别为α、β、γ，则α+β+γ=π。

2018安庆“二模”数学试题参考答案及评分标准

2018年安庆市高三模拟考试（二模）数学试题（文）参考答案一、选择题（本大题共12小题，每小题5分，共60分，每小题分别给出四个选项，只有一个选项符合题意.）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CAABBACDDBDB1.C.解析:21525125)2()12()2)(2()2)((2=∴++-=++-=+-++=-+a i a a i a a i i i i a i i a ，选C. 2.A.解析：()()()3401111214124=++=--=q q q q a qq a a S ，选A.3.解析：选A.4.B.解析：圆形纪念币的面积是ππ812182=⎪⎭⎫⎝⎛，根据几何概型得估计装饰狗的面积大约是ππ1024381500150=⨯，选B. 5.B.解析：该几何体的直观图如图所示，其体积为12222222162⨯⨯+⨯⨯⨯⨯=（3cm ）. 选B.6. A. 解析：由函数()y f x =图象相邻两条对称轴之间的距离为π2可知其周期为π，所以2π2πω==，所以()()sin 2f x x ϕ=+. 将函数()y f x =的图象向左平移π3个单位后，得到函数πsin 23y x ϕ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦图象. 因为得到的图象关于y 轴对称，所以ππ2π32k ϕ⨯+=+，z k ∈，即ππ6k ϕ=-，z k ∈. 又π2ϕ<，所以π6ϕ=-，所以π()sin 26f x x ⎛⎫=- ⎪⎝⎭，其图象关于点π012⎛⎫ ⎪⎝⎭，对称. 故选A.7.C.解析：根据程序框图的算法，得s=21，选C.文科数学参考答案（共7页）第1页8.D.解析：e xx x f e e f e x e f e x f -=⇒='⇒-'='ln 2)(1)(1)(2)( 令e x e x x f 2012)(=⇒=-='，当)(,0)(,2x f x f e x <'>单减，当)(,0)(,20x f x f e x >'<<单增，∴e x 2=时，)(x f 取得极大值.2ln 2选D.9. D. 解析：①令k z y x ===532log loglog，则kk k z y x ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=8141613141215,3,2将它们分别24次方，得,125)(,81)(,64)(244124243124242124k k k z c y b x a ======选D.②取特殊值法：取5,3,2===z y x 符合题意，易验证a b c >>，选D.10.B.解析：设双曲线的右焦点为F '，连接F P '. 因为O 是线段FF '的中点，M 为线段FP的中点，所以F P '//OM 且22F P OM a '==. 因为直线FP 与圆222x y a +=相切于点M ，所以OM FP ⊥，从而F P FP '⊥，所以点P 是以FF '为直径的圆与直线b y x a =的交点.由222(0)b y x x ax y c ⎧=>⎪⎨⎪+=⎩，，得x a y b =⎧⎨=⎩，，所以()P a b ，. 又()0F c '，，2F P a '=，所以()2224a c b a -+=.根据222b c a =-，可得2c a =. 故双曲线的离心率2ce a==. 11.D.解析：根据规律，344用去1+2+3+……+44=990个奇数，344的和式中最后一个奇数是197919902=-⨯，所以.206919831981453+++= 选D. 12.B.解析：由)1()1(-=+x f x f 知)(x f 的最小正周期是2，画出函数)(x f 的部分图像，如图所示。

2020届高考物理一轮复习专题13 电磁感应综合问题名校试题汇编(学生版)

专题13 电磁感应综合问题名校试题汇编一、选择题1.(多选)(2019·湖北省武汉市调研)如图甲所示，在足够长的光滑的固定斜面上放置着金属线框，垂直于斜面方向的匀强磁场的磁感应强度B 随时间的变化规律如图乙所示(规定垂直斜面向上为正方向).t ＝0时刻将线框由静止释放，在线框下滑的过程中，下列说法正确的是( )A.线框中产生大小、方向周期性变化的电流B.MN 边受到的安培力先减小后增大C.线框做匀加速直线运动D.线框中产生的焦耳热等于其机械能的损失2.(多选)(2019·福建省厦门市质检)如图所示，在倾角为θ的光滑固定斜面上，存在着磁感应强度大小为B 的匀强磁场，磁场方向垂直斜面向上，磁场的宽度为2L .一边长为L 的正方形导线框，由静止开始沿斜面下滑，当ab 边刚越过GH 进入磁场瞬间和刚越过MN 穿出磁场瞬间速度刚好相等.从ab 边刚越过GH 处开始计时，规定沿斜面向上为安培力的正方向，则线框运动的速率v 与线框所受安培力F 随时间变化的图线中，可能正确的是( )3.(2018·全国卷Ⅱ·18)如图，在同一水平面内有两根平行长导轨，导轨间存在依次相邻的矩形匀强磁场区域，区域宽度均为l ，磁感应强度大小相等、方向交替向上向下.一边长为32l 的正方形金属线框在导轨上向左匀速运动.线框中感应电流i 随时间t 变化的正确图线可能是( )4.(多选)(2019·方向垂直纸面向外，一正方形金属线框质量为m，电阻为R，边长为L，从虚线处进入磁场时开始计时，在外力作用下，线框由静止开始，以垂直于磁场边界的恒定加速度a进入磁场区域，t1时刻线框全部进入磁场，规定顺时针方向为感应电流I的正方向，外力大小为F，线框中电功率的瞬时值为P，通过导线横截面的电荷量为q，选项中P－t图象和q－t图象均为抛物线，则这些量随时间变化的图象正确的是()5.(多选)(2018·广西北海市一模)如图甲所示，导体框架abcd放置于水平面内，ab平行于cd，导体棒MN与两导轨垂直并与导轨接触良好，整个装置放置于垂直于框架平面的磁场中，磁感应强度B随时间变化规律如图乙所示，MN始终保持静止.规定竖直向上为磁场正方向，沿导体棒由M到N为感应电流的正方向，水平向右为导体棒所受安培力F的正方向，水平向左为导体棒所受摩擦力F f的正方向，下列图象中正确的是()6. (多选)(2019·安徽省黄山市质检)如图甲所示，闭合矩形导线框abcd 固定在匀强磁场中，磁场的方向与导线框所在平面垂直，磁感应强度B 随时间t 变化的规律如图乙所示.规定垂直纸面向外为磁场的正方向，顺时针为线框中感应电流的正方向，水平向右为安培力的正方向.关于线框中的感应电流i 与ad 边所受的安培力F 随时间t 变化的图象，下列选项中正确的是( )7.(多选)(2018·安徽省安庆市二模)如图甲所示，光滑平行金属导轨MN 、PQ 所在平面与水平面成θ角，M 、P 两端接一电阻R ，整个装置处于方向垂直导轨平面向上的匀强磁场中.t ＝0时对金属棒施加一平行于导轨的外力F ，使金属棒由静止开始沿导轨向上运动，金属棒电阻为r ，导轨电阻忽略不计.已知通过电阻R 的感应电流I 随时间t 变化的关系如图乙所示.下列关于棒的运动速度v 、外力F 、流过R的电荷量q 以及闭合回路中磁通量的变化率ΔΦΔt随时间变化的图象正确的是( )8.(多选)如图所示，竖直放置的“”形光滑导轨宽为L ，矩形匀强磁场Ⅰ、Ⅱ的高和间距均为d ，磁感应强度为B .质量为m 的水平金属杆由静止释放，进入磁场Ⅰ和Ⅱ时的速度相等.金属杆在导轨间的电阻为R ，与导轨接触良好，其余电阻不计，重力加速度为g .金属杆( )A.刚进入磁场Ⅰ时加速度方向竖直向下B.穿过磁场Ⅰ的时间大于在两磁场之间的运动时间C.穿过两磁场产生的总热量为4mgdD.释放时距磁场Ⅰ上边界的高度h 可能小于m 2gR 22B 4L 4 9.(多选)(2018·广西防城港市3月模拟)如图所示，等边闭合三角形线框，开始时底边与匀强磁场的边界平行且重合，磁场的宽度大于三角形的高度，线框由静止释放，穿过该磁场区域，不计空气阻力，则下列说法正确的是( )A.线框进磁场过程中感应电流为顺时针方向B.线框底边刚进入和刚穿出磁场时线圈的加速度大小可能相同C.线框出磁场的过程，可能做先减速后加速的直线运动D.线框进出磁场过程，通过线框横截面的电荷量不同10.(2018·陕西省咸阳市第二次模拟)如图甲所示，匝数n ＝2的金属线圈(电阻不计)围成的面积为20 cm 2，线圈与R ＝2 Ω的电阻连接，置于竖直向上、均匀分布的磁场中，磁场与线圈平面垂直，磁感应强度为B ，B －t 关系如图乙所示，规定感应电流i 从a 经过R 到b 的方向为正方向，忽略线圈的自感影响，则下列i －t 关系图正确的是( )二、非选择题1.如图甲所示，间距L＝0.5 m的两根光滑平行长直金属导轨倾斜放置，导轨平面倾角θ＝30°.导轨底端接有阻值R＝0.8 Ω的电阻，导轨间有Ⅰ、Ⅱ两个矩形区域，其长边都与导轨垂直，两区域的宽度均为d2＝0.4 m，两区域间的距离d1＝0.4 m，Ⅰ区域内有垂直导轨平面向下的匀强磁场，磁感应强度大小B0＝1 T，Ⅱ区域内的磁感应强度B随时间t变化如图乙所示，规定垂直于导轨平面向上的磁感应强度方向为正方向.t＝0时刻，把导体棒MN无初速度地放在区域Ⅰ下边界上.已知导体棒的质量m ＝0.1 kg，导体棒始终与导轨垂直并接触良好，且导体棒在磁场边界时都认为处于磁场中，导体棒和导轨电阻不计，取重力加速度g＝10 m/s2.求：(1)0.1 s内导体棒MN所受的安培力大小；(2)t＝0.5 s时回路中的电动势和流过导体棒MN的电流方向；(3)0.5 s时导体棒MN的加速度大小.2.(2018·吉林省吉林市第二次调研)如图甲所示，一边长L＝2.5 m、质量m＝0.5 kg的正方形金属线框，放在光滑绝缘的水平面上，整个装置处在方向竖直向上、磁感应强度B＝0.8 T的匀强磁场中，它的一边与磁场的边界MN重合.在水平力F作用下由静止开始向左运动，经过5 s线框被拉出磁场.测得金属线框中的电流随时间变化的图象如图乙所示，在金属线框被拉出的过程中，(1)求通过线框的电荷量及线框的总电阻；(2)分析线框运动性质并写出水平力F随时间变化的表达式；(3)已知在这5 s内力F做功1.92 J，那么在此过程中，线框产生的焦耳热是多少.3.(2018·福建省南平市适应性检测)如图所示，一对平行的粗糙金属导轨固定于同一水平面上，导轨间距L＝0.2 m，左端接有阻值R＝0.3 Ω的电阻，右侧平滑连接一对弯曲的光滑轨道.仅在水平导轨的整个区域内存在竖直向上的匀强磁场，磁感应强度大小B＝1.0 T.一根质量m＝0.2 kg、电阻r＝0.1 Ω的金属棒ab 垂直放置于导轨上，在水平向右的恒力F 作用下从静止开始运动，当金属棒通过位移x ＝9 m 时离开磁场，在离开磁场前已达到最大速度.当金属棒离开磁场时撤去外力F ，接着金属棒沿弯曲轨道上升到最大高度h ＝0.8 m 处.已知金属棒与导轨间的动摩擦因数μ＝0.1，导轨电阻不计，棒在运动过程中始终与导轨垂直且与导轨保持良好接触，取g ＝10 m/s 2.求：(1)金属棒运动的最大速率v ；(2)金属棒在磁场中速度为v 2时的加速度大小； (3)金属棒在磁场区域运动过程中，电阻R 上产生的焦耳热.4.(2018·山东省泰安市上学期期末)如图，两固定的绝缘斜面倾角均为θ，上沿相连.两细金属棒ab (仅标出a 端)和cd (仅标出c 端)长度均为L 、质量分别为2m 和m ；用两根不可伸长的柔软轻导线将它们连成闭合回路abdca ，并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上，两定滑轮间的距离也为L .左斜面上存在匀强磁场，磁感应强度大小为B ，方向垂直于斜面向上.已知斜面及两根柔软轻导线足够长.回路总电阻为R ，两金属棒与斜面间的动摩擦因数均为μ，重力加速度大小为g .使两金属棒水平，从静止开始下滑.求：(1)金属棒运动的最大速度v m 的大小；(2)当金属棒运动的速度为v m 2时，其加速度大小是多少？ 5..(2018·天津市实验中学模拟)如图所示，固定光滑金属导轨间距为L ，导轨电阻不计，上端a 、b 间接有阻值为R 的电阻，导轨平面与水平面的夹角为θ，且处在磁感应强度大小为B 、方向垂直于导轨平面向上的匀强磁场中.质量为m 、电阻为r 的导体棒与固定弹簧相连后放在导轨上.初始时刻，弹簧恰处于自然长度，导体棒具有沿导轨向上的初速度v 0.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k ，弹簧的中心轴线与导轨平行.(1)求初始时刻通过电阻R 的电流I 的大小和方向；(2)当导体棒第一次回到初始位置时，速度变为v ，求此时导体棒的加速度大小a .6.(2018·广东省惠州市模拟)如图所示，足够长的粗糙绝缘斜面与水平面成θ＝37°角放置，在斜面上虚线aa ′和bb ′与斜面底边平行，在aa ′、bb ′围成的区域中有垂直斜面向上的有界匀强磁场，磁感应强度为B ＝1 T ；现有一质量为m ＝10 g 、总电阻R ＝1 Ω、边长d ＝0.1 m 的正方形金属线圈MNQP ，让PQ 边与斜面底边平行，从斜面上端由静止释放，线圈刚好匀速穿过整个磁场区域.已知线圈与斜面间的动摩擦因数为μ＝0.5，(取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8)求：(1)线圈进入磁场区域时的速度大小；(2)线圈释放时，PQ边到bb′的距离；(3)整个线圈穿过磁场的过程中，线圈上产生的焦耳热.7.(2018·四川省凉山州三模)如图所示，光滑平行足够长的金属导轨固定在绝缘水平面上，导轨范围内存在磁场，其磁感应强度大小为B，方向竖直向下，导轨一端连接阻值为R的电阻.在导轨上垂直导轨放一长度等于导轨间距L、质量为m的金属棒，其电阻为r.金属棒与金属导轨接触良好.金属棒在水平向右的恒力F作用下从静止开始运动，经过时间t后开始匀速运动，金属导轨的电阻不计.求：(1)金属棒匀速运动时回路中电流大小；(2)金属棒匀速运动的速度大小以及在时间t内通过回路的电荷量.(3)若在时间t内金属棒移动的位移为x，求电阻R上产生的热量.8. (2018·山东省青岛市模拟)如图所示，两平行光滑金属导轨由两部分组成，左面部分水平，右面部分为半径r＝0.5 m的竖直半圆，两导轨间距离l＝0.3 m，导轨水平部分处于竖直向上、磁感应强度大小B＝1 T的匀强磁场中，两导轨电阻不计.有两根长度均为l的金属棒ab、cd，均垂直导轨置于水平导轨上，金属棒ab、cd的质量分别为m1＝0.2 kg、m2＝0.1 kg，电阻分别为R1＝0.1 Ω、R2＝0.2 Ω.现让ab棒以v0＝10 m/s的初速度开始水平向右运动，cd棒进入圆轨道后，恰好能通过轨道最高点PP′，cd 棒进入圆轨道前两棒未相碰，重力加速度g＝10 m/s2，求：(1)ab棒开始向右运动时cd棒的加速度a0；(2)cd棒刚进入半圆轨道时ab棒的速度大小v1；(3)cd棒进入半圆轨道前ab棒克服安培力做的功W.9.(2019·山东省淄博市质检)如图所示，一个质量为m、电阻不计、足够长的光滑U形金属框架MNQP，位于光滑绝缘水平桌面上，平行导轨MN和PQ相距为L.空间存在着足够大的方向竖直向下的匀强磁场，磁感应强度的大小为B.另有质量也为m的金属棒CD，垂直于MN放置在导轨上，并用一根与CD棒垂直的绝缘细线系在定点A.已知细线能承受的最大拉力为F T0，CD棒接入导轨间的有效电阻为R .现从t ＝0时刻开始对U 形框架施加水平向右的拉力，使其从静止开始做加速度为a 的匀加速直线运动.(1)求从框架开始运动到细线断裂所需的时间t 0及细线断裂时框架的瞬时速度v 0大小；(2)若在细线断裂时，立即撤去拉力，求此后过程中回路产生的总焦耳热Q .10.如图所示，平行倾斜光滑导轨与足够长的平行水平光滑导轨平滑连接，导轨电阻不计.质量分别为m 和12m 的金属棒b 和c 静止放在水平导轨上，b 、c 两棒均与导轨垂直.图中de 虚线往右有范围足够大、方向竖直向上的匀强磁场.质量为m 的绝缘棒a 垂直于倾斜导轨由静止释放，释放位置与水平导轨的高度差为h .已知绝缘棒a 滑到水平导轨上与金属棒b 发生弹性正碰，金属棒b 进入磁场后始终未与金属棒c 发生碰撞.重力加速度为g .求：(1)绝缘棒a 与金属棒b 发生弹性正碰后分离时两棒的速度大小；(2)金属棒b 进入磁场后，其加速度为其最大加速度的一半时的速度大小；(3)两金属棒b 、c 上最终产生的总焦耳热.11.(2018·湖南省长沙四县三月模拟)足够长的平行金属轨道M 、N ，相距L ＝0.5 m ，且水平放置；M 、N 左端与半径R ＝0.4 m 的光滑竖直半圆轨道相连，与轨道始终垂直且接触良好的金属棒b 和c 可在轨道上无摩擦地滑动，两金属棒的质量m b ＝m c ＝0.1 kg ，接入电路的有效电阻R b ＝R c ＝1 Ω，轨道的电阻不计.平行水平金属轨道M 、N 处于磁感应强度B ＝1 T 的匀强磁场中，磁场方向垂直轨道平面向上，光滑竖直半圆轨道在磁场外，如图所示，若使b 棒以初速度v 0＝10 m/s 开始向左运动，运动过程中b 、c 不相撞，g 取10 m/s 2，求：(1)c 棒的最大速度；(2)c 棒达最大速度时，此棒产生的焦耳热；(3)若c 棒达最大速度后沿半圆轨道上滑，金属棒c 到达轨道最高点时对轨道的压力的大小.。

安徽省安庆市2018届高三模拟考试(二模)数学(理)试卷(含答案)

2018年安庆市高三模拟考试（二模）数学试题（理）第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合}1|{<=x x A ，集合}11|{<=x x B ，则=B A （）A ．∅B ．}1|{<x xC ．}10|{<<x xD ．}0|{<x x 2．已知复数满足：i z i -=+1)2(，其中i 是虚数单位，则z 的共轭复数为（）A ．i 5351-B ．i 5351+C ．i -31D ．i +313．ABC ∆三内角C B A ,,的对边分别为c b a ,,,则“b a >”是“B A 2cos 2cos <”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．即不充分也不必要条件4．如图，四边形OABC 是边长为2的正方形，曲线段DE 所在的曲线方程为1=xy ，现向该正方形内抛掷1枚豆子，则该枚豆子落在阴影部分的概率为（）A ．42ln 23-B ．42ln 21+C ．42ln 25-D ．42ln 21+-5．阅读如图所示的程序框图，运行相应程序，则输出的x 值为（）A ．0B ．1C ．16D ．326．某几何体的三视图如图所示，则该几何体的体积是（）A ．12B ．16C ．332D ．247．函数||log |1|1)(x x x x f a ++=（10<<a ）的图象的大致形状是（）8．已知函数)sin()(ϕω+=x x f （2||,0πϕω<>）图象相邻两条对称轴之间的距离为2π，将函数)(x f y =的图象向左平移3π个单位后，得到的图象关于y 轴对称，那么函数)(x f y =的图象（）A. 关于点)0,12(π对称B. 关于点)0,12(π-对称C. 关于直线12π=x 对称 D. 关于直线12π-=x 对称9．在ABC ∆中，点D 是边BC 上任意一点，M 是线段AD 的中点，若存在实数λ和μ，使得μλ+=，则=+μλ（）A ．21B ．21-2 C ．2 D ．2- 10．在锐角ABC ∆中，B A 2=，则AC AB的取值范围是（）A ．)3,1(-B ．)3,1(C ．)3,2(D ．)2,1(11．已知实数y x ,满足⎪⎪⎪⎩⎪⎪⎪⎨⎧≥--≥≤x y x y x y 32)1(32，则1+x y 的最大值为（）A ．52B ．92C ．136D ．2112．已知函数)0(4)(>+=x x x x f ，P 是)(x f y =图象上任意一点，过点P 作直线x y =和y 轴的垂线，垂足分别为B A ,，又过点P 作曲线)(x f y =的切线，交直线x y =和y 轴于点H G ,.给出下列四个结论：①||||PB PA ⋅是定值；②⋅是定值；③||||OH OG ⋅（O 是坐标原点）是定值；④⋅是定值.其中正确的是（）A ．①②B ．①③C ．①②③D ．①②③④ 二、填空题（每题4分，满分20分，将答案填在答题纸上）13．如果nx x )13(-的展开式中各项系数之和为128，则展开式中41x 的系数是 . 14．设抛物线y x 42=的焦点为F ，点B A ,在抛物线上，且满足λ=，若23||=，则λ的值为 .15．已知由样本数据点集合}.,2,1|),{(n i y x i i =求得的回归直线方程为5.05.1ˆ+=x y ，且3=x .现发现两个数据点)1.2,1.1(和)9.7,9.4(误差较大，去除后重新求得的回归直线l 的斜率为1.2，那么，当2=x 时，y 的估计值为 .16．祖暅是我国南北朝时期杰出的数学家和天文学家祖冲之的儿子，他提出了一条原理：“幂势既同幂，则积不容异”.这里的“幂”指水平截面的面积，“势”指高.这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体体积相等.一般大型热电厂的冷却塔大都采用双曲线型.设某双曲线型冷却塔是曲线12222=-b y ax )0,0(>>b a 与直线0=x ，0=y 和b y =所围成的平面图形绕y 轴旋转一周所得，如图所示.试应用祖暅原理类比求球体体积公式的方法，求出此冷却塔的体积为 .三、解答题（本大题共6题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．已知公差不为0的等差数列}{n a 的首项21=a ，且1,1,1421+++a a a 成等比数列.（1）求数列}{n a 的通项公式；（2）设11+=n n n a a b ，*N n ∈，nS 是数列}{n b 的前n 项和，求使193<n S 成立的最大的正整数n .18．如图，四边形ABCD 是矩形，沿对角线AC 将ACD ∆折起，使得点D 在平面ABC 上的射影恰好落在边AB 上.（1）求证：平面⊥ACD 平面BCD ；（2）当2=AD AB时，求二面角B AC D --的余弦值.19．某市有两家共享单车公司，在市场上分别投放了黄、蓝两种颜色的单车，已知黄、蓝两种颜色的单车的投放比例为2：1.监管部门为了了解两种颜色的单车的质量，决定从市场中随机抽取5辆单车进行体验，若每辆单车被抽取的可能性相同.（1）求抽取的5辆单车中有2辆是蓝色颜色单车的概率；（2）在骑行体验过程中，发现蓝色单车存在一定质量问题，监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测，并规定若抽到的是蓝色单车，则抽样结束，若抽取的是黄色单车，则将其放回市场中，并继续从市场中随机地抽取下一辆单车，并规定抽样的次数最多不超过n （*N n ∈）次.在抽样结束时，已取到的黄色单车以ξ表示，求ξ的分布列和数学期望.20．已知直线1l ：x y 33=，2l ：x y 33-=，动点B A ,分别在直线1l ，2l 上移动，32||=AB ，M 是线段AB 的中点.（1）求点M 的轨迹E 的方程；（2）设不经过坐标原点O 且斜率为k 的直线l 交轨迹E 于点Q P ,，点R 满足OQ OP OR +=，若点R 在轨迹E 上，求四边形OPRQ 的面积.21．已知函数x b ax x x f ln )(2++=，曲线)(x f y =在点))1(,1(f 处的切线方程为x y 2=. （1）求a 和b 实数的值；（2）设)()()(2R m mx x x f x F ∈+-=，)0(,2121x x x x <<分别是函数)(x F 的两个零点，求证0)('21<x x F .请考生在22、23二题中任选一题作答，如果都做，则按所做的第一题记分.22．选修4-4：坐标系与参数方程已知在极坐标系中，点)6,2(πA ，)32,32(πB ，C 是线段AB 的中点，以极点为原点，极轴为x 轴的正半轴，并在两坐标系中取相同的长度单位，建立平面直角坐标系，曲线Ω的参数方程是⎩⎨⎧+-==θθsin 22cos 2y x （θ为参数）.（1）求点C 的直角坐标，并求曲线Ω的普通方程；（2）设直线l 过点C 交曲线Ω于Q P ,两点，求⋅的值. 23．选修4-5：不等式选讲已知|12|)(++-=x x x f ，不等式2)(<x f 的解集是M . （1）求集合M ；（2）设M b a ∈,，证明：||||1||2b a ab +>+. 2018年安庆市高三模拟考试（二模）数学试题（理）参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 选项 DBCABBCABDCC1．【解析】因为{}1101B x x x x x ⎧⎫=<=<>⎨⎬⎩⎭或，所{}0A B x x =<.故选D.2．【解析】. (2i)1iz +=-1i (1i)(2i)2i 5z ---==+13i 55=-，所以z 的共轭复数为13i 55+.故选B.3.【解析】根据二倍角公式、正弦定理可得22cos 2cos 212sin 12sin A B A B <⇔-<-22sin sin sin sin A B A B ⇔>⇔>a b ⇔>.故选C.4.【解析】根据条件可知，122E ⎛⎫ ⎪⎝⎭，，阴影部分的面积为()2211221112d 2ln 22ln 2ln 32ln 222x x x x ⎛⎫⎛⎫⎛⎫-=-=---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰，所以，豆子落在阴影部分的概率为42ln 23-.故选A.5.【解析】0110x t k ===，，；228x t k ===，，；1636x t k ===，，；144x t k ===，，.故选B.6.【解析】该几何体的直观图如图所示，其体积为12222222162⨯⨯+⨯⨯⨯⨯=（3cm ）.故选B.7.【解析】()()log 11()log log 101log 0.a a a ax x x f x x x x x x x --<-⎧⎪+==--<<⎨+⎪>⎩，，，，，故选C.8.【解析】由函数()y f x =图象相邻两条对称轴之间的距离为π2可知其周期为π，所以2π2πω==，所以()()sin 2f x x ϕ=+.将函数()y f x =的图象向左平移π3个单位后，得到函数第4题图第6题图第9题图数学试题（理）参考答案（共11页）第1页πsin 23y x ϕ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦图象.因为得到的图象关于y 轴对称，所以ππ2π32k ϕ⨯+=+，z k ∈，即ππ6k ϕ=-，z k ∈.又π2ϕ<，所以π6ϕ=-，所以π()sin 26f x x ⎛⎫=- ⎪⎝⎭，其图象关于点π012⎛⎫ ⎪⎝⎭，对称. 故选A. 9. 【解析】因为点D 在边BC 上，所以存在R t ∈，使得()BD tBC t AC AB==-.因为M 是线段AD 的中点，所以()()()111112222BM BA BD AB t AC t AB t AB t AC =+=-+-=-++又BM AB AC λμ=+，所以()112t λ=-+，12t μ=，所以12λμ+=-. 故选B.10.【解析】 sinB )3sin(sin sin B B C AC AB -==π2sin 33-4sin sinB BB==.因为ABC ∆是锐角三角形，所以()π02π022π0π22B B B B ⎧<<⎪⎪⎪<<⎨⎪⎪<-+<⎪⎩，，，得ππ64B <<211sin ()42B ⇒∈，.所以234sin (12)AC ABB =-∈，.故选D.11. 【解析】作可行域，如图阴影部分所示.1yx +表示可行域内的点()x y ，与点()10-，连线的斜率. 易知1142A ⎛⎫ ⎪⎝⎭，，1123B ⎛⎫ ⎪⎝⎭，，9342C ⎛⎫⎪⎝⎭，.第11题图当直线()1y k x =+与曲线y =12k =，切点为()11，，所以切点位于点A 、C 之间.因此根据图形可知，1y x +的最大值为12.故选C.数学试题（理）参考答案（共11页）第2页拓展：思考：如何求2122y x y x ++++的取值范围呢？答案：134[,]205更一般地，当直线1111:0l a x b y c ++=，2222:0l a x b y c ++=的交点不在可行域内时，111222a x b y c m ax by c ++=++的取值范围均能求出。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018年安庆市高三模拟考试（二模）语文试题本试卷共10页，22题。

全卷满分150分，考试用时150分钟。

祝考试顺利注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案的标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

在率先掌握铜冶炼技术之后，华夏民族逐渐发展出闪烁着民族文化精神和鲜明美学特质的金属艺术。

金属艺术熔炼着民族历史。

《左传》记述，夏朝君主夏启令九州牧贡献青铜铸鼎，刻以各州形胜之地和奇异之物，以一鼎象征一州，于是九州定鼎成为夏王问鼎天下的标志。

金属艺术凝聚着技术进步。

汉代长信宫灯不仅外观精美雅致，更是一件科学性、艺术性与实用性高度结合的艺术作品：灯壁可开合转向，以调节灯光的强弱和方向；灯烟经执灯宫女铜像右臂进入中空的体内，再进入盛水的灯座中，避免污染空气。

精美绝伦的制作工艺和巧妙独特的艺术构思令人叹为观止。

金属艺术也承载着一文化交流。

唐代鎏金舞马衔杯银壶就是不同民族文化交融的物证。

汉代丝绸之路带来中亚和西亚的金银器加工技术，与中原的技法交流融合，在唐代达到新的高度。

得益于精湛的揲探技法，银壶上骏马的细节才能表现清晰，口鼻眼的轮廓、躯干的肌肉线条都历历可见，形象呼之欲出。

而皮囊形的壶身，显然是借鉴了游牧民族的器物形制。

能工巧匠们萃取了各民族的艺术精华，创造出国宝级艺术珍品。

随着时间推移和社会发展，我国古代金属艺术的工艺技巧日趋精湛，作品更加注重装饰性，强调复杂的手工技法，艺术风格越来越华丽繁复。

加之金属属于贵重材质，特别是黄金和白银是古代稀有的材料，用金银等加工制成的金属艺术品，更是华美珍贵的质料与精致繁复的技艺的结晶，具有市场和艺术的双重价值。

工业革命的兴起推动世界的现代化进程，科技的飞速进步、机械化大生产的普及使得各类金属制品进入寻常百姓家，通信的发达和国际交往的频繁使得东西方艺术风格交流碰撞，追求简洁、几何化的现代审美风格逐渐风靡。

而对于传统手工艺价值的反思和对非物质文化遗产的保护也随之兴起，当代金属艺术在手工艺与机械工艺的碰撞之下应运而生。

当代金属艺术一方面重视体现传统手工艺的审美价值，强调与自然的和谐、对非完美的宽容、对过程的展示和对感性的释放；另一方面不断汲取机械工艺的优长，将新材料、新技术引入金属艺术创作，使金属艺术创作的材质从传统拓展到各类合金乃至综合材料，金属艺术工艺从传统发展到先进机械工艺乃至3D打印等。

从这个意义上来讲，当代金属艺术上承民族传统工艺的精神，下启独立审美表达、先进工艺技术与国际融合创新的木来。

（节选自王晓昕《熔古铸今话金工》，有删改）1．下列关于原文内容的理解和分析，正确的一项是（3分）A．夏启命令九州牧贡献青铜铸鼎，于是一鼎象征九州就成为夏王统治天下的标志。

B．汉代长信宫灯外观精美雅致，它的制作工艺和独特艺术构思至今仍然无法企及。

C．唐代鎏金舞马衔杯银壶萃取各个民族的艺术精华，它属于我国国宝级艺术珍品。

D．古代只有用金银加工制成的艺术品，才算质料华美珍贵与技艺精致繁复的结晶。

2．下列对原文论证的相关分析，不正确的一项是（3分）A．文章阐明了金属艺术发展意义，即熔炼民族历史、凝聚技术进步与承载文化交流。

B．文章概括了我国古代金属艺术特征，指出工业革命兴起促进当代金属艺术的诞生。

C．文章分析了当代金属艺术的两大特征，既体现传统工艺价值又汲取机械工艺优长。

D．文章先举例论证，继而对比论述古今金属艺术，最后进一步地论述当代金属艺术。

3．根据原文内容，下列说法不正确的一项是（3分）A．如果没有率先掌握铜冶炼技术，华夏民族发展独特的金属艺术就失去源头。

B．如果没有丝绸之路带来文化交流融合，唐代金属艺术就很难达到新的高度。

C．我国古代金属艺术追求作品装饰与技法复杂精湛，所以风格愈趋华丽繁复。

D．当代金属艺术创作只因引入新材料与新技术，所以其发展突破了传统限制。

（二）文学类文本阅读（本题共3小题，14分）阅读下面的文字，完成4～6题。

攀高亲蒋平“新来的唐市长是江村当年的放牛娃啊！”虽然是小道消息，但在大学生都没出过一个的小江村，不亚于发生了一场七级地震。

最先从电视里发现这个秘密的是村里的鳏夫铁葫芦：“就是三十年前，咱们村里的二愣。

当年，他爸妈过世，无依无靠的，出去乞讨前，还从我摊担里拿过两块灶糖呢！”“你那么肯定他就是二愣？没准弄错了吧。

”“千真万确，二愣那模样，化成灰我也认得！”不光是铁葫芦，村里上了年纪的老人，都跟着作了证实。

小江村出了个市长！消息不胫而走，不光是村里，乡里和县里也认为是特大喜讯。

不过，接下来的消息让大伙无论如何也喜不起来了：据内线考证，唐市长档案里的籍贯可不是小江村。

有人对铁葫芦的记忆表示怀疑，铁葫芦这边呢，则以脑袋担保，并声称可以带领大伙前去市里朝见，当面攀上这个高亲。

这的确是个好办法。

不过，唐市长眼下正率团去香港招商，只能等他回来了。

这段时间，铁葫芦成了县乡各级领导关照的重点，每日里迎来送往，觥筹交错。

村里甚至有人张罗着要将最漂亮的寡妇介绍给他续房，铁葫芦就这样完成了身份的巨变。

举起酒杯的时候，似乎自己就成了市长的代言人，只消他开口表达，唐市长就会乖乖地在县乡的联合报告上签字，一大笔扶助资金立马手到擒来。

一个星期后，唐市长终于回来了。

县长、乡长这边也准备停当，一帮人浩浩荡荡杀到市政府，把保安吓了一大跳，以为是来上访闹事的。

后一听说是唐市长的家乡人，态度马上来了180度的大转弯。

唐市长这边呢，见到这一大帮家乡人，连连摇头：“你们可能是弄错了，我不是小江村的，也不是那个什么二愣，我父母还健在呢！”面对满口酒气，大讲灶糖往事的铁葫芦，唐市长更是一脸莫名其妙：“您老人家可能是认错人了，我小时候闹牙疼，家里从来不让我吃糖的！”唐市长不认帐，县长和乡长精心准备的要钱报告便没有递上去。

碰了一鼻子灰，走出市政府大门，县乡二长的脸色都很难看。

只有铁葫芦一脸的不在乎：“他妈的，真是一年土，两年洋，三年四年不认爹和娘。

当个市长有什么了不起，退了休，还不如咱平民老百姓呢！”返回县城的时候，司机顺路叫上了在市里做生意的小姨子，小车坐不下了。

乡长就一脸歉意地对铁葫芦说：“老叔，对不住了，小车没座位了，你是不是自个想点办法……”话音未落，铁葫芦登时眉毛倒竖：“我才坐不惯你们的车呢。

告诉你们，唐市长是二愣绝对没错，刚才是见你们人多，不好意思说。

等着瞧吧，我马上让他用小车送我，比你们还先到家……”大伙都没说话，心头的闷气积得比铁葫芦还重。

最后是县长开了口：“无凭无据的，咱们这一堆大活人，凭啥被一个疯子玩得团团转呢？”乡长涨红了脸：“这老儿以前不疯的。

唉，我当初的想法，是宁肯信其有，不可信其无。

万一他说的是实话，岂不令我们措手不及！”“什么事实！纯粹一个疯子！”县长说。

“疯子！”一车人随声附和。

乡长不吱声了。

不过，铁葫芦回到村里后像是真的疯了。

每日里有人见他喝得醉醺醺的，然后站在村口的大樟树下恨恨连声，骂着唐市长：“他妈的，臭小子才当了几天官，就六亲不认了，我那两块灶糖真是送给狗吃了！”（节选自《文艺生活》，有删改）4．下列对小说相关内容和艺术特色的分析鉴赏，不正确的一项是（3分）A．“小江村出了个市长“的消息引起村民热议和县乡两级领导高度重视，家乡官民决定前去攀高亲，这说明当今社会上仍存在着市侩习气。

B．铁葫芦因当年给过二愣两块灶糖，得到县乡领导和村人礼待，在众人热捧中不免飘飘然起来，这表明他是个盲目自信且有政治野心的人。

C．家乡官民轰轰烈烈地去找唐市长，却遭遇市长不认乡亲，于是寻求扶助资金的愿望只能落空，情节的前后逆转增强了小说的幽默讽刺性。

D．小说运用语言、行为、神态等描写手法，生动地刻画了人物形象，如乡长借口拒绝铁葫芦乘车时所说的一番话，就表现了乡长虚伪势利。

5．小说以“攀高亲”为标题，有哪些作用？请简要说明。

（5分）6．小说以铁葫芦回村后好像是“真疯了”结尾，这样设计有怎样的艺术效果？请结合作品进行分析。

（6分）（三）实用类文本阅读（本题共3小题，12分）阅读下面的文字，完成7～9题。

材料一：2014年在人们逐渐习惯了用手机叫车的时候，移动支付也悄然走入大众视野——用手机结算车费比现金方便许多。

而从用户体验角度来看，我国移动支付软件的优势远不止“便捷”这一点。

社交性强是许多人对我国移动支付软件的直观感受。

美国乔治亚理工学院的中国留学生程文杰感慨于微信红包的“贴心。

微信支付将技术和传统习俗结合起来，让用户在和钱打交道时，不忘人情温暖。

中国人民大学的韩国学生李在城最欣赏移动支付的安全性。

“信用卡在你手里，也存在被盗刷的风险；相比而言，只要管住手机，移动支付就比较安全。

”移动支付的安全性离不开中国自主研发技术的保驾护航。

在智能实时风控系统的保护下，目前支付宝的交易资损率为百万分之一，远低于国际领先支付机构万分之十七的风险水平。

（摘编自刘少华、顾桥孜《移动支付是信息时代中国的“弯道超车”》）材料二：注：2017年第2季度，在余额宝交易规模继续高速增长的带动下，支付宝金融类业务交易规模继续保持高速增长。

受益于对线下扫码业务的持续投入，支付宝消费类业务和个人转账类业务的交易规模均呈现爆发式增长。

加之阿里自有电商业务移动端业务做出的规模贡献，支付宝电商类业务交易规模也保持平稳增幅。

最终，支付宝以53．70%仍然占据头名位置。

（摘编自易观《2017年第2季度第三方支付移动支付交易规模23万亿》）材料三：混血版的支付宝钱包、微信钱包正在竞速。

2016年10月，李嘉诚旗下的长江和记与蚂蚁金服宣布共同运营电子钱包“支付宝HK”。

几乎是同时，腾讯公司旗下“微信支付HK”团队也在港宣布推出了3项升级支付功能，让消费者可通过微信扫描二维码完成线上线下、不同消费场景的支付，从而给市民生活带来便利。

许多国家和地区的支付机构提前几个月，就联合支付宝升级自己的在线支付网络。

2016年11月，蚂蚁金服与泰国支付企业签订战略合作协议，将蚂蚁的普惠金融模式复制到泰国。

2017年10月，蚂蚁金服投资的韩国移动支付公司Kakao Pay用户数突破2000万，72%的韩国就业人口在用。

在芬兰，支付宝与当地最大的电子钱包ePassi开展合作。

ePassi服务本地个人用户约70万，占该国总人口的近14%。

（摘编自陈莹莹《移动支付出海：混血版钱包成抢滩先锋》）材料四：目前，支付宝已遍布海外，北上芬兰，南下澳大利亚，通过技术出海的方式，与当地合作伙伴共同打通本地移动支付市场。

来自中国的移动支付技术，带给海外的不只是支付方式的改变，更是对当地社会方方面面的深远影响。