天津大学物理化学第五版-第四章-多组分系统热力学
合集下载
《物理化学》考点精讲(第4讲 多组分系统热力学)
第4讲多组分系统热力学《物理化学》考点精讲教程（天津大学第五版）主讲人：张彩丽网学天地《物理化学》（天大第五版）考点精讲教程第4讲多组分系统热力学4.1 偏摩尔量4.2 化学势4.3 气体组分的化学势4.4 逸度及逸度因子4.5 拉乌尔定律和亨利定律4.6 理想液态混合物4.7 理想稀溶液4.8 活度及活度因子4.9 稀溶液的依数性《物理化学》（天大第五版）考点精讲教程一、偏摩尔量二、偏摩尔量的测定法举例三、吉布斯−杜亥姆方程四、偏摩尔量之间的关系4.1 偏摩尔量《物理化学》（天大第五版）考点精讲教程结果：恒温、恒压下混合后，混合物的体积不等于混合前纯组分体积之和：**B m,B C m,CV n V n V ≠+原因：①水分子之间、乙醇分子之间和水分子与乙醇分子之间的分子间相互作用不同；②水分子与乙醇分子体积及形状不同。
对所有广度量X 均存在同样的结果:B BBX n X ≠∑*一、偏摩尔量《物理化学》（天大第五版）考点精讲教程（4）偏摩尔量：X ⎛⎞∂《物理化学》（天大第五版）考点精讲教程B VV ⎛⎞∂《物理化学》（天大第五版）考点精讲教程《物理化学》（天大第五版）考点精讲教程二、偏摩尔量的测定法举例以二组分系统偏摩尔体积测定为例：三、吉布斯恒温、恒压《物理化学》（天大第五版）考点精讲教程《物理化学》（天大第五版）考点精讲教程因此：B B B d =0n X ∑B B Bd =0x X ∑或此即吉布斯−杜亥姆方程。
该方程指出，系统中各组分的偏摩尔量并非完全独立，而是相互依存的。
在恒温、恒压下，当混合物的组成发生微小变化时，如果一组分的偏摩尔量增大，则另一组分的偏摩尔量必然减小，且增大与减小的比例与混合物中两组分的摩尔分数（或物质的量）成反比。
《物理化学》（天大第五版）考点精讲教程《物理化学》（天大第五版）考点精讲教程4.2 化学势一、化学势的定义二、多相多组分系统的热力学基本方程三、化学势判据及应用举例《物理化学》（天大第五版）考点精讲教程,,C defB B B T p n G G n μ⎛⎞∂⎜⎟===⎜⎟⎝⎠∂纯物质的化学势即为其摩尔吉布斯函数：B m, B G μ=*化学势是最重要的《物理化学》（天大第五版）考点精讲教程二、多相多组分系统的热力学基本方程μ+Vd况；不仅能应用于变组成的封闭系统，也适用于开放系统。
第4章 多组分系统热力学1(天津大5版)
系统热力学平衡的决定因素
系统热力学平衡－－热平衡、力平衡、相平衡和 化学平衡 T决定热平衡 p决定力平衡
µ决定系统的相平衡和化学平衡
§4.3 气体组分的化学势
气体标准态： pӨ＝100kPa、具有理想气体性质 的纯气体。 气体B在标准态下的化学势称为该气体的标准化 学势μӨ，它只是温度的函数。
1. 纯组分理想气体的化学势
2. 多相多组分系统的热力学基本方程
（1）单相多组分系统 ）
G = G (T , p, nB, nC L)
可得 : ∂G ∂G ∂G dG = dT + dp + ∑ dnB ∂T p.nB ∂nB T . P.nC ∂p T .nB
偏摩尔量XB
VB = (∂V
UB = (∂U
∂nB
)T , p , nc
)T , p , nc
B物质的偏摩尔体积 物质的偏摩尔体积 B物质的偏摩尔热力学能 物质的偏摩尔热力学能 B物质的偏摩尔焓 物质的偏摩尔焓 B物质的偏摩尔熵 物质的偏摩尔熵 B物质的偏摩尔亥姆霍兹函数 物质的偏摩尔亥姆霍兹函数 B物质的偏摩尔吉布斯函数 物质的偏摩尔吉布斯函数
多组分单相系统的热力学公式
dU = TdS − pdV + ∑ µ BdnB
B
dH = TdS + Vdp + ∑ µ BdnB
B
dA = − SdT − pdV + ∑ µ BdnB
B
dG = − SdT + Vdp + ∑ µ BdnB
B
（2）多相多组分系统
dU = TdS − pdV + ∑∑ µ B (α ) dnB (α )
物理化学：第4章_多组分系统热力学_
Vm*,B Vm*,C Vm*,B xC
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
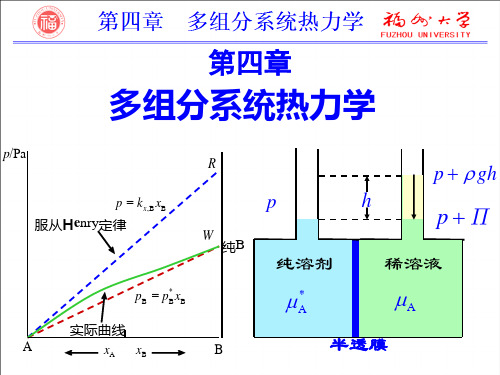
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
第四章 多组分系统热力学——【天津大学 物理化学 精】
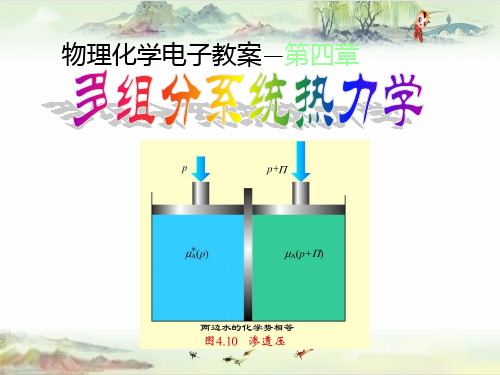
U nBUB B
H nBHB B
A nB AB
B
S nBSB B
G nBGB B
U
UB
( nB
)T , p,nc
HB
( H nB
)T , p,nc
A
AB
( nB
)T , p,nc
S
SB
( nB
)T , p,nc
G GB ( nB )T , p,nc
=B
化学势
3. 偏摩尔量的测定法举例
cm3mol-1；VBV,2A = V
2 n5BV.B340
nA
cm3mol-1
根据加合公式 V = nAVA+ nBVB
得：
由此可得，在两种溶液中H2O的偏摩尔体积分别为 VA=18.067 cm3mol-1；VA=18.045 cm3mol-1
2020/9/23
§4.2 化学势
化学势的定义
保持温度、压力和除B以外的其它组分不变， 体系的Gibbs自由能随nB的变化率称为化学势，所以 化学势就是偏摩尔Gibbs自由能。
T ,
p , nC
dnB
G S T p,nB
G p
T
,nB
V
G nB
T , p,nC
B
2020/9/23
同理
dG SdT Vdp BdnB B
dU TdS pdV BdnB B
dH TdS Vdp BdnB B
dA SdT pdV BdnB B
单相多组分系统 热力学基本方程
( nB
)T
, p,nC
若体系仅有一种组分(即纯物质)，则根据摩尔量 的定义，XB就是摩尔量。
2020/9/23
物理化学 第四章 多组分系统热力学
Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B，C形成真实液态混合物： 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时，两组分的偏摩尔体积可用下法表示： 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线，此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB，VC。
B
系统中各广度量的偏摩尔量： 对于多组分系统中的组分B，有： 偏摩尔体积： VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能： UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓： HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵： SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数：AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数： GB=(ƽG/ƽnB)T,p,n
C
几点说明： (1)偏摩尔量为两个广度性质之比，所以为强度 性质； (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下，偏导数式的下标为T，p 时才是偏摩尔量； (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中，偏摩尔量不同； (4)若系统为单组分系统，则该组分的偏摩尔量 与该组分的摩尔量相等，即： XB=X*B，m
C
=VB (数学知识：二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势，用符号μB表示：
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质，其化学势等于它的摩尔吉布斯函 数。
物理化学(天津大学第五版)第一~五章总结
第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的，与压力、温度的关系。
解：根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结，泡内密封着标准状态下的空气。
若将其中的一个球加热到100 ︒C，另一个球则维持0 ︒C，忽略连接细管中气体体积，试求该容器内空气的压力。
解：由题给条件知，（1）系统物质总量恒定；（2）两球中压力维持相同。
标准状态：因此，1.9 如图所示，一带隔板的容器内，两侧分别有同温同压的氢气与氮气，二者均可视为理想气体。
（1）保持容器内温度恒定时抽去隔板，且隔板本身的体积可忽略不计，试求两种气体混合后的压力。
（2）隔板抽取前后，H2及N2的摩尔体积是否相同？（3）隔板抽取后，混合气体中H2及N2的分压立之比以及它们的分体积各为若干？解：（1）等温混合后即在上述条件下混合，系统的压力认为。
（2）混合气体中某组分的摩尔体积怎样定义？（3）根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气，为进行实验时确保安全，采用同样温度的纯氮进行置换，步骤如下：向釜内通氮气直到4倍于空气的压力，尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解：分析：每次通氮气后至排气恢复至常压p，混合气体的摩尔分数不变。
设第一次充氮气前，系统中氧的摩尔分数为，充氮气后，系统中氧的摩尔分数为，则，。
重复上面的过程，第n次充氮气后，系统的摩尔分数为，因此。
1.13 今有0 ︒C，40.530 kPa的N2气体，分别用理想气体状态方程及van der Waals方程计算其摩尔体积。
实验值为。
解：用理想气体状态方程计算用van der Waals计算，查表得知，对于N2气（附录七），用MatLab fzero函数求得该方程的解为也可以用直接迭代法，，取初值，迭代十次结果1.16 25 ︒C时饱和了水蒸气的湿乙炔气体（即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压）总压力为138.7 kPa，于恒定总压下冷却到10 ︒C，使部分水蒸气凝结为水。
天津大学版物理化学课件第四章
即稀溶液中溶剂蒸气压下降值Δp与纯溶剂蒸气压之 比等于溶质的摩尔分数,而与溶质种类无关。 表4.4.1以甘露蜜醇的水溶液为例,列出了不同浓度下溶剂 蒸气压下降的实验值与拉乌尔定律的计算值。可以看出， 在所测的浓度范围内两者是很一致的。
表4.4.1 甘露蜜醇水溶液的蒸气压下降值(20℃)
溶质的摩尔分 数 103xB 1.769 蒸气压下降值△p/Pa 实验值 计算值 相对百分误差 %
dG -SdT Vdp B dnB
B
这四个方程时适用于均匀系统的更为普遍的热力学基本 方程，不仅适用于变组成的封闭系统，也适用于开放系 统。在封闭系统内的任一均匀部分（纯物质、混合物或 溶液）中组分B、C等的物质的量发生变化，是由于系统 内部发生了相变化或化学变化引起的。
如果将U、H、A表示成如下函数关系：
4．分配定律:
实验证明:在一定的温度、压力下，当溶质在共存的两互 不相溶液体间成平衡时，若形成的溶液的浓度不大，则 溶质在两液相中的质量浓度比为一常数。这就是能斯特 分配定律。比例系数称为分配系数，符号为K。
K bB ( ) / b( )
(4.6.18)
K是比例系数，称为分配系数。 这一经验定律可以由溶质在α、β两相间达到平衡时化学势 相等得出。
质量摩尔浓 度 b/(mol· -1) kg
0.0984
4.093
4.146
+1.3
0.2962
0.4938 0.6934 0.8913
5.307
8.817 12.34 15.80
12.29
20.48 28.83 37.23
12.41
20.60 28.83 36.95
+1.0
+0.6 0.0 -0.7
物理化学 4 多组分系统热力学
物理化学
Physical Chemistry
河北联合大学
1
of 137
第四章 多组分系统热力学
河北联合大学
2
of 137
经 典 热 力 学 系 统
简单系统
（由纯物质形成的相及组成不变 的平衡系统）
多组分系统
（相组成改变的单相或多相系统）
河北联合大学
3
of 137
多组分系统可为单相或多相。若它为多相的，则可
全部浓度范围内及理想稀溶液在小范围内均有简
单的规律性。 对溶液，将组分区分为溶剂和溶质，对溶质 与溶剂用不同标准态研究；对混合物中任意组分
均选用同样的标准态加以研究。
河北联合大学
7
of 137
混合物（mixture） 多组分均匀体系中，溶剂和溶质不加区分，
各组分均可选用相同的标准态，使用相同的经验
V VB n B T , P ,nC
nC表示，除 B 以 外，其它组分的物质 的量均不变。
除了体积，其它广度量也有偏摩尔量。
河北联合大学
16 of 137
2.偏摩尔量：
在由组分 B, C, D…形成的混合系统中，任一广度量 X 是T, p , nB , nC , nD , …的函数，即：
20 of 137
河北联合大学
应当指出， 1）只有广度量才有偏摩尔量，强度量是不存在偏摩尔量的。 2）只有恒温恒压下，系统的某一广度量随某一组分的物质 的量的变化率，才能称为偏摩尔量，任何其它条件下的变化率 均不称为偏摩尔量。
G 例：尽管 A n n B T ,V ,nC B T , p ,nC
4.1.5b
积分得:
dX X
Physical Chemistry
河北联合大学
1
of 137
第四章 多组分系统热力学
河北联合大学
2
of 137
经 典 热 力 学 系 统
简单系统
（由纯物质形成的相及组成不变 的平衡系统）
多组分系统
（相组成改变的单相或多相系统）
河北联合大学
3
of 137
多组分系统可为单相或多相。若它为多相的，则可
全部浓度范围内及理想稀溶液在小范围内均有简
单的规律性。 对溶液，将组分区分为溶剂和溶质，对溶质 与溶剂用不同标准态研究；对混合物中任意组分
均选用同样的标准态加以研究。
河北联合大学
7
of 137
混合物（mixture） 多组分均匀体系中，溶剂和溶质不加区分，
各组分均可选用相同的标准态，使用相同的经验
V VB n B T , P ,nC
nC表示，除 B 以 外，其它组分的物质 的量均不变。
除了体积，其它广度量也有偏摩尔量。
河北联合大学
16 of 137
2.偏摩尔量：
在由组分 B, C, D…形成的混合系统中，任一广度量 X 是T, p , nB , nC , nD , …的函数，即：
20 of 137
河北联合大学
应当指出， 1）只有广度量才有偏摩尔量，强度量是不存在偏摩尔量的。 2）只有恒温恒压下，系统的某一广度量随某一组分的物质 的量的变化率，才能称为偏摩尔量，任何其它条件下的变化率 均不称为偏摩尔量。
G 例：尽管 A n n B T ,V ,nC B T , p ,nC
4.1.5b
积分得:
dX X
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
G ( ) T , nB V B p
B ( ) T , x VB p
B ( ) T Vm ,B p
结论：几种纯液体在恒温恒压下，混合成理想液态混合物时，混合前 后系统的体积不变。
（ 2）
mix H 0
结论：几种纯液体在恒温恒压了混合成理想液态混合物时，混合前 后系统的焓不变，因而混合（焓）热等于零。
4．偏摩尔量与摩尔量的差别 [1]若B，C形成理想混合物 V*m，B和V*m，C为两纯液体的摩尔体积
Vm～xc作图得一条直线（见图中虚线） 截距：V*m，B 斜率：V*m，C－V*m，B
[2]若B，C形成了真实混合物 Vm～xc作图得一条曲线（见图中实线） 过d作Vm～xc曲线的切线，此切线在纵坐标轴上的 截距为该组成下两组分的偏摩尔体积VB，Vc
>0 非自发过程
化学势判据
★
3、化学势判据及应用举例 在恒温恒压下，若系统中存在有多相（α，β…），多组分（B，C …） 则：
dG dG dG
dn dn B B B B dn B B
B B B
<0 自发过程 =0 平衡状态
由享利定律可知，当溶质、溶剂和温度都一定时，亨利常数就为定值， 气体的分压越大，则该气体在溶液中的溶解度也就越大。所以增加气体的 压力有利于吸收操作。 由下表可知，随温度的升高，k值增大，因而当CO2分压相同时，随 着温度的升高，CO2的溶解度xCO2将下降。反之降低温度，则xCO2的溶解 度将增大，所以低温有利于吸收操作。
3．拉乌尔定律和亨利定律的微观解释 ※拉乌尔定律的微观解释 溶液中加入溶质 B ，单位液面上 A 分子数占液面总分子数的分数从纯 溶剂时的1下降至溶液的xA，致使单位液面上溶剂 A的蒸发速率按比例下降， 溶液中溶剂A的饱和蒸气压也相应地按比例下降。 pA=p*AxA ※亨利定律的微观解释 在溶解平衡时，气相中B在单位表面上的凝结速率与蒸发速率相等，故 气相中B的平衡分压力正比于溶液中B的摩尔分数。
全微分形式：
压力及混合 物中各组分 的物质的量 均不变时， 系统广度量 X 随温度的 变化率
温度及混合 物中各组分 的物质的量 均不变时， 系统广度量 X 随压力的 变化率；
温度、压力及除了组分 B 以外其余各组分的物 质的量均不变时，组分 B的物质的量发生了微 小的变化引起系统广度 量X 随组分B 的物质的 量的变化率。
表示纯液体B（xB=1），在温度T，压力p下的化学势
* B (l )
▲纯液体B的化学势：
▲理想液态混合物中任一分B的化学势：
如何表示纯液体 B在标准状态下（T，P0）的化学势 B (l )
纯液体 B在标准状态下的化学势
0 B ( l ) （T，P ）
纯液体B在T， p下的化学势
* B (l )
恒温恒压下非体积功等于零的条件下： dG
dn B B
B
<0 自发过程 =0 平衡状态 >0 非自发过程
>0 非自发过程
化学势判据
★
★
若此相变化能自发进行 若两相处于相平衡状态
在恒温恒压下，若任一物质B在两相中具有相同的分子形式，但化学势不等，则 相变化自发朝着化学势减少的方向进行；若两相的化学势相等，则两相处于相平 衡状态。
或
恒温、恒压下， 在足够大量的某 一定组成的混合 物中加入单位物 质的量的组分B 时所引起系统广 度量 X的增量
组分B偏摩尔量
●偏摩尔量：在温度、压力及除了组分B以外其余各组分的物质的量均不改 变时，广度量X 随组分B的物质的量nB的变化率XB称为组分B 的偏摩尔量。
注意： ▲纯物质的偏摩尔量等于其摩尔量 ▲只有广度量才有偏摩尔量 ▲只有恒温恒压下系统的广度量随某一组分的物质的量的变 化率才能称为偏摩尔量 ▲偏摩尔量和摩尔量一样，是强度量。
※一定温度、压力下，向物质的量为nc的液体组分C中，不断地加入组分B
※测量加入不同nB时，混合物的体积 V ※V－nB作图 ※过曲线上任一点作曲线的切线，此切线的斜率即为：
V ( )T , p ,nc VB nB
※组分C在此组成下的偏摩尔体积Vc
V nBVB nCVC
V n BVB VC nC
★化学势判据 （恒温恒压） ★气体的化学势 ●理想气体
B
B
dnB
<0 自发过程 =0 平衡状态 >0 非自发过程
总结2
纯
混合物 纯
●真实气体 混合物 ★拉乌尔定律 适用条件：理想液态混合物 或理想稀溶液中的溶剂 pA（溶剂）～ xA ★亨利定律 适用条件：稀溶液中的挥发性溶质 pB（溶质）～ xB
多组分系统热力 xue §4．1 偏摩尔量 1．问题的提出： ★在20℃，纯水的摩尔体积为18.09cm3/mol ，纯乙醇的摩尔体积为cm3/mol 将0.5摩尔的水与0.5摩尔的水混合，溶液体积： V＝（0.5×18.09十0.5×18.09）cm3 =18.09cm3 V nBVm , B nCVm,C 理想混合溶液
⑤拉乌尔定律的微观解释 溶液中加入溶质B，单位液面上A分子数占液面总分子数的分数从纯溶 剂时的1下降至溶液的xA，致使单位液面上溶剂A的蒸发速率按比例下降， 溶液中溶剂A的饱和蒸气压也相应地按比例下降。
2．亨利定律 ①定律： 一定温度下，稀溶液中挥发性溶质在气相中的平衡分压与其在溶液中 的摩尔分数（或质量摩尔浓度、物质的量浓度）成正比
恒温恒压下液体混合过程的吉布斯函数变△mixG＜0，说明混合过程 为自发过程。
§4．6
1．溶剂的化学势
理想稀溶液
理想稀溶液(无限稀薄溶液):溶质的相对含量趋于零的溶液。
T一定，若与理想稀溶液成平衡的气体为理想气体混合物， 溶剂遵循拉乌尔定律， 溶剂A的化学势:
§ 4． 2
化学势
化学势：混合物（或溶液）中组分B的偏摩尔吉布斯函数GB称之
1．多组分单相系统的热力学公式 若： 则：
更为普遍的热力学基本方程 适用条件：均匀（单相）系统
若U、H、A将表示成如下函数关系
比较可得：
偏摩尔量
2．多组分多相系统的热力学公式 对多组分多相系统中的α、β…每一个相，有
对系统内所有的相求和 因各相的T，p均相同
故组成a的系统的体积： 混合物的组成改变时:※ 两组分的偏摩尔体积也在改变 ※ 组成越接近某一纯组分时，该组分的偏摩尔体积 也就越接近于该纯组分的摩尔体积；
5．吉布斯一杜亥姆方程 T，p一定时， 对此式求全微分： 故必然有： 吉布斯—杜亥姆方程 偏摩尔的集合公式 已知
若为二组分混合物，则有 xBdXB＋xcdXC=0
①定律 稀溶液中溶剂的蒸气压等于同一温度下纯溶剂的饱和蒸气压与溶液 中溶剂的摩尔分数的乘积。 ②数学表达式
p*A：纯溶剂的饱和蒸气压 pA ：溶液中溶剂的饱和蒸气压 xA ： 溶液中溶剂的摩尔分数
③适用条件：理想液态混合物
或理想稀溶液中的溶剂 ④注意： 适用于溶液达气液平衡的体系
pA =气相中溶剂组分的分压
③对于其他热力学性质如H、G、S、
U等亦有类似情况。 ★0.5摩尔的水与0.5摩尔的乙醇混合中， 水 和 乙 醇的 偏 摩 尔体 积 分 别为 VB=17.0cm3/mol，Vc=57.4 cm3/mol， V=（0.5×17. 0＋0.5 ×57.4）cm3=37.2 cm3
2、偏摩尔量 组分B，C，D，…形成的混合系统中，任一广度量X
标准状态下的假想的纯态理想气体
→
压力为p的真实气体
压力为p的理想气体
→
将气体变为p→0的气体
↓
纯真实气体与理想 气体化学势的差别 是由于两者在同样 温度压力下摩尔体 积不同造成的。
↓
4．真实气体混合物中任一组分的化学势
纯 理想气体 混合物
纯 真实气体
混合物
§4 ．4
拉乌尔定律和亨利定律
1．拉乌尔定律
结论：在恒温恒压下，当混合物的组成发生微小 变化时，若一组分的偏摩尔量增大，则另一组分 的偏摩尔量必然减小，且增大与减小的比例与混 合物中两组分的摩尔分数（或物质的量）成反比。
6、偏摩尔量之间的函数关系 热力学函数之间存在有一定的函数关系 ：
H =U＋pV， A =U－TS， G =U＋pV－TS=H－TS=A＋pV 将这些公式 对混合物中 任一组分B 取偏导数， 各偏摩尔量 之间也有着 同样的关系
理想液态混合物中任一分 B的化学势为：
G ( B ) P , nB S B T
( B ) P, x S B T
B ( ) P, x S m ,B T
摩尔混合熵为： 恒压、恒温下液体的混合过程是一个自发过程
恒温下：
混合过程中:
mix H 0
mix G T mix S
（T，P）
当压力从p0变至p时 理想液态混合物中任一组分B的化学势与混合物组成的关系式
p与p0相差不大 忽略积分项
3．理想液态混合物的混合性质 相互混合 纯液体 B(n )
B
纯液体 C( nC) (1)
恒温恒压
理想液态混合物 (n= nB ＋nC)
mixV 0
理想液态混合物中任一分B的化学势为：
●偏摩尔量的集合公式
在恒温恒压条件下， dT=0，dp=0
若按混合物原有组成的比例同时微量地加入组分 B，C，…以形成混合物， 此过程中组成恒定，积分上式：
偏摩尔量的集合公式 表明：在一定温度、压力下，某一组成混合物的任一广度量等于各组分 对应的偏摩尔量与其物质的量的乘积之和
3、偏摩尔量的测定法举例
②数学表达式
pB 挥发性溶质在气相中的平衡分压 xB 挥发性溶质在溶液中的摩尔分数 kx，B 亨利系数