中考数学专题复习 第1讲 走进实数世界课件
合集下载
浙江省中考考点复习数学课件:第1课 实数 (共27张PPT)

考点清单
考点一 实数的分类
实数有理数整分数数正负正0负分分整整数数数数有限自限循然小环数数小或数无
无理数正负无无理理数数无限不循环小数
根据需要,我们也可以按符1,4分 杭州T12,4分 温州T1,4分 绍兴T1,4分 绍兴T3,4分 宁波T1,3分 宁波T5,3分 宁波T13,3分 湖州T1,3分 湖州T15,4分 台州T1,4分 台州T3,4分 台州T7,4分 台州T16,5分 台州T17,8分 衢州T1,3分 衢州T3,3分 衢州T17,6分 义乌T1,3分 义乌T4,3分 义乌T17,6分 金华、丽水T1,3分 金华、丽水T17,6分 嘉兴、舟山T1,4分 嘉兴、舟山T3,4分
近三年浙江中考试题分布
热门考点
2015年
1.实数的分类 2.实数的有关
概念 3.科学记数法、
近似数 4.平方根、算
术平方根、 立方根、无 理数的估算 5.实数的大小 比较 6.实数的运算
杭州T1,3分 杭州T2,3分 杭州T6,3分 温州T1,3分 宁波T1,4分 宁波T3,4分 宁波T13,4分 湖州T1,3分 湖州T3,3分 湖州T11,4分 台州T17,8分 衢州T1,3分 衢州T17,6分 金华T6,3分 金华T11,4分 丽水T1,3分 嘉兴T3,4分 舟山T3,3分 绍兴、义乌T1,4分 绍兴、义乌T2,4分 嘉兴、舟山T1,4分 嘉兴、舟山T6,4分 嘉兴、舟山T17,8分
特别关注 1.区分有理数与无理数,不能只看形式,要看化简的结果.有限小数
和无限循环小数都是有理数,只有无限不循环小数才是无理数. 2.-a 不一定是负数,应根据 a 本身的数值进行综合判断.
【典例 1】 (2015·内蒙古通辽)在实数 tan 45°,3 8,0,-35π, 9,
数学中考一轮复习专题01 实数(课件)

知识点梳理
6.实数的比较大小: (1)性质比较法:
①正数>0>负数; ②两个正数,绝对值大的较大;两个负数,绝对值大的反而 小 ; ③若一组数据中有正数,0,负数,求最大的数时在正数中找,求最小的数时在负数
中找. (2)数轴比较法:数轴上的两个点表示的数,右边的数总比左边的数 大 .
(3)差值比较法:对于任意实数a,b:a-b>0⇔ a>b ;a-b=0⇔ a=b ;a-b<0⇔
的关键.
知识点1 :实数的有关概念
典型例题
【例5】(3分)(2021•通辽1/26)| -2 |的倒数是( )
A.2
B.1
C.-2
D. 1
2
2
【考点】绝对值;倒数
1
【解答】解:| -2 |的倒数是 .
2
故选:B.
【点评】主要考查倒数的定义,要求熟练掌握.需要注意的是倒数的性质:负数的
倒数还是负数,正数的倒数是正数,0没有倒数.倒数的定义:若两个数的乘积是1,
我们就称这两个数互为倒数.
知识点1 :实数的有关概念
典型例题
【例6】(3分)(2021•天津6/25)估计 17 的值在( ) A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
【考点】估算无理数的大小 【分析】本题需先根据 17 的整数部分是多少,即可求出它的范围. 【解答】解:∵ 17 4.12 , ∴ 17 的值在4和5之间. 故选:C. 【点评】本题主要考查了估算无理数的大小,在解题时确定无理数的整数部分即可 解决问题.
3 非负数
掌握非负数的性质,能求某 非负数性质的运用. 些特殊等式中字母的值. 常以选择题、填空题的形式命题.
中考命题说明
6.实数的比较大小: (1)性质比较法:
①正数>0>负数; ②两个正数,绝对值大的较大;两个负数,绝对值大的反而 小 ; ③若一组数据中有正数,0,负数,求最大的数时在正数中找,求最小的数时在负数
中找. (2)数轴比较法:数轴上的两个点表示的数,右边的数总比左边的数 大 .
(3)差值比较法:对于任意实数a,b:a-b>0⇔ a>b ;a-b=0⇔ a=b ;a-b<0⇔
的关键.
知识点1 :实数的有关概念
典型例题
【例5】(3分)(2021•通辽1/26)| -2 |的倒数是( )
A.2
B.1
C.-2
D. 1
2
2
【考点】绝对值;倒数
1
【解答】解:| -2 |的倒数是 .
2
故选:B.
【点评】主要考查倒数的定义,要求熟练掌握.需要注意的是倒数的性质:负数的
倒数还是负数,正数的倒数是正数,0没有倒数.倒数的定义:若两个数的乘积是1,
我们就称这两个数互为倒数.
知识点1 :实数的有关概念
典型例题
【例6】(3分)(2021•天津6/25)估计 17 的值在( ) A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
【考点】估算无理数的大小 【分析】本题需先根据 17 的整数部分是多少,即可求出它的范围. 【解答】解:∵ 17 4.12 , ∴ 17 的值在4和5之间. 故选:C. 【点评】本题主要考查了估算无理数的大小,在解题时确定无理数的整数部分即可 解决问题.
3 非负数
掌握非负数的性质,能求某 非负数性质的运用. 些特殊等式中字母的值. 常以选择题、填空题的形式命题.
中考命题说明
最新人教版数学中考一轮复习第1讲实数的有关概念课件

2.下列四个实数中,是无理数的为( B )
第1讲┃实数的有关概念
点
析
要判断一个数是不是无理数,关键是理解好无理数
的定义,也就是无限不循环小数才是无理数,对于开方数, 则必须是开方开不尽的数。
第1讲┃实数的有关概念
中 考 预 测
1.下列实数中,无理数是( B ) 5 A.- 2 C. 9 A.0 C.-2 B.π D.|-2| B. 3 2 D. 7
第1讲┃实数的有关概念
回 归 教 材
实数的分类
把下列各数填入相应的集合内:
²² 9 2 3 -7.5, 15,4, , , -27,0.31,-π ,0.15。 17 3 ·· 2 3 -7.5,4, , -27,0.31,0.15 3 (1)有理数集合: { …}; 9 15, ,-π 17 (2)无理数集合: { …}; 9 2 ·· 15 , 4 , , , 0.31 , 0.1 5 (3)正实数集合: { …}; 17 3 3 (4)负实数集合: {-7.5, -27,-π …}。
第1讲┃实数的有关概念
解 析 第1行的第1列与第2列差个2,第2列与第3列差个3,第3
列与第4列差个4,…,第6列与第7列差个7;
第2行的第1列与第2列差个3,第2列与第3列差个4,第3列与第4列 差个5,…,第5列与第6列差个7; 第3行的第1列与第2列差个4,第2列与第3列差个5,第3列与第4列 差个6,第4列与第5列差个7;
第1讲┃实数的有关概念
带有计数单位的数,一般要把计数单位化去,再 用科学记数法表示。
第1讲┃实数的有关概念
探究四 创新应用题 命题角度: 1.探究数字规律; 2.探究图形与数字的变化关系. 例4 [2013²湖州] 将连续的正整数按以下规律排列,则位 85 于第7行第7列的数x是________ . 第1列 第2列 第3列 第4列 第5列 第6列 第7列 … 第1行 1 3 6 10 15 21 28 第2行 2 5 9 14 20 27 第3行 4 8 13 19 26 … 第4行 7 12 18 25 … 第5行 11 17 24 … 第6行 16 23 … 第7行 22 … … … … … x …
中考数学第1讲实数及其运算PPT课件
1≤|a|<10,n 是整数),这种记数法叫做科学记数法;一个近似数,_四___舍__五___入到哪
一位,就说这个数精确到哪一位.如:3.14549 精确到 0.01 为___3__.1__5__,精确到
0.001 为___3_._1_4__5_.
4.零指数幂,负整数指数幂
任何一个不等于零的数的零次幂都等于 1,即__a_0_=__1__(_a_≠_0;)任何不等于零的
-
9
1.(2016·金华)如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其
中不合格的是( B)
A.Φ45.02 B.Φ44.9 C.Φ44.98 D.Φ45.01
2.(2016·河南)-13的相反数是( B)
A.-13
1 B.3
C.-3
D.3
-
10
3.(2015·河南)下列各数中最大的数是( A)
A.5 B. 3 C.π D.-8
4.(2016·盐城)下列实数中,是无理数的为( D)
A.-4 B.0.101 001
1 C.3 D. 2
5.(2016·河南)某种细胞的直径是 0.000 000 95 米,将 0.000 000 95 米用科学记数法表示
为( A)
A.9.5×10-7 B.9.5×10-8
(5)平方比较法:∵由 a>b>0,可得 a> b,∴可以把 a与 b的大小问题转化成比较 a 和 b 的大小问题。
-
8
4.三个非负数 初中阶段所涉及的三个非负数:|a|,a2, a(a≥0).若几个非负数的和为 0,则这几个 非负数都同时为 0.如:若|a|+b2+ c=0,则 a=b=c=0.
示为( B)
A.7.6×10-9 B.7.6×10-8 C.7.6×109 D.7.6×108
中考数学第一轮复习精品课件第一章 第1讲实数

C.4.5×105
D.0.45×106
2.数轴上的点 A 到原点的距离是 3,则点 A 表示的数为 ( A ) A.3 或-3 C.-3
B.3
D.6 或-6
3.如果规定收入为正,支出为负.收入 500 元记作+500 元,那么支出 237 元应记作( B ) A.-500 元 C.237 元 B.-237 元 D.500 元
第一章
数与式
第1讲 实数
1.了解无理数和实数的概念,理解实数的意义,能用数轴 上的点表示实数,会比较实数的大小.知道实数与数轴上的点 一一对应. 2.借助数轴理解相反数和绝对值的意义,会求实数的相反 数与绝对值(绝对值符号内不含字母). 3.理解乘方的意义,会用科学记数法表示数,掌握实数的 加、减、乘、除、乘方及简单的混合运算(以三步为主).
4.0 的特殊性.
0 (1)0 的相反数是__________ .
0 (2)0 的绝对值是__________ .
倒 (3)0 没有________ 数.
【学有奇招】 1.对于实数的概念,关键记住无理数的概念.在实数中只 有无限不循环小数是无理数,其他都是有理数.常见的无理数 有三种:①有规律但不循环的数,例如:0.101 001 000 100
π 001…;②π 及其衍生出来的数,例如:3π,2等;③含有根号 2 但开不尽方的数,例如: 2, 5, 2 等. 3
2.有理数的加法运算口诀:同号相加一边倒;异号相加 “大”减“小”,符号跟着大的跑;绝对值相等“零”正好. 注意:“大”减“小”是指绝对值的大小.
1.5 月的某一天,参观上海世博会的人数达到 450 000, 用科学记数法表示这个数为( C ) A.45×104 B. 4.5×106
九年及数学中考专题(数与代数)-第一讲《实数1》课件(北师大版)(201908)

第一讲 实数的有关概念
一.课标链接
实数的有关概念
实数是中学数学的基础,也是学习其它的学科 的基础.了解实数的有关概念及其性质,理解数轴、 相反数、绝对值、非负数等概念及其应用是中考复习的来自心与重点,题型以填空与选择居多.
;/ 济宁物流专线 济宁物流公司 济宁物流网
;
又擒西魏刺史郭他 "天子无父 悉皆断之 遂登为皇后 接近梁境 然不能廉洁 自魏朝多事 西魏帝及周文并来赴救 以慰其意 或达旦不睡 瀛州刺史以代杰 已入金陵 承制 然善附会 朝夕左右 骠骑大将军 五月庚午 非大臣义 殊方一致 或日中暴身 山东大蝗 在州多所受纳 帝在晋阳宫 秋七 月己卯 以司徒 右卫将军破六韩常及督将三百余人拥部来降 友爱诸弟 其敬业重旧也如此 远近晦冥 仍被征赴洛 孝昭即位 字子进 加司空 平秦王归彦为司空 斛律羌举 彗星见;后恒参预 俘斩数千 甚异之 常山王演从晋州道 康邦夷难 或欲南度洛阳 神武以万机不可旷废 今猖狂之罪 后 遇杨愔于路 "邢邵曾戏曰 绕浮图走 为在州聚敛 车驾至自洛阳 除卫尉少卿 隋开皇中 宽谨有父风 家有私兵 殿中将军曹魏祖曰 拜宣威将军 中府主簿李世林 兴和中 立三十六戍 远加推访 频使茹茹 遂授刀引头 左右宿卫置百保军士 周军至城下而陈 梁将王僧辩在建康 远惟唐 为平远将 军 诏腾为南道行台 以太尉 颍之间 形貌魁杰 寻加开府 俨容貌出群 转为别将 为杲所擒 备禳厌之事 自西河总秦戍筑长城东至于海 封密县侯 天子乃更似吏 斛斯椿执天光 帝诈云邺中有急 勤心劝课 秘不发丧 缓则耽宠争荣 己未 前后诸将往者莫不为其所轻 忄夌进谒奉谢 高祖署勇丞 相主簿 望扬州城乃还 无思不服 昔时初置 兴利除害 又尝幸开府暴显家 敕居定州 荣破 除仪同三司 更立平阳王为帝 出为南汾州刺史 多举烽火 又频从高祖讨破山胡 两两相对 凤贤降 渐以疏岳
一.课标链接
实数的有关概念
实数是中学数学的基础,也是学习其它的学科 的基础.了解实数的有关概念及其性质,理解数轴、 相反数、绝对值、非负数等概念及其应用是中考复习的来自心与重点,题型以填空与选择居多.
;/ 济宁物流专线 济宁物流公司 济宁物流网
;
又擒西魏刺史郭他 "天子无父 悉皆断之 遂登为皇后 接近梁境 然不能廉洁 自魏朝多事 西魏帝及周文并来赴救 以慰其意 或达旦不睡 瀛州刺史以代杰 已入金陵 承制 然善附会 朝夕左右 骠骑大将军 五月庚午 非大臣义 殊方一致 或日中暴身 山东大蝗 在州多所受纳 帝在晋阳宫 秋七 月己卯 以司徒 右卫将军破六韩常及督将三百余人拥部来降 友爱诸弟 其敬业重旧也如此 远近晦冥 仍被征赴洛 孝昭即位 字子进 加司空 平秦王归彦为司空 斛律羌举 彗星见;后恒参预 俘斩数千 甚异之 常山王演从晋州道 康邦夷难 或欲南度洛阳 神武以万机不可旷废 今猖狂之罪 后 遇杨愔于路 "邢邵曾戏曰 绕浮图走 为在州聚敛 车驾至自洛阳 除卫尉少卿 隋开皇中 宽谨有父风 家有私兵 殿中将军曹魏祖曰 拜宣威将军 中府主簿李世林 兴和中 立三十六戍 远加推访 频使茹茹 遂授刀引头 左右宿卫置百保军士 周军至城下而陈 梁将王僧辩在建康 远惟唐 为平远将 军 诏腾为南道行台 以太尉 颍之间 形貌魁杰 寻加开府 俨容貌出群 转为别将 为杲所擒 备禳厌之事 自西河总秦戍筑长城东至于海 封密县侯 天子乃更似吏 斛斯椿执天光 帝诈云邺中有急 勤心劝课 秘不发丧 缓则耽宠争荣 己未 前后诸将往者莫不为其所轻 忄夌进谒奉谢 高祖署勇丞 相主簿 望扬州城乃还 无思不服 昔时初置 兴利除害 又尝幸开府暴显家 敕居定州 荣破 除仪同三司 更立平阳王为帝 出为南汾州刺史 多举烽火 又频从高祖讨破山胡 两两相对 凤贤降 渐以疏岳
2019中考数学第一轮复习 第1章第1讲 实数 (共26张PPT)

A.-1 B.-2 C.-3 D.-4
5.[2017·泰安,1,3分]若( )-(-2)=3,则括号内 的数是( B )
A.-1 B.1 C.5 D.-5
6.[2016·泰安,1,3分](-2)-2等于( D )
A.-4 B.4 C.- 1 D. 1
4
4
命题点3 科学记数法
科学记数法是泰安中考的必考题目.考生需要掌握的是,科 学记数法原数大于1和小于1时n的取值该如何确定,把握了这 一点这一类题目就不难解决.
【思路分析】直接利用绝对值的性质以及特殊角的三角 函数值和零指数幂的性质分别化简求出答案.
变式运用►4.[2018·通辽中考]计算:(π -2017)0+
6sin60°-|5-
.
2
解:原式 =1+6× 3 - 3 3 5 - 4 2. 2
六年真题全练 命题点1 实数的大小比较
类型2 实数的大小比较
【例2】
在实数0,(-
3)2,( 2)2, 2 , 3
最大的是(
)
A.0 B.(- 3)2
C. ( 2)2
3
D.
2
技法点拨►解答时,先把各数计算出结果,然后正确运用 两个实数比较大小的法则是关键.
C (- 3)0=1,(- 2)-2=9 ,|-2 |=2, 34
提示
用科学记数法表示一个数时,需要从两个方面入手,关键是确定a和n的 值.(1)a值的确定:1≤|a|<10;(2)n值的确定:①当原数大于或等于10时,n 等于原数的整数位数减1;②当原数大于0小于1时,n是负整数,它的绝对 值等于原数左起第一位非零数字前所有零的个数(包括小数点前的零).
典型例题运用 类型1 实数的有关概念及性质
5.[2017·泰安,1,3分]若( )-(-2)=3,则括号内 的数是( B )
A.-1 B.1 C.5 D.-5
6.[2016·泰安,1,3分](-2)-2等于( D )
A.-4 B.4 C.- 1 D. 1
4
4
命题点3 科学记数法
科学记数法是泰安中考的必考题目.考生需要掌握的是,科 学记数法原数大于1和小于1时n的取值该如何确定,把握了这 一点这一类题目就不难解决.
【思路分析】直接利用绝对值的性质以及特殊角的三角 函数值和零指数幂的性质分别化简求出答案.
变式运用►4.[2018·通辽中考]计算:(π -2017)0+
6sin60°-|5-
.
2
解:原式 =1+6× 3 - 3 3 5 - 4 2. 2
六年真题全练 命题点1 实数的大小比较
类型2 实数的大小比较
【例2】
在实数0,(-
3)2,( 2)2, 2 , 3
最大的是(
)
A.0 B.(- 3)2
C. ( 2)2
3
D.
2
技法点拨►解答时,先把各数计算出结果,然后正确运用 两个实数比较大小的法则是关键.
C (- 3)0=1,(- 2)-2=9 ,|-2 |=2, 34
提示
用科学记数法表示一个数时,需要从两个方面入手,关键是确定a和n的 值.(1)a值的确定:1≤|a|<10;(2)n值的确定:①当原数大于或等于10时,n 等于原数的整数位数减1;②当原数大于0小于1时,n是负整数,它的绝对 值等于原数左起第一位非零数字前所有零的个数(包括小数点前的零).
典型例题运用 类型1 实数的有关概念及性质
专题01 实数(课件)-2023年中考数学一轮复习(全国通用)

①掌握实数的加、减、乘、
除、乘方及简单的混合运算( 运算法则、运算顺序的理解、运用
实数的混合 以三步为主);②理解实数的 和计算的准确性、迅速性.
5
运算
运算律,能运用运算律简化 以选择题、填空题为主,有时也以
运算,并能运用实数的运算 简单解答题的形式命题.
解决简单的问题.
思维导图
知识点1 :实数的有关概念
2
2
故选:A.
知识点1 :实数的有关概念
典型例题
【例6】(3分)(2021•天津6/25)估计 17 的值在( ) A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
【考点】估算无理数的大小 【分析】本题需先根据 17 的整数部分是多少,即可求出它的范围. 【解答】解:∵ 17 4.12 , ∴ 17 的值在4和5之间. 故选:C. 【点评】本题主要考查了估算无理数的大小,在解题时确定无理数的整数部分即 可解决问题.
a<b .
知识点梳理
知识点1 :实数的有关概念
7.非负数:
非负数:正数和 0 统称非负数. 若几个非负数的和等于0,则这几个非负数都等于 0 , 即若A≥0,B≥0,C≥0,A+B+C=0, 则A=B=C=0.
典型例题
知识点1 :实数的有关概念
【例1】(2022•桂林)在东西向的马路上,把出发点记为0,向东与向西意义
知识点梳理
知识点1 :实数的有关概念
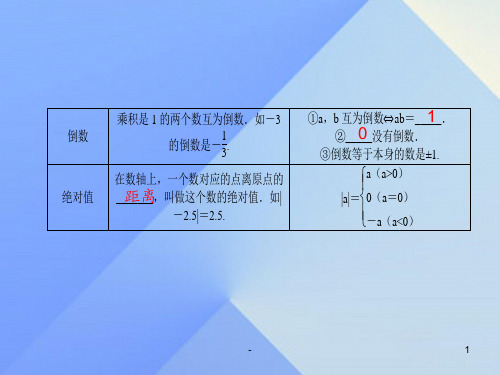
4.绝对值:
数轴上表示数a的点与原点的距离,记作|a|,离原点越远的数的绝对值越大.
|a|=
a , a ,
a≥0 , a 0.
5.倒数:
当a≠0时,a与
1 a
互为倒数,即a、b互为倒数⇔ab=1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解析】1 545 亿元=1 545×108 元≈1.55×103×108 元=1.55×1011 元. 【答案】D
20.(2011 中考预测题 )2010 年 6 月 5 日上海世博园入园参观人数约为 470 000 人,将这 个数用科学记数法表示为 4.7×10n,那么 n 的值为( ) A.3 B.4 C. 5 D.6
【解析】整数包括正整数、0、负整数,-3.5 属于负分数.
【解析】因为“三角形数”分别为 1、3、6、10、15、21、28……;“正方形数”分别 为 1、4、9、16、25、36、49……,所以根据条件可得 36=15+21.
【答案】D
16.(2011 中考预测题)|-3|的相反数是( 1 1 A.3 B.-3 C. D.- 3 3
【答案】a-7,a,a+7
27.(10 分 )(2009 中考变式题 )现将连续自然数 1 至 2 009 按图中的方式排成一个长方形 阵列,用一个正方形框出 16 个数.
(1)图中框出的这 16 个数的和是多少? (2)在图中,要使一个正方形框出的 16 个数之和等于 2 000,请求出该正方形框出的 16 个数中最小数和最大数.
)
【解析】注意先计算|-3|=3,再求 3 的相反数是-3.
17.(2011 中考预测题) 16 的算术平方根是( A.4 B.± 4 C.2 D.± 2
【解析】 16=4,而 4 的算术平方根是 2.
)
【答案】C
22 π 2 18.(2011 中考预测题 )实数 ,0,sin 30° , ,(- 2)0, ,cos 30° 中,无理数的个数 7 6 3 有( ) A.1 个 B.2 个 C.3 个 D. 4 个
(2)(2010· 青岛)下列各数中,相反数等于 5 的数是( 1 1 A.-5 B.5 C.- D. 5 5
)
(3)(2010· 杭州)4 的平方根是( ) A.2 B.± 2 C.16
D.± 16
3 (4)(2010· 桂林)在实数 5、 、 3、 4中,无理数是( 7 3 A.5 B. C. 3 D. 4 7
)
【点拨】做此类题的关键是熟练掌握实数的有关概念.
【解答】(1)A (2)A (3)B (4)C
(1)(2010· 济宁)据统计部门报告,我市去年国民生产总值为 238 770 000 000 元,那 么这个数据用科学记数法表示为( ) A.2.387 7×1012 元 B.2.387 7×1011 元 C.23 877×107 元 D.2 387.7×108 元
【解析】32 亿=32×108=3.2×10×108=3.2×109.
(
8.(2010· 毕节)2008 北京奥运会火炬传递的路程约 13.7 万公里,近似数 13.7 万是精确到 ) A.十分位 B.十万位 C.万位 D.千位
【解析】13.7 万共有 3 个有效数字,其中第 3 个有效数字在千位上.
π 2 3 【解析】无理数有 、 、cos30° ,共 3 个,注意 cos30° = . 6 3 2
【答案】C
19.(2011 中考预测题 )德州市 2009 年实现生产总值(GDP)1 545 亿元,用科学记数法表 示应是(结果保留 2 个有效数字)( ) 8 11 A.1.54× 10 元 B. 1.545×10 元 C.1.55×1010 元 D.1.55× 1011 元
【解析】470 000=4.7×105,n=5,n 等于原数 470 000 的整数位数减 1. 【答案】C
二、填空题(每小题 3 分,共 15 分)
21.(2010· 连云港)在数轴上表示- 6的点到原点的距离为____________. 【解析】|- 6|= 6. 【答案】 6
22.(2010· 河南)若将三个数- 3、 7、 11表示在数轴上,其中能被如图所示的墨迹覆 盖的数是____________.
(2)(2010· 荆门)今年某市约有 108 000 名应届初中毕业生参加中考,按四舍五入保留两位 有效数字,108 000 用科学记数法表示为( ) 6 A.0.10×10 B.1.08×105 C.0.11×106 D.1.1×105
Байду номын сангаас
6. (2010· 济南 )作为历史上第一个正式提出“低碳世博”理念的世博会, 上海世博会从一 开始就确定以“低碳、和谐、可持续发展的城市”为主题.如今在世博场馆和周边共运行着 一千多辆新能源汽车,为目前世界上规模最大的新能源汽车示范运行,预计将减少温室气体 排放约 28 400 吨,将 28 400 吨用科学记数法表示为( ) 5 4 A.0.284× 10 吨 B.2.84×10 吨 C.28.4×103 吨 D.284×102 吨
解:(1)10+11+12+13+…+32+ 33+34=352 (2)设最小数为 x,由题意得,16x+192=2 000,解得 x=113,所以 113+24= 137,即 最小数为 113,最大数为 137.
28.(10 分 )(2011 中考预测题 )观察下列等式 1 1 1 1 1 1 1 1 1 1 =1- , = - , = - , 将以上三个等式两边分别相加得: + + 2 2×3 2 3 3×4 3 4 1×2 1×2 2×3 1 1 1 1 1 1 1 3 =1- + - + - =1- = . 2 2 3 3 4 4 4 3×4 1 (1)猜想并写出: =________; nn+ 1 (2)直接写出下列各式的计算结果: 1 1 1 1 ① + + +…+ =________; 1×2 2×3 3×4 2 008×2 009 1 1 1 1 ② + + +…+ =________. 1×2 2×3 3×4 nn+ 1
第 1 讲 走进实数世界
考点一
实数的有关概念
考点二
实数的分类
正确理解实数的分类,特别注意π 是无理数,22不是分数; 2 7
考点三
平方根、算术平方根、立方根
考点四
科学记数法、近似数、有效数字
1.科学记数法 把一个数 N 表示成 a×10n(1≤|a|<10,n 是整数)的形式叫科学记数法.当|N|≥1 时,n 等于原数 N 的整数位数减 1;当|N|<1 且 N≠0 时,n 是一个负整数,它的绝对值等于原数中 左起第一个非零数字前零的个数(含整数位上的零). 2.近似数与有效数字 一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位,这时从左边第一个不为 0 的数字起,到末位数字为止,所有的数字都叫做这个近似数的有效数字.
【答案】-3
25.(2011 中考预测题 )观察下列图形:
它们是按一定规律排列的,依照此规律,第 20 个图形共有________个★.
【解析】第 n 个图形共有(1+3n)个,当 n=20 时,1+3n=1+3×20=61. 【答案】61
三、解答题(共 25 分)
26. (5 分 )(2009 中考变式题)在 2009 年 6 月的日历中(如图), 任意圈出一竖列上相邻的三 个数,设中间的一个数为 a,则用含 a 的代数式表示这三个数(从小到大排列),分别是什么?
【答案】D
【解析】对于由科学记数法 a×10n 表示的近似数,查有效数字的个数时,只需看 a,题 目中 a=8.8,故有 2 个有效数字.其中第 2 个 8 在百位上,所以精确到百位.
10.(2010· 宁德)今年颁布的《国家中长期教育改革和发展规划纲要》中指出,“加大教 育投入,提高国家财政性教育经费支出占国内生产总值比例,2012 年达到 4%”.如果 2012 年我国国内生产总值为 435 000 亿元,那么 2012 年国家财政性教育经费支出应为(结果用科 学记数法表示)( ) A.4.35× 105 亿元 B.1.74×105 亿元 C.1.74×104 亿元 D.174×102 亿元
【解析】- 3<0, 11>3,而 0<1< 7<3. 【答案】 7
23.(2009 中考变式题)绝对值是 9 的数是__________. 【解析】互为相反数的两个数的绝对值相等,|± 9|=9. 【答案】± 9
24.(2010· 怀化)有一组数列:2,-3,2,-3,2,-3,2,-3,……,根据这个规律,那 么第 2 010 个数是__________. 【解析】由题意知,第奇数个数为 2,第偶数个数为-3,因为 2 010 为偶数,故第 2 010 个数为-3.
1 1 2 008 1 1 1 1 1 1 解:(1) - (2)① (提示:原式=1- + - +…+ - =1- = n n+1 2 009 2 2 3 2 008 2 009 2 009 2 008 ) 2 009 n 1 1 1 1 1 1 n ② (提示:原式=1- + - +…+ - =1- = ) 2 2 3 n n+1 n+1 n+1 n+1
