第二章 一维极小化方法-牛顿法
一维牛顿法

一维牛顿法也称为一维牛顿-拉夫逊方法,是一种迭代的优化算法,用于求解一维非线性函数的极值点。
这种方法通过利用函数的二阶导数信息来逼近极值点,并在每次迭代中更新搜索方向,以快速收敛到最优解。
一维牛顿法的具体步骤如下:
初始化:选择初始点x0,并设定迭代终止条件,如迭代次数或函数值的收敛阈值。
计算一阶和二阶导数:计算函数f(x)在当前点xk处的一阶导数f'(xk)和二阶导数f''(xk)。
更新搜索方向和步长:根据二阶导数的信息,计算搜索方向dk和步长αk。
更新当前点:计算新的点xk+1 = xk + αk * dk。
判断终止条件:检查是否满足终止条件,如果满足则停止迭代,否则返回步骤2。
例如,对于函数f ( x ) = x 3 −2 sin ( x ) f(x) = x^3 - 2\sin(x)f(x)=x3−2sin(x),在A AA点处对函数f ( x ) f(x)f(x)展开,得到近似的二次函数φ( x ) \varphi(x)φ(x),φ( x ) \varphi(x)φ(x)的最小值在B BB点处取得,高斯牛顿法的下一步迭代点即为与B BB点横坐标相等的C CC点。
如此,只需数次,迭代能够达到很高的精度,可见牛顿法收敛速度快。
拟牛顿法算法步骤

拟牛顿法算法步骤拟牛顿法(Quasi-Newton Method)是一种用于无约束优化问题的迭代算法。
它的主要思想是利用得到的函数值和梯度信息近似估计目标函数的Hessian矩阵,并利用这个估计值来进行迭代优化。
拟牛顿法的算法步骤如下:1.初始化参数:选择初始点$x_0$作为迭代起点,设定迭代停止准则和迭代次数上限。
2. 计算目标函数的梯度:计算当前点$x_k$处的梯度向量$g_k=\nabla f(x_k)$。
3. 计算方向:使用估计的Hessian矩阵$B_k$和负梯度$g_k$来计算方向$d_k=-B_k g_k$。
4. 一维:通过线方法(如Armijo准则、Wolfe准则等)选择一个合适的步长$\alpha_k$,使得函数在方向上有明显的下降。
5. 更新参数:根据步长$\alpha_k$更新参数$x_{k+1}=x_k+\alpha_k d_k$。
6. 计算目标函数的梯度差:计算新点$x_{k+1}$处的梯度向量$g_{k+1}=\nabla f(x_{k+1})$。
7. 更新Hessian矩阵估计:根据梯度差$g_{k+1}-g_k$和参数差$\Delta x_k=x_{k+1}-x_k$,利用拟牛顿公式来更新Hessian矩阵估计$B_{k+1}=B_k+\Delta B_k$。
8.更新迭代次数:将迭代次数$k$加一:$k=k+1$。
9.判断终止:如果满足终止准则(如梯度范数小于给定阈值、目标函数值的变化小于给定阈值等),则停止迭代;否则,返回步骤310.输出结果:输出找到的近似最优解$x^*$作为优化问题的解。
拟牛顿法有许多不同的变体,最经典和最常用的是DFP算法(Davidon-Fletcher-Powell Algorithm)和BFGS算法(Broyden-Fletcher-Goldfarb-Shanno Algorithm)。
这两种算法都是基于拟牛顿公式来更新Hessian矩阵估计的,但具体的公式和更新规则略有不同,因此会产生不同的数值性能。
目标函数的几种极值求解方法

目标函数极值求解的几种方法题目:()()2221122min -+-x x,取初始点()()Tx 3,11=,分别用最速下降法,牛顿法,共轭梯度法编程实现。
一维搜索法:迭代下降算法大都具有一个共同点,这就是得到点()k x 后需要按某种规则确定一个方向()k d ,再从()k x 出发,沿方向()k d 在直线(或射线)上求目标函数的极小点,从而得到()k x 的后继点()1+k x ,重复以上做法,直至求得问题的解,这里所谓求目标函数在直线上的极小点,称为一维搜索。
一维搜索的方法很多,归纳起来大体可以分为两类,一类是试探法:采用这类方法,需要按某种方式找试探点,通过一系列的试探点来确定极小点。
另一类是函数逼近法或插值法:这类方法是用某种较简单的曲线逼近本来的函数曲线,通过求逼近函数的极小点来估计目标函数的极小点。
本文采用的是第一类试探法中的黄金分割法。
原理书上有详细叙述,在这里介绍一下实现过程:⑴ 置初始区间[11,b a ]及精度要求L>0,计算试探点1λ和1μ,计算函数值()1λf 和()1μf ,计算公式是:()1111382.0a b a -+=λ,()1111618.0a b a -+=μ。
令k=1。
⑵ 若L a b k k <-则停止计算。
否则,当()K f λ>()k f μ时,转步骤⑶;当()K f λ≤()k f μ时,转步骤⑷ 。
⑶ 置k k a λ=+1,k k b b =+1,k k μλ=+1,()1111618.0++++-+=k k k k a b a μ,计算函数值()1+k f μ,转⑸。
⑷ 置k k a a =+1,k k b μ=+1,k k μμ=+1,()1111382.0++++-+=k k k k a b a λ,计算函数值()1+k f λ,转⑸。
⑸ 置k=k+1返回步骤 ⑵。
1. 最速下降法实现原理描述:在求目标函数极小值问题时,总希望从一点出发,选择一个目标函数值下降最快的方向,以利于尽快达到极小点,正是基于这样一种愿望提出的最速下降法,并且经过一系列理论推导研究可知,负梯度方向为最速下降方向。
最优化理论方法——牛顿法
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
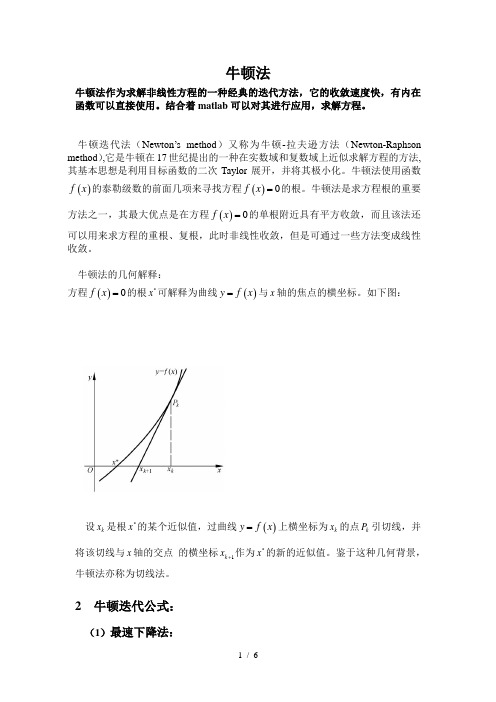
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。
第二章一维搜素解析

不存在极值点
当x x0时,f x 0,当x x0时,f x 0,则x0为极小值
当x x0时,f x 0,当x x0时,f x 0,则x0为极大值
又 f x lim f x f x0
xx0 0
x x0
0,极小值
一维函数极值条件: f x0 0,且f x 0,极大值
0,非极值
(1) 如 果 f1
f
,
2
则
留
下
的
区
间
为[a,x2
]
(2) 如 果 f1
f
,
2
则
留
下
的
区
间
为[ x1,b]
(3) 如 果 f1
f
,
2
则
留
下
的
区
间
为[ x1,x2
]
a) f a1 f b1
b) f a1 f b1
迭代
迭代是重复反馈过程的活动,
其目的通常是为了逼近所需目标或结果。
每一次对过程的重复称为一次“迭代”,
B. 当 f1> f2 时,极小点必在[x1, b]中,则
x1 a, x2 x1, f2 f1, x2 a 0.618(b a), f2 f (x2 )
(4)判断是否满足精度要求。若新区间已缩短至预 定精度要求,即 b a ,则转第5)步;否则 转第3)步,进行下一次迭代计算。
迭代
• %求第十个斐波那契数
• a0=0
• a1=1
• for i=2:10
•
a2=a0+a1
•
a0=a1;a1=a2;
• end
•
• %求不大于100的最大斐波那契数
数学中的最优化方法

数学中的最优化方法数学是一门综合性强、应用广泛的学科,其中最优化方法是数学的一个重要分支。
最优化方法被广泛应用于各个领域,如经济学、物理学、计算机科学等等。
本文将从理论和应用两个角度探讨数学中的最优化方法。
一、最优化的基本概念最优化是在给定约束条件下,寻找使某个目标函数取得最大(或最小)值的问题。
在数学中,最优化可以分为无约束最优化和有约束最优化两种情况。
1. 无约束最优化无约束最优化是指在没有限制条件的情况下,寻找使目标函数取得最大(或最小)值的问题。
常见的无约束最优化方法包括一维搜索、牛顿法和梯度下降法等。
一维搜索方法主要用于寻找一元函数的极值点,通过逐步缩小搜索区间来逼近极值点。
牛顿法是一种迭代方法,通过利用函数的局部线性化近似来逐步逼近极值点。
梯度下降法则是利用函数的梯度信息来确定搜索方向,并根据梯度的反方向进行迭代,直至达到最优解。
2. 有约束最优化有约束最优化是指在存在限制条件的情况下,寻找使目标函数取得最大(或最小)值的问题。
在解决有约束最优化问题时,借助拉格朗日乘子法可以将问题转化为无约束最优化问题,进而使用相应的无约束最优化方法求解。
二、最优化方法的应用最优化方法在各个领域中都有广泛的应用。
以下将以几个典型的应用领域为例加以说明。
1. 经济学中的最优化在经济学中,最优化方法被广泛应用于经济决策、资源配置和生产计划等问题的求解。
例如,在生产计划中,可以使用线性规划方法来优化资源分配,使得总成本最小或总利润最大。
2. 物理学中的最优化最优化方法在物理学中也是常见的工具。
例如,在力学中,可以利用最大势能原理求解运动物体的最优路径;在电磁学中,可以使用变分法来求解电磁场的最优配置;在量子力学中,可以利用变分法来求解基态能量。
3. 计算机科学中的最优化在计算机科学中,最优化方法被广泛应用于图像处理、机器学习和数据挖掘等领域。
例如,在图像处理中,可以使用最小割算法来求解图像分割问题;在机器学习中,可以使用梯度下降法来求解模型参数的最优值。
牛顿迭代法(Newton‘s Method)

牛顿迭代法(Newton’s Method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson Method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
与一阶方法相比,二阶方法使用二阶导数改进了优化,其中最广泛使用的二阶方法是牛顿法。
考虑无约束最优化问题:其中 \theta^{\ast} 为目标函数的极小点,假设 f\left( \theta \right) 具有二阶连续偏导数,若第 k 次迭代值为 \theta^{k} ,则可将f\left( \theta \right)在\theta^{k}近进行二阶泰勒展开:这里,g_{k}=x^{\left( \theta^{k} \right)}=∇f\left( \theta^{k} \right)是f\left( \theta \right) 的梯度向量在点 \theta^{k}的值, H\left( \theta^{k} \right) 是 f\left( \theta \right) 的Hessian矩阵:在点 \theta^{\left( k \right)}的值。
函数 f\left( \theta \right) 有极值的必要条件是在极值点处一阶导数为0,即梯度向量为0,特别是当H\left( \theta\right) 是正定矩阵时,函数 f\left( \theta \right) 的极值为极小值。
牛顿法利用极小点的必要条件:这就是牛顿迭代法。
迭代过程可参考下图:在深度学习中,目标函数的表面通常非凸(有很多特征),如鞍点。
因此使用牛顿法是有问题的。
如果Hessian矩阵的特征值并不都是正的,例如,靠近鞍点处,牛顿法实际上会导致更新朝错误的方向移动。
这种情况可以通过正则化Hessian矩阵来避免。
常用的正则化策略包括在Hessian矩阵对角线上增加常数α 。
正则化更新变为:这个正则化策略用于牛顿法的近似,例如Levenberg-Marquardt算,只要Hessian矩阵的负特征值仍然相对接近零,效果就会很好。
第二章 一维极小化方法

2. 若 bk a k , 停止, 且
bk a k . 否则, 2 当 f ( k ) f ( k ) 时,转 3;当 f ( k ) f ( k ) 时,转 4. x
bk 1 bk ,
3. 令 a k 1 k ,
k 1 k ,
k 1 a k 1 0.618(bk 1 a k 1 ), 计算 f ( k 1 ), 令 k : k 1, 转 2。
b) 令一阶导函数为零,解得驻点
c) 根据驻点处的二阶导函数的符号,判断驻点是否为极小点
一. 一维优化问题
古典微分法的局限性
情况1:目标函数复杂,令导函数为零时得不到解析解(例2-1,2-2)
情况2:目标函数写不出明显的表达式(例2-3)
实际化工问题中,有许多属于以上两种情况,因此必须寻求其他方法进 行求解,而借助于计算机进行的数值计算方法则能够完成这一任务
要求其满足以下两个条 件:
1. bk λk μk ak β 1 α
(1)
ak
k
uk
bk
2. 每次迭代区间长度缩短 比率相同,即
bk 1 ak 1 α(bk ak ) 另 有 : k λk /αk μk αk μk /1 α 即 ,β/α α/1
由式( )与(2)可得: 1
[ a k 1 , bk 1 ] [ a k , uk ]。
在第 k 1 次迭代时选取 k 1 , uk 1 , 则由(4)有 uk 1 a k 1 (bk 1 a k 1 )
ak 2 (bk ak )
如果令 2 1 , uk 1 k ,因此 uk 1 不必重新计算 。 则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 初始点的选取困难,甚至无法实施。 ) 初始点的选取困难,甚至无法实施。
(3)
−1 G k 的存在性和计算量问题
。
问题一: 问题一: 如何使得 f ( x k + 1 ) < f ( x k ) ?
法中, 在 Newton 法中,有
− x k +1 = x k − G k 1 g k = x k + d k
而
t k = 1。
3. 算法步骤
step 1. 给定初始点 x 0,精度 ε > 0 , k := 0
step2. 计算g k = ∇f ( x k )和G k = ∇ 2 f ( x k )
− 可逆时, 当 G k 可逆时, x k + 1 = x k − G k 1 g k 。
step3. 由方程组∇Q( x ) = g k + G k ( x − x k ) = 0 解出x k +1
− H k ≈ Gk1
↔
− 如何保证 H k > 0和 H k ≈ G k 1 ?
如何确定 ∆ H k ?
拟 Newton 条件
− 拟 Newton 条件 ↔ H k ≈ G k 1
分析: − 需满足的条件, G 分析: k 1 需满足的条件,并利用 此条件确定 H k 。
记 g ( x ) = ∇ f ( x ), g k = ∇ f ( x k ) G k = ∇ f 2 ( x k ), 则因为
f ( x ) ≈ f ( x k +1 ) + ∇f ( x k +1 )T ( x − x k +1 )
1 + ( x − x k +1 )T ∇ 2 f ( x K +1 )( x − x k +1 ) 2
g ( x ) ≈ g ( x k + 1 ) + ∇ 2 f ( x k + 1 )( x − x k + 1 )
T − − 当Gk > 0 时, ∇f ( x k )T d k = −∇f ( x k )T Gk 1 gk = − gk Gk 1 gk < 0 , 有
∴ 当Gk > 0 时, k 是下降方向。 d 是下降方向。
如果对 Newton 法稍作修正: 法稍作修正: x
k +1
= x + tk d
k
k
令
∇Q(x) = gk +Gk(x − x ) = 0
k
正定, 若 Hesse 矩阵 G k 正定,即 G k > 0,
− 则 G k 1 > 0,此时有
− x k +1 = x k − G k 1 g k
这就是 Newton 迭代公式 。
比较迭代公式
− d k = −G k 1 g k ,
x k +1 = x k + t k d k , 有
step4. 若 || ∇f ( x
k +1
) ||< ε , 停止, = x 停止, x
*
k +1
;
令 否则, k := k + 1 , 转step 4 。
4. 算法特点
收敛速度快,为二阶收敛。 初始点要选在初始点附近。
5. 存在缺点及修正
(1) f ( x k +1 ) < f ( x k ) ?
一、Newton 法
1. 问题
min f ( x )
x∈R n ∈ n
f ( x )是R 上二次连续可微函数 即f ( x ) ∈ C ( R )
2 n
2. 算法思想
x → x →L→ x → x
0 1 k k +1
→L
为了由 x 产生x
k
k +1
,用二次函数 Q( x )近似f ( x )。
f ( x) ≈ Q( x) = f ( xk ) + ∇f ( xk )T ( x − xk ) + 1 k T 2 k k + ( x − x ) ∇ f ( x )(x − x ) 2 1 k T k k T k = f ( x ) + gk ⋅ ( x − x ) + ( x − x ) Gk ( x − x ) 2 其中 g k = ∇f ( x k )T , G k = ∇ 2 f ( x k )。
xT I x
法为变尺度算法。 称 Newton 法为变尺度算法。
3.
附加某些条件使得: 如何对 H k 附加某些条件使得: (1)迭代公式具有下降性 质 (2) H k 的计算量要小 (3)收敛速度要快↔源自↔Hk > 0
H k +1 = H k + ∆H k ( ∆H k = H k +1 − H k )
t k : f ( x k + t k d k ) = min f ( x k + t d k )
则有: 则有: f ( x k + 1 ) < f ( x k ) 。
问题二: 如何克服缺点( 问题二: 如何克服缺点( 2)和( 3) ?
二、拟 Newton 算法
1.
k +1 k −1 k
( 变尺度法 )
k
迭代公式: 先考虑 Newton 迭代公式: x = x − G ∇f ( x )
迭代公式中, 在 Newton 迭代公式中,如果我们 用
− 则有: 正定矩阵 H k 替代 G k 1,则有:
x k +1 = x k − H k ∇ f ( x k )
2.
考虑更一般的形式: 考虑更一般的形式: x k +1 = x k − t k H k ∇ f ( x k )
Step 1 . 给定初始点 x 0 ,正定矩阵 H 0 , 精度 ε > 0, k := 0
step 3. 令 x k + 1 = x k + t k d k , 其中 t k : f ( x k + t k d k ) = min f ( x k + t d k )。
x k +1 = x k − t k H k ∇f ( x k ) H k ≡ I时 ⇒ 梯度法 最速下降方向 d k = −∇ f ( x k ) , 度量为 x =
− H k = G k 1时 ⇒ Newton 法 − 最速下降方向 d k = − G k 1∇ f ( x k ), 度量为 x = − xT Gk 1 x
g k ≈ g k +1 + G k +1 ( x k − x k +1 )
−1 G k +1 ( g k +1 − g k ) = x k +1 − x k ,
这样我们想到
记 y k = g k + 1 − g k , s k = x k + 1 − x k , 则有
4、拟 Newton 算法
( 变尺度法 )的一般步骤; 的一般步骤;
