定性资料统计描述
合集下载
定性资料的统计描述(公式整理)
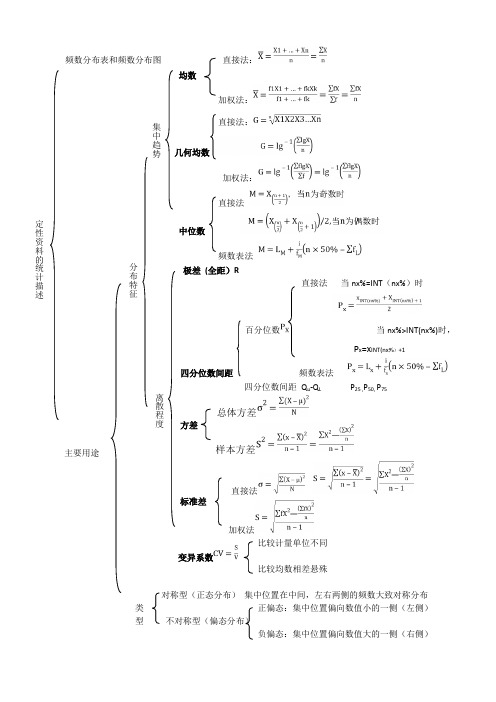
频数分布表和频数分布图 直接法：均数加权法：直接法：几何均数加权法： 直接法中位数 频数表法 极差 (全距）R直接法 当nx%=INT （nx%）时百分位数 当nx%>INT(nx%)时， P x =x INT(nx%）+1四分位数间距 频数表法四分位数间距 Q u -Q L P 25 ,P 50, P 75总体方差 样本方差直接法加权法比较计量单位不同比较均数相差悬殊对称型（正态分布） 集中位置在中间，左右两侧的频数大致对称分布 类 正偏态：集中位置偏向数值小的一侧（左侧） 型 不对称型（偏态分布）负偏态：集中位置偏向数值大的一侧（右侧）方差 标准差 变异系数 主要用途 定性资料的统计描述集中趋势离散程度分布特征集中描述 适用离散趋势适用均数 单峰对称分布资料 方差和标准差 越大，越离散 单峰对称分布资料 几何均数G对数正态分布， 观察组之间等比 变异系数CV越大，越变异不同计量单位 均数相差较大 中位数M 各种分布 不对称分布， 两端无确切值 分布不明确四分位数间距①偏态分布资料 ②两端无确切值 ③分布不明确资料概念：随机变量X 取各种值的概率称为概率分布规律，简称分布 正态分布就是一种重要的连续型随机变量的分布类型形态：呈对称钟形，在均数处最高，两侧不断降低，逐渐与横轴接近，但不与横轴相交正态分布曲线 密度函数为,分布函数，表示随机变量X 取小于或等于x 的概率①正态曲线在横轴上均数处最高。
②正态分布以均数为对中心，左右对称③正态分布有两个参数，即位置参数μ和形态参数。
特征 若固定，改变μ，曲线沿x 轴平行移动，其形态不变，若固定μ，越小，曲线越陡峭 正态分布 越大，曲线越低平，但中心在x ④正态曲线下的面积分布有规律密度函数标准正态分布(Z 分布） 分布函数标准化变换 估计总体变量值的频数分布查表过高过低均异常→双侧 应用 确定取单侧或双侧参考值 过高异常→上限 过低异常→下限 制定医学参考值范围 主要目的为减少假阳性（确诊）→99%主要目的为减少假阴性（初筛）→95% 服从正态→正态分布法不服从→百分位数法参考值范围正态分布法百分位数法确定适当的百分界限选择制定医学参考值范围方法标态 正态 面积或P -1~168.27% -1.64~1.6490% -1.96~1.96 95% -2.58~2.5899%双侧单侧双侧单侧只有上限只有下限只有上限只有下限95 P2.5~P72.5P5P9599 P0.5~P99.5P1P99。
定性资料的统计描述
（二）强度型指标
例：某企业2003年有2839名职工，该企业每年都对 职工进行体检，这一年新发生高血压病人5 例，2003年的高血压发病率为多少？
（三）相对比型指标
概念：任何两个相关联的指标A,B之比。 计算公式： 口学中的出生性别比例： 男性人口/女性人口= 19456/18340 = 1.06， 即每出生1个女婴，就有1.06个男婴出生。
分母的近似计算
假定当年每位去世者平均活了半年，每位出生 者也平均活了半年，则有： 当年全人口存活的总人年数=年初人口数×1年-去世 人数×0.5＋出生人数×0.5 或 当年全人口存活的总人年数=年终人口数×1年 ＋去世人数×0.5—出生人数×0.5
上面两个等式相加，便有 当年全人口存活的总人年数=（年初人口数＋年终人 口数）/2×1年=当年平均人口数×1年 或 当年全人口存活的总人年数=当年年中人口数 × 1年
构成比的特点
1、各构成部分的相对数之和为100%；
2、构成比的各构成部分之间存在着相互影响。
二、常用的相对数指标
用频率分布全面反映一个定性变量外，有时也可 用其他相对数指标从某个侧面来描述定性变量。 常用相对数指标大致有三种类型： 频率；强度；相对比
（一）频率型指标
频率型指标：最常见，表示某现象发生 的频率大小。 计算公式：
2、A、B也可以是相对数，如甲、乙两地的恶性肿瘤死亡率
分别是89.2/10万和65.1/10万，
则甲地恶性肿瘤死亡率是乙地的89.2/65.1=1.37（倍）。
3、A、B 可以是性质相同的两个指标，如上例甲、乙两地恶 性肿瘤死亡率相比，
也可以是性质不同的两个指标，如某医院每张病床配备的
医生人数： 368名医生/2800个床位=0.13
04定性资料的统计描述
该事物内部某一组成部分的观察单位数（例数） 构成比 100% 某事物内部的所有观察单位之和（例数之和）Βιβλιοθήκη Proportion
[说明]
构成比和率同是相对数，但应用的场合
不同。构成比之和应为100%，某一构成部分的增
减会影响其它构成部分相应的减少或增加；而某
一部分率的变化并不影响其它部分的变化。需要
Odds ratio
例4-4 母亲围孕期是否有发热或感冒病史与婴儿 神经血管畸形关系的病例对照研究的资料如下表
所示。试计算母亲围孕期是否有发热或感冒病史
引起婴儿神经血管畸形的比数比。
表4-3 母亲围孕期有否发热或感冒病史与婴儿神经血管畸形关联
发热或感冒病史 有 无 合 计
神经血管畸形组 40(a) 112(c) 152（a+c）
Standardization rate
例4-5 试对下表资料计算甲乙两个医院的标准化 率。
表 4-4 科室 甲、乙两医院治愈率的比较 甲医院 入院 治愈 治愈率 人数 人数 内科 外科 传染病科 合计 1500 500 500 975 470 475 (%) 65.0 94.0 95.0 76.8 入院 人数 500 1500 500 2500 乙医院 治愈 人数 315 1365 460 2140 治愈率 (%) 63.0 91.0 92.0 85.6
分率（‰）、万分率（/万）、或十万分率（／
10万）等来表示。计算公式为：
某事物或现象发生的实 际数 率 比例基数 某事物或现象发生的所 有可能数
Rate
公式中的“比例基数”通常依据习惯而定。 需要注意的是，率在更多情况下是一个具有时间 概念的指标，即用于说明在某一段时间内某现象 发生的强度或频率，如出生率、死亡率、发病率 、患病率等，这些指标通常是指在1年时间内发 生的频率。
定性资料统计描述
OR P1 /(1 P1) P0 /(1 P0)
P1为病例组的暴露比例或在暴露状态下的发病率 P0为对照组的暴露比例或在非暴露状态下的发病率
Odds ratio
例4-4 母亲围孕期是否有发热或感冒病史与婴儿 神经血管畸形关系的病例对照研究的资料如下表 所示。试计算母亲围孕期是否有发热或感冒病史 引起婴儿神经血管畸形的比数比。
率某某 事事 物物 或或 现现 象 有 象 际 发 可 发 数 生 能 生 比 的 数 的 例 所实 基数
Rate
公式中的“比例基数”通常依据习惯而定。
需要注意的是，率在更多情况下是一个具有时间 概念的指标，即用于说明在某一段时间内某现象 发生的强度或频率，如出生率、死亡率、发病率 、患病率等，这些指标通常是指在1年时间内发 生的频率。
R R P1 P0
P1为暴露组的发病率；P0非暴露组的发病率。
Relative risk
例4-3 某地市区非吸烟女性饮酒者和不饮酒者 的肺癌发病资料如下表所示，试计算其相对危 险度。
表4-2 某地市区非吸烟女性饮酒者和不饮酒者的肺癌发病资料
饮酒与否
发病数 观察人年数 发病率（1/10万人年）
是
Odds ratio
四、标准化率
标准化率（ standardization rate ）：比较两个不 同人群的患病率、发病率、死亡率等资料时，为 消除其内部构成（如年龄、性别、工龄、病程长 短、病情轻重等）对率的影响，可以使用标准化 率。
Standardization rate
例4-5 试对下表资料计算甲乙两个医院的标准化
P0
b
b
d
1
P0
b
d
d
由OR计算公式可以得出
P1为病例组的暴露比例或在暴露状态下的发病率 P0为对照组的暴露比例或在非暴露状态下的发病率
Odds ratio
例4-4 母亲围孕期是否有发热或感冒病史与婴儿 神经血管畸形关系的病例对照研究的资料如下表 所示。试计算母亲围孕期是否有发热或感冒病史 引起婴儿神经血管畸形的比数比。
率某某 事事 物物 或或 现现 象 有 象 际 发 可 发 数 生 能 生 比 的 数 的 例 所实 基数
Rate
公式中的“比例基数”通常依据习惯而定。
需要注意的是，率在更多情况下是一个具有时间 概念的指标，即用于说明在某一段时间内某现象 发生的强度或频率，如出生率、死亡率、发病率 、患病率等，这些指标通常是指在1年时间内发 生的频率。
R R P1 P0
P1为暴露组的发病率；P0非暴露组的发病率。
Relative risk
例4-3 某地市区非吸烟女性饮酒者和不饮酒者 的肺癌发病资料如下表所示，试计算其相对危 险度。
表4-2 某地市区非吸烟女性饮酒者和不饮酒者的肺癌发病资料
饮酒与否
发病数 观察人年数 发病率（1/10万人年）
是
Odds ratio
四、标准化率
标准化率（ standardization rate ）：比较两个不 同人群的患病率、发病率、死亡率等资料时，为 消除其内部构成（如年龄、性别、工龄、病程长 短、病情轻重等）对率的影响，可以使用标准化 率。
Standardization rate
例4-5 试对下表资料计算甲乙两个医院的标准化
P0
b
b
d
1
P0
b
d
d
由OR计算公式可以得出
定性资料的统计描述
适用条件：已知被标化组人群年龄别人 口数、死亡总数. 计算公式：
r p P P SMR ni Pi
标准组年龄 别死亡率
被标化组年 龄别人口数
标准化死亡比(SMR)
SMR是观察人群死亡率与总人群(参照人群)
相比较的指标。
计算： SMR=实际死亡数/期望死亡数＝D/E
期望死亡数：假定研究人群的年龄别死亡
45.4
SPSS进行标准化率的计算(1)
Transform Compute… Target Variable 框：sp Numeric Expression 框：p1+p2 OK
SPSS进行标准化率的计算(2)
Transform Compute… Target Variable 框：sc1 Numeric Expression 框： sp*c1/p1 OK Transform Compute… Target Variable 框：sc2 Numeric Expression 框： sp*c2/p2 OK
两样本标化率的比较应作假设检验
标准化法注意事项
各年龄组率若出现明显交叉，或非呈平行 变化趋势时，宜比较年龄组死亡率 一般情况下，直接法计算简便，易于了解， 更为常用；如原资料中有些年龄组人口过 少，致使年龄别死亡率波动较大时，宜用 间接法。
标准化率在SPSS中的实现(直接标化法)
表1 甲、乙两院某传染病治愈率/%的比较
率与标准的年龄别死亡率一样，理论上的
死亡人数。
计算标准化率的步骤
根据现有数据的条件选用直接法或间接法 选定标准：标准组应有代表性、稳定、数 据量较大的人群 应用公式计算 必要时，做假设检验
定性资料的统计描述
25
三、相对比
相对比是互不包含的两个有联系指标之比。 对比的两个指标可以性质相同，也可以性质 不同。 公式为：相对比型指标=A指标 / B指标
注意：在计算相对比中，甲、乙两个指标可 以是绝对数，也可以是相对数或平均数，可 以有不同的量纲，但是互不包含。
27
例： 某年某医院出生婴儿中，男性婴儿为 370人， 女性婴儿为358人，则出生婴儿的 性别比为多少？ 性别比为：370 / 358 ×100﹪=103﹪ 说明该医院年每出生100名女婴儿，就有103 名男婴儿出生。
30
2.相对危险度（relative risk,RR）表示在两种相同 条件下某疾病发生的概率之比。即暴露组发病率 与非暴露组发病率的比值。 某地某年男性吸烟和非吸烟的冠心病死亡资料 分组 死亡人数 观察人年数 死亡率 （1/10万人年） 43248 10673 240.5 112.4
吸烟组 104 非吸烟组 12
36
某医院某年住院病人中胃癌患者占5%，则（） A 5%是强度指标 B 5%是频率指标 C 5%是相对比指标 D 5%说明胃癌在住院病人 中的比重
37
2.使用相对数时分母不宜过小 某药物 甲治疗100人，50人有效，有效 率为50﹪。药物乙治疗5人，3人有效， 我们能否说乙药有效率为60 ﹪？能否说 乙药比甲药治疗效果好。
9
分娩方式 顺产 助产 顺产 顺产 顺产 剖宫产 顺产 剖宫产 顺产 顺产
妊娠结局 足月 足月 足月 早产 足月 足月 死产 足月 足月 足月
按年龄（2岁一组）与职业整理
年龄 18 20 22 24 26 28 30 32 34 36 38 40 合计 工人 2 9 28 50 50 34 11 14 4 2 3 0 207 管理人员 0 2 7 34 43 35 14 2 2 1 1 0 141 农民 0 6 10 28 25 10 11 3 5 1 1 2 102 商业服务 0 10 24 52 45 34 22 14 3 4 0 0 208
定性资料的统计描述
同年内死亡人数 粗死亡率＝ 1000 0 00 当年平均人口数 1年
强度型指标（近似）
同年<1周岁死亡人数 婴儿死亡率＝ 1000 0 00 当年活产儿总数
频率型指标近似
同年孕产妇死亡数 孕产妇死亡率＝ 10万/10万 当年活产儿总数
相对比型指标
统计图表
人口统计指标
例：某医生治疗了4例支气管哮喘病患者， 其中3例有效，即报告有效率为75。
请问该说法是否正确？
某医院统计1985-1990年儿科住院病人疾病种类分 布情况见表：
表 某医院儿科住院病人疾病种类分布情况 疾病种类 先天性心脏病 病人数 250 ％ 23.8
风湿性心脏病
其它
750
2. 人时资料的描述—强度
流行病学随访研究中，不同个体被观察的时间长度各 不相同，常用人时总和表示被观察的人和时间的总和。 “强度”是流行病学、统计学术语。 ——单位时间内（如年、月、日等）某事件发 生的频率。
某事件发生的个体数 强度型指标 K （ 可能发生某事件的个体 数 时间）
强度型指标通常是指一段时间内的平均概率。如人 时发病率的分子是新发生的事件数，分母是人时 数（观察人数乘以时间）的总和，多用于大人群 长时间随访的资料。
常用的相对数指标大致有三种类型：
频率(relative frequency or proportion)
强度(intensity or rate) 相对比(relative ratio)
主要内容
1. 分类资料的描述—频率和频率分布
2. 人时资料的描述—强度
3. 复合指标—相对比 4. 相对数应用中需注意的问题
新发病例数 人时发病率 观察的人时总数 新发病例数 （折合的观察人数 （ ）单 位 时 间 的 个 数 ） 院的院内感染调查中，5031名病 人共观察了127859人日（例均25.4日），其中 有596人在医院发生感染，请计算院内感染率。
定性资料的统计描述
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
某地居民年龄别癌肿患病情况统计
年龄组 （岁） （1） ＜30 30～ 40～ 50～ 60～ 总计 人口数 （2）
633000 570000 374000 143000 30250
1750250
癌肿病 人数 （3） 19 171 486 574 242 1492
×100%
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
例：
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
例：白细胞计数和分类构成比 构成比的两个特点： ⑴ 各组成部分的相对数之和为 100%； ⑵ 某一部分所占比重增大，其它部 分会相应地减少。
实际工作中，可用某一期间的平均 人口数来代表人口总数。当人口数 在一年中是均匀变动时，可用以下 两种计算方法：
年平均人口数 = 上年12月31 日人口数 + 本年12月31 日人口数 2
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
年中（7月1日零时）人口数代表全 年的平均人口数。
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
国际统一规定的统计人口数方法： ① 实际制——只统计标准时刻某地 实际存在的人口数（包括临时在 该地的人） ② 法定制——只统计某地的常住人 口数。
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
三、人口死亡统计
死亡统计资料是反映社会卫生状况和居 民健康水平的重要基础资料，也是制订 卫生工作计划、评价卫生服务效果的重 要依据。通过描述和分析不同地区、不 同人群（包括不同性别、不同年龄、不 同职业者）的死亡水平和各种死亡原因 的动态变化，反映社会经济、文化教 育、卫生服务对于居民健康的影响。
某地居民年龄别癌肿患病情况统计
年龄组 （岁） （1） ＜30 30～ 40～ 50～ 60～ 总计 人口数 （2）
633000 570000 374000 143000 30250
1750250
癌肿病 人数 （3） 19 171 486 574 242 1492
×100%
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
例：
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
例：白细胞计数和分类构成比 构成比的两个特点： ⑴ 各组成部分的相对数之和为 100%； ⑵ 某一部分所占比重增大，其它部 分会相应地减少。
实际工作中，可用某一期间的平均 人口数来代表人口总数。当人口数 在一年中是均匀变动时，可用以下 两种计算方法：
年平均人口数 = 上年12月31 日人口数 + 本年12月31 日人口数 2
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
年中（7月1日零时）人口数代表全 年的平均人口数。
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
国际统一规定的统计人口数方法： ① 实际制——只统计标准时刻某地 实际存在的人口数（包括临时在 该地的人） ② 法定制——只统计某地的常住人 口数。
QIU Yu-lan 上海交通大学医学院 QIU Yu-lan 上海交通大学医学院
三、人口死亡统计
死亡统计资料是反映社会卫生状况和居 民健康水平的重要基础资料，也是制订 卫生工作计划、评价卫生服务效果的重 要依据。通过描述和分析不同地区、不 同人群（包括不同性别、不同年龄、不 同职业者）的死亡水平和各种死亡原因 的动态变化，反映社会经济、文化教 育、卫生服务对于居民健康的影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
定性资料的统计描述
Statistical description of qualitative data
实习目的
掌握 定性资料常用描述指标 等相对数； 率 构成比 相对比
应用相对数应该注意的问题 熟悉 常用动态数列指标，率的标准化
理论复习
常用相对数及其应用：
率（frequency) 构成比 (proportion)
相对比 (ratio)
率（frequency)：
概念：是指某种现象在一定条件下，实际发生的观察单位 数与可能发生该现象的总观察单位数之比，用以说明某种 现象发生的频率大小或强度。 分类：频率和速率 （分母的观察单位总数是否引入时间因素） 计算公式：
频率 同时期实际发生某现象的观察单位数 K 某时期可能发生某现象的观察单位总数
构成比
27.27 24.24 16.67 16.67
胃肠道感染
其他 合计
4
6 66
6.06
9.09 100.00
相 对 比 (ratio)
概念：是指两个有关联的指标之比值，用以说明一个指标是另 一指标的几倍或几分之几。 计算公式：
相对比 甲指标 (或 100%) 乙指标
如：男女性别比、CV等
Dispersion：离散程度统计量 Std. deviation：标准差 Variance：方差 Distribution：分布指标 Skewness：偏度系数
Kurtosis：峰度系数
Frequencies....
绘制统计图对话框： Bar charts：条图 Pie charts：饼图
Histograms：直方图
输出结果：
Crosstables过程
Crosstabs过程主要功能：
产生二维至n维列联表（交叉表作用）
计算百分数指标、期望频数、汇总指标等 计算度量行、列变量关联度的指标及其检验 成组、配对、分层卡方检验 计算任意维列联表的确切概率值
Crosstables…
操作提示： Analyze →Descriptive Statistics →Crosstables…
2 年死亡率= 100%=0.8% 125 2
构成比 (proportion)
概念：也叫构成指标，是指一事物内部某一组成部分的观察单 位数与该事物各组成部分的观察单位总数之比，用以说明某一事 物内部各组成部分所占的比重或分布。 计算公式： 某一组成部分的观察单 位数
构成比
构成比具有以下特点： • 分子是分母的一部分，各组成部分构成比数值之和等于1或 100 • 事物内部各组成部分之间呈此消彼长关系，当其中某一组成部 分构成比数值增大，其他组成部分的构成比数值必然会减少。
率和构成比的区别
构成比 率
1.各部分可直接相加
各率不可相加
2.各部分之和等于100或1
总率不一定等于各率之和
3.某部分变化，其他部分随着变化
某率的变化，不影响其他各率
4.是说明比重和分布的，反映事物内部各 个部分之间的比例关系。
表示某现象发生的频率和强度
应用相对数时的注意事项：
分析时不能以构成比代替率（重点） 计算相对数应有足够的观察单位数：分母不能太小 应分别将分子和分母合计求合计率 相对数的比较应注意其可比性 两个样本率比较时应进行假设检验 某些情况下只能使用绝对数：传染病疫情描述，突 发事件的描述
Counts：频数 Observed：实际频数
Expected：理论频数
Percentages：百分比 Row：行百分比 Column：列百分比 Total：总百分比
例题2：
研究者希望知道不同性别和血型的交叉频数分布表， 以及不同性别和教学背景的交叉频数分布表，各种百分 比的情况，用Crosstable过程输出列联表（student.sav）
With normal curve：输出正态曲 线 Chart values：绘图指标 Frequencies：频数 Percentages：百分比
例题1：
某项调查中，研究者希望了解调查人数中一共有多少学 生，男生和女生各自为多少；各种血型的人数有多少？ 可以使用Frequencies过程输出频数表描述 （student.sav）
练习题：
1.山东省两所学校的高三毕业生的升学情况。试据 此对两所学校的升学情况进行列联表分析。（数据 练习1date.save )
课堂作业：
1.数据Employee data.sav，纪录的是不同性别的工人的学历、生日、工种、 工资等信息。 分析要求： （1）、分别统计不同性别（gender）、不同工种（jobcat）的人数；
100% 同一事物各组成部分的 观察单位总数
构成比例感染的流行病学调查发 现66例感染，感染者的感染部位分布情况见表5.3所示。
表5.3 66例感染者的感染部位分布情况
感染部位
手术创伤感染 呼吸道感染 泌尿道感染 皮肤感染
感染例数
18 16 11 11
定性资料统计描述：SPSS操作
Frequencies过程：对单个变量输出频数表，给出统计量以及绘制 条图和饼图 Crosstabs过程：对两个或多个分类变量联合描述，产生多维列联 表，还可进行分类资料的统计推断；
常用的统计表
菜单介绍：
Analyze →Descriptive Statistics →Frequencies
速率
观察时段内某现象的发生数 K 可能发生某现象的观察人时数
频率的计算
（书上例5.1） 利用2008年泸州市健康城市调查数据，对吸烟与 慢性阻塞性肺部疾病（COPD）的关系分析，结果见表5.1。试
计算该资料中吸烟者与不吸烟者患COPD的患病率。
表5.1 吸烟和不吸烟人群患COPD的情况
患COPD人数
（2）、输出关于不同性别（gender）、不同工种（jobcat）的交叉列联表； 2. 完成描述练习 题.save格式提交） 习题中的作业。（ Word 版 作业要求， 做完以后以习
小结
定性资料频数描述---- Frequencies 过程 可以产生相应的条图，圆图
可以产生频数分布表
分类变量的描述—交叉列联表输出→Crosstables
注意：1. 甲乙指标可以相同，也可以不同 2.甲乙指标可以是绝对数，也可以是 相对数或 平均数
案例辨析题：
某地1965年和1970年几种主要急性传染病发病情况如下。某 医生根据此资料中痢疾与乙脑由1965年的44.2%与3.4%分别增加 到1970年的51.9%和5.2%，认为该地1970年痢疾与乙脑的发病率 升高，该结论是否正确为什么？
Frequencies....
Percentile Values：百分位数 Quartiles：四分位数
Cut points for equal groups：分成相等的M 组
Percentile（s）：输入需计算的百分位数 Central Tendency：集中趋势统计量 Mean：算术均数
Median：中位数
动态数列，率的标准化
动态数列：一系列按照时间顺序排列起来的统计指标，用以反映事物或现 象在时间上的变化和发展趋势。常用的动态数列有 绝对增长量、发展速度与 增长速度、平均发展速度与平均增长速度。 率的标准化：标准化的意义，直接和间接标准化法的应用。 标准化：在对合计率进行比较时，如果各组观察对象内部构成不同，应考 虑对合计率进行标准化。标准化法就是采用统一的标准构成，消除因混杂因 素构成不同对总指标的影响。 直接法：已知被标化组的年龄别死亡率； 间接法：只给年龄别人口数和死亡总数；
输出结果：
率的标准化：
• （书 29页练习3）表5-4 资料分析比较甲乙两厂职工 的高血压患病率。
SPSS操作
1.数据录 入
2.分析：要生成变量 transform→compute variable... target variable: 键入 sp numeric expression：键入p1+p2 ok transform→compute variable... target variable: 键入 sp1 numeric expression：键入c1/p1*sp ok transform→compute variable... target variable: 键入 sp2 numeric expression：键入c2/p2*sp ok
2.分析：要分析的变量 Analyze→descriptive statistics→descriptive ... Variable(s): sp sp1 sp2 点击options.......选择sum continue ok
3.输出结果： 将spss输出的结果sp1之和除以sp的和，得到甲厂职工高血压标 准化患病率，sp2之和除以sp的和，得到乙厂职工高血压标准化 患病率。
未患COPD人数
合计
吸烟 不吸烟
136 161 297
2635 5409
2771 5570 8341
合计
316
计算结果：
吸烟者COPD的患病率=4.91%
不吸烟者COPD的患病率=2.89%
吸烟者COPD的患病率比不吸烟者COPD的患病率高2.02%。
速率的计算： （书上例5.2） 在一项随访研究中，对125人追踪随访了2年， 结果有2人发生了死亡，则由公式可得：
Statistical description of qualitative data
实习目的
掌握 定性资料常用描述指标 等相对数； 率 构成比 相对比
应用相对数应该注意的问题 熟悉 常用动态数列指标，率的标准化
理论复习
常用相对数及其应用：
率（frequency) 构成比 (proportion)
相对比 (ratio)
率（frequency)：
概念：是指某种现象在一定条件下，实际发生的观察单位 数与可能发生该现象的总观察单位数之比，用以说明某种 现象发生的频率大小或强度。 分类：频率和速率 （分母的观察单位总数是否引入时间因素） 计算公式：
频率 同时期实际发生某现象的观察单位数 K 某时期可能发生某现象的观察单位总数
构成比
27.27 24.24 16.67 16.67
胃肠道感染
其他 合计
4
6 66
6.06
9.09 100.00
相 对 比 (ratio)
概念：是指两个有关联的指标之比值，用以说明一个指标是另 一指标的几倍或几分之几。 计算公式：
相对比 甲指标 (或 100%) 乙指标
如：男女性别比、CV等
Dispersion：离散程度统计量 Std. deviation：标准差 Variance：方差 Distribution：分布指标 Skewness：偏度系数
Kurtosis：峰度系数
Frequencies....
绘制统计图对话框： Bar charts：条图 Pie charts：饼图
Histograms：直方图
输出结果：
Crosstables过程
Crosstabs过程主要功能：
产生二维至n维列联表（交叉表作用）
计算百分数指标、期望频数、汇总指标等 计算度量行、列变量关联度的指标及其检验 成组、配对、分层卡方检验 计算任意维列联表的确切概率值
Crosstables…
操作提示： Analyze →Descriptive Statistics →Crosstables…
2 年死亡率= 100%=0.8% 125 2
构成比 (proportion)
概念：也叫构成指标，是指一事物内部某一组成部分的观察单 位数与该事物各组成部分的观察单位总数之比，用以说明某一事 物内部各组成部分所占的比重或分布。 计算公式： 某一组成部分的观察单 位数
构成比
构成比具有以下特点： • 分子是分母的一部分，各组成部分构成比数值之和等于1或 100 • 事物内部各组成部分之间呈此消彼长关系，当其中某一组成部 分构成比数值增大，其他组成部分的构成比数值必然会减少。
率和构成比的区别
构成比 率
1.各部分可直接相加
各率不可相加
2.各部分之和等于100或1
总率不一定等于各率之和
3.某部分变化，其他部分随着变化
某率的变化，不影响其他各率
4.是说明比重和分布的，反映事物内部各 个部分之间的比例关系。
表示某现象发生的频率和强度
应用相对数时的注意事项：
分析时不能以构成比代替率（重点） 计算相对数应有足够的观察单位数：分母不能太小 应分别将分子和分母合计求合计率 相对数的比较应注意其可比性 两个样本率比较时应进行假设检验 某些情况下只能使用绝对数：传染病疫情描述，突 发事件的描述
Counts：频数 Observed：实际频数
Expected：理论频数
Percentages：百分比 Row：行百分比 Column：列百分比 Total：总百分比
例题2：
研究者希望知道不同性别和血型的交叉频数分布表， 以及不同性别和教学背景的交叉频数分布表，各种百分 比的情况，用Crosstable过程输出列联表（student.sav）
With normal curve：输出正态曲 线 Chart values：绘图指标 Frequencies：频数 Percentages：百分比
例题1：
某项调查中，研究者希望了解调查人数中一共有多少学 生，男生和女生各自为多少；各种血型的人数有多少？ 可以使用Frequencies过程输出频数表描述 （student.sav）
练习题：
1.山东省两所学校的高三毕业生的升学情况。试据 此对两所学校的升学情况进行列联表分析。（数据 练习1date.save )
课堂作业：
1.数据Employee data.sav，纪录的是不同性别的工人的学历、生日、工种、 工资等信息。 分析要求： （1）、分别统计不同性别（gender）、不同工种（jobcat）的人数；
100% 同一事物各组成部分的 观察单位总数
构成比例感染的流行病学调查发 现66例感染，感染者的感染部位分布情况见表5.3所示。
表5.3 66例感染者的感染部位分布情况
感染部位
手术创伤感染 呼吸道感染 泌尿道感染 皮肤感染
感染例数
18 16 11 11
定性资料统计描述：SPSS操作
Frequencies过程：对单个变量输出频数表，给出统计量以及绘制 条图和饼图 Crosstabs过程：对两个或多个分类变量联合描述，产生多维列联 表，还可进行分类资料的统计推断；
常用的统计表
菜单介绍：
Analyze →Descriptive Statistics →Frequencies
速率
观察时段内某现象的发生数 K 可能发生某现象的观察人时数
频率的计算
（书上例5.1） 利用2008年泸州市健康城市调查数据，对吸烟与 慢性阻塞性肺部疾病（COPD）的关系分析，结果见表5.1。试
计算该资料中吸烟者与不吸烟者患COPD的患病率。
表5.1 吸烟和不吸烟人群患COPD的情况
患COPD人数
（2）、输出关于不同性别（gender）、不同工种（jobcat）的交叉列联表； 2. 完成描述练习 题.save格式提交） 习题中的作业。（ Word 版 作业要求， 做完以后以习
小结
定性资料频数描述---- Frequencies 过程 可以产生相应的条图，圆图
可以产生频数分布表
分类变量的描述—交叉列联表输出→Crosstables
注意：1. 甲乙指标可以相同，也可以不同 2.甲乙指标可以是绝对数，也可以是 相对数或 平均数
案例辨析题：
某地1965年和1970年几种主要急性传染病发病情况如下。某 医生根据此资料中痢疾与乙脑由1965年的44.2%与3.4%分别增加 到1970年的51.9%和5.2%，认为该地1970年痢疾与乙脑的发病率 升高，该结论是否正确为什么？
Frequencies....
Percentile Values：百分位数 Quartiles：四分位数
Cut points for equal groups：分成相等的M 组
Percentile（s）：输入需计算的百分位数 Central Tendency：集中趋势统计量 Mean：算术均数
Median：中位数
动态数列，率的标准化
动态数列：一系列按照时间顺序排列起来的统计指标，用以反映事物或现 象在时间上的变化和发展趋势。常用的动态数列有 绝对增长量、发展速度与 增长速度、平均发展速度与平均增长速度。 率的标准化：标准化的意义，直接和间接标准化法的应用。 标准化：在对合计率进行比较时，如果各组观察对象内部构成不同，应考 虑对合计率进行标准化。标准化法就是采用统一的标准构成，消除因混杂因 素构成不同对总指标的影响。 直接法：已知被标化组的年龄别死亡率； 间接法：只给年龄别人口数和死亡总数；
输出结果：
率的标准化：
• （书 29页练习3）表5-4 资料分析比较甲乙两厂职工 的高血压患病率。
SPSS操作
1.数据录 入
2.分析：要生成变量 transform→compute variable... target variable: 键入 sp numeric expression：键入p1+p2 ok transform→compute variable... target variable: 键入 sp1 numeric expression：键入c1/p1*sp ok transform→compute variable... target variable: 键入 sp2 numeric expression：键入c2/p2*sp ok
2.分析：要分析的变量 Analyze→descriptive statistics→descriptive ... Variable(s): sp sp1 sp2 点击options.......选择sum continue ok
3.输出结果： 将spss输出的结果sp1之和除以sp的和，得到甲厂职工高血压标 准化患病率，sp2之和除以sp的和，得到乙厂职工高血压标准化 患病率。
未患COPD人数
合计
吸烟 不吸烟
136 161 297
2635 5409
2771 5570 8341
合计
316
计算结果：
吸烟者COPD的患病率=4.91%
不吸烟者COPD的患病率=2.89%
吸烟者COPD的患病率比不吸烟者COPD的患病率高2.02%。
速率的计算： （书上例5.2） 在一项随访研究中，对125人追踪随访了2年， 结果有2人发生了死亡，则由公式可得：