非局部时滞反应扩散方程的行波解和渐近传播速度
反应扩散方程的行波解与几类方程的多解性的开题报告

反应扩散方程的行波解与几类方程的多解性的开题报告一、研究背景反应扩散方程是生物学、化学、物理学、材料科学等多个领域中常见的数学模型之一。
该方程描述了在空间中扩散物质同时发生反应的行为,其研究具有重要意义。
其中,行波解是反应扩散方程中的一种特殊解,指方程中扰动沿着波前不断向前传播的解。
近年来,行波解在反应扩散方程解析解研究中得到了广泛应用。
另外,很多方程,包括非线性方程、拟线性方程和奇异摄动方程等,具有多解性,对其研究也非常有意义。
二、研究目的本文的研究目的是探讨反应扩散方程的行波解及几类方程的多解性。
具体研究内容包括:1. 分析反应扩散方程的基本形式及性质,并介绍行波解的概念;2. 探究反应扩散方程的行波解的构造方法;3. 研究几类方程的多解性,包括非线性方程、拟线性方程和奇异摄动方程等;4. 说明多解性的出现与方程的特殊性质的关系,并对其物理意义进行解释。
三、研究方法本文采用文献研究和数学分析相结合的方法。
首先,对反应扩散方程及相关的其他方程进行文献综述,了解其现状和研究进展。
然后,对于反应扩散方程的行波解和其他方程的多解性进行数学分析,探究其性质和构造方法,并进行例题分析和数值模拟。
最后,对研究结果进行总结和讨论,提出未来研究的方向。
四、研究意义本文的研究结果有以下几个方面的意义:1. 加深对反应扩散方程和其他一些特殊方程的理解和认识,促进其在实际场景中的应用;2. 发现和探究反应扩散方程的行波解及其他方程的多解性,有助于提高研究者对这些方程性质的认识,并为准确求解提供可能;3. 为进一步研究反应扩散方程及其他方程的特殊解提供思路和方法,开拓研究领域。
一类带时滞生物反应扩散方程的行波解

[ 0 , ] c : { ∈ C , : 0 ( ) , 0 ∈ [ 一 , 0 ]o
考察初值 问题 ,
{ ,
L v ( O ) = ( ) , 0∈[ 一 , O ] .
有
,
( 2 . 2 )
其中, 6 ( 1 , ) =m 。 a x b ( u ) , 则可知 6 在 + 上单调非减・ 由条件 ( h 1 ) 一( 2 ) 我们知存在 w w ,
( 2 ) 6 ’ ) 在R + 上存在;b ( o ) =O , b ’ ( w ) < O , d < ’ ( 0 ) .
由以上假设易知, 方程 ( 2 . 1 ) 存在两个平衡点, 分别设 为 :E =0和 E,=: ( ) , 0∈[ 0 , 1 ] , 称函数 ) , ( t ∈ [ 一 r , 】 ) 为方程( 2 . 1 ) 在[ - y , ] 的一个上( 下) 解是
1 引言
本文研究 如下一类带时滞和全局反应 的方程的行波解:
Uf
:
 ̄ 7 X
+ f ( j c — y ) 6 ( w ( t - r , y ) ) a y — d w ( f , j c )
…
( 1 . 1 )
P 一 _r 和 =e .
其 中,w ( t , ) 表示生物种群在时刻 和地点 x处的密度 函数,b ( w ( t — , ) ) 代表该生物种群 的生长函数,
指:
( ) m b / 0 ) + 6 ( 甜 ( f —r ) ) , f ∈[ 0 , ) ,
dt
( ) ( ) ( ) , 0∈[ 一 , 0 ) .
设C , =C ( [ 一 , O ] , R ) 为定义在区间[ 一 , 0 ] 到实数集R上由连续函数生成的B a n a c h 空间,C , : c ( [ 一 , , 0 ] , R + )
具有阶段结构的Gilpin-Ayala竞争系统的行波解

) 一
) e r + - r
cu r
d () z 十o 一 2z ' 一 ! () 2 () 2 ) 0 z 一c2 ) t ¨ ( —c ) 2 一c ( = . ( v e E l
、
! l: =0 i l ) l i a r () ,l a r ( =k 系统( .) 2 1在条件 :’ r一 r一 + 下是可解的. 1 2 。 = ,l 2 ) i m ( ) 2 i m ( =0
f = ( ( 一 -) C ( ) £ a ( 一l f , d u ) )
【 =( ( 一u ( 一2 £ . £ 口  ̄9£ C ( ) d v ) t ) ) t 2
其 中, () t分别表示 t U t, ) ( 时刻两种群的密度 ; o,lc 分别表示两种群的出生率和竞争系数 ,1 2 a , c,2 / , 表示非线性密度制约项 . 5构造并研究了具有离散时滞 的 Gln A a 竞争模型 : 文[] ii— yl p a
和 Zu o 建立的一般有限时滞的反应扩散方程组 波前解存 在性的理论 ,证明 了连接两个 边界平衡 解
的行波解 的存在性 。
( 词]阶段结 构 ;时滞 ;行波解 ;平衡点 ;反应扩散方程 关键 [ 中图分 类号]O 7 1 5 [ 文献标识码 ]A [ 文章编号 ]1 8 7X 21)3 00 — 5 0 —1 ( 10 — 05 0 0 8 0
【 = c + (一 戈一 d v 口一 £ ) J a u , ( 一2( xv , . f)C ‘) t) , , (
( .) 0 2
,、
其中 ∈AcR 且Q有界 , > ,u d 表示种群 I 口 t 0 d ,v t , 的扩散系数 , 和 △为n上的 Lp c n al i 算子. aa
一类单稳时滞格微分方程行波解的渐近行为及唯一性

●
Ke r s:ta ei gwa es lto y wo d rv l v o u in;mo o t bl y;ltied fe e t l q ain;t ea n n sa i t a t i r n i u to i c f ae i d ly me
( 时滞 ) 格微 分方 程是 一 类 由无 穷 多 个 ( 函微 泛
分 方程) 常微分 方 程 构成 的系 统.这 类 系统 一 方 面 来 源于 众 多 的实 际 问题 ,例 如模 拟相 变 过 程 _ 、 1 模 ] 拟 斑块 上 的人 口增 长 l 等. _ 2 另一 方 面 ,它 们 也 是偏 微分 方程 的空间 离散形式 .行 波解 是微 分 方程 的一
n n lc l if so n o - c l n e a t n we esu id Th x c s mp o i e a iro h v r — o —o a fu in a d n n l a tr ci r t de . d o i o ee a ta y t t b h vo ft ewa ep o c f e se ± ∞ wa sa l h d Alo,i wa r v d t a l t e ta eig wa e s l t n r tity i sa l se tb i e . s s t s p o e h tal h r v l v ou i s we e srcl n o
源 以常数波 速在 空 间 中传 播 等. 年来 ,( 滞 ) 近 时 格
K ()< 。 。
函
( 2 b E , , )『o 一6是 一 A ) C (0K]R ,( ) () 一 , E J O
反应扩散方程的行波解及相关的反应方程的持续生存性研究的开题报告

反应扩散方程的行波解及相关的反应方程的持续生存性研
究的开题报告
题目:反应扩散方程的行波解及相关的反应方程的持续生存性研究
研究背景:
反应扩散方程是描述物质传输及化学反应过程的一类重要方程,在物理、化学、生物学等多个领域都有广泛应用。
其中,反应扩散方程中存在自发反应以及扩散、对流等输运现象。
在很多实际应用中,自发反应往往是非线性的,这使得方程的求解变得非常困难。
为了解决这个问题,许多研究人员提出了各种方法,其中行波解方法是一种有效的分析和求解途径。
研究内容:
本研究主要围绕反应扩散方程的行波解及相关的反应方程的持续生存性展开。
具体来说,包括以下内容:
1. 探究反应扩散方程的行波解及其性质;
2. 分析反应扩散方程的稳定解和非稳定解;
3. 研究反应方程的持续生存性,即反应过程能否继续进行而不会消失;
4. 验证理论结果,并进行数值模拟。
研究意义:
本研究不仅有助于深入理解反应扩散方程及其应用,也能为相关领域的实际问题提供一定的参考和解决思路。
具体而言,本研究将为生物发展和环境污染控制等方面的实际问题提供参考。
研究方法:
本研究将采用分析和数值模拟相结合的方法,利用行波解、Lyapunov函数等数学工具,研究反应扩散方程中的行波解性质及反应方程的持续生存性。
同时,对于一部分特殊情况还将对其进行数值模拟验证,以验证理论结果的可靠性。
预期成果:
通过本研究,预计能够得到包括以下方面的成果:1. 提出反应扩散方程的行波解及其性质;2. 探究反应方程的持续生存性;3. 对一些特殊情况进行数值模拟,并验证理论结果的可靠性。
非局部时滞反应扩散方程行波解的存在性

:
(.) 1, 5
方程 (.) 前解 的存在 性 已经在 文献 [2 1] 15 波 1,6 中被研 究.
如果核函 数被取成 h , = ( 孝e÷或 h , = 1— , ( t z 一 x) ) ( t ( t对应的卷积 h 被定义 x) )e u
为
, t
( ) , = / (—s (,)s h ( t t ) xsd. ) u
十 d ≥ 。\ , , , 2 ( ) 9 ( )\ , +( , ) 乱 , \ ,
:
\ () …, 1 . 4
收稿 日期 : 0 91 —0 修订 日期: 0 10 — 0 2 0 —02 ; 2 1 — 82 E m al la g t @ 16c m ; a h @n n .d .n — i in ma h 2 .o g o j j ue uc :f
基金项 目:国家 自然科学基金 (07 07 和安徽 省高等学校 省级优 秀人才基金 (0 1QR l5 18 19 ) 2 1S L l)资助
l 7 24
数
学
物
理
学 报
、 1l ,. A 03
这个方 程 已经 被很 多研 究者 广泛研 究, 参见文 献 [. 7 如果 核 函数被取 成 hxt= t ) ] (,) ()(一丁 这 时方程 (. 被 简化 为 11 ) O (,) u t x a 一d a 2 +y ̄x , , . ,)乱 一丁) t ’(’ t “ ). ,。 ,
性链技巧和几何奇异 扰动理论 有机结合,建立了带有非局部 时滞 反应扩散 方程和对应的不带 时滞反应扩散方 程行 波解 存在性之间的 自然联系.得到如果不带 时滞反应 扩散方程行波解存 在,则在时滞充分小的条件下对应的带时滞反应扩散方程行波解也存在.
时滞反应扩散方程(组)的行波解和整体解

【正文】时滞反应扩散方程(组)的行波解和整体解一、引言时滞反应扩散方程(组)作为一类重要的非线性偏微分方程,在生物学、生态学、化学工程等领域都具有重要的应用价值。
本文将围绕时滞反应扩散方程(组)的行波解和整体解展开讨论,通过深入分析和探讨,帮助读者对这一主题有更深刻的理解。
二、时滞反应扩散方程(组)的基本形式时滞反应扩散方程是描述空间中自然界中的许多现象的重要数学模型,其一般形式可以写为:\[ u_t = d\Delta u + f(u) - \int_0^{\tau} k(s)g(u(x-s))ds \]其中,\( u(x,t) \) 是待求函数,表示空间位置为x、时间为t时的物理量;\( d \) 是扩散系数;\( f(u) \) 是物质的产生项和消耗项;\( k(\tau) \) 是时间滞后函数;\( g(u) \) 则表示物质的扩散项。
对于时滞反应扩散方程(组)的行波解和整体解的研究,需要深入理解方程中的各个参数和函数,以及它们之间的相互作用关系。
本文将分别从行波解和整体解两个方面进行探讨。
三、时滞反应扩散方程(组)的行波解行波解是非线性偏微分方程中的一类特殊解,描述了波的传播和形变过程。
对于时滞反应扩散方程(组),其行波解的研究是非常重要的。
行波解可以通过变量变换和特定的求解方法得到,通常具有局部化、稳定性和非扩散性等特点。
针对时滞反应扩散方程(组)的行波解,我们可以通过一系列的推导和分析,得到其具体的数学形式。
在得到行波解的还需要对解的性质和行为进行分析和讨论,以便更好地理解方程描述的现象和规律。
基于行波解的特点,我们可以进一步讨论时滞反应扩散方程(组)在具体问题中的应用,例如在生态系统中的物种传播和竞争问题,以及化学反应过程中的物质扩散和转化等。
通过具体的案例分析和数值模拟,可以更直观地展示行波解在实际问题中的作用和意义。
四、时滞反应扩散方程(组)的整体解除了行波解之外,时滞反应扩散方程(组)的整体解也是我们关注的重点。
【国家自然科学基金】_非局部时滞_基金支持热词逐年推荐_【万方软件创新助手】_20140802
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词 推荐指数 时滞 2 非线性抛物方程 1 非局部项 1 非局部时滞反应扩散方程 1 非局部时滞 1 适定性 1 辛方法 1 行波解 1 界带分析 1 理想 1 捕食系统 1 子结构法 1 图像处理 1 反应扩散 1 博览会 1 单调性 1 分析结构力学 1 全局稳定性 1 交叉迭代 1 上下解 1 upper-lower solutions 1 traveling wave solutions 1 reaction-diffusion system 1 partially exponential quasi-monotonicity. 1
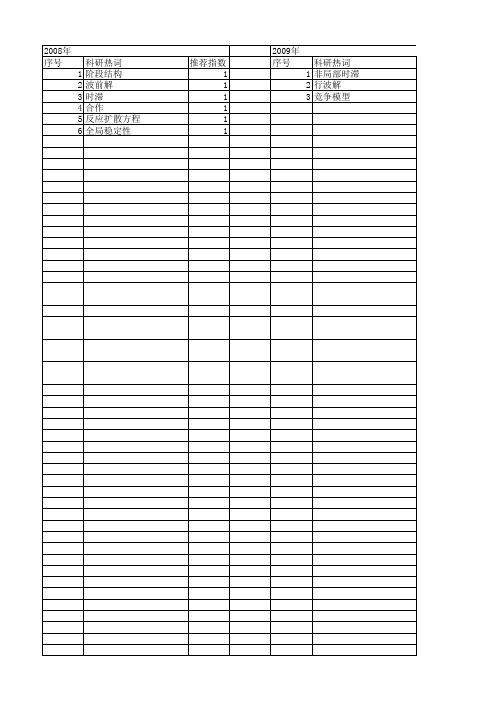
2008年 序号 1 2 3 4 5 6
科研热词 阶段结构 波前解 时滞 合作 反应扩散方程 全局稳定性
推荐指数 1 1 1 1 1 1
2009年 序号
科研热词 1 非局部时滞 2 行波解 3 竞争模型
推荐指数 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 推荐指数 非局部时滞 1 非局部 1 行波解 1 渐近波速 1 波前解 1 最小波速 1 时滞 1 扩散nicholson苍蝇方程 1 强生成核 1 发展方程 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12
2011年 科研热词 推荐指数 行波解 4 非局部扩散 2 时滞 2 非局部时滞 1 阶段结构 1 格微分方程 1 捕食-被捕食系统 1 单稳 1 几何奇异扰动理论 1 上下解方法 1 上下解 1 lotka-volterra竞争模型 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非局部时滞反应扩散方程的行波解和渐近传播速度
非局部时滞反应扩散方程的行波解和渐近传播速度
1.引言
非局部时滞反应扩散方程是一类常见的数学模型,在物理、生物学和化学等领域都有广泛的应用。
这类方程描述了物质或生物种群在非局部时滞条件下的传播、扩散和反应行为。
研究非局部时滞反应扩散方程的行波解和渐近传播速度对于理解和预测各种动态现象至关重要。
2.方程及基本概念
我们考虑一维非局部时滞反应扩散方程:
\[\frac{{\partial u}}{{\partial t}}(x,t) =
D\frac{{\partial^2 u}}{{\partial x^2}}(x,t) + f(u(x,t-\tau)), \quad x \in \mathbb{R}, t > 0\]
其中,$u(x,t)$是扩散物质或生物种群的密度函数,$D$是扩
散系数,$f(u)$是非线性的反应函数,$\tau$是时间延迟。
行波解是指方程中存在波动形式的解,其具有固定的传播速度和波形。
行波解在许多应用中具有重要的意义,例如描述火焰传播、疾病传播等。
渐近传播速度是指行波解中的波前(或波峰)传播的速度,也代表了传播或扩散过程中的特征速度。
研究行波解的渐近传播速度可以更好地理解和控制各种动态现象。
3.经典行波解的构造
对于非局部时滞反应扩散方程,我们可以使用传统的行波解方法来寻找解的形式。
根据经典的行波解构造方法,我们假设方程中的行波解可以写成如下形式:
\[u(x,t) = \phi(x - ct)\]
其中,$\phi$是波形函数,$c$是行波解的传播速度。
将波动形式的解带入方程,可以得到一个常微分方程:\[-c\phi' = D\phi'' + f(\phi(x-\tau))\]
我们可以通过适当的变换和近似方法,将上述方程进一步简化。
例如,当反应函数$f(u)$为饱和型的时候,我们可以使用Kolmogorov定理来求解波形函数$\phi$。
在一些特殊的情况下,我们还可以使用拟线性化方法来求解行波解。
4.行波解的稳定性和渐近传播速度
行波解的稳定性是指行波解是否是方程的稳定解,即初始条件的扰动是否会导致行波解的瓦解。
对于非局部时滞反应扩散方程,行波解的稳定性是一个重要的研究问题。
研究行波解的稳定性可以通过线性化方程和稳定性分析方法来进行。
将行波解进行小扰动,线性化方程可以得到一个线性的抛物型方程。
通过分析方程的特征值和特征函数,可以判断行波解的稳定性。
渐近传播速度的研究涉及到时滞因子和反应函数的具体形式。
一般来说,在反应函数的非线性程度较低时,可以使用传统的渐近传播速度公式:
\[v = \frac{{c}}{{1 + \frac{{b}}{{c}}\int_0^{\infty} e^{-cs}f'(\phi(x-\tau - s))ds}}\]
其中,$b$是非线性反应函数的线性项系数。
然而,当反应函数的非线性程度较高时,计算渐近传播速度就变得困难。
此时,研究人员通常采用数值方法或近似方法来估计渐近传播速度。
5.应用和展望
非局部时滞反应扩散方程的行波解和渐近传播速度的研究在生物学、物理学、化学等领域具有广泛应用。
例如,在生物
入侵模型中,通过研究行波解和渐近传播速度可以预测物种如何快速传播并制定相应的控制策略。
未来的研究可以进一步扩展非局部时滞反应扩散方程的应用领域,探索更加复杂的模型和更加精确的解析方法。
同时,使用数值方法和计算模拟手段来研究行波解和渐近传播速度也是一个重要的方向。
这将为我们更好地理解和预测各种动态现象提供有力的工具和理论基础
综上所述,非局部时滞反应扩散方程的行波解和渐近传播速度的研究在多个领域具有广泛应用。
传统的渐近传播速度公式适用于反应函数非线性程度较低的情况,而对于高非线性程度的情况,需要采用数值方法或近似方法来估计渐近传播速度。
未来的研究可以进一步拓展该方程的应用领域,并探索更复杂的模型和更精确的解析方法。
此外,使用数值方法和计算模拟手段来研究行波解和渐近传播速度也是重要的研究方向,这将为我们更好地理解和预测各种动态现象提供有力的工具和理论基础。
