《建筑力学》第十章_结构的几何组成分析
建筑力学课程教学大纲

《建筑力学》课程教学大纲一、本课程的地位、作用和任务《建筑力学》是水利水电建筑工程专业的一门重要的专业基础课,在本专业中起着承上启下的作用,为后续课程打基础。
《建筑力学》的任务是:教授学生掌握物体受力分析与静力平衡问题的求解方法;杆件及结构内力与变形的分析方法;关于构件的强度、刚度与稳定性的计算及构件应力、应变的方法。
通过本课程的学习,要求学生具备对常见结构、构件进行受力分析、内力与变形计算的能力,并初步具备对结构的实验分析能力。
二、教学内容和教学要求第一章绪论1、教学内容建筑力学的研究对象、研究方法、主要内容。
2、教学要求了解建筑力学课程的性质、地位和作用,了解建筑力学各部分的内容、了解建筑力学的学习方法。
第一篇、静力学第二章刚体静力分析基础1、教学内容2—1 力与力偶1)力的概念和性质2)力对点之矩3)力偶的概念和性质2—2 约束与约束反力1)约束与约束反力的概念2)工程中常见的约束与约束反力2—3 受力分析与受力图2、教学要求(1)理解力、力对点的矩、平面力偶的概念及静力学的四个公理,合力矩定理、刚体的概念;掌握平面力偶系合成的计算。
(2)了解约束的概念及荷载的分类;了解作用在构件上荷载的计算方法;掌握常见工程中的约束类型及其约束反力的确定;第三章平面力系1、教学内容3—1 平面力系向一点的简化1)力的平移定理2)平面力系向一点的简化3)力在坐标轴上的投影主矢与主矩的计算4)平面力系向一点简化结果的进一步分析3—2 平衡方程及其应用1)平面一般力系的平衡条件和平衡方程2)平面力系的几种特殊情形3)静定与超静定问题4)物体系的平衡问题2、教学要求(1)了解力的平移定理的内容;掌握力在坐标轴上的投影的概念及计算,掌握合力的投影定理;(2)理解平面一般力系的概念;了解平面一般力系向一点简化和简化结果分析。
(3)掌握平面一般力系、平面汇交力系、平面平行力系及平面力偶系的平衡方程及其应用,重点掌握常见物体支座反力的求法。
平面体系几何组成分析的方法(静定的概念)(建筑力学)
例题分析
例1.分析图示体系的几何构造性。 解析:(1)计算自由度
W 4244 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 进一步判断,依次去掉二元体DFE、BDC、BEC、BCA后,整个体系只剩下 地基了,为几何不变体系。由于去掉二元体并不改变原体系的几何构造性,因此 原体系也是几何不变体系。
二元体规则是非常好用的规则,特别是去二元体,可以大大简化体系 构件数目,使判断简化,其主要有以下几个技巧:
(1)根据需要进行链杆与刚片之间的转化,巧妙使用二元体; (2)当体系比较复杂时,可以先考虑其中的一个它部分之间的连接关系, 判定整个体系的几何构造性。
例题分析
例2.分析图示体系的几何构造性。 解析:(1)计算自由度
W 72 113 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 体系没有二元体,但体系本身是有二元体的,去掉所有二元体,只剩下一个 杆件,所以体系本身几何不变,再考虑其与地基的连接方式,判定体系几何不变。
总结与技巧
示例
例1.分析图示体系的几何构造性。
解析:(1)计算自由度
W 7277 0
体系具有成为几何不变体系的最少约束数目,需进一步判断。 (2)依次去掉二元体FAB、IED、FBJ、IDC如图所示。 (3)三角形GCH看作刚片Ⅰ,地基看作特殊刚片Ⅱ。 (4)刚片Ⅰ、Ⅱ之间通过三根链杆相连,三链杆汇交
《建筑力学》第十章结构的几何组成分析

案例二:复杂结构的几何组成分析
总结词
通过分析复杂结构的几何组成,理解超静定 结构和静定结构的区别。
详细描述
复杂结构通常由多个简单结构组合而成,通 过分析这些结构的连接方式和力的传递路径, 可以判断复杂结构是超静定结构还是静定结 构。超静定结构有多余的约束,使得结构在 力的作用下发生变形,而静定结构则没有多 余的约束,不会发生变形。
02
根据地震的烈度和频率,设计合理的抗震支撑和减震措施。
通过结构的几何组成分析,优化结构的抗震设计,提高结构的
03
抗倒塌能力。
05
案例分析
案例一:简单框架结构的几何组成分析
总结词
通过分析简单框架结构的几何组成,理解几何不变体系和几何可变体系的概念。
详细描述
简单框架结构由若干直线段组成,通过分析这些直线段的连接方式,可以判断 整个结构是几何不变体系还是几何可变体系。几何不变体系在力的作用下不会 发生变形,而几何可变体系则会发生变形。
规则二:多余约束
总结词
多余约束是指结构中存在某些约束,这些约束在限制某些自由度的同时,并没有提供稳定性或平衡性的贡献。
详细描述
多余约束规则指出,一个稳定的结构中不应该有多余的约束存在。多余的约束不仅浪费材料和资源,而且可能导 致结构在受到外力作用时出现失稳或破坏。因此,在结构的几何组成分析中,需要找出并消除多余的约束,以确 保结构的稳定性和经济性。
分析结构的支撑体系 是否合理,如支撑杆 件的布局、连接方式 等。
结构优化设计
通过分析结构的几何组成,找出 结构中的冗余杆件和不必要的约
束。
优化结构的支撑布局和连接方式, 提高结构的承载能力和刚度。
调整结构的几何形状,以改善结 构的受力分布和减少应力集中现
建筑力学第10章

[例] 试计算截面对水平形心轴 c的惯性矩。 例 试计算截面对水平形心轴y 的惯性矩。
z
10
单位: 单位:mm ①
125 C1
已算出该截面形心C的坐标为 的坐标为: 解:已算出该截面形心 的坐标为: yc=19.36mm,zc=41.9mm , 截面对轴y 的惯性矩应等于矩形①对轴y 截面对轴 c的惯性矩应等于矩形①对轴 c的惯 性矩加上矩形② 轴的惯性矩。 性矩加上矩形②对yc轴的惯性矩。即:
z2=5mm
C2
②
80
10
y
y1 ⋅ A1 + y2 ⋅ A2 = 19.36mm A1 + A2 z1 ⋅ A1 + z 2 ⋅ A2 zc = = 41.9mm A1 + A2 yc =
截面对y轴的静矩 截面对 轴的静矩 为:
S y = A1 z1 + A2 z 2 = (1250 × 62.5 + 700 × 5)mm 3 = 8.16 ×10 4 mm 3
200mm
R80mm
x
图示截面看成是矩形截面在左右各方, 解:图示截面看成是矩形截面在左右各方, 挖去两个半圆构成,因此,图示截面对x轴 挖去两个半圆构成,因此,图示截面对 轴 的惯性矩等于矩形对x轴的惯性矩减去两个 的惯性矩等于矩形对 轴的惯性矩减去两个 半圆的惯性矩, 半圆的惯性矩,即:
200 200mm
建筑力学
9.4 主惯性轴和主惯性矩
z y z
dA
I y1 =
I z1 =
Iy + Iz 2 I y + Iz
2 Iy − Iz 2
+
−
Iy − Iz 2 I y − Iz
结构力学概论几何组成分析

35
w不仅是自由度数,也是静力计算参数:
1、w>0,几何可变体系或机构,3m>2h+r,体系不能维持
静力平衡,无静力解答;
2、 无多余约束的几何不变体系, w=0, 3m=2h+r,独立的
平衡方程数等于未知力的个数。用静力平衡方程即可确定所有反 力和内力,静定结构。
3、 有多余约束的几何不变体系, w<0, 3m<2h+r,独立的
建筑力学
平面体系的几何组成分析
3
§8-2 杆件结构的计算简图
1.结构体系的简化
一般的构结都是空间结构。但是,当空间结构在某一平面内的杆 系结构承担该平面内的荷载时,可以把空间结构分解成几个平面结 构进行计算。本课程主要讨论平面结构的计算。当然,也有一些结 构具有明显的空间特征而不宜简化成平面结构。
建筑力学
平面体系的几何组成分析
1
§8-1 杆件结构力学的研究对象和任务
结构的定义: 建筑物中支承荷载而起骨架作用的部分。 结构的几何分类:
分类名称
特点
实例
杆件结构
由杆件组成的结构,是结构力 学的研究对象
梁、拱、刚架、 桁架
板壳结构
又称壁结构,几何特征是其厚 度要比长度和宽度小得多
房屋中的楼板 和壳体屋盖
9
第 9章 平面体系的几何组成分析
§9-1体系几何组成分析的意义 §9-2几何构造分析的几个概念 §9-3平面杆件体系自由度的计算 §9-4平面几何不变体系组成的基本规则 §9-5平面杆件体系的几何组成与静力特性的关系
建筑力学
平面体系的几何组成分析
10
§9-1 体系几何组成分析的意义
1、两种体系
几何可变体系:在不考虑材料应变条件的下,体系的位置和形状可以改变。 几何不变体系: 在不考虑材料应变条件的下,体系的位置和形状保持不变。
《建筑力学》课件 第十章

第二节 多跨静定梁的内力
静定梁分为单跨静定梁和多跨静定梁。第六章对单跨静定梁的内力分 析已详细阐述,这里不再重复,只介绍多跨静定梁的内力分析。
一、多跨静定梁的概念和组成 若干根梁用中间铰连接在一起,并以若干支座与地基相连或者搁置于 其他构件上所组成的静定梁,称为多跨静定梁。例如,图(a)是多跨静 定梁在公路桥中的应用;图(b)是其计算简图;图(c)是多跨静定梁各 部分之间的支承层次图。
FNCB FNBC FNCD FNDC 0 kN FNAC FNCA 10 kN
计算结果的正、负号,就是实际剪力、轴力的正、负号。
3.平面刚架内力图
平面刚架内力图的基本作法是把刚架拆成杆件,即先求各杆端内力, 然后利用杆端内力分别作各杆的内力图,将各杆的内力图合在一起就是 平面刚架的内力图。
② 作内力图。分别作各单跨梁(梁FD,DB,BA)的内力图,然后 将它们合在一起,就成为多跨静定梁的内力图,弯矩图如图(d)所示, 剪力图如图(e)所示。
(d)
(e)
结合本例,对内力分析方法作进一步讨论,可将内力分析方法归纳 为两种,一种是隔离体分析法,另一种是概念分析法。
按照先附属部分再基本部分的顺序,分别画隔离体进行受力分析的方 法,称为隔离体分析法,如本例分析采用的方法。
(a)
(b)
(c)
从图(c)可知,多跨静定梁由以下两部分构成: ① 基本部分:不依靠其他部分的存在而能独立保持其几何不
变性的部分,一般画在支承层次图的下层,例如,图(a)中的多 跨静定梁,梁AB和CD由支杆直接固定于基础,是几何不变的, 所以梁AB和CD是基本部分。
《建筑力学》第十章 结构的几何组成分析
杆件结构的几何组成分析
•学习目标:掌握自由度、约束等基本概念,掌握平面 几何不可变体系的组成规则,并能正确的进行几何组 成分析,熟悉结构的几何特征与静定性的关系。
第一节 几何组成分析的基本概念
一、几何可变体系与几何不可变体系
1.几何可变体系:几何可变体系是在不考虑材料应 变的条件下,其几何形状或位置可以改变的体系。 2.几何不可变体系:几何不可变体系是在不考虑材 料应变的条件下,其几何形状或位置不能改变的体 系。
一般工程结构在使用过程中,应保持自身的几何
形状和位置不变,必须是几何不变体系,而不能采 用几何可变体系。
3.几何组成分析 几何组成分析是指对体系的几何可变与否进行的分 析和判断。 这里只讨论平面体系的几何组成分析。 4.几何组成分析的目的 ①判别体系是否为几何不变体系,从而确定它是否 能作为结构使用; ②正确区分静定结构和超静定结构,以便选择计算 方法,为结构的内力分析打下必要的基础; ③明确体系的几何组成顺序,有助于了解结构各部 分之间的受力和变形关系,确定相应的计算顺序。
ቤተ መጻሕፍቲ ባይዱ
静定结构的几何组成特征是几何不可变且无 多余约束。 超静定结构的几何组成特征是几何不可变但 有多余约束。 通过几何组成分析可以判定结构是静定的还 是超静定的。
【例10-5】 试对如图10-16(a)所示体系进行几何 组成分析。
【解】如图10-16(b)所示,拆除杆GH、CH组成 的二元体,将铰接三角形EGJ视为刚片Ⅰ,再分别 将杆DC和地基视为刚片Ⅱ、Ⅲ,三刚片间彼此用 两两链杆形成的铰E(链杆①、②)、铰K(链杆③、 ④)、铰C(链杆⑤、⑥)连接,且三个铰不在同 一直线上,整个体系为几何不变体系且无多余约束。
建筑力学第10章 平面杆系的几何组成分析
பைடு நூலகம்12
图 10.6 虚铰
13
(3)刚性连接 刚性连接是将两个刚片以整体连接的方式进行 连接,两刚片不发生任何相对运动,即构成一个更 大的刚片。 图 10.8(a)所示的是刚片Ⅰ和刚片Ⅱ间的刚 性连接方式(可设想两者是用钢铁做的,现把它们 焊接在一起,即为刚性连接)。
14
图 10.7 位于 A、D、C 处的铰为复铰
24
图 10.17
25
10.4 几何不变体系组成规则的应用举例 在上一节中介绍了构成几何不变体系的三个基 本规则,并通过几个例题,初步了解了结构几何组 成分析的基本思路。在这里将更详细地讨论如何灵 活运用这些规则,对给定的结构作出几何组成上的 判断。
10
图 10.5 简支梁
11
2)复铰 把同时连接两个以上刚片的铰称为复铰。连接 n个刚片的复铰具有 2(n -1)个约束。 在进行几何组成分析时,会遇到同一个铰连接 多个刚片的情形,如图 10.7所示的位于 A、D、C 处的铰。可以理解为在一个已有刚片上每增加一个 刚片就需要增加一个单铰,因此连接n个刚片的复 铰相当于 n -1个单铰,也即相当于 2(n -1)个约 束。
21
图 10.13 二元体
22
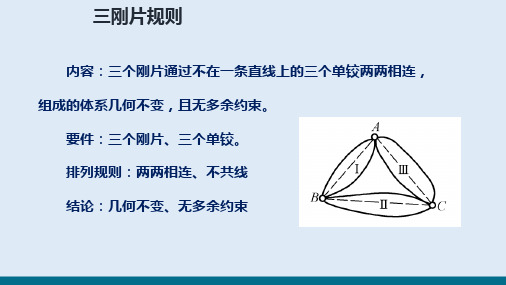
规则二(三刚片规则) 三个刚片用不在同一 条直线上的三个单铰两两相连,组成的体系为几何 不变体系,且无多余约束。
图 10.14 三刚片规则
23
规则三(二刚片规则) 两个刚片用一个铰和 一根延长线不通过此铰的链杆相连,则所得到的体 系是几何不变体系,且无多余联系。
图 10.16 二刚片规则
3
图 10.1
4
10.1.2 平面杆件体系几何组成分析的目的
只有几何不变体系才能作为承担荷载的结构, 而且杆件结构的受力性能和计算方法,都与其几何 组成有关,所以对杆件体系进行几何组成分析其目 的主要是: 1)判别体系是否为几何不变体系,从而决定它能 否作为结构使用; 2)掌握几何不变体系的组成规则,便于了解 结构的受力性能从而设计出合理的结构; 3)用以区分体系为静定结构或超静定结构, 从而选取不同的计算方法。
(完整版)建筑力学(习题答案)
建筑力学复习题一、判断题(每题1分,共150分,将相应的空格内,对的打“√”,错的打’“×”)第一章静力学基本概念及结构受力分析1、结构是建筑物中起支承和传递荷载而起骨架作用的部分。
(√)2、静止状态就是平衡状态。
(√)3、平衡是指物体处于静止状态。
(×)4、刚体就是在任何外力作用下,其大小和形状绝对不改变的物体。
(√)5、力是一个物体对另一个物体的作用。
(×)6、力对物体的作用效果是使物体移动。
(×)7、力对物体的作用效果是使物体的运动状态发生改变。
(×)8、力对物体的作用效果取决于力的人小。
(×)9、力的三要素中任何一个因素发生了改变,力的作用效果都会随之改变。
(√)10、既有大小,又有方向的物理量称为矢量。
(√)11、刚体平衡的必要与充分条件是作用于刚体上两个力大小相等,方向相反。
(×)12、平衡力系就是合力等于零的力系。
(√)13、力可以沿其作用线任意移动而不改变对物体的作用效果。
(√)14、力可以在物体上任意移动而作用效果不变。
(×)15、合力一定大于分力。
(×)16、合力是分力的等效力系。
(√)17、当两分力的夹角为钝角时,其合力一定小于分力。
(√)18、力的合成只有唯一的结果。
(√)19、力的分解有无穷多种结果。
(√)20、作用力与反作用力是一对平衡力。
(×)21、作用在同一物体上的三个汇交力必然使物体处于平衡。
(×)22、在刚体上作用的三个相互平衡力必然汇交于一点。
(√)23、力在坐标轴上的投影也是矢量。
(×)24、当力平行于坐标轴时其投影等于零。
(×)25、当力的作用线垂直于投影轴时,则力在该轴上的投影等于零。
(√)26、两个力在同一轴的投影相等,则这两个力相等。
(×)27、合力在任意轴上的投影,等于各分力在该轴上投影的代数和。
(√)28、力可使刚体绕某点转动,对其转动效果的度量称弯矩。
建筑力学与结构选型第10章 建筑结构选型
风速沿建筑物高度增大,对于受风面形状规则的矩形高层建筑, 风荷载分布可近似视为上大下小的阶梯踏步形分布。
d
b A
d
bd
bd
dh 1 2 b 2d 3 2bd 4 2bd
h /2
2/3h
h
bdh/2 5
2/3h
dh 1 2 3 4
3/4h
B
h
bdh2/3 5 bdh/3
满足建筑造型的需求:荷载路径的几何形式的改变虽 然不会影响荷载的传递效果,但对建筑外观的影响却 是深远的;而对于建筑造型复杂、平面和立面特别不 规则的建筑结构,应尽可能在结构上形成结构选型的基本原则
结构的基本功能是传递荷载 建筑结构形式千差万别,结构使用过程中的荷载也并不 确定; 所有的荷载都应具有荷载路径; 结构形式不唯一。 荷载的有效快捷传递要求所构筑的荷载路径是连续的。
竖向荷载的传递路径是“自上而下”的。 作为传递竖向荷载的结构,要求自上而下没有间断
不完全荷载路径
机械设备与电梯动力房 夜总会 客房平面图 传递结构
来自墙的荷载
客房
接待室餐厅 停车场
停车场平面图
来自柱的反作用力
(a)
(b)
水平荷载的传递路径也要求连续
可将整个建筑视为相对于地面的悬臂结构,则该悬臂结构在传递水平荷 载时不能发生间断
风1
风2 不完全荷载路径 不完全荷载路径
(a)
(b)
建筑物必须具有刚度 向下作用的重力
基础位于重力与土 的承载力之间
土的向上作用力支撑 基础传来的重量
恒载均匀分布时,建筑物的近似总重主要取决于楼面面
积和结构类型,与建筑形式无关。
