南京邮电大学2011-12研究生最优化试题标准答案[1]
最优化方法习题答案

s.t.3x1 2x2 6 x1, x2 , x3 0
解:引入剩余变量 x 4 , x5 和人工变量 x6 , x7 ,利用两阶段法得到辅助线性规划 max w x6 x7 max z' 2x1 3x2 x3
400 件,售货 600 件,五月份进货 500 件,售货 600 件,六月份进货 600 件售货 600 件时, 最大利润为 6100 元。
1.6 设市场上可买到 n 种不同的食品,第 j 种食品的单位售价为 c j ,每种食品含有 m 种基本 营养成分,第 j 种食品每一个单位含第 i 种营养成分为 aij ,每人每天对第 i 种营养成分的需 要量不少于 bi ,试确定在保持营养成分要求条件下的最经济食谱。
⑤因为 p2 , p4 线性相关, x 2 , x 4 不能构成基变量;
⑥因为 p3, p4 线性无关,可得基解 x(6) (0,0,1,1) , z6 3 ;
所以 x(2) , x(4) , x(6) 是原问题的基可行解, x(6) 是最优解,最优值是 z 3 。
(2) max z x1 x2 2x3 x4 x5
x1
x2
x3
x4
x5
x6
x7
z'
5
0
1
4
2
w
5
0
-1
2
x2
1 4
1
1 2
x7
5 2
0
-1
3
0
4
3
0
4
1
-1
3
0
2
2
-1
0
1
0
2
4
最优化理论研究生试卷_-2011516

p
s.t.
1 T p Bp 2 , 1 p 2 , p span g B g ,
1 1 其中 是信任域的半径, 而 p span g, B g 意味着 p g B g ( 和 为
两个实数), g f , B 是一个对称实矩阵。解决下面的问题:
为一个面积为 1 的正方形(如下图所示) 。
y 1 (xi, yj)
o
1
x
现在要求解满足下面两个条件的函数 z ( x, y ) :
(i) z ( x, y ) 在定义域 S 上的曲面积分 A z x, y 最小; (ii) z x, y 在定义域 S 的边界上的点 x, y 的取值为给定值。
学时 50 学分 2.5 成绩
自动化工程学院 (学生填写)
学 院
1. (10 分)对于下面的线性规划问题:
min 5 x1 x2 s.t. 2x1 1 / 2 x2 8 x1 , x2 0 x1 x2 5
,
(a) 把上面问题改写为标准型(3 分)。 (b) 采用单纯形方法算法或者单纯形表计算本问题的最小值和对应的最小解
2
定义域 S 内部的点 xr , y s 所对应的函数值 z xr , ys ,满足上面的条件(i). 解决下面的问题: (a) 写出符合题意要求的优化问题的具体形式。
共
10
页,第 8
页
6. (20 分)二维子空间最小化(2-dimensional subspace minimization)是一种信任域 方法,其问题可以描述为:
1
共
10
页,第 2
页
2011年南邮通信原理考研试题答案
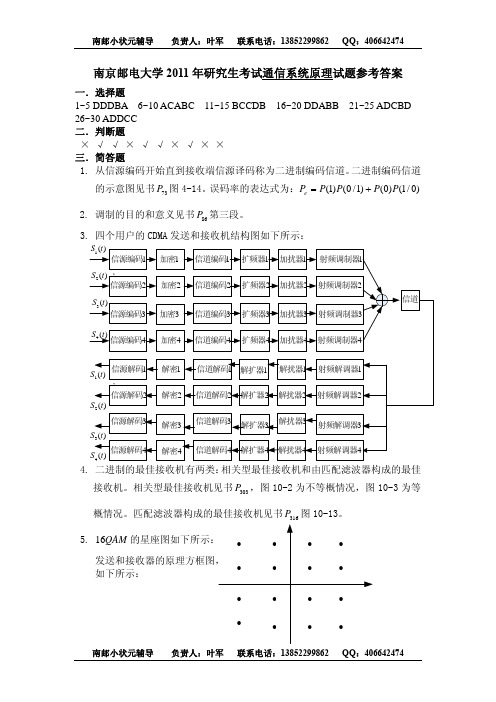
信源解码3 S3 (t )
解密3
信道解码3 解扩器3 解扰器3 射频解调器3
信源解码4 S4 (t)
解密4
信道解码4 解扩器4 解扰器4 射频解调器4
4. 二进制的最佳接收机有两类:相关型最佳接收机和由匹配滤波器构成的最佳
接收机。相关型最佳接收机见书 P303 ,图 10-2 为不等概情况,图 10-3 为等
Si Ni
1 a2 =r= 2
n0 BBPF
1 ×10−6
=
2×
2 4 ×10−14
×
2×
2 ×106
= 1.56
3)非相干解调误码率为 Pe
=
1
−
e
1 2
r
2
=
1 e −0.78 2
=
0.23
八.1)
⎡0 0 1 1 0 0 0⎤
H
= ⎢⎢1 ⎢1
11
0
1
0
0
⎥ ⎥
1 0 0 0 1 0⎥
⎢⎣1 0 1 0 0 0 1⎥⎦
S3 (t)
信道
信源编码3 加密3 信道编码3 扩频器3 加扰器3 射频调制器3
S4 (t) 信源编码4 加密4 信道编码4 扩频器4 加扰器4 射频调制器4
信源解码1 S1 (t )
解密1
信道解码1 解扩器1 解扰器1 射频解调器1
信源解码2 解密2 信道解码2 解扩器2 解扰器2 射频解调器2 S2 (t)
2) Α = [1 0 0] • G = (1 0 0 0 1 1 1)
3) 可写出全部码组,计算每个码组的码重,最小的码重就是最小汉明距离
或者直接由生成矩阵可以看出最小汉明距离为 d0 = 3
最优化试题及答案

mi 1 m *m j * g j (x*) 0最优化理论、方法及应用试题一、(30 分)1、针对二次函数f(x) 1x T Qx b T x c,其中Q是正定矩阵,试写出最速下降算法的详细步骤,并简要说明其优缺点?答:求解目标函数的梯度为g(x) Qx b,g k g(x k) Qx k b,搜索方向:从X k出发,沿g k作直线搜索以确定x k 1。
Stepl:选定X。
,计算f o,g oStep2:做一维搜索,f k i min f X k tg k , x k 1 X k tg k.Step3 :判别,若满足精度要求,则停止;否则,置 k=k+1,转步2优缺点:最速下降法在初始点收敛快,收敛速度慢。
算法简单,在最优点附近有锯齿现象,2、有约束优化问题min f (x)g i(x) 0,i 1,2,L ,ms.th j (x) 0,j 1,2,L ,l最优解的必要条件是什么?答:假设x*是极小值点。
必要条件是f,g,h函数连续可微,而且极小值点的所有起作用约束的梯度h(x*)(i 1,2丄,1)和g j(x*)( j 1,2,L ,m)线性无关,则* * * *存在1 , 2丄,I, 1, 2丄,m,使得lf(x*) i* h i(x*)i 1j*g j(x*) 0,j 1,2,L* * * * *1 ,2 ,L , l , 1 , 2 ,L ,*0, j 03、什么是起作用约束?什么是可行方向?什么是下降方向?什么是可行下降方向?针对上述有约束优化问题,如果应用可行方向法,其可行的下降方向怎样确定?答:起作用约束:若g j(x0) 0,这时点x0处于该约束条件形成的可行域边界上,它对x0的摄动起到某种限制作用可行方向:x0是可行点,某方向 p,若存在实数0 0,使得它对任意2、应用共轭梯度方法求解无约束优化问题 min X 28X |,初始点为X 0 1 1 丁 。
答:假设误差范围是0.001。
高等数学(A)下期末试卷及答案(优选.)

南京邮电大学2010/2011学年第二学期《高等数学A 》(下)期末试卷A 答案及评分标准 一、选择题(本大题分5小题,每题3分,共15分)1、交换二次积分⎰⎰x e dy y x f dx ln 01),(的积分次序为(c )(A ) ⎰⎰x e dx y x f dy ln 01),( (B )⎰⎰1),(dx y x f dy e e y(C )⎰⎰eeydx y x f dy ),(10(D )⎰⎰ex dx y x f dy 1ln 0),(2、锥面22y x z +=在柱面x y x 222≤+内的那部分面积为 (D )(A )⎰⎰-θππρρθcos 2022d d (B )⎰⎰-θππρρθcos 20222d d(C )⎰⎰-θππρρθcos 202222d d (D )⎰⎰-θππρρθcos 20222d d3、若级数∑∞=-1)2(n nn x a 在2-=x 处收敛,则级数∑∞=--11)2(n n n x na 在5=x (B ) (A ) 条件收敛 (B ) 绝对收敛 (C ) 发散(D ) 收敛性不确定 4、下列级数中收敛的级数为 (A )(A ) ∑∞=-1)13(n nn n (B )∑∞=+121n n n (C ) ∑∞=+111sin n n (D )∑∞=13!n n n 5、若函数)()2()(2222x axy y i xy y x z f -+++-=在复平面上处处解析,则实常数a 的值 为 (c )(A ) 0 (B ) 1 (C ) 2 (D ) -2二、填空题(本大题分5小题,每题4分,共20分)1、曲面122-+=y x z 在点)4,1,2(处的切平面方程为624=-+z y x2、已知)0(:222>=+a a y x L ,则=-+⎰Lds xy y x )]sin([22 32 a π 3、Ω是由曲面22y x z +=及平面)0(>=R R z 所围成的闭区域,在柱面坐标下化三重积分⎰⎰⎰+Ωdxdydz y x f )(22为三次积分为⎰⎰⎰RR dz f d d ρπρρρθ)(20204、函数x x f =)()0(π≤≤x 展开成以2π为周期的正弦级数为nx nx n n sin )1(211+∞=-=∑,收敛区间为π<≤x 05、=+-)1(i Ln2,1,0),243(2ln ±±=++k k i ππ=-]0,[Re 2zz e s z1-三、(本题8分)设),()(22xy y xg y x f z ++=,其中函数)(t f 二阶可导,),(v u g 具有二阶连续偏导数,求y x z x z ∂∂∂∂∂2,解:2112yg g y f x x z ++'=∂∂ … 3分=∂∂∂yx z2f xy ''4113122221g y x g y xyg g --++ 5分四、(本题8分)在已知的椭球面134222=++z y x 内一切内接的长方体(各边分别平行坐标轴)中,求最大的内接长方体体积。
最优化方法研究生期末考试练习题答案

《最优化方法》(研究生)期末考试练习题答案二.简答题1.;0, ,843 ,2 2-,3 34 s.t. ,95- min 2121212121≤=--≥+≥++y y y y y y y y y y 2.,065 6143≥+x x (以1x 为源行生成的割平面方程) 注意:在1x 为整数的情况下,因为3x ,04≥x ,该方程自然满足,这是割平面的退化情形,2141 41 43≥+x x (以2x 为源行生成的割平面方程)3.6648.31854.1*2)854.1()(2131.01146.1*2)146.1()(854.13*618.00)(618.0146.13*382.00)(382.03,031311111111111=+-==+-==+=-+==+=-+===μϕλϕμλa b a a b a b a 0.927.21.8540]1.8540[854.1,0)()(,*2211=+===≤x b a 近似的最优解:。
,初始的保留区间为即:。
所以,不经计算也可以看出事实上μϕλϕ4.令1.01.0)(4.04.0)(11)(7.27.2)(222222221)2(*111)1(*111)0(*121)1(*11-=-=-=-=-=-=-=-=-------x x x x x x x e x e x x f ex ex x f x e x x f e x e x x f拟合问题等价于求解下列最小二乘问题:∑=412))((mini ix f三.计算题1.分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。
取初始点()()Tx 2,21=,.1.0=ε()().1641642,2821121⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫⎝⎛=∇=⎪⎪⎭⎫⎝⎛=∇d f x x x f T方向为:从而最速下降法的搜索,在初始点,解:()()()()直至满足精度。
继续迭代方向为:从而最速下降法的搜索,,在从而求解得到:其中满足最优步长,.48/6565/19248/65-65/19265/6,65/96)65/6,65/96((-4,-16)*130/172,2 130,/17.)162(4)42()162,42()()(min )(122221)1(1)1(1*)1(*⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=∇-=-=+==-+-=--=++=+d f x x f d x f d x f d x f TTT Tλλλλλλλλλλ()()2-2- 1648/1002/1 8/1002/1,8002 2,21111⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∇-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==--f G d G G x T索方向为:从而修正的牛顿法的搜,在初始点()()()()即为所求的极小点。
南邮数字信号处理历年真题答案勘误及补充

2
2006 五、画图题
2、 H (z)
1 z1 1 0.81z2
z
z(z 1)
0.9 jz
0.9
j
,幅频相应曲线为“双峰”,图略。
七、简单计算题
3、本人认为该题条件关系式 y(n) x2 (n) 可能是笔误,应该改为 y(n) x2 (2n) ,所以 y(n)
是对 x2 (n) 的偶数点抽取,且此时未被 y(n)抽取到的 x2 (n) 的奇数点样值全为零,再参考邓
2008 年 六、说明题
1、基本解题思路如下:(图来自西电高西全 DSP 教材,注意图中 k 的取值范围有印刷错误!)
2、栅栏效应
2009 年 一、填空题 2、参考邓书第 13 页 二、选择题 2、
四、证明题 1、见吴镇扬书第 136 页
五、分析题 1、
2010 年 2、1250,2500 考点:DFT 的频率选择性。
5、{2,1,0,0,4,3} 考点:循环移位定理 二、选择题 4、A 方法一:求出零极点,几何法画出幅频相应曲线;方法二:通过计算关键频率点的
响应值来估计,当 w=0 即 z=1 时,H(1) 0;当 w=pi 即 z=-1 时,H(-1)=0,故为低通。
五、设计题 2、(2)
3、
六、综合计算题
响应曲线右移 得到 HP DF 的幅频响应曲线,类似可得, z 2 对应于 e j2w ,即把 LP DF 的幅
频响应曲线横向压缩为原来的一半得到 BS DF 的幅频响应曲线。ps:今年复试重考了本题! (6)能够分辨的两个频率分量的最小间隔 (12)半径稍小于 1 的圆上(参考张书 177 页) 3、简答题 (1)时不变:本人对该题答案所作出的时不变结论持怀疑态度,欢迎大家讨论!
南京邮电大学(已有10试题)

南京邮电大学经济与管理学院数据结构1999——2006编译原理2000——2002,2004——2005操作系统2000——2001企业管理2000,2003——2005微观经济学2004——2006,2010(2010为回忆版)经济学原理2003通信与信息工程学院通信系统原理1998——2009(1999——2000,2007——2009有答案)数字信号处理1999——2006信号与系统2003——2006信号与线性系统1997,1999——2002微机原理及应用1999——2006(注:1999——2000年试卷名称为“微机原理”;2000年试卷共7页,缺第1页)电磁场理论1998——2004数字电路1999——2000电路分析1997,1999——2004计算机学院通信系统原理1998——2009(1999——2000,2007——2009有答案)微机原理及应用1999——2006(注:1999——2000年试卷名称为“微机原理”;2000年试卷共7页,缺第1页)数据结构1999——2006编译原理2000——2002,2004——2005操作系统2000——2001光电学院通信系统原理1998——2009(1999——2000,2007——2009有答案)光学2003——2004微机原理及应用1999——2006(注:1999——2000年试卷名称为“微机原理”;2000年试卷共7页,缺第1页)信号与系统2003——2006信号与线性系统1997,1999——2002电磁场理论1998——2004数字电路1999——2000电路分析1997,1999——2004自动化学院通信系统原理1998——2009(1999——2000,2007——2009有答案)信号与系统2003——2006信号与线性系统1997,1999——2002数字信号处理1999——2006电磁场理论1998——2004数字电路1999——2000电子测量原理2004电路分析1997,1999——2004数理学院(无此试卷)传媒技术学院教育学专业基础综合(全国统考试卷)2007——2009信息网络技术研究所通信系统原理1998——2009(1999——2000,2007——2009有答案)微机原理及应用1999——2006(注:1999——2000年试卷名称为“微机原理”;2000年试卷共7页,缺第1页)数据结构1999——2006编译原理2000——2002,2004——2005操作系统2000——2001电磁场理论1998——2004数字电路1999——2000电路分析1997,1999——2004。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京邮电大学2010-2011学年研究生最优化方法试题学号 姓名 得分一、(3%×8)(1)线性规划,0 153 22 ..3 min 21212121≤≥-=--≤+-x x x x x x t s x x 的对偶规划为自由变量21212121 ,0 15 332 ..2-ax y y y y y y t s y y m ≤-≥-≤+-。
(2)在三维空间3R 中,集合},1|),,{(222z x y z y x z y x +≥≤++的极点构成的集合为 },1|),,{(222z x y z y x z y x +≥=++ 。
(3)用黄金分割法求解某个函数在区间[-1,3]上的极小点,若要求缩短后的区间的长度不大于原始区间的0.08,则需要迭代的次数为 6(4)函数65722),,(32121232221321++--+++=x x x x ax x x x x x x f 为严格凸函数,则常数a 的取值范围是||<a (5)在最速下降法,Newton 法,FR 方法,PRP 方法,DFP 方法,BFGS 方法中不具备二次终止性的算法为 最速下降法(6)求函数2221212),(x x x x f +=的极小点,取T x )1,0()0(=,用最速下降法一步得到的下一迭代点(1)x= T )0,0((7)对于无约束优化问题min 212122216432x x x x x x ---+,(1,)T p a =为目标函数在点(0,1)T 的下降方向,则a 的取值范围是 27->a(8)用内罚函数法(对数罚函数)求解0x 01 .. min 212221≥≤-+x t s x x ,其增广目标函数为212221ln )1ln(x r x r x x ---+ 二、(10%)()f x 为凸集nD R ⊂上的函数,令(){(,)|,,()}epi f x y x D y R y f x =∈∈≥,证明()f x 为凸函数的充要条件是()epi f 为凸集。
证明:⇒ 任意取两点)(),(),,(2211f epi y x y x ∈,其中,,21D x x ∈,,21R y y ∈,)(11x f y ≥)(22x f y ≥。
R D , 为凸集,R y y D x x ∈-+∈-+∴2121)1(,)1(αααα。
)(x f 为凸函数,212121)1()()1()())1((y y x f x f x x f αααααα-+≤-+≤-+∴,,)1((21x x αα-+ ),())1(21f epi y y ∈-+αα)(f epi ∴为凸集。
(5分)⇐ 任取,,21D x x ∈令),(),(2211x f y x f y ==)(),(),,(2211f epi y x y x ∈∴。
)(f epi 为凸集,=-+),)(1(),(2211y x y x αα ,)1((21x x αα-+)())1(21f epi y y ∈-+αα,)()1()()1())1((212121x f x f y y x x f αααααα-+=-+≤-+∴为凸函数。
由凸函数定义知,)(x f ∴(5分)三、(10%)设G 为n 阶正定对称矩阵,12,,,n n u u u R ∈线性无关。
k p 按如下方式生成:11p u =,1111121+++==-=-∑(,,,)T kk ik k i T i i iu Gp p u p k n p Gp ,证明12,,,n p p p 关于G 共轭。
证明:(1)2112121122111()0TT T T TT u Gp p Gp p G u p p Gu u Gp p Gp =-=-=,因此12,p p 关于G 共轭。
(4分)(2)设,(1)i j p p i j k ≤<≤关于G 共轭,即0()T j i p Gp j i =≠(2分)下证(1)j p j k ≤≤与1k p +共轭。
1111+++==-∑TkT T T k ijk jk j i T i i iu Gp p Gp p Gu p Gp p Gp ,由于0()T j i p Gp j i =≠,上式等于110++-=T k jTT jk j j Tjj u Gp p Gu p Gp p Gp 。
(4分) 由归纳法原理,命题成立。
四、(20%)(1)用单纯形方法求解下面的线性规划,0 2426 1553 ..2- min 21212121≥≥≤+≤+-x x x x x x t s x x 。
(2)若在上面的线性规划中要求变量为整数,在相应的整数规划中,请对变量1x 写出对应割平面方程。
(3)根据最后得到的单纯形表,求出该线性规划的对偶问题的最优解。
解:(1)标准型线性规划为,, 2426 1553 ..2- min 432142132121≥=++=++-x x x x x x x x x x t s x x (2分)判别数非负,最优解为T)4/3,4/15(,最优值为4/33-(8分) (2)根据单纯型表,有4151********=+-x x x 43311251211433x x x x --=--割平面方程为012512114343≤--x x 即951143≥+x x (6分)(3) 根据最后得到的单纯形表,得到该线性规划的对偶问题的最优解TTT B B C y ⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--==--127,1211353)1,2()(11*注:(1)原理正确,计算错误,若不影响最优基,扣2分,若影响最优基,扣4分 (2)割平面方程基本原理4分,(即计算错误扣2分)(3)对偶问题的最优解公式2分,结果2分(没有T B B C )(1-可以不扣分但直接写出结果没有过程要酌情扣分)五、(10%)用PRP 共轭梯度法求解 122212122123min x x x x x -+-,初始点T x )0,0( 0=。
解:.0)0,2(.),23()(01221≠-=---=T T g x x x x x g ,取T )0,2(-g p 00==∴ (1) 从0x 出发,沿0p 进行一维搜索,即求ααααϕ46)p f(x )( min 2000-=+=的极小点,得步长.31 0=α于是得到,)0,32( 0001T p x x =+=αT g )32,0(1-=.(4分) 由PRP 公式得,91/)(000110=-=g g g g g TT β故T p g p )32,92(0011=+-=β.(3分)(2) 从1x 出发,沿1p 进行一维搜索,即求3294274)p f (x )( min 2111--=+=ααααϕ 的极小点,得.231=α于是得到,)1,1( 1112T p x x =+=α此时T g )0,0(2=. 故,)1,1( 2*T x x ==.1*-=f.(3分)注:方法思路+公式正确,仅计算错误,可给分。
六、(10%)用乘子法求解问题3 x ..22 min 212221=-++x t s x x解:增广Lagrange 函数为,)3(2)3(22221212221-++-+-+=x x x x x x M σλ令,0)3(4,0)3(421222111=-++-=∂∂=-++-=∂∂x x x x Mx x x x M σλσλ 解得.423 21++==σλσx x (4分)根据乘子迭代公式,2622)3(211+++=-+-=+σσλσσλλk k k x x 当0σ>时,迭代收敛,且6*=→λλk 。
(4分) 在.423 21++==σλσx x 中令6=λ得123/2x x ==。
(2分)七、(10%)讨论Tx )3,0(*-=是否下面问题的KT 点1 09x x .. min 212221221≥+--≥+--+x x t s x x 。
解:有效集为}1{*=I ,(2分)T T T x c g x x g )6,0()(,)1,0(,)1,2()(*1*1=∇==.易见)(6*1*x c g ∇=,(4分)0,06121=>=λλ,所以*x 是KT 点。
(4分)八、(6%))设**,s z 分别是两个线性规划问题(I )0x bx .. max 1≥≤=A t s xc z T 与(II )0x kb x .. max 2≥+≤=A t s xc z T 的最优值,*1y 是(I )的对偶问题的最优解。
求证:k y z s T *1**+≤。
证明:(I )与(II )的对偶规划分别为(DI) 0y c y .. min ≥≥TT A t s yb 与 (DII) 0y cy ..)( min ≥≥+TT A t s yk b (2分)(I )的最优值与(DI )的最优值相同,得*1*y b z T =,(2分)*1y 是(DI )对偶规划的最优解,且(DI )与(DII )约束条件相同,从而*1y 是(DII )的可行解。
*1y 在(DII )的目标函数值不小于最优值,即**1)(s y k b T ≥+.因此k y z s T*1**+≤。
(2分)注:此题别的方法可类似给分。
