求匀加速直线运动的物体的平均速度
高中物理平均速度3个公式

高中物理平均速度3个公式高中物理平均速度3个公式1、平均速度=△x/△t(△x=位移,△t=通过这段位移所用的时间)。
2、2×V1×V2÷(V1+V2)=平均速度。
(前半路程平均速度V1,后半路程平均速度V2) 平均速度是一个描述物体运动平均快慢程度和运动方向的矢量,它粗略地表示物体在一个段时间内的运动情况。
3、v=(v0+v1)/2,适用于匀变速直线运动。
平均速度的公式v=x/t与v=(v0+v1)/2两者的区别是适用的范围不一样:v=x/t:总位移除总时间,任何时候都适用。
v=(v0+v1)/2:只适用于匀加速,匀减速,或匀速直线运动。
物理复习方法和技巧夯实基础知识尽管近几年来教材在变,大纲在变,高考也在变,但基本概念、基本规律和基本思路不会变,它们是高考物理考查的主要内容和重点内容,而主干知识又是物理知识体系中的最重要的知识,学好主干知识是学好物理的关键,是提高能力的基础。
在备考复习中,不仅要求记住这些知识的内容,而且还要加强理解,熟练运用,既要“知其然”,又要“知其所以然”。
要立足于本学科知识,把握好要求掌握的知识点的内涵和外延,明确知识点之间的内在联系,形成系统的知识网络。
新课程知识应用性较强,与素质教育的教改目标更加接近,容易成为命题点。
注重学科思想方法的掌握学习物理的目的,就是要在掌握知识的同时,领悟其中的科学方法,培养独立思考和仔细审题的习惯和能力。
为什么感到物理课听起来容易,做起来难。
问题就在于没有掌握物理学科科学的研究方法,而是死套公式。
为此,在物理复习过程中要适时地、有机地将科学方法如:理想化、模型法、整体法、隔离法、图象法、逆向思维法、演绎法、归纳法、假设法、排除法、对称法、极端思维法、等效法、类比和迁移法等进行归纳、总结,使之有利于消化吸收,领悟其精髓,从而提高解题能力和解题技巧。
研究题型,分类归档高考把能力考查放在首位,就必须对知识点考查的能力要求上不断翻新变化。
匀加速直线运动的各种公式及比例关系

匀加速直线运动的 各种公式及比例关系● 匀变速直线运动(回忆)1、平均速度:()01=2t s v v v t =+2、有用推论:2202t v v as -=3、中间时刻速度:()/2012t t v v v v ==+4、末速度:0t v v at =+5、中间位置速度:220/22t s v v v +=6、位移:20122t v s v t at vt t =+== 7、 加速度:0t v v a t-=8、实验用推论:2S aT ∆=1m/s=3.6km/h;● 自由落体运动1、初速度:00v =;末速度:t v gt =2、下落高度:212h gt =3、有用推论:22t v gh =● 竖直上抛运动1、位移:2012s v t gt =-2、末速度:0t v v gt =-3、有用推论:2202t v v gs -=-4、上升最大高度:202v h g = 5、往返时间:02v t g=✓ 上升与下落过程具有对称性,如在同点速度等值反向等。
● 平抛运动1、水平、竖直方向速度:0x v v =;y v gt =3、水平方向位移:0x v t =4、竖直方向位移:212y gt =5、运动时间:22y ht g g==6、合速度:()22220t x y v v v v gt =+=+7、合速度与水平方向夹角:0tan y xv gtv v β==7、合位移:22s x y =+8、位移与水平方向夹角:0tan 2y gt x v α== 9、水平、竖直方向加速度:0x a =;y a g =✓ 运动时间由下落高度h (y )决定与水平抛出速度无关;✓θ与β的关系为tanβ=2tanα;例一个做匀加速直线运动的物体,在头4s内经过的位移为24m,在第二个4s内经过的位移是60m.求这个物体的加速度和初速度各是多少?(稍难)(稍难)● 初速度为零的匀加速直线运动中的比例关系***设T 为时间单位,则有:✓ 1s 末、2s 末、3s 末、…、ns 末的瞬时速度之比:123:::...:1:2:3:...:n v v v v n =1T 末、2T 末、3s 末、…、nT 末的瞬时速度之比:123:::...:1:2:3:...:n v v v v n =✓ 1s 末、2s 末、3s 末、…、ns 末的位移之比:2222123:::...:1:2:3:...:n s s s s n =1T 末、2T 末、3s 末、…、nT 末的位移之比:2222123:::...:1:2:3:...:n s s s s n =✓ 第一个1s 内、第二个1s 内、…、第n 个1s 内的位移之比:()12::...:1:3:...:21n s s s n =-第一个T 内、第二个T 内、…、第n 个T 内的位移之比:()12::...:1:3:...:21n s s s n =- ✓ 通过连续相等的位移所用时间之比:()()()123::: (1)21:32:...:1n t t t t n n =----●追击和相遇问题●两种典型追击问题(1)速度大者(匀减速)追速度小者(匀速)①当v1=v2时,A末追上B,则A、B永不相遇,此时两者间有最小距离;②当v1=v2时,A恰好追上B,则A、B相遇一次,也是避免相撞刚好追上的临界条件;③当v1>v2时,A已追上B,则A、B相遇两次,且之后当两者速度相等时,两者间有最大距离。
匀变速直线运动的四个基本公式

第二章 匀变速直线运动的研究 一、四个基本公式1、 匀变速直线运动速度随时间变化规律公式:at v v +=02、匀变速直线运动位移随时间变化规律公式:2021at t v x += 【例1】以10 m/s 的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2 s 内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s 内汽车的位移是多大?3、匀变速直线运动位移与速度的关系:ax v v 2202=-【例2】身高为2 m 的宇航员,用背越式跳高,在地球上能跳2 m ,在另一星球上能跳5 m ,若只考虑重力因素影响,地球表面重力加速度为g ,则该星球表面重力加速度约为( ) A.52g B.25g C.15g D.14g 【例7】一辆车由静止开始作匀变速直线运动,在第8 s 末开始刹车,经4 s 停下来,汽车刹车过程也是匀变速直线运动,那么前后两段加速度的大小之比和位移之比x 1 ׃ x 2分别是( )A 、=1:4 ,x 1 ׃ x 2=1:4B 、=1:2,x 1 ׃ x 2=1:4C 、=1:2 ,x 1 ׃ x 2=2:1 C 、=4:1 ,x 1 ׃ x 2=2:1【例6】一只小球自屋檐自由下落,在Δt =0.25 s 内通过高度为Δh =2 m 的 窗口,求窗口的顶端距屋檐多高?(取g =10 m/s2)4、匀变速直线运动平均速度公式:(v0+v1)/2 通过图像关系证明二、 匀变速直线运动的三个推论1、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:试证明此结论:2、某段位移内中间位置的瞬时速度2x v 与这段位移的初、末速度0v 与t v 的关系为:()220221t x v v v +=试证明此结论:【例3】一列从车站开出的火车,在平直轨道上做匀加速直线运动,已知这列火车的长度为l , 火车头经过某路标时的速度为v 1,而车尾经过这个路标时的速度为v 2,求: (1)火车的加速度a ;(2)火车中点经过此路标时的速度v ; (3)整列火车通过此路标所用的时间t 。
几种常见匀变速直线运动解题方法

几种常见匀变速直线运动解题方法一.一般公式法.一般公式法是指选用速度、位移和时间的关系式,它们均是矢量式,使用时应注意方向性.一般以v的方向为正方向,其余与正方向相同者取正,与正方向相反者取负.二.平均速度法.定义式v=xt,对任何性质的运动都适用,而公式v=12(v0+v t)只适用于匀变速直线运动.三.中间时刻速度法.利用“任一段时间t的中间时刻的瞬时速度等于这段时间t内的平均速度”,即v t2=v.此公式适用于任何一个匀变速直线运动.有些题目应用它可以避免常规解法中用位移公式列出的含有t2的复杂式子,从而简化解题过程,提高解题速度.四.比例法.对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的重要结论的比例关系,用比例法求解问题.五.逆向思维法.逆向过程处理(逆向思维)是把运动过程的“末态”作为“初态”的反向研究问题的方法.如:物体做匀加速运动可看成做反向的匀减速运动,物体做匀减速运动可看成做反向的匀加速运动.该方法一般用在末状态已知的情况中.六.图象法应用v-t图象,可把较复杂的问题转变为较为简单的数学问题解决,尤其是用图象定性分析,可避开繁杂的计算,快速找出答案.七.巧用推论Δx=x n+1-x n=aT2解题.匀变速直线运动中,在连续相等的时间T内的位移之差为一恒量,即x n+1-x n=aT2.对一般的匀变速直线运动问题,出现相等的时间间隔时,应优先考虑用Δx=aT2求解.自由落体运动1.钢球A自塔顶自由落下2 m时,钢球B自离塔顶6 m距离处自由落下,两钢球同时到达地面,不计空气阻力,则塔高为( D )A.24m B.16m C.12m D.8m2.甲、乙两物体分别从10m和20m高处同时自由落下,不计空气阻力,下面描述正确的是( D )A.落地时甲的速度是乙的1/2 B.落地的时间甲是乙的2倍C.甲、乙两物体在最后1s内下落的高度相等 D 下落1s时甲的速度与乙的速度相同3.把自由落体运动总路程从上到下分成相等的两段,则上、下两段路程的平均速度之比为( B )A.1∶4 B.(2-1)∶1 C.1∶2 D.1∶(2-l)4.甲乙两球从同一高度相隔1s先后自由下落,在下落过程中( AD )A.两球速度差始终不变 B.两球速度差越来越大C.两球距离始终不变 D.两球距离越来越大匀变速直线运动提高小练1.(2013·无锡模拟)如图所示,一小球分别以不同的初速度,从光滑斜面的底端A 点向上做直线运动,所能到达的最高点位置分别为a 、b 、c ,它们距斜面底端A 点的距离分别为s 1、s 2、s 3,对应到达最高点的时间分别为t 1、t 2、t 3,则下列关系正确的是( C )A.s 1t 1=s 2t 2=s 3t 3B.s 3t 3>s 2t 2>s 1t 1C.s 1t12=s 2t 22=s 3t 32 D.s 1t 12>s 2t 22>s 3t 32 2.(2014·启东质检)汽车以20m /s 的速度做匀速直线运动,刹车后的加速度大小为 5m/s 2,那么开始刹车后2 s 内与开始刹车后6 s 内汽车通过的位移之比为( C ) A .1∶1 B .1∶3C .3∶4D .4∶33、 一辆公共汽车进站后开始刹车,做匀减速直线运动,开始刹车后的第1s 内和第2s 内位移大小依次为9m 和7m.则刹车后6s 内的位移是( C )A .20mB .24mC .25mD .75m4、小石子从离地某一高度处由静止自由落下,某摄影爱好者恰好拍 到了它下落的一段轨迹AB .该爱好者用直尺量出轨迹的长度,如图所示,已知曝光时间为11 000s ,则小石子出发点离A 点的距离约为( C ) A .6.5 m B .10 mC .20 mD .45 m5、做匀加速直线运动的物体,先后经过A 、B 两点时的速度分别为v 和7v ,经历的时间为t ,则(C D )A .前半程速度增加3.5vB .前t 2时间内通过的位移为11v t 4C .后t 2时间内通过的位移为11v t 4D .后半程速度增加2v6.一位同学在某星球上完成自由落体运动实验:让一个质量为2 kg 的小球从一定的高度自由下落,测得在第5 s 内的位移是18 m ,则( D )A .物体在2 s 末的速度是20 m/sB .物体在第5 s 内的平均速度是3.6 m/sC .物体在第2 s 内的位移是20 mD .物体在5 s 内的位移是50 m7、.(2013·佛山一模)如图1-2-5所示,一小球从A 点由静止开始沿斜面向下做匀变速直线运动,若到达B 点时速度为v ,到达C 点时速度为2v ,则x AB ∶x BC 等于( C )A .1∶1B .1∶2C .1∶3D .1∶48、某列车离开车站后做匀加速直线运动,从某时刻开始计时,前1 s 内的位移为10 m ,前2 s 内的位移为25 m ,则前 3秒内的位移为( B )A .40 mB .45 mC .50 mD .55 m9、一个质点正在做匀加速直线运动,用固定的照相机对该质点进行闪光照相,闪光时间间隔为1 s ,分析照片得到的数据,发现质点在第1次、第2次闪光的时间间隔内移动了0.2 m ;在第3次、第4次闪光的时间间隔内移动了0.8 m ,由上述条件可知( B )A .质点运动的加速度是0.6 m/s 2B .质点运动的加速度是0.3 m/s 2C .第1次闪光时质点的速度是0.1 m/sD .第2次闪光时质点的速度是0.3 m/s| 多阶段匀变速直线运动问题10、(2014·江都模拟)珠海航展现场空军八一飞行表演队两架“歼-10”飞机表演剪刀对冲,上演精彩空中秀。
高一物理讲义——速度与位移的关系

高一物理速度与位移的关系【知识点】【典例精析】1、正在沿水平直轨道匀加速运行的列车长为L ,列车通过长也为L 的桥,设列车刚开始过桥和恰好完全通过桥的速度分别是v 1和v 2,则列车的加速度大小等于( )A 、L v v 2122-B 、Lv v 22122-C 、Lv v 42122-D 、无法计算2、光滑斜面的长度为L ,一物体自斜面顶端由静止开始匀加速滑至底端,经历的时间为t ,则下列说法不正确的是( ) A 、物体运动全过程中的平均速度是L tB 、物体在2t 时的瞬时速度为是2L tC 、物体运动到斜面中点时瞬时速度为是2LtD 、物体从顶点运动到斜面中点所需的时间是22t 3、光滑斜面长为L ,物体从斜面顶端由静止开始匀加速下滑,当物体的速度是到达斜面底端速度的13时,它沿斜面下滑的距离是( ) A 、19L B 、16LC 、13L D 、33L4、如图所示,物体A 在斜面上由静止匀加速滑下x 1后,又匀减速地在平面上滑过x 2后停下,测得x 2=2x 1,则物体在斜面上的加速度a 1与在平面上的加速度a 2的大小关系为( )A 、a 1=a 2B 、a 1=2a 2C 、a 1=12a 2 D 、a 1=4a 2 5、某航母跑道长200 m ,飞机在航母上滑行的最大加速度为6 m/s 2,起飞需要的最低速度为50 m/s 。
要使飞机正常起飞,需要借助弹射系统获得的最小初速度为( ) A 、5 m/s B 、10 m/s C 、15 m/s D 、20 m/s6、由静止开始做匀加速直线运动的物体,当经过S 位移的速度是v 时,那么经过位移为2S 时的速度是( ) A 、vB 、2vC 、2vD 、4v7、矿井里的升降机,由静止开始匀加速上升,经过5秒钟速度达到6m/s后,又以这个速度匀速上升10秒,然后匀减速上升,经过10秒恰好停在井口,以向上为正方向(1)画全过程的v﹣t图象(2)求匀加速上升阶段的加速度(3)求匀减速上升阶段位移(4)求全过程总位移(5)画全过程的a﹣t图象.【随堂练习】1、如图所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度x x等于()为v,到达C点时速度为2v,则:AB BCA、1:1B、1:2C、1:3D、1:42、下列所给的图象中能反映作直线运动物体回到初始位置的是()(多选)A、B、C、D、3、一物体做匀减速直线运动,初速度为10m/s,加速度大小为2m/s2,则物体在停止运动前1s内的平均速度为()A、5.5m/sB、5m/sC、1m/sD、0.5m/s4、2011年1月11日,我国隐形战斗机“歼20”震撼亮相,并胜利完成首飞.战斗机返航时,在跑道上滑行约240m后停了下来,用时约6s.战斗机着地时的速度约为()A、80m/sB、60m/sC、40m/sD、70m/s5、一物体做匀加速直线运动,在第1个t s内位移为x1,第2个t s内位移为x2,则物体在第1个t s末的速度是()A、B、C、D、6、某一时刻a、b两物体以不同的速度经过某一点,并沿同一方向做匀加速直线运动,已知两物体的加速度相同,则在运动过程中()(多选)A、a、b两物体速度之差保持不变B、a、b两物体速度之差与时间成正比C、a、b两物体位移之差与时间成正比D、a、b两物体位移之差与时间平方成正比7、一个做匀加速直线运动的小球,在第1s内通过1m,在第2s内通过2m,在第3s内通过3m,在第4s内通过4m.下面有关小球的运动情况的描述中,正确的是()(多选)A、小球在这4s内的平均速度是2.5m/sB、小球在第3s和第4s这两秒内的平均速度是3.5m/sC、小球在第3s末的瞬时速度是3m/sD、小球的加速度大小为2m/s28、酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间。
匀变速直线运动公式、规律总结

匀变速直线运动公式、规律总结一.基本规律:v2s v ,三.自由落体运动和竖直上抛运动: v(4)通过连续相等的位移所用时间之比为:t 1∶t 2∶t 3∶…… :t n =1∶(12-)∶(23-)∶……… ∶(1--n n )课时4:匀速直线运动、变速直线运动基本概念(例题)一.变速直线运动、平均速度、瞬时速度:例1:一汽车在一直线上沿同一方向运动,第一秒内通过5m,第二秒内通过10m,第三秒内通过20m,第四秒内通过5m,则最初两秒的平均速度是_________m/s,则最后两秒的平均速度是_________m/s,全部时间的平均速度是_________m/s.例2:做变速运动的物体,若前一半时间的平均速度为4m/s,后一半时间的平均速度为8m/s,则全程内的平均速度是_________m/s;若物体前一半位移的平均速度为4m/s,后一半位移的平均速度为8m/s,则全程内的平均速度是_________m/s.例1例2例3例4)例51、下列说法中正确的是:()A.路程就是位移B.路程大,位移一定大C.路程是标量,总是正值;位移是矢量,既有大小又有方向D.物体运动的轨迹是直线时,位移的大小等于路程2、(2001年)某测量员是这样利用回声测距离的:他站在两平行峭壁间某一位置鸣枪,经过1.00s第一次听到回声,又经过0.50s再次听到回声. 已知声速为340m/s,则两峭壁间的距离为m.。
3、下列说法中正确的是:()A.平均速度即为速度的平均值B.瞬时速率是指瞬时速度的大小C.火车以速度v经过某一段路,v是指瞬时速度D.子弹以速度v从枪口射出,v是指平均速度4、某同学在百米赛跑中,以6m/s的速度从起点冲出,经过50m处的速度为8.2m/s,在他跑完全程中间时刻t'=6.25s时速度为8.3m/s,最后以8.4m/s冲过终点,他的百米平均速度大小为_________m/s.5、甲、乙两辆汽车沿平直公路从某地同时驶向同一目标,甲车在前一半时间内以速度v1做匀速运动,后一半时间内以速度v2做匀速运动;乙车在前一半路程中以速度v1做匀速运动,后一半路程中以速度v2做匀速运动,则:()A.甲先到达B.乙先到达C.甲、乙同时到达D.不能确定6、根据给出的速度、加速度的正负,下列对运动性质的判断正确的是:()A.v0>0,a<0,物体做加速运动B.v0<0,a<0,物体做加速运动C.v0<0,a>0,物体做减速运动D.v0>0,a>0,物体做加速运动7、关于物体的运动,下面哪种说法是不可能的:()A.加速度在减小,速度在增加B.加速度方向始终变化,而速度不变C.加速度和速度的大小都在变化,加速度最大时,速度最小,速度最大时,加速度最小D.加速度方向不变而速度方向变化8、小球由静止沿斜面滚下,在第1s内通过1m,在第2s内通过2 m,在第3s内通过3m,在在第4s内通过4m,下列有关小球运动的描述正确的是:()A.小球在这4s内的平均速度是2.5m/sB.小球在第3、4s内的平均速度是3.5m/sC.小球在第3s末的瞬时速度是3m/sD.小球在斜面上做匀加速直线运动9、一物体沿直线启动后每通过1m距离速度就增加0.5m/s,通过20m距离后速度达到10m/s,则该物体的运动为:()A.匀加速运动B.匀速运动C.变加速运动D.无法判断10、物体从静止出发,做匀加速直线运动,紧接着又做匀减速直线运动到达B点时恰好停止.在先后两个运动过程中:()A.物体通过的路程一定相等B.两次运动的加速度大小一定相等C.平均速度一定相同D.所用的时间一定相等11、(1992年)两辆完全相同的汽车,沿水平直路一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车. 已知前车在刹车过程中所行的距离为s,若要保证两辆车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为()A、s;B、2s;C、3s;D、4s;12、(1994年)将物体竖直向上抛出后,能正确表示其速率v随时间t的变化关系的图线是下图中图( ).。
匀变速直线运动的推论整理
1 2 x2 a 2 2 1 2 x3 a 3 2
故 x1 : x2
: x3 : 1 : 4 : 9 :
(3)第一秒、第二秒、第三秒……位移之比
1 2 x = a 1 第一秒内位移 Ⅰ 2
(m)
1 1 3 2 2 第二秒内位移 xⅡ= a 2 a 1 a 2 2 2 1 1 5 2 2 第三秒内位移 xⅢ = a 3 a 2 = a 2 2 2
②为确定解题结果是否正确,用不同方法求 解是一有效措施。 ③一般应该先用字母代表物理量进行运算, 得出用已知量表达未知量的关系式,然后 再把数值代入。 这样做能够清楚地看出未知量与已知 量的关系,计算也比较简便。
四个比例式:初速为零的匀加速直线运动 的几个常用的比例式:
• • • • • • • (1)1秒末、2秒末、3秒末……瞬时速度 之比
位移公式:
速度位移公式:
v v 2ax
2 2 0
二、3个推论与一种方法
1. 2.
v
v0 v 2
vt
2
Vx
2
V02 V 2 2
2
3. x2 x1 x3 x2 aT 4.
逆向思维法
练习1:一物体做初速为零的匀加速直线运 动。求:
(1)1秒末、2秒末、3秒末……瞬时速度 之比 由速度公式
4.汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这 连续的3个1 s内汽车通过的位移之比为( B ) A.1∶3∶5 C.1∶2∶3 B.5∶3∶1 D.3∶2∶1
解析:末速度为零的匀减速直线运动可以看作反向的初速度 为零的匀加速直线运动处理,初速度为零的匀加速直线运动 第1秒内、第2秒内、第3秒内……的位移之比为
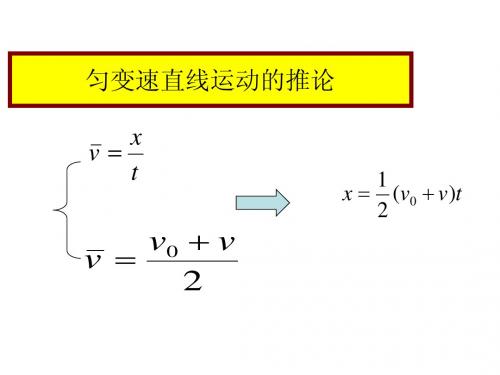
第13讲 匀变速直线运动平均速度公式和位移差公式的应用(解析版)

第13讲匀变速直线运动平均速度公式和位移差公式的应用如图1所示,如果匀变速直线运动的初速度为v 0,末速度为v ,这段时间中间时刻的瞬时速度为2t v ,试推导v -=v 0+v2=2t v .图1答案方法一解析法在匀变速直线运动中,对于这段时间t ,其中间时刻的瞬时速度2t v =v 0+12at ,该段时间的末速度v =v 0+at ,由平均速度的定义式和匀变速直线运动的位移公式整理加工可得v =xt =v 0t +12at 2t =v 0+12at =2v 0+at 2=v 0+v 0+at 2=v 0+v 2=2t v ,即v =v 0+v 2=2t v .方法二图像法这段时间位移x =v 0+v2t 平均速度v =x t =v 0+v2中间时刻的瞬时速度对应梯形中位线高,故2t v =v 0+v2一、匀变速直线运动的平均速度公式1.平均速度公式:v =2t v =v 0+v2(1)匀变速直线运动中任意一段时间t 内的平均速度等于该段时间的中间时刻的瞬时速度,还等于该段时间初、末速度矢量和的一半.(2)若同时涉及位移与时间而不涉及加速度,选用平均速度公式及中间时刻瞬时速度公式2tv=x t ,v 0+v 2=x t .2.三个平均速度公式的比较v =x t适用于任何运动;v =v 0+v 2及v =2tv 仅适用于匀变速直线运动.例题1.某汽车从车站由静止开出,做匀加速直线运动,运动了12s 时,发现还有乘客没上来,于是汽车立即做匀减速直线运动至停下,共历时20s ,运动了50m ,求汽车在上述运动中的最大速度的大小.【答案】5m/s【解析】由于汽车在前、后两阶段均做匀变速直线运动,设最大速度为v m ,则x 1=v m2t 1①x 2=v m2t 2②由①+②得x 1+x 2=v m2(t 1+t 2)解得v m =2(x 1+x 2)t 1+t 2=5m/s.对点训练1.2019年6月6日,中国科考船“科学”号对马里亚纳海沟南侧系列海山进行调查,船上搭载的“发现”号遥控无人潜水器完成了本航次第10次下潜作业,“发现”号下潜深度可达6000m 以上,如图2所示.潜水器完成作业后上浮,上浮过程初期可看作匀加速直线运动.今测得潜水器相继经过两段距离为8m 的路程,第一段用时4s ,第二段用时2s ,则其加速度大小是()图2A.23m/s 2 B.43m/s 2C.89m/s 2 D.169m/s 2【答案】A【解析】根据匀变速直线运动中间时刻的速度等于平均速度可知:v 1=84m/s =2m/s ;v 2=82m/s =4m/s再根据加速度的定义可知:a =Δv Δt =4-23m/s 2=23m/s 2.故选A.例题2.(多选)一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其速度-时间图像如图所示,那么0~t 0和t 0~3t 0两段时间内()A .加速度大小之比为3∶1B .位移大小之比为1∶2C .平均速度大小之比为2∶1D .平均速度大小之比为1∶1【答案】BD【解析】加速度a =Δv Δt ,由题图知Δt 1=t 0,Δt 2=2t 0,则a 1a 2=21,A 项错误;位移大小之比等于v -t 图线与t 坐标轴所围图形的面积之比,即x 1x 2=12,B 项正确;平均速度v =v 0+v 2,v1v 2=1,C 项错误,D 项正确.对点训练2.一物体从固定斜面上某点由静止开始沿斜面做匀加速直线运动,经过3s 后到达斜面底端,并在水平地面上做匀减速直线运动,又经过9s 停止,已知物体经过斜面和水平地面交接处时速度大小不变,则物体在斜面上的位移与在水平地面上的位移之比是()A .1∶1B .1∶2C .1∶3D .3∶1【答案】C 【解析】设物体到达斜面底端时的速度为v ,则物体在斜面上的平均速度v 1=v2,在斜面上的位移x 1=v 1t 1=v2t 1在水平地面上的平均速度v 2=v2,在水平地面上的位移x 2=v 2t 2=v2t 2所以x 1∶x 2=t 1∶t 2=1∶3,故选C.一、位移差公式Δx =aT 21.内容:做匀变速直线运动的物体,在任意两个连续相等的时间T 内的位移差是个常量,即Δx =aT 2.2.推导:如图3,x 1=v 0T +12aT 2,x 2=v 0·2T +12a (2T )2-(v 0T +12aT 2)=v 0T +32aT 2,所以Δx =x 2-x 1=aT 2.图33.应用(1)判断物体是否做匀变速直线运动如果Δx =x 2-x 1=x 3-x 2=…=x n -x n -1=aT 2成立,则a 为一恒量,说明物体做匀变速直线运动.(2)求加速度利用Δx =aT 2,可求得a =ΔxT2.例题3.(多选)(2019·长春外国语学校月考)一质点做匀加速直线运动,第3s 内的位移是2m ,第4s 内的位移是2.5m ,求:(1)第2s 内的位移大小;(2)第3s 末的速度大小;(3)质点的加速度大小.【答案】(1)1.5m (2)2.25m/s(3)0.5m/s 2【解析】(1)由x 3-x 2=x 4-x 3可知,第2s 内的位移大小x 2=1.5m ;(2)第3s 末的瞬时速度等于2~4s 内的平均速度,所以v 3=x 3+x 42T =2.25m/s ;(3)由Δx =aT 2,得a =x 4-x 3T 2=0.5m/s 2.对点训练3.从斜面上某一位置每隔0.1s 静止释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个小球后,对在斜面上滚动的小球拍下如图4所示的照片(照片与实际大小相同),测得x AB =15cm ,x BC =20cm.求:图4(1)小球的加速度的大小;(2)拍摄时小球在B 点时的速度的大小;(3)拍摄时C 、D 间的距离x CD ;(4)A 点的上方滚动的小球还有几个.【答案】(1)5m/s 2(2)1.75m/s (3)0.25m (4)2个【解析】(1)由推论Δx =aT 2可知,小球加速度为a =Δx T 2=x BC -x AB T 2=(20-15)×10-20.12m/s 2=5m/s 2.(2)由题意知B 点对应AC 段的中间时刻,所以B 点的速度等于AC 段的平均速度,即v B =x AC 2T =(20+15)×10-22×0.1m/s =1.75m/s.(3)由于连续相等时间内位移差恒定,所以x CD -x BC =x BC -x AB ,得x CD =2x BC -x AB =2×20×10-2m -15×10-2m =0.25m.(4)设A 点处小球的速度为v A ,由于v A =v B -aT =1.25m/s ,所以A 点处小球的运动时间为t A =v Aa =0.25s ,所以在A 点的上方滚动的小球还有2个.二、逐差法求加速度1.纸带上提供的数据为偶数段.(1)若已知连续相等时间内的两段位移.由x 2-x 1=aT 2,得a =x 2-x 1T2(2)若已知连续相等时间内的四段位移.可以简化成两大段AC 、CE 研究x Ⅰ=x 1+x 2x Ⅱ=x 3+x 4t AC =t CE =2Ta =x Ⅱ-x Ⅰ(2T )2=(x 3+x 4)-(x 1+x 2)4T 2(3)若已知连续相等时间内的六段位移可以简化成两大段AD 、DG 研究x Ⅰ=x 1+x 2+x 3x Ⅱ=x 4+x 5+x 6a =x Ⅱ-x Ⅰ(3T )2=(x 4+x 5+x 6)-(x 1+x 2+x 3)9T 2.2.纸带上提供的数据为奇数段可以先舍去一个较小的数据,选取偶数段数据再利用上述方法求解.例题4.在“探究小车速度随时间变化的规律”的实验中,打点计时器打出的一条纸带如图5所示,A 、B 、C 、D 、E 是在纸带上所选的计数点,相邻两计数点间的时间间隔为0.1s ,各计数点与A 计数点间的距离在图中已标出.则在打B 点时,小车的速度为________m/s ,并可求得小车的加速度大小为________m/s 2.图5【答案】0.260.4【解析】由纸带数据经计算可知小车在做匀变速直线运动,根据匀变速直线运动某段时间中间时刻的瞬时速度等于该段时间内的平均速度,可知v B =xAC 2T =52.0×10-30.2m/s =0.26m/s ,根据匀变速直线运动的推论Δx =aT 2,可知加速度a =x CE -x AC 4T 2=120.0-2×52.04×0.12×10-3m/s 2=0.4m/s 2.对点训练4.研究小车匀变速直线运动的实验装置如图6所示.其中斜面倾角θ可调,打点计时器的工作频率为50Hz ,纸带上相邻两计数点间的距离如图5所示,其中每两个相邻计数点之间还有四个点未画出.图6图7(1)部分实验步骤如下:A .测量完毕,关闭电源,取出纸带B .接通电源,待打点计时器工作稳定后放开小车C .将小车停靠在打点计时器附近,小车尾部与纸带相连D .把打点计时器固定在斜面上,让纸带穿过限位孔上述实验步骤的正确顺序是________.(用步骤前的字母填写)(2)图7中标出的相邻两计数点间的时间间隔T =________s.(3)打计数点5时小车的瞬时速度大小的计算式为v 5=________.(4)为了充分利用纸带上的测量数据,减小误差,小车加速度大小的计算式应为a =________.【答案】(1)DCBA(2)0.1(3)x 4+x 52T(4)(x 4+x 5+x 6)-(x 1+x 2+x 3)9T 2【解析】(1)实验步骤:先固定打点计时器,再放置小车,然后接通电源,释放小车,最后关闭电源,取出纸带,所以实验步骤的正确顺序是DCBA.(2)每两个相邻计数点之间还有四个点没有画出,所以相邻两计数点间的时间间隔T =0.02s ×5=0.1s.(3)根据匀变速直线运动某段时间中间时刻的瞬时速度等于该段时间的平均速度,有v 5=x 4+x 52T.(4)根据逐差法计算加速度,有a =(x 4+x 5+x 6)-(x 1+x 2+x 3)9T 2.1.一辆汽车在水平地面上沿直线行驶,在0~2t 时间内做匀加速直线运动,速度由0变为v .在2t ~3t 时间内做匀减速直线运动,速度由v 变为0,在这两段时间内,下列说法正确的是()A .加速度的大小之比为2∶1B .位移的大小之比为2∶1C .平均速度的大小之比为1∶2D .平均速度的大小之比为2∶1【答案】B【解析】根据题意作出汽车运动的v -t 图像,如图所示.根据图像的斜率表示加速度,可得加速度的大小之比a 1∶a 2=v 2t ∶vt =1∶2,故A 错误;位移的大小之比x 1∶x 2=12v ·2t ∶12v t =2∶1,故B 正确;平均速度的大小之比v 1∶v 2=0+v 2∶v +02=1∶1,故C 、D 错误.2.如图是物体做直线运动的v -t 图像,由图可知,该物体()A .0~2s 内和0~4s 内的位移不相等B .0~2s 内和0~4s 内的平均速度大小不相等C .第1s 内和第4s 内的位移大小不相等D .第3s 内和第4s 内的加速度不相同【答案】B【解析】0~2s 内物体的位移x 2=(1+2)×12m =1.5m ,则平均速度v 2=x 2t 2=0.75m/s.0~4s 内物体的位移x 4=1.5m =x 2,则平均速度v 4=x 4t 4=0.375m/s ,A 错,B 对.第1s 内和第4s 内位移大小均为0.5m ,C 错.第3s 内和第4s 内加速度均为-1m/s 2,D 错.3.(多选)做直线运动的物体的v -t 图像如图所示.由图像可知()A .前10s 物体的加速度为0.5m/s 2,后5s 物体的加速度为-1m/s 2B .15s 末物体回到出发点C .前15s 内物体的位移为37.5mD .前10s 内物体的平均速度为2.5m/s 【答案】ACD【解析】在v -t 图像中,图线斜率表示加速度,故前10s 物体的加速度为a 1=v -v 0t 1=5-010m/s 2=0.5m/s 2,后5s 物体的加速度为a 2=0-55m/s 2=-1m/s 2,故A 正确;v -t 图线与时间轴所围“面积”表示位移,故物体在前15s 内的位移为x =12×15×5m =37.5m ;前10s内的平均速度v =x 1t 1=12×10×510m/s =2.5m/s ,故B 错误,C 、D 正确.4.(多选)如图所示,物体做匀加速直线运动,A 、B 、C 、D 为其运动轨迹上的四点,测得AB =2m ,BC =3m ,且物体通过AB 、BC 、CD 所用的时间均为0.2s ,则下列说法正确的是()A .物体的加速度为20m/s 2B .物体的加速度为25m/s 2C .CD =4m D .CD =5m 【答案】BC 【解析】由匀变速直线运动的规律,连续相等时间内的位移差为常数,即Δx =aT 2,可得:a =BC -AB T 2=25m/s 2,故A 错误,B 正确;根据CD -BC =BC -AB ,可知CD =4m ,故C 正确,D 错误.5.一物体从静止开始做匀加速直线运动,已知第3s 内与第2s 内的位移之差是6m ,则可知()A .物体运动的加速度大小为3m/s 2B .第2s 末的速度大小为12m/sC .第1s 内的位移大小为1mD .物体在前4s 内的平均速度大小为15m/s 【答案】B 【解析】根据Δx =aT 2可得物体运动的加速度a =Δx T 2=612m/s 2=6m/s 2,A 错误;第2s 末的速度v 2=at 2=6×2m/s =12m/s ,B 正确;第1s 内的位移x 1=12at 12=12×6×12m =3m ,C 错误;物体在前4s 内的位移x 4=12at 42=12×6×42m =48m ,则物体在前4s 内的平均速度v =x 4t 4=484m/s =12m/s ,D 错误.6.(多选)如图,一质点从A 点开始做匀加速直线运动,随后依次经过B 、C 、D 三点.已知AB 段、CD 段距离分别为5m 、13m ,质点经过AB 段、BC 段、CD 段时间相等,均为1s ,则()A .质点的加速度大小为4m/s 2B .质点的加速度大小为2m/s 2C .质点在C 点的速度大小为11m/sD .质点在B 点的速度大小为6m/s 【答案】AC 【解析】AB 、BC 、CD 段时间相等,均为T =1s 由x 3-x 1=2aT 2得a =x 3-x 12T 2=13-52×12m/s 2=4m/s 2由x 2-x 1=x 3-x 2得BC 段长度x 2=9m B 点对应AC 段的中间时刻,v B =v AC =x 1+x 22T =5+92×1m/s =7m/s C 点对应BD 段的中间时刻,v C =vBD =x 2+x 32T =9+132×1m/s =11m/s ,故A 、C 正确.7.(1)电火花计时器使用________电源(选填“直流”或“交流”),工作电压为________V.(2)在某次用打点计时器(工作频率为50Hz)测定已知做匀变速直线运动物体的加速度实验中,所获得的纸带如图所示.选好0点后,每5个间隔点取一个计数点(中间的4个点图中未画出),依次取得1、2、3、4点,测得的数据如图所示.则纸带的加速度大小为________m/s 2,“1”这一点的速度大小为________m/s.(结果均保留三位有效数字)【答案】(1)交流220(2)0.8000.461【解析】(1)电火花计时器使用交流电源,工作电压为220V ;(2)每5个间隔点取一个计数点,所以相邻的计数点间的时间间隔T =0.1s ,由逐差法得:a =(x 4+x 3)-(x 2+x 1)4T 2=6.61+5.80-5.01-4.204×(0.1)2×10-2m/s 2=0.800m/s 2,根据匀变速直线运动时间中点的速度等于该过程中的平均速度,可以求出打纸带上1点时的速度大小:v 1=x 022T =(4.20+5.01)×10-20.2m/s ≈0.461m/s.8.如图所示为“测定小车做匀加速直线运动加速度”的实验中得到的一条纸带,舍去开始比较密集的点,按时间顺序标注0、1、2、3、4、5共六个计数点,相邻两计数点间有四个点没有画出,相邻两计数点间的距离已在图中标出.已知交变电源的频率为50Hz.(1)图中纸带________(选填“左”或“右”)端与小车相连;(2)相邻两计数点间的时间间隔为________s ;(3)由图给数据可以计算出小车运动的加速度a =________m/s 2(保留2位有效数字);(4)打下计数点2时小车的速度v 2=________m/s(保留2位有效数字);(5)若继续取计数点6、7,则计数点6、7之间的距离应为________cm.【答案】(1)左(2)0.1(3)2.0(4)0.80(5)17.00【解析】(1)根据纸带数据可知纸带左端与小车相连.(2)相邻两计数点间的时间间隔T =0.02s ×5=0.1s.(3)小车的加速度a =x 34-x 013T 2=11.00-5.003×0.12×10-2m/s 2=2.0m/s 2.(4)根据某段时间内的平均速度等于这段时间中间时刻的瞬时速度,再结合速度公式v =v 0+at ,可得v 2=x 01T +a ×32T =5.000.1×10-2m/s +2.0×32×0.1m/s =0.80m/s.(5)由题图和逐差法可知x 67-x 34=x 34-x 01,解得x 67=2x 34-x 01=(2×11.00-5.00)cm =17.00cm.9.在“研究小车做匀变速直线运动”的实验中,电源频率为50Hz,如图8为一次记录小车运动情况的纸带,图中A、B、C、D、E、F、G为相邻的计数点,在相邻计数点之间还有4个点未画出.图8(1)根据纸带可知,相邻计数点之间的时间间隔为____s,打C点时小车的瞬时速度为v C=______m/s,小车运动的加速度a=________m/s2.(后两空结果保留两位有效数字)(2)若交流电的频率变为51Hz而未被发觉,则测得的小车的速度值与真实值比较将偏________(选填“大”或“小”).(已知打点周期T与交流电的频率关系为T=1f)【答案】(1)0.10.200.50(2)小【解析】(1)电源频率为50Hz,则相邻两个点之间的时间间隔为0.02s,由于相邻计数点之间还有4个点未画出,所以相邻计数点之间的时间间隔为T=0.1s;利用中间时刻的速度等于这段时间内的平均速度即可求得v C=x BD2T=(5.38-1.30)×10-22×0.1m/s≈0.20m/s;根据Δx=aT2可得加速度为:a=(x FG+x EF+x DE)-(x AB+x BC+x CD)9T2,代入数据可得:a=0.50m/s2.(2)当交流电的频率变为51Hz时,打点的时间间隔减小,所以相邻计数点之间的时间间隔T减小,而此时还是以50Hz对应的打点周期去计算,根据v=xt可知测得的小车的速度值与真实值比较将偏小.10.疫情期间“停课不停学”,小明同学在家自主开展实验探究.用手机拍摄物体自由下落的视频,得到分帧图片,利用图片中小球的位置来测量当地的重力加速度,实验装置如图9所示.图9(1)家中有乒乓球、小塑料球和小钢球,其中最适合用作实验中下落物体的是.(2)下列主要操作步骤的正确顺序是.(填写各步骤前的序号)①把刻度尺竖直固定在墙上②捏住小球,从刻度尺旁静止释放③手机固定在三角架上,调整好手机镜头的位置④打开手机摄像功能,开始摄像(3)停止摄像,从视频中截取三帧图片,图片中的小球和刻度如图10所示.已知所截取的图片相邻两帧之间的时间间隔为16s ,刻度尺的分度值是1mm ,由此测得重力加速度为________m/s 2.图10【答案】(1)小钢球(2)①③④②(3)9.6(9.5~9.7均可)【解析】(1)小钢球受到的空气阻力可忽略,可认为是自由落体运动.(2)安装好器材后,先打开手机摄像功能,再由静止释放小球.这类似于使用打点计时器时先接通电源,再释放纸带,故顺序是①③④②.(3)由题图读得球心的位置坐标x 1=2.50cm ,x 2=26.50cm ,x 3=77.20cm ,由(x 3-x 2)-(x 2-x 1)=gT 2,T =16s 解得g ≈9.6m/s 2.。
