大地坐标转换成施工坐标公式修订稿
cad大地坐标转施工坐标方法
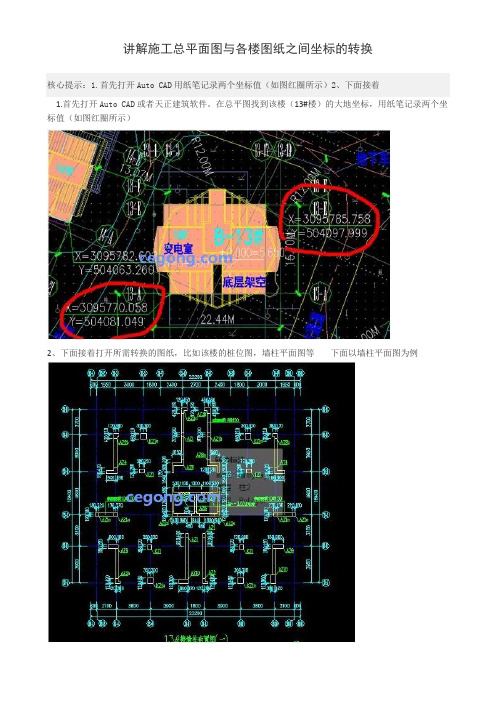
讲解施工总平面图与各楼图纸之间坐标的转换
核心提示：1.首先打开Auto CAD用纸笔记录两个坐标值（如图红圈所示）2、下面接着
1.首先打开Auto CAD或者天正建筑软件。
在总平图找到该楼（13#楼）的大地坐标，用纸笔记录两个坐标值（如图红圈所示）
2、下面接着打开所需转换的图纸，比如该楼的桩位图，墙柱平面图等下面以墙柱平面图为例
3.在图形输入L，定义一个点的坐标，注意：这里先输入Y值再输入X值，且不输小数点，坐标输好后回车，直线的第二个点任意。
接着L，输入第二个点的坐标
4.输好之后用天正建筑里的【坐标标注】核对坐标数值
5.然后输入命令AL 选中要转换的图形将图纸上的点和刚刚输入的两个坐标点依次对齐。
就OK了
6 .将图纸上对应的点和刚刚输入的两个坐标点依次对齐。
图形对齐完毕
7.下图为已经转换好的坐标图，可以用坐标标注任意一点的坐标值。
CAD大地坐标转换施工坐标
CAD大地坐标转换施工坐标概述在工程建设和土地测量中，CAD（计算机辅助设计）软件常用于设计、绘图和地理信息系统（GIS）分析。
CAD软件使用大地坐标系统来表示和显示地理位置。
然而，当需要在实际施工场地上进行施工时，常常需要将CAD中的大地坐标转换为施工坐标。
本文将介绍CAD大地坐标和施工坐标的定义，并详细阐述CAD大地坐标转换为施工坐标的方法。
CAD大地坐标和施工坐标的定义CAD大地坐标CAD大地坐标是基于地球椭球体的经纬度坐标系统，通常使用经度和纬度以及海拔高度来表示地球上的点。
在CAD软件中，经度表示东西方向的距离，纬度表示南北方向的距离，海拔高度表示地点相对于平均海平面的高度。
CAD大地坐标采用具体的坐标系，如WGS84、GCS Beijing 1954等。
不同的坐标系在选取和计算上均有一些差异，因此在进行坐标转换时需要注意。
施工坐标施工坐标通常以某一现实地物为基准，以便实际施工测量、放样和布控。
施工坐标一般采用平面坐标系统，如UTM（世界通用横轴墨卡托投影）坐标系，其中坐标以东西方向和南北方向的距离表示。
施工坐标通常以某个已知的控制点为基准进行测量，通过在实地上测量和计算，可以得到各个构件或测量点的坐标。
施工坐标以X和Y坐标表示平面位置，没有海拔高度。
CAD大地坐标转换施工坐标的方法CAD大地坐标转换为施工坐标的方法需要对大地坐标进行投影转换和坐标系转换。
1.投影转换大地坐标通常使用经纬度表示，但施工坐标使用平面坐标表示。
因此，需要将大地坐标进行投影转换，将经纬度转换为平面坐标。
常用的投影方法有经纬度转UTM投影和经纬度转高斯克吕格投影。
经纬度转UTM投影是将经纬度坐标投影到地球上的UTM坐标系中，其中每个地区根据其位置采用不同的投影带。
经纬度转高斯克吕格投影是将经纬度坐标投影到高斯克吕格投影坐标系中，用于较小的区域。
2.坐标系转换投影转换后的大地坐标已经是平面坐标，但仍然使用大地坐标系。
测量坐标转换建筑坐标公式
测量坐标转换建筑坐标公式引言在建筑测量过程中，坐标转换是一项重要的工作。
它涉及将不同坐标系下的位置信息进行转换，以满足具体测量需求。
本文将介绍测量坐标转换中常用的建筑坐标公式，包括平面坐标转换、高程坐标转换以及三维坐标转换。
1. 平面坐标转换平面坐标转换主要涉及将不同测量坐标系下的平面坐标互相转换。
常见的平面坐标系有国家大地坐标系、UTM坐标系等。
建筑测量中常用的公式如下：1.1 国家大地坐标系转化为局部坐标系国家大地坐标系是基于地球的椭球体模型建立的坐标系。
当需要将国家大地坐标系转换为局部坐标系时，可以使用以下公式进行计算：X_Local = X_Geo - X_OriginY_Local = Y_Geo - Y_Origin其中，X_Local和Y_Local表示转换后的局部坐标，X_Geo和Y_Geo表示国家大地坐标系下的坐标，X_Origin和Y_Origin表示局部坐标系的原点坐标。
1.2 UTM坐标系转化为局部坐标系UTM坐标系是一种经纬度的投影坐标系，以地区为单位进行划分。
当需要将UTM坐标系转换为局部坐标系时，可以使用以下公式进行计算：X_Local = X_UTM - X_OriginY_Local = Y_UTM - Y_Origin其中，X_Local和Y_Local表示转换后的局部坐标，X_UTM和Y_UTM表示UTM坐标系下的坐标，X_Origin和Y_Origin表示局部坐标系的原点坐标。
2. 高程坐标转换高程坐标转换主要涉及将不同坐标系下的高程信息互相转换。
常见的高程坐标系有大地水准面、局部高程坐标系等。
建筑测量中常用的公式如下：2.1 大地水准面转化为局部高程坐标系大地水准面是以地球引力为基准的坐标系，用于表示地球表面高程。
当需要将大地水准面转换为局部高程坐标系时，可以使用以下公式进行计算：H_Local = H_Geo - H_Origin其中，H_Local表示转换后的局部高程坐标，H_Geo表示大地水准面下的高程，H_Origin表示局部高程坐标系的起始高程。
大地坐标转施工坐标教程
大地坐标转施工坐标教程1. 引言大地坐标和施工坐标是在土木工程和测量学中经常使用的两种坐标系统。
大地坐标系统使用地球的形状作为参考，可以描述地球上的任意一个点的位置；而施工坐标系统则是基于具体的建筑或工程项目而设立的，用于指导施工过程。
在土木工程中，常常需要将大地坐标转换为施工坐标，以便在实际施工中准确定位。
本文将介绍大地坐标转施工坐标的基本原理和步骤。
2. 坐标系统简介2.1 大地坐标系统大地坐标系统使用地球的形状作为参考，以经度和纬度表示一个点在地球上的位置。
经度表示一个点的东西方位置，纬度表示一个点的南北方位置。
经度的取值范围为-180°到+180°，纬度的取值范围为-90°到+90°。
2.2 施工坐标系统施工坐标系统是基于具体的建筑或工程项目而设立的，用于指导施工过程。
施工坐标一般使用直角坐标系，以一个基准点为原点，建立x、y、z三个轴向表示一个点的位置。
3. 大地坐标转施工坐标的基本原理大地坐标转施工坐标的基本原理是通过坐标变换公式将大地坐标转换为施工坐标。
坐标变换公式由几何关系和坐标变换参数组成。
3.1 几何关系几何关系是指大地坐标系和施工坐标系之间的空间关系。
常用的几何关系有平移、旋转、缩放等。
3.2 坐标变换参数坐标变换参数是指将大地坐标转换为施工坐标所需的参数。
坐标变换参数包括基准点的大地坐标、基准点的施工坐标、坐标系旋转角度等。
4. 大地坐标转施工坐标的步骤4.1 确定基准点首先需要确定一个基准点，作为大地坐标和施工坐标转换的起始点。
基准点的选择应符合工程实际需要，并且容易测量、计算。
4.2 计算坐标变换参数利用基准点的大地坐标和施工坐标，结合已知的几何关系，计算坐标变换参数。
这些参数将作为坐标变换公式的输入。
4.3 建立坐标变换公式根据几何关系和坐标变换参数，建立大地坐标与施工坐标之间的坐标变换公式。
这个公式将用于实际的坐标转换计算。
施工坐标和大地测量坐标转换
施工坐标和大地测量坐标转换在工程测量领域中，施工坐标和大地测量坐标是两种常见的坐标系统。
施工坐标是指以某一参考坐标系为基准的坐标系统，用于实际施工中的测量和定位。
而大地测量坐标是指以地球形状和地球椭球体参数为基础建立的坐标系统，用于精确测量和导航等应用。
由于两种坐标系统的基准和计算方法不同，因此在实际应用中，需要进行施工坐标和大地测量坐标的转换。
施工坐标系统施工坐标系统是为了满足实际施工需求而建立的坐标系统。
在施工坐标系统中，通常以某一固定点作为原点，建立直角坐标系，以确定工程测量点的位置。
施工坐标系统的建立通常考虑了工程项目的需要，可以更好地满足施工测量的要求。
施工坐标系统主要包括平面坐标和高程坐标两个方面。
平面坐标是指在施工坐标系中，点的水平位置坐标，一般采用直角坐标系表示，以东西方向和南北方向的直角坐标值表示。
而高程坐标是指点的垂直位置坐标，一般采用高程值表示，可以表示点相对于某一参考面的高度。
大地测量坐标系统大地测量坐标系统是为了满足精确测量和导航等需求而建立的坐标系统。
在大地测量坐标系统中，通常以地球椭球体参数作为基础，建立球坐标系或椭球坐标系，以确定地球上点的位置。
大地测量坐标系统的建立考虑了地球形状的要素，可以更精确地表示和计算地球上点的位置。
大地测量坐标系统主要包括经纬度和大地高两个方面。
经纬度是指点在地球上的位置，通常用度表示，用于确定点在赤道和子午线上的位置。
大地高是指点相对于重力等势面的高度，通常用米表示，可以表示点相对于地球表面的高度。
施工坐标和大地测量坐标的转换在实际工程测量应用中，施工坐标和大地测量坐标之间的转换是一个重要的问题。
由于两种坐标系统的基准和计算方法不同，因此需要进行转换，以保证数据的准确性和一致性。
施工坐标到大地测量坐标的转换将施工坐标转换为大地测量坐标的过程称为施工坐标到大地测量坐标的正算。
正算的主要目的是将施工坐标转换为大地测量坐标，以满足精确测量和导航等需求。
大地坐标转换为施工坐标
**** 大桥关于大地坐标转化为施工坐标的报告**** 监理公司：**** 大桥为特大型桥梁，对测量精度要求高、施工难度大。
在实际施工测量当中，例如承台等结构尺寸比较简单的结构，在模板的安装的时候需要不断的测量、调整，直到满足要求。
在上述过程中需要用放样模式来确定设计位置，待模板调整后又要切换到测量模式检查坐标的偏差，如果没有满足要求，又需要切换到放样模式来确定设计位置。
如此反复，给我们施工放样带来了不必要的时间浪费，根据特大跨径桥梁施工的特点方便大桥测量定位，我项目部拟大地坐标系转化为独立的施工坐标系。
转化方法及过程从国家坐标系转换到施工坐标系，具体转换公式：E X X1 cos Y Y1 sinF Y Y1 cos X X1 sin （做了修改）施工坐标系以桥轴线为E轴，且以桩号增加方向为正向；以垂直于E轴为F 轴，水平向右为正向。
高程采用设计提供的85黄海高程，式中E、F 为转换后的施工坐标系坐标；X、丫为国家坐标系下坐标，Xl、Y为施工坐标原点在国家坐标系下坐标；表示桥轴正向在国家坐标系下的方位角。
本桥梁起点桩号为K119+大地坐标为X:，丫:，方位角为289° 2' 5具体转化过程如下：以DQ06 为例DQ06大地坐标为X:，丫:。
F 丫丫1 cos X X1 sin4351.265 5380.6574 cos 289.0494444 5157.7791 5034.6566 sin 289.04944441013.2052（做了修改）E X X1 cos 丫丫1 sin5157.7791 5034.6566 cos289.0494444 4351.265 5380.6574 sin 289.0494444 219.1972见下图：由上可知，DQ06的施工坐标为（X:, Y:）。
用以上公式同样可以求出控制点施工坐标，列表如下:****大桥的快速、优质的完成。
望贵单位批准。
大地坐标转施工坐标(fx5800)
大地坐标与工程坐标相互转化数学模式α:工程坐标系+X轴方位角β: M点在工程坐标系中的方位角δ: M点在大地坐标系中的方位角R: M点到工程坐标系原点距离R=X/cosβ=Y/sinβR=(N-N0)/cosδ=(E-E0)/sinδM(X,Y): M点在工程坐标系的坐标M(N,E): M点在大地坐标系的坐标δ=α+β1: M点由大地坐标系坐标转换为工程坐标系坐标X= R*cosβ=R*cos(δ-α)=R*(cosδ*cosα+sinδ*sinα)=(N-N0)*cosα+(E-E0)*sinαY= R*sinβ=R*sin(δ-α)= R*(sinδ*cosα-cosδ*sinα)=(E-E0)*cosα-(N-N0)*sinα2: M点由工程坐标系坐标转换为大地坐标系坐标N=N0+R*cos(α+β)=N0+R*(cosαcosβ-sinα*sinβ)=N0+X*cosα-Y*sinαE=E0+R*sin(α+β)=E0+R*(sinαcosβ+cosα*sinβ)=E0+X*sinα+Y*cosα大地坐标转施工坐标CSHS 程序标题〃CS→HS〃↙〃DD⇒SG〃◢Deg:Fix 3:Clrstat:FreqOff:Cls↙〃XO=〃?A:〃YO=〃?B:〃DX=〃?C:〃DY=〃?D:〃XI=〃?E:〃YI=〃?F:tan-1((F-B)÷(E-A)) →G↙0→K↙Lbl 1↙K+1→K:Norm 1:〃n=〃:K◢Fix 3:〃Xn=〃?X↙While X≠0↙〃Yn=〃?Y↙(X-A)cos(G)+（Y-B)sin(G)+C→U↙(Y-B)cos(G)-（X-A)sin(G)+D→V↙U→List X［K］:V→List Y［K］:Cls↙〃XP=〃: Locate 5,1,U:〃YP=〃: Locate 5,2,V◢Goto 1：WhlieEnd↙〃CSHS→END〃程序运行说明：先输入大地原点，再输入对应的测量坐标和施工坐标，作为3个已知数据再输入要转换的点，可重复输入，按0终止。
cad大地坐标转换施工坐标怎么转换
CAD大地坐标转换施工坐标的转换方法在土木工程和建筑施工中，CAD（计算机辅助设计）软件被广泛使用以进行绘图和设计。
在进行施工过程中，有时需要将CAD中的大地坐标转换为施工坐标，以便更准确地安排建筑和土木结构。
本文将介绍CAD大地坐标转换为施工坐标的常用方法。
什么是大地坐标和施工坐标？在开始讨论转换方法之前，我们先来了解一下大地坐标和施工坐标的概念。
大地坐标大地坐标是用来表示地球上某一点位置的坐标系统。
在大地坐标系统中，地球被划分为经度（longitude）和纬度（latitude）的坐标网格。
经度用来表示东西方向上的位置，纬度则用来表示南北方向上的位置。
施工坐标施工坐标是指在具体施工工地内部建筑或土木结构上使用的坐标系统。
这种坐标系统通常以某一固定点为起点，并使用局部坐标系，以便更方便地进行施工工作。
大地坐标到施工坐标的转换方法为了将CAD中的大地坐标转换为施工坐标，我们需要以下的转换步骤：1.确定旋转角度：首先，我们需要确定局部施工坐标系相对于大地坐标系的旋转角度。
这可以通过观察施工场地的实际情况并进行测量来确定。
2.坐标平移：接下来，我们需要进行坐标平移，以便将施工区域的某一点对应到大地坐标系的原点上。
通过测量起始点在大地坐标系中的坐标，我们可以计算出平移的距离。
3.坐标旋转：使用所确定的旋转角度，对CAD中的所有点进行坐标旋转。
旋转后得到的坐标即为相对于施工坐标系的结果。
4.坐标缩放：根据需要，可以在转换过程中进行坐标缩放，以适应施工坐标系的单位。
转换示例以下是一个具体的转换示例，以帮助更好地理解大地坐标到施工坐标的转换过程。
假设有一个CAD绘图文件，其中有一组点的大地坐标为：•点A：经度 120.456，纬度 31.789•点B：经度 120.453，纬度 31.790•点C：经度 120.458，纬度 31.791我们已经确定旋转角度为 45°，并测量了起始点在大地坐标系中的位置。
施工坐标(A,B)与大地测量坐标(X,Y)之间的几种换算方法
CAD软件功能来实现坐标换算的方法.
方法四:AutoCAD软件UCS法
AutoCAD有UCS命令设置用户坐标系,
用该命令来建立AB坐标系,也可实现坐标
转换.
具体步骤:
(1)数据预处理,求出待求点D相对于
基准点Ⅳ的,A(同方法二).
始坐标系.
(6)运行ID命令,端点捕捉方法读出D
点坐标为(627449.40,55920.86).与方法
三同理,调换计算机屏幕上的纵横轴值,即得
D点XY坐标(55920.86,627449.40).
方法五:AutoCAD软件ROTATE法
利用AutoCAD软件ROTATE旋转功能,
亦可实现坐标旋转转换.
调换一下计算机提供的纵横轴值,即可
得点D的XY坐标(55920.86,627449.40).
该方法对各数据不进行任何的预处理,
直接机械地将相关数据输入计算中,完全由
计算机软件来完成换算.若本身是用GPCAD
软件设计出图,已设置好新坐标系,直接用步
骤(5)就可得出换算结果,很是方便简单.但
其局限性也是显而易见的——要购有GP-
XY坐标系)与数学笛卡尔直角坐标系(或计
算机图形处理器)的纵横轴是不匹配的(图
3).工程图纸上的点(,B)(或(,))对应于
数学笛卡尔坐标系(或计算机图形)中的点
(,)或(,).坐标值进出计算机和套用数
学公式时应注意.
方法一:坐标轴平移和旋转公式法
新坐标系Y,}.系的原点不在,y系的
原点,却在X,系中有坐标=Xo和y=
当然,上述五种转换法对建北,磁北一致
时仍适用,只是夹角一O了.
施工坐标(A,B)与大地测量坐标(X,Y)之间的几种换算方法
施工坐标（A,B）与大地测量坐标（X,Y）之间的几种换算方法施工坐标(,B)与大地测量坐标(,y)之间的几种换算方法杨成贵(四川石油蔷面葡察设计研究院).『]3'摘要总图设计施工图阶段,常常引入施工坐标系,施工坐标值与大地测量坐标值之间就存在一个换算问题本文针对建北与磁北不一致时(即施工坐标系与大地测量坐标系之问有一旋转角),结合工程实践,归纳总结出五种简便易行的坐标换算方法.主翘词大地测量施工坐标值计算方法AB坐标系(即施工坐标系).然后在AB坐标问题的提出系下以设定的基准点为参照,推算确定各个工程设计中,为方便设计和施工放线,常建构筑物的AB坐标,来达到给建构筑物定常在XY坐标系(即测量坐标系)基础上引入位的目的.图l某油库征地边界线示意图(xY坐标AB坐标)建北成都某油库(圉1).由测量成果表可得征地界址点的XY坐标.为方便施工定位,我*扬成贵,助理工程师,1971年生;1994年毕业于武汉测绘科技大学城镇建设学院城市规划专业,获工学学士.现主要从事总图设计工作.地址:(6iO0l7)四川省成都市小关庙后街28号.电话:(028)6917700389.十天然气与石油们以点为基准点,MP为纵轴设置AB坐标系,且建北与磁北夹角为北偏东37.45(由和P两点得出),继而在AB坐标系下确定出各构筑的AB坐标,但是图面上界址点和库内建构筑分属两套坐标系统(XY坐标系和AB坐标系),界址点就难以用现有坐标值有效直观地控制库内建构筑的定位.速就要求我们统一坐标系,即要求我们将各界址点的XY坐标换算成AB坐标靖边至西安输气管道工程某基地平面布置图中(图2).引入了AB坐标,以站3(.一55912.63,y0—627599.45)相当于A0—500.00,B.一500.00为基准,建北与磁北夹角为北偏东l7..然后在AB坐标系下较简便地给基地内各建构筑物定了位,而某些特殊要求的建构筑物(如该基地综合楼上通讯塔,即图2中点D(A一464.00,B=354.10),仅知道AB坐标是不够的,应通讯专业要求,还要给出其相应的XY坐标.如何将AB坐标换算成相应的XY坐标就又摆在了设计人面前.下面就以图2中通讯塔坐标换算为例,详细讲述五种坐标换算方法.数学公式法图2某工矿基地平面布置示意图(AB坐标xY坐标)首先得强调的是:工程中AB坐标系(或XY坐标系)与数学笛卡尔直角坐标系(或计算机图形处理器)的纵横轴是不匹配的(图3).工程图纸上的点(,B)(或(,))对应于数学笛卡尔坐标系(或计算机图形)中的点(,)或(,).坐标值进出计算机和套用数学公式时应注意.方法一:坐标轴平移和旋转公式法新坐标系Y,}.系的原点不在,y系的原点,却在X,系中有坐标=Xo和y=ro;并有OX轴与OX轴之间有旋转角0(弧度,逆时针方向为正)则有数学公式:』一'一...+'r—in(1)lY一(一.)sin~(—D)c0f—o+Xcc~+YsinO{—+置sjn+c0s(2)在工程上,以(o,)为基准点M(山,)设置AB坐标系,且建北与磁北有夹角(逆时针(即北偏西)为正).则有公式(参见图4):rA.+'.c~o(Y (3)lB一0+(X一0)sinO+(Y一】0)cosO=X0+(AAncos+(BBnsing{—.一(一.)s.n+(—.)c.s第l6卷第l期扬成贵:施工坐标(^,口)与大地测量坐标(,y)之间的几种换算方法}^J一0'X=100P(1O.O,蚰工程图中:纵轴为轴()轴数学坐标系及计算机图形器中l轴为()轴^(盛北)/.一Xain口L-/,^\//o\ArI\△h口图4具体到图2中通讯塔坐标转换,有:^=464,00,A0=500.00,Xo=55912,63B=354.10,BD=500.O0,Yo=627599.45日一一17.(建北为北偏东故取负值)将上述值代入公式(4)中,则可得D点相应的XY坐标:X一55912,63+(464—5O0)coS(一17)+(354,10--500)sin(一17)一55912.63(一36)×cos(一17)+(一145.9)×sin(一17)=55912,63—34.427+42.657=55920.86r=627599.45一(464—500)sin(一17)354.1—500)cos(一17)一627599.45一l0.525到∞\l刺乙,O图5XY坐标系下P(r,d)AB坐标系下P(r,)其中——点P的向径ia,——点P在极坐标系的角弧度有(0≤d,fl<~360.)#~a--O天然气与石油极轴分别为OY,OB算成直角坐标值本方法就是借助极坐标来实现转换,再将转换后的极坐标折算成直角坐标.具体步骤:(1)数据预处理,求出AA,AB.AA=A--n==464--500一——36△=B—B0=354.1—500=一145.9(2)在AB坐标系,求出D点相对于M点的极坐标(r,),(注意是以MB方向为极轴.)r=&B2==丽_1一150.275=a…g(面A,4)ecg(二)一(180+13.86)=193.86(O≤fl~360.,注意象限)图(3)参照图5画出AB坐标系及XY坐标系之间的旋转关系及D点位置(如图6),以极坐标方法实现D点的坐标转换,即在XY 坐标系下点D的极坐极为:D(r,)其中一+口(口在建北为北偏西时为正)具体到通讯塔,有=150.276,d一193.86+(一l7),即:D(150.276,176.86)(4)在XY坐标系下,将极坐标O(r,a)换AX=rsina=rsin(+)=150.276sin(176.86)=8.23AY=rcosa=rcos(+)一l50.276c∞(176.86)一一l50.05(5)在J】lf点XY坐标值基础上,纵横轴值分别加上AX,△y即为D点的XY坐标. X—X0+AX一559l2.63+8.23=55920.86Y=Yo+AY一527599.45一l5O.05=627449.40方法二较之方法一,公式分解后较简单易记.但步骤较多并面临一个确定象限角的问题,还涉及反三角函数等.计算机图形处理法从前面两种方法中,我们不难看出:数学公式法计算麻烦,需要不断进行逐点校对.因此,我们都希望用直观的换等方法来代替传统的,抽象的数学公式法.计算机图形编辑器及相关工程软件的出现,给我们带来了极大的便利.方法三:GPCAD软件法GPCAD是杭州飞时达电脑技术公司开发的规划总圈设计软件包.利用该软件包中"设置坐标系"这一功能菜单,按照具体设计要求在XY坐标系下设置好AB坐标系.用IDD命令点取图中任意位置,程序自动计算出该点的AB坐标,并将该点的XY坐标一并读出.具体步骤:(1)进入GPCAD工作环境;(2)点取功能菜单{系统H设置坐标,图层…—设置坐标系(3)选择"建立"选项,程序提示:选择参考点<O,O>:[选定当前坐标系建,二北磁第l6卷第l期杨成贵:施工坐标,B)与大地测量坐标(x,y)之间的几种换算方法47中的某一点<可用捕捉>]627599.25.559l2.63取该点的坐标值d0,O>;[给定参考点在新坐标系中的坐标]500.00,500.00输入+B轴旋转角度(定义+轴角度):一17.[给定新建坐标系(AB坐标系)与原坐标系(XY坐标系)水平轴之间的旋转角<逆时针为正>];(4)在新建坐标系下,画线MD,以确定待求点D的位置:Command:Linefrompoint:500,500topoint:354.10,464.00(5)用IDD命令点取D点(端点捕捉),从计算机上读出D点:B施工坐标(354.10,464.10)对应x—r测量坐标(627449.40,55920.86)调换一下计算机提供的纵横轴值,即可得点D的XY坐标(55920.86,627449.40).该方法对各数据不进行任何的预处理,直接机械地将相关数据输入计算中,完全由计算机软件来完成换算.若本身是用GPCAD软件设计出图,已设置好新坐标系,直接用步骤(5)就可得出换算结果,很是方便简单.但其局限性也是显而易见的——要购有GP-CAD软件包,而GPCAD本身远不及Auto_ CAD软件普及;下面就介绍两种基于AuCAD软件功能来实现坐标换算的方法.方法四:AutoCAD软件UCS法AutoCAD有UCS命令设置用户坐标系,用该命令来建立AB坐标系,也可实现坐标转换.具体步骤:(1)数据预处理,求出待求点D相对于基准点Ⅳ的,A(同方法二).(2)进入AutoCAD图形编辑器,在当前(XY)坐标系下找到点M(627599.45, 55912.63).并画出方向角为0的直线(建北为北偏西时,0取正).(3)运行UCS命令,用三点法设置用户坐标系(以埘为原点,MN为水平轴).(4)在新建坐标系下,画线MD(0,0)(A,△).'5)再运行UCS命令,空回车.恢复到原始坐标系.(6)运行ID命令,端点捕捉方法读出D点坐标为(627449.40,55920.86).与方法三同理,调换计算机屏幕上的纵横轴值,即得D点XY坐标(55920.86,627449.40).方法五:AutoCAD软件ROTATE法利用AutoCAD软件ROTATE旋转功能,亦可实现坐标旋转转换.具体步骤:(I)数据预处理,求出AA,△(同方法二)(2)进入Aq~oCAD图形编辑器,视当前坐标系为AB坐标系,基准点为坐标原点(0,0).画线MD(O,0)一(△占,△)以确定D点相对于点的位置.(3)运行ROTATE命令,以点为基点旋转一(建北为北偏西时,0取正).(4)运行ID命令,用端捕捉方式得出D点旋转后的坐标值D(△y,△x)为(一l5O.05,8.23).再调换纵横轴值与点的XY坐标值相加,即得点D的XY坐标:x一o+AX=55912.63+8.23—55920.86Y—d-△y627599.45—15O.05=627449.40结束语I.五种换算方法的比较(表I),设计人员可据自身习惯以及手上现有软件和工具,选择相应的坐标换算法.有条件的,笔者建议天然气与石油1998芷用计算机图形处理法,特别对于需要对多个具体工程中,可用一种方法来换算计算,点进行坐标换算时(如图1),更显其优越性.表1五种方法综台比较表数学公式法方法一,坐标轴平移和旋转公式法方法二,投坐标公式法计算器计算器公式只一十,一次性出结果但:公式长,运算易错公式有五十,公式易记但:要分五步才得出结果,井涉及象限角,运算易错方法三,GPCAD软件法方法四,AutoCAD软件UCS法处理法方法五,Aut0cAD软件ROTATE法计算机(带GPCAD软件包)计算机(带AutoCAD软件)计算机(带AutoCAD软件)最简单,直观,明了但:局限性大(要购有GPCAD为前提)简单,直观,明了通用性强(AutoCAD很普及),但:有少量的数据预处理直观根普及)注:AB坐标xY坐标,建北为北偏西时,取正值.用另一种方法来校对,验算,达到自检的目的.2.本文是以由AB坐标换算成相应的XY坐标为例论述的.若是XY坐标换算成AB坐标(如图1).则:方法一,用公式3;方法三,同理;方法二,四,五,用x,y(或AX,)换A,B(找AA,△B)来上机操作或代八公式亦可实现转换,值则在建北为北偏东时取正值3.本文重点论述的是建北与磁北之间有一夹角0.当建北与磁北一致时,换算较简单:参照基准点倒有:AA=AX,AB=AY,在倒点相应的坐标轴上简单的增减AX,AY(或AA,△日).即可实现转换.当然,上述五种转换法对建北,磁北一致时仍适用,只是夹角一O了.参考文献l[美]A?科恩M?科恩.国民强等译.数学手册.工人出版杜,1987,122陈高波等.GPCAD操作手册.杭州飞时达电脑技术公司,t995,123邱玉春.AutoCAD操作手册.电子工业出敝社,1989,54王莉等.计算机图形学殛其在工程中的应用.交通出版社,1992,3f审稿人高级工程师杨秀田lI收稿日期1997--10--14)』计算机图形D理处预糍濑通但。
cad大地坐标转施工坐标方法
讲解施工总平面图与各楼图纸之间坐标的转换
核心提示：1.首先打开Auto CAD用纸笔记录两个坐标值（如图红圈所示）2、下面接着
1.首先打开Auto CAD或者天正建筑软件。
在总平图找到该楼（13#楼）的坐标，用纸笔记录两个坐标值（如图红圈所示）
2、下面接着打开所需转换的图纸，比如该楼的桩位图，墙柱平面图等下面以墙柱平面图为
3.在图形输入L，定义一个点的坐标，注意：这里先输入Y值再输入X值，且不输小数点，坐标输好后回车，直线的第二个点任意。
接着L，输入第二个点的坐标
4.输好之后用天正建筑里的【坐标标注】核对坐标数值
5.然后输入命令AL 选中要转换的图形将图纸上的点和刚刚输入的两个坐标点依次对齐。
就OK了
6 .将图纸上对应的点和刚刚输入的两个坐标点依次对齐。
图形对齐完毕
7.下图为已经转换好的坐标图，可以用坐标标注任意一点的坐标值。
大地坐标怎么转换施工坐标
大地坐标怎么转换施工坐标在土木工程和建筑领域中，施工坐标是一种用于测量和定位施工位置的坐标系统。
而大地坐标系则是一种用于表示地理位置的坐标系统。
在实际工程中，有时需要将大地坐标转换为施工坐标，以便准确地定位建筑结构和相关设备。
本文将介绍大地坐标如何转换为施工坐标的方法和步骤。
1. 大地坐标系统大地坐标系统是一种基于地球椭球体的坐标系统，用于描述地球上的地理位置。
在大地坐标系统中，经度表示东西方向的角度，纬度表示南北方向的角度。
经度的范围为-180°到+180°，纬度的范围为-90°到+90°。
例如，纬度为0°的点位于赤道上，纬度为90°的点位于北极圈上。
2. 施工坐标系统施工坐标系统是一种用于描述施工位置的坐标系统，与大地坐标系统有所不同。
在施工坐标系统中，通常采用直角坐标系，以某个参考点为原点，沿着水平方向和垂直方向建立坐标轴。
施工坐标通常用X、Y和Z三个坐标值表示，分别表示东西方向、南北方向和垂直方向的距离。
一般来说，施工坐标的原点是一处明确的参考点，如建筑物的角点或地面标志物。
3. 大地坐标转换施工坐标的步骤要将大地坐标转换为施工坐标，需要进行一系列的计算和转换。
下面是将大地坐标转换为施工坐标的基本步骤：步骤1：确定参考点首先需要确定施工坐标系的参考点，通常是建筑物的某个角点或地面标志物。
该参考点将作为施工坐标的原点。
步骤2：计算大地方位角和距离根据已知的大地坐标和参考点的坐标，可以计算两点之间的大地方位角和距离。
大地方位角是指从参考点到目标点的方向角度，以正北方向为基准。
大地距离是指从参考点到目标点的直线距离。
步骤3：转换大地方位角为施工方位角由于大地方位角是以正北方向为基准的，而施工坐标通常是以某个参考方向为基准的。
因此，需要通过一定的转换将大地方位角转换为施工方位角。
转换的方法可以是旋转坐标轴或加减一个常数。
步骤4：计算施工坐标根据已知的大地距离和施工方位角，可以计算出目标点相对于参考点的X、Y 和Z坐标值。
大地坐标转换施工坐标
大地坐标转换施工坐标在土木工程和建筑领域中，大地坐标和施工坐标是非常重要的概念。
大地坐标是指以地球椭球体为基准的坐标系统，用于描述地球表面上的点的位置。
而施工坐标则是指以工程项目为基准的坐标系统，用于指示工程项目中各个建筑物、道路和设施的位置。
大地坐标与施工坐标之间的转换是在土木工程和建筑项目中必不可少的任务。
1. 大地坐标大地坐标是一种用来表示地球表面上点的位置的坐标系统。
它基于地球的椭球体模型，考虑了地球的曲率和地球椭球体的形状差异。
大地坐标系统通常使用经纬度和海拔高度来描述一个点的位置。
经度表示一个点在地球表面上东西方向上的位置，而纬度表示一个点在地球表面上南北方向上的位置。
海拔高度则表示一个点相对于海平面的高度。
大地坐标系统可以通过全球定位系统（GPS）等卫星导航系统进行测量和确定。
2. 施工坐标施工坐标是一个以特定建筑项目为基准的坐标系统。
它通常是在工程项目开始时建立的，用于确定各个建筑物、道路和设施的位置。
施工坐标系统与大地坐标系统之间的转换通常涉及到一个坐标转换模型，该模型可以将一个点的大地坐标转换为施工坐标，或者将施工坐标转换为大地坐标。
施工坐标系统常用于土木工程和建筑项目中的测量、定位和设计等阶段。
3. 大地坐标转换施工坐标大地坐标转换施工坐标是指将一个点的大地坐标转换为施工坐标，或者将施工坐标转换为大地坐标的过程。
这个转换过程中需要考虑到多个因素，包括坐标系之间的差异、转换模型的选择和计算方法等。
下面简要介绍大地坐标转换施工坐标的一般步骤：步骤一：确定参考坐标系在进行大地坐标转换施工坐标之前，首先需要确定参考坐标系。
参考坐标系是一个确定的坐标系统，用来规定大地坐标和施工坐标之间的转换规则。
常见的参考坐标系包括WGS84、北京54坐标系等。
步骤二：进行坐标转换模型选择根据需要进行坐标转换的精度要求以及计算复杂度，选择适合的坐标转换模型。
常用的大地坐标转换施工坐标的模型包括带高斯投影的平面坐标系转换和三参数转换等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大地坐标转换成施工坐标公式Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】大地(高斯平面)坐标系工程坐标系转换大地坐标系--->工程坐标系?========================待转换点为P，大地坐标为：Xp、Yp?工程坐标系原点o:大地坐标：Xo、Yo工程坐标：xo、yo工程坐标系x轴之大地方位角：adX=Xp-XodY=Yp-YoP点转换后之工程坐标为xp、yp:xp=dX*COS(a)+dY*SIN(a)+xoyp=-dX*SIN(a)+dY*COS(a)+yo工程坐标系--->大地坐标系========================待转换点为P，工程坐标为：xp、yp工程坐标系原点o:大地坐标：Xo、Yo工程坐标：xo、yo工程坐标系x轴之大地方位角：adx=xp-xody=yp-yoP点转换后之工程坐标为xp、yp:xp=Xo+dx*COS(a)-dy*SIN(a)yp=Yo+dx*SIN(a)+dy*COS(a)坐标方位角计算程序置镜点坐标：ZX?ZY后视点坐标：HXHY方位角：W两点间距离:SLb10←｛A,B,C,D｝←A〝ZX=〞:B〝ZY=〞:C〝HX=〞:D〝HY=〞:W=tg1((D-B)÷(C-A)):(D-B)>0=>(C-A)>0=>W=W:∟∟(D-B)>0=>(C-A)<0=>W=W+180:∟∟(D-B)<0=>(C-A)<0=>W=W+180:∟∟(D-B)<0=>(C-A)>0=>W=360+W∟∟W=W◢S=√((D-B)2+(C-A)2)◢Goto?0←CASIO?fx－4500p坐标计算程序根据坐标计算方位角W＝W＋360△W：“ALF(1~2)＝”L1?A“X1＝”：B“Y1＝”：Pol(C“X2”－A，D“Y2”－B：“S＝”▲W＜0直线段坐标计算L1X“X(0)”：Y“Y(0)”：S“S(0)”：A“ALF”L2Lb12L3{L}：L“LX”L4M“X(Z)”＝X＋(L－S)cosA▲L5?N“Y(Z)”＝Y＋(L－S)sinA▲L6{B}：B“B(L)”：Q“Q”L7?O“X(L)”＝M＋Bcos(A＋Q＋180)▲L8?P“Y(L)”＝N＋Bsin(A＋Q＋180)▲L9{C}：C“B(R)”L10?U“X(R)”＝M＋Ccos(A＋Q)▲L11?V“Y(R)”＝N＋Csin(A＋Q)▲L12Goto2园曲线段坐标计算L1S“S(0)-Km”：X“X(0)”：Y“Y(0)”：A“ALF”：R“R”：K“K(L＝1,R＝2)”L2Lb12L3{L}：L“L(X)”L4V＝180／π×（L－S）／R：W＝V／2L5C＝A＋(-1)K×W：D＝2RsinW：F＝A＋(-1)K×VL6M“X(Z)”＝X＋DcosC▲L7?N“Y(Z)”＝Y＋DsinC▲L8{E}：E“B(L)”：Q“Q”L9?O“X(L)”＝M＋Ecos(F＋Q＋180)▲L10?P“Y(L)”＝N＋Esin(F＋Q＋180)▲L11{G}：G“B(R)”L12?T“X(R)”＝M＋Gcos(F＋Q)▲L13?U“Y(R)”＝N＋Gsin(F＋Q)▲L14Goto2正向缓和曲线段坐标计算L1S“ZH-Km”：X“X(ZH)”：Y“Y(ZH)”：A“ALF”：R“R”：H“LS”：K“K(L＝1,R＝2)”L2Lb12L3{L}：L“L(X)”L4D＝30（L－S）2／π／R／H：C＝L－S－（L－S）5／90／（R×H）2：B＝A＋D(-1)K：E＝A＋3D(-1)KL5U“X(Z)”＝X＋CcosB▲L6?V“Y(Z)”＝Y＋CsinB▲L7{G}：G“B(L)”：Q“Q”L8?F“X(L)”＝U＋Gcos(E＋Q＋180)▲L9?I“Y(L)”＝V＋Gsin(E＋Q＋180)▲L10{J}：J“B(R)”L11?M“X(R)”＝U＋Jcos(E＋Q)▲L12?N“Y(R)”＝V＋js in(E＋Q)▲L13Goto2卵形曲线坐标计算X＝1,D＝2)”L1?S“Km-YH”：E“X(YH)”：F“Y(YH)”：G“ALF”：B“R1”：D“A”：K“K(L＝1,R＝2)”：Q“R1-R2 L2Lb12L3{Z}：Z“L(X)”L4J“L1”＝D2／B：R“RP”＝D2B／(D2＋(-1)Q(Z－S)B)：L“LP”＝D2／RL5M＝(L－J)－(L5－J5)／40／D4＋(L9－J9)／3456／D8L6?N＝(L3－J3)／6／D2－(L7－J7)／336／D6＋(L11－J11)／42240／D10L7T＝G－(-1)Q(-1)K×J2×90／D2／πL8X“X(Z)”＝E＋(-1)QMcosT－(-1)KNsinT▲L9?Y“Y(Z)”＝F＋(-1)QMsinT＋(-1)KNcosT▲L10?A“ALF(P)”＝G＋(-1)K(Z－S)×90×(1／B＋1／R)／πL11{H}：H“B(L)”：U“Q”L12W“X(L)”＝X＋Hcos(A＋U＋180)▲L13?V“Y(L)”＝Y＋Hsin(A＋U＋180)▲L14{C}：C“B(R)”L15?I“X(R)”＝X＋Ccos(A＋U)▲L16?P“Y(R)”＝Y＋Csin(A＋U)▲L17Goto2公路逐桩坐标计算4800程序公路逐桩坐标计算程序(可以计算对称、不对称缓和曲线)Lb1?0Z=V=W=V+2：Fixm｛K｝Lb11K>Z[W+5Z+4]=>W=W+1:Goto1⊿(判断桩号在哪个交点范围，就是该交点曲线起点至下一交点曲线起点) S=K-Z[W+5Z+3]（计算该桩号与曲线起点的距离）R=Z[W+2Z+2]：L=Z[W+3Z+2]:E=Z[W+4Z+2]（读取该交点曲线要素R、Ls1、Ls2）Pol（Z[W]-Z[W-1],Z[W+Z+2]-Z[W+Z+1]）（计算该交点与下一交点直线方位角）J<0=>J=J+360⊿A=JPol（Z[W-1]-Z[W-2],Z[W+Z+1]-Z[W+Z]）（计算该交点与上一交点直线方位角）J<0=>J=J+360⊿C=A-J:A=J?（计算偏角）W=V+2=>Goto2⊿（如果桩号在起点与第一交点曲线起点之间，则转Lb12）I=Abs（tan（c÷2））M=L÷2-L^3÷240R^2:N=E÷2-E^3÷240R^2P=L^2÷6R-L^4÷336R^3-R（1-cos（90L÷πR））Q=E^2÷6R-E^4÷336R^3-R（1-cos（90E÷πR））D=（P-Q）I÷2:F=（P+Q+2R）I÷2M=F+M-D:Q=F+N+DN=πRAbsC÷180+（L+E）÷2X=Z[W-1]-McosAY=Z[W+Z+1]-MsinAM=Z[W-1]+Qcos（A+C）V=Z[W+Z+1]+Qsin（A+C）Q=AbsC÷CS≤L=>P=0:Goto3⊿（如果桩号在第一缓和曲线内，则转Lb13）S≤N-E=>S=S-L:Goto4⊿（如果桩号在圆曲线内，则转Lb14）S≤N=>S=N-SQ=-Q:A=A+C-180:X=M:Y=V:L=E：P=180:Goto3⊿（如果桩号在第二缓和曲线内，则转Lb13）P=A+C:S=S-N:D=M+ScosP:F=V+SsinPGoto6（如果桩号在直线内，则转Lb16）Lb12P=A+CD=Z[W-1]+ScosPF=Z[W+Z+1]+SsinP:Goto6Lb1?3I=S-S^5÷40R^2÷L^2+S^9÷3456R^4÷L^4J=Q（S^3÷6RL-S^7÷336R^3÷L^3）P=P+A+90QS^2÷πRL:Goto5Lb1?4M=90（2S+L）÷πRI=RsinM+L÷2-L^3÷240R^2J=Q（L^2÷24R+R（1-cosM））P=A+QMLb1?5D=X+IcosA-js inA:F=Y+JcosA+IsinALb16D″X=″◢（结果显示X坐标）F″Y=″◢（结果显示Y坐标）P″AT=″◢（结果显示该桩号方位角）{BO}：B″S″O″⊿″（输入边桩距离，交角）P=P+OL″XB″=D+BcosP◢（结果显示边桩X坐标）M″YB″=F+BsinP◢（结果显示边桩Y坐标）以上是坐标计算程序，括号内是程序计算的大致原理及说明，中间部分为直线、圆曲线、缓和曲线计算的各种公式，大家也知道，书上也有。
该程序是最基本的，如再加几条语句就可以处理断链。
该程序还需变量输入，把整条线路曲线要素一次输入到4800中，就可以计算线路任意中、边桩坐标。
曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序曲线任意里程中边桩坐标正反算(CASIOfx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQX js)和两个子程——正算子程序(SUB1)、反算子程序(SUB2)序构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。
另外也可以将本程序中核心算法部分的两个子程序移植到其它相关的程序中，用于对曲线任意里程中边桩坐标进行正反算。
本程序也可以在CASIOfx-4500P计算器及CASIOfx-4850P计算器上运行。
二、源程序1.主程序(TYQX js) "=>XY"："=>SZ"：N：U"X0"：V"Y0"：O"S0"：G"F0"：H"LS"：P"R0"：R"RN"：Q：C=1÷P：D=(P-R)÷(2HPR)：E=180÷π：N=1=>Goto1：≠>Goto2Δ←┘Lbl?1：{SZ}：SZ：W=Abs(S-O)：Prog?"SUB1"：X"XS"=X◢Y"YS"=Y◢Goto?1←┘Lbl?2：{XY}：XY：I=X：J=Y：Prog?"SUB2"：S"S"=O+W◢Z"Z"=Z◢Goto2 2.正算子程序(SUB1) M=1-K：X=U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G+QEFW (C+FWD))+Acos(G+QEMW(C+MWD)))：Y=V+W(Asin(G+QEKW(C+KWD))+Bsin(G+ QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD)))：F=G+QEW(C+ WD)+90：X=X+ZcosF：Y=Y+ZsinF 3.反算子程序(SUB2) T=G-90：W=Abs((Y-V)cosT-(X-U)sinT)：Z=0：Lbl0：Prog"SUB1"：L=T+QEW(C+ WD)：Z=(J-Y)cosL-(I-X)sinL：AbsZ<1E-6=>Goto1：≠>W=W+Z：Goto?0Δ←┘Lbl?1：Z=0：Prog?"SUB1"：Z=(J-Y)÷sinF三、使用说明1、规定(1)以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。