正弦量的向量表示法..
合集下载
正弦量的三要素及相量表示法基尔霍夫
第五章
正弦电流电路导论
内容提要
1.正弦量的相量表示法； 2.两类约束的相量形式； 3.正弦电流电路的分析计算； 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流：随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值：时变电压和电流在任一时刻的数值，用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解：
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω：每秒变化的弧度。单位：弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系：
1 f T
2 2 f T
* 电网频率（工频）：我国：50Hz；美国和日本：60Hz * 无线通信频率： 30 kHz ～ 30GMHz ◆ 相位和初相位 ①相位：正弦波的 (ωt ψ ) 。 ②初相位 ：t =0 时的相位。 ③规定：初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量：表示正弦量的复数称为相量。
相量表示法：用模值等于正弦量的最大值（或有效值）、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即：相量 Im （或 I ）
j
模用最大值表示时，为最 I ψ 大值相量，即 I m m
正弦电流电路导论
内容提要
1.正弦量的相量表示法； 2.两类约束的相量形式； 3.正弦电流电路的分析计算； 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流：随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值：时变电压和电流在任一时刻的数值，用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解：
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω：每秒变化的弧度。单位：弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系：
1 f T
2 2 f T
* 电网频率（工频）：我国：50Hz；美国和日本：60Hz * 无线通信频率： 30 kHz ～ 30GMHz ◆ 相位和初相位 ①相位：正弦波的 (ωt ψ ) 。 ②初相位 ：t =0 时的相位。 ③规定：初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量：表示正弦量的复数称为相量。
相量表示法：用模值等于正弦量的最大值（或有效值）、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即：相量 Im （或 I ）
j
模用最大值表示时，为最 I ψ 大值相量，即 I m m
正弦量的相量表示法教案
《电工学（少学时）》第三章正弦量的相量表示法学习目标： 1. 掌握复数的基本知识。
2 ．掌握正弦量的相量表示法。
重点：正弦量的相量表示法。
难点：相量图一、相量法的引入一个正弦量可以用三角函数式表示，也可以用正弦曲线表示。
但是用这两种方法进行正弦量的计算是很繁琐的，有必要研究如何简化。
由于在正弦交流电路中 , 所有的电压、电流都是同频率的正弦量，所以要确定这些正弦量，只要确定它们的有效值和初相就可以了。
相量法就是用复数来表示正弦量。
使正弦交流电路的稳态分析与计算转化为复数运算的一种方法。
二、复数概述1 ．复数：形如的式子称为复数，为复数的实部，为复数的虚部，、均为实数，为虚数单位。
图 4-3 复数的图示法2 ．复数的图示法式中为复数 A 的模，为复数 A 的辐角。
3 ．复数的表示形式及其相互转换其中代数式常用于复数的加减运算，极坐标式常用于复数的乘除运算。
4 ．复数的运算法则①相等条件：实部和虚部分别相等（或模和辐角分别相等）。
②加减运算：实部和实部相加（减），虚部和虚部相加（减）。
③乘法运算：模和模相乘，辐角和辐角相加。
④ 除法运算：模和模相除，辐角和辐角相减。
三、相量表示法1 ．正弦量与复数的关系= sin( ψ )= [ ]= [ ]正弦电压等于复数函数的虚部，该复数函数包含了正弦量的三要素。
2 ．相量 ---- 分有效值相量和最大值相量① 有效值相量：= / ψ② 最大值相量：= / ψ3 ．相量图在复平面上用一条有向线段表示相量。
相量的长度是正弦量的有效值I ，相量与正实轴的夹角是正弦量的初相。
这种表示相量的图称为相量图。
例 4-4 ：。
写出表示 1 和2 的相量，画相量图。
解： 1 =100 /60 ° V2 =50 /-60 ° V相量图见图 4-4 。
例 4-5: 已知 1 =100 sin A ， 2 =100 sin( -120 ° )A ，试用相量法求 1 + 2 ，画相量图。
正弦量的向量表示
试求uAB ，并画出相量图。
解:(1) 用相量法计算：
UA 220 0 V
N
UB 220 120V
UC 220 120V
+ +A
UA
–
U–B
UAB -
N
+– U+–C
B C
由KVL定律可知
UAB UA UB 220 0V 220 120 V
UAB 220 V 220 cos (120 ) jsin (120) V
【例3】已知同频率的正弦量的解析式分别为
i=10sin(ωt+30°), 并绘出相量图。
, 写出电流和电压的相量
,
u 220 2 sin(t 45)
••
I 、U
【例 1】
•
I
10
30 5 2 30A
2
•
U
220
2
45V
2
相量图如图所示。
＋j ·I
30°
O
45°
＋1
U·
注意:
①相量只是表示正弦量，而不等于正弦量。
Um、U、Im、I
复数及四则运算
1.复数
A a jb
模 r A a2 b2
辐 角
arctan b
a
( 2 )
a r cos
b
r sin
＋j b
r
O
P a ＋1
2. 复数的四种形式 (1) 复数的代数形式
(2) 复数的三角形式 (3) 复数的指数形式 (4) 复数的极坐标形式
A a jb
A r cos jrsin
A re j
A r A
3、相量表示法
5-3 正弦量的相量表示法
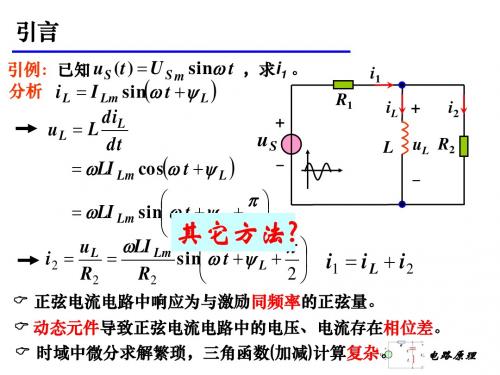
或
I m Ime
j i
I m i
I Ie
I i
电路原理
§5-3 正弦量的相量表示法 相量 正弦量
j u
Um U m e
u(t ) Im(Ume ) u(t ) Im( 2Ue )
i (t ) Im( I me
j t
j t
U U u
I m Ime
A2 A2e j 2 A2 2 a2 jb2
加减运算 A1 A2 (a1 a2 ) j (b1 b2 )
j ( ) 乘法运算 A1 A2 A1 A2e 1 2 A1 A2( 1 2 )
A1 A1 j ( 1 2 ) A1 除法运算 e ( 1 2 ) jA1 A2 A2 A2 j 1 90o jA1 A1e A1 1 90o
e jt Im 2U e jt ut Im U m
2)相量运算与复数运算相同，但必须是同频率的相 量才能进行运算。 3)已知时间正弦量可唯一确定对应的相量，而相量 只包含了正弦量的两个要素。 、 U U m 、U 4)注意符号区分：ut 、 、U m
正弦量 幅值 有效值 幅值相量 有效值相量
Im(虚部)
b1
A1
A1
a1
A1 j 1 90 o jA1 A1e A1 1 90o j
1
Re(实部)
0
jA1
电路原理
§5-3 正弦量的相量表示法
常用相量表示形式：
Ue j U
U U U (cos j sin ) U
4.2 正弦量的相量表示法
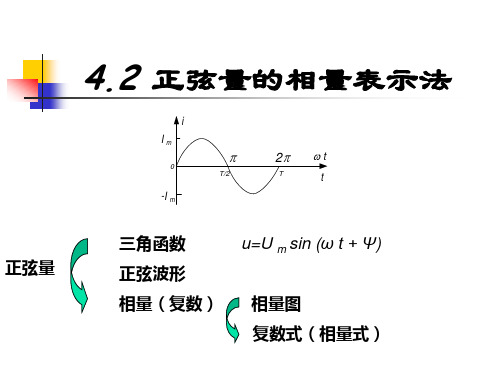
(1)2+(2)2
Im
I1m cos 1 I2m cos 2 I1m sin 1 I2m sin 2
2
2
(1)÷(2)
I1m sin 1 I2 m sin 2 arctan I cos I cos 1m 1 2m 2
将本题中 的I1m=100A, I2m=60A, Ψ1=45°, Ψ2=-30°
代入可得：
Im
70.7 52
2
70.7 30 129A
2
70.7 30 ' arctan 18 20 70.7 52
故得
i=129sin(ωt+18°20′)A
4.2 正弦量的相量表示法
i Im
0
T/2
2
T
t
t
-I m
三角函数
u=U m sin (ω t + Ψ) 相量图 复数式（相量式）
正弦量
正弦波形
相量（复数）
4.2.1 旋转有向线段表示正弦量
a. 在 u=U m sin (ω t + Ψ) 中
y A
Um 表示正弦电压的最大值 （A的长度） ω 表示正弦电压的角频率 Ψ 表示正弦电压的初相位
c.复数的三种表示方法： A=a+j b 实部
a2 b2 b arcty a r
b
虚轴 +1 A r
虚部
0 a
实轴 +1
a=r cos ψ
b=r sin ψ
复数的模 复数的辐角
A=a+j b= r cos ψ+j r sin ψ = r (cos ψ + j sin ψ)
第二节正弦量的相量表示法第三节电阻元件伏安关系的向
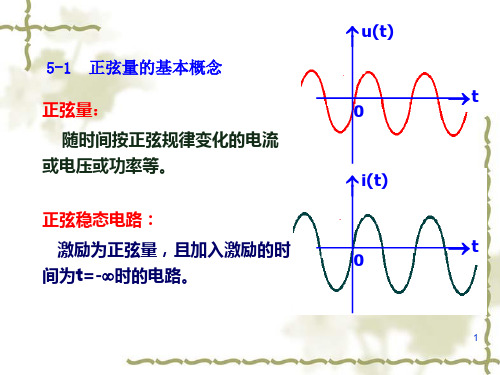
i(t) 11.18 2 cos(t 10.3) 21
例2 图示电路，已知：
+ u1(t) -
u1(t) 6 2 cos(t 30)
-
u2 (t) 4 2 cos(t 60)
u3(t)Biblioteka u2(t)+
求 u3(t)
解： 正弦量以相量表示，有
•
U1 630
•
U2 460
•
••
U3 U1 U2 (5.19 j3) (2 j3.45)
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2）平均功率: P 1
T
p(t)dt
T0
0
p(t)
UI
3）无功功率: Q UI
X
LI
2
U X
2 L
(Var)
0
意义:反映电感元件与电源进行能量交换的最大速率.
t
12
i(t) 2I cos(t i )
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2）平均功率: P 1
T
p(t)dt
T0
0
3）无功功率: Q UI
XCI 2
U2 XC
(Var)
p(t)
UI
0
意义:反映电容元件与电源进行能量交换的最大速率.
3 j4
8 j6
例2：写出下列正弦量的时域形式：
•
U1 3 j4
•
U 2 8 j6
u1(t) 5 2 cos(t 126.9)
正弦量的向量表示法
arctg (70.7 30) 1820
70.7 52
i 129sin(t 1820)A
③ 正弦量的复数表示法
复数简介
一、复数的几种表示形式 1. 代数形式（直角坐标形式）
A a jb j 1
a 称为实部
b称为虚部
均为实数，复矢量 在实、虚轴的投影
2. 三角形式
则 A a jb cos j sin
六、相量运算
•
设： A e j 则
•
•
B A e j e j( )
当 90时
••
•
B A e j90 e j( 90) j A
e j90 cos90 j sin 90 j
••
•
C A e j90 e j( 90) j A
••
•
•
D A e j90 • e j90 A e180 A
•
Um 200 220V
•
U 20020V 200e j20V
但不能写成：
u 200 2 sin(314 t 20) 200 220 200 2e j20
•
例2： 已知 f 1000Hz, I 0.530 A, 求i。
解： 2f 6280rad / s
i 0.5 2 sin(6280t 30) A
注意：① 幅值相量正弦量，它们存在一定得对应关系。
•
U m Ume ju Umu u Um sin(t u )
② 幅值相量反映了振幅和初相位的两个要素。
•
U m Ume ju Umu
③ 旋转因子 ejt 反映了另一要素t。
例1： u 200 2 sin(314 t 20)V
其相量形式：
i2 I 2m sin(t 2 ) 60 sin(t 30) A
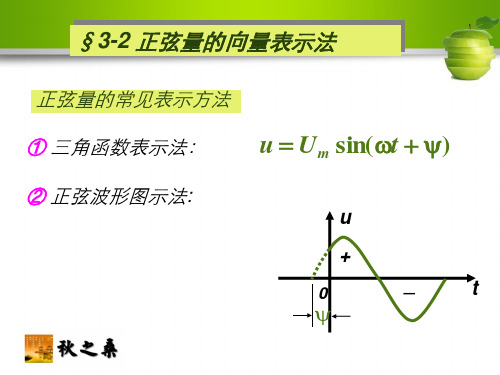
70.7 52
i 129sin(t 1820)A
③ 正弦量的复数表示法
复数简介
一、复数的几种表示形式 1. 代数形式（直角坐标形式）
A a jb j 1
a 称为实部
b称为虚部
均为实数，复矢量 在实、虚轴的投影
2. 三角形式
则 A a jb cos j sin
六、相量运算
•
设： A e j 则
•
•
B A e j e j( )
当 90时
••
•
B A e j90 e j( 90) j A
e j90 cos90 j sin 90 j
••
•
C A e j90 e j( 90) j A
••
•
•
D A e j90 • e j90 A e180 A
•
Um 200 220V
•
U 20020V 200e j20V
但不能写成：
u 200 2 sin(314 t 20) 200 220 200 2e j20
•
例2： 已知 f 1000Hz, I 0.530 A, 求i。
解： 2f 6280rad / s
i 0.5 2 sin(6280t 30) A
注意：① 幅值相量正弦量，它们存在一定得对应关系。
•
U m Ume ju Umu u Um sin(t u )
② 幅值相量反映了振幅和初相位的两个要素。
•
U m Ume ju Umu
③ 旋转因子 ejt 反映了另一要素t。
例1： u 200 2 sin(314 t 20)V
其相量形式：
i2 I 2m sin(t 2 ) 60 sin(t 30) A
电工基础3、3正弦量的相量表示法
1、复数的几种表示方法
复数的代数表达式为： A=a+jb
复数的三角形式为： A=rcos θ +jrsin θ
复数的极坐标形式为： A=r θ
复数的指数形式为: A=re j θ
2、加减运算
•A±B=(a1±a2)+j(b1±b2)
3、乘除运算
A·B=r1r2 θ1+θ2
A r1 1 2
A
数A的幅角； A在实轴上的投影a是它的实部； b
r
A在虚轴上的投影b称为其虚部。 0 a
＋1
复数A的代数表达式为：A=a+jb 由图又可得出复数A的模r和幅角θ分别为：
r a2 b2 极坐标形式： A=r θ
arctan b
a
＋j
br
0 a
A 由图还可得出复数A与模 a r cos
Z1Z2 3 00 ×3 -900 = 9 -900
Z1 Z2
3-j3
3 2 -450
= 2.12 -450
1. 已知复数A=4+j5，B=6-j2。试求A+B、 A-B、A×B、A÷B。
2. 已知复数A=30 30°，B=40 60°。试 求A+B、A-B、A×B、A÷B。
A+B=（4+6）+j（5-2）=10+j3≈10.4 16.70
3.3.1
1、复数的图形表示
1）复数用点表示
A1=1+j A2=-3 A3=-3-j2 A4=3-j
复数及其运算规律
+j
3
2
A2
1
A1
-3 -2 -1 0 1 2 3 +1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i i2
因此，总电流 i 的幅值为
I m (I1m cos 1 I 2m cos 2 ) (I1m sin 1 I 2m sin 2
总电流 i 的初相位为
2
i1
1 2 2 )
I1m sin 1 I 2m sin 2 arctg ( ) I1m cos 1 I 2m cos 2
则
A a jb cos j sin
与代数形式的关系
a cos a 2 b 2 或 b b sin arctg a
2001-02-10
南京航空航天大学
3. 指数形式 由欧拉公式：
e
j
cos j sin
§3-2 正弦量的向量表示法
正弦量的常见表示方法 ① 三角函数表示法： ② 正弦波形图示法:
u U m sin( t )
u
+ _
2001-02-10 1 sin( t 1 ) A
i i1 i2
i
i2 2I 2 sin( t 2 ) A
Ume
j ( t u )
Um cos(t u ) jUm sin(t u )
很明显，上式的虚部恰好是 u，即
u I m U me
2001-02-10
j (t u )
U
m
sin(t u )
南京航空航天大学
u I m U m e j (t u ) I m U m e j u e jt jt I m U m e
式中 ①
Im [ ] 为取“虚部”的运算符。
U m U m e ju U m u
称为正弦量 u 的“幅值相量” 同样有： U U Ue j
（最大值相量） 有效值相量
2001-02-10
南京航空航天大学
相量 U m 正好体现了正弦量的量特征：初相、幅值，而没能体现t。
Um
u U m sin( t )V
b t t a
P
1
0
0 t
t
Um
u
OP=Um cos (t+) + j Um sin(t+)
= Um e j(t+)
2001-02-10
= Um t +
南京航空航天大学
四、利用向量表示正弦交流量
设正弦电压
u U m sin(t u )
i1 i2
求
i i1 i2 2 I1 sin( t 1 ) 2 I 2 sin( t 2 ) ......
2001-02-10
南京航空航天大学
例题 分析
• 对如图电路，设
i i2
i1 I1m sin(t 1 ) 100sin(t 45) A
南京航空航天大学
2001-02-10
由此，代入数据I m1=100A, I m2=60A, 1=45, 2= –30 则：
Im (70.7 52) 2 (70.7 30) 2 122.7 2 40.7 2
129A
70.7 30 arctg ( ) 1820 70.7 52
A B = 1 2 ( 1 + 2)
2001-02-10 南京航空航天大学
B=a2+jb2= 22
三、旋转矢量 设
A A
e
jt
1t
——称为旋转因子（ ejt ）
则Ae jt
表示将A逆时针旋转一角度t
故称 A e jt 为旋转矢量。
2001-02-10
复数 A (cos j sin ) e j
4. 极坐标形式
A
2001-02-10
南京航空航天大学
二、复数运算
加、减宜用代数形式 例：A=a1+jb1 B=a2+jb2
A B = (a1 a2) + j(b1 b2)
乘、除宜用极坐标形式 例： A=a1+jb1=11
i2 I 2m sin(t 2 ) 60sin(t 30) A
i1
试求总电流 i 。
解 用 三 角 函 数 式 求 解
i i1 i2 I 1m sin(t 1 ) I 2 m sin(t 2 ) I 1m (sin t cos 1 cost sin 1 ) I 2 m (sin t cos 2 cost sin 2 ) ( I 1m cos 1 I 2 m cos 2 ) sin t ( I 1m sin 1 I 2 m sin 2 ) cost
i 129sin(t 1820) A
2001-02-10
南京航空航天大学
③ 正弦量的复数表示法
复数简介
一、复数的几种表示形式 1. 代数形式（直角坐标形式）
A a jb
j 1
a 称为实部
b称为虚部
2001-02-10
均为实数，复矢量 在实、虚轴的投影
南京航空航天大学
2. 三角形式
南京航空航天大学
正弦量的旋转矢量表示
Um
P1
a1 a2
+j
t
P0 t 0
Um
u U m sin( t )V
b b1
t 2
t1
0
P1
a
+1
0 t1
t 2
t
P2
b2
Um
P2
2001-02-10
南京航空航天大学
※旋转矢量与瞬时值之间的关系
Um
P
j
P0 t 0
2001-02-10 南京航空航天大学
两个同频率正弦量相加仍得到一个正弦量，设此正弦量为
i I m sin( t ) I m cos sin t I m sin cos t
则
I m cos I1m cos 1 I 2m cos 2 I m sin I1m sin 1 I 2m sin 2
但对于分析线性电路来说，电路中电压、电流都是和电源同频率的正弦量。
注意：① 幅值相量正弦量，它们存在一定得对应关系。
U m U me