必修2第四章导学案
必修二Unit4导学案

必修二Unit4 导学案1 Introduction&Vocabulary 编写:定稿:审核:时间:月日学生姓名:班级:学号:课前自主预习目标方案●重点单词1.enemy n.敌人2. reserve v.保护区3.hunt v.打猎4. wild adj. 野生的5.protection n.保护6.peace n.和平7.apply v.申请,应用8. suggest v.建议,暗示9.rub v.摩擦10.contain v.包含11.affect v.影响effect n.影响12.attention n.注意●重点短语e into being形成2.as a result 结果,因此3.die out (动,植物物种)灭绝4.in danger of 处于危险中5.get dressed 穿上衣服6.would like“想,愿意”7.pay more attention to 注意8.protect …from / against保护使不受……伤害课后自主反思与测评Ⅰ. 单词拼写1. He went through the forest under the p_______ of his dog.2. The soldiers lined up for their daily i by their officers.3. Ancient people h______ for food.4.I invited her to dinner but she did not r_______.5.Orange juice c_________ vitamin c.6. Geography _______ (影响)people’s ways of living.7. In today’s economy, you need to have specific skills to ____________(成功)。
人教版高中化学(必修2)第四章同步导学案4.1.2 海水资源的开发利用

第四章化学与自然资源的开发利用第一节第2课时海水资源的开发利用1.了解海水资源及其利用。
2了解海水淡化的方法,掌握海水的蒸馏。
3掌握海水化学资源的开发和利用,即海水制盐,海水提镁、提溴、提碘。
4了解海水综合利用的重要方向。
►自主探究自主学习探究归纳一、海水水资源的利用1.类型海水水资源的利用主要包括海水的和海水的。
2.海水的淡化1主要方法:、和等。
2海水的蒸馏①主要仪器:A:;B:;C:。
②冷凝水的流向:口进,口出。
③A中加入碎瓷片的目的是。
二、海水化学资源的开发利用1.海水中的元素1常量元素99%:除、两种元素外,含有Cl、Na、K、Mg、Ca、S、C、F、B、Br、Sr等11种元素。
2微量元素1%:常量元素之外的元素,总计含有80多种。
3特点:种类很多,总储量很大,但许多元素的富集程度很低。
2.海水化学资源的开发利用1从海水中制得的NaCl除食用外,还用作工业原料,如生产、、以及氯气、、等含氯化工产品。
2从海水中制取钾、镁、溴及其化工产品,是在传统海水制盐工业上的发展。
自我测评►———————————————————做一做1.判断正误:1用蒸馏法进行海水淡化是物理变化。
分析:蒸馏是利用物质沸点不同进行分离的方法,没有发生化学变化。
2甲状腺肿大的病人应适量多食海带。
分析:碘元素缺乏导致甲状腺肿大,海带中含有丰富的碘元素,因此适当多食用海带能帮助甲状腺肿大的病人康复。
3海水中含有溴元素,不需要经过化学反应即能得到溴单质。
分析:海水中溴元素是以溴离子的形式存在,需要发生氧化反应才能生成溴单质。
2.思考:海带中含有碘,海带能使淀粉溶液变蓝吗?1海带中碘的提取和碘元素的检验1海带中提碘①流程海带→灼烧→浸泡→氧化→过滤→提纯→碘单质。
②主要化学反应2I-+H2O2+2H+===I2+2H2O或Cl2+2I-===I2+2Cl-。
③主要物理原理单质碘用苯或四氯化碳萃取,分液后用蒸馏的方法将碘和有机溶剂分开。
高中生物必修2导学案:第4单元 基因的表达
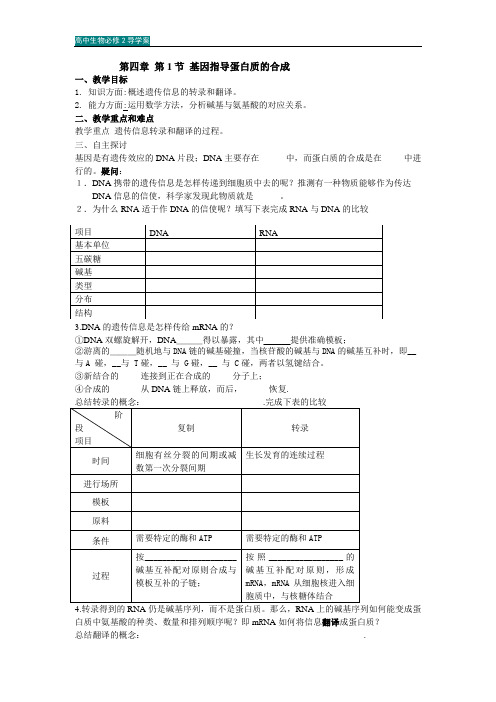
第四章第1节基因指导蛋白质的合成一、教学目标1. 知识方面:概述遗传信息的转录和翻译。
2. 能力方面:运用数学方法,分析碱基与氨基酸的对应关系。
二、教学重点和难点教学重点遗传信息转录和翻译的过程。
三、自主探讨基因是有遗传效应的DNA片段;DNA主要存在______中,而蛋白质的合成是在_____中进行的。
疑问:1.DNA携带的遗传信息是怎样传递到细胞质中去的呢?推测有一种物质能够作为传达DNA信息的信使,科学家发现此物质就是______。
2.为什么RNA适于作DNA的信使呢?填写下表完成RNA与DNA的比较3.DNA的遗传信息是怎样传给mRNA的?①DNA双螺旋解开,DNA___得以暴露,其中___提供准确模板;②游离的___随机地与DNA链的碱基碰撞,当核苷酸的碱基与DNA的碱基互补时,即__与A 碰,__与 T碰,__ 与 G碰,__ 与 C碰,两者以氢键结合。
③新结合的_____连接到正在合成的_____分子上;④合成的_______从DNA链上释放,而后,______恢复.4.转录得到的RNA仍是碱基序列,而不是蛋白质。
那么,RNA上的碱基序列如何能变成蛋白质中氨基酸的种类、数量和排列顺序呢?即m R NA如何将信息翻译成蛋白质?总结翻译的概念:__________________________________________________.思考:①碱基和氨基酸的对应关系如何?一个碱基决定一个氨基酸只能决定4种,4 =4,不行。
二个碱基决定一个氨基酸只能决定16种,42=16,不行。
三个碱基决定一个氨基酸只能决定64种,43=64,足够有余。
最终,我们知道_______________决定一个氨基酸,___________________称作一个密码子。
如右图所示一条mRNA 片段,有3个密码子,分别是_______,______,_________U U A G AU A U C 请大家查密码子表,分析密码子的特点:一个密码子决定一个特定的氨基酸;(2)有的氨基酸可能有一个以上的密码子;(3)起始密码子、终止密码子。
【人教A版】高中数学必修二:第4章《圆与方程》导学案设计(含答案) 第四章 4.2.1

4.2.1 直线与圆的位置关系[学习目标] 1.理解直线和圆的三种位置关系.2.会用代数与几何两种方法判断直线和圆的位置关系.知识点一 直线与圆的位置关系及判断思考 用代数法与几何法判断直线与圆的位置关系时,二者在侧重点上有什么不同? 答 代数法与几何法都能判断直线与圆的位置关系,只是角度不同,代数法侧重于“数”的计算,几何法侧重于“形”的直观. 知识点二 圆的切线问题 1.求圆的切线的方法(1)求过圆上一点(x 0,y 0)的圆的切线方程:先求切点与圆心的连线的斜率k ,则由垂直关系,知切线斜率为-1k ,由点斜式方程可求得切线方程.如果k =0或k 不存在,则由图形可直接得切线方程为y =y 0或x =x 0. (2)求过圆外一点(x 0,y 0)的圆的切线方程:几何法:设切线方程为y -y 0=k (x -x 0),即kx -y -kx 0+y 0=0.由圆心到直线的距离等于半径,可求得k ,切线方程即可求出.并注意检验当k 不存在时,直线x =x 0是否为圆的切线. 代数法:设切线方程y -y 0=k (x -x 0),即y =kx -kx 0+y 0,代入圆的方程,得到一个关于x 的一元二次方程,由Δ=0求得k ,切线方程即可求出.并注意检验当k 不存在时,直线x =x 0是否为圆的切线. 2.切线段的长度公式(1)从圆外一点P (x 0,y 0)引圆(x -a )2+(y -b )2=r 2的切线,则P 到切点的切线段长为 d =(x 0-a )2+(y 0-b )2-r 2.(2)从圆外一点P (x 0,y 0)引圆x 2+y 2+Dx +Ey +F =0的切线,则P 到切点的切线段长为d =x 20+y 20+Dx 0+Ey 0+F .题型一 直线与圆的位置关系的判断例1 已知直线方程mx -y -m -1=0,圆的方程x 2+y 2-4x -2y +1=0.当m 为何值时,圆与直线(1)有两个公共点; (2)只有一个公共点; (3)没有公共点.解 方法一 将直线mx -y -m -1=0代入圆的方程化简整理得, (1+m 2)x 2-2(m 2+2m +2)x +m 2+4m +4=0. ∵Δ=4m (3m +4),∴当Δ>0,即m >0或m <-43时,直线与圆相交,即直线与圆有两个公共点;当Δ=0,即m =0或m =-43时,直线与圆相切,即直线与圆只有一个公共点;当Δ<0,即-43<m <0时,直线与圆相离,即直线与圆没有公共点.方法二 已知圆的方程可化为(x -2)2+(y -1)2=4, 即圆心为C (2,1),半径r =2.圆心C (2,1)到直线mx -y -m -1=0的距离 d =|2m -1-m -1|1+m 2=|m -2|1+m 2.当d <2,即m >0或m <-43时,直线与圆相交,即直线与圆有两个公共点;当d =2,即m =0或m =-43时,直线与圆相切,即直线与圆只有一个公共点;当d >2,即-43<m <0时,直线与圆相离,即直线与圆没有公共点.反思与感悟 直线与圆位置关系判断的三种方法:(1)几何法:由圆心到直线的距离d 与圆的半径r 的大小关系判断. (2)代数法:根据直线与圆的方程组成的方程组解的个数来判断.(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系,但有一定的局限性,必须是过定点的直线系.跟踪训练1 若直线4x -3y +a =0与圆x 2+y 2=100有如下关系:①相交;②相切;③相离.试分别求实数a 的取值范围. 解 方法一 (代数法)由方程组⎩⎪⎨⎪⎧4x -3y +a =0,x 2+y 2=100,消去y ,得25x 2+8ax +a 2-900=0. Δ=(8a )2-4×25(a 2-900)=-36a 2+90 000. ①当直线和圆相交时,Δ>0, 即-36a 2+90 000>0,-50<a <50; ②当直线和圆相切时,Δ=0, 即a =50或a =-50; ③当直线和圆相离时,Δ<0, 即a <-50或a >50. 方法二 (几何法)圆x 2+y 2=100的圆心为(0,0),半径r =10, 则圆心到直线的距离d =|a |32+42=|a |5, ①当直线和圆相交时,d <r , 即|a |5<10,-50<a <50; ②当直线和圆相切时,d =r , 即|a |5=10,a =50或a =-50; ③当直线和圆相离时,d >r , 即|a |5>10,a <-50或a >50. 题型二 圆的切线问题例2 过点A (4,-3)作圆(x -3)2+(y -1)2=1的切线,求此切线的方程. 解 因为(4-3)2+(-3-1)2=17>1,所以点A 在圆外.(1)若所求直线的斜率存在,设切线斜率为k , 则切线方程为y +3=k (x -4).即kx -y -3-4k =0, 因为圆心C (3,1)到切线的距离等于半径1, 所以|3k -1-3-4k |k 2+1=1,即|k +4|=k 2+1, 所以k 2+8k +16=k 2+1.解得k =-158.所以切线方程为y +3=-158(x -4),即15x +8y -36=0. (2)若直线斜率不存在,圆心C (3,1)到直线x =4的距离也为1,这时直线与圆也相切,所以另一条切线方程是x =4. 综上,所求切线方程为15x +8y -36=0或x =4.反思与感悟 1.过一点P (x 0,y 0)求圆的切线方程问题,首先要判断该点与圆的位置关系,若点在圆外,切线有两条,一般设点斜式y -y 0=k (x -x 0)用待定系数法求解,但要注意斜率不存在的情况,若点在圆上,则切线有一条,用切线垂直于过切点的半径求切线的斜率,再由点斜式可直接得切线方程.2.一般地,有关圆的切线问题,若已知切点则用k 1·k 2=-1(k 1,k 2分别为切线和圆心与切点连线的斜率)列式,若未知切点则用d =r (d 为圆心到切线的距离,r 为半径)列式.跟踪训练2 圆C 与直线2x +y -5=0相切于点(2,1),且与直线2x +y +15=0也相切,求圆C 的方程.解 设圆C 的方程为(x -a )2+(y -b )2=r 2. 因为两切线2x +y -5=0与2x +y +15=0平行, 所以2r =|15-(-5)|22+12=4 5.所以r =2 5.所以|2a +b +15|22+1=r =25,即|2a +b +15|=10;①|2a +b -5|22+1=r =25,即|2a +b -5|=10.② 又因为过圆心和切点的直线与切线垂直, 所以b -1a -2=12.③联立①②③,解得⎩⎪⎨⎪⎧a =-2,b =-1.故所求圆C 的方程为(x +2)2+(y +1)2=20. 题型三 圆的弦长问题例3 求直线x -3y +23=0被圆x 2+y 2=4截得的弦长.解 方法一 直线x -3yy +23=0和圆x 2+y 2=4的公共点坐标就是方程组⎩⎨⎧x -3y +23=0,x 2+y 2=4的解. 解这个方程组,得⎩⎨⎧x 1=-3,y 1=1,⎩⎪⎨⎪⎧x 2=0,y 2=2. 所以公共点的坐标为(-3,1),(0,2),所以直线x -3y +23=0被圆x 2+y 2=4截得的弦长为(-3-0)2+(1-2)2=2. 方法二 如图,设直线x -3y +23=0与圆x 2+y 2=4交于A ,B 两点,弦AB 的中点为M ,则OM ⊥AB (O 为坐标原点), 所以|OM |=|0-0+23|12+(-3)2= 3.所以|AB |=2|AM |=2OA 2-OM 2 =222-(3)2=2. 反思与感悟求直线与圆相交时弦长的两种方法:(1)几何法:如图1,直线l 与圆C 交于A ,B 两点,设弦心距为d ,圆的半径为r ,弦长为|AB |,则有⎝⎛⎭⎫|AB |22+d 2=r 2. 即|AB |=2r 2-d 2.(2)代数法:如图2所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A (x 1,y 1),B (x 2,y 2), 则|AB |=(x 1-x 2)2+(y 1-y 2)2 =1+k 2|x 1-x 2| =1+1k2|y 1-y 2|, 其中k 为直线l 的斜率.跟踪训练3 直线x +2y -5+5=0被圆x 2+y 2-2x -4y =0截得的弦长为( ) A.1 B.2 C.4 D.46 答案 C解析圆的方程可化为C:(x-1)2+(y-2)2=5,其圆心为C(1,2),半径r=5.如图所示,取弦AB的中点P,连接CP,则CP⊥AB,圆心C到直线AB的距离d=|CP|=|1+4-5+5|12+22=1.在Rt△ACP中,|AP|=r2-d2=2,故直线被圆截得的弦长|AB|=4.数形结合思想例4直线y=x+b与曲线x=1-y2有且只有一个交点,则b的取值范围是()A.|b|= 2B.-1<b≤1或b=-2C.-1≤b<1D.非以上答案分析曲线x=1-y2变形为x2+y2=1(x≥0),表示y轴右侧(含与y轴的交点)的半圆,直线y=x+b表示一系列斜率为1的直线,利用数形结合思想在同一平面直角坐标系内作出两种图形求解.解析曲线x=1-y2含有限制条件,即x≥0,故曲线并非表示整个单位圆,仅仅是单位圆在y轴右侧(含与y轴的交点)的部分.在同一平面直角坐标系中,画出y=x+b与曲线x=1-y2(就是x2+y2=1,x≥0)的图象,如图所示.相切时,b=-2,其他位置符合条件时需-1<b≤1.故选B.答案B解后反思求解直线与曲线公共点的问题,首先要借助图形进行思考;其次要注意作图的完整准确,使得图形能够反映问题的全部;最后在求解中还要细心缜密,保证计算无误.1.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是()A.相离B.相切C.相交但直线不过圆心D.相交且直线过圆心答案C解析方法一圆心(0,0)到直线kx-y+1=0的距离d=11+k2≤1<2=r,∴直线与圆相交,且圆心(0,0)不在该直线上.方法二 直线kx -y +1=0恒过定点(0,1),而该点在圆内,故直线与圆相交,且圆心不在该直线上.2.已知点M (a ,b )在圆O :x 2+y 2=1外,则直线ax +by =1与圆O 的位置关系是( ) A.相切 B.相交 C.相离 D.不确定 答案 B解析 ∵点M (a ,b )在圆x 2+y 2=1外,∴a 2+b 2>1. ∴圆心(0,0)到直线ax +by =1的距离d =1a 2+b2<1=r ,则直线与圆的位置关系是相交. 3.平行于直线2x +y +1=0且与圆x 2+y 2=5相切的直线的方程是( ) A.2x -y +5=0或2x -y -5=0 B.2x +y +5=0或2x +y -5=0 C.2x -y +5=0或2x -y -5=0 D.2x +y +5=0或2x +y -5=0 答案 D解析 依题意可设所求切线方程为2x +y +c =0,则圆心(0,0)到直线2x +y +c =0的距离为|c |22+12=5,解得c =±5.故所求切线的直线方程为2x +y +5=0或2x +y -5=0. 4.设A 、B 为直线y =x 与圆x 2+y 2=1的两个交点,则|AB |等于( ) A.1 B. 2 C. 3 D.2 答案 D解析 直线y =x 过圆x 2+y 2=1的圆心C (0,0), 则|AB |=2.5.过原点的直线与圆x 2+y 2-2x -4y +4=0相交所得弦的长为2,则该直线的方程为________. 答案 2x -y =0解析 设所求直线方程为y =kx ,即kx -y =0.由于直线kx -y =0被圆截得的弦长等于2,圆的半径是1,因此圆心到直线的距离等于12-⎝⎛⎭⎫222=0,即圆心(1,2)位于直线kx -y =0上.于是有k -2=0,即k =2,因此所求直线方程是2x -y =0.1.判断直线和圆的位置关系的两种方法中,几何法要结合圆的几何性质进行判断,一般计算较简单.而代数法则是通过解方程组进行消元,计算量大,不如几何法简捷.2.一般地,在解决圆和直线相交时,应首先考虑圆心到直线的距离,弦长的一半,圆的半径构成的直角三角形.还可以联立方程组,消去y ,组成一个一元二次方程,利用方程根与系数的关系表达出弦长l =k 2+1·(x 1+x 2)2-4x 1x 2=k 2+1|x 1-x 2|.3.研究圆的切线问题时要注意切线的斜率是否存在.过一点求圆的切线方程时,要考虑该点是否在圆上.当点在圆上时,切线只有一条;当点在圆外时,切线有两条.一、选择题1.直线l :y -1=k (x -1)和圆x 2+y 2-2y =0的位置关系是( ) A.相离 B.相切或相交 C.相交 D.相切 答案 C解析 l 过定点A (1,1),∵12+12-2×1=0,∴点A 在圆上,∵直线x =1过点A 且为圆的切线,又l 斜率存在, ∴l 与圆一定相交,故选C.2.已知直线l 过圆x 2+(y -3)2=4的圆心,且与直线x +y +1=0垂直,则l 的方程是( ) A.x +y -2=0 B.x -y +2=0 C.x +y -3=0 D.x -y +3=0答案 D解析 圆x 2+(y -3)2=4的圆心为点(0,3),又因为直线l 与直线x +y +1=0垂直,所以直线l 的斜率k =1.由点斜式得直线l :y -3=x -0,化简得x -y +3=0.3.已知圆C 与直线x -y =0及x -y -4=0都相切,圆心在直线x +y =0上,则圆C 的方程为( )A.(x +1)2+(y -1)2=2B.(x -1)2+(y +1)2=2C.(x -1)2+(y -1)2=2D.(x +1)2+(y +1)2=2答案 B解析 由条件,知x -y =0与x -y -4=0都与圆相切,且平行,所以圆C 的圆心C 在直线x -y -2=0上.由⎩⎪⎨⎪⎧x -y -2=0,x +y =0,得圆心C (1,-1).又因为两平行线间距离d =42=22,所以所求圆的半径长r =2,故圆C 的方程为(x -1)2+(y +1)2=2.4.过点P (-3,-1)的直线l 与圆x 2+y 2=1相切,则直线l 的倾斜角是( ) A.0° B.45° C.0°或45° D.0°或60° 答案 D解析 设过点P 的直线方程为y =k (x +3)-1,则由直线与圆相切知|3k -1|1+k 2=1,解得k =0或k =3,故直线l 的倾斜角为0°或60°.5.圆x 2+y 2-4x +6y -12=0过点(-1,0)的最大弦长为m ,最小弦长为n ,则m -n 等于( )A.10-27B.5-7C.10-3 3D.5-322答案 A解析 圆的方程x 2+y 2-4x +6y -12=0化为标准方程为(x -2)2+(y +3)2=25. 所以圆心为(2,-3),半径长为5. 因为(-1-2)2+(0+3)2=18<25, 所以点(-1,0)在已知圆的内部, 则最大弦长即为圆的直径,即m =10. 当(-1,0)为弦的中点时,此时弦长最小. 弦心距d =(2+1)2+(-3-0)2=32, 所以最小弦长为2r 2-d 2=225-18=27, 所以m -n =10-27.6.在圆x 2+y 2+2x +4y -3=0上且到直线x +y +1=0的距离为2的点共有( ) A.1个 B.2个 C.3个 D.4个 答案 C解析 圆心为(-1,-2),半径r =22,而圆心到直线的距离d =|-1-2+1|2=2,故圆上有3个点满足题意.7.直线y =kx +3与圆(x -3)2+(y -2)2=4相交于M ,N 两点,若|MN |≥23,则k 的取值范围是( ) A.⎣⎡⎦⎤-34,0 B.⎝⎛⎦⎤-∞,-34∪[0,+∞) C.⎣⎡⎦⎤-33,33 D.⎣⎡⎦⎤-23,0 答案 A解析 设圆心为C ,弦MN 的中点为A ,当|MN |=23时,|AC |=|MC |2-|MA |2=4-3=1.∴当|MN |≥23时,圆心C 到直线y =kx +3的距离d ≤1. ∴|3k -2+3|k 2+(-1)2≤1,∴(3k +1)2≤k 2+1. 由二次函数的图象可得 -34≤k ≤0. 二、填空题8.设直线ax -y +3=0与圆(x -1)2+(y -2)2=4相交于A ,B 两点,且弦AB 的长为23,则a =________. 答案 0解析 圆心到直线的距离d =|a -2+3|a 2+1=22-(3)2=1,解得a =0. 9.圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________. 答案 (x -2)2+(y -1)2=4解析 设圆C 的圆心为(a ,b )(b >0),由题意得a =2b >0,且a 2=(3)2+b 2,解得a =2,b =1.所以所求圆的标准方程为(x -2)2+(y -1)2=4.10.在平面直角坐标系xOy 中,直线x +2y -3=0被圆(x -2)2+(y +1)2=4截得的弦长为________. 答案2555解析 圆心为(2,-1),半径r =2.圆心到直线的距离d =|2+2×(-1)-3|1+4=355,所以弦长为2r 2-d 2=222-(355)2=2555.11.若直线l :y =x +b 与曲线C :y =1-x 2有两个公共点,则b 的取值范围是_______. 答案 [1,2)解析 如图所示,y =1-x 2是一个以原点为圆心,长度1为半径的半圆,y =x +b 是一个斜率为1的直线,要使直线与半圆有两个交点,连接A (-1,0)和B (0,1),直线l 必在AB 以上的半圆内平移,直到直线与半圆相切,则可求出两个临界位置直线l 的b 值,当直线l 与AB 重合时,b =1;当直线l 与半圆相切时,b = 2.所以b 的取值范围是[1,2). 三、解答题12.已知圆C :(x -1)2+(y -2)2=25,直线l :(2m +1)x +(m +1)y -7m -4=0(m ∈R ). (1)求证不论m 取什么实数,直线l 与圆恒交于两点; (2)求直线被圆C 截得的弦长最小时的l 的方程.(1)证明 因为l 的方程为(x +y -4)+m (2x +y -7)=0(m ∈R ),所以⎩⎪⎨⎪⎧2x +y -7=0,x +y -4=0,解得⎩⎪⎨⎪⎧x =3,y =1, 即l 恒过定点A (3,1).第11页 共11页 因为圆心为C (1,2),|AC |=5<5(半径),所以点A 在圆C 内,从而直线l 与圆C 恒交于两点.(2)解 由题意可知弦长最小时,l ⊥AC .因为k AC =-12,所以l 的斜率为2. 又l 过点A (3,1),所以l 的方程为2x -y -5=0.13.已知直线l 过点P (1,1)并与直线l 1:x -y +3=0和l 2:2x +y -6=0分别交于点A ,B ,若线段AB 被点P 平分,求:(1)直线l 的方程;(2)以原点O 为圆心且被l 截得的弦长为855的圆的方程. 解 (1)依题意可设A (m ,n ),B (2-m,2-n ), 则⎩⎪⎨⎪⎧ m -n +3=0,2(2-m )+(2-n )-6=0,即⎩⎪⎨⎪⎧m -n =-3,2m +n =0, 解得A (-1,2).又l 过点P (1,1),易得直线AB 的方程为x +2y -3=0, 即直线l 的方程为x +2y -3=0.(2)设圆的半径长为r ,则r 2=d 2+⎝⎛⎭⎫4552,其中d 为弦心距,d =35,可得r 2=5,故所求圆的方程为x 2+y 2=5.。
必修2第四单元导学案

Book 2 Unit 2 Computers学习目标1 To master the usage of words and expressions.2 To learn the method of developing English system and be able to use the new words and phrases by self-directed study and cooperation.3 Study with passion and try your best to enjoy English learning.使用说明及方法指导1 依据预习案掌握重点词汇和句式,进行知识梳理;熟记基础知识。
2.将预习中不能解决的问题和自主学习的收获一并填写到后面“我的疑问与收获”处。
预习案1. signal v.发信号n.信号signal sb to do sth示意某人做某事signal sb that 示意1)This announcement signaled a clear change of policy._______________________________________________2) He signaled ________________________他打手势让他们前进。
3) In our class, when the bell rang and the teacher closed his book, it was a ____for everyone to stand up.A. signalB. chanceC. markD. measure2. arise vi.发生,出现,产生,起身,起床,上升1) We keep them informed of any changes as they arise.如有任何变化,我们随时通知他们。
2) A new crisis has arisen and we have to think of a way to deal with it..新危机已经出现, 我们的想一个办法来解决它。
必修二Unit 4导学案

Unit 4. Wildlife protection------Language pointsPeriod1.一.自主探究:1.look after____________2.die out____________3.as a result___________4.set up ___________5.nature reserves ___________6.bring back ___________7.leave sb in peace ___________8.with no hunting ___________9.in danger of disappearing ___________10.have some progress in ___________二.语言点1.decrease v. & n. (1)vi. & vt. 降低,减少,使(变小)decrese to 减少到…… decrease by 减少了……会员减少至300人。
The member decreased three hundred.会员减少了300人。
The members decreased three hundred. 2. die out : disappear completely,extinct 灭绝Dinosaurs have long before.die of.指由于疾病,情感,饥寒等原因而造成的死亡,指死于内因。
die from .指死于外因。
He died drinking/smoking/overwork/accident.More and more people died cancer.die off :死去;先后死去The members of the family had all for no reason.die away: (光、声音)慢慢消失(风)停下来He hid behind the door until the footsteps had .渴望某人/物渴望做某事long before.before long.不久以后他就去美国继续深造了。
人教新课标高中英语必修二Unit4Wildlifeprotection导学案(4)

①这些措施将有助于降低生产成本。
willhelp
thecostofproduction.
②人口出生率正在下降。
Thebirthrateis
.
答案:① Thesemeasures;decrease
② onthedecrease
2.suggest vt .建议;提出(意见、计划、理论等) ;暗示;表明 常用结构: suggest+doing 建议做 …… suggestsb./sb. ’ sdoingsth. 建议某人做某事(不说 suggestsb.todosth. ) suggeststh.to sb. 向某人提议 …… (不能说 suggestsb.sth.)
increaseto/by... 增加到 / 了 …… onthedecrease/increase 在减少 / 增加 易混辨析
reduce/decrease reduce 强调在 “数量、大小,程度或强度 ”方面下降或减少。
decrease 侧重强调 “稳定地,逐渐地,不断地 ”减少。 Theyaremakingeveryefforttodecreasetheproductioncost. 他们正在尽力降低生产成本。
高中英语必修 2Unit4Wildlifeprotection
精品文档
精品导学案(含答案解析)
Unit4Wildlifeprotection
核心单词
1.decrease
v.减少;(使)变小;变少
n. 减少;降低;减少的数量,其后常接介词
in/of
联想拓展
decrease(sth.)to/by... 减少到 / 了 …… increasevi.&vt .增加;增长;增强 n.增加;增加的数量
高二数学必修二 第四章《圆与方程》4.1圆的方程导学案

高二数学必修2 第四章 圆与方程第四章 圆与方程§4.1圆的方程§4.1.1圆的标准方程(1)【学习目标】1.能根据圆心、半径写出圆的标准方程.2.利用圆的标准方程,会判断点与圆的位置关系.【学习重点】求圆的标准方程.【学习难点】根据不同的已知条件,判断点与圆的位置关系.【学习过程】一、自主学习(阅读课本第118-119页,完成自主学习)1.已知两点(2,5),(6,9)A B -,求它们之间的距离?若已知(3,8),(,)C D x y -,求它们之间的距离.2.图中哪个点是定点?哪个点是动点?动点具有什么性质?3.具有什么性质的点的轨迹称为圆? 圆心和半径分别确定了圆的_______和_______.4.我们知道,在平面直角坐标系中,确定一条直线的条件是两点或一点和倾斜角,那么,在平面内确定圆的条件是什么?5.在平面直角坐标系中,若一个圆的圆心(,)C a b ,半径为r (其中,,a b r 都是常数, 0r >),圆的标准方程为__________________________________.6.当圆心在原点时,圆的标准方程是_________________ .思考:圆的标准方程222()()x a y b r -+-=中,只要求出___、___、___,这时圆的方程就被确定,因此确定圆的标准方程,需三个独立条件,其中____是圆的定位条件,_____是圆的定形条件.二、合作探究例1:写出圆心为(2,3)A -半径长等于5的圆的方程,判断12(5,7),(1)M M --是否在这个圆上.推广:设点00(,)M x y ,圆的方程为222()()x a y b r -+-=.1,M 在圆上⇔2200()()x a y b -+- 2r ;2,M 在圆外⇔2200()()x a y b -+- 2r ;3,M 在圆内⇔2200()()x a y b -+- 2r ;例2:圆的一条直径的两个端点分别是(2,0),(2,2)A B -,求圆的标准方程,并判断点(0,0),C (2,2)D -与该圆的位置关系推广:已知圆的一条直径的端点分别是1222(,),(,),A x y B x y 求证此圆的方程是1212()()()()0.x x x x y y y y --+--=三、达标检测1.写出下列各圆的标准方程.(1) 圆心在原点,半径是3;(2) 圆心在(3,4)C(3) 经过点(5,1)P ,圆心在点(8,3)C -;2.写出下列各圆的圆心坐标和半径:(1) 22(1)6x y -+= (2) 22(1)(2)9x y ++-= (3) 22(2)(3)3x y -++=3.已知圆心在点(3,4),C --且经过原点,求该圆的标准方程,并判断点12(,0),(1,1),P P -- 3(3,4)P -和圆的位置关系.四、学习小结1.圆的标准方程 .2.求圆的标准方程的方法有:高二数学必修2 第四章 圆与方程§4.1.1圆的标准方程(2)【学习目标】会用待定系数法求圆的标准方程.【学习重点】掌握求圆的标准方程的思路方法.【学习难点】领会用数形结合求圆的标准方程的思想.【学习过程】一、自主学习(阅读课本第119-120页,完成自主学习)1.圆的定义是什么?2.圆的标准方程是怎样的?3.点M(x 0,y 0)与圆(x -a )2+(y -b )2=r 2的关系的判断方法:(1)当点M(x 0,y 0)在圆(x -a )2+(y -b )2=r 2上时,点M 的坐标_____方程(x -a )2+(y -b )2=r 2.(2)当点M(x 0,y 0)不在圆(x -a )2+(y -b )2=r 2上时,点M 的坐标______方程(x -a )2+(y -b )2=r 2.(3)用点到圆心的距离和半径的大小来说明应为:1°点到圆心的距离大于半径⇔点在圆外⇔_________________.2°点到圆心的距离等于半径⇔点在圆上⇔_________________.3°点到圆心的距离小于半径⇔点在圆内⇔_________________.二、合作探究例1:ABC ∆的三个顶点的坐标分别是(5,1),(2,8),(7,3)A B C --,求它的外接圆的方程.例2:求经过点(1,1)A ,(2,2)B -,且圆心在直线:10l x y -+=上的圆的标准方程.三、达标检测1.写出下列各圆的标准方程:(1) 圆心在y 轴上,半径长为1,且过点(1,2)的圆的方程;(2)圆心在x 轴上,半径长为1,且过点(2,1)的圆的方程.2.圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4),(0,2)A B --,求圆C 的标准方程.3.求经过两点(1,4),(3,2)A B -且圆心在y 轴上的圆的方程.四、学习小结1.确定圆的方程主要方法是_____________法,即列出关于a 、b 、r 的方程组,求a 、b 、r 或直接求出圆心(a ,b )和半径r ,一般步骤为:1°根据题意,设所求的圆的标准方程________________;2°根据已知条件,建立关于__________________的方程组;3°解方程组,求出___________的值,并把它们代入所设的方程中去,就得到所求圆的方程.2.思想方法总结:高二数学必修2 第四章 圆与方程§4.1.2圆的一般方程(1)【学习目标】能用圆的一般方程确定圆的圆心、半径.【学习重点】把握圆的一般方程的代数特征,能根据已知条件待定方程中的系数,,D E F .【学习难点】根据已知条件选择待定圆的标准方程或一般方程.【学习过程】一、自主学习(阅读课本第121-122页,完成自主学习)1.写出圆心为(,)a b ,半径为r 的圆的标准方程_______________________________.2.将以(,)C a b 为圆心, r 为半径的圆的标准方程展开并整理得________________.3.如果2222,2,D a E b F a b r =-=-=+-,得到方程____________________,这说明圆的 方程还可以表示成另外一种非标准方程形式.4.思考:能不能说方程220x y Dx Ey F ++++=所表示的曲线一定是圆呢?二、合作探究1.222()()x a y b r -+-=中0r >时表示___ _;0r =时表示____________;2.把式子220x y Dx Ey F ++++=配方得_________________________________.(ⅰ)当2240D E F +->时,表示以_________为圆心,_____________ _为半径的圆; (ⅱ)当2240D E F +-=时,方程只有实数解x =______y =______,即只表示__________; (ⅲ)当2240D E F +-<时,方程______(有或没有)实数解,因而它_________________.方程220x y Dx Ey F ++++=表示的曲线_________(一定或不一定)是圆;但圆的方程都能写成_________________的形式,只有当_____________时,它表示的曲线才是圆. 我们把形如220x y Dx Ey F ++++=表示圆的方程称为圆的_________方程.3.圆的一般方程形式上的特点:(1)x 2和y 2的系数_______且________. (2)没有_________这样的二次项.例1:判断下列二元二次方程是否表示圆的方程?如果是,请求出圆的圆心及半径.(1) 224441290x y x y +-++= (2) 2220x y by ++=例2:求过三点(0,0),(1,1),(4,2)O M N 的圆的一般方程,并求圆的半径长和圆心坐标.三、达标检测1.判断下列方程(1) 2260x y y +-=(2)222460x y x y +-+-=(3)224220200x y mx my m +-++-=能否表示圆,若能表示圆,求出圆心和半径.2.ABC ∆的三个顶点分别为(1,5),(2,2),(5,5)A B C ---,求其外接圆的一般方程.四、学习小结用待定系数法求圆的方程的步骤是:1.____________________________________________2._____________________________________________3._____________________________________________高二数学必修2 第四章 圆与方程§4.1.2圆的一般方程(2)【学习目标】掌握圆的一般方程及其特点,会由圆的方程求出圆心、半径会用待定系数法求圆的一般方程.【学习重点】圆的一般方程的特征和求圆的一般方程.【学习难点】用相关点法求轨迹方程.【学习过程】一、自主学习(阅读课本第122-123页,完成自主学习)1.将下列圆的方程化为标准方程,并写出圆心坐标和半径:(1)222220(0);(2)22420.x y my m x y ax ++=≠++-=2.圆C :222440x y x y +--+=的圆心到直线3440x y ++=的距离_____d =.二、合作探究例:已知线段AB 的端点B 的坐标是(4,3),端点A 在圆22(1)4x y ++=上运动,求线段AB 的中点M 的轨迹方程.三、达标检测1.求以(1,1)A -为圆心,且经过点(0,1)B 的圆的一般方程.2.若(5,0),(1,0),(3,3)A B C --三点的外接圆为圆M ,求圆M 的方程,若点(,3)D m 在圆M 上,求m 的值.3.求圆心在直线230x y --=上,且过点(5,2),(3,2)A B -的圆的方程.4.已知点P 在圆的C :2286210x y x y +--+=上运动,求线段OP 的中点坐标M 的轨迹方程.四、学习小结相关点法求轨迹方程的步骤:1._______________________________________________________;2._______________________________________________________;3._______________________________________________________;4._______________________________________________________;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 第一节 开发利用金属矿物和海水资源金属矿物的开发利用(1)【学习目标】1. 了解金属元素在自然界中的存在形态2.重点掌握金属冶炼的原理,熟悉金属冶炼的步骤以及方法。
【教学重点】了解化学方法在金属矿物开发中的作用【教学难点】学生在掌握金属冶炼的一般原理基础上,了解适用于不同金属的冶炼方法【教学方法】探究法【知识链接】金属活动顺序表【学习内容】知识点:1、金属的存在:除了金、铂等少数金属外,绝大多数金属以 的形式存在于自然界。
2、金属冶炼的含义:简单地说,金属的冶炼就是把金属从矿石中提炼出来。
金属冶炼的实质是把金属元素从化合态还原为游离态,即M +n(游离态)。
3、金属冶炼的一般步骤:(1) : ,提高矿石中有用成分的含量。
(2) :利用氧化还原反应原理,在一定条件下,用还原剂把金属从其矿石中还原出来,得到金属单质(粗)。
(3) :采用一定的方法,提炼纯金属。
4、金属冶炼的方法① 热分解法在金属活动顺序中,位于汞以后的不活泼金属可以直接用 的方法从其化合物中还原出来。
例如:氧化汞分解:氧化银分解:②热还原法对于金属活动顺序表中Zn-Cu段的金属的冶炼可以通过来完成,常用的还原剂有、、等。
例如:氧化铁和一氧化碳反应:氧化铜和氢气反应:对于一些高熔点的金属如铁、铬、锰、钨等可以用冶炼。
实验:观察〖实验4-1〗,完成下列表格讨论:⑴在实验中为什么要在铝与氧化铁混合粉末的上面加少量的氯酸钾固体,中间插一根用砂纸打磨过的镁条?⑵这个实验说明什么?③电解法对于金属活动顺序表中Zn前面非常活泼的金属,采用一般的还原剂很难将它们还原出来,工业上常用冶炼,例如:电解熔融的氯化镁:电解熔融的氯化钠:电解熔融的氧化铝:5、 (1)回收金属的意Ⅳ义:节约矿物资源,节约能源,减少环境污染。
(2)废旧金属的处理方法:回收利用。
回收金属的实例:a.废旧钢铁用于炼钢;b.废铁屑用于制铁盐;c.从电影业、照相业、科研单位和医院X光室回收的定影液中,可以提取金属银。
【归纳小结】常见金属的冶炼原理【过关训练】1、冶炼金属一般有下列四种方法:①1焦炭法②水煤气法③活泼金属置换法④电解法。
古代有(Ⅰ)火烧孔雀石炼铜(Ⅱ)湿法炼铜;现代有(Ⅲ)铝热法炼铬(Ⅳ)从光卤石中炼镁,对它们的冶炼方法的分析不正确的是( )A.(Ⅰ)用①B.(Ⅱ)用②C.(Ⅲ)用③D.(Ⅳ)用④2、下列冶炼方法中,可以将化合物中的金属元素还原为金属单质的是( )A.加热Al 2O 3B.加热CaCO 3C.电解熔融NaClD.氯化钠与铝粉高温共热3、冶炼金属常用以下几种方法:①以C 、CO 或H 2做还原剂 ②热分解法 ③利用铝热反应原理还原 ④电解法。
下列金属各采用哪种方法还原最佳。
(用序号填写下列空白。
)(1)Fe 、Zn 、Cu 等中等活泼金属_____________。
(2)Na 、Mg 、Al 等活泼或较活泼金属_________。
(3)Hg 、Ag 等不活泼金属__________________。
(4)V 、Cr 、Mn 、W 等高熔点金属____________。
4、宋朝初期,我国已将湿法炼铜应用于生产,其反应原理为( )A 、CuO+H 2==Cu+H 2OB 、CuO+CO==CO 2+CuC 、Fe+CuSO 4==Cu+FeSO 4D 、Cu 2(OH)2CO 3==2CuO+H 2O+CO 2↑5、下列关于金属冶炼的说法不正确的是 ( )A.金属冶炼是指用化学方法将金属由化合态转变为游离态B.天然矿藏很少只含有一种金属元素,往往含有较多杂质C.金属的冶炼方法主要有热分解法,热还原法和电解法三种方法D.金属冶炼一定要用到还原剂6、工业上用铝土矿(主要成分为Al 2O 3、Fe 2O 3、SiO 2)提取氧化铝做冶炼铝的原料,提取的操作过程如下:不溶物铝土矿 沉淀(甲)2O3滤液(1)写出步①中发生的化学方程式:(2)写出滤液甲中一种溶质与过量NaOH溶液反应进入滤液乙所发生的化学方程式:第四章第一节开发利用金属矿物和海水资源海水资源的开发利用(2)【学习目标】1.了解海水资源开发和利用的前景及化学在其中可以发挥的作用;2.体验工业生产的复杂性、艰苦性。
3.认识到关心科学、研究科学和探索科学的精神。
【学习重点】了解海水资源开发和利用。
【学习难点】从海水中提取镁、钾、溴、碘等化工产品原理及方法。
【知识链接】海水中提取食盐【学习内容】知识点1、海水水资源的利用a.海水是一个远未开发的巨大化学资源宝库。
海水中含有多种元素,其中11种元素的含量较高,其余为元素。
常从海水中提取,并在传统海水制盐工业基础上制取镁、钾、溴及其化合物。
b.海水水资源的利用主要包括:海水淡化和直接利用海水进行循环冷却。
海水淡化的方法:主要有蒸馏法、电渗析法、离子交换法等.其中蒸馏法的历史悠久,技术和工艺也比较完善,但成本较高.c. 描述蒸馏原理和过程,思考蒸馏实验操作中有哪些注意事项?浓缩海水溴单质溴化氢硫酸溴单质2、海水化学资源的开发利用【实验讨论】①海带为什么不能用水冲洗?②海带剪碎后,为什么要用酒精润湿?③实验中用H2O2氧化I—,写出反应的离子方程式。
用H2O2氧化I—有何优点?(2)海水提溴:①向硫酸酸化的海水中通入适量的,使溴离子(主要以溴化钠存在)转化为溴单质,涉及的化学方程式为:;②向含溴单质的水溶液中通入空气和水蒸气,将溴单质吹入的吸收塔内,使溴单质蒸气、水和吸收剂二氧化硫相互反应生成溴化氢和硫酸,以达到富集的目的,涉及的化学方程式为:;③向吸收塔的溶液内通入适量的氯气得到溴单质,用四氯化碳萃取、分液得到产品溴,涉及的化学方程式为:。
【归纳小结】1.海水资源的淡化和利用2.海水中提取碘和溴的原理和实验操作方法【过关训练】1.水资源非常重要,联合国确定2003年为国际淡水年,以下关于水的说法错误的是()A.蒸馏法是海水淡化的方法之一B.淡水的密度小于海水的密度C.融化的雪水中矿物质含量比深井水中的少D.0℃以上,温度越高,水的密度越小2.医生建议因缺少某种元素而导致甲状腺肿大的病人多吃海带,这是由于海带中含有较丰富的()A.碘元素B.铁元素C.钾元素D.锌元素3.一位海上遇难的水手随着木排在海上漂流,他用完了淡水,感到口渴异常,但他不喝海水,因为他知道海水会致命,主要原因是()A.海水有苦涩味,根本喝不下去B.海水中含有多种盐,能使肠胃腐烂致人死亡C.海水中有许多微生物,有些微生物能致人死亡D.海水会造成人体水分从血液和组织中脱离出来,使人脱水死亡4.从海水中提取下列物质,可以不涉及化学变化的是()A、MgB、NaClC、Br2D、K5.下列哪种试剂加入到含有Br—的溶液中,可以将Br—氧化为Br2()A、I2B、I—C、Cl2D、Cl—6.海带中含碘元素。
从海带中提取碘有如下步骤:①通入足量Cl2;②将海带焙烧成灰后加水搅拌;③加CCl4振荡;④用分液漏斗分液;⑤过滤。
合理的操作顺序是()A.①②③④⑤B.②⑤①③④C.①③⑤②④D.②①③⑤④7.全球海水中溴的藏量丰富,约占地球溴总藏量的99%,故溴有“海洋元素”之称,海水中溴含量为65mg/L。
其工业提取方法有:(1)空气吹出纯碱吸收法。
方法是将氯气通入到富含溴离子的海水中,使溴置换出来,再用空气将溴吹出,用纯碱溶液吸收,最后用硫酸酸化,即可得到溴单质。
该方法涉及到的反应有:①(写出离子方程式);②Br2+3CO32-=BrO3-+ 5Br-+3CO2↑; ③BrO3-+ 5Br-+6H+=3Br2+3H2O。
其中反应②中氧化剂是;还原剂是。
(2)空气吹出SO2吸收法。
该方法基本同(1),只是将溴吹出后是用SO2来吸收的,使溴转化为氢溴酸,然后再用氯气氧化氢溴酸即得单质溴。
写出溴与二氧化硫反应的化学方程式:_ 。
(3)溶剂萃取法。
该法是利用单质溴在水中和溶剂中溶解度的不同的原理来进行的。
实验室中萃取用到的实验仪器名称是。
下列可以用于海水中溴的萃取试剂的。
①乙醇②四氯化碳③硝酸④裂化汽油第四章第二节资源综合利用环境保护【学习目标】(1)了解煤、石油的组成,掌握煤、石油的综合利用。
(2)掌握环境污染的几种类型及防治,了解其危害。
(3)了解绿色化学的含义。
【重点难点】掌握煤、石油的综合利用【基础知识】一、煤的综合利用1.煤的组成:_______________________________________________.主要含有___________元素,还含有少量的等元素.2.煤的综合利用主要是通过____________、___________和__________,获得洁净的燃料和多种化工原料.(1)煤的干馏①煤的干馏原理:把煤隔绝空气加强热使它分解的过程,如右图:②煤干馏的主要产物和用途(阅读课本)(2)煤的气化煤的气化是。
煤气化的主要反应是__________________ 。
(3)煤的液化煤的液化是。
直接液化是______________________,间接液化是_________________。
二、石油的综合利用1.石油的成分:_____________________________________________________。
2.石油的分馏(1)石油的分馏原理: ______ ____________ __。
实验如图所示,将100 mL石油注入到蒸馏烧瓶中,再加入几片碎瓷片以防石油暴沸.然后加热,分别收集60℃~150℃和150℃~300℃时的馏分,就可以得到汽油和煤油.(2)石油的分馏产物:石油气、汽油、煤油、柴油、重油等.3.石油的裂化和裂解(1)裂化的目的:提高轻质液体燃料的产量.(2)裂化的原理:石油的裂化是_________________________ 。
(3)裂解的目的:获得乙烯、丙烯、甲烷等重要化工基本原料.三、天然气的综合利用天然气既是一种清洁的化石燃料,更是一种重要的化工原料.主要用于和___________等四、合成材料1.三大合成材料________________ ________________ _________________2.写出下列反应方程式:乙烯合成聚乙烯________________________________________丙烯合成聚丙烯________________________________________聚苯乙烯的加聚________________________________________聚氯乙烯的加聚________________________________________五. 绿色化学绿色化学核心是___________________________________________________原子经济是指____________________________________________________,此时原子利用率为________,请求出书后“思考与交流”中两种生产工艺的原子利用率分别为_____________、______________【自主探究】你能列举出多少种环境污染?【过关训练】1.有关化石燃料的说法正确的是( )A.因为地球上的蕴藏量是无限的。
