正方体长方体表格
长方体和正方体的表面积(定稿)

跟踪小练笔
练一练:求下列图形的表面积。(单位:厘米)
4
24 5
4 4
1、(1)计算上面的面积是( B )。
(2)计算右面的面积是( C )。
(3)计算后面的面积是( A )。
1.5
3
1.2
A. 3×1.5 B. 3×1.2 C. 1.2×1.5
(单位:厘米)
2、一个正方体的棱长为3厘米,他的表面积是
( C )平方厘米。
A.3×3×4 B.3×3×3 C.3×3× 6
分析在计算下列物体面积时,应 考虑几个面的面积。
1、给长方体饼干罐的四周贴一圈商标纸。 四个面
2、给礼堂内长方体柱子刷油漆。 四个面 3、要将一个长方体的游泳池内部贴上瓷砖。 五个面 4、用木料做一个抽屉。 五个面 5、粉刷教室的墙壁(黑板门窗除外)。 五个面
说一说该求哪部分的面积
制一个长方体无 盖鱼缸,求所需 玻璃的面积。
粉刷教室时,粉刷 教室四面墙壁,求 粉刷的面积。。
说一说该求哪部分的面积
给一个长方体罐头 盒贴包装纸,求包 装纸的面积。
给一个长方体的领 操台刷上油漆,求 粉刷的面积。。
三、知识应用
亮亮家要给一个长0.75m,宽0.5m,高1.6m的简易衣柜换 布罩(如下图,没有底面)。至少需要用布多少平方米?
我们借助长方体表面展开图来研究。 将一个长方体的表面展开:
二、合作探索
上
二、合作探索
上 后
下 前
二、合作探索
上 后
下 前
二、合作探索
长方体、正方体表面积、体积所有计算公式

长方体:
1、长方体的棱长和=(长+宽+高)×4
包装礼盒用的绳子=长×2+宽×2+高×4+绳头长
2、长方体的表面积= 长×宽×2+长×高×2+宽×高×2
(没有盖的)长方体的表面积=长×宽+长×高×2+宽×高×2 (上下面不计算)长方体的表面积=长×高×2+宽×高×2
3、通风管的表面积=长×宽×4(长与宽相等)
通风管的面积=长×宽×2+宽×高×2(长与宽不相等)4、长方体的体积=长×宽×高
长方体的体积=底面积×高
正方体:
1、正方体的棱长和=棱长×12
2、正方体的表面积= 棱长×棱长×6
(没有盖的)正方体的表面积= 棱长×棱长×5
(上下面不计算)正方体的表面积=棱长×棱长×4
3、正方体的体积=棱长×棱长×棱长
正方体的体积=底面积×高。
长方体正方体表面积体积公式

长方体正方体表面积体积公式
长方体和正方体的表面积和体积公式是数学中常用的公式,可以用来计算立体图形的面积和体积。
下面是具体的公式:
长方体表面积公式:S(表面积) = 2(a1a2a3) (其中 a1、a2、a3 分别为长、宽、高)
长方体体积公式:V(体积) = a1a2a3 (其中 a1、a2、a3 分别为长、宽、高)
正方体表面积公式:S(表面积) = 6a2 (其中 a 为正方体的棱长) 正方体体积公式:V(体积) = a3 (其中 a 为正方体的棱长)
其中,a1、a2、a3 分别表示长方体或正方体的一个面的面积,V 表示体积,S 表示表面积,正方体有 6 个面,每个面都是相同的正方形,所以正方体的表面积为 6a2。
长方体和正方体的体积和表面积公式都是用来描述立体图形大
小和形状的公式,可以用来计算立体图形的面积和体积,帮助人们更好地理解和探究数学问题。
正方体、长方体展开图
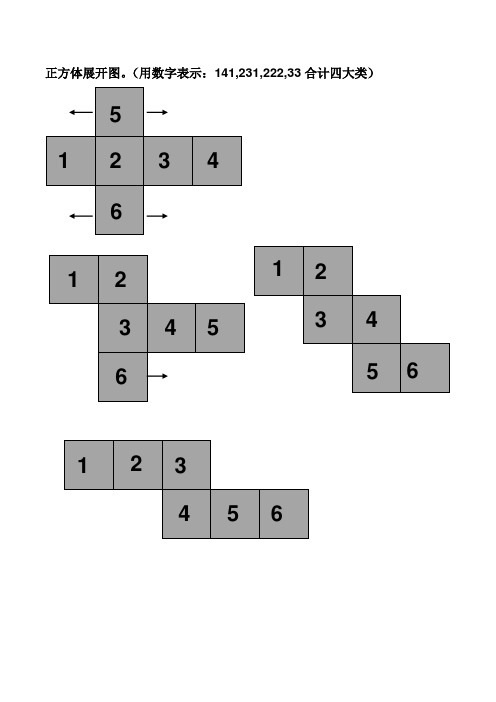
正方体展开图。
(用数字表示:141,231,222,33合计四大类)
长方体展开图类似正方体第一类141。
各位家长:
空间观念的培养不是一朝一夕能建立,必须在实践-----表象-----想像等基础之上,所以务必请家长和孩子一起先实践。
第一步:
用铅化纸照样子剪一剪。
第二步:
先拼一拼,拼的时候想一想这个正方体的上下前后左右各是数字几?第三步:
不拼想像。
直接说出正方体的上下前后左右各是数字几?
(比如以3为底面时,上、前、后、左、右格式数字几)
如果有困难,可以拼一拼(拼成半成品)帮助想像。
人教版五年级数学下册第三章长方体和正方体第三节长方体和正方体的体积ppt课件

公有的质因数
2 18 30 3 9 15 35
独有的质因数
所以,18和30的最大公因数=2×3=6; 18和30的最小公倍数= 2×3×3×5=90。 为了便于区分,可以简单归纳为: 最大公因数乘半边,最小公倍数乘半圈。
6 18
30
3
5
求两个数的最大公因数与最小公 倍数时,用合数作除数有助于提 高计算速度。
计量体积就要用体积单位,常用的体积单位有
立方厘米 立方分米 立方米
1立方厘米
棱长1厘米的正方体,体积是1立方厘米
1立方厘米
棱长1分米的正方体,体积是1立方分米
1米
1分米
1分米
1立方分米
棱长1米的正方体,体积是1立方米
1米
1立方厘米
上图含( 4个 )1立方厘米, 体积就是(4立方厘米 )
一个物体里含有多少个体积 单位,它的体积就是多少。
长/分米 宽/分米
长
5
方
4
体
10
1 3 2 棱长/米
正
6
方 体
30
0.4
高/分米 2 5 4
体积/分米 3
10 60 80
体积/米3
216 27000 0.064
3、判断正误并说明理由。 ( 1)0.2 3=0.2×0.2×0.2;( √ )
( 2)5X 3=10X;( × )
( 3 )一个正方体棱长4分米,它的体
(分数的意义)
一个物体、一些物体等都可以看作一个整体, 把这个整体平均分成若干份,这样的一份或 几份都可以用分数来表示。
单位“1”与分数单位的区别
单位“1”表示:一个物体、一些物体等都可 以看作一个整体,一个整体可以用自然数1来 表示,通常把它叫做“1”。 分数单位表示:把单位“1”平均分成若干份, 表示其中一份的数叫分数单位。
长方体正方体面积体积公式

长方体正方体面积体积公式长方体公式
长方体是一种具有六个面的三维物体,每个面都是矩形。
其表面积和体积公式如下:
表面积:2(长 x 宽 + 宽 x 高 + 高 x 长)
体积:长 x 宽 x 高
正方体公式
正方体是一种特殊的长方体,其所有边长相等。
其表面积和体积公式如下:
表面积:6(边长)²
体积:边长³
具体实例
假设有一个长方体,其长为 5 cm,宽为 3 cm,高为 2 cm。
表面积:2(5 cm x 3 cm + 3 cm x 2 cm + 2 cm x 5 cm) = 56 cm²
体积:5 cm x 3 cm x 2 cm = 30 cm³
假设有一个正方体,其边长为 4 cm。
表面积:6(4 cm)² = 96 cm²
体积:4 cm³ = 64 cm³
其他公式
除了基本公式外,还有一些适用于特殊情况的附加公式:
侧表面积(长方体):2(长 + 宽) x 高
底面积(长方体):长 x 宽
对角线长度(长方体):√(长² + 宽² + 高²)
对角线面积(正方体):√(3) x 边长
内切球半径(正方体):边长 / 2
应用场景
这些公式在解决涉及长方体和正方体的几何问题时至关重要。
它们可用于计算包装、建筑和工程中的表面积和体积。
青岛版五年级数学下册课件第7单元长方体和正方体

50cm
= 6200(平方厘米) 答:至少需要6200平方厘米的纸板。
二、合作探索
根据刚才的解题过程,你能总结出长方体的表面积计算公式吗?
前、后面: 50×30×2 = 3000(平方厘米) 左、右面: 20×30×2 = 1200(平方厘米) 上、下面: 50×20×2 = 2000(平方厘米)
三、自主练习
1.下面的平面图哪些可以折成长方体或正方体?
长方体
长方体
长方体
正方体
三、自主练习
2.右图是一个长方体。
(1)上面的面积是( 24 )平方厘米; (2)前面的面积是( 30 )平方厘米;
(3)右面的面积是( 20 )平方厘米;
(4)表面积是( 148 )平方厘米。
三、自主练习
3. 计算下面图形的表面积。
的占地面积是多少,列式为
20×20
辨析:不能正确区分求物体的占地面积还是表面积。
三、自主练习
9.计算下面图形的表面积。
答:12×8×4+8×8×2=512(cm2)
辨析:易把特殊长方体(有2个面是正方形)当作
=34(米)
答:至少需要34米铝条。
下面:5×0.5=2.5(平方米)
答:前面是15平方米、右面 是1.5平方米、下面是2.5平
方米。
三、自主练习
4.哪几个面可以围成一个长方体?
① ③ ⑦
⑤
②
④
⑥
⑧
三、自主练习
5. 用12个棱长是1厘米的小正方体拼成一个长方体,有几种不
同的拼法?拼成的长方体的长、宽、高各是多少?
情境导入 合作探索 自主练习 回顾反思 课后作业
长方体和正方体基本知识

长方体和正方体基本知识1、长方体和正方体的特征:长方体和正方体都有8个顶点、12条棱、6个面。
长方体一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
在一个长方体中,相对的2个面完全相同,相对的4条棱长度相等。
正方体是由6个完全相同的正方形围成的立体图形,所有的棱长度相等。
相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。
2、长方体和正方体的关系正方体是长、宽、高都相等的特殊的长方体。
可用下右面的集合图来表示:3、棱长和长方体棱长和=长×4+宽×4+高×4=(长+宽+高)×4正方体棱长和=棱长×124、正方体的展开图(见第2页)长正方体的展开图都有六个面;判断一个展开图能不能折叠成长正方体,关键是看看每个面有没有相对的面。
5、长方体或正方体6个面的总面积,叫做它的表面积。
计算表面积时要先弄清楚有没有缺面。
6、物体所占空间的大小叫做物体的体积长方体体积=长×宽×高(V 长=abh ) 正方体体积=棱长×棱长×棱长(V 正=a 3)计量体积要用体积单位,常用的体积单位有立方米、立方分米和立方厘米,分别写作m ³,dm ³和cm ³。
①棱长是1cm 的正方体,体积是1 cm ³;②棱长是1dm 的正方体,体积是1 dm ³;③棱长是1m 的正方体,体积是1 m ³7、长方体或正方体底面的面积叫做底面积。
长方体(或正方体)底面的体积=底面积×高(V=sh )8、箱子、油桶、仓库等所能容纳物体的体积,叫做他们的容积。
计量容积,一般就用体积单位。
计量液体容积时,常用容积单位升和毫升,写成L 和mL 。
9、 可以用排水法计量不规则物体的体积。
不规则物体的体积=总体积-水的体积。
10、长方体 正方体 1³=1 2³=8 3³=27 4³=64 5³=125 6³=216。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形体
相同点
不同点
联系
面
棱
顶点
面的
形状
面的
大小
棱的
长度
长方体
()个
()条
()个
正方体
长方体和正方体的特征
形体
相同点
不同点
联系
面
棱
顶点
面的
形状
面的
大小
棱的
长度
长方体
( )个
( )条
( )个
正方体
长方体和正方体的特征
形体
相同点
不同点
联系
面
棱
长方体
( )个
( )条
1dm²=100cm²
( )个
正方体
长方体和正方体的棱长和、表面积
棱长和
表面积
意义
12条棱的总长度
长方体或正
方体6个面
的总面积
计算
方法
C长=4a+4b+4c
C正=12a
S长=2ab+2ah+2bh=2(ab+ah+bh)
S正= 6a²
常用
单位
m
dm
cm
m²
dm²
cm²
单位间
的进率
1m=10dm
1dm=10cm
1m²=100dm²
