第9讲_动力学分析和力
理论力学第9章

重点:求解质点和平动刚体的两类动力学问题 难点:理解惯性坐标系与非惯性坐标系
§ 9-1 动力学的基本定律
质点动力学的基础是牛顿三大定律 第一定律 (惯性定律) 不受力作用的质点,将保持静止或作匀速直线运动。 ——惯性 第二定律(力与加速度之间关系定律) d (mv ) F dt 在经典力学范围内,质点的质量是守恒的,因此有:
例9-3 已知:一圆锥摆,如图所示。质量m=0.1kg 的小球系 于长 l=0.3 m 的绳上,绳的另一端系在固定点O,并与 60 铅直线成 角。 求:如小球在水平面内作匀速圆周运动,小球 的速度与绳的张力。
解: 以小球为研究的质点
选取在自然轴上投影的运动微 分方程,得: v2 m F sin θ F cos mg 0 ρ 其中:ρ l sin θ mg F 1.96 N cos
动力学
导言
动力学:研究物体的机械运动与作用力之间的关系 动力学的基本问题大致分为两类: 1.已知运动求力; 2.已知力求运动。 具体学习以下内容: 质点动力学基本方程; 普遍定理:动量定理、动量矩定理、动能定理; 达朗贝尔原理; 虚位移原理
力学模型
1. 质点:具有一定质量而几何形状和尺寸大小可以 忽略不计的物体。 例如:研究卫星的轨道时,卫星 —— 质点 刚体作平动时,刚体 —— 质点
1.已知质点的运动规律,求作用于质点上的力
求两次导数得到质点的加速度,代入质点的 运动微分方程中,即可求解——求微分问题 2.已知质点上所受的力,求质点的运动规律 按作用力的函数规律进行积分,并根据具体 问题的运动条件确定积分常数——求积分问题
3.混合问题:第一类与第二类问题的混合.
例9-1 已知:曲柄连杆机构如图所示.曲柄OA以匀角速度
动力学问题解析方法总结

动力学问题解析方法总结动力学是研究物体在力的作用下随时间变化的规律的学科,广泛应用于物理学、工程学、生物学等领域。
在解决动力学问题时,我们需要运用一系列的方法和技巧来分析和求解。
本文将针对动力学问题解析方法做一个总结,介绍常用的方法和技巧,以及其适用范围和应用实例。
一、拉格朗日方程拉格朗日方程是解析力学中的重要方法,适用于描述质点、刚体和多体系统的运动。
通过将系统的动能和势能表示为广义坐标的函数,在广义坐标下建立拉格朗日函数,然后通过对拉格朗日函数进行变分,得到系统的拉格朗日方程。
拉格朗日方程能够简化复杂的多自由度系统的动力学问题,使得求解更加便捷。
例如,一个常见的应用是求解一个弹簧振子的运动方程。
通过将系统的动能和势能表示为弹簧伸长量的函数,建立拉格朗日函数,然后利用拉格朗日方程求解出振子的运动方程。
这个方法可以推广到更复杂的系统,如双摆、陀螺等。
二、哈密顿方程哈密顿方程是解析力学中与拉格朗日方程相对应的一种方法。
通过将拉格朗日函数转换成哈密顿函数,建立哈密顿方程,可以得到对应于拉格朗日方程的广义动量和广义坐标的演化方程。
哈密顿方程在一些特定问题的求解中更为有效,特别是在涉及到正则变换和守恒量的问题中。
例如,对于一个自由粒子在势场中运动的问题,通过将拉格朗日函数转换成哈密顿函数,然后利用哈密顿方程求解出粒子的运动方程。
这个方法具有一定的普适性,适用于多体系统的动力学问题求解。
三、牛顿第二定律牛顿第二定律是经典力学中最基本的定律之一,描述了质点受力后的运动规律。
根据牛顿第二定律,物体的加速度与作用于物体的合力成正比,与物体的质量成反比。
通过建立物体的运动方程,可以求解物体在给定力下的运动轨迹和运动状态。
例如,对于一个斜抛运动的问题,我们可以根据牛顿第二定律建立物体在水平和竖直方向上的运动方程,然后通过求解这个方程组,得到物体的运动轨迹和飞行时间等信息。
牛顿第二定律适用于描述质点的运动,是解决实际问题常用的方法。
第九章-曲柄连杆机构动力学分析
Pj m j a m j R 2 cos m j R 2 cos2 PjI PjII
(2)、旋转惯性力Fr=mrRω2 2、沿气缸中心线的总作用力F 总作用力F是缸内气体作用力Fg与往复惯性力的代数和 F=Fg+Fj 气体作用力 D 2 Fg p g - p? g 4
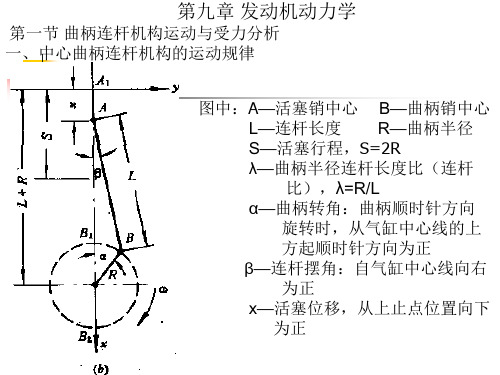
1、活塞位移x:
x ( L R) ( L cos R cos )
2 2
R(1 cos ) L(1 1 sin )
(精确式)
R x R(1 cos ) (1 cos 2 ) x I x II (近似式) 4
近似式与精确式相比误差很小,如当λ =1/3.5时,曲柄转角为 90度时误差为最大,在0.003R左右,此精度在工程上已足够。
பைடு நூலகம்
(精确式)
1 2 L sin 1 1 3 cos2 (近似式) 2
2
在α =90º 或270º 时达到极值:
Le
2 (1 2 )1 / 2
(精确式)
1 (近似式) 2 摆动角速度和角加速度精确式中分母均近似等于 1 ,因此两者均 随α 近似按简谐规律变化。
L L 1 m j m p m 1 m p m l L 作旋转运动的不平衡质量mr,包括曲柄换算质量mk和连杆换算
L1 mr mk m 2 mk1 2mk 2 mL R L
到大头中心的质量m2,集中作用于曲柄销中心,即
三、曲柄连杆机构作用力和力矩 1、惯性力 、 (1)旋转惯性力 (1)、 往复惯性力
2、活塞速度:
sin( ) v R cos
核反应堆物理分析(第九讲)核反应堆动力学

3
• 解决反应性的迅速变化引起的中子通量密度 随时间的瞬态变化:中子动力学(neutron kinetics)。 • 反应堆瞬态过程中,存在着一些反馈效应, 本章不考虑。
4
8.1 缓发中子的作用
1.1 基本概念:
裂变中子(fission neutron): 由裂变过程产生 并保持它们初始能量的中子。 分为瞬发和 缓发两种。
39
3.2 常数缓发中子源近似
• 由于先驱核半衰期较长,在某些反应性瞬变 中(e.g.停堆插棒)可以认为缓发中子源保持 为常数:
C (t ) = l / k
i =1 i i
6
n0
eff
• 可得解析解: n0 0 − n(t ) = [ 0 exp( t) − ] 0 − l / keff
36
(p241)
37
8.3* 点堆方程的近似解法
• 方程(iii)、(iv)是个耦合的一阶微分方程组, 同时由于反应性的反馈作用(温度效应、中毒 等),该方程一般也是非线性的: 6 dn (t ) − = n(t ) + i Ci (t ) (iii )
dt l / keff
i =1
• 缓发中子产生率= i Ci (r , t )
i =1
18
6
• 考虑缓发中子的单群扩散方程:
1 ( r , t ) 2 = D (r , t ) − a (r , t ) + (1 − )k a (r , t ) v t + i Ci (r , t )
t /T
实际使用的还有倍增周期Td,,Td=0.693T
第9章平面连杆机构的动力分析与平衡

第9章平面连杆机构的动力分析与平衡平面连杆机构是由若干个连杆组成的机械系统,常用于研究机械系统的动力学性质。
对于平面连杆机构的动力分析与平衡,主要是研究其运动学和动力学方程,并进行相应的力和动量平衡计算。
以下将从运动学和动力学两个方面进行详细介绍。
1、运动学分析平面连杆机构的运动学分析是研究机构的位置、速度和加速度的关系。
其中,位置分析主要是根据连杆的几何性质,通过连杆的长度、夹角和初始位置等参数,确定连杆机构的位置关系。
速度分析主要是研究各连杆的线速度和角速度之间的关系,通过运用位移法和速度图解法,可以求解各连杆关节处的速度。
加速度分析主要是研究各连杆的线加速度和角加速度之间的关系,可以通过速度分析的基础上运用动图解法求解。
2、动力学分析平面连杆机构的动力学分析是研究机构中各连杆所受力和动量的关系,进而分析机构的运动特性。
动力学分析主要包括力分析和动量平衡两个方面。
力分析主要是研究在给定外部载荷下,各连杆之间的约束力和连接力,分析力的大小、方向和位置。
动量平衡主要是研究机构质点的动量矩等于零,根据牛顿第二定律和冲量动量定理,可以建立平面连杆机构的运动方程,进而求解各连杆的加速度和力。
平面连杆机构的平衡主要涉及到静平衡和动平衡两个方面。
静平衡要求在机构基准位置时,机构中各连杆和连接处的力矩之和等于零,可以通过力分析和力矩平衡方程求解。
动平衡要求机构中各连杆的质心加速度等于零,在给定外部载荷和给定输入力矩的情况下,可以通过动量平衡方程求解。
总结来说,平面连杆机构的动力分析与平衡需要进行运动学和动力学的分析,通过建立力分析和动量平衡方程,求解各连杆的加速度和力,进而研究机构的运动特性和平衡性。
对于平面连杆机构的动力分析与平衡研究,可以为机械设计和动力学性能优化提供理论依据。
1机械原理课件_东南大学_郑文纬_第七版第09章_平面机构的力分析111解析

惯性力:是一种虚拟加在有变速运动的构件上的力。
惯性力是是阻力还是驱动力? 当构件减速时,它是驱动力;加速时,它是阻力 特点:在一个运动循环中惯性力所作的功为零。低速机械的惯性力 一般很小,可以忽略不计。
二、研究机构力分析的目的
确定运动副反力。
因为运动副中反力的大小和性质对于计算机构各个零 件的强度、决定机构中的摩擦力和机械效率、以及计 算运动副中的磨损和确定轴承型式都是有用的已知条 件。
选定一点B, 再选定另一点为K
可以任意选择两个代换点
B b B
S k S
K
mB mK m mB (b) mK k 0
mk mB bk
K
mb mK bk
动代换
两质量点动代换: 选定一点B; 则另一点为K。
不能同时任意选择两个代换点
mB mK m
K k
mB (b) mK k 0
例 9- 6
例9-6 p367
5 E Aω 1
1
Fi5 G5
6 Fr
D B 2 3
4
在如图所示的牛头刨床机构 中,已知:各构件的位置 和尺寸、曲柄以等角速度 w1顺时针转动、刨头的重 力G5、惯性力Fi5及切削 阻力(即生产阻力)Fr。
C
试求:机构各运动副中的反力及需要施于曲柄1上的平 衡力偶矩(其他构件的重力和惯性力等忽略不计)。
π
Fi 2 Fi 2b Fi 2k
5、动静法应用
不考虑摩擦时机构动静法分析的步骤:
1. 求出各构件的惯性力,并把其视为外力加于产生 该惯性力的构件上; 2. 根据静定条件将机构分解为若干个杆组和平衡力 作用的构件; 3. 由离平衡力作用最远的杆组开始,对各杆组进行 力分析; 4. 对平衡力作用的构件作力分析。
机械工程中的动力学分析
机械工程中的动力学分析引言:机械工程是一门研究机械结构和运动规律的学科,其中动力学分析是机械工程中的重要内容之一。
动力学分析的目的是研究物体在力的作用下的运动规律,通过分析物体的运动状态和力的关系,可以揭示物体的力学特性,并为机械系统的设计和优化提供理论依据。
本教案将从运动学和动力学两个方面,对机械工程中的动力学分析进行深入探讨。
一、运动学分析运动学是研究物体运动状态和运动规律的学科,是动力学分析的基础。
在机械工程中,运动学分析可以通过描述物体的位置、速度和加速度等运动参数来研究物体的运动规律。
1. 位置分析位置是描述物体在空间中的位置信息,可以用坐标系来表示。
在机械工程中,常用的坐标系包括笛卡尔坐标系、极坐标系和柱坐标系等。
通过确定物体在坐标系中的位置,可以揭示物体的运动轨迹和位置变化规律。
2. 速度分析速度是描述物体运动快慢和方向的物理量,可以用矢量来表示。
在机械工程中,速度可以分为线速度和角速度两种。
线速度是物体在直线运动中单位时间内所经过的路程,角速度是物体在旋转运动中单位时间内所转过的角度。
通过分析物体的速度变化,可以了解物体的加速度和运动状态。
3. 加速度分析加速度是描述物体运动变化率的物理量,是速度变化率的导数。
在机械工程中,加速度可以分为线加速度和角加速度两种。
线加速度是物体在直线运动中单位时间内速度的变化量,角加速度是物体在旋转运动中单位时间内角速度的变化量。
通过分析物体的加速度变化,可以了解物体的动力学特性和运动规律。
二、动力学分析动力学是研究物体运动规律和力的作用关系的学科,是机械工程中的核心内容。
在机械工程中,动力学分析可以通过分析物体的运动状态和力的关系,揭示物体的力学特性和运动规律。
1. 牛顿定律牛顿定律是经典力学的基础,描述了物体在力的作用下的运动规律。
根据牛顿定律,物体的运动状态由力的作用决定,力的大小和方向决定了物体的加速度。
通过分析物体所受的力和运动状态,可以计算物体的加速度和运动轨迹。
第9讲安培力的计算
第9讲安培力的计算欢迎来到第9讲!在本节课中,我们将学习安培力的计算方法。
安培力是指通过电流在两个导体之间产生的力。
它是一个矢量量,其大小与电流的大小成正比,方向垂直于电流的方向和两个导体之间的距离。
安培力的计算公式如下:F = BIL sin θ其中,F表示安培力的大小,B表示磁感应强度,I表示电流的大小,L表示导体的长度,θ表示电流与磁场方向之间的夹角。
在使用这个公式时,我们需要注意几个要点。
首先,磁感应强度B是由外部磁场决定的,它的大小和方向在给定的环境中是固定的。
其次,电流I是通过导体流动的电荷的总量,单位是安培(A)。
导体的长度L是指电流所通过的导体的长度。
最后,夹角θ是电流方向和磁场方向之间的夹角,它的取值范围是0到180度。
接下来,让我们通过几个例子来学习如何计算安培力。
第一个例子,假设有一根长度为2米的导线,电流大小为5安培,在一个磁感应强度为0.5特斯拉的磁场中。
如果电流方向和磁场方向之间的夹角为30度,我们可以使用安培力的计算公式计算出安培力的大小。
F = (0.5特斯拉) * (5安培) * (2米) * sin(30度) = 2.5牛顿因此,根据给定的条件,这根导线所受的安培力为2.5牛顿。
第二个例子,假设有一根长度为3米的导线,在一个磁感应强度为0.8特斯拉的磁场中,电流大小为10安培。
如果电流方向与磁场方向垂直,即夹角为90度,我们可以使用安培力的计算公式计算出安培力的大小。
F = (0.8特斯拉) * (10安培) * (3米) * sin(90度) = 0牛顿由于sin(90度)等于1,因此该导线所受的安培力为0牛顿。
这是因为电流方向与磁场方向垂直,所以安培力的大小为0。
在实际应用中,安培力的计算常常用于直流电动机、电磁铁等电磁装置的设计和分析中。
通过计算电流通过导体时所受到的安培力,我们可以了解电流对导体的作用,并相应地设计和优化电磁设备。
此外,安培力的计算也有助于我们理解电磁感应、电动力学等领域的物理现象。
动力学基础知识梳理
动力学基础知识梳理动力学是物理学中研究物体运动规律的领域,它主要关注物体受力和速度、加速度等因素之间的相互关系。
本文将对动力学的基础知识进行梳理,帮助读者更好地理解这一重要物理学分支。
一、力的概念和力的作用力是动力学的基础概念之一,定义为使物体发生变化(比如加速度、形状改变等)的原因。
力的作用可以描述为三个要素:力的大小、方向和作用点。
1.1 力的大小力的大小通常用牛顿(N)作为单位。
力的大小可以通过测量物体的质量和加速度来计算。
牛顿第二定律指出,力等于质量乘以加速度:F = m ×a。
其中,F表示力,m表示物体的质量,a表示物体的加速度。
1.2 力的方向力的方向是力所施加的物体的运动方向。
对于力的方向,我们常常采用坐标系,将力的方向与坐标轴建立关联。
1.3 力的作用点力的作用点是指力所施加的物体上的一个特定点。
在力同时作用于物体的多个点时,物体上不同点受到的力有可能不同。
二、牛顿三定律牛顿三定律是动力学中的重要法则,它描述了力与物体运动之间的关系。
2.1 第一定律:惯性定律牛顿第一定律也称作惯性定律,它表明物体在没有受到外力作用时将保持静止或匀速直线运动的状态。
若物体受到外力,则它将发生加速度变化。
2.2 第二定律:动量定律牛顿第二定律也称作动量定律,它给出了力、质量和加速度之间的关系。
根据牛顿第二定律,力等于质量乘以加速度:F = m × a。
2.3 第三定律:作用-反作用定律牛顿第三定律也称作作用-反作用定律,它指出对于任何一对相互作用的物体,它们之间的作用力与反作用力的大小相等、方向相反,并且作用在不同的物体上。
三、动力学中的其他重要概念除了力和牛顿三定律,动力学中还有其他一些重要概念需要掌握。
3.1 弹性碰撞弹性碰撞是指碰撞过程中物体之间能量守恒的现象。
在弹性碰撞中,物体之间的动能和动量都能够得到保持。
3.2 动能和势能动能是物体由于其运动而具有的能量,它与物体的质量和速度有关。
结构力学中的动力学分析研究
结构力学中的动力学分析研究动力学是结构力学中的重要研究领域之一,主要研究结构在外部力的作用下的运动和振动规律。
动力学分析对于预测结构的响应和安全性评估具有重要意义。
本文将从动力学分析的基本理论、数值模拟方法以及应用领域等方面进行探讨。
1.基本理论动力学分析的基本理论是基于牛顿第二定律,根据结构物体上各个部分的质量、惯性、位移和力的关系进行研究。
基于质点的动力学理论可以方便地应用于刚体和弹性结构的动力学分析。
而对于柔性结构来说,需要引入振动理论来描述结构的运动性质。
2.数值模拟方法动力学分析通常是通过数值模拟方法来实现的。
常用的数值模拟方法包括有限元方法、边界元方法、模态超级位置法等。
其中,有限元方法是最为常用的方法之一,它可以将结构分割成有限数量的单元,通过离散化的力学方程求解结构的动力学响应。
边界元方法则针对无限域的问题,通过模拟结构表面的运动来计算结构的响应。
模态超级位置法则是利用小振动的结构模态进行求解。
3.应用领域动力学分析在结构工程中有广泛的应用。
它可以用于评估结构在自然灾害(如地震、风灾)等外部力作用下的安全性能。
动力学分析还可以用于分析机械系统、飞行器和航天器的动力学行为。
此外,动力学分析还可用于优化结构设计、评估材料的动态性能以及模拟结构的振动响应等方面。
4.动力学分析的挑战与发展尽管动力学分析在结构力学中具有重要意义,但其研究也面临许多挑战。
首先是复杂结构的动力学分析问题,如非线性振动和混合动力学问题,并需要开发相应的数值模拟方法。
其次,对于大规模结构的动力学分析,需要考虑计算效率和计算精度的平衡。
此外,结构的材料非线性和边界条件非线性等因素也是动力学分析中需要考虑的问题。
未来,随着计算能力的提升和数值方法的发展,动力学分析将更好地满足工程实践的需求。
总之,动力学分析在结构力学中起着重要的作用,它通过数值模拟方法研究结构在外部力作用下的运动和振动规律,并应用于结构的安全性评估、设计优化和动态响应预测等方面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y x
θ1
(x1, y1) d1 m1
例1
• 先求刚体的动能与位能(旋转式运动) 先求刚体的动能与位能(旋转式运动) 假设连杆质量用等效连杆末端的点质量表示 • 连杆1: 1 连杆2: 1 2 ɺ2 2 K1 = m d1 θ1 K2 = m2v2 1 2 2 P = −m gd1 cosθ1 P = m2 gy2 1 1 2
力矩 惯量 向心加速度系数 哥氏加速度系数 重力
ɺɺ ɺ ɺɺ D θ12 D D θ1θ2 D T D D θ1 D 1 11 12 111 122 112 121 = + + + 1 ɺ2 ɺ ɺ T D D ɺɺ D D222θ2 D212 D221θ2θ1 D2 θ 22 2 211 2 21
2 D = (m + m2 )d12 + m2d2 + 2m2d1d2 cosθ2 11 1 有效惯量: 2 D22 = m2d2
2 D 耦合惯量: 12 = D21 = m2d2 + m2d1d2 cosθ2 向心加速度系数: D111 = 0
D = −m2d1d2 sin θ2 122 D211 = m2d1d2 sin θ2 D222 = 0
2 1 2 2 1 2 2 1 2 2 2 1 2 1 1 2 2 1 2
T2 =
d ∂L ∂L 2 2ɺ ɺ ɺ − = (m2d2 + m2d1d2 cosθ2 )θɺ + m2d2θɺ + m2d1d2 sin θ2θ12 1 2 ɺ dt ∂θ2 ∂θ2 + m2 gd2 sin(θ1 +θ2 )
Fi =
d ∂L ∂L − , i =1,2,..., n ɺ dt ∂qi ∂qi d ∂L ∂L d ∂L ∂L , , , ɺ ɺ dt ∂θ1 ∂θ1 dt ∂θ2 ∂θ2
求取
代入拉格朗日方程式
T= 1
d ∂L ∂L 2 2 ɺɺ ɺɺ − = [(m + m2 )d12 + m2d2 + 2m2d1d2 cosθ2 ]θ1 + (m2d2 + m2d1d2 cosθ2 )θ2 1 ɺ ∂θ dt ∂θ1 1 ɺɺ ɺ − 2m d d sin θ θ θ − m d d sin θ θ 2 + (m + m )gd sin θ + m gd sin( θ +θ )
拉格朗日函数
ɺ L(qi , qi ) = K − P
拉格朗日函数
q = [q1
系统总的动能
系统总的势能
q 2 ⋯ q n ]是表示动能和势能的广义
坐标
ɺ ɺ q = [q1 ɺ ɺ q 2 ⋯ q n ] 是相应的广义速度
机器人系统动能
连杆 i 的动能 K i 为连杆质心线速度引起 的动能和连杆角速度产生的动能之和:
构造拉格朗日函数L=K-P:
1 2 ɺ ɺ 1 ɺ ɺ ɺ2 ɺ ɺɺ L = K − P = (m + m2 )d12θ12 + m2d2 (θ12 + 2θ1θ2 +θ2 ) + m2d1d2 cosθ2 (θ12 +θ1θ2 ) 1 2 2 + (m + m2 )gd1 cosθ1 + m2 gd2 cos(θ1 +θ2 ) 1
2 21 1 22 2 211 1 222 2 212 1 2 221 2 1
2
ɺɺ ɺ ɺɺ D θ12 D D θ1θ2 D T D D θ1 D 111 122 112 121 1 11 12 = + + + 1 ɺ2 ɺ ɺ T D D ɺɺ D θ2 211 D222θ2 D212 D221θ2θ1 D2 22 2 21
哥氏加速度系数: D = D = −m2d1d2 sin θ2 112 121
D212 = D221 = 0
重力项: D1 = (m1 + m2 )gd1 sin θ1 + m2 gd2 sin(θ1 +θ2 ) D2 = m2 gd2 sin(θ1 +θ2 )
作业
平面 RP机器人如图所示,用拉格朗日方法 求其动力学方程。
θ2
d2 m2
(x2, y2)
x 2 = d1 sin θ1 + d 2 sin(θ1 + θ 2 ) y 2 = − d1 cos θ1 − d 2 cos(θ1 + θ 2 ) ɺ ɺ ɺ x 2 = d1 cos θ1θ1 + d 2 cos(θ1 + θ 2 )(θ1 + θ 2 ) ɺ ⇒ ɺ ɺ ɺ ɺ y 2 = d1 sin θ1θ1 + d 2 sin(θ1 + θ 2 )(θ1 + θ 2 ) 2 ɺ2 ɺ2 v2 = x2 + y 2 2 2 ɺ ɺ ɺ ɺ ɺ ɺ ɺ ɺ ⇒ v 2 = d 12θ12 + d 2 (θ12 + 2θ1θ 2 + θ 22 ) + 2d1 d 2 cos θ 2 (θ12 + θ1θ 2 )
经整理:
ɺ ɺ ɺ ɺ ɺɺ ɺ ɺ T1 = D11θɺ + D12θɺ2 + D111 θ12 + D122 θ 22 + D112θ1θ 2 + D121θ 2θ1 + D1 1 ɺ ɺ ɺ ɺ ɺɺ ɺ ɺ T = D θɺ + D θɺ + D θ 2 + D θ 2 + D θ θ + D θ θ + D
Pi = − mi g Pci
T
机器人系统的势能为各连杆势能之和:
P = ∑ Pi
i =1 n
拉格朗日方程
d ∂L ∂L − =τi ɺ dt ∂q i ∂q i (i = 1,2,..., n)
τ i 是广义力,代表 n 个关节的驱动力或 力矩;若 i 是移动关节,i 就是力,若 i τ τ 是转动关节, i பைடு நூலகம்是力矩。
系统的总动能和总势能:
1 1 2 ɺ2 2 ɺ2 ɺ ɺ ɺ2 ɺ2 ɺ ɺ K = K1 + K2 = (m + m2 )d1 θ1 + m2d2 (θ1 + 2θ1θ2 +θ2 ) + m2d1d2 cosθ2 (θ1 +θ1θ2 ) 1 2 2 P = P + P = −(m + m2 )gd1 cosθ1 − m2 gd2 cos(θ1 +θ2 ) 1 2 1
1 1i T i i T K i = mi v ci v ci + ω i I i ω i 2 2
系统总动能为 n 个连杆动能之和:
K = ∑ Ki
i =1 n
机器人系统势能
设连杆 i 的势能为 Pi ,连杆 i 的质心在 {0}坐标系中的位置矢量为 Pci ,重力加速度 矢量在 {0}坐标系中为 g ,则
研究机器人动力学的方法
牛顿——欧拉法(Newton-Euler) 拉格朗日法(Lagrange) 高斯法(Gauss) 凯恩法(Kane) 旋量对偶数法 罗伯逊——魏登堡法(RobersonWittenburg)
研究动力学的目的
动力学正问题与机器人仿真有关; 动力学逆问题是为了实时控制的需要,利用动 力学模型,实现最优控制,以期达到良好的动 态性能和最优指标; 可利用动力学方程来考察不同惯量负载对机器 人的影响,以及根据期望的加速度来考察某些 负载的重要性。
第9讲 机器人动力学
机器人动力学问题
机器人动态性能不仅与运动学相对位置有关, 还与机器人的结构形式、质量分布、执行机构 的位置、传动装置等因素有关。 机器人动态性能由动力学方程描述,动力学是 考虑上述因素,研究物体运动和受力之间的关 系。
机器人动力学问题
动力学正问题:根据关节驱动力或力矩计算机 器人的运动(关节位移、速度和加速度),即 研究机器人手臂在关节力矩作用下的动态响应。 动力学逆问题:已知轨迹对应的关节位移、速 度和加速度,求出所需要的关节力或力矩;进 而选择设计出能提供足够力及力矩的驱动器。
