平面桁架程序计算原理及程序编制
桁架计算_精品文档

桁架计算引言桁架是一种通过连接许多杆件和节点来形成稳定结构的建筑体系。
它常被用于搭建临时或永久性的大型结构,如广告牌、天桥、悬索桥等。
在设计和计算桁架结构时,需要考虑到各种力学和结构上的因素,以确保桁架的稳定性和可靠性。
本文将介绍桁架计算的一般原理和方法。
桁架的基本概念桁架由两种基本要素构成:杆件和节点。
杆件是桁架结构中的线状元素,通常是直线或弧线形状,其作用是传递和承载力。
节点是桁架结构中的连接点,用于连接和固定杆件,同时也能分担一部分力。
桁架计算的步骤桁架计算通常可以分为以下几个步骤:1.确定桁架的几何形状和尺寸:根据设计要求和实际需求,确定桁架的长度、宽度和高度等几何参数。
2.确定桁架的节点和杆件数量:根据桁架的几何形状,确定桁架的节点数量和杆件数量,并给予它们编号。
3.选择杆件材料和荷载信息:根据桁架的设计要求和实际使用环境,选择合适的杆件材料,并确定荷载信息,包括重力荷载、风荷载等。
4.建立荷载模型和边界条件:根据实际情况,建立桁架的荷载模型,并确定桁架的边界条件,如支撑方式、固定方式等。
5.进行力学计算:根据桁架的几何形状、节点和杆件数量、杆件材料和荷载信息,利用力学原理和方法,进行桁架的力学计算,包括静力分析、动力分析等。
6.分析结果和优化设计:根据计算结果,分析桁架的稳定性和可靠性,如受力情况、变形等,如果需要,对桁架进行优化设计,以提高其性能。
7.编制计算报告和施工图纸:将计算结果整理成计算报告和施工图纸,以便后续的施工和检验过程。
桁架计算的常用方法桁架计算主要依靠力学原理和方法,其中常用的方法包括以下几种:1.静力学方法:通过平衡力的方法,计算桁架在静态荷载作用下的受力情况。
常用的方法有切向力平衡法、截面法、节点法等。
2.动力学方法:通过考虑桁架的质量和荷载的动态响应,计算桁架在动态加载下的受力情况。
常用的方法有模态分析、响应谱法等。
3.有限元法:将桁架离散为许多小的有限元,利用有限元法进行分析和计算。
平面桁架程序计算原理及程序编制

对于该平面桁架,有
杆号 L
△L
1
2
3
4
a
a
a
sqrt(2)a
v1
u1-u2
v2
(u1+ v1)/ sqrt(2)
把上述值代入应变能表达式,得到
5 sqrt(2)a (v2- u2)/ sqrt(2)
U E 2 F a v 1 2 ( u 1 u 2 ) 2 v 2 2 ( u 1 v 2 ) 2 /2 2 ( v 2 u 2 ) 2 /2 2
的内力。
5-5 结构计算简图的数据结构
完整而确切描述一个平面桁架结构的数据有三个方面:
(1)结构本体描述数据(NW, IESG, NU, X, Y, HL, HR)
(2)性质数据(EF)
(3)荷载数据(PX, PY)
➢NW为节点总数 ➢IESG杆件总数 ➢NU可动节点总数 ➢X, Y 节点坐标 ➢HL, HR 每根杆件两端节点编号 ➢EF 性质数据 ➢PX, PY 外载荷数据
FAFBN
FA和FB在x轴、y轴方向的分量分别为:
F A xF Ac o s N c o s
F A yF AsinNsin
F B xF BcosN cos
F B yF BsinN sin
把 F A x 、F B x 、 F A y 、 F B y 排列成列向量 P ,则有
FAx cos
式中 L 为杆的伸长, L 为杆的长度, N 为杆的
内力,EF / L 称为单根杆的刚度(单元刚度阵)。
注意⊿L= uB-uA,并且由平衡关系得到
FAFBNE L F(uAuB)
可把FA、FB排成列向量{N},uA, uB,排成列向 量{u},系数阵排成矩阵RD,即
平面桁架有限元分析及程序设计

0 1 0 ui ui v e vi 0 0 0 i u k u 0 1 0 j j vj 0 0 0 vj
单元轴力:
N
AE 1 0 l
ui ui v v i 1 0 S i u u j j v j v j
1杆和3杆位移:
N1l1 14 34 E1 A1
N 2l2 24 E2 A2
P
第二章 平面桁架有限元分析及程序设计
超静定桁架
1杆轴力竖向分量:
E1 A1 E1 A1 cos2 N1 y N1 cos 14 cos v4 k1v4 l1 l1
2杆轴力:
第二章 平面桁架有限元分析及程序设计
超静定桁架
代入平衡方程:
2N1y N2 y P
(2k1 k2 )v4 P
P v4 2k1 k2
结构的整体刚度系数
1
l2
2
l1 l1
3
4 P
k1v4 k1P N1 cos cos (2k1 k2 ) cos
k2 P N 2 k2v4 2k1 k2
因此:
e
0 0
0 0
e
0 U i V 0 i U j V j
cos
sin
F T F
0 0
其中,[T]为转换矩阵:
转换矩阵的性质
T 0 0 0 0
式中:
S AE
l
cos
sin
平面桁架杆件内力的虚位移原理求解

平面桁架杆件内力的虚位移原理求解
平面桁架是指由桁架杆件组成的平面结构,它是一种比较常见的结构类型,在建筑工程中有广泛应用。
平面桁架杆件内力的虚位移原理是指用来求解平面桁架杆件内力的方法。
虚位移原理是基于桁架结构的平衡原理,根据桁架结构的挠度方程可以求解桁架杆件的虚位移。
求解虚位移的步骤如下:
1.确定桁架杆件的位置关系和支座约束条件,并根据桁架
的几何形状建立坐标系。
2.确定桁架的荷载状态,根据桁架的荷载状态确定桁架的
内力状态。
3.建立桁架的节点虚位移表,并根据节点虚位移表解出桁
架杆件的虚位移。
4.根据桁架杆件的虚位移和杆件的截面尺寸计算杆件的内
力。
在求解平面桁架杆件内力的过程中,需要注意桁架的几何形状、
荷载状态、支座约束条件等因素,并根据这些因素建立相应的计算模型。
在求解过程中,还要注意桁架杆件的截面尺寸、杆件材料的弹性模量等因素,以保证计算结果的准确性。
虚位移原理是一种通用的求解平面桁架杆件内力的方法,在建筑工程中有广泛应用。
但是,在实际应用中,还要注意桁架杆件的几何形状、荷载状态、支座约束条件等因素的变化,并作出相应的调整。
建筑力学基本计算1平面桁架的计算

建筑力学基本计算1平面桁架的计算1、基本概念和计算要求在学习静定平面桁架的的简化及其分类时,要注意如下几点:1) 分析实际桁架受力情况比较复杂,影响杆件内力的因素很多,在计算时必须抓主要矛盾,对实际桁架作必要的简化。
2) 要懂得理想桁架的基本假定,及由此所得的力学特性,学会画出理想桁架的计算模型,和各类杆件的名称。
3) 能用平面一般力系的平衡条件,熟练的求出桁架的支座反力。
2、基本计算方法桁架的基本计算方法主要有结点法和截面法及其联合运用:1) 学会结点法的基本原理在选取结点的过程中,由于平面汇交力系只有2个平衡方程,所以,每次选取的结点,其未知的杆件轴力不得多于两个。
2) 充分利用某些杆件和结点的特殊情况在桁架中常有些特殊形状的结点,通常可以直观地求解出结点上某些杆件的轴力,可以给计算带来很大方便,如:(1) 只有两根杆件构成的结点,当结点上无荷载作用时,两杆轴力皆为零。
如图1(a )。
(2) 三杆汇交的结点,而其中两杆共线图1(b ),当结点上无荷载时,第三杆必为零杆,而共线两杆的内力相等且性质相同(即同为拉力或同为压力)。
3) 学会截面法的基本原理在选取截面截取桁架的过程中,由于平面一般力系只有三个平衡方程,所以,每次截取后切断各 图1杆的未知轴力个数应不超过3个。
而且这三个力彼此既不平行也不汇交于一点。
在计算少数指定杆件轴力时,用截面法特别方便。
4)一般在复习考试中,主要是要学会如何联合应用结点法和截面法来计算桁架中指定杆件的轴力。
要注意结点法和截面法各自的特点,使用最灵活的手段,最快速的求出杆件轴力。
3、计算步骤和常用方法考试要求一般为求桁架指定杆件的轴力问题,指定杆件不超过三根。
通常先求桁架的支座反力;然后根据具体题目要求,利用某些特殊结点,看是否可以判断出某些杆件的轴力;再考虑使用一次结点法和一次截面法(也可以是两次结点法或两次截面法)基本可以求出指定杆件的轴力。
在解题过程中,要充分注意计算桁架轴力的技巧:结点法的核心是投影方程,投影轴应选为除计算轴力的杆件外其余轴力未知杆件的垂直方向;截面法的核心在于针对具体情况,选取最合适的截面。
平面桁架有限元C#编程

1题目结构如图所示: 杆的弹性模量E 为200000Mpa ,横截面面积A 为3250mm 2。
图 1 桁架示意图2实验材料PC 机一台,Microsoft Visual Studio 软件,Ansys 软件。
3实验原理(1)桁架结构特点桁架结构中的桁架指的是桁架梁,是格一种梁式结构。
桁架结构常用于大跨度的厂房、展览馆、体育馆和桥梁等公共建筑中。
由于大多用于建筑的屋盖结构,桁架通常也被称作屋架。
结构上由光滑铰链连接,载荷只作用于节点处,只约束线位移,各杆只有轴向拉伸和压缩。
(2)平面桁架有限元分析1、单元分析局部坐标系中的干单元如图所示:图 2 局部坐标系中的杆单元以下公式描述了整体位移和局部位移之间的关系:U=Tu 其中U=[ U ix U iy U jx U jy ],T=[cos θ−sin θ00sin θcos θ0000cos θ−sin θ00sin θcos θ],u=[u ix u iy u jx u jy ]U 和u 分别代表整体坐标系和局部坐标系XY 系和局部坐标系xy 下节点i 和节点j 的位移。
T 是变形从局部坐标转换到整体坐标系下的变换阵,类似的局部力和整体力也有以下关系:F=Tf其中F=[ F ixF iy F jx F jy ] ,是整体坐标系下施加在节点i 和j 上的力的分量而且f=[ f ix f iy f jx f jy ],代表局部坐标系下施加在节点i和j上的分量。
在假设的二力杆条件下,杆只能沿着局部坐标系的x方向变形,内力也总是沿着局部坐标系x的方向,因此将y方向的位移设置为0,局部坐标系下内力和位移通过刚度矩阵有如下关系:[f ixf iyf jxf jy]=|k0−k00000−k0k00000|=[U ixU iyU jxU jy]这里k=k eq=AE/L,写成矩阵形式有:f=Ku将f和u替换成F和U有:T-1F=KT-1U将方程两边乘以T得到:F=TKT-1U其中T-1是变换矩阵T的逆矩阵,替换方程中的TKT-1和U矩阵的值,相乘后得到:[F ixF iy F jx F jy]= k[cos2θsinθcosθ−cos2θ−sinθcosθsinθcosθsin2θ−sinθcosθ−sin2θ−cos2θ−sinθcosθcos2θsinθcosθ−sinθcosθ−sin2θsinθcosθsin2θ][U ixU iyU jxU jy]上述方程代表了施加外力、单元刚度矩阵和任意单元节点的整体位移之间的关系。
2015-平面桁架有限元程序设计_任务书
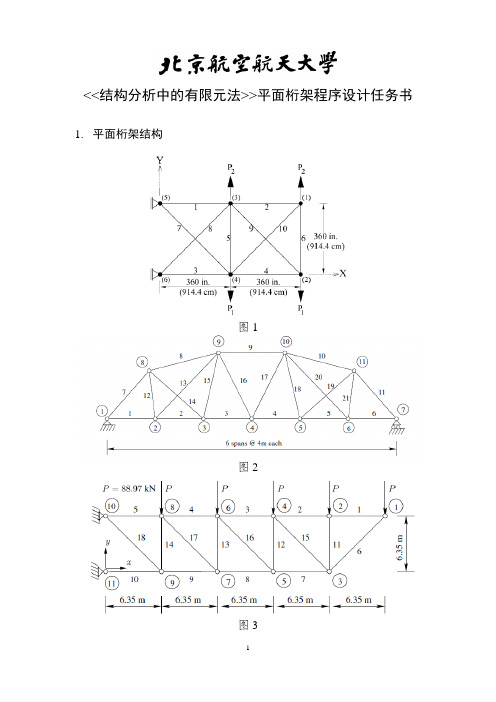
<<结构分析中的有限元法>>平面桁架程序设计任务书1.平面桁架结构
图1
图2
图3
基于平面桁架静力有限元分析理论自行编写平面桁架有限元分析程序,并利用自编程序对图1、图2和图3所示三个平面桁架结构形式进行变形和应力分析,其中结构材料、结构尺寸和外载荷可自行设定。
2.程序编写和报告撰写要求
(1)编制的程序要求具有一定的“通用性”,通过“输入文件”形式读
入具体分析结构的结点个数、结点坐标、单元个数、单元结点信息、单元材料信息、单元刚度和结点外载荷信息等,从而实现程序的通用性;
(2)提交形式:程序和计算分析报告电子版发至邮箱:
xjwang@),程序和计算分析报告打印版一份;
(3)提交时间:2015年5月28日前。
平面桁架内力和位移计算的框图与程序

有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
14
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
15
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
16
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
4-14)
在式(3-5)中,ann 对应 bn,1; aii 对应 bi,1;aij 对应 bi,j-I+1。把这些关系带入
后,得等带向后回运算格式
pn
对于i pi
pn
(bpn有 成n1i 生 功1m命 ,,inn(ji就 有id会 思12a1,,ni就有 索,)j会希 就i,11做有望 会pi 收, 有) /获有 思bi1信 路 心 ,就 有会 努有 力
பைடு நூலகம்
成功, 0有思0索就0会有0思路,有努力 就会有收获
2
2.坐标变换
杆端力和杆端位移的坐标变换是通过单元坐标变换矩T阵e 即式(1-34 )完成的,令 Cx cos , C y sin ,则
Cx Cy 0 0
Te
Cy
Cx
0
0
0
0
Cx
C
y
4
4.半带存贮和带消去法
在计算连续梁程序中,由于整体刚度矩阵所占计算机存贮量小,顾采
用高斯顺序消元法解刚度方程.如果方程组的系数矩阵是对称矩阵,可以
证明在第 k 轮消元后,由第(K+1)至第 n 个方程的系数仍是对称矩阵.为了
减小运算次数,在整个消元过程中,只要存贮系数矩阵上三角部分的元素.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-2 矩阵位移法算例
如图所示平面桁架,各根杆的截面积F相等,材料的 弹性模量E相同,在两个单位力P=1的外荷载作用下, 用位移法计算节点位移和各杆内力。
P 1
P 2
节点总数: NW=4 可动节点数:NU=2 位移未知数总数:NDISP=2*NU=4
4
平面桁架结构
3
u1
v2 u1 2a
平面桁架结构
应用上述各杆内力和位移关系后,便可建立以位移 为未知数的节点平衡方程。
平面桁架程序计算原理及程序编制
节点平衡方程为
N 2N 4cos450P0 N1N4cos4500
N 2N 5cos450P0 N3N5cos4500
注意:节点自由度排序和节点平衡方程相对应。
平面桁架程序计算原理及程序编制
W
v u
1 2
注意:节点自由 度排序和节点平 衡方程相对应。
v 2
平面桁架程序计算原理及程序编制
单元局部刚度阵
考虑单根杆件在位移下产生的内力。
根据虎克定律,对于任意一根杆,有:
N EF L L
式中 L 为杆的伸长,L 为杆的长度,N 为杆的内 力, E F 称为单根杆的刚度(单元刚度阵)。
进一步有内力和节点位移之间的关系
N E L F (u B u A )c o s (v B v A )s in 平面桁架程序计算原理及程序编制
对于每根杆件(以两端节点编号A和B定出 角) 应用上述公式,有
N1
EF
v1 a
N2
EF
u1
u2 a
N3
EF
v2 a
N4
EF
u1 v1 2a
N5
EF
其中
1212
r11 r12 r13 r14
1
Rr21
r22
r23
r24
EF/
a
2
2
rr3411
r32 r42
r33 r43
rr3444
1
0
结构刚度矩阵
1 22 1 1
22 0
0
1
0 1 1
22 1
22
0
0
1 22
1212
而外力向量为:
平面桁架程序计算原理及程序编制
P1 P
P
结构有限元程序设计基本原理
——平面桁架程序的计算原理及程序编制
平面桁架程序计算原理及程序编制 平面桁架程序的计算原理5-01 矩阵位移法 5-02 矩阵位移法算例 5-03 最小总势能原理的应用 5-04 矩阵位移法的求解步骤 5-05 结构计算简图的数据结构 5-06 位移未知数的确定 5-07 单根杆件的分析 5-08 结构总刚度矩阵的形成 5-09 杆件内力的计算 5-10 能量原理和矩阵位移法
将各杆的内力用位移表示的方程代入上式,有
E a F1212u1212v1u20P
E a F 212u 1 1212 v100 P
未知 数为 节点
E a F u10 1212 u2212v2 P
位移
E a F00212u21212v2P
平面桁架程序计算原理及程序编制
写成矩阵形式 RWP,即正则方程。
U E 2 F a v 1 2 ( u 1 u 2 ) 2 v 2 2 ( u 1 v 2 ) 2 /2 2 ( v 2 u 2 ) 2 /2 2
由上式可见,公式中只有位移的二次项,也就是说 是位移的一个二次齐次函数,或者说是一个位移的 二次型。(位移的正定二次型,应变能总是正的)
平面桁架程序计算原理及程序编制
根据最小总势能原理,在所有可能的位移状态中, 真正发生的位移状态使总势能为最小。即函数对 自变量的偏微商为零,即
最小总势能原理与位移法都是以位移为未知 数使变形状态预先满足连续条件。现对上述 例题采用最小总势能原理进行求解。
• 总势能由两部分组成
➢结构的弹性应变能 U ➢外力由于结构变位所产生的势能 V
平面桁架程序计算原理及程序编制
由于桁架结构的杆件只能承受拉压力,所以 单根杆件的应变能为
U EF(L)2 / L 2
P P
2 3
0
P
P 4 0
采用高斯消元法求得位移为
u13.824a/EF
v11.000a/EF
u2 u1
v2 v1
利用每根杆的内力-位移关系计算杆内力
N1 1 N3 1
N5 1.412
N2 0 N4 1.412
平面桁架程序计算原理及程序编制
5-3 最小总势能原理的应用
平面桁架程序计算原理及程序编制
5-1 矩阵位移法
• 桁架是由离散杆件组成的构架结构,杆件的端点 借助于无摩擦的铰连接起来。
• 桁架主要靠各杆中的轴向拉力或压力来传递作用 在桁架节点上的荷载,杆件的任何弯曲均忽略不 计。
• 用有限元分析桁架时,桁架中的每根杆件都是一 个单元,称为杆单元。它是一维单元。
平面桁架程序计算原理及程序编制
现在计算外力势能。外力 P 产生势能的原因是当节
点发生位移时,外力要作功。所作功的负值便是它
们具有势能的改变量,如果取未变形位置外力的势
能为零,有
P
P
1
2
VPu1Pu2
4
3
平面桁架结构
将 U 和 V 相加,得到总势能。
由于V 是位移的一次函数,总势能就成为位 移的二次非齐次函数。
不同分类: (1)平面桁架/空间桁架 (2)静定桁架/超静定桁架
平面桁架程序计算原理及程序编制
求解方法
力法:以力未知数,必须预先满足平衡条件,然 后通过连续条件求解未知力;超静定基的选取。 • 位移法:以位移为未知数,各杆件的变形由相连 接的节点位移确定(变形协调条件),通过各个 节点的平衡方程求出未知位移,再由位移计算出 各杆件的内力;各节点的平衡方程也可由最小总 势能原理推导。 以平面桁架结构分析的程序设计为例,介绍结构分 析和程序设计的方法。
对于整个桁架应变能是所有杆件应变能的叠 加,即
U12k51(EF)k(L)k2/Lk
平面桁架程序计算原理及程序编制
对于该平面桁架,有
杆号 L
△L
1
2
3
4
a
a
a
sqrt(2)a
v1
u1-u2
v2
(u1+ v1)/ sqrt(2)
把上述值代入应变能表达式,得到
5 sqrt(2)a (v2- u2)/ sqrt(2)
L
用RD来表示单元刚度阵,于是
RD EF L
胡克定律可表达如下
NRDL 平面桁架程序计算原理及程序编制
y
u v
A A
A
u v
B B
B
x
由单根杆件的变形几何关系可得
L uco s vsin (u B u A )co s (vB vA )sin
角是杆件轴线与 x 方向的夹角,由 x 正向逆时 针向转至杆轴的角度为正。
