平面桁架位移法求解程序设计修正版
平面桁架杆件内力的虚位移原理求解

平面桁架杆件内力的虚位移原理求解平面桁架杆件内力的虚位移原理求解平面桁架杆件内力的虚位移法就是通过对一个平面桁架杆件分别在不同的横截面处作轴力作用,从而求出在相互之间的杆件的虚位移及节点内部力,以此作为最终求解这个结构内力的手段。
该原理具有可操作性好、局部支座独立性强、保守性好等特点,是解决桁架杆件内力不确定性和复杂性的有效方法。
具体步骤如下:一、选取横截面在选取横截面时,首先确定受力过程,即在该结构中确定各结构件的受力情况或作用力方向。
根据力学原理,如果在任意结构单元面上作当量的力和力矩都是等价的,那么就可以合理的在该杆件的横截面上选取合理的横截面去分析这一结构横截面单元的内力。
二、确定虚力系数接下来,我们需要根据上一步确定的受力情况,确定每一横截面上的虚力系数。
虚力系数是根据横截面单元元素的面积、材料的刚度等诸多因素而确定的。
虚力系数的计算公式是:Q=m*b/d,其中m为横截面单元的面积,b和d为杆件的刚度,以及杆件的厚度。
三、计算横截面的虚力根据已经确定的虚力系数,就可以求出每一横截面单元上的虚力,即就可以由横截面上的受力确定每一单元上的虚力值。
四、求解节点上的抗力根据虚位移原理及上面确定的横截面单元虚力,就可以求出这个桁架杆件上每个节点处的抗力。
该原理指出:节点处的抗力可以由所有横截面单元虚力的总和相加得到,即按下式求解:F1=Q1-Q2+Q3-Q4,其中Q1指的是横截面1上的虚力,Q2指的是横截面2上的虚力,以此类推。
五、求解内力最后,根据以上分析,就可以求出该平面桁架杆件上每个节点处的抗力,从而求出这个结构的主/副矩,悬臂梁杆件的弯矩、压弯构件的压力矩、支座上反力等内力。
通过分析可以看出,平面桁架杆件内力的虚位移法是解决桁架结构内力问题的有效方法,具有可操作性好、局部支座独立性强、保守性好等特点,在实际工程中得到广泛应用。
桁架计算(TRUSS)

桁架内力计算程序(TRUSS)一、程序功能及编制方法桁架内力计算程序(TRUSS),能计算任意平面和空间桁架(包括网架)在结点荷载作用下各结点的位移和各杆的轴力。
程序采用变带宽一维数组存储总刚度矩阵,先处理法引进支座条件。
计算结果输出各结点的位移和各杆的轴力。
二、程序使用方法使用方法与“APF”程序相同。
用文件编辑编辑器建立数据文件后即可运行。
计算结果将写在结果文件中。
三、数据文件填写格式数据文件填写格式大致与APF程序相似。
1.总信息:T,NJ,NE,NR,NB,NP,EO,DS其中:T——桁架类型,平面桁架 T=2,空间桁架 T=3。
NR——支座约束数。
其他变量与APF程序相同。
2.结点坐标数组XYZ(NJ, 3)每个结点填一行,每行三个数分别填写结点的x,y,z三个坐标数值,平面桁架只填x,y 值(单位:m)。
3.单元信息数组G(NE)采用紧缩存储方式,每个单元填一个数。
把单元的左端、右端结点号和杆的类型号三个数紧缩为一个数。
例如某单元左端结点号为15,在端结点号为8,类型号为3,则写成0.15083,一般格式为0.×××××。
4.单元截面信息数组AI(NB)填写各类单元的杆截面面积(m2)。
5.约束信息数组R(NR)采用紧缩存储方式,每个约束(支座链杆)填一个数。
把约束作用的作用点写在该数的整数部分,约束的方向写在小数部分。
x方向的约束为“l”,y方向的约束为“2”。
例如某支座链杆作用在 17号结点上,方向沿整体坐标 y方向,则写为 17.2,一般格式为××.×。
6.结点荷载信息数组F(NP,2)每个结点荷载填一行,每行两个数。
前一个数用紧缩方式填写荷载作用的结点号和作用方向,格式与约束信息的格式相同。
后一个数为荷载的数值。
单位为kN,与整体坐标方向一致者为正值,相反者为负值。
例如,作用在16号结点上,数值为183.5 kN,方向向下的力,则写成:16.2,-183.5(这里,假定坐标轴y轴向上)。
弹性力学与有限元分析第二章-平面桁架有限元分析及程序设计

x
由单元①的刚度方程:
Fj
①
k
① ji
i
①
k
① jj
j
①
k
① ji
2
k
① jj
1
由单元③的刚度方程:
Fj
③
k
③ ji
i
③
k
③ jj
j
③
k
③ ji
3
k
③ jj
1
§2.3 结点平衡与整体刚度矩阵的集成
代入结点1的平衡条件:
k
l
xi
)
(dx j
dxi
)
(
yj
l
yi )
(dy j
dyi )
(dx j dxi ) (dy j dyi )
cos sin
由于杆件的变形产生位移:
ui dxi vi dyi
u j dxj v j dy j
因此,杆件应变为:
dl l
l
(ui
uj)
l
(vi
vj)
杆件轴力为:
(2k1 k2 )v4 P
结构的整体刚度系数
v4
P 2k1
k2
12 3
l2 l1 l1
4 P
N1
N1y
cos
k1v4
cos
k1P
(2k1 k2 ) cos
N2
k2v4
k2P 2k1 k2
位移法求解超静定结构。
§2.1 平面桁架单元的离散
结构的离散化:尽量将结构离散成数量最少的等截面直 杆单元
kki③ ③jii
ki③j
k
③ jj
3 3 3 3
§2.3 结点平衡与整体刚度矩阵的集成
平面桁架程序计算原理及程序编制

对于该平面桁架,有
杆号 L
△L
1
2
3
4
a
a
a
sqrt(2)a
v1
u1-u2
v2
(u1+ v1)/ sqrt(2)
把上述值代入应变能表达式,得到
5 sqrt(2)a (v2- u2)/ sqrt(2)
U E 2 F a v 1 2 ( u 1 u 2 ) 2 v 2 2 ( u 1 v 2 ) 2 /2 2 ( v 2 u 2 ) 2 /2 2
的内力。
5-5 结构计算简图的数据结构
完整而确切描述一个平面桁架结构的数据有三个方面:
(1)结构本体描述数据(NW, IESG, NU, X, Y, HL, HR)
(2)性质数据(EF)
(3)荷载数据(PX, PY)
➢NW为节点总数 ➢IESG杆件总数 ➢NU可动节点总数 ➢X, Y 节点坐标 ➢HL, HR 每根杆件两端节点编号 ➢EF 性质数据 ➢PX, PY 外载荷数据
FAFBN
FA和FB在x轴、y轴方向的分量分别为:
F A xF Ac o s N c o s
F A yF AsinNsin
F B xF BcosN cos
F B yF BsinN sin
把 F A x 、F B x 、 F A y 、 F B y 排列成列向量 P ,则有
FAx cos
式中 L 为杆的伸长, L 为杆的长度, N 为杆的
内力,EF / L 称为单根杆的刚度(单元刚度阵)。
注意⊿L= uB-uA,并且由平衡关系得到
FAFBNE L F(uAuB)
可把FA、FB排成列向量{N},uA, uB,排成列向 量{u},系数阵排成矩阵RD,即
平面桁架程序的计算原理及程序编制共70页PPT

41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
2015-平面桁架有限元程序设计_任务书
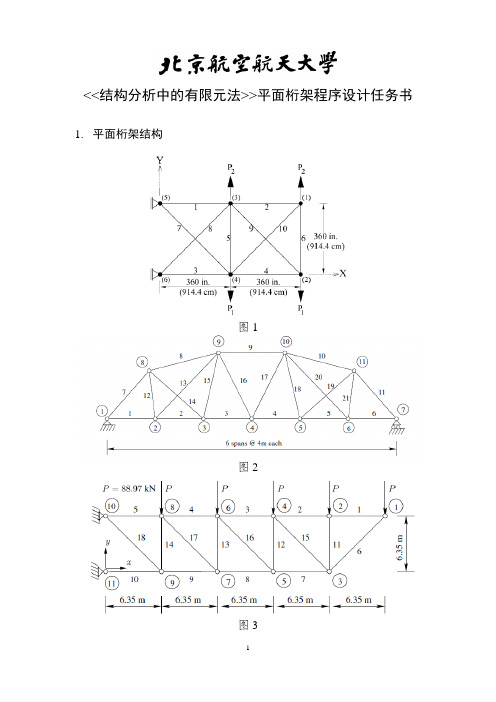
<<结构分析中的有限元法>>平面桁架程序设计任务书1.平面桁架结构
图1
图2
图3
基于平面桁架静力有限元分析理论自行编写平面桁架有限元分析程序,并利用自编程序对图1、图2和图3所示三个平面桁架结构形式进行变形和应力分析,其中结构材料、结构尺寸和外载荷可自行设定。
2.程序编写和报告撰写要求
(1)编制的程序要求具有一定的“通用性”,通过“输入文件”形式读
入具体分析结构的结点个数、结点坐标、单元个数、单元结点信息、单元材料信息、单元刚度和结点外载荷信息等,从而实现程序的通用性;
(2)提交形式:程序和计算分析报告电子版发至邮箱:
xjwang@),程序和计算分析报告打印版一份;
(3)提交时间:2015年5月28日前。
平面桁架内力和位移计算的框图与程序

有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
14
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
15
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
就会有收获
16
有生命就会有希望,有信心就会有 成功,有思索就会有思路,有努力
4-14)
在式(3-5)中,ann 对应 bn,1; aii 对应 bi,1;aij 对应 bi,j-I+1。把这些关系带入
后,得等带向后回运算格式
pn
对于i pi
pn
(bpn有 成n1i 生 功1m命 ,,inn(ji就 有id会 思12a1,,ni就有 索,)j会希 就i,11做有望 会pi 收, 有) /获有 思bi1信 路 心 ,就 有会 努有 力
பைடு நூலகம்
成功, 0有思0索就0会有0思路,有努力 就会有收获
2
2.坐标变换
杆端力和杆端位移的坐标变换是通过单元坐标变换矩T阵e 即式(1-34 )完成的,令 Cx cos , C y sin ,则
Cx Cy 0 0
Te
Cy
Cx
0
0
0
0
Cx
C
y
4
4.半带存贮和带消去法
在计算连续梁程序中,由于整体刚度矩阵所占计算机存贮量小,顾采
用高斯顺序消元法解刚度方程.如果方程组的系数矩阵是对称矩阵,可以
证明在第 k 轮消元后,由第(K+1)至第 n 个方程的系数仍是对称矩阵.为了
减小运算次数,在整个消元过程中,只要存贮系数矩阵上三角部分的元素.
平面桁架杆件内力的虚位移原理求解

平面桁架杆件内力的虚位移原理求解平面桁架是由若干个杆件和连接节点组成的结构系统。
在静力学中,我们需要确定杆件的内力分布,以便分析框架结构的稳定性和强度。
在这个过程中,虚位移原理是一种常用的求解方法。
虚位移原理是基于杆件内力是虚功平衡的原理。
根据虚功原理,任意一种变形状态下,根据外力做的虚功与内力做的虚功之和等于零。
在平面桁架中,变形可以由杆件的伸缩变形和节点的转动变形来描述。
假设在特定的荷载条件下,各杆件的长度变化为ΔL,各节点转动角为Δθ。
那么我们可以将每个杆件的内力分解为水平分力、垂直分力和弯矩。
根据虚功原理,我们可以得到以下方程:∑(F_x*ΔL+M*Δθ)=0∑(F_y*ΔL)=0这里,F_x和F_y表示水平和垂直分力,M表示弯矩。
上述两个方程是根据平衡条件得到的。
在求解过程中,通常将虚移位分解为水平和垂直方向的分量,即:ΔL_x=∂u/∂x*Δx+∂u/∂y*ΔyΔL_y=∂v/∂x*Δx+∂v/∂y*Δy其中u和v是位移函数,表示节点的水平和垂直位移,Δx和Δy是节点在x和y方向的位移增量。
通过将虚位移代入虚功方程,我们可以得到:∑(F_x*∆L_x+F_y*∆L_y+M*∆θ)=0这个方程称为平面桁架杆件内力求解的虚功原理方程。
通过这个方程,我们可以求解每个杆件的内力。
具体的求解过程可以分为以下几步:1.根据给定的初始条件,假设节点的位移增量Δx、Δy和Θ;2.对于每个节点,根据虚功方程计算杆件的水平力、垂直力和弯矩;3.根据每个杆件的几何特性和材料属性,计算杆件的伸缩变形和转动变形;4.根据计算得到的杆件力和变形,更新节点的位移增量;5.重复步骤2-4,直到计算收敛,即内力和位移增量不再变化。
通过以上步骤,我们可以求解平面桁架杆件的内力分布。
总结起来,平面桁架杆件内力的虚位移原理求解主要是基于虚功原理。
通过将虚位移代入虚功方程,结合平衡条件和杆件的几何特性和材料性质,可以求解出每个杆件的内力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录摘要 ............................................................................ - 3 -第一章题目的意义...................................................... - 4 -第二章理论分析......................................................... - 4 -2.1位移法的基本概念.. (4)2.2平面桁架分析的基本问题 (7)第三章程序设计框图..................................................- 12 -第四章程序代码........................................................- 13 -4.1计算平面桁架位移法的程序代码 .. (13)第五章应用..............................................................- 16 -5.1例一 .. (16)5.2例二 (19)第六章结论······························································- 22 -参考文献 ·····································································- 22 -平面桁架位移法计算的MAPLE程序设计摘要本文利用位移法编写MAPLE程序来计算平面桁架各节点位移、各杆的轴力。
通过虚设位移和约束处的位移处理,由位移表示出杆件轴力,把杆件轴力和支反力转化为节点力,建立节点力的平衡方程,根据线性代数知识求解多元一次方程组,求解出杆件内力。
所以,通过MAPLE输入特征矩阵和约束条件,采用后处理方法编写MAPLE程序代码计算出平面桁架各节点位移、约束处的支反力和各杆件内力。
本文通过2个计算实例表明其计算结果较为理想。
关键词:平面桁架;位移法;MAPLE;程序设计平面桁架位移法的MAPLE程序设计第一章题目的意义平面桁架在我们的生活中到处可见,房屋、桥梁、电视塔等等都可以发现,因而平面桁架的求解变得尤为重要。
在以往我们学过的力学知识中,我们发现平面桁架求解是相当复杂的,运算量比较的大,然而我们利用的平面桁架位移法的MAPLE程序设计则大大降低了运算量,也极大的提高了运算精度。
第二章理论分析2.1位移法的基本概念位移法是计算超静定结构的另一种基本的、也是有效的方法,不仅如此,对于静定结构,位移法也是一种计算方法。
力法从未知力/缀余力入手,力法的基本原理,是对于超静定结构中任意两点的相对变形都是0,也就说所有的力在该位置上产生的变形之和为0,因此力法可以称之为位移协调法。
位移法与之相对应,即对于处于平衡状态下的结构体系来讲,结构中的任意一点或任意组成部分也是处于平衡状态的,因此该点或部分必然存在内力的平衡,以内力平衡为基础所构建的线性方程组来求解结构内力,也是一种极佳的方法。
因为结构的内力与变形之间存在着必然的、确定的联系,因此结构的内力平衡一般从位移为未知量来入手,最终求得结构内力。
这种以位移为初始未知数求解结构内力的方法称为位移法。
位移法的基本原理,是以在小变形的基础的结构体系中,内力是可以叠加的,位移也是可以叠加的。
结构中的受力、变形是可以分阶段、分次发生的,分阶段、分次发生的受力、变形是可以线性叠加的,叠加的结果与这些力、变形同时发生的结构所产生的内力、变形是相同的。
位移法可按两种思路求解结点位移和杆端弯矩:典型方程法和平衡方程法。
下面给出典型方程法的解题思路和解题步骤。
1、截面直杆的转角位移方程各种因素共同作用下杆端弯矩的表达式称为转角位移方程。
①两端固定梁转角位移方程:②一端固定一端铰支梁转角位移方程:③ 一端固定一端定向支承梁转角位移方程:④已知杆端弯矩,可由杆件的矩平衡方程求出剪力:其中是相应的简支梁在荷载作用下的杆端剪力;M AB,M BA的正负按位移法规定。
2、直接列平衡方程法:位移法方程实质上是静力平衡方程。
对于结点角位移,相应的是结点的力矩平衡方程;对于结点线位移,相应的是截面的投影平衡方程。
用基本体系方法计算时,是借助于基本体系这个工具,以达到分步、分项写出平衡方程的目的。
也可以不用基本体系,直接由转角位移方程,写出各杆件的杆端力表达式,在有结点角位移处,建立结点的力矩平衡方程;在有结点线位移处,建立截面的投影平衡方程。
这些方程也就是位移法的基本方程。
正负号的规定结点转角、杆转角、杆端弯矩和剪力一律以顺时针为正。
其中:形常数(刚度系数)2.2 平面桁架分析的基本问题要解决平面桁架问题,首先,要了解平面桁架的基本假设:1.各杆件都用光滑铰链链接。
2.各杆件都是直的,其轴线位于同一平面内,且通过铰链的中心。
3.荷载与支座的约束反力都作用在节点上且位于轴线的平面内。
4.各杆件的自重或略去不计,或平均分配到杆件两端的节点上。
桁架中各杆件都是二力杆,杆件的内力都是轴力。
其次,在平面桁架分析的基本问题中,我们利用理论力学进行分析的方法一般有:1.节点法:假想地截取平衡桁架的一部分为分离体,若分离体只包含一个节点,称为节点法。
节点处的平衡力系为平面汇交力系。
2.截面法:若分离体包含两个以上的节点,称为截面法,为平面任意力系的平衡。
3.节点法和截面法的混合应用。
用结构力学进行分析的方法有:1.节点法:假想地截取平衡桁架的一部分为分离体,若分离体只包含一个节点,称为节点法。
节点处的平衡力系为平面汇交力系。
2.截面法:若分离体包含两个以上的节点,称为截面法,为平面任意力系的平衡。
3.节点法和截面法的混合应用。
用结构力学进行分析的方法有:1.力法:是以多余未知力为基本未知量,基本未知量的数目等于结构的超静定次数。
2.位移法:是以独立的结点位移(结点角位移与独立结点线位移)为基本未知量,基本未知量的数目与超静定的次数无关。
关于位移法的简例(《结构力学Ⅰ》【第二版】包世华p274)先举一个简单的桁架例子,以便于具体地了解位移法的基本思路。
图7-1a 为一个对称结构,承受对称荷载Fp 。
结点B 只发生竖向位移⊿,水平位移为零。
在位移法中,把此竖向位移⊿选作基本未知量。
这是因为:如果能设法把位移⊿求出,那么各杆的伸长变形即可求出,从而各杆的内力就可求出,整个问题也就迎刃而解了。
由此看出,位移⊿确是一个关键的未知量。
现在进一步讨论如何求基本未知量⊿的问题。
计算分为两步: 第一步,从结构中选取一个杆件进行分析。
图7-2a 中杆AB ,如已知杆端B 沿杆轴向的位移u i (即杆的伸长),则杆端力F Ni 应为 i i i Ni u l EA F (7-1) 式中E 、A i 、l i 分别为杆件的弹性模量、截面面积和长度。
系数EA i / l i 是使杆端产生单位位移时所需施加的杆端力,称为杆件的刚度系数。
式(7-1)表明杆件的杆端力F Ni 与杆端位移u i 之间的关系,称为杆件的刚度方程。
图 7 - 1 图 7 - 2第二步,把各杆件综合成结构。
综合时各杆在B 端的位移是相同的,即都由B 改变到B ’,此为变形协调条件,各杆端位移u i 与基本未知量⊿间的关系为(图7-2b )i i a u sin ∆= (a ) 再考虑结点B 的平衡条件∑Fy=0,得(图7-1b )∑==51sin i p i N F a F(b )其中各杆的轴力FNi 可由(7-1)表示,再利用式(a )可用基本未知量⊿表示,代入式(b ),既得p i i ii F a l EA =∆∑=251sin (c ) 这就是位移法的基本方程,它代表平衡方程,是用位移表示的平衡方程。
由此可求出基本未知量⊿= ∑=512sin i i ai ipl EA F (d )至此,完成了位移法计算中的关键一步。
基本未知量⊿求出以后,其余为题就迎刃而解了。
例如,为了求各杆的轴力,可将式(d )代入(a ),再代入式(7-1),可得i i i i i i i i a l EA a l EA FN 251sin sin ∑== (e) 将图7-1a 的尺寸代入式(d )和(e ),设各杆EA 相同,得 EAa F p 637.0=∆ F N1=F N5=0.159F pF N2=F N4=0.255F pF N3=0.319F p在图7-1a 中,如只有2根杆,结构是静定的;当杆数大于(或等于)3时,结构是超静定的,均可用上述方法计算。
可见,用位移法计算时,计算方法并不因结构的静定或超静定而有所不同。
第三章程序设计框图第四章程序代码4.1 计算平面桁架位移法的程序代码>restart:with(linalg):with(plots):printlevel:=0:interface( showassumed=0):Warning, the protected names norm and trace have been redefined and unprotectedWarning, the name changecoords has been redefined>XY:=matrix([[0,0],[1.5,0],[2.25,0],[3,0],[4.5,0],[3,-0.5 ],[1.5,-0.5]]):>NE:=matrix([[1,2,E,A],[2,3,E,A],[3,4,E,A],[4,5,E,A],[5,6 ,E,A],[4,6,E,A],[3,6,E,A],[6,7,E,A],[3,7,E,A],[2,7,E,A],[ 1,7,E,A]]):>NP:=matrix([[1,2,-8],[2,2,-8],[3,2,-6],[4,2,-8],[5,2,-8] ]):> NC:=matrix([[1,1],[1,2],[5,2]]):初始数据的处理>truss:=proc()平面桁架位移法求解子程序global XY,NE,NP,NC:localx1,y1,x2,y2,L,cosa,sina,k1,T1,T2,T,ss,a,f,solu,k,i,j,uv,p p,ff,nf:uv:=matrix(rowdim(XY)*2,1,0):pp:=matrix(rowdim(XY)*2,1,0) :ff:=matrix(rowdim(NE),1,0):nf:=matrix(rowdim(XY)*2,1,0): ht:=(XY,NE)->display(plot([seq([XY[i,1],XY[i,2]],i=1..row dim(XY))],style=point,color=red,symbol=circle,symbolsize= 30),plot([seq([[XY[NE[i,1],1],XY[NE[i,1],2]],[XY[NE[i,2], 1],XY[NE[i,2],2]]],i=1..rowdim(NE))],color=blue,thickness =2),textplot([seq([XY[i,1],XY[i,2],i],i=1..rowdim(XY))],c olor=red),axes=none):绘图程序代码for k from 1 to rowdim(XY) do;虚设位移uv[2*k-1,1]:=u[k];uv[2*k,1]:=v[k];od;for k from 1 to rowdim(NC) do;约束处的位移处理i:=NC[k,1]: j:=NC[k,2]:uv[2*i-2+j,1]:=0:od;for k from 1 to rowdim(NE) do; 有虚设位移求杆件内力i:=NE[k,1]: j:=NE[k,2]:x1:=XY[i,1]: y1:=XY[i,2]:x2:=XY[j,1]: y2:=XY[j,2]:L:=sqrt((x2-x1)**2+(y2-y1)**2):cosa:=(x2-x1)/L :sina:=(y2-y1)/L:k1:=NE[k,3]*NE[k,4]/L:T1:=cosa*k1: T2:=sina*k1:T:=matrix([[-T1,-T2,T1,T2]]);ss:=matrix([[uv[2*i-1,1]],[uv[2*i,1]],[uv[2*j-1,1]],[uv[2 *j,1]]]);ff[k,1]:=det(simplify(multiply(T,ss))):od;for k from 1 to rowdim(NE) do;把轴力化为节点力i:=NE[k,1]: j:=NE[k,2]:x1:=XY[i,1]: y1:=XY[i,2]:x2:=XY[j,1]: y2:=XY[j,2]:L:=sqrt((x2-x1)**2+(y2-y1)**2):cosa:=(x2-x1)/L : sina:=(y2-y1)/L:pp[2*i-1,1]:=pp[2*i-1,1]-cosa*ff[k,1]:pp[2*i,1]:=pp[2*i,1 ]-sina*ff[k,1]:pp[2*j-1,1]:=pp[2*j-1,1]+cosa*ff[k,1]:pp[2*j,1]:=pp[2*j,1 ]+sina*ff[k,1]:od;for k from 1 to rowdim(NC) do;把支座反力引入节点力i:=NC[k,1]: j:=NC[k,2]:pp[2*i-2+j,1]:=X[i,j]+pp[2*i-2+j,1]:od;for k from 1 to rowdim(NP) do;已知载荷的处理i:=NP[k,1]: j:=NP[k,2]:nf[2*i-2+j,1]:=NP[k,3]:od;for k from 1 to rowdim(NC) do;约束出的位移由支反力替代i:=NC[k,1]: j:=NC[k,2]:uv[2*i-2+j,1]:=X[i,j]:od;for k from 1 to 2*rowdim(XY) do;节点平衡方程f[k]:=pp[k,1]=nf[k,1];od;solu:=solve({seq(f[i],i=1..rowdim(XY)*2)},{seq(uv[i,1],i= 1..rowdim(XY)*2)});位移与支座反力的求解ff:=subs(solu,evalm(ff)):for k from 1 to rowdim(NE) do;i:=NE[k,1]: j:=NE[k,2]:print(F[N,i,j]=evalf(ff[k,1],4)):od;ht(XY,NE);end proc:> truss();子程序的引用=F-33.00N12,,F=-33.00,,N23F=-33.00,,N34F-33.00=,,N4534.79F=N56,,-8.000F=N46,,-5.408F=N36,,37.50=F,,N67-5.408F=N37,,-8.000=F,,N2734.79=FN17,,第五章应用5.1 例一>XY:=matrix([[0,0],[0,6],[3,0],[3,3],[3,7],[6,0],[6,6],[6 ,8],[9,0],[9,9],[12,0],[12,6],[12,8],[15,0],[15,3],[15,7] ,[18,0],[18,6]]):>NE:=matrix([[1,2,E,A],[1,3,E,A],[1,4,E,A],[2,5,E,A],[5,4,E,A],[5,8,E,A],[4,3,E,A],[4,6,E,A],[4,7,E,A],[3,6,E,A],[6,7,E,A],[6,9,E,A],[7,8,E,A],[7,9,E,A],[7,10,E,A],[8,10,E ,A],[9,10,E,A],[10,12,E,A],[10,13,E,A],[9,11,E,A],[9,12,E ,A],[12,13,E,A],[13,16,E,A],[15,16,E,A],[16,18,E,A],[12,15,E,A],[17,18,E,A],[15,17,E,A],[14,17,E,A],[14,15,E,A],[11,14,E,A],[11,15,E,A],[11,12,E,A]]):> NP:=matrix([[5,2,-10],[8,2,-10]]):> NC:=matrix([[1,1],[1,2],[17,2]]):➢ truss();⏹= F ,,N 120. = F ,,N 1315. = F ,,N 14-21.21 = F ,,N 250. = F ,,N 54-10. = F ,,N 580. = F ,,N 430. = F ,,N 46-7.08 = F ,,N 47-14.14 = F ,,N 3615. = F ,,N 67 4.993 = F ,,N 6910. = F ,,N 78-10. = F ,,N 79-11.18 = F ,,N 710-7.070 = F ,,N 8100.= F ,,N 91010.= F ,,N 1012-7.070= F ,,N 10130.= F ,,N 911 5.= F ,,N 9120.= F ,,N 12130.= F ,,N 13160.= F ,,N 15160.= F ,,N 16180.= F ,,N 1215-7.070= F ,,N 17180.= F ,,N 1517-7.070= F ,,N 1417 5.= F ,,N 14150.= F ,,N 1114 5.= F ,,N 1115-.01= F ,,N 1112-.015.2 例二>XY:=matrix([[0,0],[2,-2],[2,0],[4,-2],[4,0],[6,-2],[6,0] ,[8,0],[10,-2],[10,0],[12,-2],[12,0],[14,-2],[14,0],[16,0 ]]):>NE:=matrix([[1,2,E,A],[1,3,E,A],[2,3,E,A],[2,4,E,A],[3,4 ,E,A],[3,5,E,A],[5,4,E,A],[4,6,E,A],[4,7,E,A],[5,7,E,A],[ 6,7,E,A],[6,8,E,A],[7,8,E,A],[6,9,E,A],[8,9,E,A],[8,10,E, A],[9,10,E,A],[9,11,E,A],[10,11,E,A],[10,12,E,A],[11,12,E ,A],[11,13,E,A],[11,14,E,A],[12,14,E,A],[13,14,E,A],[13,1 5,E,A],[14,15,E,A]]):> NP:=matrix([[5,2,-10],[8,2,-10]]):> NC:=matrix([[1,1],[1,2],[15,2]]): >truss();17.68F=N12,,-12.50=FN13,,-12.50=FN23,,F=12.50,,N2417.68=F,,N34F-25.=N35,,-10.F=N54,,27.50=FN46,,F=-3.535,,N47-25.=FN57,,F=2.500,,N67F-3.535=N68,,-27.50=FN78,,F=30.,,N69F-10.60=N89,,F=-22.50N810,,F=7.500,,N91022.50=FN911,,-10.60=FN1011,,-15.F=N1012,,= F ,,N 11120.= F ,,N 11137.500= F ,,N 111410.60= F ,,N 1214-15.= F ,,N 1314-7.500= F ,,N 131510.60= F ,,N 1415-7.500第六章结论本次课程利用结构力学位移法编写MAPLE程序计算平面桁架的受力。
