第六章 平面简单桁架..
合集下载
结构体系篇--桁架结构讲义PPT(51张)

梯形屋架
用于屋面坡度较小的屋盖中,
受力性能比三角形屋架优越,
适用于较大跨度或荷载的工 业厂房。
用于无檩体系屋盖,屋面材 料大多用大型屋面板。
(四)轻型钢屋架 屋架的上弦一般用小角钢、下弦和腹杆用小角钢或圆钢。
适用于:跨度<=18m,柱距4~6m,设置有起重量
<=50KN的中、轻级工作制桥式吊车的工业建筑和跨度 <=18m的民用房屋的屋盖结构。 结构型式:三角形、三铰拱和梭形屋架。 常用:三角形屋架。
三角形、三铰拱屋架适用于斜坡屋面,屋面坡度通常取
1/2~1/3,梭形屋架的屋面坡度较平坦,通常取1/12~1/8。
(五)混凝土屋架 常见形式有:梯形、折线形、拱形、无斜腹杆屋架等。 根据是否对屋架下弦施加预应力,分为:钢筋混凝土屋架和
预应力混凝土屋架,前者适用跨度为15~24m,后者适用跨
度为18~36m或更大。 1、梯形屋架
按几何组成方式可以分:简单桁架、联合桁架 (由几个简单桁架按几何不变体系的简单组成规 则联合组成)和复杂桁架(不同于前两种的其他 静定桁架)。
按是否存在水平推力分:无推力的梁式桁架(与相应的实 体梁结构比较,掏空率大,上下弦杆联合抗弯,腹杆主要 抗剪,受力合理,用材经济)和有推力的拱式桁架(拱圈 与拱上结构联为一体,整体性好,便于施工,跨越能力强, 节省钢材)。
梯形屋架受力性能比三角形屋架合理,可用于跨度较大房 屋适用跨度为12~18m。
(二)钢-木组合屋架
形式:(1)豪式、(2)芬
克式、(3)梯形、(4)下折式。
由于不易取得符合下弦材质 标准的上等木材,特别是原木和
方木干燥较慢,干裂缝对下弦不
利,采用钢拉杆作为屋架的下弦, 每平方米建筑面积的用钢量增加
单辉祖工力-6静力学专题1

yC
yili li
yi li l
xC
zili li
zi li l
z
C Pi
P
zi
zC
O
yi
xi
xC y
x
yC
2. 确定重心的常用方法
• 当物体具有对称轴、对称面或对称中心时,它 的重心一定在对称轴、对称面或对称中心上。
• 对于几何形状较复杂的均质物体,往往采用分 割法和负面积法
S 3 = 9. 81kN
YA +S2 ·sin 60°-P1 = 0 S 2 = 1. 15kN
● 零力杆的判断 零力杆:杆件内力为零的杆件
节点只连接两根不共线的杆件
0 0
节点无外力 则此两根杆为零力杆
节点只连接两根不共线的杆件
0
外力作用线沿某一根杆
则另一根杆为零力杆
节点连接三根杆件
0
若其中两根共线且节点无外力
称重法
• 然后将其一端支承于 A 点,另一端放在磅称 B上, 测得两点的水平距离 l 及 B 处的约束反力 FB , 假定为 G , 由
∑MA( F ) = 0 , P xC - FB l = 0
xc
FBl P
G P
l
O x
zi
yi yC
P
zC
xi
xC y
为了求坐标 zC, 将物体连同直角坐 标系 Oxyz 一起绕 x 轴逆时针旋转90°
重力的方向并无改变 对 x 轴取矩,有
P zC = (P1z1 + P2z2 + …+ Pnzn) = ∑Pi zi
重心的坐标公式
z
y
Mi
△Vi Mi
PCi P
水工钢结构第六章钢桁架讲解

单斜杆与弦杆的连接
2、结点板的形状及其厚度 结点板的作用主要是通过它将交汇于结点上的腹杆连接到弦杆上, 并传递和平衡结点上各杆内力。
3、腹杆角钢的切割和腹杆长度的确定 4、腹杆的焊接
二、结点板的计算
由静力平衡条件有:
节点板只在弦杆与腹杆之间传力,不直接参与传递弦杆内力,弦杆 若在节点板处断开,应设置拼接角钢在两弦杆间直接传力。
一、支撑
平面桁架在其本身平面内具有较大的刚度,但在垂直于桁架平面 方向(桁架平面外)不能保持其几何不变,即使桁架上弦与檩条 或屋面等铰接相连桁架仍会侧向倾倒。为了防止桁架侧向倾倒破 坏和改善桁架工作性能,对于平面桁架体系,必须设置支撑系统 (水工结构中也称为联结系)。
桁架间的支撑
桁架间的支撑
桁架支撑的作用主要是: (一):桁架支撑的作用主要是:
2. 下弦横向水平支撑
布置原则:一般情况均应设置下弦横向水平支撑。只有当桁架跨度比较 小(L≤18m),且没有悬挂式吊车,或虽有悬挂吊车但起重吨位不大, 厂房内也无较大的振动设备时,可不设下弦横向水平支撑。 布置位置:与上弦横向水平支撑布置在同一柱间,以形成空间稳定体。
• 3. 纵向水平支撑 • 布置位置:在屋架下弦(三角形屋架可在下弦或上弦)端
4、施工图设计分为施工设计和详图设计两个阶段,设计文件(图纸) 的名称相应为施工图和施工详图,施工图是编制施工详图的依据, 施工详图则是施工图的深化和补充。 5、随着国内钢结构生产企业技术能力的提高,向国际惯用做法靠拢, 施工图由设计院完成,施工详图由生产企业的技术科完成。
(4)承受并传递水平荷载。 (5)保证结构安装时的稳定且便于安装。
(二):支撑的布置 桁架的支撑按照布置方向分为横向支撑和纵向支撑。 1.上弦横向水平支撑
2、结点板的形状及其厚度 结点板的作用主要是通过它将交汇于结点上的腹杆连接到弦杆上, 并传递和平衡结点上各杆内力。
3、腹杆角钢的切割和腹杆长度的确定 4、腹杆的焊接
二、结点板的计算
由静力平衡条件有:
节点板只在弦杆与腹杆之间传力,不直接参与传递弦杆内力,弦杆 若在节点板处断开,应设置拼接角钢在两弦杆间直接传力。
一、支撑
平面桁架在其本身平面内具有较大的刚度,但在垂直于桁架平面 方向(桁架平面外)不能保持其几何不变,即使桁架上弦与檩条 或屋面等铰接相连桁架仍会侧向倾倒。为了防止桁架侧向倾倒破 坏和改善桁架工作性能,对于平面桁架体系,必须设置支撑系统 (水工结构中也称为联结系)。
桁架间的支撑
桁架间的支撑
桁架支撑的作用主要是: (一):桁架支撑的作用主要是:
2. 下弦横向水平支撑
布置原则:一般情况均应设置下弦横向水平支撑。只有当桁架跨度比较 小(L≤18m),且没有悬挂式吊车,或虽有悬挂吊车但起重吨位不大, 厂房内也无较大的振动设备时,可不设下弦横向水平支撑。 布置位置:与上弦横向水平支撑布置在同一柱间,以形成空间稳定体。
• 3. 纵向水平支撑 • 布置位置:在屋架下弦(三角形屋架可在下弦或上弦)端
4、施工图设计分为施工设计和详图设计两个阶段,设计文件(图纸) 的名称相应为施工图和施工详图,施工图是编制施工详图的依据, 施工详图则是施工图的深化和补充。 5、随着国内钢结构生产企业技术能力的提高,向国际惯用做法靠拢, 施工图由设计院完成,施工详图由生产企业的技术科完成。
(4)承受并传递水平荷载。 (5)保证结构安装时的稳定且便于安装。
(二):支撑的布置 桁架的支撑按照布置方向分为横向支撑和纵向支撑。 1.上弦横向水平支撑
第06章 静力学专题-桁架、重心

yili li
yi L
li
zC
zili li
zi li
L
极限为:
xdl
ydl
xC
C
L
,
yC
C
L
,
zdl
zC
C
L
z
O x
Pi zi
yi yC
C
P zC
xi
xC y
本章小结
1. 了解桁架的构成、结构特点以及桁架杆件内力的求解 方法;
§6.1 桁架 基本三角形 三个铰链为节点连接的三根杆构成的三角形 平面简单桁架
平面简单桁架节点和杆件数的关系 桁架节点数为n,杆件数为m,则 m-3=2(n-3) 即 m=2n-3 或 m+3=2n
§6.1 桁架 无冗杆桁架 从桁架中抽出任何一根杆,原有的几何形状不能保持, 没有多余杆件的桁架 有冗杆桁架 从桁架中抽出一根杆或几根杆件,原有的几何形状能 保持,桁架有多余杆件
S
xdS
ydS
xC
S
S
,
yC
S
S
,
zdS
zC
S
S
z ds
Pi
C
zi
PzC
O
yi
xi
xC y
x
yC
§6.3 重心
如果物体是均质等截面的细长线段,其截面尺寸与 其长度 L 相比是很小的,则重心公式为
xC
xili li
xi li
L
yC
(3)、节点连接三根杆,其中两根共线,并且在此节 点上无外载荷,则第三根杆件为零杆
工程力学平面桁架问题课件PPT

本节只讨论平面简单桁架内力的计算。
15
注意
工 1、一般要求所有杆件的内力时,采用节点法;只需要 程 求桁架中某一根或某几根杆件的内力时,采用截面法。 力 学 2、两种方法一般都是先要取整体为研究对象,根据平
面力系平衡 方程求出支座约束反力。 下面通过例子说明两种方法的应用。
16
例一
工 程 力 学
FBy
C
31
例三 已知P1,P2,P3, 尺寸如图。求1,2,3杆所受力。
工
程 力
若再求4,5杆受力
FAy
FBy
学 取节点D考虑
Fx 0 F5 Fy 0 F4
32
零杆:
工 程 力 学
所谓“零杆”,即是内力为零的杆。 当荷载改变后,“零杆”可以变为非零杆。因此,为 了保证结构的几何形状在任何荷载作用下都不会改变, 零杆不能从桁架中除去。
工 程 力 学
A
B
如果两支承点是简支的,很容易证明此桁架是静定的。
13
关于平面理想桁架的基本假设
组成桁架的杆件的轴线都在同一平面内的桁架称为平面桁架。 只需要求桁架中某一根或某几根杆件的内力时,采用截面法。
关 所于谓平“零面杆理”,想即桁是架内的(力1基为本)零假各的设杆杆。 在端点用光滑铰链相连接,连接点称为节点
已知:静止的桁架如图所示,AD=DE=EH=HB=a。
已请知指P出1图,中P2桁,架P内3,力(尺2为寸零)如的图杆杆。件的? 自重相对载荷可以忽略不计
一节点上有三根杆件,如果节点上无外力的作用,其中两根共线,则另一杆为零杆.
工 (2) 杆的自重相对载荷可以忽略不计
(3) 载荷及支座反力均作用在节点上。 否则,称之为空间桁架。
简单平面桁架的内力计算
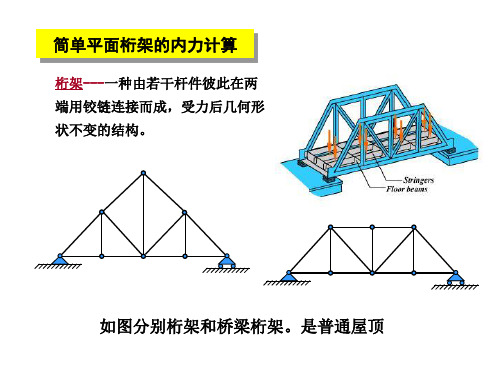
思考题
C
D
用截面法求杆1,2,3的内力。 用截面m,并取上半部分。 m
a
1
E 2 F
3
m
a B
F
a
x
0, 求出杆2的内力F2。
C
A
a
a
F
M
0, 求出杆3的内力F3。
M
D
0, 求出杆1的内力F1。
3. 计算桁架杆件内力的方法
节点法—— 应用共点力系平衡条件,逐一研究桁架上每个
节点的平衡。
截面法—— 用应用平面任意力系的平衡条件,研究桁架由 截面切出的某些部分的平衡。
例3-10 如图平面桁架,求各杆内力。已知铅垂力FC=4 kN, 水平力FE=2 kN。
F E a A a C a a B
FE
a
C
FAx
解得
FC
FCE 2 2 kN ,
FCD 2 kN
FDE
D
8.取节点D,受力分析如图。 列平衡方程
FDB
FDC
F
x
0,
FDB FDC 0
F E a D
FAy
A a
FE
a
F
FB
B
y
0,
FDE 0
解得
a
C
FAx
FC
FDB 3 kN ,
FDE 0
9.取节点B,受力分析如图。
D
FC
解: 节点法
1.取整体为研究 对象,受力分析如图。
FAy
A a C F
E
a
FE
a
FB
B
a
FAx
D
FC
3.列平衡方程。
简单桁架

基本结构
零杆:Zero force members
F2 F1
F
F3
F2
F1 F1
F2
Which members are zero force members?
一、节点法(Method of Joints)
1、先求支座反力;
2、逐个取节点研究(汇交力系)。
3、假设未知力方向背离节点,即受拉为正。
例3-13 平面桁架 P=10kN
各杆件轴线的交点称为节点(joint)。
为简化计算特作如下假设: 1.桁架在的各杆均为直杆。 2.节点都抽象化为光滑铰链连接。 3.外力都作用在节点上且作用在平面内。 4.自重不计(或均匀分配在节点上)。 满足上述假设的桁架称为理想桁架,各杆为二力杆。 5.静定桁架,无多余杆件,拆除任一根则结构活动变形。 (以三角形为基本结构)。
§3—6.平面静定桁架的内力分析
桁架:由直杆两端焊接或铆接而成的几 何形状不变的结构。
平面桁架(Plane Truss):各杆都在同一平 面内。
杆件轴线的交点称为节点(joint)。
§3—6.平面静定桁架的内力分析
桁架:由直杆两端焊接或铆接而成的几何形状不变的结构。 平面桁架(Plane Truss):各杆都在同一平面内。
以一个截面截取结构的一部分研究。
注意:
1、选取受力情况简单的一段; 2、截取的结构上的力系为平面任意力系,可求三个未知数, 一般截割不超过三根杆,若多于三根杆时,必须可以求出一部 分未知数。 3、设杆受拉为正。 4、选取合适的力矩中心。
例3-14 平面桁架
m
各杆长度等于1m,
P1=10kN,P2=7kN。 求:1、2、3杆的内力。
F1 10kN F2 8.66kN
零杆:Zero force members
F2 F1
F
F3
F2
F1 F1
F2
Which members are zero force members?
一、节点法(Method of Joints)
1、先求支座反力;
2、逐个取节点研究(汇交力系)。
3、假设未知力方向背离节点,即受拉为正。
例3-13 平面桁架 P=10kN
各杆件轴线的交点称为节点(joint)。
为简化计算特作如下假设: 1.桁架在的各杆均为直杆。 2.节点都抽象化为光滑铰链连接。 3.外力都作用在节点上且作用在平面内。 4.自重不计(或均匀分配在节点上)。 满足上述假设的桁架称为理想桁架,各杆为二力杆。 5.静定桁架,无多余杆件,拆除任一根则结构活动变形。 (以三角形为基本结构)。
§3—6.平面静定桁架的内力分析
桁架:由直杆两端焊接或铆接而成的几 何形状不变的结构。
平面桁架(Plane Truss):各杆都在同一平 面内。
杆件轴线的交点称为节点(joint)。
§3—6.平面静定桁架的内力分析
桁架:由直杆两端焊接或铆接而成的几何形状不变的结构。 平面桁架(Plane Truss):各杆都在同一平面内。
以一个截面截取结构的一部分研究。
注意:
1、选取受力情况简单的一段; 2、截取的结构上的力系为平面任意力系,可求三个未知数, 一般截割不超过三根杆,若多于三根杆时,必须可以求出一部 分未知数。 3、设杆受拉为正。 4、选取合适的力矩中心。
例3-14 平面桁架
m
各杆长度等于1m,
P1=10kN,P2=7kN。 求:1、2、3杆的内力。
F1 10kN F2 8.66kN
水工钢结构第六章

三角形桁架
上弦坡度:一般大于1:5,适用于轻屋面材料 的屋架。跨度在18m以下由小角钢和圆钢组成的轻 型钢屋架,比较经济。
三角形悬臂式桁架 多用于海洋采油平台上直升飞机场承重支架。
二、桁架的基本尺寸:跨度L、高度H
跨度L主要决定于结构的使用要求。 桁架高度H与组合梁的高度相似,主要应根据经济 和刚度的要求而定。
对屋架设计应考虑以下三种荷载组合: 1)全跨永久荷载+全跨可变荷载; 2)全跨永久荷载+半跨可变荷载; 3)全跨屋架、支撑及天窗架自重+半跨檩条、 屋面板和活(或雪)荷载。
二、桁架杆件的内力计算 桁架杆件内力的计算是根据理想的桁架计算简 图进行的,即假定节点为理想的铰,桁架中所有杆 件的轴线为直线且都在同一平面内,各杆轴线相交 于节点中心,荷载作用于节点上,在这些条件下, 可用结构力学的方法,如图解法、节点法或截面法 以及刚度法等。
(d)单斜式:对称,结点形状相同, 加工方便。 (e)交叉式:可以承受动力荷载。
(a)(c)再分式
(b)(d)K形
(e)菱形
第三节 一、支撑 1、支撑的作用
桁架间的支撑和压杆的计算长度
支撑的主要作用是: 1)保证桁架体系的空间几何稳定性。 2)为桁架弦杆提供必要的侧向支承点,可以减少 受压弦杆在桁架平面外的计算长度,提高桁架的侧向 刚度及稳定性。 3)支撑与桁架弦杆配合,承受垂直于桁架平面 的各种荷载所引起的侧向弯曲及扭转作用,提高结 构的侧向抗弯刚度和抗扭刚度。 4)使结构具有空间整体作用,改善桁架的工作性 能。 5)支撑又可以保证结构安装的方便及可靠性。
(二)钢管截面 钢管壁厚较薄,而截面材料分布离几何中心较远, 且各方面的回转半径均等,与其它型钢截面相比回转 半径较大,相应的长细比较小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 用节点法求解。
1. 求支座约束力。 以整体为研究对象, 受力分析如图所示。 列平衡方程:
A
C 1 3 4 5 D B
30
2
2m
F
2m
F 0, F 0 F 0, F F F 0 M F 0, F 2 F 4
x Bx A y By B A
1 B
F1 = 125 kN (压) F2 =52.6 kN (拉)
FB
y
2
B
A
FA
C
50 kN m 100 kN m F1 1 E D 5
B
y x
1m
F2 2
F
1m
3 4 H
6
1m
G
F4 m
1m
1m
FB 87.5kN, FA 62.27 5kN
北京林业大学
BEIJING FORESTRY UNIVERSITY
桁架的实际节点 理想节点
焊接或铆接,杆的端点不能转动, 可承受力矩。
光滑铰链, 不能承受力矩
5
北京林业大学
BEIJING FORESTRY UNIVERSITY
平面简单桁架内力计算的基本假设
① 杆件用光滑的铰链连接;
② 直杆;
③ 桁架所受的载荷均作用在节点上,且在桁架
的平面内; ④ 杆重不计或平均分配在杆件两端的节点上。 — 桁架内各杆均为二力杆。
F
x
0,
F5 F2 0
F2
D
F3 F5
x
F5 8.66kN
结论: F1 10 kN (压), F2 F5 8.66 kN(拉),
F
F3 10 kN (拉),F4 10 kN (压)。
19
请同学们思考:
F3 ? , F5 ? 能否直接得 到?如何求?
Ay
F1 8.73 kN (压) F2 2.82 kN (拉) F3 12.32 kN (拉)
24
北京林业大学
BEIJING FORESTRY UNIVERSITY
例题 5
试计算图示平面桁架杆1、2、3的内力。
100 kN
A C D 2 F 1m G 1 E
50 kN
B
3
H
1m
1m
1m
20
北京林业大学
BEIJING FORESTRY UNIVERSITY
例题4
如图所示平面桁架,各杆件的长度都等于1 m。在节点E、
G、F上分别作用载荷FE =10 kN,FG = 7 kN ,FF = 5 kN 。
求:杆1、2、3的内力。
y
C
1 2
D
F B
FF
x
A
E
3
G
FE
FG
21
北京林业大学
BEIJING FORESTRY UNIVERSITY
北京林业大学
BEIJING FORESTRY UNIVERSITY
第六章 静力学专题 — 平面简单桁架
1
北京林业大学
BEIJING FORESTRY UNIVERSITY
一、平面桁架
2
北京林业大学
BEIJING FORESTRY UNIVERSITY
桁架:
由杆组成,杆杆间用铰链连接,且受力后几何形 状不变的系统。
y
D
A
C 1 3 4 5 D
FBy
B
30
2
FA
2m
FBx
F
2m
F3 F5
x
F3 F 10kN, F5 F2 8.66kN
FBx 0, FA FBy 5 kN
y
A
F2
F
y
C
F1
30
F2
FA
30
x
F1 F3
F4
x
F4 10kN
F1 10 kN, F2 8.66 kN
F1 F4
3
1 4
F2
F1 F2 , F3 8 F4
北京林业大学
BEIJING FORESTRY UNIVERSITY
例题 1
试计算图示平面桁架杆1、2、3的内力。
F
M H
F D
B
a
N a
0
3
K a
-F
2
1
F
0
G
0
C
0 0 a
A
0 a
解: F1 0,
F2 F (压), F3 0
(压 )
100 kN
解得:F3 = 87.5 kN
A
C D
n
F1
2
50 kN
5
1 E 3
B
FB
y x
1m
F
1m
G
F2 F3 6 4 F6
H 1m
1m
n
FB 87.5kN, FA 62.29 5kN
1m
北京林业大学
BEIJING FORESTRY UNIVERSITY
作 业
P110:
习题 6 — 1, 6
7
北京林业大学
BEIJING FORESTRY UNIVERSITY
四、特殊杆件的内力判断
☆ 两杆节点无载荷、且两杆不在 一条直线上时,该两杆是零杆。 ☆ 三杆节点无载荷、其中两杆在
1
2
F1
F1 F2 0
F2
3
F3
一条直线上,另一杆必为零杆
F1
F3 0
2
1
F2 F3
2
F1 F2
☆ 四杆节点无载荷、其中两两 在一条直线上,同一直线上两 杆内力等值、同性。
30
五、求平面桁架各杆内力的两种方法 2、截面法 — 适于校核部分杆件内力。
适当地选取一截面,假想地把桁架截开,再 考虑其中任一部分的平衡,求出被截杆件的
内力。
截开的每部分均受一平面任意力系的作用,
只能列写三个独立的平衡方程,因而只能求
解三个未知量。— 不宜截断三杆以上。
13
北京林业大学
BEIJING FORESTRY UNIVERSITY
C
1
A
3
4 5
FBy
B
0
FA
30
2 D
FBx
F
2m
解得:
FBx 0, FA FBy 5 kN
2m
16
2. 再依次取节点为研究对象,求各杆的内力。 假定各杆均受拉力。 (1)先以节点A为研究对象
y
A A C 1 3 4
FBy
B
30
2 D
5
F1
30
FA
2m x
FBx
F
2m
F2
FA
FBx 0, FA FBy 5 kN
E
F3
FE
列平衡方程:
M F 0 F 0 F M F 0
E y D
解得:
F1 sin 60 1 FAy 1 0 FE F2 sin 60 0 F3 sin 60 1 FE 0.5 FAy 1.5 FAx sin 60 1 0
五、求平面桁架各杆内力的两种方法 1、节点法 — 适于求解全部杆件的内力。
分别考虑各节点的平衡。 每个节点都受一平面汇交力系的作用,只能 列写两个独立的平衡方程,因而只能求解两 个未知量。— 每个节点只能有两未知力杆
注意选择节点顺序。
12
北京林业大学
BEIJING FORESTRY UNIVERSITY
A
C
1 2 E 3
D
F
FF
B
x
FAx
G
FAy
FE
FG
FB
F 0, F F 0 F 0, F F F F 0 M F 0, F sin 60 1 F
x Ax F y Ay E G B B F
G
1 +FE 2 FAy 3 0
解: 用节点法求解。
1. 先求桁架的支座约束力。 2. 再求杆的内力。 节点A:F4、F5 节点C:F1、F6
节点E:F2、F3
y C 1 D
7
F
4
A
5
6 2
E 3
8
FAx
9 10 B G 11
FF
x
FAy
FE
FG
FB
22
解: 用截面法求解。
y
1. 先求桁架的支座约束力。
取桁架整体为研究对象, 受力分析如图所示。 列平衡方程:
1m
FB 87.5kN, FA 62.28 5kN
北京林业大学
BEIJING FORESTRY UNIVERSITY
解: F3 = ?
能否用截面法求?如何求?
假想截面n-n截断杆1、2、3、6,研究右侧.
M B F 0,
FA
50 1+F2 cos 45 1+F 1 0
9
北京林业大学
BEIJING FORESTRY UNIVERSITY
例题 2
已知: P,d。求:1、2、3、4 四杆的内力。
K
0 0 B 0 0 0 2P 1 2 0 3 0 4 0 0 0 -P -P 0D 0 C G J I
2P
H
0
F
E
A
d
P
5d
F2
y
解:由零杆判式知: F1 F3 F4 0
