老树新芽_抛物线性质30条 (1)
北师大版高中数学选择性必修第一册 第二章 3.2 抛物线的简单几何性质

出明亮的、照射很远的平行光束,又能发射出较暗的、照射近距离的光线,
这也就是汽车的远光灯和近光灯.那么它的工作原理是什么?
知识点拨
抛物线的简单几何性质
名师点析1.抛物线没有渐近线,在画图时不要把抛物线画成双曲线一支的
形状,因为双曲线的开口越来越开阔,而抛物线的开口越来越扁平.
(
)
A.1
B.2
C.3
D.4
答案 C
解析 ∵P(x0,y0)在抛物线 y2=4x 上,∴02 =4x0,
2
则点 P 与点(5,0)的距离 d= (0 -5) + 02 =
02 -100 + 25 + 40 =
(0 -3)2 + 16.
∵x0≥0,∴当x0=3时,点P与点(5,0)的距离最小,此时x0=3.
变式训练3(2020吉林长春实验中学高二检测)如果P1,P2,…,Pn是抛物线
C:y2=4x上的点,它们的横坐标依次为x1,x2,…,xn,F是抛物线C的焦点,若
x1+x2+…+xn=10,则|P1F|+|P2F|+…+|PnF|=(
A.n+10
B.n+20
C.2n+10
D.2n+20
)
答案 A
2
1
将点 M(1,-2)的坐标代入,得 n=-2,
1
∴x =-2y.
2
1
故所求抛物线的标准方程为 y =4x 或 x =-2y.
2
2
反思感悟 把握三个要点确定抛物线的简单几何性质
(1)开口:由抛物线标准方程看图象开口,关键是看准二次项是x还是y,一次
二次函数的像与性质抛物线的变化规律

二次函数的像与性质抛物线的变化规律二次函数的像与性质:抛物线的变化规律二次函数是高中数学中的一个重要概念,它描述了一类特殊的函数关系,被广泛应用于数学建模和实际问题的解决中。
本文将探讨二次函数的像与性质,以及抛物线的变化规律。
1. 二次函数的定义和基本性质二次函数的一般形式为:f(x) = ax^2 + bx + c,其中a、b、c为实数且a≠0。
在二次函数中,x是自变量,f(x)是因变量,表示y的值。
1.1 抛物线的开口方向二次函数的性质之一是抛物线的开口方向。
当a>0时,抛物线开口向上,形状像一个"U";当a<0时,抛物线开口向下,形状像一个"∩"。
1.2 抛物线的顶点二次函数的顶点是抛物线的最高点(当a<0时)或最低点(当a>0时)。
顶点的横坐标为-h/2a,纵坐标为k=f(-h/2a),其中h为二次函数一次项系数b的相反数。
1.3 对称轴二次函数的对称轴是通过抛物线顶点的直线。
它也是抛物线的对称轴,将抛物线分为两个对称的部分。
2. 二次函数对x的平移和伸缩二次函数在平面直角坐标系中具有一些特殊的平移和伸缩性质。
2.1 平移二次函数可以通过在x轴和y轴方向上平移来改变其位置。
对于函数f(x) = ax^2 + bx + c,若对于任意常数h和k,当x变为x-h时,f(x)变为f(x-h)+k,即平移了h个单位,若对于任意常数p,当y变为y+k 时,f(x)变为pf(x),即平移了k个单位。
2.2 伸缩二次函数可以通过改变系数a来进行垂直方向上的伸缩,通过改变系数b进行水平方向上的伸缩。
具体来说,当a的绝对值变大时,抛物线向纵轴拉伸;当a的绝对值变小时,抛物线向纵轴压缩;而当b的绝对值变大时,抛物线向横轴伸展;当b的绝对值变小时,抛物线向横轴收缩。
3. 二次函数的零点和判别式二次函数的零点即方程f(x) = 0的解,而判别式可以用来判断二次函数的零点的性质。
高二上学期数学人教A版(2019)选择性必修第一册3.3.2抛物线的简单几何性质教案

第三章圆锥曲线的方程3.3 抛物线3.3.2 抛物线的简单几何性质一、教学目标1、掌握抛物线的范围、对称性、顶点、离心率等几何性质;2、能根据抛物线的几何性质对抛物线方程进行讨论,在此基础上列表、描点、画抛物线图形;3、在对抛物线几何性质的讨论中,注意数与形的结合与转化.二、教学重点、难点重点:掌握抛物线的范围、对称性、顶点、离心率等几何性质难点:灵活根据抛物线的几何性质解决抛物线的有关问题三、学法与教学用具1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.2、教学用具:多媒体设备等四、教学过程(一)创设情景,揭示课题【情景一】抛物线的魅力展现【情景二】抛物线的标准方程与图形【思考】类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质?(二)阅读精要,研讨新知【类比、发现】抛物线的简单几何性质解读【例题研讨】阅读领悟课本134P 例3、例4(用时约为2-3分钟,教师作出准确的评析.)例3已知抛物线关于x 轴对称,它的顶点在原点,并且经过点(2,M -,求它的标准方程.解:依题意,可设抛物线的标准方程为22(0)y px p =>,因为点(2,M -在抛物线上,所以 2(22p -=⨯,解得2p = 因此,所求抛物线的标准方程是24y x =.例4斜率为1的直线l 经过抛物线24y x =的焦点F ,且与抛物线相交于,A B 两点,求线段AB 的长. 解:由已知,抛物线的焦点为(1,0)F , 准线方程为1x =-,如 图3.3-4, 设1122(,),(,)A x y B x y ,,A B 两点到准线的距离分别为,A B d d ,由抛物线的定义, 可知12||1,||1A B AF d x BF d x ==+==+,于是12||||||2AB AF BF x x =+=++ 由已知,设直线:1l y x =-由2216104y x x x y x=-⎧⇒-+=⎨=⎩,所以126x x +=,所以,12||28AB x x =++= 所以,线段AB 的长是8.【小组互动】完成课本136P 练习1、2、3、4,同桌交换检查,老师答疑. 【练习答案】【例题研讨】阅读领悟课本136P 例5、例6(用时约为2-3分钟,教师作出准确的评析.)例5经过抛物线焦点F 的直线交抛物线于,A B 两点,经过点A 和抛物线顶点的直线交抛物线的准线于点D ,求证:直线DB 平行于抛物线的对称轴.证明:如图3.3-5, 以抛物线的对称轴为x 轴,抛物线的顶点为原点,建立平面直角坐标系Oxyz .设抛物线的方程为22(0)y px p => ①点2000(,)(0)2y A y y p ≠, 则直线OA 的方程为02py x y = ② 抛物线的准线方程是2px =-③联立②③,可得2D p y y =-,当220y p ≠时,直线AF 的方程为02202()2py py x y p =-- ④ 联立①④,消去x ,可得2222000()0y y y p y y p ---=即200()()0y y y y p -+=,可得2B p y y =-所以D B y y =,即DB 平行于x 轴. 当220y p =时,易知结论成立.所以,直线DB 平行于抛物线的对称轴.例6如图3.3-6, 已知定点(,)B a h -,BC x ⊥轴于点C M 是线段OB 上任意一 点,MD x ⊥轴于点D ME BC ⊥于点E ,OE 与MD 相交于点P ,求点P 的轨迹方程.解:设点(,),(,)P x y M x m ,其中0x a ≤≤ 则点(,)E a m .由题意,直线OB 的方程为hy x a =-① 因为点M 在OB 上,所以hm x a=- ②所以点P 的横坐标x 满足②.直线OE 的方程为my x a= ③因为点P 在OE 上,所以点P 的坐标(,)x y 满足③.将②代人③,消去m ,得22(0)a x y x a h=-≤≤,即点P 的轨迹方程 【发现】例6中,设点B 关于y 轴的对称点为A ,则方程22(0)a x y x a h=-≤≤对应的轨迹是常见的抛物拱AOB (图3.3-7).抛物拱在现实中有许多原型,如桥拱(图3.3-8)、卫星接收天线等,抛掷出的铅球在空中划过的轨迹也是抛物拱的一部分.【小组互动】完成课本138P 练习1、2、3、4、5,同桌交换检查,老师答疑. 【练习答案】(三)探索与发现、思考与感悟1.已知F 是抛物线2y x =的焦点, ,A B 是该抛物线上的两点, ||||3AF BF +=,则线段AB 的中点到y 轴的距离为( )A.34B.1C.54D. 74解:由已知,12p =,由抛物线的定义,有||||()()322A B A B p pAF BF x x x x p +=+++=++=,所以532A B x x p +=-=,故线段AB 的中点到y 轴的距离为54. 故选C.2.设F 为抛物线24y x =的焦点, ,,A B C 为抛物线上不同的三点,点F 是ABC ∆的重心, O 为坐标原点,,,OFA OFB OFC ∆∆∆的面积分别为123,,S S S ,则222123S S S ++= ( )A.9B.6C.3D.2解:设112233(,),(,),(,)A x y B x y C x y ,由已知(1,0)F ,所以112233111||,||,||222S y S y S y === 所以2222221231231231()4S S S y y y x x x ++=++=++, 因为点F 是ABC ∆的重心,所以1233x x x ++=,所以2221233S S S ++=. 故选C.3. 已知点P 是抛物线24y x =上的动点,点P 在y 轴上的射影是M ,点(7,8)A ,则||||PA PM +的最小值是________.解:如图,由24y x =,得2p =,所以(1,0)F ,||||||12pPM PF PF =-=-,所以2||||||||1||1(71)(80)19PA PM PA PF AF +=+-≥-=-+-=答案:9(四)归纳小结,回顾重点抛物线的简单几何性质图形焦点位置 x 轴的正半轴上 x 轴的负半轴上 y 轴的正半轴上y 轴的负半轴上标准方程 22(0)y px p =>22(0)y px p =->22(0)x py p =>22(0)x py p =->范围 0,x y R ≥∈0,x y R ≤∈,0x R y ∈≥,0x R y ∈≤对称性 关于x 轴对称关于x 轴对称关于y 轴对称关于y 轴对称顶点 (0,0)(0,0)(0,0)(0,0)离心率 1e =1e =1e =1e =(五)作业布置,精炼双基1. 完成课本138P 习题3.3 5、6、9、10、11、12、132. 阅读140P 《圆锥曲线的光学性质及其应用》3. 阅读143P 《小结》4. 完成 复习参考题3五、教学反思:(课后补充,教学相长)。
抛物线-高考数学复习

视角3 与抛物线有关的最值问题
2-3 (2023·十堰二模)已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C的准线与
坐标轴相交于点P,点M(3,2),且△MFP的面积为2,若Q是抛物线C上一点,则
△FMQ周长Biblioteka 最小值为( B)A.4+ 2
B.4+2 2
C.4+ 10
D.4+2 10
【解析】由题可知,△MFP 的面积为12×p×2=2,则 p=2,故 F(1,0),准线 l 的方 程为 x=-1,|MF|= (3-1)2+22=2 2. 如图,点 Q 到准线距离为|QQ′|.因为△FMQ 的周长为|MF|+|QM|+|QF|=
过F的直线交C于A,B两点,线段AB的中点D在x轴上方且其横坐标为1,|AB|=3, 则直线AB的斜率为____2__.
【解析】 设A(x1,y1),B(x2,y2),D(1,m)(m>0),则x1+x2=2.又|AB|=x1+x2+p=
3,所以p=1,所以C:y2=2x. 由题意知直线 AB 的斜率存在,故可设直线
研题型 能力养成 举题说法
1 (2) (2023·石家庄期末)已知抛物线 C:y2=2x 的焦点为 F,准线为 l,点 P 在 C
上,过点 P 作准线 l 的垂线,垂足为 A,若∠FPA=π3,则|PF|=
( D)
A.1
B. 2
C. 3
D.2
【解析】因为|PF|=|PA|,∠FPA=π3,所以∠PAF=∠PFA=π3.如图, 设准线 l 与 x 轴交于点 Q. 因为 PA∥QF,所以∠AFQ=∠PAF=π3.因为|QF|=p=1,所以|AF| =2,所以在等边三角形 PAF 中,|PF|=2.
5
链教材 夯基固本 激活思维
抛物线的几个常见结论及其用

抛物线的几个常见结论及其应用抛物线中有一些常见、常用的结论,了解这些结论后在做选择题、填空题时可迅速解答相关问题,在做解答题时也可迅速打开思路。
结论一:若AB 是抛物线22(0)y px p =>的焦点弦(过焦点的弦),且11(,)A x y ,22(,)B x y ,则:2124p x x =,212y y p =-。
例:已知直线AB 是过抛物线22(0)y px p =>焦点F , 求证:11AF BF+为定值。
结论二:(1)若AB 是抛物线22(0)y px p =>的焦点弦,且直线AB 的倾斜角为α,则22sin PAB α=(α≠0)。
(2)焦点弦中通径(过焦点且垂直于抛物线对称轴的弦)最短。
例:已知过抛物线29y x =的焦点的弦AB 长为12,则直线AB 倾斜角为 。
AB 倾斜角为3π或23π。
结论三:两个相切:(1)以抛物线焦点弦为直径的圆与准线相切。
(2)过抛物线焦点弦的两端点向准线作垂线, 以两垂足为直径端点的圆与焦点弦相切。
例:已知AB 是抛物线22(0)y px p =>的过焦点F 的弦,求证:(1)以AB 为直径的圆与抛物线的准线相切。
(2)分别过A 、B 做准线的垂线,垂足为M 、N ,求证:以MN 为直径的圆 与直线AB 相切。
结论四:若抛物线方程为22(0)y px p =>,过(2p ,0)的直线与之交于A 、B 两点,则OA ⊥OB 。
反之也成立。
结论五:对于抛物线22(0)x py p =>,其参数方程为222x pt y pt =⎧⎨=⎩,,设抛物线22x py =上动点P 坐标为2(22)pt pt ,,O 为抛物线的顶点,显然222OP pt k t pt==,即t 的几何意义为过抛物线顶点O 的动弦OP 的斜率.例 直线2y x =与抛物线22(0)y px p =>相交于原点和A 点,B 为抛物线上一点,OB 和OA 垂直,且线段AB长为,求P 的值.解析:设点A B ,分别为22(22)(22)A A B B pt pt pt pt ,,,, 则112A OA t k ==,12B OA OBt k k ==-=-. A B ,的坐标分别为(84)2p p p p ⎛⎫- ⎪⎝⎭,,,.AB∴=.2p =∴. 练习:1.过抛物线2(0)y ax a =>的焦点F 作一直线交抛物线于P Q ,两点, 若线段PF 与FQ 的长分别是p q ,,则11pq+= 故114a pq+=】2.设抛物线22(0)y px p =>的焦点为F ,经过点F 的直线交抛物线 于A B ,两点.点C 在抛物线的准线上,且BC x ∥轴. 证明直线AC 经过原点O .【证明:抛物线焦点为02p F ⎛⎫ ⎪⎝⎭,.设直线AB 的方程为2px my =+, 代入抛物线方程,得2220y pmy p --=.若设1122()()A x y B x y ,,,, 则212y y p =-.BC x ∵∥轴,且点C 在准线12CO pk y =; 又由2112y px =,得1112AO y p k x y ==, 故CO AO k k =,即直线AC 经过原点O .】3.已知抛物线的焦点是(11)F ,,准线方程是20x y ++=,求抛物线的方程以及顶点坐标和对称轴方程.【解:设()P x y ,是抛物线上的任意一点,由抛物线的定义得=.整理,得222880x y xy x y +---=,此即为所求抛物线的方程.抛物线的对称轴应是过焦点(11)F ,且与准线20x y ++=垂直的直线,因此有对称轴方程y x =.设对称轴与准线的交点为M ,可求得(11)M --,,于是线段MF 的中点就是抛物线的顶点,坐标是(00),】1.抛物线的顶点坐标是(10)A ,,准线l 的方程是220x y --=,试求该抛物线的焦点坐标和方程.解:依题意,抛物线的对称轴方程为220x y +-=.设对称轴和准线的交点是M ,可以求得6255M ⎛⎫- ⎪⎝⎭,.设焦点为F ,则FM 的中点是A ,故得焦点坐标为4255F ⎛⎫ ⎪⎝⎭,. 再设()P x y ,是抛物线上的任一点,根据22444120x y xy x y ++--=,即为所求抛物线的方程.例2 已知A B ,为抛物线24x y =上两点,且OA OB ⊥,求线段AB 中点的轨迹方程.。
描写老树出新芽的句子唯美(精选2篇)

描写老树出新芽的句子唯美(篇一)1. 在岁月的刻痕中,老树坚守着自己的根基,从细枝末节绽放出崭新的生机。
2. 宛如神奇的魔法般,老树凭借着顽强的生命力,不断向阳光伸展,催生出一片片焕然一新的新芽。
3. 即便四季变迁,岁月更替,老树对生命的渴望从未改变,它用新芽诉说着生命的延续。
4. 经历岁月的雕琢,老树的树干如同一部厚重的历史巨著,而新芽则是其中崭新的篇章。
5. 虽然岁月留下了白发,老树却依然用新芽为自己的生命故事增添了一抹鲜艳的色彩。
6. 当春风拂面,老树顽强地伸展出新的枝条,仿佛在歌颂生命的美好。
7. 老树的新芽是自然界对生命力的最美赞歌,展现着永恒不灭的希望。
8. 老树虽已经历过风雨,然而,新芽的绽放让它重获新生,在岁月的长河中不断书写新的篇章。
9. 即使老树枯黄萧条,新芽却仍在默默绽放,向世界传递着生命的坚毅。
10. 老树的新芽如同一位美丽的舞者,跳动着欢快的节拍,唤醒大地的生机。
11. 就像春天拂面的微风,老树的新芽带来了温暖和希望。
12. 在繁忙的都市之中,老树的新芽仿佛是大地恢复自然的弥漫香气。
13. 纵使岁月已经残酷地浸染了老树的枝干,新芽却仍旧守望着生命的初衷。
14. 老树凭借顽强的生命意志,不断向天空的蓝递交新芽的盛开。
15. 无论风吹雨打,老树的新芽始终带着温柔的勃发,展示着生命的纯真与美丽。
16. 在老树的枝条间,新芽犹如一串串琥珀,为大地增添了生机与活力。
17. 老树的新芽仿佛是对上苍深情的告白,表达着自己不屈的生命态度。
18. 老树虽已见过太多的世面,新芽却总能为它带来新的惊喜和感动。
19. 大自然给予老树新芽的馈赠,仿佛是对它坚韧不拔的崇敬。
20. 老树的新芽如同一颗颗希望的种子,细细吮吸着生命的阳光和露水。
21. 即使风霜雨雪摧残了老树,新芽依旧奋力生长,为它展现新的生命力。
22. 老树宛如一位智者,新芽则是他智慧的结晶,点亮了懂得感悟生命的人们。
23. 老树的新芽带给人们希望的眷顾,为他们的心灵撒播了温暖的种子。
高中数学选修一第2章 2.7.2 抛物线的几何性质人教B版讲义
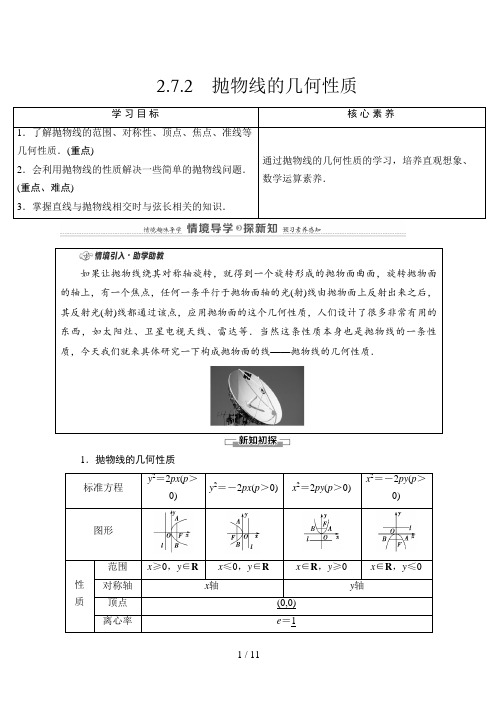
2.7.2 抛物线的几何性质学习目标核心素养1.了解抛物线的范围、对称性、顶点、焦点、准线等几何性质.(重点)2.会利用抛物线的性质解决一些简单的抛物线问题.(重点、难点)3.掌握直线与抛物线相交时与弦长相关的知识.通过抛物线的几何性质的学习,培养直观想象、数学运算素养.如果让抛物线绕其对称轴旋转,就得到一个旋转形成的抛物面曲面,旋转抛物面的轴上,有一个焦点,任何一条平行于抛物面轴的光(射)线由抛物面上反射出来之后,其反射光(射)线都通过该点,应用抛物面的这个几何性质,人们设计了很多非常有用的东西,如太阳灶、卫星电视天线、雷达等.当然这条性质本身也是抛物线的一条性质,今天我们就来具体研究一下构成抛物面的线——抛物线的几何性质.1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0) x2=2py(p>0)x2=-2py(p>0)图形性质范围x≥0,y∈R x≤0,y∈R x∈R,y≥0 x∈R,y≤0 对称轴x轴y轴顶点(0,0)离心率e=1思考1:抛物线x2=2py(p>0)有几条对称轴?[提示]有一条对称轴.思考2:抛物线的范围是x∈R,这种说法正确吗?[提示]抛物线的方程不同,其范围就不一样,如y2=2px(p>0)的范围是x≥0,y∈R,故此说法错误.思考3:参数p对抛物线开口大小有何影响?[提示]参数p(p>0)对抛物线开口大小有影响,因为过抛物线的焦点F且垂直于对称轴的弦的长度是2p,所以p越大,开口越大.2.焦点弦设过抛物线焦点的弦的端点为A(x1,y1),B(x2,y2),则y2=2px(p>0)|AB|=x1+x2+py2=-2px(p>0)|AB|=p-(x1+x2)x2=2py(p>0)|AB|=y1+y2+px2=-2py(p>0)|AB|=p-(y1+y2)1.思考辨析(正确的打“√”,错误的打“×”)(1)抛物线是中心对称图形.( )(2)抛物线的范围为x∈R.( )(3)抛物线关于顶点对称.( )(4)抛物线的标准方程虽然各不相同,但离心率都相同.( )[答案](1)×(2)×(3)×(4)√[提示](1)×在抛物线中,以-x代x,-y代y,方程发生了变化.(2)×抛物线的方程不同,其范围不同,y2=2px(p>0)中x≥0,y∈R.(3)×(4)√离心率都为1,正确.2.设抛物线y2=8x上一点P到y轴的距离是6,则点P到该抛物线焦点F的距离是( )A .8B .6C .4D .2 A [∵抛物线的方程为y 2=8x , ∴其准线l 的方程为x =-2, 设点P (x 0,y 0)到其准线的距离为d , 则d =|PF |,即|PF |=d =x 0-(-2)=x 0+2, ∵点P 到y 轴的距离是6, ∴x 0=6, ∴|PF |=6+2=8.]3.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2),若x 1+x 2=6,则|AB |= .8 [∵y 2=4x ,∴2p =4,p =2.∵由抛物线定义知:|AF |=x 1+1,|BF |=x 2+1, ∴|AB |=x 1+x 2+p =6+2=8.]4.顶点在原点,对称轴是x 轴,并且顶点与焦点的距离等于6的抛物线方程是 .y 2=24x 或y 2=-24x [∵顶点与焦点距离为6,即p2=6,∴2p =24,又对称轴为x轴,∴抛物线方程为y 2=24x 或y 2=-24x .]由抛物线的几何性质求标准方程【】(1)平面直角坐标系xOy 中,有一定点A (2,1),若线段OA 的垂直平分线过抛物线y 2=2px (p >0)的焦点,则该抛物线的标准方程是 .(2)抛物线的顶点在原点,对称轴重合于椭圆9x 2+4y 2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.(1)y 2=5x [线段OA 的垂直平分线为4x +2y -5=0,与x 轴的交点为⎝ ⎛⎭⎪⎫54,0,∴抛物线的焦点为⎝ ⎛⎭⎪⎫54,0,∴其标准方程是y 2=5x .](2)解:椭圆的方程可化为x24+y29=1,其短轴在x 轴上,∴抛物线的对称轴为x 轴,∴设抛物线的方程为y 2=2px 或y 2=-2px (p >0). ∵抛物线的焦点到顶点的距离为3, 即p2=3,∴p =6, ∴抛物线的标准方程为y 2=12x 或y 2=-12x , 其准线方程分别为x =-3和x =3.用待定系数法求抛物线方程的步骤提醒:求抛物线的方程时要注意抛物线的焦点位置.不同的焦点设出不同的方程.[跟进训练]1.已知抛物线关于x 轴对称,它的顶点在坐标原点,其上一点P 到准线及对称轴距离分别为10和6,求抛物线方程.[解] 设抛物线方程为y 2=2ax (a ≠0),点P (x 0,y 0). 因为点P 到对称轴距离为6,所以y 0=±6, 因为点P 到准线距离为10,所以⎪⎪⎪⎪⎪⎪x0+a 2=10.① 因为点P 在抛物线上,所以36=2ax 0.②由①②,得⎩⎨⎧a =2,x0=9或⎩⎨⎧a =18,x0=1或⎩⎨⎧a =-18,x0=-1或⎩⎨⎧a =-2,x0=-9.所以所求抛物线方程为y 2=±4x 或y 2=±36x .抛物线性质的应用【例2】(1)抛物线y 2=4x 的焦点为F ,准线为l ,点A 是抛物线上一点,且∠AFO =120°(O 为坐标原点),AK ⊥l ,垂足为K ,则△AKF 的面积是 .(2)已知正三角形AOB 的一个顶点O 位于坐标原点,另外两个顶点A ,B 在抛物线y 2=2px (p >0)上,求这个三角形的边长.(1)43 [如图,设A (x 0,y 0),过A 作AH ⊥x 轴于H , 在Rt △AFH 中,|FH |=x 0-1, 由∠AFO =120°,得∠AFH =60°, 故y 0=|AH |=3(x 0-1), 所以A 点的坐标为错误!,将点A 坐标代入抛物线方程可得3x 20-10x 0+3=0, 解得x 0=3或x 0=13(舍),故S △AKF =12×(3+1)×23=43.](2)解:如图所示,设正三角形OAB 的顶点A ,B 在抛物线上,且坐标分别为A (x 1,y 1),B (x 2,y 2),则y 21=2px 1,y 2=2px 2.又|OA |=|OB |,所以x 21+y 21=x 2+y 2, 即x 21-x 2+2px 1-2px 2=0, 整理得(x 1-x 2)(x 1+x 2+2p )=0. ∵x 1>0,x 2>0,2p >0, ∴x 1=x 2,由此可得|y 1|=|y 2|, 即线段AB 关于x 轴对称. 由此得∠AOx =30°, 所以y 1=33x 1,与y 21=2px 1联立, 解得y 1=23p .∴|AB |=2y 1=43p .利用抛物线的性质可以解决的问题(1)对称性:解决抛物线的内接三角形问题. (2)焦点、准线:解决与抛物线的定义有关的问题. (3)范围:解决与抛物线有关的最值问题. (4)焦点:解决焦点弦问题.提醒:解答本题时易忽略A ,B 关于x 轴对称而出错.[跟进训练] 2.已知双曲线x2a2-y2b2=1(a >0,b >0)的两条渐近线与抛物线y 2=2px (p >0)的准线分别交于A 、B 两点,O 为坐标原点,若双曲线的离心率为2,△AOB 的面积为3,求抛物线的标准方程.[解] 由已知得c a =2,所以a2+b2a2=4,解得ba=3.即渐近线方程为y =±3x ,而抛物线准线方程为x =-p 2,于是A ⎝ ⎛⎭⎪⎫-p 2,-32p ,B ⎝ ⎛⎭⎪⎫-p 2,32p ,从而△AOB 的面积为12·3p ·p 2=3.可得p =2,因此抛物线开口向右,所以标准方程为y 2=4x .焦点弦问题[探究问题]以抛物线y 2=2px (p >0)为例,回答下列问题: (1)过焦点F 的弦长|AB |如何表示?还能得到哪些结论? [提示] ①|AB |=2⎝ ⎛⎭⎪⎫x0+p 2(焦点弦长与中点关系).②|AB |=x 1+x 2+p =2psin2θ(θ为AB 的倾斜角).③A ,B 两点的横坐标之积、纵坐标之积为定值,即x 1·x 2=p24,y 1·y 2=-p 2.④S △AOB =p22sin θ.⑤1|AF|+1|BF|=2p(定值). (2)以AB 为直径的圆与直线l 具有怎样的位置关系?[提示] 如图,AB 是过抛物线y 2=2px (p >0)焦点F 的一条弦,设A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),相应的准线为l .所以以AB 为直径的圆必与准线l 相切. (3)解决焦点弦问题需注意什么?[提示] 要注意抛物线定义在其中的应用,通过定义将焦点弦长度转化为端点的坐标问题,从而可借助根与系数的关系进行求解.【例3】已知抛物线方程为y 2=2px (p >0),过此抛物线的焦点的直线与抛物线交于A ,B 两点,且|AB |=52p ,求AB 所在直线的方程.[思路探究] 根据弦长求出直线斜率,进而求得直线方程. [解] ∵过焦点的弦长|AB |=52p ,∴弦所在的直线的斜率存在且不为零,设直线AB 的斜率为k ,且A (x 1,y 1),B (x 2,y 2). ∵y 2=2px 的焦点为F ⎝ ⎛⎭⎪⎫p 2,0.∴直线方程为y =k ⎝ ⎛⎭⎪⎫x -p 2.由⎩⎨⎧y =k ⎝ ⎛⎭⎪⎫x -p 2,y2=2px ,整理得k 2x 2-(k 2p +2p )x +14k 2p 2=0(k ≠0),∴x 1+x 2=k2p +2pk2,∴|AB |=x 1+x 2+p =k2p +2pk2+p , 又|AB |=52p ,∴k2p +2p k2+p =52p ,∴k =±2.∴所求直线方程为y =2⎝ ⎛⎭⎪⎫x -p 2或y =-2⎝⎛⎭⎪⎫x -p 2.1.(改变问法)本例条件不变,求弦AB 的中点M 到y 轴的距离. [解] 设AB 中点为M (x 0,y 0), 由例题解答可知2x 0=x 1+x 2=32p ,所以AB 的中点M 到y 轴的距离为34p .2.(变换条件)本例中,若A 、B 在其准线上的射影分别为A 1,B 1,求∠A 1FB 1. [解] 由例题解析可知AB 的方程为y =k ⎝⎛⎭⎪⎫x -p 2,即x =1k y +p2,代入y 2=2px 消x 可得y 2=2p k y +p 2,即y 2-2pky -p 2=0,∴y 1y 2=-p 2, 由A 1点的坐标为⎝ ⎛⎭⎪⎫-p 2,y1,B 1点的坐标为⎝ ⎛⎭⎪⎫-p 2,y2,得kA 1F =-y1p ,kB 1F =-y2p. ∴kA 1F ·kB 1F =y1y2p2=-1, ∴∠A 1FB 1=90°.解决过焦点的直线与抛物线相交有关的问题时,一是注意直线方程和抛物线方程联立得方程组,再结合根与系数的关系解题,二是注意焦点弦长、焦半径公式的应用.解题时注意整体代入思想的运用,简化运算.1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.2.解决抛物线的轨迹问题,可以利用抛物线的标准方程,结合抛物线的定义. 3.抛物线y 2=±2px (p >0)的过焦点的弦长|AB |=x 1+x 2+p ,其中x 1,x 2分别是点A ,B 横坐标的绝对值;抛物线x 2=±2py (p >0)的过焦点的弦长|AB |=y 1+y 2+p ,其中y 1,y 2分别是点A ,B 纵坐标的绝对值.4.求抛物线的方程常用待定系数法和定义法;直线和抛物线的弦长问题、中点弦问题及垂直、对称等可利用判别式、根与系数的关系解决;抛物线的综合问题要深刻分析条件和结论,灵活选择解题策略,对题目进行转化.1.若抛物线y 2=2x 上有两点A 、B 且AB 垂直于x 轴,若|AB |=22,则抛物线的焦点到直线AB 的距离为( )A .12B .14C .16D .18A [线段AB 所在的直线方程为x =1,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫12,0,则焦点到直线AB 的距离为1-12=12.]2.在抛物线y 2=16x 上到顶点与到焦点距离相等的点的坐标为( ) A .(42,±2) B .(±42,2) C .(±2,42)D .(2,±42)D [抛物线y 2=16x 的顶点O (0,0),焦点F (4,0),设P (x ,y )符合题意,则有错误!⇒错误!⇒错误!所以符合题意的点为(2,±42).]3.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 是抛物线上一点,若OA →·AF→=-4,则点A 的坐标是( )A .(2,±22)B .(1,±2)C .(1,2)D .(2,22)B [由题意知F (1,0),设A ⎝ ⎛⎭⎪⎫y204,y0,则OA →=⎝ ⎛⎭⎪⎫y204,y0,AF →=⎝ ⎛⎭⎪⎫1-y204,-y0,由OA →·AF →=-4得y 0=±2,∴点A 的坐标为(1,±2),故选B .]4.已知AB 是过抛物线2x 2=y 的焦点的弦,若|AB |=4,则AB 的中点的纵坐标是 .158[设A (x 1,y 1),B (x 2,y 2),11 / 11 由抛物线2x 2=y ,可得p =14. ∵|AB |=y 1+y 2+p =4,∴y 1+y 2=4-14=154,故AB 的中点的纵坐标是y1+y22=158.] 5.已知点P (1,m )是抛物线C :y 2=2px 上的点,F 为抛物线的焦点,且|PF |=2,直线l :y =k (x -1)与抛物线C 相交于不同的两点A ,B .(1)求抛物线C 的方程;(2)若|AB |=8,求k 的值.[解] (1)抛物线C :y 2=2px 的准线为x =-p 2, 由|PF |=2得:1+p 2=2,得p =2. 所以抛物线的方程为y 2=4x .(2)设A (x 1,y 1),B (x 2,y 2),由错误!可得k 2x 2-(2k 2+4)x +k 2=0,Δ=16k 2+16>0,∴x 1+x 2=2k2+4k2. ∵直线l 经过抛物线C 的焦点F ,∴|AB |=x 1+x 2+p =2k2+4k2+2=8, 解得k =±1,所以k 的值为1或-1.。
苏教版 高中数学选择性必修第一册 抛物线的几何性质 课件1

而|AB|=|AF|+|BF|=x1+ p +x2+ p =x1+x2+p,所以|AB|=5+3=8.
2
2
(2)设A(x1,y1),B(x2,y2),
由抛物线定义知|AB|=|AF|+|BF|=x1+x2+p=x1+x2+3,
所以x1+x2=6,于是线段AB的中点M的横坐标是3.
又准线方程是x=- 3 ,所以点M到准线的距离为3+ 3 = 9 .
焦点弦 如图,线段AB是抛物线y2=2px(p>0)过焦点F的一条弦,称为焦点 弦.设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0). 过A,M,B分别向抛物线的准线作垂线,垂足分别为A1,M1,B1,则 根据抛物线的定义有|AF|=|AA1|,|BF|=|BB1|, 故|AB|=|AF|+|BF|=|AA1|+|BB1|. 因为MM1是梯形AA1B1B的中位线, 所以|AB|=|AA1|+|BB1|=2|MM1|.
故设 A(3,m),代入 y2=8x 得 m2=24;所以 m=2 6或 m=-2 6,
所以 A(3,2 6),B(3,-2 6),所以|OA|=|OB|= 33,
所以△OAB 的周长为 2 33+4 6.
总结
把握三个要点确定抛物线的简单几何性质 (1)开口:由抛物线标准方程看图象开口,关键是看准二次项 是 x 还是 y,一次项的系数是正还是负. (2)关系:顶点位于焦点与准线中间,准线垂直于对称轴. (3)定值:焦点到准线的距离为 p;过焦点垂直于对称轴的弦(又 称为通径)长为 2p;离心率恒等于 1.
离心率
抛物线上的点到焦点的距离与到准线的距离之比称为抛物线的 离心率,用e表示. 根据抛物线的定义可知,抛物线的离心率e=1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
124=3. 212y y p =-;
4. '90AC B ∠=;
5. ''90A FB ∠=;
6. 123222()2sin p
p
AB x x p x α=++=+=;
7. 112
AF BF P +=;
8. A 、O 、'B 三点共线;
9. B 、O 、'A 三点共线;
10. 2
2sin AOB P S α=;
11. 23()2AOB
S P
AB =(定值);
12. 1cos P
AF α=-;1cos P BF α=+;
13. 'BC 垂直平分'B F ;
14. 'AC 垂直平分'A F ;
15. 'C F AB ⊥;
16. 2AB P ≥;
17. 1
1
'('')22CC AB AA BB ==+;
18. AB 3
P K =
y ; 19. 2
p 22y tan =x -α; 20. 2A'B'4AF BF =⋅;
21. 1C'F A'B'2
=. 22. 切线方程 ()x x m y y +=00
性质深究
一)焦点弦与切线
1、 过抛物线焦点弦的两端点作抛物线的切线,两切线交点位置有
何特殊之处?
结论1:交点在准线上
先猜后证:当弦x AB ⊥轴时,则点P 的坐标为⎪⎭
⎫ ⎝⎛
-0,2p 在准线上. 证明: 从略
结论2 切线交点与弦中点连线平行于对称轴
结论3 弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.
2、上述命题的逆命题是否成立?
结论4 过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点
先猜后证:过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点.
结论5过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.
3、AB 是抛物线px y 22
=(p >0)焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B 的切线相交于P ,PQ 与抛物线交于点M .则有
结论6P A ⊥PB .
结论7PF ⊥AB .
结论8 M 平分PQ .
结论9 P A 平分∠A
1AB
,PB 平分∠B 1BA .
结论2=
结论11PAB
S ∆2min p =
二)非焦点弦与切线
思考:当弦AB 不过焦点,切线交于P 点时,
也有与上述结论类似结果:
结论12 ①p y y x p 221=,2
21y y y p += 结论13 P A 平分∠A 1AB ,同理PB 平分∠B 1BA .
结论14 PFB PFA ∠=∠
结论15 点M 平分PQ
结论16 2
PF =
相关考题
1、已知抛物线y x 42=的焦点为F ,A ,B 是抛物线上的两动点,且FB AF λ=(λ>0),过A ,B 两点分别作抛物线的切线,设其交点为M ,
(1)证明:AB FM ⋅的值;
(2)设ABM ∆的面积为S ,写出()λf S =的表达式,并求S 的最小值.
2、已知抛物线C 的方程为y x 42=,焦点为F ,准线为l ,直线m 交抛物线于两点A ,B ;
(1)过点A 的抛物线C 的切线与y 轴交于点D ,求证:DF AF =;
(2)若直线m 过焦点F ,分别过点A ,B 的两条切线相交于点M ,求证:AM ⊥BM ,且点M 在直线l 上.
3、对每个正整数n ,()n n n y x A ,是抛物线y x 42=上的点,过焦点F 的直线F A n 交抛物线于另一点()n n n t s B ,, (1)试证:4-=⋅n n s x (n ≥1)
(2)取n n x 2=,并C n 为抛物线上分别以A n 与B n 为切点的两条切线的交点,求证:
122121+-=++++-n n n FC FC FC (n ≥1)。
