用拉伸法测钢丝杨氏模量——实验报告
用拉伸法测钢丝杨氏模量――实验报告

用拉伸法测钢丝杨氏模量――实验报告本实验使用拉伸法测定钢丝的杨氏模量。
实验过程包括测量原始尺寸和断裂强度,计算应力和应变,绘制应力-应变曲线,利用斜率计算杨氏模量。
一、实验原理1.杨氏模量:杨氏模量也称弹性模量,是研究力学学科中的一项重要物理量,它描述了物体在受力时,单位应力下的应变程度。
可以表示为弹性模量E,其计算公式为E=σ/ε,其中σ为应力,ε为单位应变。
2.拉伸法:拉伸法是测定材料弹性性质的常用方法之一。
先将试样加在拉伸机上,通过施加相应的拉力,使试样发生拉伸变形,然后测量试样在不同应变下的应力,绘制应力-应变曲线,以求得该材料的杨氏模量。
二、实验步骤1.准备实验设备,将钢丝放在拉伸机上。
2.用卡尺测量钢丝的初始长度、直径和断裂长度,记录数据。
3.用拉伸机分别在不同的拉力下进行拉伸,记录拉力和试样的应变。
4.计算每个密度下的应力,应力=拉力/试样横截面积。
5.计算每个密度下的应变,应变=延长长度/原始长度。
6.根据应力-应变曲线,计算杨氏模量。
三、实验数据试样长度:5m原始直径:2.5mm断裂长度:8m钢丝密度:7.85g/cm³拉伸试验数据如下:|拉力F(N)|延长长度L(mm)|试样直径D(mm)||:-:|:-:|:-:||0|0|2.5||50|2|2.5||100|4|2.6||150|6|2.7||200|8|2.8||250|10|2.9||300|12|3.0||350|14|3.1||400|16|3.2||450|18|3.3||500|20|3.4||550|22|3.5||600|24|3.6||650|26|3.7||700|28|3.8||750|30|3.9||800|32|4.0|四、实验计算1.计算实验数据中的横截面积试样横截面积=π*(D/2)²=π*(2.5/2)²=4.91mm² 2.计算每个密度下的应力应力=F/S=700/4.91=142.6N/mm²应变=L/L0=28/5000=0.00564.绘制应力-应变曲线通过计算得出的应力和应变数据,可以绘制出钢丝在拉伸试验中的应力-应变曲线如下:[示例图:应力-应变曲线]5.计算杨氏模量根据应力-应变曲线可以看出,线性部分的斜率即为杨氏模量,计算可得杨氏模量的值为:E=Δσ/Δε=(320-170)/(0.004-0.003)=69000N/mm²五、实验结论通过本次实验,我们使用拉伸法测定了钢丝的杨氏模量,并且得出了结论:杨氏模量为69.0×10⁹N/mm²。
测钢丝的杨氏模量(实验篇)

测钢丝的杨氏模量实验简介材料受力后发生形变。
在弹性限度内,材料的胁强与胁变(即相对形变)之比为一常数,叫弹性模量。
条形物体(如钢丝)沿纵向的弹性模量叫杨氏模量。
测量杨氏模量有拉伸法、梁的弯曲法、振动法、内耗法等等,本实验采用拉伸法测杨氏模量。
实验原理任何物体(或材料)在外力作用下都会发生形变。
当形变不超过某一限度时,撤走外力则形变随之消失,为一可逆过程,这种形变称为弹性形变,这一极限称为弹性极限。
超过弹性极限,就会产生永久形变(亦称塑性形变),即撤除外力后形变仍然存在,为不可逆过程。
人们在研究材料的弹性性质时,希望有这样一些物理量,它们与试样的尺寸、形状和外加的力无关。
于是提出了应力F/S(即力与力所作用的面积之比)和应变△L/L(即长度或尺寸的变化与原来的长度或尺寸之比)之比的概念。
在胡克定律成立的范围内,应力和应变之比是一个常数,即E=(F/S)/(△L/L)=FL/S△L (1)E被称为材料的杨氏模量,它是表征材料性质的一个物理量,仅与材料的结构、化学成分及其加工制造方法有关。
某种材料发生一定应变所需要的力大,该材料的杨氏模量也就大。
杨氏模量的大小标志了材料的刚性。
通过式E=(F/S)/(△L/L)=FL/S△L 在样品截面积S上的作用应力为F,测量引起的相对伸长量△L/L,即可计算出材料的杨氏模量E。
因一般伸长量△L很小,故常采用光学放大法,将其放大,如用光杠杆测量△L。
光杠杆是一个带有可旋转的平面镜的支架,平面镜的镜面与三个足尖决定的平面垂直,其后足即杠杆的支脚与被测物接触,如图5.3.1-1。
当杠杆支脚随被测物上升或下降微小距离△L时,镜面法线转过一个角,而入射到望远镜的光线转过角,如图5.3.1-2所示,当很小时,(2)式中为支脚尖到刀口的垂直距离(也叫光杠杆的臂长),根据光的反射定律,反射角和入射角相等,故当镜面转动角时,反射光线转动角,由图可知(3)式中为镜面到标尺的距离,为从望远镜中观察到的标尺移动的距离。
用拉伸法测量钢丝的杨氏模量

用拉伸法测量钢丝的杨氏模量段心蕊 PB05000826 九号台一 实验目的:掌握利用光杠杆测定微小形变的方法,在数据处理中,采用逐差法和作图法得出测量结果,掌握这两种数据处理的方法。
二 实验原理:(1)在弹性限度内,材料的应力与应变之比为一常数,叫弹性模量。
条形物体沿纵向的弹性模量叫杨氏模量,用E 来表示,则L S FL L L S F E ∆=∆=/)//()/(杨氏模量是表征材料性质的一个物理量,仅与材料的结构、化学成分及其加工制造方法有关。
杨氏模量的大小标志了材料的刚性。
(2)由于一般伸长量ΔL 很小,故常采用光学放大法,将其放大,如用光杠杆测量ΔL 。
当杠杆支脚随被测物上升或下降微小距离ΔL 时,镜面法线转过一个θ角,而入射到望远镜的光线转过2θ角。
当θ很小时,D blL D b l L 2/2tan /tan =∆⇒⎭⎬⎫≈=∆=≈θθθ 其中l 为支脚尖到刀口的垂直距离(也叫光杠杆的臂长),D 为镜面到标尺的距离,b 为从望远镜中观察到的标尺移懂得距离。
从而得到 ()4/22d SSlbDLFE π==三实验仪器:光杠杆、砝码、望远镜、标尺、螺旋测微器、卷尺。
四实验内容:1调节仪器(1)调节放置光杠杆的平台与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线大体重合。
(2)调节支架底脚螺丝,确保平台水平,调平台的上下位置,使管制器顶部与平台的上表面共面。
(3)光杠杆的调节,光杠杆和镜尺组是测量金属丝伸长量ΔL的关键部件。
光杠杆的镜面和刀口应平行。
使用时刀口放在平台的槽内,支脚放在管制器的槽内,刀口和支脚尖应共面。
(4)镜尺组的调节,调节望远镜、直尺和光杠杆三者之间的相对位置,使望远镜和反射镜处于同等高度,调节望远镜目镜视度圈,使目镜内分划板刻线(叉丝)清晰,用手轮调焦,使标尺像清晰。
2测量(1)砝码托的质量为m0,记录望远镜中标尺的读数r0作为钢丝的起始长度。
(2)在砝码托上逐次加500g砝码(可加到3500g),观察每增加500g时望远镜中标尺上的读数r i,然后再将砝码逐次减去,记下对应的读数,r i’取两组对应数据的平均值r。
钢丝杨氏模量的测定实验报告

钢丝杨氏模量的测定实验报告篇一:用拉伸法测钢丝杨氏模量——实验报告用拉伸法测钢丝杨氏模量——实验报告杨氏弹性模量测定仪;光杠杆;望远镜及直尺;千分尺;游标卡尺;米尺;待测钢丝;砝码等。
【实验原理】1.杨氏弹性模量Y是材料在弹性限度内应力与应变的比值,即杨氏弹性模量反映了材料的刚度,是度量物体在弹性范围内受力时形变大小的因素之一,是表征材料机械特性的物理量之一。
2.光杠杆原理伸长量Δl比较小,不易测准,本实验利用了光杠杆的放大原理对Δl进行测量。
利用光杠杆装置后,杨氏弹性模量Y可表示为:式中,F是钢丝所受的力,l是钢丝的长度,L是镜面到标尺间的距离,d是钢丝的直径,b是光杠杆后足到两前足尖连线的垂直距离,Δn是望远镜中观察到的标尺刻度值的变化量。
3. 隔项逐差法隔项逐差法为了保持多次测量优越性而采用的数据处理方法。
使每个测量数据在平均值内都起到作用。
本实验将测量数据分为两组,每组4个,将两组对应的数据相减获得4个Δn,再将它们平均,由此求得的Δn 是F 增加4千克力时望远镜读数的平均差值。
【实验步骤】1.调整好杨氏模量测量仪,将光杠杆后足尖放在夹紧钢丝的夹具的小圆平台上,以确保钢丝因受力伸长时,光杠杆平面镜倾斜。
2.调整望远镜。
调节目镜,使叉丝位于目镜的焦平面上,此时能看到清晰的叉丝像;调整望远镜上下、左右、前后及物镜焦距,直到在望远镜中能看到清晰的直尺像。
3.在钢丝下加两个砝码,以使钢丝拉直。
记下此时望远镜中观察到的直尺刻度值,此即为n0 值。
逐个加砝码,每加1个,记下相应的直尺刻度值,直到n7,此时钢丝下已悬挂9个砝码,再加1个砝码,但不记数据,然后去掉这个砝码,记下望远镜中直尺刻度值,此为n7’,逐个减砝码,每减1个,记下相应的直尺刻度值,直到n0’。
4. 用米尺测量平面镜到直尺的距离L;将光杠杆三足印在纸上,用游标卡尺测出b;用米尺测量钢丝长度l;用千分尺在钢丝的上、中、下三部位测量钢丝的直径d,每部位纵、横各测一次。
用拉伸法测钢丝杨氏模量实验报告
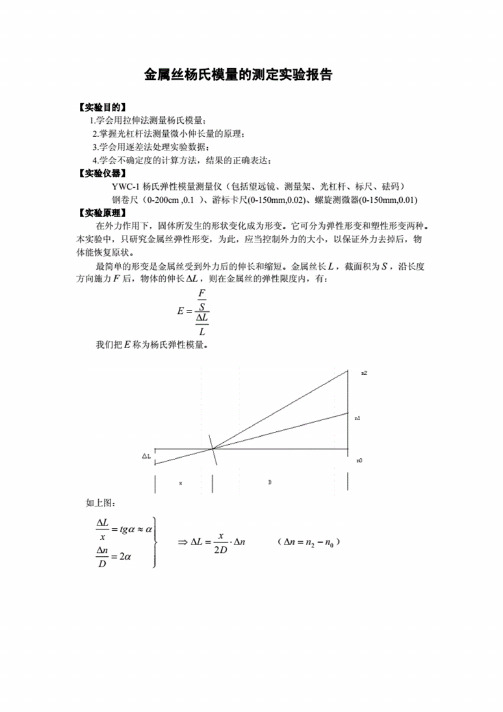
金属丝杨氏模量的测定实验报告【实验目的】1.学会用拉伸法测量杨氏模量:2.掌握光杠杆法测量微小伸长量的原理:3.学会用逐差法处理实验数据;4.学会不确定度的计算方法,结果的正确表达:【疝仪器】YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、破码)钢卷尺(0-200cm,0.1)、游标K•尺(0-150mm,0.02)、螺旋测微器(0-150mm,0.01)【实验原理】在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属统弹性形变,为此.应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属统受到外力后的伸长和缩短。
金属税长乙,截面积为S,沿长度方向施力F后,物体的伸长则在金属统的弹性限度内.有:FE=i~L我们把E称为杨氏弹性模量。
8FLD F 1 , — —m£ = _5_ = ^_ _ ,亶 X7^1 X •——---M L W _L真实测量时放大倍数为4倍,即E=2£[实验内容】<一>仪器调整1、 杨氏弹性模量测定仪底座调节水平:2、 平面镜镜面放置与测定仪平面垂直:3、 将望远镜放置在平面镜正前方1.5-2.0m 左右位置上:4、 粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像:5、 调节物镜焦距能看到尺子清晰的像.调节目镜焦距能清晰的看到叉统:6、 调节叉税在标尺±2"〃以内,并使得视差不超过半格。
〈二〉测量1、 记下无挂物时刻度尺的读数〃°:2、 依次挂上】00g 的虢码,8次,计下〃],〃2,〃3,〃4,〃5,〃6,〃7 :3、 依次取下 100g 的瑟码,8 次,计下 no 〃[ ,〃2 ,〃3 ,〃4,〃S ,〃6:4、 用米尺测量出金属税的长度L (两K •口之间的金属统)、镜面到尺子的距离。
大学物理实验 报告实验21 用拉伸法测杨氏模量
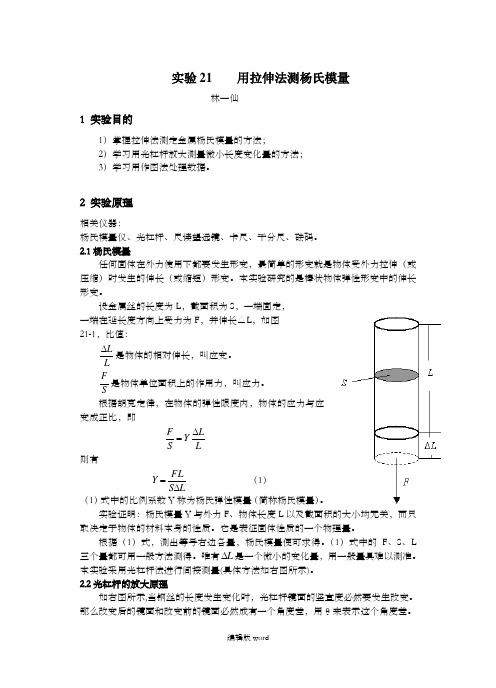
实验21 用拉伸法测杨氏模量林一仙1 实验目的1)掌握拉伸法测定金属杨氏模量的方法;2)学习用光杠杆放大测量微小长度变化量的方法; 3)学习用作图法处理数据。
2 实验原理相关仪器:杨氏模量仪、光杠杆、尺读望远镜、卡尺、千分尺、砝码。
2.1杨氏模量任何固体在外力使用下都要发生形变,最简单的形变就是物体受外力拉伸(或压缩)时发生的伸长(或缩短)形变。
本实验研究的是棒状物体弹性形变中的伸长形变。
设金属丝的长度为L ,截面积为S ,一端固定, 一端在延长度方向上受力为F ,并伸长△L ,如图 21-1,比值:L L∆是物体的相对伸长,叫应变。
SF是物体单位面积上的作用力,叫应力。
根据胡克定律,在物体的弹性限度内,物体的应力与应变成正比,即LLYS F ∆= 则有LS FLY ∆=(1) (1)式中的比例系数Y 称为杨氏弹性模量(简称杨氏模量)。
实验证明:杨氏模量Y 与外力F 、物体长度L 以及截面积的大小均无关,而只取决定于物体的材料本身的性质。
它是表征固体性质的一个物理量。
根据(1)式,测出等号右边各量,杨氏模量便可求得。
(1)式中的F 、S 、L 三个量都可用一般方法测得。
唯有L ∆是一个微小的变化量,用一般量具难以测准。
本实验采用光杠杆法进行间接测量(具体方法如右图所示)。
2.2光杠杆的放大原理如右图所示,当钢丝的长度发生变化时,光杠杆镜面的竖直度必然要发生改变。
那么改变后的镜面和改变前的镜面必然成有一个角度差,用θ来表示这个角度差。
从下图我们可以看出:hLtg ∆=θ (2) 这时望远镜中看到的刻度为1N ,而且θ201=ON N ∠,所以就有:DN N tg 012-=θ(3) 采用近似法原理不难得出:L hDN N N ∆=-=∆201(4)这就是光杠杆的放大原理了。
将(4)式代入(1)式,并且S=πd 2,即可得下式:Nh d FLD Y ∆∆=π28 这就是本实验所依据的公式。
杨氏模量测量实验报告

杨氏模量测量实验报告一、实验目的1、学会用拉伸法测量金属丝的杨氏模量。
2、掌握用光杠杆放大法测量微小长度变化量。
3、学会使用游标卡尺、螺旋测微器等测量长度的仪器。
4、学习用逐差法处理实验数据。
二、实验原理1、杨氏模量的定义杨氏模量是描述固体材料抵抗形变能力的物理量。
对于一根长度为L、横截面积为 S 的均匀金属丝,在受到沿长度方向的拉力 F 作用时,伸长量为ΔL。
根据胡克定律,在弹性限度内,应力 F/S 与应变ΔL/L成正比,比例系数即为杨氏模量 E,其表达式为:E =(F/S)/(ΔL/L) = FL/(SΔL)2、光杠杆放大原理光杠杆是一个附有三个尖足的平面镜,其前两尖足放在平台的沟内,后足尖置于与金属丝下端相连的圆柱体上。
当金属丝被拉长时,光杠杆的后足尖随圆柱体下降ΔL,使光杠杆绕前足尖转动一微小角度θ。
此时,反射光线相对入射光线偏转2θ 角。
设平面镜到标尺的距离为D,光杠杆后足尖到两前足尖连线的垂直距离为 b,则有:ΔL =bθ/2D 由于θ 很小,tanθ ≈ θ,所以ΔL =bΔx/2D ,式中Δx 为标尺上的读数变化量。
三、实验仪器杨氏模量测量仪、光杠杆、望远镜及标尺、螺旋测微器、游标卡尺、砝码、米尺等。
四、实验步骤1、调整杨氏模量测量仪(1)调节底座水平,使金属丝铅直。
(2)将光杠杆放在平台上,使其前两足尖位于沟槽内,后足尖置于与金属丝下端相连的圆柱体上,调整光杠杆平面镜的俯仰角度,使其与平台垂直。
(3)调节望远镜及标尺,使其与光杠杆平面镜等高,且望远镜光轴水平,标尺与望远镜光轴垂直。
2、测量金属丝的长度 L用米尺测量金属丝的长度,测量多次,取平均值。
3、测量金属丝的直径 d用螺旋测微器在金属丝的不同部位测量直径,测量多次,取平均值。
4、测量光杠杆常数 b用游标卡尺测量光杠杆后足尖到两前足尖连线的垂直距离 b,测量多次,取平均值。
5、测量望远镜中标尺的初始读数 n₀在未加砝码时,通过望远镜读取标尺的读数 n₀。
钢丝的杨氏模量实验报告

一、实验目的1. 学习使用拉伸法测定钢丝的杨氏模量;2. 掌握光杠杆法测量微小伸长量的原理;3. 学会用逐差法处理实验数据;4. 学会计算不确定度,并正确表达实验结果。
二、实验原理杨氏模量(E)是材料在弹性限度内应力(σ)与应变(ε)的比值,即 E =σ/ε。
它是衡量材料刚度和抵抗形变能力的物理量。
本实验采用拉伸法测定钢丝的杨氏模量,利用光杠杆放大原理测量微小伸长量,通过计算得出杨氏模量。
三、实验仪器1. YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码)2. 钢卷尺(0-200cm,0.1cm)3. 千分尺(0-150mm,0.02mm)4. 游标卡尺(0-25mm,0.01mm)5. 米尺四、实验步骤1. 调整杨氏模量测量仪,确保平台水平。
2. 将光杠杆放置于平台上,旋松固定螺丝,移动杠杆使其前两锥形足尖放入平台的沟槽内,后锥形足尖放在管制器的槽中,再旋紧螺丝。
3. 调节平面镜的仰角,使镜面垂直,即光杠杆镜面法线与望远镜轴线大致重合。
4. 利用望远镜上的准星瞄准光杠杆平面镜中的标尺刻度,调节望远镜的焦距,使标尺清晰可见。
5. 在钢丝下端悬挂砝码,使钢丝产生微小伸长。
6. 观察望远镜中的标尺刻度变化,记录光杠杆后足到两前足尖连线的垂直距离b 和望远镜中观察到的标尺刻度值的变化量n。
7. 重复步骤5和6,进行多次测量,记录数据。
8. 使用逐差法处理实验数据,计算杨氏模量的平均值。
五、数据处理1. 根据公式 E = 2δlb/Slb,计算杨氏模量E,其中δ为砝码质量,l为钢丝长度,b为光杠杆后足到两前足尖连线的垂直距离,S为钢丝截面积。
2. 计算不确定度,根据公式ΔE = Δδ/2δ + Δl/l + Δb/b + ΔS/S,其中Δδ、Δl、Δb、ΔS分别为δ、l、b、S的不确定度。
3. 根据计算结果,分析实验误差来源,讨论实验结果与理论值的差异。
六、实验结果与分析1. 通过实验,我们测定了钢丝的杨氏模量,计算结果为 E =2.02×10^5 MPa。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金属丝杨氏模量的测定实验报告
【实验目的】
1.学会用拉伸法测量杨氏模量;
2.掌握光杠杆法测量微小伸长量的原理;
3.学会用逐差法处理实验数据;
4.学会不确定度的计算方法,结果的正确表达;
【实验仪器】
YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码) 钢卷尺(0-200cm , )、游标卡尺(0-150mm,、螺旋测微器(0-150mm,
【实验原理】
在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L ,截面积为S ,沿长度方向施力F 后,物体的伸长L ∆,则在金属丝的弹性限度内,有:
F
S E L
L
=∆ 我们把E 称为杨氏弹性模量。
如上图:
⎪⎪⎭
⎪⎪⎬⎫=∆≈=∆ααα2D n tg x L n D x L ∆⋅=∆⇒2 (02n n n -=∆) n x d FLD L
n D
x d F
L L S F E ∆⋅=∆=∆=228241ππ 真实测量时放大倍数为4倍,即E=2E
【实验内容】
<一> 仪器调整
1、杨氏弹性模量测定仪底座调节水平;
2、平面镜镜面放置与测定仪平面垂直;
3、将望远镜放置在平面镜正前方左右位置上;
4、粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像;
5、调节物镜焦距能看到尺子清晰的像,调节目镜焦距能清晰的看到叉丝;
6、调节叉丝在标尺cm 2±以内,并使得视差不超过半格。
<二>测量
1、 记下无挂物时刻度尺的读数0n ;
2、依次挂上100g 的砝码,8次,计下7654321,,,,,,n n n n n n n ;
3、依次取下100g 的砝码,8次,计下n 0‘,'
7'65'4'3'2'1,,,,,,'n n n n n n n ; 4、用米尺测量出金属丝的长度L (两卡口之间的金属丝)、镜面到尺子的距离D ;
5、用游标卡尺测量出光杠杆x 、用螺旋测微器测量出金属丝直径d 。
<三>数据处理方法——逐差法
1. 实验测量时,多次测量的算术平均值最接近于真值。
但是简单的求一下平均还
是不能达到最好的效果,我们多采用逐差法来处理这些数据。
2. 逐差法采用隔项逐差:
4
)()()()(37261504n n n n n n n n n -+-+-+-=∆ 3. 注:上式中的n ∆为增重400g 的金属丝的伸长量。
【实验数据记录处理】
【结果及误差分析】
1. 光杠杆、望远镜和标尺所构成的光学系统一经调节好后,在实验过程中就不可
在移动,否则,所测的数据将不标准,实验又要重新开始;
2. 不准用手触摸目镜、物镜、平面反射镜等光学镜表面,更不准用手、布块或任
意纸片擦拭镜面;
2砝码,将金属丝拉直,作为一个基准点;
3.实验测数据前没有事先放上去一个kg
4.用游标卡尺在纸上测量x值和螺旋测微器测量读数时易产生误差;
5.测量金属丝长度时没有找准卡口;
6.米尺使用时常常没有拉直,且应该注意水平测量D,铅垂测量L;
7.在加减砝码是应该注意轻放,避免摇晃。
附:真实数据图。
