大学物理实验-报告实验用拉伸法测杨氏模量.doc
用拉伸法测钢丝杨氏模量――实验报告

用拉伸法测钢丝杨氏模量――实验报告本实验使用拉伸法测定钢丝的杨氏模量。
实验过程包括测量原始尺寸和断裂强度,计算应力和应变,绘制应力-应变曲线,利用斜率计算杨氏模量。
一、实验原理1.杨氏模量:杨氏模量也称弹性模量,是研究力学学科中的一项重要物理量,它描述了物体在受力时,单位应力下的应变程度。
可以表示为弹性模量E,其计算公式为E=σ/ε,其中σ为应力,ε为单位应变。
2.拉伸法:拉伸法是测定材料弹性性质的常用方法之一。
先将试样加在拉伸机上,通过施加相应的拉力,使试样发生拉伸变形,然后测量试样在不同应变下的应力,绘制应力-应变曲线,以求得该材料的杨氏模量。
二、实验步骤1.准备实验设备,将钢丝放在拉伸机上。
2.用卡尺测量钢丝的初始长度、直径和断裂长度,记录数据。
3.用拉伸机分别在不同的拉力下进行拉伸,记录拉力和试样的应变。
4.计算每个密度下的应力,应力=拉力/试样横截面积。
5.计算每个密度下的应变,应变=延长长度/原始长度。
6.根据应力-应变曲线,计算杨氏模量。
三、实验数据试样长度:5m原始直径:2.5mm断裂长度:8m钢丝密度:7.85g/cm³拉伸试验数据如下:|拉力F(N)|延长长度L(mm)|试样直径D(mm)||:-:|:-:|:-:||0|0|2.5||50|2|2.5||100|4|2.6||150|6|2.7||200|8|2.8||250|10|2.9||300|12|3.0||350|14|3.1||400|16|3.2||450|18|3.3||500|20|3.4||550|22|3.5||600|24|3.6||650|26|3.7||700|28|3.8||750|30|3.9||800|32|4.0|四、实验计算1.计算实验数据中的横截面积试样横截面积=π*(D/2)²=π*(2.5/2)²=4.91mm² 2.计算每个密度下的应力应力=F/S=700/4.91=142.6N/mm²应变=L/L0=28/5000=0.00564.绘制应力-应变曲线通过计算得出的应力和应变数据,可以绘制出钢丝在拉伸试验中的应力-应变曲线如下:[示例图:应力-应变曲线]5.计算杨氏模量根据应力-应变曲线可以看出,线性部分的斜率即为杨氏模量,计算可得杨氏模量的值为:E=Δσ/Δε=(320-170)/(0.004-0.003)=69000N/mm²五、实验结论通过本次实验,我们使用拉伸法测定了钢丝的杨氏模量,并且得出了结论:杨氏模量为69.0×10⁹N/mm²。
用拉伸法测量金属丝的杨氏模量实验报告

用拉伸法测量金属丝的杨氏模量实验报告《用拉伸法测量金属丝的杨氏模量实验报告》
嘿,朋友们!今天我来给大家讲讲我做的这个超有趣的用拉伸法测量金属丝杨氏模量的实验!(就像我们要探索一个神秘的宝藏一样刺激!)
实验开始前,那根金属丝乖乖地躺在那儿,仿佛在等待着我们去揭开它的秘密呢。
(这不就像一个等待被唤醒的小战士嘛!)我和小伙伴们可兴奋了,都迫不及待地想开始。
我们小心地把金属丝安装在实验装置上,这过程就好像在给它打扮一样,得特别仔细。
(就跟给宝贝穿衣服一样不能马虎呀!)然后,慢慢给它施加拉力,看着它一点点被拉长,哇,那种感觉真奇妙!(这就像看着小树苗一点点长大一样神奇!)
在测量数据的时候,我们可是全神贯注,眼睛瞪得大大的,生怕错过一点。
(那认真的样子,就像侦探在寻找关键线索呢!)每一个数据都感觉好重要啊!“哎呀,这个数字读对了没?”我还时不时问小伙伴。
经过一番努力,终于测得了所有的数据。
这时候大家都特别有成就感。
(就像打了一场大胜仗一样开心!)
分析数据的时候,才发现这里面可藏着大学问呢。
就好像解开一道复杂的谜题一样。
(哎呀,原来这里面有这么多门道啊!)
这次实验,让我对杨氏模量有了更深刻的理解,也让我感受到了科学实验的魅力。
(真的太棒啦!)以后我还要多做这样的实验,探索更多的科学奥秘呢!(大家也快来试试呀!)。
大学物理实验 报告实验21 用拉伸法测杨氏模量

真验21 用推伸法测杨氏模量之阳早格格创做林一仙1 真验脚段1)掌握推伸法测定金属杨氏模量的要领;2)教习用光杠杆搁大丈量微弱少度变更量的要领;3)教习用做图法处理数据.2 真验本理相闭仪器:杨氏模量仪、光杠杆、尺读视近镜、卡尺、千分尺、砝码.所有固体正在中力使用下皆要爆收形变,最简朴的形变便是物体受中力推伸(或者压缩)时爆收的伸少(或者收缩)形变.本真验钻研的是棒状物体弹性形变中的伸少形变.设金属丝的少度为L,截里积为S,一端牢固,一端正在延少度目标上受力为F,并伸少△L,如图21-1,比值:L L∆是物体的相对于伸少,喊应变. SF是物体单位里积上的效率力,喊应力. 根据胡克定律,正在物体的弹性极限内,物体的应力与应形成正比,即 则有LS FLY ∆=(1) (1)式中的比率系数Y 称为杨氏弹性模量(简称杨氏真验道明:杨氏模量Y 与中力F 、物体少度L 以及截里积的大小均无闭,而只与决断于物体的资料自己的本量.它是表征固体本量的一个物理量.根据(1)式,测出等号左边各量,杨氏模量即可供得.(1)式中的F 、S 、L 三个量皆可用普遍要领测得.唯有L ∆是一个微弱的变更量,用普遍量具易以测准.本真验采与光杠杆法举止间接丈量(简曲要领如左图所示).如左图所示,当钢丝的少度爆收变更时,光杠杆镜里的横曲度必定要爆收改变.那么改变后的镜里战改变前的镜里必定成有一个角度好,用θ去表示那个角度好.从下图咱们不妨瞅出:hL tg ∆=θ (2)那时视近镜中瞅到的刻度为1N ,而且θ201=ON N ∠,所以便有:DN N tg 012-=θ(3)采与近似法本理没有罕见出:L hDN N N ∆=-=∆201(4)那便是光杠杆的搁大本理了.将(4)式代进(1)式,而且S=πd2,即可得下式: 那便是本真验所依据的公式. 2.3 真验步调1)将待测金属丝下端砝码钩上加砝码使它伸曲.安排仪器底部三足螺丝,使G 仄台火仄.2)将光杠杆的二前足置于仄台的槽内,后足置于C 上,安排镜里与仄台笔曲.3)安排标尺与视近镜收架于符合位子使标尺与视近镜以光杠杆镜里核心为对于称,并使镜里与标尺距离D约为安排.4)用千分尺丈量金属丝上、中、下曲径,用卷尺量出金属丝的少度L.5)安排视近镜使其与光杠杆镜里正在共一下度,先正在视近镜表里附近找到光杠杆镜里中标尺的象(如找没有到,应安排或者上下移动标尺的位子或者微调光杠杆镜里的笔曲度).再把视近镜移到眼睛天圆处,分离安排视近镜的角度,正在视近镜中即可瞅到光杠杆镜里中标尺的反射象(纷歧定很浑晰).6)安排目镜,瞅浑十字叉丝,安排调焦旋钮,瞅浑标尺的反射象,而且忽视好.若有视好,应继承小心安排目镜,曲到忽视好为止.查看视好的办法是使眼睛上下移动,瞅叉丝与标尺的象是可相对于移动;若有相对于移动,道明有视好,便应再调目镜曲到叉丝与标尺象无相对于疏通(即忽视好)为止.记下火仄叉丝(或者叉丝接面)所对于准的标尺的初读数N0,N普遍应调正在标尺0刻线附近,若好得很近,应上下移动标尺或者查看光杠杆反射镜里是可横曲.7)屡屡将砝码沉沉天加于砝码钩上,并分别记下读数N'1、N'2、…、Ni',共搞5次.8)屡屡缩小砝码,并依次记下记读数N i ''-1,N i ''-2,…、N ''0.9)当砝码加到最大时(如)时,再测一次金属丝上、中、下的曲径d ,并与挂砝码时对于应的曲径供仄衡值,动做金属丝的曲径d 值.10)用卡尺测出光杠杆后足尖与前二足尖的距离h ,用尺读视近镜的测距功能测出D (少短叉丝的刻度好乘100倍).11)用图解法处理真验数据决定丈量截止及丈量没有决定度.1)光杠杆及镜尺系统已经调佳,中途没有得再任性变动,可则所测数据无效.2)加、减砝码要小心,须用脚沉沉托住砝码托盘,没有得碰动仪器;而且需待钢丝伸缩宁静后圆可读数. 3)正在丈量钢丝伸少量历程中,没有成中途停顿而改测其余物理量(如d 、L 、D 等),可则若中途受到其余搞扰,则钢丝的伸少(或者收缩)值将爆收变更,引导缺面删大. 3 数据处理1) 真验数据记录表格表1相闭数据的丈量序次 F(×9.789N)Ni(加,cm) Ni(减,cm)Nd(1kg) (mm)d(6kg) (mm)L(cm )D(c m) H(cm)1 01502 3 4 56——2) 用做图法处理数据决定NF ∆∆的丈量截止及没有决定度;3) 估计钢丝的杨氏模量的丈量截止及没有决定度.cm m Hu0012.03002.03==∆=;cm m L u 029.0305.03==∆=;4真验截止: 5思索题(计划)1)本真验为什么用分歧仪器去测定各个少度量? 2)光杠杆法是可用去丈量一齐薄金属片的薄度?怎么样丈量?3)安排光杠杆镜尺系统时,若逢到下列局里时您将怎么样处理(即怎么样安排)?(1)用视近镜找标尺的像时,瞅到了光杠杆的镜里,而瞅没有到标尺的像.(2)某一共教已调佳的光杠杆系统(他确已调佳了),但是您去瞅时感触标尺的像很朦胧.。
大学物理实验 报告实验21 用拉伸法测杨氏模量
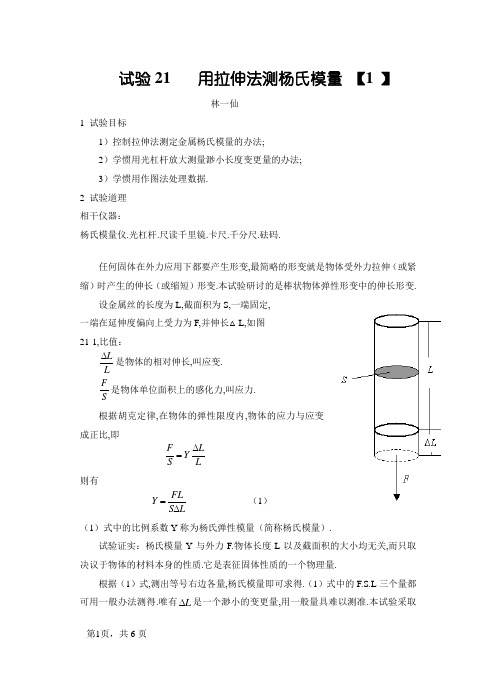
试验21 用拉伸法测杨氏模量 【1 】林一仙1 试验目标1)控制拉伸法测定金属杨氏模量的办法; 2)学惯用光杠杆放大测量渺小长度变更量的办法; 3)学惯用作图法处理数据. 2 试验道理 相干仪器:杨氏模量仪.光杠杆.尺读千里镜.卡尺.千分尺.砝码.任何固体在外力应用下都要产生形变,最简略的形变就是物体受外力拉伸(或紧缩)时产生的伸长(或缩短)形变.本试验研讨的是棒状物体弹性形变中的伸长形变.设金属丝的长度为L,截面积为S,一端固定, 一端在延伸度偏向上受力为F,并伸长△L,如图 21-1,比值:L L∆是物体的相对伸长,叫应变. SF是物体单位面积上的感化力,叫应力. 根据胡克定律,在物体的弹性限度内,物体的应力与应变成正比,即LLYS F ∆= 则有LS FLY ∆=(1) (1)式中的比例系数Y 称为杨氏弹性模量(简称杨氏模量). 试验证实:杨氏模量Y 与外力F.物体长度L 以及截面积的大小均无关,而只取决议于物体的材料本身的性质.它是表征固体性质的一个物理量.根据(1)式,测出等号右边各量,杨氏模量即可求得.(1)式中的F.S.L 三个量都可用一般办法测得.唯有L ∆是一个渺小的变更量,用一般量具难以测准.本试验采取光杠杆法进行间接测量(具体办法如右图所示).如右图所示,当钢丝的长度产生变更时,光杠杆镜面的竖直度必定要产生转变.那么转变后的镜面和转变前的镜面必定成有一个角度差,用θ来暗示这个角度差.从下图我们可以看出:hLtg ∆=θ (2) 这时千里镜中看到的刻度为1N ,并且θ201=ON N ∠,所以就有:DN N tg 012-=θ(3) 采取近似法道理不可贵出:L hDN N N ∆=-=∆201(4)这就是光杠杆的放大道理了.将(4)式代入(1)式,并且S=πd2,即可得下式:N h d F LD Y ∆∆=π28这就是本试验所根据的公式. 2.3 试验步调1)将待测金属丝下端砝码钩上加砝码使它伸直.调节仪器底部三脚螺丝,使G 平台程度.2)将光杠杆的两前足置于平台的槽内,后足置于C 上,调剂镜面与平台垂直. 3)调剂标尺与千里镜支架于适合地位使标尺与千里镜以光杠杆镜面中间为对称,并使镜面与标尺距离D 约为阁下.4)用千分尺测量金属丝上.中.下直径,用卷尺量出金属丝的长度L.5)调剂千里镜使其与光杠杆镜面在同一高度,先在千里镜外面邻近找到光杠杆镜面中标尺的象(如找不到,应阁下或高低移动标尺的地位或微调光杠杆镜面的垂直度).再把千里镜移到眼睛地点处,联合调剂千里镜的角度,在千里镜中即可看到光杠杆镜面中标尺的反射象(不一定很清楚).6)调节目镜,看清十字叉丝,调节调焦旋钮,看清标尺的反射象,并且疏忽差.如有视差,应持续仔细调节目镜,直到疏忽差为止.检讨视差的办法是使眼睛高低移动,看叉丝与标尺的象是否相对移动;如有相对移动,解释有视差,就应再调目镜直到叉丝与标尺象无相对活动(即疏忽差)为止.记下程度叉丝(或叉丝交点)所瞄准的标尺的初读数N0,N0一般应调在标尺0刻线邻近,若差得很远,应高低移动标尺或检讨光杠杆反射镜面是否竖直.7)每次将砝码轻轻地加于砝码钩上,并分离记下读数N'1.N'2.….N i',共做5次.8)每次削减砝码,并依次记下记读数N i''-1,N i''-2,….N''0.9)当砝码加到最大时(如)时,再测一次金属丝上.中.下的直径d,并与挂砝码时对应的直径求平均值,作为金属丝的直径d值.10)用卡尺测出光杠杆后足尖与前两足尖的距离h,用尺读千里镜的测距功效测出D(长短叉丝的刻度差乘100倍).11)用图解法处理试验数据肯定测量成果及测量不肯定度.1)光杠杆及镜尺系同一经调好,半途不得再随意率性变动,不然所测数据无效.2)加.减砝码要仔细,须用手轻轻托住砝码托盘,不得碰动仪器;并且需待钢丝伸缩稳固后方可读数.3)在测量钢丝伸长量进程中,不成半途停留而改测其他物理量(如d.L.D等),不然若半途受到别的干扰,则钢丝的伸长(或缩短)值将产生变更,导致误差增大.3 数据处理1)试验数据记载表格表1相干数据的测量次序 F(×9.789N)Ni(加,cm) Ni(减,c m) N d(1kg) (mm) d(6kg)(mm)L(cm)D(c m) H(cm)1 01502 3 4 56——2) 用作图法处理数据肯定NF∆∆的测量成果及不肯定度;())/(1090.61005.015.7789.900.100.622m N N N F F N FA B A B ⨯=⨯-⨯-=--=∆∆%0.1103.3107.610.7305.0200.5305.022255222222=⨯+⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯=⎪⎪⎭⎫⎝⎛∆+⎪⎪⎭⎫ ⎝⎛∆=⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆=--∆∆∆∆N u F u N u F u E BANFN F NF)/(10069.01090.6%0.122m N NFE NF NF u⨯=⨯⨯=∆∆⨯=∆∆∆∆ 3) 盘算钢丝的杨氏模量的测量成果及不肯定度.)/(1063.11090.6842.70450.014.31015000.98882112222m N N h d F LD Y ⨯=⨯⨯⨯⨯⨯⨯⨯=∆∆=π cm m Hu0012.03002.03==∆=;cm m L u 029.0305.03==∆=;cm m D u 9.2100305.03==∆=()cm m d dS u9.2100305.00047.032222=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫⎝⎛∆+= ()%5.2100.1102.2101.1107.3107.8%0.1842.70012.0450.09.221509.200.98029.02484482222222222=⨯+⨯+⨯+⨯+⨯=+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=-----∆∆E N F H d D L Y H u d u D u L u E )/(10039.0%5.21063.121111m N E Y Y Yu⨯=⨯⨯=⨯=4试验成果:())683.0(%5.2/1004.063.1211=⎪⎩⎪⎨⎧=⨯±=±=p E mN Y Y Y Y u 5思虑题(评论辩论)1)本试验为什么用不合仪器来测定各个长器量?2)光杠杆法可否用来测量一块薄金属片的厚度?若何测量?3)调节光杠杆镜尺体系时,若碰到下列现象时你将若何处理(即若何调节)?(1)用千里镜找标尺的像时,看到了光杠杆的镜面,而看不到标尺的像.(2)某一同窗已调好的光杠杆体系(他确已调好了),但你去看时觉得标尺的像很隐约.。
拉伸法测量金属丝的杨氏模量实验报告

拉伸法测量金属丝的杨氏模量实验报告《拉伸法测量金属丝的杨氏模量实验报告》
嘿,朋友们!今天我要来给你们讲讲我做的拉伸法测量金属丝杨氏模量的实验,那可真是一次超级有趣的体验啊!
实验开始前,我就像要去探险一样兴奋!我准备好了各种器材,那根金属丝就静静地躺在那里,好像在等着我去揭开它的秘密。
我心里想着:“这根小小的金属丝里到底藏着怎样的奥秘呢?”
然后我和小伙伴们一起动手啦!我们小心翼翼地把金属丝安装到实验装置上,就像在给一个小宝贝安家一样。
我还打趣地说:“嘿,可得轻点儿对它呀!”大家都笑了。
当我们开始施加拉力的时候,那种感觉就像是在和金属丝拔河一样。
它一开始还有点不情愿呢,不过慢慢地就开始伸长啦!看着它一点点变化,我心里那个激动啊,哎呀,真的很难形容!就好像看着一颗种子慢慢发芽长大。
在测量数据的过程中,我们可真是一丝不苟啊!每一个数值都像是宝贝一样,生怕记错了。
我和小伙伴还互相提醒:“嘿,你可看准了啊,别出差错!”这感觉就像是在完成一项超级重要的任务。
经过一番努力,终于得出了结果!哇,那种满足感简直爆棚!就好像我们征服了一座小山一样。
这次实验让我深刻地体会到了科学的魅力,它就像一个神秘的宝藏,等着我们去挖掘。
总之,这次实验真的是太棒了!你们也快去试试吧,绝对会让你们大开眼界的!。
用拉伸法测金属丝的杨氏模量实验报告

用拉伸法测金属丝的杨氏模量实验报告用拉伸法测金属丝的杨氏模量实验报告引言:杨氏模量是材料力学性质的重要指标之一,它描述了材料在拉伸过程中的刚度和变形能力。
本实验通过拉伸金属丝的方法来测量杨氏模量,旨在了解金属丝的力学性质,并探讨拉伸过程中的变形行为。
实验装置和步骤:实验装置主要包括拉伸机、金属丝样品、刻度尺、电子天平和计算机。
具体的实验步骤如下:1. 将金属丝样品固定在拉伸机的夹具上,并调整夹具使其与拉伸机的拉伸轴心对齐。
2. 通过调整拉伸机的拉伸速度和加载范围,使实验能够在合适的条件下进行。
3. 使用刻度尺测量金属丝的初始长度,并记录下来。
4. 启动拉伸机,开始对金属丝进行拉伸。
5. 在拉伸过程中,使用电子天平测量金属丝的质量,并记录下来。
6. 当金属丝断裂时,停止拉伸机的运行,并记录下金属丝的最终长度。
实验数据处理:根据实验步骤所得到的数据,可以计算出金属丝的应力和应变。
应力定义为单位面积上的力,可以通过施加在金属丝上的拉力除以金属丝的横截面积得到。
应变定义为单位长度上的变形量,可以通过金属丝的伸长量除以初始长度得到。
根据胡克定律,应力与应变之间的关系可以用以下公式表示:应力 = 弹性模量× 应变其中,弹性模量即为杨氏模量。
通过绘制应力-应变曲线,可以得到金属丝的杨氏模量。
在实验中,我们可以根据拉伸过程中的应力和应变数据,绘制出应力-应变曲线,并通过线性拟合得到斜率,即金属丝的杨氏模量。
实验结果和讨论:根据实验数据处理得到的应力-应变曲线,我们可以得到金属丝的杨氏模量。
实验结果显示,金属丝的杨氏模量为XXX GPa(Giga Pascal)。
这个结果与文献中的数值相符合,证明了实验方法的可靠性。
在拉伸过程中,金属丝会发生塑性变形,即超过了材料的弹性限度。
这是因为金属丝在受到拉力的作用下,晶体结构发生了位错滑移,导致金属丝的形状发生变化。
当拉力超过金属丝的极限强度时,金属丝会发生断裂。
大学物理实验《用拉伸法测金属丝的杨氏弹性模量》

三、实验中注意:实验测量中,发现增荷和减荷时读数相关差较大,当荷重按比例增加时,?n不按比例增加,应找出原因,重新测量。这种情况可能发生的原因有:
1、金属丝不直,初始砝码太轻,没有把金属丝完全拉直。
2、杨氏弹性模量仪支柱不垂直,使金属丝下端的夹头不能在金属框内上下自由滑动,摩擦阻力太大。
1
3、加减砝码时动作不够平衡,导致光杠杆足尖发生移动。
1、万能试验机法:在万能试验机上做拉伸或压缩试验,自动记录应力和应变的关系图线,从而计算出杨氏弹性模量。
2、静态拉伸法(本实验采用此法),它适用于有较大形变的固体和常温下的测量,它的缺点是:①因为载荷大,加载速度慢,含有驰豫过程。所以它不能很真实地反映出材料内部结构的变化。②对脆性材料不能用拉伸法测量;③不能测量材料在不同温度下的杨氏弹性模量。
8LD?n??F?KF 2?dbE
8LD
?d2bE由此式作?n?F图线,应得一直线。从图线中计算出直线的斜率K,再由K?
即可计算出E。
3
篇二:大学物理实验用拉伸法测金属丝的杨氏模量
用拉伸法测金属丝的杨氏模量
材料在外力作用下产生形变,其应力与应变的比值叫做弹性模量,它是反映材料抵抗形变能力的物理量,杨氏模量是固体材料的纵向弹性模量,是选择机械构件的依据之一,也是工程技术中研究材料性质的常用参数。测定弹性模量的方法很多,如拉伸法、振动法、弯曲法、光干涉法等,本实验采用拉伸法测定金属丝的杨氏弹性模量,研究拉伸正应力与应变之间的关系。
用拉伸法测金属丝的杨氏模量参考报告

用拉伸法测金属丝的杨氏模量参考报告在物理实验的世界里,测量材料的性质总是让人充满好奇。
今天我们来聊聊金属丝的杨氏模量,简单点说,就是一种描述材料在受力时如何变形的方式。
这项实验用的是拉伸法,听起来挺简单的,但其实蕴含着不少奥妙。
首先,我们得了解一下实验的基本设备。
拉伸测试机是关键。
它就像一位耐心的老师,慢慢施加力道,直到金属丝发生明显的变化。
我们使用的是一根标准的金属丝,直径和材质都有所规定。
准备好这些,心里就像打了鸡血一样,期待接下来的过程。
在实验开始前,必须仔细测量金属丝的初始长度和直径。
没有好的数据,后面的计算就像无源之水,难以为继。
用卡尺小心翼翼地量,生怕一不小心就把结果搞错。
记得那时候,心里默默祈祷,希望一切顺利。
测量完成后,记录数据是必不可少的,确保我们在后面能轻松搞定计算。
当拉伸机缓缓施加力量时,金属丝开始变形,仿佛在低声诉说着它的故事。
每一次拉伸,都是一次挑战。
我们认真观察着,目不转睛,生怕错过任何细微的变化。
随着力量的增大,金属丝的长度逐渐拉长,直至达到极限,最终它会发生断裂。
那一刻,仿佛整个世界都静止了,时间都在为这一瞬间而停滞。
接下来,断裂后的一切都得仔细分析。
我们需要记录下每个阶段的力量和对应的变形量。
通过这些数据,我们能够计算出金属丝的杨氏模量。
这个公式其实并不复杂,简而言之,就是应力与应变的比值。
应力是施加的力量除以横截面积,而应变则是长度的变化除以原始长度。
计算过程中,心中充满期待。
把数据代入公式后,金属丝的杨氏模量赫然出现在眼前。
这个数值就像一个特殊的标签,代表着这根金属丝的特性。
高杨氏模量意味着材料比较坚硬,而低杨氏模量则表明材料更柔韧。
通过这些,我们能更好地理解金属丝在各种应用中的表现。
在这个实验中,最让我印象深刻的其实是那种耐心和细致的态度。
科学实验从来不是一蹴而就的,更多时候是需要一点一滴地积累。
每一次观察,每一次记录,都在为结果添砖加瓦。
就像古人云“千里之行,始于足下”,每一步都至关重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验21 用拉伸法测杨氏模量林一仙1 实验目的1)掌握拉伸法测定金属杨氏模量的方法;2)学习用光杠杆放大测量微小长度变化量的方法; 3)学习用作图法处理数据。
2 实验原理相关仪器:杨氏模量仪、光杠杆、尺读望远镜、卡尺、千分尺、砝码。
2.1杨氏模量任何固体在外力使用下都要发生形变,最简单的形变就是物体受外力拉伸(或压缩)时发生的伸长(或缩短)形变。
本实验研究的是棒状物体弹性形变中的伸长形变。
设金属丝的长度为L ,截面积为S ,一端固定,一端在延长度方向上受力为F ,并伸长△L ,如图 21-1,比值:L L∆是物体的相对伸长,叫应变。
SF是物体单位面积上的作用力,叫应力。
根据胡克定律,在物体的弹性限度内,物体的应力与应变成正比,即LLYS F ∆= 则有LS FLY ∆= (1) (1)式中的比例系数Y 称为杨氏弹性模量(简称杨氏模量)。
实验证明:杨氏模量Y 与外力F 、物体长度L 以及截面积的大小均无关,而只取决定于物体的材料本身的性质。
它是表征固体性质的一个物理量。
根据(1)式,测出等号右边各量,杨氏模量便可求得。
(1)式中的F 、S 、L 三个量都可用一般方法测得。
唯有L ∆是一个微小的变化量,用一般量具难以测准。
本实验采用光杠杆法进行间接测量(具体方法如右图所示)。
2.2光杠杆的放大原理如右图所示,当钢丝的长度发生变化时,光杠杆镜面的竖直度必然要发生改变。
那么改变后的镜面和改变前的镜面必然成有一个角度差,用θ来表示这个角度差。
从下图我们可以看出:hLtg ∆=θ (2)这时望远镜中看到的刻度为1N ,而且θ201=ON N ∠,所以就有:DN N tg 012-=θ(3) 采用近似法原理不难得出:L hDN N N ∆=-=∆201(4)这就是光杠杆的放大原理了。
将(4)式代入(1)式,并且S=πd 2,即可得下式:N h dFLD Y ∆∆=π28 这就是本实验所依据的公式。
2.3 实验步骤1)将待测金属丝下端砝码钩上加1.000kg 砝码使它伸直。
调节仪器底部三脚螺丝,使G 平台水平。
2)将光杠杆的两前足置于平台的槽内,后足置于C 上,调整镜面与平台垂直。
3)调整标尺与望远镜支架于合适位置使标尺与望远镜以光杠杆镜面中心为对称,并使镜面与标尺距离D 约为1.5米左右。
4)用千分尺测量金属丝上、中、下直径,用卷尺量出金属丝的长度L 。
5)调整望远镜使其与光杠杆镜面在同一高度,先在望远镜外面附近找到光杠杆镜面中标尺的象(如找不到,应左右或上下移动标尺的位置或微调光杠杆镜面的垂直度)。
再把望远镜移到眼睛所在处,结合调整望远镜的角度,在望远镜中便可看到光杠杆镜面中标尺的反射象(不一定很清晰)。
6)调节目镜,看清十字叉丝,调节调焦旋钮,看清标尺的反射象,而且无视差。
若有视差,应继续细心调节目镜,直到无视差为止。
检查视差的办法是使眼睛上下移动,看叉丝与标尺的象是否相对移动;若有相对移动,说明有视差,就应再调目镜直到叉丝与标尺象无相对运动(即无视差)为止。
记下水平叉丝(或叉丝交点)所对准的标尺的初读数N 0,N 0一般应调在标尺0刻线附近,若差得很远,应上下移动标尺或检查光杠杆反射镜面是否竖直。
7)每次将1.000kg 砝码轻轻地加于砝码钩上,并分别记下读数N '1、N '2、…、N i ',共做5次。
8)每次减少1.000kg 砝码,并依次记下记读数N i ''-1,N i ''-2,…、N ''0。
9)当砝码加到最大时(如6.000kg )时,再测一次金属丝上、中、下的直径d ,并与挂1.000kg 砝码时对应的直径求平均值,作为金属丝的直径d 值。
10)用卡尺测出光杠杆后足尖与前两足尖的距离h ,用尺读望远镜的测距功能测出D (长短叉丝的刻度差乘100倍)。
11)用图解法处理实验数据确定测量结果及测量不确定度。
2.4注意事项1)光杠杆及镜尺系统一经调好,中途不得再任意变动,否则所测数据无效。
2)加、减砝码要细心,须用手轻轻托住砝码托盘,不得碰动仪器;而且需待钢丝伸缩稳定后方可读数。
3)在测量钢丝伸长量过程中,不可中途停顿而改测其他物理量(如d 、L 、D 等),否则若中途受到另外干扰,则钢丝的伸长(或缩短)值将发生变化,导致误差增大。
3 数据处理1) 实验数据记录表格表1相关数据的测量次序F(×9.789N) N i (加,cm)N i (减,cm)Nd(1kg) (mm)d(6kg) (mm)L(cm )D(c m)H(cm)1 1.000 0 -0.05 -0.02 0.442 0.440 98.00 150 7.842 2 2.000 1.38 1.65 1.52 0.465 0.4603 3.000 2.90 2.95 2.92 0.438 0.4554 4.000 4.30 4.45 4.38 5 5.000 5.72 5.90 5.81 66.0007.12——7.122) 用作图法处理数据确定NF∆∆的测量结果及不确定度;())/(1090.61005.015.7789.900.100.622m N N N F F N FA B A B ⨯=⨯-⨯-=--=∆∆ %0.1103.3107.610.7305.0200.5305.022255222222=⨯+⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯=⎪⎪⎭⎫⎝⎛∆+⎪⎪⎭⎫ ⎝⎛∆=⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆=--∆∆∆∆N u F u N u F u E BANFN F NF)/(10069.01090.6%0.122m N NFE NF NF u⨯=⨯⨯=∆∆⨯=∆∆∆∆ 3) 计算钢丝的杨氏模量的测量结果及不确定度。
)/(1063.11090.6842.70450.014.31015000.98882112222m N N h d F LD Y ⨯=⨯⨯⨯⨯⨯⨯⨯=∆∆=π cm m Hu0012.03002.03==∆=;cm m L u 029.0305.03==∆=;cm m D u 9.2100305.03==∆=()cm m d dS u9.2100305.00047.032222=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛∆+= ()%5.2100.1102.2101.1107.3107.8%0.1842.70012.0450.09.221509.200.98029.02484482222222222=⨯+⨯+⨯+⨯+⨯=+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=-----∆∆E N F H d D L Y H u d u D u L u E )/(10039.0%5.21063.121111m N E Y Y Yu⨯=⨯⨯=⨯=4 实验结果:())683.0(%5.2/1004.063.1211=⎪⎩⎪⎨⎧=⨯±=±=p E mN Y Y Y Y u5 思考题(讨论)1)本实验为什么用不同仪器来测定各个长度量?2)光杠杆法能否用来测量一块薄金属片的厚度?如何测量?3)调节光杠杆镜尺系统时,若遇到下列现象时你将如何处理(即如何调节)? (1)用望远镜找标尺的像时,看到了光杠杆的镜面,而看不到标尺的像。
(2)某一同学已调好的光杠杆系统(他确已调好了),但你去看时感到标尺的像很模糊。
XXXX项目可行性研究报告报告日期XXXX年XXXX月XXXX日目录第一节项目概况一、项目背景二、投资方简介三、目标公司简介第二节拟投资行业及市场概况第三节项目实施的必要性与可行性一、项目实施的必要性二、目标公司市场分析三、项目实施的可行性第四节项目内容及实施方案第五节项目效益分析一、经营收入估算二、经营总成本估算三、经营利润与财务评价第六节项目风险分析及对策一、市场风险及对策二、技术风险及对策三、财务风险及对策……第七节投资方案一、收购定价二、预计投资总额三、资金来源与支付四、后续发展方案第六节报告结论第一节项目概况一、项目背景说明项目提出的背景、投资理由、拟投资国家的投资环境、在可行性研究前已经进行的工作情况及其成果、重要问题的决策和决策过程等情况。
二、投资方简介1、投资方基本情况及经营情况包括目标公司基本工商注册信息、产业布局、主要产品及用途、员工情况、股权结构及控股方信息、行业地位、历史沿革等。
2、投资方实力和优势分析三、目标公司简介1、基本信息包括目标公司基本工商注册信息、产业布局、主要产品及用途、员工情况、股权结构及控股方信息、行业地位、历史沿革等。
2、经营情况(1)经营情况公司的产品在市场上进行销售、服务的发展现状,包括历年产量、销售收入等。
(2)资产负债情况公司主要财务指标,要求能够反映公司盈利能力、经营能力、偿债能力等。
第二节拟投资行业及市场概况1、国内相关行业及市场概况2、国际相关行业及市场概况第三节项目实施的必要性与可行性一、项目实施的必要性主要围绕公司战略目标,根据公司产业资源协同发展的需要以及产品规划,结合产业政策等有关因素的支持与制约,论证项目投资的必要性。
二、目标公司市场分析运用统计分析原理,分析目标公司产品销售变化及市场发展趋势。
1、市场规模研究目标公司产品及行业的整体规模,具体包括目标公司产品及行业在指定时间的产量、销售收入等。
2、行业分析主要包括行业内主要品牌市场占有率、行业总销售量年增长率、行业发展方向、市场发展方向等。
3、竞争格局包括主要竞争企业基本资料、主要品牌经营策略、竞争品牌近三年发展情况、行业竞争态势未来发展预测等。
三、项目实施的可行性主要表现在以下方面:技术可行性。
主要分析目标企业产品技术现状与规划是否符合公司战略,技术部门对目标公司实施的技术在行业内进行比选和评价,合理评估其技术先进性。
经济可行性。
主要从企业理财的角度进行资本预算,评价项目的财务盈利能力,预测项目投资回收期、净现值等财务指标。
社会影响。
主要从资源配置的角度衡量项目的价值,评价项目在符合区域经济发展目标、有效配置经济资源、增加供应、创造就业、改善环境等方面的效益。
风险因素及对策。
主要对项目的市场风险、技术风险、财务风险、法律风险及社会风险等风险因素进行评价,制定规避风险的对策,为项目全过程的风险管理提供依据。
第四节项目效益分析一、经营收入估算根据行业及公司历史数据对目标公司未来五年经营收入进行合理预测。
二、经营总成本估算合理估算目标公司未来五年主营业务成本、期间费用和税金支出等。
三、经营利润与财务评价合理估算目标公司未来五年的盈利水平,并估算项目投资回收期、内部收益率、净现值等财务指标。
