必修2三视图练习及答案
必修2三视图练习及答案
高一数学必修二练习一、选择题1．下边的几何物体中，哪一个正视图不是三角形 A ．竖放的圆锥 B ．三棱锥( )C．三棱柱D．竖放的正四棱锥2．以下几何体各自的三视图中，有且只有两个视图是同样的是( )A ．①②B．①③C．①④ D ．②④3．已知几何体的三视图A ．四棱台，圆台(如图 )，则这个几何体自上而下挨次为()B ．四棱台，四棱台C．四棱柱，四棱柱 D ．不可以判断4．某四棱锥的三视图如下图，该四棱锥的表面积是( )A ． 32 B． 16＋16 2C． 48 D． 16＋32 25.以下命题中正确的选项是()A.平行于圆锥的一条母线的截面是等腰三角形6.若一个几何体的正视图和侧视图都是等腰三角形，俯视图是圆，则这个几何体可能是（Ａ．圆柱Ｂ．三棱柱Ｃ．圆锥Ｄ．球体7、三视图均同样的几何体有（）Ａ．球Ｂ．正方体Ｃ．正四周体Ｄ．以上都对）8．给出以下命题：①假如一个几何体的三视图是完整同样的，则这个几何体是正方体；②假如一个几何体的正视图和俯视图都是矩形，则这个几何体是长方体；③假如一个几何体的三视图都是矩形，则这个几何体是长方体；④假如一个几何体的正视图和侧视图都是等腰梯形，则这个几何体是圆台．此中正确命题的个数是( )A ． 0 B． 1 C． 2 D ．3*9 ．某简单几何体的一条对角线长为a，在该几何体的正视图、侧视图与俯视图中，这条对角线的投影都是长为2的线段，则a 等于 ( )A. 2B.3C． 1 D． 2二、填空题10、三视图的正视图、俯视图、侧视图分别是从、、察看同一个几何体，画出的空间几何体的图形．（正前方，正上方，正左方）11、圆台的正视图、侧视图都是12．把边长为 1 的正方形ABCD 沿对角线BD，俯视图是折起形成三棱锥．（全等的等腰梯形，两个齐心圆）C－ ABD ，其主视图与俯视图如下图，则其左视图的面积为________．高一数学《空间几何体的三视图和直观图》练习题A组1．右图是一块带有圆形空洞和方形空洞的小木板，则以下物体中既能够堵住圆形空洞，又能够堵住方形空洞的是（）2．利用斜二测画法获得的①三角形的直观图必定是三角形；②正方形的直观图必定是菱形；③等腰梯形的直观图能够是平行四边形；④菱形的直观图必定是菱形.以上结论正确的选项是（）A．①②B．①C．③④D．①②③④3．等腰梯形ABCD ,上底边 CD=1, 腰 AD=CB=2, 下底 AB=3 ，按平行于上、下底边取x 轴，则直观图A′B′C′D′的面积为 _______．4．一个三角形在其直观图中对应一个边长为 1 正三角形，原三角形的面积为.5．一天，小莹站在室内，室内有一面积为 3 平方米的玻璃窗，她站在离窗子 4 米的地方向外看，他能看到窗前方一幢楼的面积为.（楼层之间的距离为20 米）6．如图，E、F 分别是正方体的面 ADD 1A 1、面 BCC 1B 1的中心，则四边形 BFD 1E 在该正方体的面上的正投影可能是（要求把可能的图的序号都填上）。
2019届(北师大版)数学必修二课时作业：1.3三视图(含答案)
2019届北师大版数学精品资料温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。
关闭Word文档返回原板块。
课时提升作业(三)三视图一、选择题(每小题3分，共18分)1.(2014·江西高考)一几何体的直观图如图，下列给出的四个俯视图中正确的是( )【解析】选B.因为俯视图是几何体在下底面上的投影，所以选B.2.(2014·福州高一检测)一个几何体的三视图形状都相同，大小均相等，则该几何体不可以是( )A.球B.三棱锥C.正方体D.圆柱【解析】选D.圆柱的三视图分别是矩形，矩形，圆，不可能三个视图都一样，球的三视图都是圆，三棱锥的三视图都是三角形，正方体的三视图都是正方形.3.(2014·广州高一检测)如图，△A′B′C′为正三角形，与底面不平行，且CC′>BB′>AA′，则多面体的主视图为( )【解析】选D.因为△A′B′C′为正三角形，面A′B′BA向前，所以主视图不可能是A，B，C，只能是D.4.一个几何体由几个相同的小正方体组合而成，它的主视图、左视图、俯视图如图所示，则这个几何体包含的小正方体的个数是( )A.7B.6C.5D.4【解析】选C.由三视图知小正方体底层4个，上层1个，共5个.【变式训练】该几何体的三视图如图所示，则搭成该几何体需要的小正方体的块数是( )A.8B.7C.6D.5【解析】选C.由主视图和左视图，知该几何体由两层小正方体拼接成，由俯视图可知，最下层有5个小正方体，由主、左视图知上层仅有一个小正方体，则共有6个小正方体.5.(2013·四川高考)一个几何体的三视图如图所示，则该几何体的直观图可以是( )【解析】选D.根据几何体的三视图中正视图与侧视图一致，并且俯视图是两个圆，可知只有选项D适合，故选D.6.(2014·北京高一检测)一个长方体去掉一个长方体，所得几何体的主视图与左视图分别如图所示.则该几何体的俯视图为( )【解题指南】从主视图和左视图上分析，去掉长方体的位置所在的方位，然后判断俯视图的正确图形.【解析】选C.由主视图可知去掉的长方体在正视线的方向，从左视图可以看出去掉的长方体在原长方体的左侧，可知俯视图为C.二、填空题(每小题4分，共12分)7.下图中三视图表示的几何体是________.【解析】由主视图和左视图知为柱体，又底面为四边形，所以此几何体为四棱柱.答案：四棱柱8.如图所示，图①②③是图④表示的几何体的三视图，其中图①是____________，图②是____________，图③是____________(填写视图名称).【解析】由三视图可知，①为主视图，②为左视图，③为俯视图. 答案：主视图左视图俯视图9.(2014·南昌高一检测)一个三棱柱的左视图和俯视图如图：则该三棱柱主视图的面积为________.【解析】由题知主视图如图，其高与左视图中三角形的高相等，由俯视图的高为2，知左视图的底边为2，故左视图为正三角形，而主视图的长为1，高为，则主视图的面积为1×=.答案：三、解答题(每小题10分，共20分)10.画出如图所示物体的三视图.【解析】此物体的三视图如图所示：11.(2014·洛阳高一检测)如图所示是一个半圆柱OO1与三棱柱ABC A1B1C1的组合体，其中，圆柱OO1的轴截面ACC1A1是边长为4的正方形，△ABC为等腰直角三角形，AB⊥BC，试画出此组合体的三视图.【解析】由题意可知几何体的主视图与左视图都是中间有一条线段的矩形，俯视图由半圆与等腰三角形组成，如图：一、选择题(每小题4分，共16分)1.(2014·阜阳高一检测)如图是长和宽分别相等的两个矩形，给定下列三个命题：①存在三棱柱，其主视图俯视图如图；②存在四棱柱其主视图，俯视图如图；③存在圆柱，其主视图、俯视图如图.其中真命题的个数是( )A.3B.2C.1D.0【解析】选A.对于①可以为放倒的直三棱柱；②可以为长方体；③可以为放倒的圆柱.2.(2014·泸州高一检测)将一个正方体沿其棱的中点截去两个三棱锥后所得几何体如图所示，则其俯视图为( )【解题指南】根据正方体的几何特征，分析几何体俯视图外轮廓的形状及截面截正方体表面所得的棱能否看到，进而得到答案.【解析】选C.将一个正方体沿其棱的中点截去两个三棱锥后所得几何体的俯视图满足：外轮廓是一个正方形，左上角能看到上底面被截所成的棱，为实线，右下角看不到下底面被截所成的棱，为虚线，故选C.3.如图，直三棱柱的所有棱长均为2，主视图和俯视图如图所示，则其左视图的面积为( )A.2B.2C.4D.4【解题指南】先确定出左视图的形状，再求面积.【解析】选B.左视图是长为2，宽为底面三角形的高，即为的矩形.所以S=2×=2.4.(2014·湖南高考)一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于( )A.1B.2C.3D.4【解题指南】先由三视图画出直观图，判断这个几何体是底面是边长为6，8，10的直角三角形，高为12的躺下的直三棱柱，底面的内切圆的半径就是做成的最大球的半径.【解析】选B.由三视图画出直观图如图，判断这个几何体是底面是边长为6，8，10的直角三角形，高为12的躺下的直三棱柱，直角三角形的内切圆的半径为r==2，这就是做成的最大球的半径.二、填空题(每小题5分，共10分)5.(2014·淮北高一检测)正方形ABCD的边长为3cm，以直线AB为轴，将正方形旋转一周，所得几何体的主视图的周长是__________cm.【解析】正方形旋转一周，所得几何体是圆柱，主视图是矩形，矩形的长为6cm，宽是3cm，因此，所得几何体的主视图的周长为2×(6+3)=18(cm).答案：186.用n个体积为1的正方体搭成一个几何体，其主视图、左视图都是如图所示的图形，则n的最大值与n的最小值之差是________.【解析】由主视图、左视图可知，正方体个数最少时，底层有3个小正方体，上面有2个，共5个；个数最多时，底层有9个小正方体，上面有2个，共11个.故n的最大值与最小值之差是6.答案：6三、解答题(每小题12分，共24分)7.如图是根据某一种型号的滚筒洗衣机抽象出来的几何体，数据如图所示(单位：cm).试画出它的三视图.【解析】这个几何体是由一个长方体挖去一个圆柱体构成的，三视图如图所示.【拓展延伸】画三视图的诀窍由三视图的作图原则可知：(1)主视图和俯视图共同反映了物体左右方向的尺寸.(2)主视图和左视图共同反映了物体上下方向的尺寸.(3)俯视图和左视图共同反映了物体前后方向的尺寸.因此画一个物体的三视图不仅要确定其形状，而且要确定三视图之间的线段大小关系.画三视图时一般遵循从下层向上层，从左边到右边的原则.【变式训练】如图，BC⊥CD，且CD⊥MN，ABCD绕AD所在直线MN旋转，在旋转前，点A可以在DM上选定.当点A选在射线DM上的不同位置时，形成的几何体大小、形状不同，分别画出它的三视图并比较异同.【解析】(1)当点A在图(a)中射线DM的位置时，绕MN旋转一周所得几何体为底面半径为CD的圆柱和圆锥叠加而成，其三视图如图(a).(2)当点A在图(b)中射线DM的位置时，即点A是B到MN作垂线的垂足时旋转后的几何体为圆柱，其三视图如图(b).(3)当点A在图(c)中所示位置时，其旋转所得几何体为圆柱中挖去同底的圆锥，其三视图如图(c).(4)当点A位于点D时，如图(d)中，旋转体为圆柱中挖去同底等高的圆锥，其三视图如图(d).8.如图是由小立方块组成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，请画出它的主视图和左视图.【解题指南】从俯视图可以看出，其主视图应该是3列，每列的立方块的个数分别是4，4，3；左视图应该是4列，每列的立方块的个数分别是3，3，4，3，由此可以想象该几何体的形状，得到其主视图和左视图.【解析】该几何体的主视图和左视图如图：【变式训练】某座楼由相同的若干个房间组成，该楼的三视图如图所示，其中图中每一个小矩形表示一个房间.该楼有几层？最多有多少个房间？画出房间最多时此楼的大致形状.【解析】由主视图和左视图可知，该楼共3层，由俯视图可知该楼一层共5个房间，结合主视图和左视图可知二楼最多有四个房间，三楼一个房间，故最多有10个房间，此时楼的大致形状如图所示.关闭Word文档返回原板块。
北师大高中数学必修二随堂巩固验收： 三视图 含解析
1．如图，甲、乙、丙是三个立体图形的三视图，与甲、乙、丙相对应的标号是()
①长方体；②圆锥；③三棱锥；④圆柱．
A．③①②B．①②③C．③②④D．④②③
[答案] D
2．已知三棱柱ABC—A1B1C1如右图所示，以BCC1B1的前面为
正前方，画出的三视图正确的是()
[解析]主视图是矩形，左视图是三角形，俯视图是矩形，中间有一条线．
[答案] A
3．已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的主视图的面积不可能等于()
A．1 B. 2 C.2－1
2 D.
2＋1
2
[解析]当正方体的主视图为边长为1的正方形时，面积取得最小值1，当正方体的主视图为宽为1，长为2的矩形时，面积取得最
大值2，故主视图的面积S满足1≤S≤2，观察选项知，2－1 2
不
在此区间内．故本题正确答案为C.
[答案] C
4．将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的左视图为()
[解析]还原正方体后，将D1，D，A三点分别向正方体右侧面作垂线．D1A的射影为C1B，且为实线，B1C被遮挡应为虚线．[答案] B。
（完整版）高中数学3三视图课后习题（带答案）
（完整版）高中数学3三视图课后习题（带答案）332 正视图侧视图俯视图图1 三视图课后习题1.（陕西理5）某几何体的三视图如图所示，则它的体积是A ．283π-B ．83π-C ．82π-D ．23π2.（全国新课标理6）。
在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为3.（湖南理3）设图1是某几何体的三视图，则该几何体的体积为A ．9122π+B ．9182π+C ．942π+D ．3618π+4.（广东理7）如图1－3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为A ．63 B ．93C ．123D ．1835.（北京理7）某四面体的三视图如图所示，该四面体四个面的面积中，最大的是A ．8B ．62C ．10D ．826.（安徽理6）一个空间几何体的三视图如图所示，则该几何体的表面积为（A ）48 （B ）32+817 （C ）48+817 （D ）807.（辽宁理15）一个正三棱柱的侧棱长和底面边长相等，体积为32，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是．8.（天津理10）一个几何体的三视图如右图所示（单位：m ），则该几何体的体积为__________3m9.（2010湖南文数）13.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h= cm10．（2010浙江理数）（12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是___________3cm .11．（2010辽宁文数）（16）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为 .12.（2010辽宁理数）（15）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.13.（2010天津文数）（12）一个几何体的三视图如图所示，则这个几何体的体积为。
高中数学1.2.1空间几何体的三视图练习新人教版A版必修2【含答案】
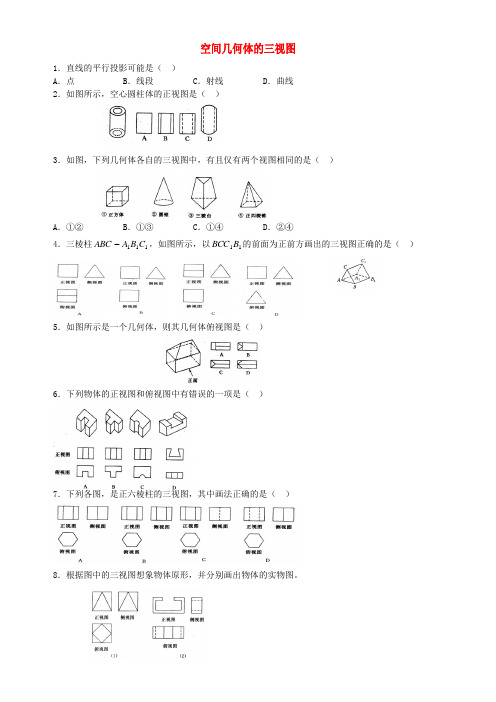
空间几何体的三视图1．直线的平行投影可能是（ ）A ．点B ．线段C ．射线D ．曲线2．如图所示，空心圆柱体的正视图是（ ）3．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）A ．①②B ．①③C ．①④D ．②④4．三棱柱111C B A ABC ，如图所示，以11B BCC 的前面为正前方画出的三视图正确的是（）5．如图所示是一个几何体，则其几何体俯视图是（ ）6．下列物体的正视图和俯视图中有错误的一项是（ ）7．下列各图，是正六棱柱的三视图，其中画法正确的是（ ）8．根据图中的三视图想象物体原形，并分别画出物体的实物图。
10．如图，E 、F 分别是正方体1AC 的面11A ADD 和面11B BCC 的中心，则四边形E BFD 1在该正方体的面上的正投影（投射线垂直于投影面的投影）可能是图中 （把所有可能图形的序号都填上）。
空间几何体的直观图1．利用斜二测画法叙述正确的是（ ）A ．正三角形的直观图是正三角形B ．平行四边形的直观图是平行四边形C ．矩形的直观图是矩形D ．圆的直观图一定是圆2．下列结论正确的是（ ）A ．相等的线段在直观图中仍然相等B ．若两条线段平行，则在直观图中对应的两条线段仍然平行C ．两个全等三角形的直观图一定也全等D ．两个图形的直观图是全等的三角形，则这两个图形是全等三角形3．直角坐标系中一个平面图形上的一条线段AB 的实际长度为4cm ，若AB//x 轴，则画出直观图后对应的线段=''B A ，若y AB //轴，则画出直观图后对应的线段B A ''= 。
4．水平放置的ABC ∆的斜二测直观图如图所示，已知2,3=''=''C B C A ，则AB 边上的中线的实际长度为 。
四、典例剖析1．已知一个正方形的直观图是一个平行四边形，其中有一边长为4，则此正方形的面积是（ ）A ．16B ．64C ．16或64D ．都不对分析：根据直观图的画法，平行于x 轴的线段长度不变，平行于y 轴的线段变为原来的一半，于是长为4的边如果平行于x 轴，则正方形边长为4，面积为16，边长为4的边如果平行于y 轴，则正方形边长为8，面积是64。
人教A版2019高中数学必修二学案12空间几何体的三视图和直观图 含答案
空间几何体的三视图和直观图 1.2空间几何体的三视图2.1&12.2 中心投影与平行投影1．，思考并完成以下问题～14预习课本P11[新知初探]1．投影的定义由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影．其中，把光线叫做投影线，把留下物体影子的屏幕叫做投影面．2．中心投影与平行投影平行投影下，与投影面平行的平面图形留下的影子，与这个平面图形的形状和] [点睛大小完全相同；而中心投影则不同． 3．三视图[点睛] 三视图中的每种视图都是正投影．[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)直线的平行投影是直线( )(2)圆柱的正视图与侧视图一定相同( )(3)球的正视图、侧视图、俯视图都相同( )答案：(1)× (2)× (3)√2.一个几何体的三视图如图所示，则该几何体可以是( )A．棱柱 B．棱台D．圆台 C．圆柱解析：选D 先观察俯视图，再结合正视图和侧视图还原空间几何体．由俯视图是圆环可排除A、B，由正视图和侧视图都是等腰梯形可排除C，故选D.3．沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是( )解析：选D 从上面看依然可得到两个半圆的组合图形，注意看得到的棱画实线．中心投影与平行投影[典例] 下列命题中正确的是( )．矩形的平行投影一定是矩形A．B．平行投影与中心投影的投影线均互相平行C．两条相交直线的投影可能平行D．如果一条线段的平行投影仍是一条线段，那么这条线段中点的投影必是这条线段投影的中点[解析] 平行投影因投影线的方向变化而不同，因而平行投影的形状不固定，故A不正确．平行投影的投影线互相平行，中心投影的投影线相交于一点，故B不正确．无论是平行投影还是中心投影，两条直线的交点都在两条直线的投影上，因而两条相交直线的投影不可能平行，故C不正确．两条线段的平行投影长度的比等于这两条线段长度的比，故D正确．[答案] D[活学活用]OABCDABCDEBBCCF′的中心，点′为面′-′′如图所示，点′的中心，点为正方体BCDOEF在该正方体的面上的正投影可能是________(为′′填出所′的中点，则空间四边形有可能的序号)．ABCDBBCC′上的投影为②，在后侧面解析：在下底面′上的投影为③，在右侧面DDCC′上的投影为①.′答案：①②③由几何体画三视图[典例] 画出如图所示的正四棱锥的三视图．正四棱锥的三视图如图所示．] 解[[活学活用]ABCABC，如图所示，则其三视图为( ) 1．已知三棱柱-111CC可见，为实线，只有A其正视图为矩形，侧视图为三角形，俯视图中棱解析：选A 1符合．2．画出如图所示的物体的三视图．解：三视图如图所示．由三视图还原几何体[典例] 根据如图所示的三视图，画出几何体．[解]由正视图、侧视图可知，该几何体为简单几何体的组合体，结合俯视图为大正方形里有一个小正方形，可知该组合体上面为一个正方体，下面为一个下底面是正方形的倒置的四棱台．如图所示．[活学活用]若某几何体的三视图如图所示，则这个几何体的直观图可以是( )中所给几中所给几何体的正视图、俯视图不符合要求；D解析：选B 由题意知，A和CB. B.故选何体的侧视图不符合要求；由侧视图可判断该几何体的直观图是视图与计算BDABCD折起，形成三棱锥沿对角线所示，将一边长为1的正方形[典例] 如图1ABDC)，其正视图与俯视图如图2所示，则侧视图的面积为-(2211 C. A. B. D. 2424BDBCDA的中点，由俯] 由正视图可以看出，点在面上的投影为[解析BDCABD的中点，所以其侧视图为如图所示视图可以看出上的投影为点在面21221，于是侧视图的面积为××的等腰直角三角形，直角边为＝. 22224A答案[]]活学活用[的正方形，则该正方体的正视图的面的正方体的俯视图是一个面积为11 已知棱长为) ( 积不可能等于．．．2 B. A．1122－1＋ C.D. 22解析：选C 由正方体的俯视图是面积为1的正方形可知正方体的正视图的面积范围属于[1，2 ]，故选C.层级一学业水平达标ABCABC所在平面平行，则经过中心投影后所得的三角形，选定的投影面与△．已知△1．ABC( 与△)A．全等 B．相似D．以上都不正确C．不相似ABC相B 根据中心投影的概念和性质可知，经过中心投影后所得的三角形与△解析：选似．2．如图是一个物体的三视图，则此三视图所描述的物体的直观图是( )解析：选D 由三视图知D正确．3．一几何体的直观图如图，下列给出的四个俯视图中正确的是( )解析：选B 由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形．4．若某几何体的正视图、侧视图、俯视图完全相同，则该几何体的正视图不可能是( )解析：选D 满足选项A的有三棱锥，满足选项B的有球，满足选项C的有正方体，故选D. 5．一个长方体去掉一角，如图所示，关于它的三视图，下列画法正确的是( )由于去掉一角后，出现了一个小三角形的面．正视图中，长方体上底面和解析：选A错；侧视图中的线应是虚右边侧面上的三角形的两边的正投影分别和矩形的两边重合，故B D 错．线，故C错；俯视图中的线应是实线，故的中几何体体何可能是下列视图为一个三角形，则这个几的6．一个几何体正．________(填入所有可能的几何体前的编号) ①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱．解析：三棱锥、四棱锥和圆锥的正视图都是三角形，当三棱柱的一个侧面平行于水平面，底面对着观测者时其正视图是三角形，四棱柱、圆柱无论怎样放置，其正视图都不可能是三角形．答案：①②③⑤两底面之间(7.若一个正三棱柱的三视图如图所示，则这个三棱柱的高．________和________的距离)和底面边长分别是解析：正三棱柱的高同侧视图的高，侧视图的宽度恰为底面正三角形的4.高，故底面边长为42 答案：CCAACDEFBABCDA的′′′中，′′，8.如图所示，在正方体，-分别是′)(填序号中点，则下列判断正确的是________．ABCDBFDE′内的正投影是正方形；在面①四边形DAADBFDE②四边形′′内的正投影是菱形；在面′AABBAEDDABFD′内的投影是全等的平行四边′内的正投影与在面在面′③四边形′′形．ADBCEBFDABCD，所以正投，内的投影分别是点解析：①四边形，′的四个顶点在面，AGDGDAE，则的中点′影是正方形，即①正确；②设正方体的棱长为2，则＝1，取，连接GAEGDEAEDDAAGDAEDBFD，知四在面′，且′内的正投影是四边形′＝′，由′∥′四边形AGDEAEDEEAGD不是菱形，即②不正5＝，所以四边形，边形′是平行四边形，但＝1′′确．对于③，由②可知两个正投影所得四边形是全等的平行四边形，从而③正确．答案：①③．画出如图所示的三棱柱的三视图．9．解：三棱柱的三视图如图所示：10．如图(1)所示是实物图，图(2)和图(3)是其正视图和俯视图，你认为正确吗？如不正确请改正．解：不正确，正确的正视图和俯视图如图所示：层级二应试能力达标1．以下关于几何体的三视图的论述中，正确的是( ) ．球的三视图总是三个全等的圆A．．正方体的三视图总是三个全等的正方形B ．正四面体的三视图都是正三角形C ．圆台的俯视图是一个圆DDA 正视方向不同，正方体的三视图不一定是三个全等的正方形，B错误；C，解析：选A.显然错误，故选．一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是2)(不可能是该锥体的俯视图，C解析：选C 由几何体的俯视图与侧视图的宽度一样，可知C.故选的等边三角形．若三棱柱3.已知三棱柱的侧棱与底面垂直，且底面是边长为2)( 的正视图(如图所示)的面积为8，则侧视图的面积为4 A．8 B．334D．C．2aaa该三棱柱的侧视图是一个＝8，所以4.解析：选C 设该三棱柱的侧棱长为，则2＝，所以侧视图的面积为，另一边长等于三棱柱底面等边三角形的高，为4矩形，一边长为3C.43.故选一四面体的三视图如图所示，则该四面体四个面中最大的面积4.)是(2 ．BA．23 D．3 BCDA，由三-解析：选D 由四面体的三视图知其直观图为如图所示的正方体中的四面体2.视图知正方体的棱长为1S 22，×2×2所以＝2＝ABD△231S 2×22×3，＝2×2＝ADC△221S，22＝2×2×2＝ABC△2．1S2.×2×2＝＝BCD△2D.23.所以所求的最大面积为故选DBCBABCDACDPA内一-是上底面5.如图所示，在正方体中，点11111111ABCP-．的正视图与侧视图的面积的比值为动点，则三棱锥________ABCP的正视图与侧视图为等底等高的三角形，故它解析：三棱锥-1.们的面积相等，面积比值为1答案：的正方形，则这个正6.已知一正四面体的俯视图如图所示，它是边长为2 cm2.四面体的正视图的面积为______cm DCAABCDB，在此正方体中作出一个解析：构造一个棱长为2 cm 的正方体-1111CDAB2 cm符合题意的正四面体2-2 cm，易得该正四面体的正视图是一个底边长为，高为112.22 cm的等腰三角形，从而可得正视图的面积为2答案：2yx的7．如图，是一个棱柱的三视图，请根据三视图的作图原则列出方程组，求出，值．解：由题意，可知1032? {yxyyxyx，＋6410－4＝，－＝＋.，＝＝解得?33?8．图为长方体木块堆成的几何体的三视图，求组成此几何体的长方体木块共有多少块？解：由正视图可知有两列，由侧视图可知有两排，再结合俯视图可得，几．块．如图所示，其中小长方形中的数字表示13块，上面一层有何体共分两层，下面一层有 )．1＋＝4(块此位置木块的块数，所以长方体木块共有2＋1 1.2.3 空间几何体的直观图18，思考并完成以下问题预习课本P16～[新知初探]1．用斜二测画法画平面图形的直观图的步骤xyO，画直观图时，把它们画成轴和(1)在已知图形中取互相垂直的轴，两轴相交于点xyOxOy′＝45°(或′，且使∠′对应的′′轴和′轴，两轴相交于点135°)，它们确定的平面表示水平面．xyxy′轴的轴的线段，在直观图中分别画成平行于′轴或(2)已知图形中平行于轴或线段．xy轴的线段，长已知图形中平行于轴的线段，在直观图中保持原长度不变，平行于(3)度变为原来的一半．2．用斜二测画法画空间几何体的直观图的步骤(1)画底面，这时使用平面图形的斜二测画法即可．zzOx′轴的夹角为90°，并画出高线画(′轴，′轴过点与原图高线相′，且与(2)等，画正棱柱时只需要画侧棱即可)，连线成图．(3)擦去辅助线，被遮线用虚线表示．画水平放置的平面图形的直观图，关键是确定多边形顶点的位置，借助于(1)] 点睛[平面直角坐标系确定顶点后，只需把这些顶点顺次连接即可． 135°)．(2)用斜二测画法画直观图要掌握水平长不变，垂线长减半，直角画45°(或[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)AAxyA＝用斜二测画法画水平放置的∠轴和时，若∠轴，且∠的两边分别平行于(1)A＝45°( 90°，则在直观图中，∠ )(2)用斜二测画法画平面图形的直观图时，平行的线段在直观图中仍平行，且长度不变( )答案：(1)× (2)×2．如图所示为某一平面图形的直观图，则此平面图形可能是下图中的( )解析：选A 由直观图知，原四边形一组对边平行且不相等，为梯形，且梯形两腰不能与底垂直．ABCABC的面积为________．3.已知△的直观图如图所示，则原△ABCACABACAB＝，，且解析：由题意，易知在△3. 中，＝⊥61S＝×6×3＝9.∴ABC△2答案：9水平放置的平面图形的直观图[典例] 画水平放置的直角梯形的直观图，如图所示．OBCDOBx轴，垂直于中，以底边所在直线为[解] (1)在已知的直角梯形OBODyxyxOy′＝′轴和′的腰′轴，使∠所在直线为轴建立平面直角坐标系．画相应的′45°，如图①②所示．1xOBOByODODDx′轴的平行′轴上截取，过点′(2)在′作′轴上截取′′＝′＝，在2llxCDCDCBC′，如图②′′使得′.′＝.连接线，在上沿′轴正方向取点OBCDOBCD.的直观图．如图③′就是直角梯形′′′所得四边形(3)．][活学活用)．45°的平行四边形的直观图(尺寸自定画一个锐角为yxOxOy′，其中∠′解：(1)画轴．如图①，建立平面直角坐标系′，再建立坐标系yxO′′＝45°.′1DOBOByOxAOAO′＝′＝(2)描点．如图②，在轴上截取′轴上截取′′′＝，在，′2DCCCxDODDD.′∥′，过点′轴，且′作′＝′DABC′′′，′.(3)连线．连接ABCDDBCA的直观′′即为一个锐角为(4)成图．如图③，四边形′′45°的平行四边形图．空间几何体的直观图 2的正三棱台的直观图．] 画出一个上、下底面边长分别为1,2，高为[典例xOyzOxy，使∠(1)[解] 画轴．如图，画轴、轴、轴相交于点xOz＝90°.＝45°，∠ABABOx＝画下底面．以(2)2为线段中点，在，使，轴上取线段3BCCAOCOCABCy为正三棱台的＝.连接在，轴上取线段，使，则△2 下底面的直观图．OyOxOOOOxOyOOz，建′′∥′∥，过点′作，′(3)画上底面．在轴上取′，使′＝2yxOxyO的画′立坐标系′中，类似步骤′′′.在′(2)CAB′法得上底面的直观图△′′.CCAABB′，去掉辅助线，将被遮住的部分(4)′，′，连线成图．连接CBAABC′即为要求画的正三棱台的直观图．′′-画成虚线，则三棱台．[活学活用]如图是一个几何体的三视图，用斜二测画法画出它的直观图．xyzxOyxOz＝90°.＝45°，∠轴、轴，使∠解：(1)画轴．如图①，画轴、(2)画底面．由三视图知该几何体是一个简单组合体，它的下部是一个正四棱台，上部ABCDzOOOO′等于三视图中，在′，使轴上截取是一个正四棱锥，利用斜二测画法画出底面OOxOxOyOyOxOy′画出上的平行线′相应高度，过′与′作的平行线′，利用′′′，′ABCD′. 底面′′′OzPPO′等于三视图中相应的高度． (3)画正四棱锥顶点．在，使上截取点PAPBPCPDAABBCCDD，整理得到三视图，，′成图．连接(4)，′，′，′′，′，′′表示的几何体的直观图，如图②.直观图的还原与计算ABCD的水平放置边四形的直观图是如]典[例图ABCDABCD)( 的面积是′，则原四边形′′′．2 10 B．14 A．2．14C．28D DBCABCDAADy′′≠′∥′′，解析] ∵′，′′∥′′轴，′[∴原图形是一个直角梯形．DA′，′＝4又1S∴原直角梯形的上、下底及高分别是2,5,8，故其面积为＝228.5)×8＝C[答案]][活学活用CBAABCaABC′的面积′是正三角形，且它的边长为的平面直观图△，那么△′已知△)( 为3322aa B.A.846622aa C.D. 168S23CAB′′△′2aS，，且解析：选D 由于＝＝ABC△S44ABCaaSS. ＝×所以＝＝ABCBAC△′′△′44416△223622层级一学业水平达标OxOyOzOxOy′，，′，轴画成对应的′1．根据斜二测画法的规则画直观图时，把，′OzxOyxOz′的度数分别为( ′′′，则∠′′′)′与∠A．90°，90° B．45°，90°D．45°或135°，90°C．135°，90°xOy′的度数应为45°或根据斜二测画法的规则，∠′135°，∠′解析：选DxOz′指的是画立体图形时的横轴与纵轴的夹角，所以度数为90°.′′xOy′平面上，则圆柱的高应画成( ) 的圆柱的底面画在．若把一个高为210 cm′′z10 cm′轴且大小为．平行于A．z5 cm B．平行于′轴且大小为z10 cm C．与45°且大小为′轴成z5 cmD．与45°且大小为′轴成zz的线段，在直观图中的方向和长度都与原来保持一轴上或在解析：选A 平行于)轴( 致．)1 cm的正方形的直观图，可能是下面的( 3．利用斜二测画法画边长为C 正方形的直观图是平行四边形，且边长不相等，故选C项．解析：选CDAB′中4.如右图所示的水平放置的三角形的直观图，′是△′′CADABCADyAB′′′′边的中点，且′′′，′平行于′轴，那么′，′ACABAD)三条线段对应原图形中线段，( ，中ACAB A．最长的是，最短的是ABAC B．最长的是，最短的是ADAB C．最长的是，最短的是ACAD D．最长的是，最短的是CByABCADBCDAD′的中′轴，所以在△，又因为中，′′′∥⊥解析：选C 因为′是ADACDBCAB.点，所以>是＝中点，所以ABC，有一边在水平线上，用斜二测画法作出的直观图是正三角形．水平放置的△5ABCABC)是′( ′′，则△ B．直角三角形．锐角三角形A C．钝角三角形 D．任意三角形ABCABC′′将△为钝角三角形．′还原，由斜二测画法知，△解析：选CBABCOxOy中，点如图所示，在平面直角坐标系水平放置的正方形6.B′到，则由斜二测画法画出的该正方形的直观图中，顶点的坐标为(4,4)x．′轴的距离为________xEB′轴于点⊥′解析：由斜二测画法画出的直观图如图所示，作ECEBCBEECBB＝＝45°，所以′′，在Rt△′′′中，′，∠′＝22CB2. ＝′′sin 45°＝2×22答案：CBOA′是水平放置的一个平面图形的直观′′7.如图，矩形′xCCOBAO′轴，则原平面图形的面′∥′，3′＝′，6′＝′图，其中积为________．DBCyDO，所以原平面′＝解析：在直观图中，设2′′′与′轴的交点为3′，则易得2.＝26的平行四边形，所以其面积为366×62图形为一边长为6，高为2答案：36CBOA，则在在直观图中，四边形′′2 cm′′为菱形且边长为8.2OABCxOy.，面积为________cm中原四边形)为________(坐标系填形状OABC为矩形，其中解析：由题意，结合斜二测画法可知，四边形2SOCOABCOA．的面积)＝2×4＝＝2 cm，8(cm＝4 cm，所以四边形8答案：矩形．已知几何体的三视图如图所示，用斜二测画法画出它的直观图．9xOzzxOyxy轴，使∠解：(1)画轴．如图①，画＝90°.轴，＝45°，∠轴，OOzOOO′等于三轴上截取画圆台的两底面．利用椭圆模板，画出底面⊙(2)′，使，在OyxOOyOOOx的作′′，′视图中相应的长度，过点的平行线′作′，类似底面⊙的平行线O法作出上底面⊙′.POOPOzOP′(3)画圆锥的顶点．在′′上截取等于三视图中′的长度．，使BABPAPBA，整理得到三视图所表示的几何体的直观图，(4)成图．连接，′，′′，′.如图②CBOA，它是水平放置的一个cm′′′的边长为′如图，正方形10.1平面图形的直观图．请画出原来的平面图形的形状，并求原图形的周长与面积．AOOAxOyx；，在1 轴上取＝cm′′＝解：如图，建立直角坐标系BOOBy；2 cm2′＝′2＝轴上取在．xB的在过点轴的平行线上取CBCB1 cm.′＝′＝CABO，各点，即得到了原图形．连接，，OABC为平行四边形，由作法可知，22BCOBOC＋，＝3 cm＝8＝＋12SOABC.的周长为(3＋1)×2＝8 cm，面积为2 cm∴平行四边形2＝1×22＝应试能力达标层级二．已知一个建筑物上部为四棱锥，下部为长方体，且四棱锥的底面与长方体的上底面15001∶尺寸一样，长方体的长、宽、高分别为20 m,5 m,10 m，四棱锥的高为8 m．如果按)的比例画出它的直观图，那么在直观图中，长方体的长、宽、高和棱锥的高应分别为(4 cm,1 cm,2 cm,1.6 cm ．A4 cm,0.5 cm,2 cm,0.8 cm ．B4 cm,0.5 cm,2 cm,1.6 cm ．C4 cm,0.5 cm,1 cm,0.8 cm．D4 cm,1 cm,2 cm解析：选C 由比例尺可知，长方体的长、宽、高和棱锥的高应分别为4 cm,0.5 cm,2 cm,1.6 cm.和1.6 cm，再结合直观图，图形的尺寸应为yAB边平行于2.用斜二测画法画出的某平面图形的直观图如图所示，2ABCDADBCx，则原平面图的面积为，平行于2 cm轴．已知四边形2轴，DCAB)′的面积为′( ′′形．4 cmA．22 2 cm4B．C．DBADABC′为直角梯形，上、′′依题意，可知∠解析：选C ′＝45°，22 88 cm 2 cmD则原平面图形BADACADBCB′，且长度为梯形′，′相等，高为′，且长度分别与′下底边分别为′，2ABCD.22倍，所以原平面图形的面积为的高的8 cm的等腰梯13．一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为)形，则该平面图形的面积等于(212 1A.＋＋B．2222．2＋．C21＋D的直角梯形．计算得面积22，高为平面图形是上底长为1，下底长为1＋D 解析：选2＋为2.ABCBC′＝4的斜二测直观图如图所示，已知′4.水平放置的△，ACBCyABCAB)( 边上的中线的长度为中′轴，则△′∥′，3′＝′．7373 A.B. 255C．D. 2BCACACBCABC＝＝⊥3，即△，解析：选A 由斜二测画法规则知为直角三角形，其中73ABAB A. .边上的中线长度为故选＝73，8，所以22.________ cm5．有一个长为5 cm，宽为4 cm的矩形，则其直观图的面积为2S，由平面图形的面积与直观图的面积间的关＝5×4＝20(cm)解析：该矩形的面积为22SS)52(cm系，可得直观图的面积为．＝′＝42答案：5BAOBAOB′如图所示，△6.的直观图，点′′表示水平放置的△′OBAOBAOOxAx上的′2′轴垂直，且在′＝′轴上，，则△′′与的边 ________．高为OBOAOBOBhB的长度相等，，由直观图中边解析：设△′与原图形中边的边′上的高为11OBBhAOBOOBSShAO上的的边＝4＝22××2.′′×故△′及′，则＝22，得×直观图原图222.高为424答案：BDACACABC，求其水平放上的高cm＝7.如图所示，△12 中，12 ＝cm，边置的直观图的面积．yyOOxx′＝45°，作′，使∠′解：法一：画′′轴，′轴，两轴交于1BDACABCACBD′＝，△的直观图如图所示，则＝′′＝，＝12 cm6 cm′212SCABDB＝，所以′′的高为 cm′＝3故△′′2CAB′′△′2212×32＝)182(cm，2.2×即水平放置的直观图的面积为182 cm112BDABCAC，由平面图＝的面积为法二：△·)×12×12＝72(cm222ABC2形的面积与直观图的面积间的关系，可得△的水平放置的直观图的面积是×72＝1842 (cm．)8．已知某几何体的三视图如下，请画出它的直观图(单位：cm)．解：画法：xyzOxOyxOz＝建系：如图①，画轴，，使∠轴，＝45°，∠轴，三轴相交于点(1)90°. xOByOAOBOA′为邻边，以轴上取线段和′＝(2)画底：在轴上取线段2 ＝8 cm，在cm OBBA′.′作平行四边形zOCCxy轴的平行线，并在平行线上分，过定点：在(3)分别作轴上取线段轴，＝4cm CDCCCDCCCDDC′.′和′为邻边作平行四边形别截取4 cm＝，2 cm.′＝以ACBDBD′，并加以整理(′′，去掉辅助线，将被遮挡的部分改为虚，′成图：连接(4)线)，就得到该几何体的直观图(如图②)．。
高中数学 必修二 空间几何体及三视图课后练习一(含解析)新人教A版必修2
高中数学空间几何体及三视图课后练习一（含解析）题1如图所示的几何体，关于其结构特征，下列说法不正确的是( )．A．该几何体是由两个同底的四棱锥组成的几何体B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中有1个为四边形，另外8个为三角形题2如下图所示，将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度，则倾斜后水槽中的水形成的几何体是( )．A．棱柱 B．棱台 C．棱柱与棱锥组合体D．不能确定题3已知四棱锥P－ABCD水平放置如图所示，且底面ABCD是正方形，侧棱PA⊥底面ABCD，PA ＝AB．试画出该几何体的三视图．题4cm．若正三棱锥（底面是正三角形）的主视图与俯视图如下，则左视图的面积为2题5一个三棱柱的底面是正三角形，三视图如图所示，求这个三棱柱的表面积和体积．题6如图所示为长方体木块堆成的几何体的三视图，此几何体共由几块木块堆成．题7长方体的主视图、俯视图如图所示，则其左视图面积为（）A．3 B．4 C．12 D．16题8某几何体的三视图如图所示，那么这个几何体是（）．A．三棱锥B．四棱锥C．四棱台D．三棱台题9某个几何体的三视图如图所示，其中正视图与侧视图是完全相同的图形，则这个几何体的体积为多少？题10某四面体的三视图如图所示，该四面体四个面的面积中，最大的是（）(A) 8 (B) (C)10 (D)题11一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱题12如图是一个倒置的四棱柱的两种摆放，试分别画出其三视图，并比较它们的异同．课后练习详解题1答案：D ．详解：四个选项中C 、D 矛盾，所以答案从这两个里选一个，又根据图形几何体有8个面． 题2答案：A ．详解：当固定AB 或CD 中的一边时，可形成以左右侧面为底面的棱柱；当固定AD 或BC 中的一边时，可形成以前后侧面为底面的棱柱．题3答案：见详解．详解：该几何体的三视图如下：注意侧视图的直角顶点位置．题4 答案：342cm ． 详解:三棱锥的左视图肯定还是三角形，需求三角形的底边长和高．根据俯视图知左视图的是边长为的三角形，又由主视图知，，1324S ∴==2cm ． 题5答案：这个三棱柱的表面积为（48+83）cm 2,体积为163cm 3.详解：由三视图易知，该三棱柱的形状如图所示：由左视图可得三棱柱的高为4cm,正三角形ABC和正三角形A′B′C′的高为23cm.∴正三角形ABC的边长为|AB|=sin601×42sin60°2).∴该三棱柱的表面积为S=3×4×4+2×21×42sin60°×3).体积为V=S底·|AA′|=2故这个三棱柱的表面积为2,体积为cm3.题6答案：4．详解:画出三视图复原的几何体，即可判断长方体的木块个数．由直视图知，由4块木块组成．故答案为：4．题7答案：A．详解：根据物体的主视图与俯视图可以得出，物体的长与高以及长与宽，进而得出左视图面积=宽×高．由主视图易得高为1，由俯视图易得宽为3．则左视图面积=1×3=3．题8答案：B．详解：由所给三视图可以判定对应的几何体是四棱锥．题9cm3详解：几何体是正四棱锥，底面是对角线长为2cm，则112232V=⨯⨯⨯= 3题10答案：C．详解：由三视图还原几何体如下图，该四面体四个面的面积中最大的是∆PAC，面积为10，选C．题11答案：①②③⑤．题12详解：如图：。
高中数学必修二《立体几何》练习题
立体几何一、选择题1、（2016年北京高考）某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）A.B. C. D. 【答案】A2、（2016年山东高考）有一个半球和四棱锥组成的几何体，其三 视图如右图所示，则该几何体的体积为（A ） （B ） （C ） （D ） 【答案】C3、（2016年全国I高考）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相1613121π32+31π32+31π62+31π62+1垂直的半径.若该几何体的体积是28π3，则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π【答案】A4、（2016年全国I 高考）平面过正方体ABCD A 1B 1C 1D 1的顶点A ，//平面CB 1D 1，平面ABCD =m ，平面ABB 1 A 1=n ，则m ，n 所成角的正弦值为（A ） （B ） （C ） （D ） 【答案】A5、（2016年全国II 高考）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（A ）20π （B ）24π （C ）28π （D ）32π 【答案】C6、（2016年全国III 高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为α-ααI αI22313（A ）（B ）（C ）90 （D ）81 【答案】B7、（2016年全国III 高考）在封闭的直三棱柱内有一个体积为V 的球，若，，，，则V 的最大值是（A ）4π （B ） （C ）6π （D ）【答案】B二、填空题1、（2016年上海高考）如图，在正四棱柱中，底面的边长为3，与底面所成角的大小为，则该正四棱柱的高等于____________【答案】2、（2016年四川高考）已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是__________．18+54+111ABC A B C -AB BC ⊥6AB =8BC =13AA =92π323π1111D C B A ABCD -ABCD 1BD 32arctan3、（2016年天津高考）已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示（单位：m），则该四棱锥的体积为_______m3.【答案】24、（2016年全国II高考）是两个平面，是两条直线，有下列四个命题：（1）如果，那么.[（2）如果，那么.（3）如果，那么.（4）如果，那么与所成的角和与所成的角相等.其中正确的命题有．.(填写所有正确命题的编号）【答案】②③④5、（2016年浙江高考）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是 cm2，体积是 cm3.,αβ,m n,,//m n m nαβ⊥⊥αβ⊥,//m nαα⊥m n⊥//,mαβα⊂//mβ//,//m nαβmαnβ【答案】 6、（2016年浙江高考）如图，在△ABC 中，AB =BC =2，∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD =DA ，PB =BA ，则四面体PBCD 的体积的最大值是 .【答案】三、解答题1、（2016年北京高考） 如图，在四棱锥中，平面平面，，，，，，（1）求证：平面；（2）求直线与平面所成角的正弦值；（3）在棱上是否存在点，使得平面？若存在，求的值；若不存在，说明理由. 【解】⑴∵面面 面面723212P ABCD -PAD ⊥ABCD PA PD ⊥PA PD =AB AD ⊥1AB =2AD =AC CD ==PD ⊥PAB PB PCD PA M //BM PCD AMAP∵，面∴面∵面∴又∴面⑵取中点为，连结，∵∴∵∴以为原点，如图建系易知，，，，则，，，设为面的法向量，令，则与面夹角有⑶假设存在点使得面设，由（2）知，，，，有∴∵面，为的法向量∴即∴∴综上，存在点，即当时，点即为所求.' 2、（2016年山东高考）在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O的直径，FB 是圆台的一条母线.（I ）已知G ,H 分别为EC ，FB 的中点，求证：GH ∥平面ABC ； （II ）已知EF =FB =AC =，AB =BC .求二面角的余弦值.【解】(Ⅰ)连结，取的中点，连结， 因为，在上底面内，不在上底面内， 所以上底面，所以平面； 又因为，平面，平面，所以平面； 所以平面平面，由平面，所以平面． (Ⅱ) 连结，以为原点，分别以为轴， 建立空间直角坐标系．，，于是有，，，， 可得平面中的向量，, 于是得平面的一个法向量为， 又平面的一个法向量为， 设二面角为，12F BC A --FC FC M HM GM,GM//EF EF GM GM//GM//ABC MH//B C⊂BC ABC ⊄MH ABC MH//ABC GHM//ABC ⊂GH GHM GH//ABC OB B C AB = OB A ⊥∴O O O O OB,OA,'z y,x,BC AB ,32AC 21FB EF ==== 3)(22=--='FO BO BF O O )0,0,3A(2)0,0,3C(-2)0,3B(0,2)3,3F(0,FBC )3,(30,-=)0,,(3232=FBC )1,3,3(1-=n ABC )1,0,0(2=n A -BC -F θ B则． 二面角的余弦值为．3、（2016年上海高考）将边长为1的正方形（及其内部）绕的旋转一周形成圆柱，如图，长为，长为，其中与在平面的同侧。
2019-2020学年高中数学北师大版必修2一课三测：1.3 三视图 含解析
§3三视图填一填1。
三视图的概念三视图包括主视图（又称正视图）、俯视图，侧视图（通常选择左侧视图,简称左视图)．2．三视图的画法规则(1)主、俯视图反映物体的长度—-“长对正”．(2)主、左视图反映物体的高度-—“高平齐"．（3)俯、左视图反映物体的宽度-—“宽相等”．3．由基本几何体形成的组合体的两种基本形式(1）将基本几何体拼接．(2)从基本几何体中切掉或挖掉部分.判一判1。
任何一个几何体都可画出三视图．（√）2．主视图和左视图都是矩形的几何体一定是长方体．（×)3．主视图的高就是看到的几何体的高．（×)4．画三视图时应保证光线与投射面垂直．（√)5．同一个物体的主视图可能不同．（√)6．画三视图时,被遮住的部分可不画．(×)7．圆柱的三视图都是矩形．（×）8．三视图可以是全等的三角形．（√）想一想1.提示：常见几何体正视图侧视图俯视图长方体矩形矩形矩形正方体正方形正方形正方形圆柱矩形矩形圆圆锥等腰三角形等腰三角形圆圆台等腰梯形等腰梯形两个同心的圆球圆圆圆2.画组合体三视图的“四个步骤”是什么?提示：（1)析：分析组合体的组成形式；(2)分：把组合体分解成简单几何体；(3）画：画分解后的简单几何体的三视图；（4)拼：将各个三视图拼合成组合体的三视图．3．画三视图时要注意避免出现哪些问题？提示：(1)没有确定主视方向直接画图；（2)三个视图摆放位置混乱；（3）未遵循长、宽、高的画图原则；（4）看不见的边界轮廓线未画成虚线．4．由三视图还原几何体的步骤是什么？提示：思考感悟:练一练1。
以下说法正确的是( )A．任何物体的三视图都与物体摆放位置有关B．任何物体的三视图都与物体摆放位置无关C．有的物体的三视图与物体的摆放位置无关D．正方体的三视图一定是三个全等的正方形答案：C2．有一个几何体的三视图如图所示，这个几何体应是一个________．答案:四棱台3．水平放置的下列几何体，主视图是长方形的是________．(填序号)答案：①③④4．一个圆柱的三视图中，一定没有的图形是（)A．矩形B．圆C．三角形D．正方形答案:C5．根据如图所示的俯视图，找出对应的物体．（1）对应________；(2)对应________；(3）对应________；(4）对应________；(5)对应________．答案：(1)（D) （2）(A) （3)（E) （4)（C)(5)（B）知识点一简单几何体的三视图1。
高中数学必修2考点知识专题训练3---空间几何体的三视图(含答案解析)
ൌ
ை ை
ൌ
.
答案:
9.画出如图所示的几何体的三视图.
解:该几何体的三视图如图所示.
3/8
10.如图是一个几何体的三视图,想象该几何体的结构特征,画出该几何体的形状.
解:由于俯视图中有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合 体;结合侧视图和正视图,可知该几何体的上面是一个圆柱,下面是一个长方体.该几何体 的形状如图所示.
高中数学必修 2 考点知识专题训练
空间几何体的三视图
课时过关·能力提升
一、基础巩固
1.下列视图不属于三视图的是( )
A.正视图
B.侧视图
C.后视图
D.俯视图
答案:C
2.如果一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其
圆心,那么这个棱柱
C.圆锥
D.圆柱
8.若线段
AB
平行于投影面,O
是线段
AB
上一点,且
ை ை
ൌ
,
点ܣᇱ,
ܱᇱ,
ܤᇱ分别是
'ܱ'ܣ ܣ, ܱ, ܤ在投影面上的投影点, 则 ܱ' 'ܤൌ __________________.
解析:由题意知 AB∥A'B',OO'∥AA',OO'∥BB',
则有
'ை' ை''
答案:D 4.在下列几何体各自的三视图中,有且仅有两个视图相同的是( )
1/8
A.①②
B.①③
C.①④
D.②④
解析:①正方体,三个视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三个视图各不 相同;④四棱锥,正视图和侧视图相同.
高中数学人教版必修2作业1-2-12空间几何体的三视图2
1.2.1、2 空间几何体的三视图基础巩固一、选择题1．下列投影是平行投影的是()A．俯视图B．路灯底下一个变长的身影C．将书法家的真迹用电灯光投影到墙壁上D．以一只白炽灯为光源的皮影[答案] A[解析]三视图是由平行投影形成的，而B、C、D中由电灯发出的光得到的投影是中心投影．2．对几何体的三视图，下列说法正确的是()A．正视图反映物体的长和宽B．俯视图反映物体的长和高C．侧视图反映物体的高和宽D．正视图反映物体的高和宽[答案] C3．某空间几何体的正视图是三角形，则该几何体不可能是()A．圆柱B．圆锥C．四面体D．三棱柱[答案] A4．小周过生日，公司为她预订的生日蛋糕(示意图)如下图所示，则它的正视图应该是() [答案] B[解析]A为俯视图，注意到封闭的线段情形，正视图应该是B．5．一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台[答案] D[分析]利用三视图逐个排除错误选项即可．[解析]由俯视图可排除A，B，由正视图可排除C，故选D．6．若一个几何体的三视图如下图所示，则这个几何体是()A．三棱锥B．四棱锥C．三棱柱D．四棱柱[答案] B[解析]由俯视图可知底面为四边形，由正视图和侧视图知侧面为三角形，故几何体为四棱锥．二、填空题7．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号)．①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱．[答案]①②③⑤[解析]三棱锥、四棱锥和圆锥的正视图都是三角形，当三棱柱的一个侧面平行于水平面，底面对着观测者时其正视图是三角形，四棱柱、圆柱无论怎样放置，其正视图都不可能是三角形．8．下图中三视图表示的几何体是________.[答案]四棱柱三、解答题9．如图，四棱锥的底面是正方形，顶点在底面上的射影是底面正方形的中心，试画出其三视图．[解析]所给四棱锥的三视图如下图．[点评](1)画三视图时，务必做到正视图与侧视图的高度一致(即所谓的高平齐)、正视图与俯视图的长度一致(即所谓的“长对正”)、侧视图与俯视图的宽度一致(即所谓的“宽相等”)．(2)习惯上将侧视图放在正视图的右侧，将俯视图放在正视图的下方．[拓展提高](1)三视图中各种数据的对应关系：①正视图中AB的长对应原四棱锥底面多边形的左右方向的长度，AC、BC的长则不对应侧棱的长，它们对应四棱锥的顶点到底面左、右两边的距离．②侧视图中，EF的长度对应原四棱锥底面的前后长度，GE、GF的长度则是四棱锥顶点与底面前后两边的距离．③俯视图中HIJK的大小与四棱锥底面的大小形状完全一致，而OK，OI，OJ，OH 的大小，则为四棱锥的顶点在底面上的投影到底面各顶点的距离．(2)误区警示：正视图、侧视图中三角形的腰长有的学生会误认为是棱锥的侧棱长，实则不然．弄清一些数据的对应关系，是后面进行相关计算的前提．10．依所给实物图的形状，画出所给组合体的三视图．[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体，在中心以中心轴为轴线挖去一个小圆柱，故其三视图如下：能力提升一、选择题1．下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④[答案] D[解析]①正方体，三视图均相同；②圆锥，正视图和侧视图相同；③三棱台，三视图各不相同；④圆台，正视图和侧视图相同．[点评]熟悉常见几何体的三视图特征，对于画几何体的直观图是基本的要求．下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体长方体圆柱圆锥圆台球[答案] C[分析]本题是组合体的三视图问题，由几何体的正视图和侧视图均如左图所示知，几何体下面为圆柱或直四棱柱，上面是圆柱或直四棱柱或底面是直角三角形的直三棱柱．[解析]A，B，D都可能是该几何体的俯视图，C不可能是该几何体的俯视图，因为它的正视图上面应为如右图所示的矩形．3．如图所示，画出四面体AB1CD1三视图中的正视图，以面AA1D1D为投影面，则得到的正视图可以为()[答案] A[分析]依次确定四面体AB1CD1的每一条棱在面AA1D1D上的投影即可．[解析]显然AB1，AC，B1D1，CD1分别投影得到正视图的外轮廓，B1C为可见实线，AD1为不可见虚线．故A正确．4．若某几何体的三视图如图所示，那么这个几何体是()A．三棱锥B．四棱锥C．四棱台D．三棱台[答案] B[解析]根据三视图的特征可以断定是四棱锥，由正视图和侧视图可知，该四棱锥底面中，必定有一组对边平行，另一组对边不平行．二、填空题5．下列图形：①三角形；②直线；③平行四边形；④四面体；⑤球．其中投影不可能是线段的是________.[答案]②④⑤[解析]三角形的投影是线段或三角形；直线的投影是点或直线；平行四边形的投影是线段或平行四边形；四面体的投影是三角形或四边形；球的投影是圆．6．已知某一几何体的正视图与侧视图如图所示，则下列图形中，可以是该几何体的俯视图的图形有________.[答案]①②③④三、解答题7．说出下列三视图表示的几何体：[解析]8．根据下列图中所给出的一个物体的三视图，试画出它的形状．[答案]所对应的空间几何体的图形为：。
2017-2018学年高中数学人教B版必修2教师用书：第1章 1
1.1.5 三视图1.能画出简单空间图形的三视图.(重点)2.能识别三视图所表示的立体模型.(重点)3.利用三视图的画法及其特征作组合体的三视图.(难点)4.三视图、直观图、原空间几何体形状之间的相互转化.(难点)教材整理三视图阅读教材P21～P23“例1”以上内容，完成下列问题.1.正投影的定义和性质(1)定义：在物体的平行投影中，如果投射线与投射面垂直，则称这样的平行投影为正投影.(2)性质①垂直于投射面的直线或线段的正投影是点；②垂直于投射面的平面图形的正投影是直线或直线的一部分.2.三视图的分类及画法(1)分类图1164(2)三视图的画法规则①主、俯视图都反映物体的长度——“长对正”；②主、左视图都反映物体的高度——“高平齐”；③俯、左视图都反映物体的宽度——“宽相等”.(3)三视图的排列顺序：先画主视图，左视图在主视图的右边，俯视图在主视图的下边.如果一个几何体的主视图和左视图都是长方形，那么这个几何体不可能是( )A.长方体B.圆柱C.三棱柱D.正三棱锥【解析】长方体和圆柱的主视图和左视图可能是长方形，当三棱柱为直棱柱时，其主视图和左视图可能都是长方形.【答案】 D(1) (2) (3)图1165【精彩点拨】确定正前方→画主视图→画左视图→画俯视图【自主解答】三视图如图①②③所示.1.务必做到长对正，宽相等，高平齐.2.三视图的安排方法是主视图与左视图在同一水平位置，且主视图在左，左视图在右，俯视图在主视图的正下方.3.若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法.1.画出如图1166所示几何体的三视图.图1166【解】图为正六棱柱，主视图和左视图都是矩形，主视图中有两条竖线，左视图中有一条竖线，俯视图是正六边形..【导学号：45722021】图1167【精彩点拨】欲画出该几何体的三视图，先弄清它是由什么简单几何体按什么方式构成的，然后确定主视、左视、俯视的方向，最后按三视图的画法规则画出它的三视图.【自主解答】该物体是由一个正六棱柱和一个圆柱组合而成的，主视图反映正六棱柱的三个侧面和圆柱的侧面，左视图反映正六棱柱的两个侧面和圆柱的侧面，俯视图反映该物体投影后是一个正六边形和一个圆(中心重合)，故它的三视图如图.画组合体的三视图的“四个步骤”1.析：分析组合体的组成形式.2.分：把组合体分解成简单几何体.3.画：画分解后的简单几何体的三视图.4.拼：将各个三视图拼合成组合体的三视图.2.画出如图1168所示的几何体的三视图.图1168【解】探究1该几何体是什么吗？并试着画出图形.图1169【提示】由三视图可知，该几何体为正四棱锥，如图所示.探究2 如何结合三视图还原几何体？【提示】根据三视图还原几何体，要仔细分析和认真观察三视图并进行充分的想象，然后结合三视图的形状，从不同的角度去还原.看图和想图是两个重要的步骤，“想”于“看”中，形状分析的看图方法是解决此类问题的常用方法.根据三视图(如图1170所示)想象物体原形，指出其结构特征，并画出物体的实物草图.图1170【精彩点拨】由主视图、左视图确定几何体为锥体，再结合俯视图确定其是四棱锥，由俯视图可知其底面形状，再结合主视图、左视图所给信息画直观图.【自主解答】由俯视图知，该几何体的底面是一直角梯形；再由主视图和左视图知，该几何体是一四棱锥，且有一侧棱与底面垂直，所以该几何体如图所示.由三视图还原几何体时，一般先由俯视图确定底面，由主视图与左视图确定几何体的高及位置，同时想象视图中每一部分对应实物部分的形状.3.如图1171是一个物体的三视图，则此三视图所描述的物体是下列哪个几何体？( )图1171【解析】由俯视图可知该几何体为旋转体，由主视图、左视图可知该几何体由圆锥、圆柱组合而成.【答案】 D1.下列哪个几何体的三视图可能全是一样的平面图形( )A.长方体B.圆柱C.正四棱锥D.正方体【答案】 D2.已知某物体的三视图如图1172所示，那么这个物体的形状是( )图1172A.长方体B.圆柱C.正方体D.圆锥【解析】俯视图是圆，所以为旋转体，可排除A、C，又主、左视图为矩形，所以不是圆锥，排除D.故选B.【答案】 B3.水平放置的下列几何体，主视图是长方形的是______(填序号).①②③④图1173【解析】①③④的主视图为长方形，②的主视图为等腰三角形.【答案】①③④4.一物体及其主视图如图1174：①②③④图1174则它的左视图与俯视图分别是图形中的________.【解析】左视图是矩形中间有条实线，应选③；俯视图为矩形中间有两条实线，且为上下方向，应选②.【答案】③②5.如图1175所示的三视图表示的几何体是什么？画出物体的形状.【导学号：45722022】图1175【解】该三视图表示的是一个四棱台，如图.。
数学必修二1-2-2三视图练习题5页word
三视图练习题一、选择题1．对几何体的三视图，下列说法正确的是()A．正视图反映物体的长和宽B．俯视图反映物体的长和高C．侧视图反映物体的高和宽D．正视图反映物体的高和宽[答案] C2．一个空间几何体的正视图与侧视图均为全等的等腰三角形，俯视图为一个圆及其圆心，那么这个几何体为()A．棱锥B．棱柱C．圆锥D．圆柱[答案] C3．(2019－2019·安徽淮南高三模拟)下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④[答案] D[解析]①正方体，三视图均相同；②圆锥，正视图和侧视图相同；③三棱台，三视图各不相同；④圆台，正视图和侧视图相同．[点评]熟悉常见几何体的三视图特征，对于画几何体的直观图是基本的要求．下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体长方体圆柱圆锥圆台球4.一个几何体的三视图如图，则组成该几何体的简单几何体为()A．圆柱和圆锥B．正方体和圆锥C．四棱柱和圆锥D．正方体和球[答案] C[解析]由正视图和侧视图可知，该几何体的上部可能为棱锥或圆锥，下部可能为棱柱和圆柱，结合俯视图为圆和圆心及正方形知，上部是圆锥，下部是四棱柱．5．一个几何体的三视图如图，则组成该组合体的简单几何体为()A．圆柱与圆台B．四棱柱与四棱台C．圆柱与四棱台D．四棱柱与圆台[答案] B[解析]该几何体形状如图．上部是一个四棱柱，下部是一个四棱台．6．(2019·北京理，3)一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如下图所示，则该几何体的俯视图为()[答案] C[解析]由正视图和侧视图知，该长方体上面去掉的小长方体，从正前方看在观察者左侧，从左向右看时在观察者右侧，故俯视图为C.7．如图所示几何体的正视图和侧视图都正确的是()[答案] B8．(2019·新课标全国高考)在一个几何体的三视图中，主视图和俯视图如下图所示，则相应的侧视图可以为()[答案] D[解析]此几何体为一个半圆锥和一个半三棱锥的组合体，只有D项符合题意．9．如图所示，在正方体ABCD－A1B1C1D1中，M、N分别是BB1、BC的中点，则图中阴影部分在平面ADD1A1上的正投影是() [答案] A[解析]N点投影为AD中点，M点投影为AA1中点，故选A.10．某几何体的三视图如图所示，那么这个几何体是()A．三棱锥B．四棱锥C．四棱台D．三棱台[答案] B[解析]由正视图与侧视图知，该几何体为棱锥，由俯视图知，该几何体是四棱锥．二、填空题11．下列图形：①三角形；②直线；③平行四边形；④四面体；⑤球．其中投影不可能是线段的是________．[答案]②④⑤[解析]三角形的投影是线段成三角形；直线的投影是点或直线；平行四边形的投影是线段或平行四边形；四面体的投影是三角形或四边形；球的投影是圆．12．(2019·烟台高一检测)已知某一几何体的正视图与侧视图如图所示，则下列图形中，可以是该几何体的俯视图的图形有________．[答案]①②③④13．(2019－2019·湖南高三“十二校联考”)一个几何体的三视图如图所示，其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形，则用________个这样的几何体可以拼成一个棱长为4的正方体．[答案] 3[解析]该几何体是四棱锥，其底面是边长为4的正方形，高等于4，如图(1)所示的四棱锥A－A1B1C1D1，如图(2)所示，三个相同的四棱锥A－A1B1C1D1，A－BB1C1C，A －DD1C1C可以拼成一个棱长为4的正方体．三、解答题14．如图所示是一个四棱柱铁块，画出它的三视图．[答案]正视图、俯视图、侧视图分别如图所示．15．依所给实物图的形状，画出所给组合体的三视图．[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体，在中心以中心轴为轴线挖去一个小圆柱，故其三视图如下：16．说出下列三视图表示的几何体：[解析]17．根据下列图中所给出的一个物体的三视图，试画出它的形状．[答案]所对应的空间几何体的图形为：。
新高中人教B版数学必修二同步练习：1.1.5_三视图(含答案)
1.1.5 三视图【课时目标】1．了解正投影的概念；2．理解三视图的原理和视图间的相互关系，能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简单组合)的三视图．1．正投影在物体的平行投影中，如果投射线与投射面垂直，则称这样的平行投影为__________．2．三视图(1)一个投射面水平放置，叫做______________，投射到水平投射面的图形叫__________．一个投射面放置在正前方叫做____________，投射到直立投射面内的图形叫__________，和直立、水平两个投射面都垂直的投射面叫做______________，投射到侧立投射面内的图形叫做__________．(2)将空间图形向水平投射面、直立投射面、侧立投射面作正投影，然后把这三个投影按一定的布局(俯视图放在________的下面，长度与__________一样，左视图放在__________的右面，高度与__________一样，宽度与__________的宽度一样即“长对正、高平齐、宽相等”)放在一个平面内，这样构成的图形叫做空间图形的__________．一、选择题1．下列说法正确的是()A．任何几何体的三视图都与其摆放的位置有关B．任何几何体的三视图都与其摆放的位置无关C．有的几何体的三视图与其摆放的位置无关D．正方体的三视图一定是三个全等的正方形2．如图所示的一个几何体，哪一个是该几何体的俯视图()3．如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④4．一个长方体去掉一个小长方体，所得几何体的主视图与左视图分别如图所示，则该几何体的俯视图为()5．如图所示的正方体中，M、N分别是AA1、CC1的中点，作四边形D1MBN，则四边形D1MBN在正方体各个面上的正投影图形中，不可能出现的是()6．一个长方体去掉一角的直观图如图所示，关于它的三视图，下列画法正确的是()二、填空题7．根据如图所示俯视图，找出对应的物体．(1)对应________；(2)对应________；(3)对应________；(4)对应________；(5)对应________．8．若一个三棱柱的三视图如图所示，则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________．9．用小正方体搭成一个几何体，如图是它的主视图和左视图，搭成这个几何体的小正方体的个数最多为________个．三、解答题10．在下面图形中，图(b)是图(a)中实物画出的主视图和俯视图，你认为正确吗？如果不正确，请找出错误并改正，然后画出左视图(尺寸不作严格要求)．11．(1)如图是截去一角的长方体，画出它的三视图．(2)如图，螺栓是棱柱和圆柱的组合体，画出它的三视图．能力提升12．对如图所示的几何体正确的说法是()A．如果把(1)作为主视图，则(2)、(3)分别是俯视图和左视图B．如果把(2)作为主视图，则(1)、(4)分别是俯视图和左视图C．如果把(3)作为主视图，则(2)、(1)分别是俯视图和左视图D．如果把(4)作为主视图，则(2)、(1)分别是俯视图和左视图13．用小立方体搭成一个几何体，使它的主视图和俯视图如图所示，搭建这样的几何体，最多要几个小立方体？最少要几个小立方体？在绘制三视图时，要注意以下三点：1．若两相邻物体的表面相交，表面的交线是它们的原分界线，在三视图中，分界线和可见轮廓都用实线画出，不可见轮廓用虚线画出．2．一个物体的三视图的排列规则是：俯视图放在主视图的下面，长度和主视图一样．左视图放在主视图的右面，高度和主视图一样，宽度和俯视图一样，简记为“长对正，高平齐，宽相等”．3．在画物体的三视图时应注意观察角度，角度不同，往往画出的三视图不同．1．1．5 三视图答案知识梳理1．正投影2．(1)水平投射面俯视图直立投射面主视图侧立投射面左视图(2)主视图主视图主视图主视图俯视图三视图作业设计1．C[球的三视图与其摆放位置无关．]2．C3．D[在各自的三视图中①正方体的三个视图都相同；②圆锥有两个视图相同；③三棱台的三个视图都不同；④正四棱锥有两个视图相同．]4．C[由三视图中的主、左视图得到几何体的直观图如图所示，所以该几何体的俯视图为C．]5．D6．A7．(1)D(2)A(3)E(4)C(5)B8．2 4解析三棱柱的高同左视图的高，左视图的宽度恰为底面正三角形的高，故底边长为4．9．710．解图(a)是由两个长方体组合而成的，主视图正确，俯视图错误，俯视图应该画出不可见轮廓线(用虚线表示)，左视图轮廓是一个矩形，有一条可视的交线(用实线表示)，正确画法如图所示．11．(1)解该图形的三视图如图所示．(2)解该物体是由一个正六棱柱和一个圆柱组合而成的，正视图反映正六棱柱的三个侧面和圆柱侧面，左视图反映正六棱柱的两个侧面和圆柱侧面，俯视图反映该物体投影后是一个正六边形和一个圆(中心重合)．它的三视图如图所示．12．D[物体有不同的放法得到不同的视图，所以把不同的图作为主视图就是考查各种不同的放法时物体的三视图．若(2)为主视图，说明物体已经竖起来放，显然此时(1)(3)(4)里面没有适合的视图作为左视图和俯视图；若(3)为主视图，则俯视图(2)中的正方体小块的位置不正确；若(1)为主视图，则俯视图(2)中的正方体小块的位置不正确．所以D正确，故选D．]13．解由于主视图中每列的层数即是俯视图中该列的最大数字，因此，用的立方块数最多的情况是每个方框都用该列的最大数字，即如图①所示，此种情况共用小立方块17块．数字可减少到最少的1，即如图②所示，这样的摆法只需小立方块11块．。
必修二-三视图-直观图新课练习加答案
∠ABC＝45°，AB=AD＝1，DC⊥BC，这个平面图形的面积为_____
27．已知△ABC的平面直观图△A′B′C′是边长为a的正三角形，那么原△ABC的面积为____________.
28．水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为.
19．D
【解析】
20．A
【解析】
21．B
【解析】B错误.因为平行于y轴的线段,其对应的线段平行于y′轴,长度变为原来的一半.
22．B
【解析】根据斜二测画法的要求知,正方形的直观图为平行四边形.
23．C.
【解析】由几何体知，该物体是由一个长方体和一个截角三棱柱组成的，结合它们的轮廓线和交线，它的俯视图应为C.
C.梯形的直观图不是梯形
D.正三角形的直观图一定为等腰三角形
23．如图(1)所示的一个几何体，在图(2)中是该几何体俯视图的是( )
(1)
(2)
24．如右图，平行四边形OPQR是四边形OPQR的直观图，若OP＝3, OR＝1，则原四边形OPQR的周长为.
25．如图为一个棱长为2cm的正方体被过其中三个顶点的平面削去一个角后余下的几何体，试画出它的正视图．
B.原图中平行于y轴的线段,其对应线段平行于y′轴,长度不变
C.画与坐标系xOy对应的坐标系x′O′y′时,∠x′O′y′可等于135°
D.作直观图时,由于选轴不同,所画直观图可能不同
22．斜二测画法所得直观图,以下说法正确的是( )
A.等腰三角形的直观图仍是等腰三角形
B.正方形的直观图为平行四边形
9．C
【解析】由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的左侧，
高中数学人教A版必修2《空间几何体及三视图》课后练习二(含解析)
（同步复习精讲辅导）北京市-高中数学空间几何体及三视图课后练习二（含解析）新人教A版必修2题1有一个三棱锥和一个四棱锥，棱长都相等，问它们的一个侧面重叠后，还有几个暴露面？题2A．①②③ B．②③ C．②③⑤ D．①⑤题3说出下列图中两个三视图分别表示的几何体．(1) (2)题4已知正三棱锥V－ABC的正视图和俯视图如图所示．求出侧视图的面积．题5已知一个空间几何体的三视图如图所示，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ ）．A ．4cm 3B ．5cm 3C ．6cm 3D ．7cm 3题6 如图是由大小相同的长方体木块堆成的几何体的三视图，则此几何体共由几块木块堆成．题7一个长方体的主视图和左视图如图所示（单位：cm ），则俯视图的面积是_______．题8如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为22 主视图 2 左视图 44，且垂直于底面，该三棱锥的主视图是（）题9某几何体的三视图如图所示，则它的体积是________．题10某几何体的一条棱长为根号7，在该几何体的正视图中，这条棱的投影是长为根号6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b 的最大值为_______．题11某几何体的正视图和侧视图均为如图1所示，则该几何体的俯视图不可能是：（）A．（1），（3） B．（2），（4）C．（1），（2），（3）D．（1），（2），（3），（4）题12若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（）．A．3523cm3 B．3203cm3 C．2243cm3 D．1603cm3课后练习详解题1答案：5个．详解：如图①，三棱锥S—A′B′C′有四个暴露面；如图②，四棱锥V—ABCD有五个暴露面，且它们的侧面都是完全相同的正三角形；如图③，当三棱锥S—A′B′C′的侧面A′B′C′与四棱锥V—ABCD的侧面AVD完全重合后，四点S、A、B、V共面. 同样四点S、D、C、V也共面（证明如下），此时，新几何体共有5个面．证明：如图所示，过V作VS′∥AB，则四边形S′ABV为平行四边形，有∠S′VA=∠VAB=60°，从而ΔS′VA为等边三角形，同理ΔS′VD也是等边三角形，从而ΔS′AD也是等边三角形，得到以ΔVAD为底，以S′与S重合．这表明ΔVAB与ΔVSA共面，ΔVCD与ΔVSD共面，故共有5个暴露面．题2答案：D详解: ①正确，正四面体是每个面都是等边三角形的四面体，如正方体ABCDA1B1C1D1中的四面体ACB1D1；②错误，如图所示，底面△ABC为等边三角形，可令AB＝VB＝VC＝BC＝AC，则△VBC为等边三角形，△VAB和△VCA均为等腰三角形，但不能判定其为正三棱锥；③错误，必须是相邻的两个侧面；④错误，如果有两条侧棱和底面垂直，则它们平行，不可能；⑤正确，当两个侧面的公共边垂直于底面时成立；⑥错误，当底面是菱形时，此说法不成立．题3答案：图（1）是正六棱锥；图（2）是两个相同的圆台组成的组合体．题4答案：6．详解：如图．根据三视图间的关系可得BC ＝23， 侧视图中VA ＝42－(23×32×23)2＝12＝23，∴S △VBC ＝12×23×23＝6． 题5答案：选A ．详解:由三视图可知，几何体如图所示，底面为直角梯形ABCD ，且 ,,2cm,4cm,2cm,2cm ADBC AD AB AD BC PA AB ⊥====()2241124332ABCD V S PA ⨯+∴=⋅=⨯⨯=cm 3题6答案：5．详解：由三视图可知：此几何体最少由5块木块堆成，如图所示：故答案为5．题7答案：6cm 2．详解：根据给出的长方体的主视图和左视图可得，俯视图的长方形的长与主视图的长方形的宽相等为3，俯视图的长方形的宽与左视图的长方形的宽相等为2．俯视图是边长分别为3和2的长方形，因而其面积为6cm 2．题8答案：B ．详解：通过观察图形，三棱锥的正（主）视图应为高是4，底面边长为3的直角三角形． 故应选B ．题9答案：8－23π． 详解：分析图中所给的三视图可知，对应空间几何图形，应该是一个棱长为2的正方体中间挖去一个半径为1，高为2的圆锥，则对应体积为：V ＝2×2×2－13π×12×2＝8－23π． 题10 答案：4．详解：根据三视图的平行投影的法则，由题意，、a 、b分别作为三个面的对角线．可得2222222,8a b a b ++=⨯+= ∴4a b +===．题11 答案：B ． 详解：由该几何体的正视图和侧视图均为已知图所示，所以该几何体是由上下两部分组成的，其上面是一个球，而下面可能是①直四棱柱，②直三棱柱，③圆柱．根据长对正，宽相等的原则，底面图形的长和宽应该相等，据此可得出答案． 由该几何体的正视图和侧视图均为已知图所示，所以该几何体是由上下两部分组成的，其上面是一个球，根据长对正，宽相等的原则，底面图形的长和宽应该相等故该几何体的俯视图（1）、（3）皆有可能．（2）中的正视图和侧视图不是轴对称图形，（4）中正三角形的底边和高不相等，不满足要求．题12答案：B详解：该空间几何体为一四棱柱和一四棱台组成的,四棱柱的长宽都为4，高为2, 体积为4×4×2=32四棱台的上下底面分别为边长为4和8的正方形，高为2，所以体积为所以该几何体的体积为32+3224=．3224)8844(2312222=+⨯+⨯⨯3320。
北师大高中数学必修二课后作业4 三视图 含解析
课后作业(四)(时间45分钟)学业水平合格练(时间20分钟)1．下列几何体各自的三视图中，有且仅有两个视图相同的是()①长方体②圆锥③三棱台④正四棱锥A．①②B．①③C．①④D．②④[解析]②圆锥和④正四棱锥的主视图和左视图相同．[答案] D2．某几何体的主视图和左视图均如下图所示，则该几何体的俯视图不可能是()[解析]A是两个圆柱的组合体，B是一个圆柱和一个四棱柱的组合体，C选项的主视图和左视图不相同，D可以是一个底面为等腰直角三角形的直三棱柱与一个四棱柱的组合体．[答案] C3．如图所示的三视图表示的几何体可能是()A．圆台B．四棱台C．四棱锥D．三棱台[解析]由三视图可知，该几何体是四棱台．[答案] B4．某空间几何体的主视图是三角形，则该几何体不可能是()A．圆柱B．圆锥C．四面体D．三棱柱[解析]圆柱的主视图不可能是三角形．[答案] A5．若一个几何体的三视图如下图所示，则这个几何体是()A．三棱锥B．四棱锥C．三棱柱D．四棱柱[解析]由俯视图可知底面为四边形，由主视图和左视图知侧面为三角形，故几何体为四棱锥．[答案] B6．水平放置的下列几何体，主视图是长方形的是________(填序号).[解析]①③④的主视图为长方形，②的主视图为等腰三角形．[答案]①③④7．一物体及其主视图如图：则它的左视图与俯视图分别是图形中的________．[解析]左视图是矩形中间有条实线，应选③；俯视图为矩形中间有两条实线，且为上下方向，应选②.[答案]③②8．如图所示，在正方体ABCD－A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P－ABC的主视图与左视图的面积的比值为________．[解析]三棱锥P－ABC的主视图与左视图为等底等高的三角形，故它们的面积相等，面积比值为1.[答案] 19．如图，四棱锥的底面是正方形，顶点在底面上的射影是底面正方形的中心，试画出其三视图．[解]所给四棱锥的三视图如下图．10．如图所示的螺栓是由棱柱和圆柱构成的组合体，试画出它的三视图．[解]三视图如图所示．应试能力等级练(时间25分钟)11．如果用□表示1个立方体，用表示2个立方体叠加，用表示3个立方体叠加，那么图中由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是()[解析]从正前方观察，有两层，下边一层有3个立方体，且中间为3个立方体叠加；第二层中间有一个立方体，且有2个立方体叠加，故选B.[答案] B12．如图所示为一个简单几何体的三视图，则其对应的几何体是()[解析]对于A，该几何体的三视图恰好与已知图形相符，故A 符合题意；对于B，该几何体的主视图的矩形中，对角线应该是虚线，故不符合题意；对于C，该几何体的主视图的矩形中，对角线应该是从左上到右下的方向，故不符合题意；对于D，该几何体的左视图的矩形中，对角线应该是虚线，故不符合题意．故选A.[答案] A13．已知某组合体的主视图与左视图相同(其中AB＝AC，四边形BCDE为矩形)，则该组合体的俯视图可以是图中的________．(把你认为所有正确图象的序号都填上)[解析]由主视图和左视图可知几何体为锥体和柱体的组合体．(1)若几何体为圆柱与圆锥的组合体，则俯视图为③；(2)若几何体为棱柱与圆锥的组合体，则俯视图为④；(3)若几何体为棱柱与棱锥的组合体，则俯视图为①；(4)若几何体为圆柱与棱锥的组合体，则俯视图为②.[答案]①②③④14．如图是一个棱柱的三视图，根据三视图的作图原则，则x＝________，y＝________.[解析] 棱柱的底面是一个直角三角形，根据“长对正、高对平、宽相等”的原则可知两直角边分别为x ＋y －2(或8)和x －y ＋5(或3y )，则⎩⎨⎧ x ＋y －2＝8，x －y ＋5＝3y即⎩⎨⎧ x ＋y ＝10，x －4y ＝－5解得⎩⎨⎧ x ＝7，y ＝3.[答案] 7 3 15．如图，该几何体是由一个长方体木块锯成的．(1)判断该几何体是否为棱柱；(2)画出它的三视图．[解] (1)是棱柱．因为该几何体的前、后两个面互相平行，其余各面都是矩形，而且相邻矩形的公共边都互相平行．(2)该几何体的三视图如图．。
必修二空间几何体的三视图(附答案)
空间几何体的三视图[学习目标] 1.了解中心投影和平行投影.2.能画出简单空间图形的三视图.3.能识别三视图所表示的立体模型.知识点一投影的概念及分类1.投影的定义由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影.其中，我们把光线叫做投影线，把留下物体影子的屏幕叫做投影面.2.投影的分类3.当图形中的直线或线段不平行于投影线时，平行投影都具有下述性质：①直线或线段的平行投影仍是直线或线段；②平行直线的平行投影是平行或重合的直线；③平行于投影面的线段，它的投影与这条线段平行且等长；④与投影面平行的平面图形，它的投影与这个图形全等；⑤在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比.知识点二三视图的概念及特征1.定义：光线从几何体的前面向后面正投影，得到投影图，这种投影图叫做几何体的正视图；光线从几何体的左面向右面正投影，得到投影图，这种投影图叫做几何体的侧视图；光线从几何体的上面向下面正投影，得到投影图，这种投影图叫做几何体的俯视图.几何体的正视图、侧视图和俯视图统称为几何体的三视图，三视图是正投影.2.基本特征：一个几何体的侧视图和正视图高度一样，俯视图与正视图长度一样，侧视图与俯视图宽度一样.思考 画三视图时一定要求光线与投影面垂直吗？ 答 是.由画三视图的规则要求可知光线与投影面垂直.题型一 中心投影与平行投影 例1 下列说法中：①平行投影的投影线互相平行，中心投影的投影线相交于一点；②空间图形经过中心投影后，直线还是直线，但平行线可能变成了相交的直线；③两条相交直线的平行投影是两条相交直线.其中正确的个数为( )A.0B.1C.2D.3 答案 B解析 由平行投影和中心投影的定义可知①正确；空间图形经过中心投影后，直线可能变成直线，也可能变成一个点，如当投影中心在直线上时，投影为点；平行线有可能变成相交线，如照片中由近到远物体之间的距离越来越近，最后相交于一点，②不正确；两条相交直线的平行投影是两条相交直线或一条直线，③不正确.跟踪训练1 已知△ABC ，选定的投影面与△ABC 所在平面平行，则经过中心投影后所得的△A ′B ′C ′与△ABC ( ) A.全等 B.相似 C.不相似 D.以上都不对答案 B解析 本题主要考查对中心投影的理解.根据题意画出图形，如图所示.由图易得OA OA ′＝AB A ′B ′＝OB OB ′＝BC B ′C ′＝OC OC ′＝AC A ′C ′，则△ABC ∽△A ′B ′C ′.题型二画空间几何体的三视图例2如图是按不同方式放置的同一个圆柱，阴影面为正面，画出其三视图.解三视图分别如图所示.跟踪训练2螺栓是棱柱和圆柱构成的组合体，如图，画出它的三视图.解该物体是由一个正六棱柱和一个圆柱组合而成的，正视图反映正六棱柱的三个侧面和圆柱侧面，侧视图反映正六棱柱的两个侧面和圆柱侧面，俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).三视图如图所示.题型三由三视图还原空间几何体例3根据以下三视图想象物体原形，并画出物体的实物草图.(1)(2)解(1)此几何体上面可以为圆柱，下面可以为圆台，所以实物草图可以如图.(2)此几何体上面可以为圆锥，下面可以为圆柱，所以实物草图可以如图.反思与感悟由三视图还原空间几何体的步骤：跟踪训练3已知如下三视图，试分析该几何体结构特征并画出物体的实物草图.解由三视图可知该几何体为四棱锥，对应空间几何体如图：数形结合思想例4某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为a的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为6和b的线段，求a2＋b2的值. 分析本题考查某几何体的一条棱长和它在三视图中的投影长的关系，这种关系比较抽象，不易理解，我们可以结合长方体的体对角线在三个面上的投影来理解这个问题.解如图所示，设长方体的长、宽、高分别为m，n，k，体对角线长为7，体对角线在三个相邻面上的投影长分别为a，6，b.则由题意，得m 2＋n 2＋k 2＝7，n 2＋k 2＝6，解得m ＝1或m ＝－1(舍去)，则⎩⎪⎨⎪⎧k 2＋1＝a ，n 2＋1＝b ，所以(a 2－1)＋(b 2－1)＝6，即a 2＋b 2＝8.解后反思 本题主要是根据题意利用数形结合思想构造一个长方体，通过长方体把a ，b 集中在方程中求解.画出所给几何体的三视图例5 画出如图所示物体的三视图.分析 首先正视图与侧视图的高要相等，其次侧视图的宽与俯视图的宽一致. 解 该几何体的三视图如图所示：解后反思 本例的侧视图中有一条看不到的棱，在绘图时应用虚线，常见错误是将此虚线误绘成实线，这一点在绘制三视图时尤其要重视.1.一条直线在平面上的平行投影是()A.直线B.点C.射线D.直线、射线或点2.若一个几何体的正视图和侧视图都是等腰三角形，俯视图是带圆心的圆，则这个几何体可能是()A.圆柱B.三棱柱C.圆锥D.球体3.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为()4.如图所示，正三棱柱(底面是正三角形的直三棱柱)ABC－A1B1C1的正视图是边长为4的正方形，则此正三棱柱的侧视图的面积为()A.8 3B.4 3C.2 3D.165.有一个正三棱柱(俯视图为正三角形)的三视图如图所示，则这个三棱柱的高和底面边长分别为________.一、选择题1.一个几何体的三视图如图所示，则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台2.某空间几何体的正视图是三角形，则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱3.一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为()4.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()5.已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于()A.32 B.1 C.2＋12 D. 26.一几何体的直观图如图所示，下列给出的四个俯视图中正确的是()7.某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为()A.1B. 2C. 3D.2二、填空题8.如图所示，桌面上放着一个半球，则它的三视图中，与其他两个视图不同的是______(填“正视图”“侧视图”或“俯视图”).9.如图，在正方体ABCD－A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P－ABC的正视图与侧视图的面积的比值为________.10.已知一几何体的三视图如下，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何体(或图形)的4个顶点，这些几何体(或图形)是________.(写出所有正确结论的编号)①矩形；②不是矩形的平行四边形；③有三个面为直角三角形，有一个面为等腰三角形的四面体；④每个面都是等腰三角形的四面体；⑤每个面都是直角三角形的四面体.11.一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于________.三、解答题12.如图是一个几何体的正视图和俯视图.(1)试判断该几何体是什么几何体；(2)画出其侧视图，并求该平面图形(侧视图)的面积.13.一个物体由几块相同的正方体组成，其三视图如图所示，试据图回答下列问题：(1)该物体有多少层？(2)该物体的最高部分位于哪里？(3)该物体一共由几个小正方体构成？当堂检测答案1.答案 D解析当直线与投影线平行时，投影是一个点；当直线与投影线垂直时，投影是一条直线；当直线与投影线相交，但不垂直时，投影是一条射线.2.答案 C解析由圆锥的三视图可知这个几何体可能是圆锥.3.答案 D解析从左往右看，主体的轮廓是一个长方形，长方体的对角线可以看见，且该对角线是从左下角往右上角倾斜的.4.答案 A解析由正视图可知三棱柱的高为4，底面边长为4，所以底面正三角形的高为23，所以侧视图的面积为4×23＝8 3.故选A.5.答案2,4解析由正三棱柱三视图中的数据，知三棱柱的高为2，底面边长为23×23＝4.课时精练答案一、选择题1.答案 D解析先观察俯视图，再结合正视图和侧视图还原空间几何体.由俯视图是圆环可排除A，B，由正视图和侧视图都是等腰梯形可排除C，故选D.2.答案 A解析由三视图知识，知圆锥、四面体、三棱柱(放倒看)都能使其正视图为三角形，而圆柱的正视图不可能为三角形，故选A.3.答案 C解析正视图中小长方形在左上方，对应俯视图应该在左侧，排除B、D，侧视图中小长方形在右上方，排除A，故选C.4.答案 D解析由几何体的正视图和俯视图可知，该几何体的底面为半圆和等腰三角形，其侧视图可以是一个由等腰三角形及底边上的高构成的平面图形.5.答案 D解析正方体的侧视图面积为2，正视图和侧视图完全相同，所以面积也为 2.6.答案 B解析几何体俯视图的轮廓是矩形，几何体的上部的棱都是可见线段，所以C，D不正确；几何体的最上面的棱与正视图方向垂直，所以A不正确.7.答案 C解析由三视图可知，该几何体是由一个正方体切掉部分后留下的一个四棱锥.如图所示，所以最长的棱长为12＋12＋12＝ 3.二、填空题8.答案俯视图解析该半球的正视图与侧视图均为半圆，而俯视图是一个圆，所以俯视图与其他两个视图不同.9.答案 1解析依题意得三棱锥P－ABC的正视图与侧视图分别是一个三角形，且这两个三角形的底边长都等于正方体的棱长，底边上的高也都等于正方体的棱长，因此三棱锥P－ABC的正视图与侧视图的面积的比值为1.10.答案①③④⑤解析由三视图知该几何体是底面为正方形的长方体.故①可能，如图，由图可知，②不可能，③④⑤都有可能.11.答案 2解析由图可得该几何体为三棱柱，因为正视图、侧视图、俯视图的内切圆最小的是正视图(直角三角形)所对应的内切圆，所以最大球的半径为正视图中直角三角形的内切圆的半径r. 由题意，得8－r＋6－r＝82＋62.解得r＝2.三、解答题12.解 (1)由该几何体的正视图和俯视图可知该几何体可以是一个正六棱锥.(2)该几何体的侧视图如图所示：其中AB ＝AC ，AD ⊥BC ，且BC 的长是俯视图中正六边形对边间的距离，即BC ＝3a ，AD是正棱锥的高，则AD ＝3a .所以该平面图形(侧视图)的面积为12×3a ×3a ＝32a 2.13.解 (1)该物体一共有两层，从正视图和侧视图都可以看出来.(2)该物体最高部分位于左侧第一排和第二排.(3)从侧视图及俯视图可以看出，该物体前后一共三排，第一排左侧2个，右侧1个；第二排左侧2个，右侧没有；第三排左侧1个，右侧1个.该物体一共由7个小正方体构成.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高一数学必修二练习
一、选择题
1．下面的几何物体中，哪一个正视图不是三角形( )
A．竖放的圆锥B．三棱锥 C．三棱柱 D．竖放的正四棱锥
2．下列几何体各自的三视图中，有且只有两个视图是相同的是( )
A．①② B．①③ C．①④ D．②④
3．已知几何体的三视图(如图)，则这个几何体自上而下依次为( )
A．四棱台，圆台 B．四棱台，四棱台 C．四棱柱，四棱柱 D．不能判断
4．某四棱锥的三视图如图所示，该四棱锥的表面积是( )
A．32 B．16＋16 2 C．48 D．16＋322
5.下列命题中正确的是( )
A.平行于圆锥的一条母线的截面是等腰三角形
B.平行于圆台的一条母线的截面是等腰梯形
C.过圆锥顶点的截面是等腰三角形
D.过圆台一个底面中心的截面是等腰梯形
6. 若一个几何体的正视图和侧视图都是等腰三角形，俯视图是圆，则这个几何体可能是（）
Ａ．圆柱Ｂ．三棱柱Ｃ．圆锥Ｄ．球体
7、三视图均相同的几何体有（）
Ａ．球Ｂ．正方体Ｃ．正四面体Ｄ．以上都对
8．给出下列命题：
①如果一个几何体的三视图是完全相同的，则这个几何体是正方体；
②如果一个几何体的正视图和俯视图都是矩形，则这个几何体是长方体；
③如果一个几何体的三视图都是矩形，则这个几何体是长方体；
④如果一个几何体的正视图和侧视图都是等腰梯形，则这个几何体是圆台．
其中正确命题的个数是( )
A．0 B．1 C．2 D．3
*9．某简单几何体的一条对角线长为a，在该几何体的正视图、侧视图与俯视图中，这条对角线的投影都是长为2的线段，则a等于( )
A. 2
B. 3 C．1 D．2
二、填空题
10、三视图的正视图、俯视图、侧视图分别是从、、观察同一个几何体，画出的空间几何体的图形．（正前方，正上方，正左方）
11、圆台的正视图、侧视图都是，俯视图是．（全等的等腰梯形，两个同心圆）
12．把边长为1的正方形ABCD沿对角线BD折起形成三棱锥C－ABD，其主视图与俯视图如图所示，则其左视图的面积为________．
高一数学《空间几何体的三视图和直观图》练习题
A组
1．右图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（）
2．利用斜二测画法得到的
①三角形的直观图一定是三角形；②正方形的直观图一定是菱形；
③等腰梯形的直观图可以是平行四边形；④菱形的直观图一定是菱形.
以上结论正确的是（）
A．①②B．①C．③④D．①②③④
3．等腰梯形ABCD,上底边CD=1, 腰AD=CB=2 , 下底AB=3，按平行于上、下底边取x轴，则直观图A′B′C′D′的面积为_______．
4．一个三角形在其直观图中对应一个边长为1正三角形，原三角形的面积为 .
5．一天，小莹站在室内，室内有一面积为3平方米的玻璃窗，她站在离窗子4米的地方向外看，他能看到窗前面一幢楼的面积为 .（楼层之间的距离为20米）
6．如图，E、F分别是正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的正投影可能是（要求把可能的图的序号都填上）。
7．一个物体由几块相同的正方体叠成，它的正视图、侧视图、俯视图如图所示，请回答下列问题：
（1）该物体共有层？
（2）最高部分位于哪个位置？（在三视图中把相应正方体涂黑以标记）
（3）一共需要个小正方体？
B组
8．一个画家有14个边长为1m的正方体，他在地面上把它们摆成如右图所示的形式，然后他把露出的表面都涂上颜色，那么被涂
上颜色的总面积为 .
9．在阳光下一个大球放在水平面上, 球的影子伸到距球与地面接触点10米处, 同一时刻, 一根长1米一端接触地面且与地面垂
直的竹竿的影子长为2米, 则该球的半径等于米。
10．右图是由一些大小相同的小正方体组成的几何体的主视图和俯视图。
（1）请你画出这个几何体的各种可能的左视图；
（2）若组成这个几何体的小正方形的块数为n，请你写出n的所有可能值。
11．小华身高1.6米，一天晚上回家走到两路灯之间，如右图所示，他发现自己的身影的顶部正好在A路灯的底部，他又向前走了
5米，又发现身影的顶部正好在B路灯的底部。
已知两路灯之间的距离为10米，（两路灯的高度是一样的）。
求：（1）路灯的高度；
（2）当小华走到B路灯下时，他在A路灯下的身影有多长？。