热学教案(第五章).ppt
合集下载
工程热力学(511章)教案 沈道维版

定温、定熵、多变压缩消耗理论功的比较:
8-2 余隙容积的影响
余隙容积:当活塞运动到上死点位置时,在活塞顶面与气缸盖间有一定的空隙,该空隙的容积称为余隙容积。
1)对生产量的影响:降低排气量。
2)对理论耗功的影响:不论有无余隙,压缩单位质量气体所消耗的理论压气功相同。
8-4叶轮式压气机的工作原理
✓与活塞式压气机相比,叶轮式压气机结构紧凑,输气量大,输气均匀且运转平稳,效率高。
缺点是单级增压比小、摩擦损耗大。
✓叶轮式压气机分为离心式与轴流式两种型式。
轴流式压气机:
离心式压气机:
课后作业无
9-3活塞式内燃机的理想循环一、混合加热理想循环(萨巴德循环)
二、定压加热理想循环(狄塞尔循环)
三、定容加热理想循环(奥托循环)
9-6 燃气轮机装置循环
燃气轮机的特点:
1.开式循环(open cycle),工质流动
2.运转平稳,连续输出功
3.启动快,达满负荷快
4.压气机消耗了燃气轮机产生功率的很大部分,但重量功率比(specific weight of engine)仍较大
循环示意图:
循环原理图:
课后作业9-1。
人教版物理《热学》电子教案50页PPT

人教版物理热学》电子教案
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
热力学第五章6162474页PPT文档
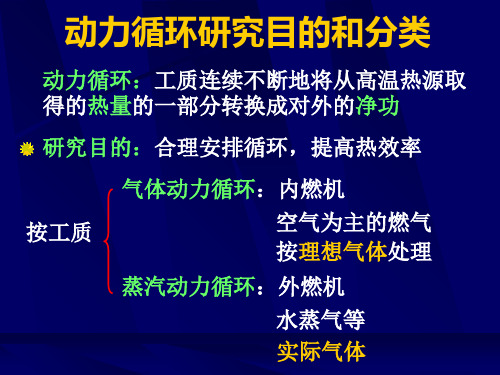
四冲程高速柴油机的理想化
1. 工质
p3 4
定比热理想气体
工质数量不变
2
P-V图p-v图
2’
2. 0—1和1’ —0抵消 开口闭口循环
3. 燃烧外界加热
p0 0
5 1’
1
4. 排气向外界放热
V
5. 多变绝热
6. 不可逆可逆
理想混合加热循环(萨巴德循环)
分析循环吸热量,放热量,热效率和功量
p
3
4
T
4 3
1
2’ 喷柴油
V
2 开始燃烧
2—3 迅速燃烧,近似 V
p↑5~9MPa
四冲程高速柴油机工作过程
3—4 边喷油,边膨胀
p3 4
近似 p 膨胀
t4可达1700~1800℃
2 2’
4 停止喷柴油
5
4—5 多变膨胀
p0
1’
p5=0.3~0.5MPa
0
1
t5500℃
V
5—1’ 开阀排气, V 降压
1’—0 活塞推排气,完成循环
p 3
T
3
2
2
4
4
1
1
v
s
定容加热循环的计算Βιβλιοθήκη 吸热量T3
q1cvT3T2
放热量(取绝对值)
2
4
q2cvT4T1
1
热效率
s
t
wq1q21q21T 4T 1
q1 q1
q1 T 3T 2
定容加热循环的计算
热效率
T
t
1 T4 T3
T1 T2
1
T1
T4 T1
T2
T3 T2
大学物理第五章PPT课件

Q be W abe (a E )8 4208
29J2
p
负号表示放热
c
(3)若Ed - Ea=167 J,求系统沿ad及db变
化时,各吸收了多少 a
热量?
0
-
b e
d V
24
W a dW ad 4 bJ 2
Q a d W a d ( E d E a ) 2J 09
又 E b E aE 2J 08
p
o V1 dV
-
dl
Ⅱ V2 V
6
注意 功是过程量,其数值大小与过程有关, 只给定初态和末态并不能确定功的数值.
dQ dE PdV
或
QE2
E1
v2 v1
PdV
5.1.4 理想气体的等体过程、等压过程 和等温过程
热力学第一定律可以应用于气体、液体 和固体系统,研究它们的变化过程.
-
7
1. 等体过程 气体体积保持不变的过程叫做等体过程.
QT WP1V1lnV V12 在等温膨胀过程中,理想气体所吸收的 热量全部转换为对外所做的功.
-
12
5.1.5 气体的摩尔热容
定 义 1 摩尔的某种物质温度升高(或降低) 1K 所吸收(或放出)的热量.
同一气体在不同的过程中有不同的热容.
1 . 等体摩尔热容
设:1摩尔气体在等体过程中吸取热量dQV 温度升高dT
p1VV12
1 .0 1 15 3 0 11 .4 0 1
2.5 5160 Pa
-
29
5.2 循环过程 卡诺循环
5.2.1 循环过程 5.2.2 卡诺循环
-
30
5.2.1 循环过程
1. 定义
《热学》(第二版)电子教案-杨体强编 第5章 热力学第一定律 第5章 热力学第一定律

压强空间—多孔塞实验,节流过程。
节流膨胀后温度降低—正焦耳—汤姆孙效应(正效应)。 节流膨胀后温度升高—负焦耳—汤姆孙效应(负效应)。
S1
p1
V1
T1 p1
l1
S1
p1
S2
p2
V2
T2
p2
l2
S2
p2
做功 吸热
A A L A R p 1 S 1 l 1 p 2 S 2 l 2 p 1 V 1 p 2 V 2
功与过程(路径)有关,它是过程量,不是状态量。
[例题] 在定压下,气体体积从V1 变被压缩到V2 (1)设过程为 准静态过程,试计算外界对系统所做的功。(2)若为非静态过
程结果如何?
[解]
(1)
A V V 1 2p d V pV V 1 2d V p (V 2 V 1)
A 外界对系统做正功
参考文献: 1.杨体强:《大学物理》1991,12,: 2.赵凯华:《热学》(高等教育出版社,1998),; 3.包科达:《热物理学基础》(高等教育出版社,2001),。
三、理想气体内能 焓的表达式
在实际气体压强趋于零的极限情形下,内能只是温度的函数,与 体积无关。这一规律也叫焦耳定律。
综合气体物态方程及气体内能的实验规律,提出理想气体的概念 是:
热质:没有重量的物质,热的物体含有较多的热质,冷物体含 有较少的热质;热质既不能产生也不能消灭,只能从较热的物体传 到较冷的物体,在热传递过程中热质量守恒是物质量守恒的表现。
1798年,伦福德(Rumford)由实验揭示出热质不守恒。
焦耳( ,1818─1889) 实验表明:热量是物体中大量微粒机械运 动的宏观表现。
热功当量
热量不是传递着的热质,而是传递着的能量。 做功与传热是使系统能量发生变化的两种不同的方式。 1956年国际规定的热功当量精确值为: 1 cal(热化学卡)= 4.184 0 J 1 cal(国际蒸汽表卡)= 4.186 8 J 1 cal(15 0C卡)= 4.185 5 J
节流膨胀后温度降低—正焦耳—汤姆孙效应(正效应)。 节流膨胀后温度升高—负焦耳—汤姆孙效应(负效应)。
S1
p1
V1
T1 p1
l1
S1
p1
S2
p2
V2
T2
p2
l2
S2
p2
做功 吸热
A A L A R p 1 S 1 l 1 p 2 S 2 l 2 p 1 V 1 p 2 V 2
功与过程(路径)有关,它是过程量,不是状态量。
[例题] 在定压下,气体体积从V1 变被压缩到V2 (1)设过程为 准静态过程,试计算外界对系统所做的功。(2)若为非静态过
程结果如何?
[解]
(1)
A V V 1 2p d V pV V 1 2d V p (V 2 V 1)
A 外界对系统做正功
参考文献: 1.杨体强:《大学物理》1991,12,: 2.赵凯华:《热学》(高等教育出版社,1998),; 3.包科达:《热物理学基础》(高等教育出版社,2001),。
三、理想气体内能 焓的表达式
在实际气体压强趋于零的极限情形下,内能只是温度的函数,与 体积无关。这一规律也叫焦耳定律。
综合气体物态方程及气体内能的实验规律,提出理想气体的概念 是:
热质:没有重量的物质,热的物体含有较多的热质,冷物体含 有较少的热质;热质既不能产生也不能消灭,只能从较热的物体传 到较冷的物体,在热传递过程中热质量守恒是物质量守恒的表现。
1798年,伦福德(Rumford)由实验揭示出热质不守恒。
焦耳( ,1818─1889) 实验表明:热量是物体中大量微粒机械运 动的宏观表现。
热功当量
热量不是传递着的热质,而是传递着的能量。 做功与传热是使系统能量发生变化的两种不同的方式。 1956年国际规定的热功当量精确值为: 1 cal(热化学卡)= 4.184 0 J 1 cal(国际蒸汽表卡)= 4.186 8 J 1 cal(15 0C卡)= 4.185 5 J
第五版传热学课件第五章
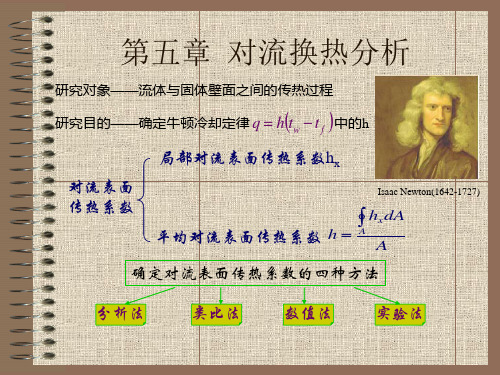
惯性力
对稳态流动:
体积力
压强梯度
黏滞力
u v 0
当只有重力场作用时:
X g x
Y g y
四、能量微分方程式
推导依据—— 内能增量=导热热量+对流热量
1.导热热量:
t x dy x t y dx y 2t x dx 2 dxdy x方向导入的净热量: x x x x
u x p 2 u v x 表面法向应力 表面切向应力 yx xy v y x y p 2 y
将其代入Navier-Stokes方程,并采用连续方程化简,得到:
2u 2u u u u p x方向: u x v y X x x 2 y 2 2v 2v v v v p y方向: u x v y Y y x 2 y 2
冷凝器
锅炉
四、换热表面几何因素 (壁面尺寸、粗糙度、形状及与流体的相对位置)
定型尺寸——换热中有决定意义的尺寸,以此特征 尺寸作为分析计算的依据,能准确反映物体形状对 换热的影响
对流表面传热系数h的多参数函数
h f u, t w , t f , , c p , , , , l
1 1 11 1
1
1 1 ? 1 2
~02
小量,可除去
3.y方向动量方程:
2v 2v v v p u v 2 2 x x y y y
11 1
热学课件chapter5

如果 A B ,则 WA ' WB ' ,
那么 QB 2 'QA2 ' WA 'WB ' 0.
于是,对于 A + B逆 组成
的大系统,T1 处不变,
大系统从T2 处吸收的热量
QB 2 QA2 ' 全部转化为功,
高温热源 (温度 T1 )
QA1
A
WA '
QA 2 '
QB1
在两个平衡态之间热温比的积分与
可逆过程的路径无关,从而由之可定义一个态函数。
2. 熵变的定义
由系统吸收的热量与温度的比值沿可逆路径的积分
定义的态函数称为系统的熵变,记为S,即有
S S f Si
j
j
j
j
i
i
i
i
因为 Q j ' Q j ,
则上式即
Ti
Qi
Ti
Qj
Tj
Tj
0.
n
对 i、j 统一记为 k,对k 求和,即得
k 1
Qk
0.
Tk
其中等号适用于可逆过程,不等号适用于不可逆过程。
dQ
n
若
, 则 Ti Ti 1 Ti 0, Qi dQ, 于是有
QB 2 'QA 2 '
这表明,在 = 的情况下,
> 的假设实际不成立。
低温热源 T2
(b) 对第二条定理的证明(续)
如图,假设A 不可逆、B可逆,
高温热源 T1
如果 WA ' WB ' ,
QA1
QB1
则 QA1 QA2 ' QB1 QB 2 ' ,
那么 QB 2 'QA2 ' WA 'WB ' 0.
于是,对于 A + B逆 组成
的大系统,T1 处不变,
大系统从T2 处吸收的热量
QB 2 QA2 ' 全部转化为功,
高温热源 (温度 T1 )
QA1
A
WA '
QA 2 '
QB1
在两个平衡态之间热温比的积分与
可逆过程的路径无关,从而由之可定义一个态函数。
2. 熵变的定义
由系统吸收的热量与温度的比值沿可逆路径的积分
定义的态函数称为系统的熵变,记为S,即有
S S f Si
j
j
j
j
i
i
i
i
因为 Q j ' Q j ,
则上式即
Ti
Qi
Ti
Qj
Tj
Tj
0.
n
对 i、j 统一记为 k,对k 求和,即得
k 1
Qk
0.
Tk
其中等号适用于可逆过程,不等号适用于不可逆过程。
dQ
n
若
, 则 Ti Ti 1 Ti 0, Qi dQ, 于是有
QB 2 'QA 2 '
这表明,在 = 的情况下,
> 的假设实际不成立。
低温热源 T2
(b) 对第二条定理的证明(续)
如图,假设A 不可逆、B可逆,
高温热源 T1
如果 WA ' WB ' ,
QA1
QB1
则 QA1 QA2 ' QB1 QB 2 ' ,
热学教学教案

教学效果:通过案例分析,学生能够更好地理解热学知识,提高学习兴趣和积极性
4
第一课时:热学基础知识介绍
第二课时:热力学第一定律
第三课时:热力学第二定律
Hale Waihona Puke 第四课时:热力学第三定律第五课时:热学实验介绍
第六课时:热学习题讲解
热学基础知识:1-2周
复习与考试:11-12周
热学实验:9-10周
热力学第一定律:3-4周
熵增的原因:系统内部分子热运动导致熵增
熵增的应用:解释自然界的不可逆现象,如热量的传递和扩散
熵增的限制:熵增不能超过系统的最大熵值,否则系统将崩溃
3
添加标题
添加标题
添加标题
添加标题
通过实例分析帮助学生理解
讲解热学基本概念和原理
利用多媒体教学手段,如动画、视频等,增强教学效果
设计课堂讨论和实验,让学生动手操作,加深对理论知识的理解
热力学第三定律:7-8周
热力学第二定律:5-6周
布置作业:每周一次,内容与本周学习内容相关
练习题目:难度适中,涵盖知识点
作业提交:按时提交,逾期视为未完成
作业批改:及时批改,反馈给学生
5
课堂观察:观察学生的课堂表现,评估学生的学习情况
作业评价:通过学生的作业,评估学生的学习效果
测试评价:通过测试,评估学生的学习成绩和掌握程度
热力学第二定律:熵增原理,表示在一个自发过程中,系统的熵总是增加的
热传导:通过固体或液体中的分子或原子之间的碰撞传递热量
热交换:通过两种或多种不同温度的物体之间的接触传递热量
热辐射:通过电磁波传递热量,不需要介质
热对流:通过流体(液体或气体)的流动传递热量
熵增原理:系统自发过程总是朝着熵增的方向进行
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010级物理学专业热学教案
第5章热力学第二定律与熵
3.两种表述的等效性证明:热力学与统计物理 5.1.4 热力学第二定律的实质 1.热力学第二定律的实质:
在一切与热相联系的自然现象中他们自发 地实现的过程都是不可逆的。
2010级物理学专业热学教案
第5章热力学第二定律与熵
5.2卡诺定理 5.2.1卡诺定理 1.卡诺定理: (1)在相同的高温热源和相同的低温热源之间工 作的一切可逆热机,其效率都相等,而与工作物质 无关。 (2)在相同高温热源与相同低温热源之间工作的 一切热机中,不可逆热机的效率不可能大于可逆热 机的效率。
S
S0
CV ,m
ln
T T0
R ln V
V0
如以T、p表示则有:
S
Байду номын сангаас
S0
C p ,m
T ln
T0
R ln
p p0
2010级物理学专业热学教案
第5章热力学第二定律与熵
5.3.4 熵增加原理 1.某些不可逆过程中熵变的计算: 2.熵增加原理: (1)克劳修斯不等式: 有卡诺定理,工作在相同热源之间的热机,
dQ
S T S0
2010级物理学专业热学教案
第5章热力学第二定律与熵
3.不可逆过程中熵的计算: 方法有三种: (1)设计一个连接相同初、末态的任一可 逆过程,用定义式计算; (2)计算出熵作为状态参量的函数形式, 再以初、末两状态参量代入计算熵的变化;
2010级物理学专业热学教案
第5章热力学第二定律与熵
2010级物理学专业热学教案
热学教案
物理学与电子工程学院 张可言
2011年5-6月
2010级物理学专业热学教案
第5章热力学第二定律与熵
5.1 热力学第二定律的表述及其实质 5.1.1 两种表述及其等效性 1.开尔文表述: (1)表述:
不可能从单一热源吸收热量,使之完全 变为有用功而不产生其它影响。
b可 逆 T
a不 可 逆 T
a dQ b dQ
b可 逆 T
a不 可 逆 T
b dQ a不可逆 T Sb Sa
可逆
b V
或
dS dQ
T
2010级物理学专业热学教案
第5章热力学第二定律与熵
对于绝热过程: dQ 0 ,则dS≥0。 结论:热力学系统从一个平衡态绝热地到达 另一个平衡态的过程中,它的熵永不减少; 如果过程是可逆的,则熵不变,如果过程是 不可逆的,则熵增加。
G.熵的单位是:JK-1。
2010级物理学专业热学教案
第5章热力学第二定律与熵
2.关于熵应注意的问题:
(1)若变化路径是不可逆的,则
Sb Sa
b dQ aT
不成立;
(2)熵是态函数,系统状态已经确定,熵也
被确定。通常表示为:S T ,V ,S T , p
(3)若某一可逆过程的初态确定,设熵为S0, 则任一态的熵为:
(5)第二类永动机(开尔文表述):
第二类永动机不可能制造成功。
2010级物理学专业热学教案
第5章热力学第二定律与熵
2.克劳修斯表述:
(1)表述:
不可能把热量从低温热源传到高温热源而
不产生其它影响。
(2)间接证明:
制冷机:
冷
Q2 Q1 Q2
Q2 A
反证:A=0,Q1=Q2,η→∞,这是不可能实
现的。
第5章热力学第二定律与熵
dQ
对可逆过程, l T 只与起始点有关,与过程无关。 (3)态函数——熵:
A.力学中,力做功与路径无关,由此引入 状态函数——势能。 函数B—.—l dTQ熵对。可逆过程与路径无关,也引入状态
C.具体形式:
2010级物理学专业热学教案
第5章热力学第二定律与熵
ΔE p
(2)间接证明: 反正:如某些热机从单一热源吸取热量,并全 部转变为有用功,则由热力学第一定律:
2010级物理学专业热学教案
第5章热力学第二定律与熵
Q1 Q2 W 100%
Q1
Q1
故:Q2=0,这是实际做不到的。
(3)单一热源:
温度均匀的热源。
(4)无其它影响:
除传热、作功以外无其它过程。
4.理想气体的熵:
由 TdS dU pdV
可得: dS 1 dU pdV
T
对于理想气体:dU CV ,mdT , p RT
V
则:
dS
CV ,m
dT T
R
dV V
S S0
T
C T0
V ,m
dT T
R ln V
V0
2010级物理学专业热学教案
第5章热力学第二定律与熵
在温度变化不大时,CV ,m 可视为常数。则有:
2010级物理学专业热学教案
第5章热力学第二定律与熵
5.3 熵与熵增加原理
5.3.1克劳修斯等式
P
1.条件:
过程为可逆过程。
2.表达式:
V
1 Q2 1 T2
Q1
T1
2010级物理学专业热学教案
第5章热力学第二定律与熵
因为|Q1|、|Q2|都为正,
Q1 Q2 0 T1 T2
如果定义Q均以吸热为正,则Q2为负,因此有:
b a F dr E p
,即熵
b dQ
S
S
aT
注意:熵是状态函数,与过程无关。
D.一般式:
Sb
Sa
b dQ
a可 逆 T
对无限小过程: TdS dQ可逆 或
dS dQ可逆
T
2010级物理学专业热学教案
第5章热力学第二定律与熵
E.热力学第一定律:
TdS dU pdV
F.熵的引入,最早是克劳修斯1854年引入的dQ ,其本质是热量转变为功的一种本领。由于 是广延量,T是强度量,因此,S也是广延量。
2010级物理学专业热学教案
第5章热力学第二定律与熵
(1)前提: 推导过程为可内过程。 (2)克劳修斯等式变形:
P a
II
I
b V
dQ b dQ a dQ 0
lT
aI T
bII T
b dQ b dQ
aII T
aII T
由于I、II路径是任意选择的,由此可得结论:
2010级物理学专业热学教案
其效率不可能大于可逆卡诺热机,因而有:
2010级物理学专业热学教案
第5章热力学第二定律与熵
卡诺
→ → → 1 Q2 1 T2
Q1
T1
Q2 T2 Q1 T1
Q1 Q2 0 T1 T2
dQ 0 T
P a
(2)不可逆过程的熵:
不可逆
由
dQ T
0
有:
→ → a dQ b dQ
0
Q1 Q2 0 T1 T2
则: 2 Qi 0
T i 1 i
P a
II
I
b V
2010级物理学专业热学教案
第5章热力学第二定律与熵
如果一个循环是任意循环,则可将任意 循环分为无数多个小卡诺循环来描述,则有:
Qi 0
T i 1 i
,即:
5.3.2 熵和熵的计算 1.态函数熵的引入:
dQ T
0
