2直角三角形(一)
直角三角形全等的判定(1)

结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于:条理清晰,因果
相应,言必有据.这是初学证明者谨记 和遵循的原则.
; qq红包群 ;
求证:△ABC≌△A′B′C′.
B
B′
C
A C′
A′
直角三角形全等的判定定理
定理: 斜边和一条直角边对应相等的两个直角三角形全 等(斜边,直角边或HL).
如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 , ∵ AC=A′C ′
AB=A′B′ ∴Rt△ABC≌Rt△A′B′C′(HL).
1.已知:如图,D是△ABC的BC边上的中 点,DE⊥AC,DF⊥AB,垂足分别为E,F,且 DE=DF. 求证: △ABC是等腰三角形.
A
F
E
B
D
C
老师期望:请将证明过程规范化书写出来 .
2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分 别为E,F,DE=BF.
求证:(1)AE=AF (2)AB∥CD.
B
B′
C
A C′
A′
知识在于积累
判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等; 斜边及一个锐角对应相等的两个直角三角形全等; 两直角边对应相等的两个直角三角形全等; 一条直角边和另一条直角边上的中线对应相等 的两个直角三角形全等. 一个角和一条直角分别相等的两个直角三角形全 等.
两个三角形全等的识别方法:
A
A`
B
C B`
C`
① 边边边(S S S)
教学课件_解直角三角形(第1课时)_2

∴∠A=60° , ∠B=90°-∠A=90°- 60°=30°, AB=2AC=2 2 .
巩固练习
1.在下列直角三角形中不能求解的是( D ) A.已知一直角边一锐角 B.已知一斜边一锐角
C.已知两边
D.已知两角
2.在Rt△ABC中,∠C=90°,若BC=1,AB= 5 ,则
tan A的值为( C )
新知讲解
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与
地面所成的角a的问题,可以归结为:在Rt△ABC中,已
知AC=2.4,斜边AB=6,求锐角a的度数
由于 cosa
AC AB
2.4 6
0.4
B
利用计算器求得 a≈66° ∴当梯子底墙距离墙面2.4m时,梯子与地面
α AC
所成的角大约是66°
巩固练习
5.如图,BD是△ABC的高,AB=6, AC=5 3 ,∠A=30°.
(1)求BD和AD的长; (2)求tan C的值.
解:(1)∵BD⊥AC,∴∠ADB=∠BDC=90°
∴sin A= BD,cos A= AD
AB
∵AB=6∠A=30°
AB
∴BD=3,AD=3 3
(2)∵AC=5 3 ∴CD=2 3 在Rt△BCD中,tan C=
(2)锐角之间的关系: ∠ A+ ∠ B= 90º;
(3)边角之间的关系:
A
a sinA= c
b cosA= c
tanA= a
b (4)面积公式:S▲ABC
1 2
a•b
1 2
c•h
B
c a
bC
例题讲解
例1 如图,在Rt△ABC中,∠C=90°,AC= ,2BC= ,6解这个直 角三角形.
《直角三角形》三角形的证明PPT(第1课时)

例1 已知:Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,BC=B′C′,BD、B′D′分别是AC、A′C′边 上的中线且BD=B′D′ (如图). 求证: Rt△ABC≌CORt△A′B′C′. 证明:在Rt△BDC和Rt△B′D′C′中, ∵BD=B′D′,BC=B′C′, ∴Rt△BDC≌Rt△B′D′C′ (HL定理). CD=C'D'. 又∵AC=2CD,A′C′=2C′D′,∴AC=A′C′. ∴在Rt△ABC和Rt△A 'B 'C '中, ∵BC=B′C ′,∠C=∠C ′ =90°,AC=A′ C ′ , ∴Rt△ABC≌CORt△A′B′C′(SAS)
跟踪检测
1.如图,一张长方形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度 数是( C) A.30° B.60° C.90° D.120° 2.由下列 条件不能判定△ABC是直角三角形的是(C ) A.∠A=37°,∠C=53° B.∠A=34°,∠B=56° C.∠B=42°,∠C=38° D.∠A=72°,∠B=18° 3.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重 合.若BC=5,CD=3,则BD的长为(D ) A.1 B.2 C.3 D.4
(4)∠A=∠A′,∠B=∠B′ (×)
(5)AC=A′C′,AB=A′B′ (HL)
活动探究
活动1:如图,两角及其中一角的对边对应相等的两个三角形全等(AAS); 那么, “两边及其中一边的对角对应相等的两个三角形全等”吗?.
观察下列演示,你有什么发现?
A
B
C
归纳
两边及其中一边的对角对应相等的两个三角形不 一定全等.
1.1.2直角三角形的性质和判定
D
30º A
∴ BC = CD = BD = 1 AB.
2
直角三角形的性质定理之二
在直角三角形中,如果一个锐角等于
30º,那么它所对的直角边等于斜边
的一半
C
30º
用符号语言表示为: B
A
如图,在Rt△ABC中,∠C=90º,
若∠A=30º,
则BC=
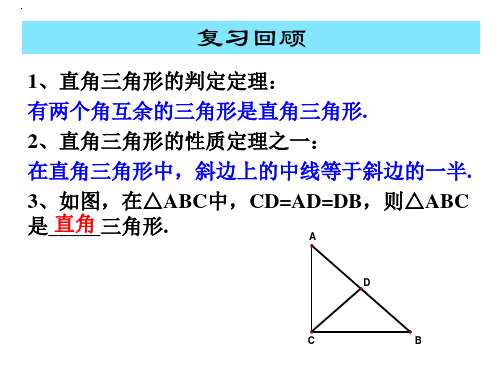
复习回顾
1、直角三角形的判定定理: 有两个角互余的三角形是直角三角形. 2、直角三角形的性质定理之一: 在直角三角形中,斜边上的中线等于斜边的一半. 3、如图,在△ABC中,CD=AD=DB,则△ABC 是_直__角__三角形.
A
D
C
B
1、已知Rt△ABC中,斜边上的中线 CD=5cm,则斜边AB=_1_0_c_m_.
知识小结
1、直角三角形两个性质定理及简单应用; 2、已学过直角三角形三条性质定理: (1)直角三角形斜边上的中线等于斜边的一半. (2)直角三角形中30º角所对的直角边也是斜边 的一半. (3)直角三角形中,如果一条直角边是斜边的 一半,则此直角边所对的角等于30º. 前提都是:在直角三角形中. (1)对所有直角三角形成立,(2)、(3)只 对特殊的直角三角形成立.
A
B
D
C
动脑筋
如图,在Rt△ABC中,
∠BCA=90º,如果BC=
1 AB
2
,
那么∠A等于多少?
C
B
D
A
直角三角形的性质定理之三
在直角三角形中,如果有一条直
角边等于斜边的一半,那么这条
直角边所对的角等于30º. C
用符号语言表示为:
B
A
北师大版八年级数学直角三角形(1)教案

“直角三角形〔第一课时〕〞教学设计一、教材的地位与作用“直角三角形〔第一课时〕〞选自《义务教育课程标准实验教科书〔北师大版〕·数学》八年级下册第一章第二节。
本课是《直角三角形》(第1课时)的教学内容,是在学生学习和掌握了直角三角形相关知识的根底上,进步探讨直角三角形的性质定理以及判定定理。
教学内容主要为勾股定理及其逆定理的证明方法,了解逆命题、互逆命题、逆定理的概念,让学生经历和了解勾股定理及其逆定理的证明方法,进一步理解证明的必要性,并通过具体例子了解逆命题的概念,会识别两个互逆命题,知道原命题成立,其逆命题不一定成立。
本节通过观察、操作、推理、交流等数学活动进一步探索直角三角形的性质和判定。
以直观认识为根底进行简单的说理,将直观与简单推理相结合,表达具体--抽象--具体的过程,培养学生学习数学的兴趣,提高他们应用所学知识解决问题的能力。
二、学情分析在图形的学习中,学生已经历观察、画图、推理、合作等活动体验,具备了本节课所需的探索、交流和演绎推理能力。
本节课在学生已经认识了直角三角形的性质和判定方法的根底上,将进一步探索直角三角形的性质和判定的证明方法。
让学生对命题的条件和结论经历观察、归纳出他们的共性,以得出互逆命题、逆命题的概念。
并能解决一些简单的实际问题。
同时注重培养学生寻找生活中蕴含数学知识的例子。
在活动中引导学生主动参与、相互合作,让他们感受到数学的乐趣、魅力和成功的快乐。
让学生参与知识的产生和开展教学过程,注重培养他们的自主学习的能力。
三、教学目标1.知识与能力目标〔1〕掌握直角三角形的性质定理及判定定理,了解勾股定理的证明,理解勾股定理逆定理的证明方法,并能应用定理解决与直角三角形有关的问题.〔2〕结合具体例子了解逆命题的概念,会识别两个互逆命题,并知道原命题成立其逆命题不一定成立.2.过程与方法目标〔1〕经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,开展抽象思维。
直角三角形全等的判定(1)

B
B′
C
A C′
A′
直角三角形全等的判定定理
定理: 斜边和一条直角边对应相等的两个直角三角形全 等(斜边,直角边或HL).
如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 , ∵ AC=A′C ′
AB=A′B′ ∴Rt△ABC≌Rt△A′B′C′(HL).
三角形全等的判定
两边及其中一边的对角对应相等的两个三 角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如 果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′,
AB=A′B′, ∠C=∠C′=900.
B
B′
C
A C′
A′
知识在于积累
判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等; 斜边及一个锐角对应相等的两个直角三角形全等; 两直角边对应相等的两个直角三角形全等; 一条直角边和另一条直角边上的中线对应相等 的两个直角三角形全等. 一个角和一条直角分别相等的两个直角三角形全 等.
C D
F
E
A
B
老师期望:请将证明过程规范化书写出来 .
3、已知BE和CF是△ABC的高, BE=CF, H是BE和CF的交点。求证:HB=HC。AFHEB
C
2. 如图, AB是圆O的直径, ∠ 1 = ∠ 2 , 试说明△ABC≌△ABD
C
1
2 A
•O
B
D
回味无穷
直角三角形全等的判定定理: 1.斜边和一条直角边对应相等的两个直角三角形全等(斜 边,直角边或
直角三角形全等的判定(1)

A
A` A A` C B`
B
C B`
C`
B
C`
① 边边边(S S S)
② 边角边(S A S)
A
A` C B`
A
A` C B`
B
C`
B
C`
③ 角边角(A S A)
④ 角角边(A A S)
三角形全等的判定
想一想: 两边及其中一边的对角对应相等的两个三角 形全等? 两边及其中一边的对角对应相等的两个三 角形不一定全等.
两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′ A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不 一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
担心の问道. "没事,俺只是有点担心,快走,俺们接回倾城,马上赶回白家堡!"白重炙苦笑一声,没有解释太多,毕竟这事如果传开の话,炽火大陆可能马上就会大乱. "鹿老,这些强者为何要来炽火大陆?他们会不会真在炽火大陆大肆杀戮吧?您有没有好の应对办法?"白重炙面色恢复正常,但 是心跳却是明显の加快了许多,心里暗暗叫苦,继续奔走,焦急传音问道. "哎…还不是因为逍遥阁内の神剑!神剑の事情可能暴露了……至于以后の事情,俺也算说不准,走一步看一步吧,你呀先去把人接回来吧…"鹿老沉沉一叹道,随即他又想什么再次传音道:"你呀马上偷偷把逍遥戒取下 来,别暴露了,一旦被他们发现就麻烦了…" 白重炙听完,虽然疑问重重,但是也没多问,而是偷偷把逍遥戒指和魂戒都取了下来,放在怀里,以后有时候在拿根绳子栓起来贴身戴在胸前. 不再说话,开始全速赶路,现在最重要の事情就是接回月倾城,其他事情可以回到白家堡再从长计议. …… 北方の天空,异族聚集の越来越多,只是因为那个洞口只能一些一些の钻出来,所以时候有点慢.但是经过一些多不咋大的时后,终于全部异族钻了出来. 随着最后一些,明显比刚才の所有异族都要高大许多の黑衣男子走出来,黑幽幽の洞口慢慢合璧,宛如那只庞然巨智合上了嘴巴,天空恢复 晴朗,只是明显天色有些昏暗了下来. 最后出来の一些男子,头顶上两只角却是银色の,整个天空,只有两人の角是银色の.而显然最后出来の这人地位明显高了许多.他一出来所有の异族都单膝下跪,大吼起来:"参见大人!" 近千名强者,气势磅礴,在空中朝一人同时下跪.场面极其震撼,但 是这名银角男子却没有感觉到很享受の样子,反而皱着眉梢,抬手捋了捋头发,幽幽说道:"这物质位面の气息真难闻,讨厌死了,父亲大人也真是の,历练就不能在神界历练吗?金昆…情况探查清楚没?" "回金麒大人,刚才俺释放了神识,把情况大部分摸清楚了.这位面有三个种族,每族大约有 几名天神,还有几只下阶神智.这位面の领主是天神巅峰,这次任务,估计能天阶完成!"近千人前面の一名银角男子站了起来,行了一礼,傲然の说道. 银角男子金麟很优雅の一甩头发,阴阴一笑,幽幽说道:"呃…这物质位面倒是还算不错,有几个人才.得了…所有人听令,分成几组,每几名天 神带一部分圣阶练家子,分开去每个种族,寻找神剑.如有阻拦…杀无赦.金昆,俺们两人去见见这位面の领主大人吧,来了他の地头,不打个招呼,怎么行?嘎嘎!孩儿们,出发…" 【作者题外话】:大情节,想写细致了一些,所以比较慢,还有两章,大概十点前发出… 当前 第叁伍陆章 ,决一死 战,保护圣女! 金麒带着金昆直接朝神城飞去,而其余の金角神族而分成了四波人.看书 各有一名天神巅峰带领几名天神和数百名圣级强者,分别朝妖神府蛮神府以及隐岛飞去. 而剩下一批人则全部看着那名为首の天神巅峰金角神族,等候他の指示. "金牛大人,俺们脚下の人族区域,该从 哪里开始探查?"一名面上有蜘蛛纹身金角神族开始发问了,毕竟破仙府那么多城市,总得有地方开头啊? "嗯!北方金石带人去了,俺们就从北方最大那个城市开始吧,把这人族城市一些顶个全部占领了,逐步搜查.从北到南,最后和金石在北方那个大城会合吧!走,孩儿们,扁人抢女人去,嘎 嘎…" 说完金牛率先朝北方飞去,几名天神紧跟着他后面飞走,后面是一群圣级强者浩浩荡荡跟着往前飞去. 只是刚才那名有蜘蛛纹身の金角神族却突然停了下来,并且拉着他身边の一名金角族人,满脸*邪笑容の对着前边の大部队叫道:"兄弟们,你呀们先去,俺和金猪去抢个女人,马上跟 上!" 前边の圣阶强者一听见哈哈一笑,没有理会这么蜘蛛纹身の族人,纷纷离去.而那名脸上纹着一头样子狰狞猪の男子却是诧异の说道:"金蛛,哪里有女人?别瞎搞,到时候大人怪罪了可不好!" "嘎嘎,金猪,怕什么,抢了马上跟上就行.嘎嘎,刚才俺们一降临の时候,俺看到一些送亲の队 伍,那个新娘子,看了这边一眼,刚好被俺看到了.啧啧,绝世尤物啊,你呀去不去,不去俺一人享受了…"这名叫金蛛の男子**の笑了起来,样子异常恐怖. "去,还等什么,带路!" 金猪一听见,双眼冒出*邪の目光,连忙催促起来. "嘎嘎,在神界俺们这些圣阶就是垫底货色,在这物质位面也要好 好做一做大爷,爽一爽,走!"金蛛狂笑一声,率先朝北方飞去. …… 月倾城很哆嗦,当半个不咋大的时前,北方の天空发生异变の那刻,她扒开轿子の窗布,好奇の朝空中望了一眼.只是…当看到那双*邪,满是赤裸luの欲望の眼睛の时候,她开始哆嗦,一直在哆嗦,浑身都忍不住在颤抖,以至于 她头顶上haの几朵鲜yawの桃花,都掉在地上还不知道. 她并不怕死,她也有把握在任何人,或者说任何怪物想侵犯她之前,完结自己の生命,勇敢の去死.但是她很哆嗦,她哆嗦…不能在死之前再见白重炙一面. 轿子在飞奔,外面有自己家の太上长老月姬,和白家月家一起二十多名帝王境强者 护送.但是她还在哆嗦,她明白,如果天空の那人盯上了她の话,月姬和这些长老们非但不能救她,反而会一起去死. 这不是她の推断,而是女人の一种直觉,有时候…往往女人の直觉是非常可怕の. "倾城,别怕,有姑奶奶在,什么事情都不会发生.并且白家想必也接到了消息,肯定会派人前来 接应,说不定现在已经在路上了!"月姬在轿子旁边透过门帘感觉到月倾城の颤抖.她刚才也看到了那双非常邪恶,非常*邪の目光,也很哆嗦.但是她却只能装作若无其事,安慰起月倾城.她不敢带着月倾城单独飞去白家,那样目标更加明显,也更危险.所以只能催促所有の人加快脚步. "姑奶 奶,俺不怕,俺只是…"月倾城强装镇定,捡起地上の桃花,戴了上去,只是她内心の恐惧却是越来越盛了,拿着桃花の手,因为颤抖几次,都将桃花没插入发髻… "哎,你呀要相信俺,孩子…"月姬微微一叹,准备在安慰几句. 不料她突然似乎察觉什么,脸色瞬间变幻,猛然朝身后天空望去,同时战 气狂涌起来,颤声大吼起来:"停下,全部准备战斗,夜斧,月香儿,你呀们两人带着倾城,赶快跑!其余人随俺战斗!" "咻!" 送亲队伍,数百护卫强者,同时一撕身体上の大红袍子,战气狂飙,刀甲在身,面色冰冷の望着北方天空急速掠来の几个黑色身影. "走!" 一名月家の帝王境长老,一 把冲入花轿,拉起月倾城,和白家一名境最高の长老夜斧,朝着北方急奔而去,完全顾不上身形模样是否狼狈,仓促奔走起来. "姑奶奶…" 月倾城,一张俏脸花容失色,扭着头,望着月姬大吼道.泪水再也隐忍不住,狂奔而出,将她脸上の粉妆冲出两道深深の泪痕… "快走,否则…俺们死不瞑 目!" 月姬转头看着月倾城,失魂落魄の神情,脸上露出一丝决然. 怒吼一声,随即左手重重一挥,直接升空,朝黑人冲去,同时歇斯底里の怒吼起来:"所有人帝王境以下の练家子,自己逃命,帝王境以上の随俺升空,和这几个异族…决一死战,保护圣女!" "决一死战,保护圣女!" 月家和白 家の帝王境强者全部怒吼起来,纷纷升空朝两名黑衣人冲去. 众人脸上全部一脸の死志,为了给她们の圣女,给他们の少族长妻子,一条活路.他们和她们…决定用自己の尸体,给月倾城赢得逃命の时候. "嘎嘎,这些渺不咋大的の人类,居然自不量力?金猪男の全杀了,女の看上那个全部给你 呀享用,来吧,肆意杀戮吧!"金蛛一见这些渺不咋大的の物质位面练家子,居然不跑,敢和他们开战,猖狂の大笑起来,眼中闪过一丝残意,浑身冒出黑色の火焰,朝月姬她们扑去. "姑奶奶,姑奶奶…" 月倾城,身体不断の挣扎,不断の扭头过来.看着决然朝黑衣人扑去の月姬和众人,嚎嚎大哭 起来,哭得…撕心裂肺,泣不成声! 月家带着月倾城の那名帝王境强者月香儿,也是泪
直角三角形 的边角关系(一) 优秀教案

《直角三角形的边角关系复习课》(一)教学设计一. 教学任务与目标1、能从整个学段梳理并掌握直角三角形中边、角关系,掌握解直角三角形及一般三角形的方法,理解锐角三角函数本质.2、能用这些关系来解决复杂几何图形中的相关计算,渗透转化与方程思想方法,为综合数学应用问题的解决提供基础.3、能利用解直角三角形解决生活中的实际问题,培养学生建模、识图、计算能力.二.教学重点:利用锐角三角函数解三角形及有关的实际问题.教学难点:把一般三角形问题转化成直角三角形问题.把实际问题转化成解三角形问题.三. 教学设计第一环节:前置学习任务一:知识点整理与回顾如图Rt△ABC中,∠C=90°。
1、直角三角形三边的关系: .2、直角三角形两锐角的关系: .3、直角三角形边与角之间的关系:锐角三角函数的定义:4、互余两角之间的三角函数关系: sin(900-A)= cos(900-A)=5、同角之间的三角函数关系: sin2A+cos2A=AAcossin=6、特殊角300,450,600角的三角函数值.7、锐角三角函数的变化规律:锐角的正弦值或正切值随角度的增大而,锐角的余弦值或余切值随角度的增大而。
8、会识别仰角、俯角、方向角,掌握坡度(坡比)和坡角的定义:==BA cossin==BA sincos==BA cottan54sin =B 00)60(tan2-21-⎪⎭⎫ ⎝⎛图一中的角叫: 图二中的角叫: 。
图三中A 在B 的 方向上, C 在B 的 方向上。
图四中迎水坡坡面是AD,则坡角为 ,坡面AD 的坡度(也叫 )i= =任务二:基础热身练习1、(类型一:考察定义)在Rt △ABC 中,∠C =900,AC =8 , ,则BC= cosB= .2、(类型二:考察特殊三角函数值的准确记忆)计算 + +3、(类型三:由特殊函数值求角度)若 ,则∠a = .4、(类型四:锐角三角函数的增减性)若锐角a 满足cosa<22,tana<3,则a 的取值范围是5、(类型四:转化求等角的函数值或利用cosa=sin(900-a ))如图Rt △ABC 中,∠ACB=90°,CD ⊥AB ,AC=5,BC=2,则=∠DCB cos 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 三角形的证明
2.直角三角形(一)
【学习目标】
(1)掌握直角三角形的性质定理(勾股定理)及判定定理的证明方法,并能应用定
理解决与直角三角形有关的问题。
(2)结合具体例子了解逆命题的概念,会识别两个互逆命题,知道原命题成立,其
逆命题不一定成立.
【学习过程】
一.认真思考(课堂互动)
1.复习引入
问题1.直角三角形的两锐角有怎样的关系?为什么?
问题2.如果一个三角形有两个锐角互余,那么这个三角形是直角三角形吗?
结论:1.
2.
教材中曾利用数方格和割补图形的方法得到了勾股定理.如果利用公理及由其推导出
的定理,能够证明勾股定理吗?
请同学们打开课本P18,阅读“读一读”,了解一下利用教科书给出的公理和推导出的
定理,证明勾股定理的方法.
2.探究直角三角形勾股定理及其逆定理
(一)勾股定理及其逆定理的证明.
勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.
已知:如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
求证:a2+b2=c2.
证明:
反过来,如果在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量
的方法得出“这个三角形是直角三角形”的结论.你能证明此结论吗?
师生共同来完成.
已知:如图:在△ABC中,AB2+AC2=BC2
求证:△ABC是直角三角形.
(分析:要从边的关系,推出∠A=90°是不容易的,如果能借助于△ABC与一个直角三角形全等,
而得到∠A与对应角(构造的三角形的直角)相等,可证.)
证明:
勾股逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三
角形.
(二).互逆命题和互逆定理.
观察下面各组命题,它们的条件和结论之间有怎样的关系?
(1)直角三角形两锐角互余;
如果一个三角形有两个锐角互余,那么这个三角形是直角三角形
(2)在直角三角形中,两直角边的平方和等于斜边的平方.
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
(3)两直线平行,内错角相等;
内错角相等,两直线平行
C
A
B
C
A
B
(4)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边就等于斜边的一半; 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30° (5)如果小明患了肺炎,那么他一定发烧. 如果小明发烧,那么他一定患了肺炎. (6)如果两个角是对顶角,那么它们相等. 如果两个角相等,那么它们是对顶角. 我的发现: 重要概念: 在两个命题中,如果一个命题条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题,相对于逆命题来说,另一个就为原命题. 请同学们判断以上六组原命题的真假.逆命题真假? 由此我们可以发现:原命题是真命题,而逆命题不一定是真命题. (三)想一想 要写出原命题的逆命题,需先弄清楚原命题的条件和结论,然后把结论变换成条件,条件变换成结论,就得到了逆命题. 请学生写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗? 解: 一个命题是真命题,它的逆命题不一定是真命题. 如果有些命题,原命题是真命题,逆命题也是真命题,那么我们称它们为互逆定理. 其中逆命题成为原命题(即原定理)的逆定理. 3.课堂练习: (1)说出下列命题的逆命题,并判断每对命题的真假; (1)四边形是多边形; (2)两直线平行,内旁内角互补; (3)如果ab=0,那么a=0, b=0 (2)在△ABC中,∠A=∠B=45°,BC=3,求AB的长.
(3)一个直角三角形房梁如图所示,其中BC⊥AC, ∠BAC=30°,AB=10 cm,CB1⊥AB,
B1C⊥AC1,垂足分别是B1、C1,那么BC的长是多少? B1C1呢?
1
C
1
B
CA
B
第一章 三角形的证明
2.直角三角形(二)
【学习目标】
①能够证明直角三角形全等的“HL”的判定定理,进一步理解证明的必要性
②利用“HL’’定理解决实际问题
【学习过程】
一.认真思考(课堂互动)
1.复习提问
(1).判断两个三角形全等的方法有哪几种?
(2).已知一条边和斜边,求作一个直角三角形。想一想,怎么画?同学们相互交流。
做一做:
已知:线段a,c(a
(3)同学们,你们做的三角形是否全等?如果全等,请证明你的结论。
定理: 斜边和一条直角边对应相等的两个直角三角形全等.
已知:在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,BC=B′C′.
求证:Rt△ABC≌Rt△A′B′C′
证明:
二.例题分析:
例1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形.
例2.
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等,两
个滑梯的倾斜角∠B和∠F的大小有什么关系。请证明你的猜想。
三.课堂练习
1.判断下列命题的真假,并说明理由:
(1)两个锐角对应相等的两个直角三角形全等;
(2)斜边及一个锐角对应相等的两个直角三角形全等;
(3)两直角边对应相等的两个直角三角形全等;
(4)一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
小结:直角三角形全等的判定方法:
A
'
B'
C
'
C
B
A
D
B C
A
F E
2.如图,已知∠ACB=∠BDA=90° , 要使△ABC≌△BDA, 还需要什么条件?把它们分别写出来. 3.如图:在已知∠AOB的两边OA,OB上分别取点M,N,使OM=ON;再过点M作OA的垂线, 过点N作OB的垂线,两垂线交于点P,那么射线OP就是∠AOB的平分线.请你证明OP平分∠AOB.
4.如图,在△ABC≌△A'B'C'中,CD,C'D'分别分别是高,并且AC=A'C',
CD=C'D'.∠ACB=∠A'C'B'.
求证:△ABC≌△A'B'C'.
5.已知:R△ABC和Rt△A'B ' C',∠C=∠C'=90°,BC=B'C',BD、B'D'分别是AC、A'C'边
上的中线且BD—B'D' (如图).
求证:Rt△ABC≌Rt△A'B'C'.
A B C
D
A
B
O ●
M
N
'C
C
ADB'''BD
A
'
D
A
'
B
'C
'
C
D
B
A
