三角函数的定义域、值域和最值
三角函数的定义域、值域

要使y 1 sin z有最小值- 1,
必须
2
z
2
2k ,k z
2
要使y 1 sin z有最大值 1,
1 x 2k
必须
2
z
2
2k ,k z
1
x
2
2k
x
4k
2 x
35
2
4k
3
使原函数取得最小值的集合是
2 32
3
y sin x
x
|
x
5
3
4k ,k
Z
y sin x
角
练习 求函数 y=cos2x+4sin x 的最值及取到最大值和最小值 时的 x 的集合.
解 y=cos2x+4sin x=1-sin2x+4sin x =-sin2x+4sin x+1=-(sin x-2)2+5.
∴当 sin x=1,即 x=2kπ+2π,k∈Z 时,ymax=4; 当 sin x=-1 时,即 x=2kπ-2π,k∈Z 时,ymin=-4. 所以 ymax=4,此时 x 的取值集合是{x|x=2kπ+π2,k∈Z}; ymin=-4,此时 x 的取值集合是{x|x=2kπ-π2,k∈Z}.
2
所以结论要相反 y sin z 最小
3.二次函数的某些知识点
例 求函数 y=sin2x-sin x+1,x∈R 的值域.
解 设 t=sin x,t∈[-1,1],f(t)=t2-t+1. ∵f(t)=t2-t+1=t-122+34. ∵-1≤t≤1, ∴当 t=-1,即 sin x=-1 时,ymax=f(t)max=3;
x x sinx
忘掉的同学再去看看课本, 后面的老师还会讲到
课堂小结
第7章 三角函数(课件)高一数学单元复习(沪教版2020必修第二册)

2π
f 3 的值;
解析 :
-2
由题意,f(x)=-cos 2x- 3sin 2x=
π
3
1
sin 2x+ cos 2x=-2sin2x+6 ,
2
2
故
2π
4π π
f 3 =-2sin 3 +6 =-2sin
3π
=2.
2
考点2、三角函数的奇偶性与单调性
π
π
π,且在4,2 上单调递增的奇函数是
3π
A.y=sin2x+ 2
π
B.y=cos2x- 2
π
C.y=cos2x+ 2
π
D.y=sin2-x
3π
2x+
解析:y=sin
2 =-cos
π
y=cos2x-2 =sin
在_________________________
_______上是递增函数, 在
[2kπ,2kπ
单调性
____________
π
3π
上是递增函数
+2kπ, +2kπ
____
在2
2
____________
(k∈Z)上是递减函数
_______
上是递减函数
在__________________
2x 为偶函数,排除 A;
常见函数定义域和值域

常见函数定义域和值域1. 线性函数 f(x) = mx + b定义域: 实数集 R值域: 实数集 R2. 二次函数f(x) = ax^2 + bx + c (a ≠ 0)定义域: 实数集 R值域: 当 a > 0 时, 值域为 [c - b^2 / (4a), +∞)当 a < 0 时, 值域为 (-∞, c - b^2 / (4a)]3. 平方根函数f(x) = √x定义域: [0, +∞)值域: [0, +∞)4. 绝对值函数 f(x) = |x|定义域: 实数集 R值域: [0, +∞)5. 分数函数 f(x) = 1 / x定义域: 实数集 R 除去 0值域: 实数集 R 除去 06. 指数函数f(x) = a^x (a > 0, a ≠ 1)定义域: 实数集 R值域: 当 a > 1 时, 值域为(0, +∞)当 0 < a < 1 时, 值域为(0, +∞)7. 对数函数f(x) = log_a(x) (a > 0, a ≠ 1)定义域: (0, +∞)值域: 实数集 R8. 三角函数正弦函数 f(x) = sin(x)定义域: 实数集 R值域: [-1, 1]余弦函数 f(x) = cos(x)定义域: 实数集 R值域: [-1, 1]正切函数 f(x) = tan(x)定义域: 实数集 R 除去(2n + 1)π/2, n 为整数值域: 实数集 R以上是一些常见函数的定义域和值域的介绍。
需要注意的是,一些函数的定义域和值域可能会受到其他条件的限制,因此在实际应用中需要进一步分析。
高中数学《三角函数》详解+公式+精题(附讲解)

高中数学《三角函数》详解+公式+精题(附讲解)引言三角函数是中学数学的基本重要容之一,三角函数的定义及性质有许多独特的表现,是高考中对基础知识和基本技能进行考查的一个容。
其考查容包括:三角函数的定义、图象和性质,同角三角函数的基本关系、诱导公式、两角和与差的正弦、余弦、正切。
两倍角的正弦、余弦、正切。
、正弦定理、余弦定理,解斜三角形、反正弦、反余弦、反正切函数。
要求掌握三角函数的定义,图象和性质,同角三角函数的基本关系,诱导公式,会用“五点法”作正余弦函数及的简图;掌握基本三角变换公式进行求值、化简、证明。
了解反三角函数的概念,会由已知三角函数值求角并能用反三角函数符号表示。
由于新教材删去了半角公式,和差化积,积化和差公式等容,近年的高考基本上围绕三角函数的图象和三角函数的性质,以及简单的三角变换来进行考查,目的是考查考生对三角函数基础知识、基本技能、基本运算能力掌握情况。
2.近年来高考对三角部分的考查多集中在三角函数的图象和性质,重视对三角函数基础知识和技能的考查。
每年有 2 — 3 道选择题或填空题,或 1 — 2 道选择、填空题和 1 道解答题。
总的分值为 15 分左右,占全卷总分的约 10 左右。
( 1 )关于三角函数的图象立足于正弦余弦的图象,重点是函数的图象与 y=sinx 的图象关系。
根据图象求函数的表达式,以及三角函数图象的对称性。
如 2000 年第( 5 )题、( 17 )题的第二问。
( 2 )求值题这类问题在选择题、填空题、解答题中出现较多,主要是考查三角的恒等变换。
如 2002 年( 15 )题。
( 3 )关于三角函数的定义域、值域和最值问题( 4 )关于三角函数的性质(包括奇偶性、单调性、周期性)。
一般要先对已知的函数式变形,化为一角一函数处理。
如 2001 年( 7 )题。
( 5 )关于反三角函数, 2000 — 2002 年已连续三年不出现。
( 6 )三角与其他知识的结合(如 1999 年第 18 题复数与三角结合)今后有关三角函数仍将以选择题、填空题和解答题三种题型出现,难度不会太大,会控制在中等偏易的程度;三角函数如果在解答题出现的话,应放在前两题的位置,放在第一题的可能性最大,难度不会太大。
(完整版)最全三角函数的图像与性质知识点总结
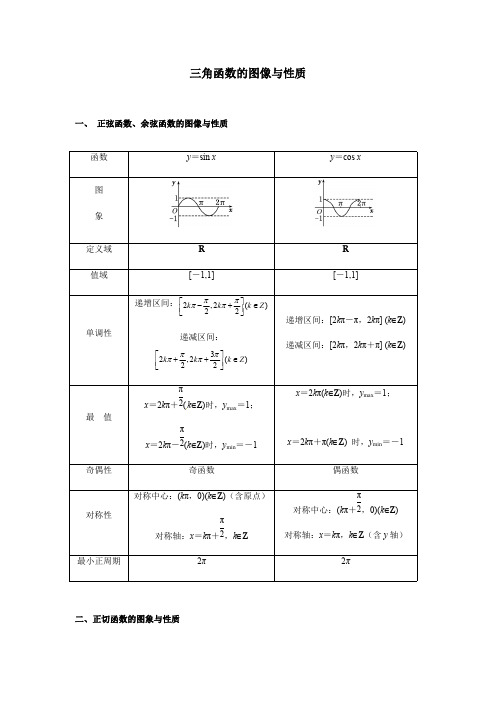
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y =sin x y =cos x图象定义域RR 值域[-1,1][-1,1]单调性递增区间:2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间:32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间:[2k π-π,2k π] (k ∈Z )递减区间:[2k π,2k π+π] (k ∈Z )最 值x =2k π+(k ∈Z )时,y max =1;π2x =2k π-(k ∈Z )时,y min =-1π2x =2k π(k ∈Z )时,y max =1;x =2k π+π(k ∈Z ) 时,y min =-1奇偶性奇函数偶函数对称性对称中心:(k π,0)(k ∈Z )(含原点)对称轴:x =k π+,k ∈Zπ2对称中心:(k π+,0)(k ∈Z )π2对称轴:x =k π,k ∈Z (含y 轴)最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心:(含原点)(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一:先平移后伸缩方法二:先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意:平移变换或伸缩变换都是针对自变量x 而言的,因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
高三高考文科数学《三角函数》题型归纳与汇总

高三高考文科数学《三角函数》题型归纳与汇总高考文科数学题型分类汇总:三角函数篇本文旨在汇总高考文科数学中的三角函数题型,包括定义法求三角函数值、诱导公式的使用、三角函数的定义域或值域、三角函数的单调区间、三角函数的周期性、三角函数的图象变换和三角函数的恒等变换。
题型一:定义法求三角函数值这类题目要求根据三角函数的定义,求出给定角度的正弦、余弦、正切等函数值。
这类题目的难点在于熟练掌握三角函数的定义,以及对角度的准确度量。
题型二:诱导公式的使用诱导公式是指通过对已知的三角函数进行代数变形,得到新的三角函数值的公式。
这类题目需要熟练掌握各种诱导公式,以及灵活应用。
题型三:三角函数的定义域或值域这类题目要求确定三角函数的定义域或值域。
需要掌握各种三角函数的性质和图象,以及对函数的定义域和值域的概念和计算方法。
题型四:三角函数的单调区间这类题目要求确定三角函数的单调区间,即函数在哪些区间上单调递增或单调递减。
需要掌握各种三角函数的性质和图象,以及对函数单调性的判定方法。
题型五:三角函数的周期性这类题目要求确定三角函数的周期。
需要掌握各种三角函数的性质和图象,以及对函数周期的计算方法。
题型六:三角函数的图象变换这类题目要求根据给定的变换规律,确定三角函数图象的变化。
需要掌握各种三角函数的性质和图象,以及对图象变换的计算方法。
题型七:三角函数的恒等变换这类题目要求根据已知的三角函数恒等式,进行变形和推导。
需要掌握各种三角函数的恒等式,以及灵活应用。
2)已知角α的终边经过一点P,则可利用点P在单位圆上的性质,结合三角函数的定义求解.在求解过程中,需注意对角终边位置进行讨论,避免忽略或重复计算.例2已知sinα=0.8,且α∈[0,π2],则cosα=.答案】0.6解析】∵sinα=0.8,∴cosα=±√1-sin²α=±0.6XXXα∈[0,π2],∴cosα>0,故cosα=0.6易错点】忘记对cosα的正负进行讨论思维点拨】在求解三角函数值时,需注意根据已知条件确定函数值的正负,避免出现多解或无解的情况.同时,需根据角度范围确定函数值的取值范围,避免出现超出范围的情况.题型二诱导公式的使用例3已知tanα=√3,且α∈(0,π2),则sin2α=.答案】34解析】∵ta nα=√3,∴α=π/30<α<π/2,∴0<2α<πsin2α=sin(π-2α)=sinπcos2α-cosπsin2α=-sin2α2sin2α=0,∴sin2α=0sin2α=3/4易错点】忘记利用诱导公式将sin2α转化为sin(π-2α)思维点拨】在解决三角函数的复合问题时,可利用诱导公式将一个三角函数转化为其他三角函数的形式,从而简化计算.同时,需注意根据角度范围确定函数值的取值范围,避免出现超出范围的情况.题型三三角函数的定义域或值域例4已知f(x)=2sinx+cosx,则f(x)的值域为.答案】[−√5,√5]解析】∵f(x)=2sinx+cosx=√5(sin(x+α)+sin(α-x)),其中tanα=-121≤sin(x+α)≤1,-1≤sin(α-x)≤15≤f(x)≤√5f(x)的值域为[−√5,√5]易错点】忘记利用三角函数的性质将f(x)转化为含有同一三角函数的形式思维点拨】在确定三角函数的定义域或值域时,可利用三角函数的性质将其转化为含有同一三角函数的形式,从而方便计算.同时,需注意对于复合三角函数,需先将其转化为含有同一三角函数的形式,再确定其定义域或值域.题型四三角函数的单调区间例5已知f(x)=sin2x,则f(x)在区间[0,π]上的单调递增区间为.答案】[0,π/4]∪[3π/4,π]解析】∵f'(x)=2cos2x=2(2cos²x-1)=4cos²x-2f'(x)>0的充要条件为cosx12f(x)在[0,π/4]∪[3π/4,π]上单调递增易错点】忘记将f'(x)化简为含有同一三角函数的形式,或对于三角函数的单调性判断不熟练思维点拨】在求解三角函数的单调区间时,需先求出其导数,并将其化简为含有同一三角函数的形式.然后,利用三角函数的单调性进行判断,得出函数的单调区间.题型五三角函数的周期性例6已知f(x)=sin(2x+π),则f(x)的周期为.答案】π解析】∵sin(2x+π)=sin2xcosπ+cos2xsinπ=-sin2xf(x)的周期为π易错点】忘记利用三角函数的周期性质思维点拨】在求解三角函数的周期时,需利用三角函数的周期性质,即f(x+T)=f(x),其中T为函数的周期.同时,需注意对于复合三角函数,需先将其转化为含有同一三角函数的形式,再确定其周期.题型六三角函数的图象变换例7已知f(x)=sinx,g(x)=sin(x-π4),则g(x)的图象相对于f(x)的图象向左平移了.答案】π4解析】∵g(x)=sin(x-π4)=sinxcosπ4-cosxsinπ4g(x)的图象相对于f(x)的图象向左平移π4易错点】忘记利用三角函数的图象变换公式,或对于三角函数的图象不熟悉思维点拨】在求解三角函数的图象变换时,需利用三角函数的图象变换公式,即y=f(x±a)的图象相对于y=f(x)的图象向左(右)平移a个单位.同时,需对于各种三角函数的图象有一定的了解,以便准确判断图象的变化情况.题型七三角函数的恒等变换例8已知cosα=12,且α∈(0,π2),则sin2α的值为.答案】34解析】∵cosα=12,∴sinα=√3/2sin2α=2sinαcosα=√3/2×1/2=3/4易错点】忘记利用三角函数的恒等变换公式思维点拨】在求解三角函数的恒等变换时,需熟练掌握三角函数的基本恒等式和常用恒等式,从而简化计算.同时,需注意根据已知条件确定函数值的正负,避免出现多解或无解的情况.已知角α的终边所在的直线方程,可以通过设出终边上一点的坐标,求出此点到原点的距离,然后利用三角函数的定义来解决相关问题。
三角函数的图象与性质(自制)

x
R 最大值与最小值点恰好都在x 2 y 2 R 2上, 则f ( x ) 的最小正周期为 A.1 B.2 C .3 D.4
的图象上, 相邻的一个
析 : 本题主要考查三角函数的图象的性质 : 对称 中心与对称轴及最大值与最小值之间的关系.
依题意知 : 函数f ( x )的周期T f ( x )的最大值为 3.
f ( x )max 0
当x 0时分子为 1, 分母为1, 最小值为 1.
析 : f ( x) =-
sin x 1 3 2cos x 2sin x 1 1( 1 cos x 2 ) 1 sin x .
sin x 1 (1 sin x )2 (1 cos x )2
1 cos x 2 ) 表示点(1, 1)与单位圆上的点连线的斜率 1 sin x 的平方,为(0, ) (
故f ( x ) [1,0]
例4 : 对于函数f ( x ) a sin x bx c(其中a , b R, c z ), 选取a , b, c的一组值计算f (1)与f ( 1), 所得出的正确 结果一定不正确的是( 2011福建) A.4, 6 B.3,1 C .2, 4 D.1, 2
| t | 2
必须的哟!
故f ( t )在[ 2, 2]上为减函数, f ( x )min
9 9 2 2; f ( x )max 2 2. 2 2
练1.(2011上海理8)函数y sin(
2
2
x )cos(
6
x )的最大值为
.
析 : y sin(
x )cos(
1 积化和差 : sin sin [sin( ) sin( )] 2
第四章 专题研究 三角函数的值域与最值

授 人 以 渔
1+k 4± 7 解之得 k= 3
课 时 作 业
4- 7 4+ 7 ∴函数 f(x)的值域为[ , ] 3 3
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
课 前 自 助 餐
sinx (2)f(x)= cosx
sinx≤cosx sinx>cosx
作出图象 2 由图象知,-1≤y≤ 2
授 人 以 渔
探究3 借助一些代数式的几何意义或三角函 数的图象可直观地求出函数的值域,从而减 少运算量.
课 时 作 业
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
课 前 自 助 餐
专题训练
授 人 以 渔 课 时 作 业
高考调研· 新课标高考总复习
课 时 作 业
高考调研· 新课标高考总复习
高三数学(理)
第四章
专题研究
题型三 数形结合求三角函数的值域
课 前 自 助 餐
授 人 以 渔
2-sinx 例 3 (1)求函数 f(x)= 的值域. 2+cosx 1 1 (2) 已 知 f(x) = (sinx + cosx) - |sinx - 2 2 cosx|,求 f(x)的值域. 2-sinx 【解析】 (1)函数 f(x)= ,可看作 2+cosx 点(2,2)(-cosx,sinx)两点连线的斜率. 点(-cosx,sinx)的轨迹为 x2+y2=1.
高三数学(理)
第四章
专题研究
专题研究
课 前 自 助 餐
三角函数的值域与最值
专题要点
1.
函数 定义域 值域 y=sinx R [-1,1] cosx R [-1,1] tanx π {x|x≠kπ+ ,k∈Z} 2 R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的定义域、值
域和最值
-CAL-FENGHAI.-(YICAI)-Company One1
三角函数的定义域、值域和最值
一 知识点精讲: 1 三角函数的定义域
(1)r y =αsin 定义域为R. (2)r x
=αcos 定义域为R.
(3)x y =
αtan 定义域为 ⎭
⎬⎫
⎩⎨⎧∈+≠Z k k ,2|ππαα. (4)y x =αcot 定义域为
{}Z k k ∈≠,|παα.
2 三角函数的值域 ① )0(,sin ≠+=a b x a y 型
当0>a 时,],[b a b a y ++-∈ ; 当0<a 时 ],[b a b a y +-+∈ ② c x b x a y ++=sin sin 2型
此类型的三角函数可以转化成关于sinx 的二次函数形式。
通过配方,结合
sinx 的取值范围,得到函数的值域。
x sin 换为x cos 也可以。
③ x b x a y cos sin +=型
利用公式a
b
x b a x b x a =++=+φφtan ),sin(cos sin 22, 可以转化为一个三角函数的情形。
④x x b x x a y cos sin )cos (sin ++=型
利用换元法,设x x t cos sin +=, ]2,
2[-∈t ,则2
12cos sin -=
t x x ,
转化为关于t 的二次函数2
22122b
at t b t b at y -+=-+=. ⑤x x c x b x a y cos sin cos sin 22++=型
这是关于x x cos ,sin 的二次齐次式,通过正余弦的降幂公式以及正弦的倍角公式,2
2sin cos sin ,22cos 1cos ,22cos 1sin 22x
x x x x x x =+=-=
, 可转化为p x n x m y ++=2cos 2sin 的形式。
⑥ d
x c b
x a y ++=
sin sin 型 可以分离常数,利用正弦函数的有界性。
⑦b
x a
x y ++=
cos sin 型 可以利用反解的思想方法,把分母乘过去,整理得,
a by x y x -=-cos sin ,11,
1)sin(2
2
≤+-+-=
-y
a by y
a by x φ, 通过解此不等式可得到
y 的取值范围。
或者转化成两点连线的斜率。
以上七种类型是从表达的形式上进行分类的,如果x 有具体的角度范围,则再进行限制。
二 典例解析:
例1.求下列函数的定义域
(1)x x y 2cos 2sin 33--=; (2))2
1(cos log sin +=x y x . (3)
x x y cos lg 252+-=;
例2.求下列函数的值域
(1) 3sin 2+-=x y (2)4sin 5cos 22-+=x x y ;
(3)x x x x y 22cos 2cos sin 4sin 5+-=; (4)x x x x y cos sin cos sin ++= (5)2sin 31
sin 3++=x x y ; (6)2
cos 2sin ++=x x y
(7)x x y cos )6
sin(π
-=. (8))
4
(
tan 1)4
(tan 12
2x x y -+--=
ππ
(9)求函数x x
x x
y 2sin cos sin 12sin +--=的值域.
三 课堂练习:
1.若αααα则,11sec csc cos 2-=-⋅所在的象限是
( ) A .第二象限 B .第四象限
C .第二象限或第四象限
D .第
一或第三象限 2.不解等式:
(1)21sin -<x (2)21
cos >x
3.已知)(cos ),2
3
,21()(x f x f 则的定义域为-的定义域为____________.
4.求下列函数的定义域 (1)1tan 1
-=
x y (2).251sin 2x
x y -+
=
5.求下列函数的值域 (1)1cos 2-=x y
(2).sin 1cos sin 22x
x
x y +=
(3)].,[2sin 2
1
cos sin 1ππ-∈+++=x x x x y (4).sin cos 3x x y -=
(5)x
y sin 21
+= (6) 1cot 4tan 22++=x y
6.有一块扇形铁板,半径为R ,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都半径或弧在扇形的上,求这个内接矩形的最大面积.。
