博弈论原理 第5讲 不完全信息静态博弈
合集下载
不完全信息静态博弈
• （3）、信念不同出现的均衡的答案也会不同。 ）、信念不同出现的均衡的答案也会不同 ）、信念不同出现的均衡的答案也会不同。 • • • • （4）、由于参与者的收益函数具有不确定性，因而不可能通过 ）、由于参与者的收益函数具有不确定性， ）、由于参与者的收益函数具有不确定性 求解最大化的方式找到最优策略，换句话说， 求解最大化的方式找到最优策略，换句话说，就是什么策略都可 能成为最优策略，任何结果都有可能是博弈的均衡解。 能成为最优策略，任何结果都有可能是博弈的均衡解。这样得不 出结果。 出结果。
囚徒因境2 囚徒因境2的扩展式表达
2、囚徒因境2的扩展式的理解 、囚徒因境2
）、该博弈有两个开始点 行动的时候， • （1）、该博弈有两个开始点 ）、该博弈有两个开始点(X1和X2)，在囚徒 行动的时候， 和 ，在囚徒1行动的时候 囚 • 徒1分不清他到底位于哪一个节点，是X3、X4、X5，还是 。 分不清他到底位于哪一个节点， 分不清他到底位于哪一个节点 、 、 ，还是X6。 • （2）、博弈的扩展式有三个信息集，它们分别 ）、博弈的扩展式有三个信息集 ）、博弈的扩展式有三个信息集，它们分别{X1}，{X2}和 ， 和 • {X3，X4，X5，X6}。 ， ， ， 。 • • • • ）、由于该博弈有两个开始点 （3）、由于该博弈有两个开始点、可以理解为两个不同的博 ）、由于该博弈有两个开始点、 但关键是，这两个博弈被一条虚线连接起来， 弈，但关键是，这两个博弈被一条虚线连接起来，因而它又是一 个博弈。它既是两个博弈又是一个博弈， 个博弈。它既是两个博弈又是一个博弈，从逻辑上来说这是矛盾 因而我们不可能直接分析它。 的，因而我们不可能直接分析它。
• 豪尔绍尼转换的主要思路 • 以类型概念构造对不完全信息的招述， 在此基础上构造统一的模型来描述局中人 在博弈中对不完全信息的处理，从而将不 完全信息博弈转化为不完美信息的完全信 息博弈。
博弈论——不完全信息静态博弈
3 不完全信息静态博弈3.1 简介博弈论在1970年代之后逐渐进入主流经济学体系，主要是由于它在不完全信息条件下的经济分析中表现出特别的优势。
不完全信息指经济活动中一部分经济主体的某些特征对于其他主体来说是不清楚的。
如在拍卖商品或工程招投标中。
信息不完全又称为信息不对称，即其他局中人没有特定局中人清楚特定局中人自身的特征。
不完全信息静态博弈就是假定某些局中人具有其他局中人不清楚的某些特征的静态博弈。
但对于局中人本身来说，他自身的这些不为人所知的特征对于他自己来说是清楚的，因而称这些特征为局中人自己拥有的“私人信息”（private information）。
在博弈论中，习惯地将局中人的“私人信息”集中表现为局中人的支付函数特征，也就是说，局中人的私人特征将完全通过其支付函数特征表征出来，而不完全信息就表现为一些局中人不清楚另一局中人的支付函数，当然，每个局中人是完全清楚自己的支付函数的。
3.2 理论: 静态贝叶斯博弈和贝叶斯纳什均衡在假定局中人拥有私人信息的情况下，其他局中人对特定局中人的支付函数类型并不清楚，局中人不知道他在与谁博弈，在1967年前，博弈论专家认为此时博弈的结构特征是不确定的，无法进行分析。
Harsanyi （1967、1968）提出了一种处理不完全信息博弈的方法，即引入一个虚拟的局中人——“自然N ”。
N 首先行动，决定每个局中人的特征。
每个局中人知道自己的特征，但不知道其他局中人特征。
这种方法将不完全信息静态博弈变成一个两阶段动态博弈，第一个阶段是自然N 的行动选择，第二阶段是除N 外的局中人的静态博弈。
这种转换被称为“Harsanyi 转换”，它将不完全信息博弈转换为完全但不完美信息博弈。
局中人拥有的私人信息为他的“类型”，由其支付函数决定，故常将支付函数等同于类型。
用i θ表示局中人i 的一个特定类型，i H 表示局中人i 所有可能类型的集合，即i i H ∈θ，称i H 为局中人i 的类型空间，n i ,,1 =。
第五章 不完全信息静态博弈
不完全信息的古诺模型 5
不完全信息的古诺模型 6
三、静态贝叶斯博弈的战略式表述
参与人的类型
要准确地表示静态贝叶斯博弈，关键的问题是反映这种博弈中各参与 人虽然清楚自己的支付函数，却无法确定其他参与人支付函数这一特征。 解决这个问题的前提和基本思路：某些参与人虽然不能确定其他 参与人在一定策略组合下的支付，但至少知道其他参与人的支付有哪 几种可能的结果，而哪种可能的结果会出现则取决于其他参与人属于 哪种“类型”。 定义：一个参与人自己清楚而他人无法完全清楚的私人内部消息、有 关情况或数据等(所有个人信息)，即所有不是共同知识的信息称为参 与人的类型。 上述方法实际上是将博弈中某些参与人对其他参与人支付的不了 解，转化成为对这些参与人“类型”的不了解，是一种“追根溯源 ”的思想方法。
与人不知道其他参与人的支付或支付函数。
暗标拍卖 注：不完全信息并不是完全没有信息，实际上不完全信息的博弈方至 少必须有关于其他博弈方支付分布的可能范围和分布概率的知识，否则 博弈方的决策选择就会完全失去依据，我们的博弈分析也就无意义了。
1. 不完全信息博弈例子：市场进入博弈
潜在进入企业(参与人1) 决定是否进入一个新的产业， 但不知道在位企业(参与人2) 的成本函数，不知道在位者 决定默许还是斗争。假设在 位者的成本有两种可能的成 本函数：高成本或低成本(称 为类型)。
四、海萨尼转换 2
海萨尼（Harsanyi，1967-1968）提出了一种在前述将对支付的不了解
转化为对类型的思路的基础上，进一步将不完全信息静态博弈转化为完全 但不完美信息动态博弈进行分析的思路，被称为海萨尼转换。
之后，
四、海萨尼转换 3
N
在位者 1 p 高成本 低成本
博弈论_不完全信息静态博弈
贝叶斯纳什均衡的存在性
贝叶斯纳什均衡的存在性定理 定理3.1.2，见书上第62页，不讲定理的证明 它与第24页的定理2.2.3的比较。定理3.1.2所
要用到的前提条件更强，其原因在于： 在贝叶斯博弈中，局中人i的收益是纯策略下
的期望收益。或，局中人i的收益函数ui(s-i, si, ti)可以随着类型的变化而变化；当ui是si的凹函 数时，其凸组合“∑pi(t-i|ti)×ui(s-i(t-i), si, ti), t-i∈T-I”也是si的凹函数；若拟凹则不成立
义3.1.2做比较 此定义是对纯策略下贝叶斯纳什均衡定义的一
个直接扩展，其中E(ui)是局中人i在混合策略 组合下，对其收益函数ui的数学期望 定理3.1.3：混合策略组合是贝叶斯纳什均衡 的充分必要条件 定理3.1.4：贝叶斯纳什均衡的存在性定理
求解行业博弈的贝叶斯纳什均衡
条件概率 标记混合策略的符号 标记期望收益的符号 计算不同类型下的期望收益 书上的方法：由混合策略下贝叶斯纳什均衡的
对局中人2的计算
局中人 1建厂 高成本
进入
不进入
局中人 1建厂 低成本
进入
不进入
建厂 , -4/3 , 0 建厂 , -4/3 , 0
不建厂 , 1 , 0 不建厂 , 1 , 0
合成后的支付矩阵
局中人 1建厂 高成本
进入
不进入
局中人 1建厂 低成本
进入
不进入
建厂 0, -4/3 2, 0 建厂 1.5, -4/3 3.5, 0
混合策略
在贝叶斯博弈G＝[N, {Ti}, P, {Si(ti)}, {ui}]中，局中人i 在类型ti∈Ti下，为每一个纯策略以概率进行选择，则 xi(ti) ＝(x1(i)(ti), x2(i)(ti), ···, xm_i(i)(ti))称为局中人i在类型 ti下的一个混合策略。有时简写为xi。
博弈论与信息经济学 不完全信息静态博弈
不完全信息和贝叶斯纳什均衡
定义：在静态贝叶斯G {A1, , An ; 1, , n ; p1, , pn ;u1, , un}博弈中， 纯策略贝叶斯纳什均衡是一个类型依存策略组
合a (θ) (a1 (1 ),
,
a
n
(
n
))，其中，每个参与人
i
在给定自己的类
型
i
和其他参与人依存策略
a
i
(θ i
不完全信息和贝叶斯纳什均衡
n 人不完全信息静态博弈的时间顺序为：
⑴自然给定类型向量θ 察到 i ，但参与人
(1, ,
j（ i
n ) ，其中，i ）只知道 p j
(θ j
i
|
，参与人 i 观 j )，观察不
到 i；
⑵参与人同时选择行动，参与人 i 从可行集 Ai (i )中选择行
动 a i，n 人的行动组合为a (a1, , an )；
p(i ,i ) p(i )
p(i ,i ) p(i ,i )
ii
这里，p(i ) 是边缘概率。如果类型的分布是独立的，pi (i i ) p(i )
不完全信息和贝叶斯纳什均衡
贝叶斯纳什均衡是完全信息静态博弈纳什均衡概念在不完 全信息静态博弈上的扩展。不完全信息静态博弈又称为静 态贝叶斯博弈。 ◆定义：n人静态贝叶斯博弈的战略式表述包括：参与人的类 型空间 1, , n，条件概率 p1 ,..., pn ，类型依存战略空间
A11,..., An n ，和类型依存支付函数u1(a1, , an ;1),..., un (a1, , an ;n )
参与人i知道自己的类型 i i ，条件概率 pi pi (i i ) 描述 给定自己属于 i 的情况下，参与人i有关其他参与人类型 i i的不确定性。我们用 G {A1, , An ;1, ,n ; p1, , pn ;u1, ,un} 代表这个博弈。
不完全信息静态博弈
假设我们观察到一个人干了一件好事,那么,这个人 是好人的后验概率为: P(GP |GT)= P(GT|GP定张三是好人的先验概率是0.5, 那么, 在观察到张三干了一就好事后,我们如何修正他是好 人的先验概率依赖于我们认为这间好事好到什么程度. 1,这是一件非常好的好事,好人一定干,坏人决不可能 干,即P(GT|GP)=1, P(GT|BP)=0
进入者似乎是与两个不同的在位者博弈, 一个是高成本的在位者,一个是低成本的 在位者.
不完全信息古诺模型 参与人的类型是成本函数.假设逆需求函数 为P = a-q1-q2,每个企业的单位成本不变, 为ci,则企业的利润函数为: πi = qi (a-q1-q2-ci), i=1,2
假设企业1的单位成本c1是共同知识,企 业2的单位成本可能是高的也可能是低的, 企业2知道自己的成本类型,但企业1只 知道企业2属于这两种类型的概率分布 和1-,是共同知识. 进一步假设 a = 2, h c 2 = 1.25, = 0.5 c1 = 1, l c2 = 0.75,
不完全信息静态博弈: 不完全信息静态博弈:贝叶斯纳什均衡
完全信息博弈的基本假设是所有的参与人都知 道博弈的结构,博弈的规则,和博弈的支付函 数.例如在"市场进入"博弈中,进入者知道 在位者的偏好,战略空间和各种战略组合下的 利润水平,反之亦然.当然,这个假设在许多 情况下是不成立的.
哈桑尼( 哈桑尼(Harsanyi)定义了"贝叶斯纳什均衡": )定义了"贝叶斯纳什均衡" 贝叶斯均衡是纳什均衡在不完全信息博弈中的 扩展:
在静态不完全信息博弈中,参与人同时行动,没有机 会观察到其他人的选择; 每个参与人仅知道其他参与人类型的概率分布而不知 道其真实类型; 他不可能准确地知道其他参与人实际上会选择什么战 略,但是,他能正确地预测到其他参与人的选择是如 何依赖于其各自的类型的 决策目标就是在给定自己的类型和别人的类型依从战 略的情况下,最大化自己的期望效用.
第五章 不完全信息静态博弈及应用 《博弈论与经济》 PPT课件
p(t-iti ) p(ti )
p(t-i ti )
p(t-i ti
)
pi
t-i
▪ 它描写了参与人i依据自己的类型 ti 对其余局中人类型 t-i 的推断或信
念。
▪ 以下用
G T1, T2,, Tn; A1, A2,, An; u1, u2,, un; P1, P2,, Pn
弈模型。
表示贝叶斯博
因而局中i人的策略是定义在局中人的信息集 上，Ti 取值于行动集合
的映射A：i
si : Ti Ai
▪
▪
si (ti ) ai , ti Ti , ai Ai
▪ 局中人的条件期望 支付函数
▪ 由于局中人i的支付函数 ui ui (a1, a2 ,, an ; t1, t2 ,, tn ) 是随机的，因而需 用期望支付作为决策的依据。对给定的其余局中人的策略组合
参与人2关于参与人1的最优反应策略为 s2(t) (C, D)
▪ 2. 求参与人1关于参与人2的最优反应策略。
▪ 对于固定的 s2(t)，参与人1选择 s1 a1 ，最大化自己的期望支付，即
求解最大化问题
▪
max u1(a1, s2 (t1),t1) (1- )u1(a1, s2(t2 ),t2) a1
己以及对手的支付值，因为支付还依赖于对手的成本是H还是L。而局 中人对于对手的这一私人信息还不了解，这样当然无法选择出对自己 有利的策略。为解决这个问题，海萨尼提出了解决的方法—海萨尼转 换。
▪ 海萨尼转换
▪ 1.海萨尼从不完全信息模型的特征入手，引入一个概念，类
型： ti Ti , i 1,2,, n 。Ti 称为局中人的类型空间或类型集合，
▪ 故 ： (C, (C, D)) 是贝叶斯纳什均衡。
5 不完全信息静态博弈
第5章
不完全信息静态博弈
[贝叶斯博弈]
1. 贝叶斯博弈简介
• 在第2章中，我们学习了关于完全信息静 态博弈，以及如何求解其纳什均衡。
• 在完全信息博弈中，局中人了解每个人 的特征(type).
• 然而，在很多情况下，博弈参加者并不 了解其对手的特征。
•
例如:
1. 谈判双方不了解彼此对于谈判目标的 评价。 2. 企业可能不知道竞争对手的成本函数。
• Jerry选择 (D,P)时， Michelle选择 D 的期望收益为2p。
如果 p>1/3, 那么， Michelle 选择 D, Jerry 选择 (D,P)是贝叶斯纳什均衡的。
• 所有博弈都可以被划分为完全信息或不 完全信息博弈。
• 不完全信息博弈: 至少一个局中人不知道 其他人的“类型”。
不完美信息 vs.不完全信息博弈
• 在不完美信息博弈中，局中人不知道其 他局中人所选择的行动。但是，知道他 们的类型。
• 也可以说, 在不完全信息博弈中，正在进 行的博弈状况不是“共同知识”。
但是, 局中人1不知道局中人2处于哪种状 态，他认为处于两种状态的概率各为1/2， 这是他的信念(belief)。
• 接下来，求解博弈均衡的核心理念是， 给定对方的选择，以及关于对方行动的 信念，自己做出的选择是最优的。
• 局中人1不知道局中人2的类型，所以， 要作出理性的选择，他需要形成关于对 方各个行动的信念。
• 给定这些信念，他就可以计算自己各种 行动的期望收益。
• 例如，局中人1了解到，当他选择B时， 如果局中人2愿意与自己在一起，会选择 B, 如果不愿意与自己在一起则选择S。
• 那么局中人选择B的期望收益为： ½ ·2 + ½ ·0 = 1
不完全信息静态博弈
[贝叶斯博弈]
1. 贝叶斯博弈简介
• 在第2章中，我们学习了关于完全信息静 态博弈，以及如何求解其纳什均衡。
• 在完全信息博弈中，局中人了解每个人 的特征(type).
• 然而，在很多情况下，博弈参加者并不 了解其对手的特征。
•
例如:
1. 谈判双方不了解彼此对于谈判目标的 评价。 2. 企业可能不知道竞争对手的成本函数。
• Jerry选择 (D,P)时， Michelle选择 D 的期望收益为2p。
如果 p>1/3, 那么， Michelle 选择 D, Jerry 选择 (D,P)是贝叶斯纳什均衡的。
• 所有博弈都可以被划分为完全信息或不 完全信息博弈。
• 不完全信息博弈: 至少一个局中人不知道 其他人的“类型”。
不完美信息 vs.不完全信息博弈
• 在不完美信息博弈中，局中人不知道其 他局中人所选择的行动。但是，知道他 们的类型。
• 也可以说, 在不完全信息博弈中，正在进 行的博弈状况不是“共同知识”。
但是, 局中人1不知道局中人2处于哪种状 态，他认为处于两种状态的概率各为1/2， 这是他的信念(belief)。
• 接下来，求解博弈均衡的核心理念是， 给定对方的选择，以及关于对方行动的 信念，自己做出的选择是最优的。
• 局中人1不知道局中人2的类型，所以， 要作出理性的选择，他需要形成关于对 方各个行动的信念。
• 给定这些信念，他就可以计算自己各种 行动的期望收益。
• 例如，局中人1了解到，当他选择B时， 如果局中人2愿意与自己在一起，会选择 B, 如果不愿意与自己在一起则选择S。
• 那么局中人选择B的期望收益为： ½ ·2 + ½ ·0 = 1
05 不完全信息静态博弈解析
例如：
经过海萨尼转换后
N
正常 [P] 乙 招 甲 招 不招 招 不招 甲 不招 甲 招 不招 招 招 有义气 [1- P] 乙 不招 甲 不招
(-5，-5)
(0，-8)
(-8，0)
(－1，1) (-11，-5) (-6，-8)
(-8，0)
(－1，1)
2 不完全信息博弈
在一些博弈中，经常出现其中的一方或双方 都具有私人信息（即一方知道而对方不知道的信 息）。 如:消费者在购物时，知道物品对自己的效用大小， 而商家不知道；但商家知道商品的质量如何，而 消费者未必清楚。
如果各参与人的类型空间只有一个元素，则 退化为完全信息静态博弈
静态贝叶斯博弈的一般表达式：
空间 Ai ( i ), 类型依存支付函数 ui (a1 ,, an ; i)。参与人i知道
i
参与人i (i 1,, n)的类型空间i , 条件概率 Pi , 类型依存策略
自己的类型 i i , 条件概率 p ( i | i)描述给定自己属于 i G { A1 ,, An ;1 ,, n ; p1 ,, pn ; u1 ,, un }代表这个博弈。
引例2：不完全信息的古诺模型 厂商2的成本有两种可能，是厂商2的私人信息，厂商1 只知道其可能性（概率分布），因此厂商1对厂商2的得益 不完全清楚。
1 海萨尼（Harsanyi）转换
引入虚拟参与人“自然”
对自然来讲在所有后果间是无差异的 自然的选择提供了被选择的参与人真实类型的概率分 布 分布函数是共同知识 “不完全信息”转换为“完全但不完美信息”
u
4 静态贝叶斯博弈的应用举例
1)不完全信息的古诺（Cournot）模型
不完全信息表现在： 企业2的成本有两种可能，是企业2的私人信息， 企业1只知道可能性（概率分布），因此企业1对企业 2的得益不完全清楚。企业1的单位成本是共同知识。
不完全信息静态博弈
第八章 不完全信息静态博弈这一章里我们讨论不完全信息静态博弈，也称为贝叶斯博弈(Bayes)。
不完全信息博弈中，至少有一个参与者不能确定另一参与者的收益函数。
非完全信息静态博的一个常见例子是密封报价拍卖(sealed —bid auction)：每一报价方知道自己对所售商品的估价，但不知道任何其他报价方对商品的估价；各方的报价放在密封的信封里上交，从而参与者的行动可以被看作是同时的。
静态贝叶斯博弈问题的主要来源也是现实经济活动，许多静态博弈关系都有不完全信息的特征，研究贝叶斯博弈不仅是完善博弈理论的需要，也是解决实际问题的需要。
8.1 静态贝叶斯博弈和贝叶斯纳什均衡为了更好的说明不完全信息与完全信息之间的差异，我们用一个典型静态贝叶斯博弈作为例子，自然的引进静态贝叶斯博弈概念。
考虑如下两寡头进行同时决策的产量竞争模型。
其中市场反需求函数由Q a Q P -=)(给出，这里21q q Q +=为市场中的总产量。
企业1的成本函数为1111)(q c q C =，不过企业2的成本函数以θ的概率为222)(q c q C H =，以θ-1的概率为222)(q c q C L =，这里H L c c <。
并且信息是不对称的：企业2知道自己的成本函数和企业1的成本函数，企业1知道自己的成本函数，但却只知道企业2边际成本为高的概率是θ，边际成本为低的概率是θ-1(企业2可能是新进入这一行业的企业，也可能刚刚发明一项新的生产技术)。
上述一切都是共同知识：企业1知道企业2享有信息优势，企业2知道企业1知道自己的信息优势，如此等等。
现在我们来分析这个静态贝叶斯博弈。
一般情况下，企业2的边际成本较高时选择较低的产量，边际成本较低时，选择较高的产量。
企业1从自己的角度，会预测到企业2根据其成本情况将选择不同的产量。
设企业1的最佳产量选择为*1q ，企业2 边际成本为H c 时的最佳产量选择为)(*2H c q ，企业2 边际成本为L c 时的最佳产量选择为)(*2L c q ，如果企业2的成本较高，它会选择)(*2H c q 满足：类似地，如果企业2的成本较低，)(*2L c q 应满足：从而，企业l 为了使利润最大化，选择*1q 应满足：三个最优化问题的一阶条件为：及 ]})()[(1(])([({211*21*2*1c c q a c c q a q L H ---+--=θθ 三个一阶条件构成的方程组的解为：及 3)1(2*1L H c c c a q θθ-++-=把这里的*1q 、)(*2H c q 和)(*2L c q 与成本分别为1c 和2c 的完全信息古诺均衡相比较，假定1c 和2c 的取值可使得两个企业的均衡产量都为正，在完全信息的条件下，企业的产出为3/)2(*j i i c c a q +-=。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
贝叶斯纳什均衡
不完全信息博弈-无法避免的不确定性
有一次，主人派伊索进城。半路上，他遇见一位法官。法官严厉 地盘问：“你要去哪儿？” 伊索回答说“不知道” 。法官起了 疑心，派人把伊索关进了监狱，严加审问。“法官先生，要知道， 我讲的是实话。”伊索说，“我确实不知道我会进监狱”。
5.1 不完全信息与不完全信息静态博弈
二、静态贝叶斯博弈的表示 在静态贝叶斯博弈中，各博弈方虽然知道自己的 得益函数，但却无法了解其他博弈方的得益函数，按照 一般静态博弈分析方法无法解决该问题。为此，我们可 以这样来考虑：虽然一些博弈方(如博弈方k)不能确定 其他博弈方在一定策略组合下的得益，但一般知道其他 博弈方(如博弈方i)的得益有哪些可能的结果，而具体哪 种可能的结果会出现则取决于博弈方属于哪种“类型” （Type）。这些“类型”是博弈方自己清楚而他人博弈 方无法完全清楚的有关私人内部信息。
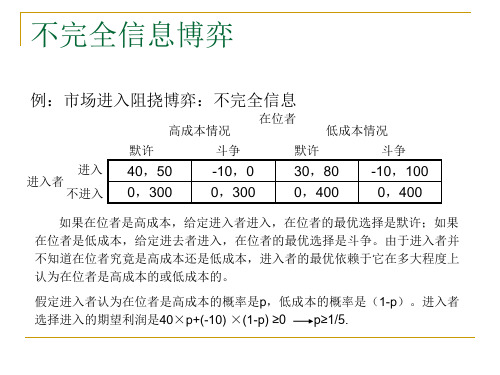
低成本情况 斗争 -10,100 0,400
进入者关于在位者成本信息是不完全的，进入者的最优选择依赖于他在多大程度上 认为在位者是低成本的。 假定进入者认为在位者是高成本的概率是p，低成本的概率是（1-p），那么，进入 者选择进入的期望利润是p（40）+（1-p）（-10），选择不进入的利润是0，因此， 进入者的最优选择是：如果p>=1/5，进入，如果p<1/5，当p=1/5时，进入与不进 入是无差异的，我们假定其进入。
密封拍卖一般有这样几个基本特征： （1）各方的报价放在密封的信封里上交 （2）在统一的时间里公证开标； （3 ）每一个报价方知道自己对标的的估 价，但不知 道其他报价方对标的的估价 （4）一般是标价最高者中标
显然, 拍卖或招投标问题属于不完全信息博弈，包括不 完全信息静态博弈和不完全信息动态博弈。
将计就计：真正的“信息不对称”
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
一个古董商发现一个人用珍贵的茶碟做猫食碗，于是假装对这只猫很感兴趣，要 丛主人手里买下，主人不卖，为此古董商出了大价钱。成交之后，古董商装做不在意 地说：这个碟子它已经用惯了，就一块送给我吧。猫主人不干了：你知道用这个碟子， 我已经卖了多少只猫了？
著名的BF实验
把几只蜜蜂和几只苍蝇放进一个玻璃瓶中，然后将瓶子平放，让瓶底朝向窗户，结果会怎样呢？ 你会看到，蜜蜂不停地在瓶底寻找出口，直到累死为止，而苍蝇则在不到两分钟内全部逃出。为什 么呢？因为蜜蜂喜欢光亮而且有智力，于是他们坚定的认为，出口一定在有光亮的地方，于是他们 不停地重复这一合乎逻辑的行为。而苍蝇呢？它们对事物的逻辑毫不在意，而是到处乱飞，探索有 可能出现的任何机会，于是他们成功了。 实验、试错、冒险、即兴发挥、迂回前进、混乱、随机应变，所有这些都有助于应付变化，要善 于打破固定的思维模式，要有足够的探索未知领域的学习能力。
然而，司马懿不知道自己和对方在不同行动策略下 的支付，而诸葛亮是知道的，他们对博弈结构的了 解是不对称的，诸葛亮拥有比司马懿更多的信息， 因此这是一个信息不对称的博弈。
1
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈
着博弈方 i 不同的收益函数的可能情况。其取值是博弈方 i 自己知道而其他博弈方并不 清楚的，反映了静态贝叶斯博弈中信息不完全的特征。根据上述思路，静态贝叶斯博 弈可一般表达为 G {A1 ,, An ; T1 ,Tn , u1 ,, u n } ，其中 Ai 为博弈方 i 的策略空间，Ti 是博弈方 i 的类型空间，
3
5.2 海萨尼转换 关于海萨尼转换
工商管理学院
School .Busi Admin
5.2 海萨尼转换 海萨尼转换的原理
工商管理学院
School .Busi Admin
海萨尼（Harsanyi）1967年提出了一种进一步将 不完全信息静态博弈转化为完全但不完美信息动态 博弈进行分析的思路，被称为“海萨尼转换 （Harsany Transformation）”
将计就计：掌握的正确信息越多，获胜的可能就越大
有一个卖草帽的人，有一天叫卖归来，在一棵大树旁 打起了瞌睡，等他醒来的时候，发现身边的帽子都不 见了，抬头一看，树上有很多猴子，模仿人的样子把 帽子戴在头上，他想到猴子喜欢模仿人的动作，就拿 下自己的帽子扔在地上，猴子也学他，纷纷将帽子扔 在地上。于是卖帽子的人检起帽子回家去了，并将这 个故事告诉了他的子孙。 很多年后，他的孙子继承了卖帽子的家业，有一天， 他也在大树旁睡着了，而帽子也同样被猴子拿走了， 他想起爷爷的办法，拿下帽子扔在地上。可是猴子非 但没有照他的做，还把扔在地下的帽子也拣走了，临 走时还说：我爷爷早告诉我了，你这个老骗子要玩什 么把戏。
5.1 不完全信息与不完全信息静态博弈 自然选择参与人的类型
行动
接受
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
你
不接受
-50，0 0， 0 100，20 0， 0
几个静态贝叶斯博弈的例子
密封拍卖（Sealed-bid Auction）
2
5.1 不完全信息与不完全信息静态博弈 我们假设卖主不设定成 交的最低限价，未中标 者没有成本。显然这种 暗标拍卖是发生在投标 人之间的，在同时开标 的情况下（即同时选择） 展开的一次性静态博弈， 各个博弈方的策略是他 们各自提出的标价；中 标博弈方的得益是其对 标的的估价与成交价格 之差，未中标博弈方的 利益则为0。
拍卖和招投标是比较典型的不完全信息静态博弈。由拍 卖或招投标问题构成的博弈模型的共同特征就是都属于 不完全信息博弈，包括不完全信息静态博弈和不完全信 息动态博弈。而密封拍卖就可以构成一个典型的不完全 信息静态博弈，也就是静态贝叶斯博弈。
求爱博弈： 品德优良者求爱
20x+ （-100）（1-x）=0 当x大于5/6时，接受求爱
(a1 ,, a n ) 和类型 ti 的函数。
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
5.2 海萨尼转换
在位者 高成本情况 合作 进入者 进入 不进入 40,50 0,300 斗争 -10, 0 0, 300 合作 30,80 0,400
工商管理学院
在上述的博弈中，进入者似乎在与两个 在位者博弈，一个是高成本的在位者， 一个是低成本的在位者；如果在位者有T 种不同的成本函数，进入者就相当于与T 个不同的在位者博弈。 1967年以前，博弈论专家认为这样的不 完全信息是没法分析的。
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
如果用 ti 表示博弈方 i 的类型，用 Ti 表示博弈方 i 的类型空间， t i Ti ，用
ui (a1 ,, an , t i ) 表示博弈方 i 在策略组合 (a1 ,, an ) 下的得益，每一类型 ti 都对应
通过上述思想和方法, 我们就将博弈中一些博弈方 对其他博弈方得益的不了解，转化成对这些博弈方 “类型”的不了解，这样我们在分析静态贝叶斯博 弈的时候，就必须将关注各博弈方的得益转向关注 各博弈方的策略组合以及各自的“类型”。
ui (a1 ,, an , t i ) 为博弈方
i 的得益 , 它是策略组合
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈
工商管理学院
School .Busi Admin
在密封拍卖中，中标博 弈方的利益除了取决于 标价以外，还取决于他 对拍卖标的物的估价， 买价估价是私人信息， 因此在密封拍卖博弈中， 各个博弈方对其他博弈 方中标的实际得益无法 确知，只能自己判断， 这说明上述暗标拍卖博 弈确实是不完全信息博 弈, 是静态贝叶斯博弈。
工商管理学院
School .Busi Admin
在孔明与司马懿的博弈中，对于司马懿而言，孔明有谨 慎和冒险两种类型。 由于司马懿不知道双方行动的支付，根据其策略我们可 以假设他对此次博弈的预期支付为：
孔明 冒险 司 马 懿 守城 进攻 后退 获胜，被擒 不胜不败，逃 脱 弃城 获胜，被擒 不胜不败，逃 脱 守城 被伏击，逃脱 不胜不败，逃 脱 谨慎 弃城 获胜，被擒 不胜不败，逃 脱
工商管理学院
School .Busi Admin
5.1 不完全信息与不完全信息静态博弈 关于不完全信息
工商管理学院
School .Busi Admin
第五讲
1 2 3
不完全信息静态博弈
不完全信与不完全信息静态博弈 海萨尼转换
在生活中我们会碰到这样的问题，比如一个乞丐向你乞讨，你愿意帮助别人， 但不知道他是真的乞丐还是骗子，该如何决定呢？ 在博弈中，不完全信息的博弈称为“贝叶斯博弈”。不完全信息是指至少有一 个博弈方不完全清楚其他某些博弈方的得益或得益函数。不完全信息的静态博 弈也就是后面即将要讲的“静态贝叶斯博弈”。 不完全信息的静态博弈主要探讨如何在不确定性的情况下做出理性、一致的决 策，换句话说，首先必须承认自己虽然没有办法做到无所不知，但也不至于一 无所知，而应该或尽可能有效运用自己所知的一切为自己谋利。
进入
求爱者
不进入
你
默许 进入 不进入
100，－100 0， 0
斗争
-50，0 0， 0