人教版七年级数学上册图形的认识初步单元检测题
人教版七年级上册数学《几何图形初步》单元测试题(含答案)

人教版数学七年级上学期第四章单元测试满分:100分时间:90分钟一、选择题(每题3分,共30分)1.下列各图中,∠1与∠2互为补角的是( )学#科#网...学#科#网...A. AB. BC. CD. D2.下列语句错误的是( )A. 延长线段ABB. 延长射线ABC. 直线m和直线n相交于点PD. 在射线AB上截取线段AC,使AC=3 cm3.下列立体图形中,都是柱体的为( )A. AB. BC. CD. D4.如图,表示∠1的其他方法中,不正确的是( )A. ∠ACBB. ∠CC. ∠BCAD. ∠ACD5.如图所示的表面展开图所对应的几何体是( )A. 长方体B. 球C. 圆柱D. 圆锥6.如图所示的物体从上面看到的形状是( )A. AB. BC. CD. D7.下列各图中,经过折叠能围成一个正方体的是( )A. B. C. D.8.在直线上顺次取A,B,C三点,使得AB=5 cm,BC=3 cm,如果O是线段BC的中点,那么线段AO的长度是( )A. 8 cmB. 7.5 cmC. 6.5 cmD. 2.5 cm9.如图,∠AOC=∠DOE=90°,如果∠AOE=65°,那么∠COD的度数是( )A. 90°B. 115°C. 120°D. 135°10.用折纸的方法,可以直接剪出一个正五边形(如图).方法是:拿一张长方形纸对折,折痕为AB,以AB的中点O为顶点将平角五等分,并沿五等分的线折叠,再沿CD剪开,使展开后的图形为正五边形,则∠OCD 等于( )A. 108°B. 90°C. 72°D. 60°二、填空题(每题3分,共24分)11.如图,射线OA表示____________方向,射线OB表示____________方向.12.已知线段AB=8 cm,在直线AB上画线段BC,使它等于3 cm,则线段AC=__________.13.如图,图中线段有________条,射线有________条.14.计算:(1)90.5°-25°45′=__________;(2)5°17′23″×6=__________.15.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOC的度数是________.16.将线段AB延长至点C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8 cm,则AB=________ cm.17.如图,将一副三角尺叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=________.18.如图是由一些小立方块所搭立体图形分别从正面、左面、上面看到的图形,若在所搭立体图形的基础上(不改变原立体图形中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.三、解答题(19,21题每题6分,20,22,24题每题10分,其余每题12分,共66分)19.如图,A,B两个村庄在河m的两侧,连接AB,与m交于点C,点D在m上,连接AD,BD,且AD=BD.若要在河上建一座桥,使A,B两村来往最便捷,则应该把桥建在点C还是点D?请说明理由.20.如图,已知线段a,b,画一条线段,使它等于3a-b(不要求写画法).21.如图所示的立体图形是由七块积木搭成的,这几块积木是大小相同的正方体,请画出这个立体图形分别从正面、左面、上面看到的图形.22.如图,点C是AB的中点,D,E分别是线段AC,CB上的点,且AD=AC,DE=AB,若AB=24 cm,求线段CE的长.23.如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.(1)求出∠AOB及其补角的度数;(2)①请求出∠DOC和∠AOE的度数;②判断∠DOE与∠AOB是否互补,并说明理由.24.如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60 cm,求绳子的原长.25.已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE 与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.参考答案一、选择题(每题3分,共30分)1.下列各图中,∠1与∠2互为补角的是( )学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...A. AB. BC. CD. D【答案】D【解析】【分析】根据互为补角的两个角的和等于180°对各选项分析判断即可得解.【详解】A、∠1+∠2不一定等于180°,故不一定是互为补角关系,故本选项错误;B、∠1+∠2=90°,是互为余角关系,故本选项错误;C、∠1与∠2是对顶角,不一定互补,故本选项错误;D、∠1与∠2互为补角关系,故本选项正确,故选D.【点睛】本题考查了余角和补角,熟练掌握补角的概念是解题的关键.2.下列语句错误的是( )A. 延长线段ABB. 延长射线ABC. 直线m和直线n相交于点PD. 在射线AB上截取线段AC,使AC=3 cm【答案】B【解析】【分析】利用有关直线、射线、线段的知识逐项判定即可.【详解】A、延长线段AB,说法正确,故A选项不符合题意;B、射线只能反向延长,所以延长射线AB说法错误,故B选项符合题意;C. 直线m和直线n相交于点P,说法正确,故C选项不符合题意;D、在射线AB上截取线段AC,使AC=3 cm,说法正确,故D选项不符合题意,故选B.【点睛】本题主要考查了直线、射线、线段,解题的关键是熟记有关直线、射线、线段的知识.3.下列立体图形中,都是柱体的为( )A. AB. BC. CD. D【答案】C【解析】【分析】根据柱体是上下一样粗的几何体逐项进行分析可得答案.【详解】A选项中有锥体,故A选项不符合题意;B选项中有锥体,故B选项不符合题意;C选项中全是柱体,故C选项符合题意;D选项中有台体,故D选项不符合题意,故选C.【点睛】此题主要考查了认识立体图形,关键是掌握各种图形的特点.4.如图,表示∠1的其他方法中,不正确的是( )A. ∠ACBB. ∠CC. ∠BCAD. ∠ACD【答案】B【解析】【分析】根据角的表示方法,一个顶点有多个角时,不能用单个大写字母表示,由此进行判断即可. 【详解】A 选项符合角的表示方法,不符合题意;B选项以C点为顶点的角有多个,故∠C不能表示∠1,符合题意;C选项符合角的表示方法,不符合题意;D选项符合角的表示方法,不符合题意;故选B.【点睛】此题主要考查角的表示方法,熟练掌握是解题关键.5.如图所示的表面展开图所对应的几何体是( )A. 长方体B. 球C. 圆柱D. 圆锥【答案】D【解析】【分析】观察表面展开图有圆和扇形,由此即可确定.【详解】A选项展开图中没有圆,不符合题意;B选项展开图不是平面,不符合题意;C选项展开图中没有扇形,不符合题意;D选项展开图中有圆和扇形,符合题意,故选D.【点睛】此题主要考查立体图形的展开图,熟知常见几何体表面展开图是解题关键.6.如图所示的物体从上面看到的形状是( )A. AB. BC. CD. D【答案】D【解析】【分析】从上面观察所给几何体,结合选项即可得出答案.【详解】从上面观察所给几何体可以看到是一个有直径的圆环,如图所示:故选D.【点睛】此题主要考查三视图的知识,熟练掌握是解题关键.7.下列各图中,经过折叠能围成一个正方体的是( )A. B. C. D.【答案】A【解析】由平面图形的折叠及正方体的展开图解题,注意只要有“田”、“凹”字格的展开图都不是正方体的表面展开图。
七年级数学上学期第四单元几何图形初步测试卷5套带答案
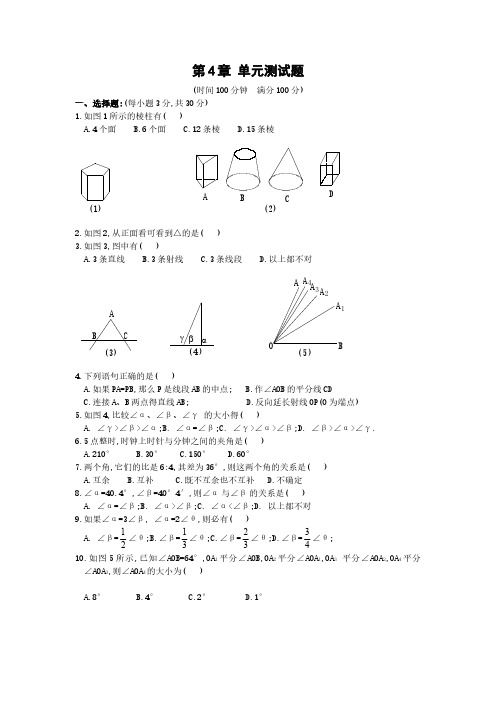
第4章 单元测试题(时间100分钟 满分100分)一、选择题:(每小题3分,共30分)1.如图1所示的棱柱有( )A.4个面B.6个面C.12条棱D.15条棱C(2)A DB2.如图2,从正面看可看到△的是( )3.如图3,图中有( )A.3条直线B.3条射线C.3条线段 D.以上都不对4.下列语句正确的是( )A.如果PA=PB,那么P是线段AB的中点;B.作∠AOB的平分线CDC.连接A、B两点得直线AB;D.反向延长射线OP(O为端点)5.如图4,比较∠α、∠β、∠γ 的大小得( )A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.6.5点整时,时钟上时针与分钟之间的夹角是( )A.210°B.30°C.150°D.60°7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )A.互余B.互补C.既不互余也不互补D.不确定8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对9.如果∠α=3∠β, ∠α=2∠θ,则必有( )2310.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )A.8°B.4°C.2°D.1°二、填空题:(每小题3分,共30分)11.已知线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,则线段CD=______.12.如图,从城市A 到城市B 有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.13.57.32°=_______°_______′_______″;27°14′24″=_____°.14.已知∠a=36°42′15″,那么∠a 的余角等于________.15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.16.表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.航线铁路公路(6)A B18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.19.已知线段AB=acm,点A 1平分AB,A 2平分AA 1,A 3平分AA 2,……,____________cm.20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.三、解答题:(21、24、25、26每题6分,22、23题每题8分)21.根据下列语句画图:(1)画∠AOB=120°;(2)画∠AOB 的角平分线OC;(3)反向延长OC 得射线OD;(4)分别在射线OA、OB、OD 上画线段OE=OF=OG=2cm;(5)连接EF、EG、FG;(6)你能发现EF、EG、FG 有什么关系?∠EFG、∠EGF、∠GEF 有什么关系?22.已知线段AB=10cm,直线AB 上有一点C ,且BC=4cm,M 是线段AC 的中点,求AM 的长.23.如图,直线AB、CD 交于O 点,且∠BOC=80°,OE 平分∠BOC,OF 为OE 的反向延长线.(1)求∠2和∠3的度数.(2)OF平分∠AOD吗?为什么?24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).北D CA B26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.参考答案一、选择题1.D2.C3.C4.D5.C6.C7.B8.B9.C 10.B二、填空题11.12cm 12.两点之间,线段最短 13.57、19、12;27.2414. 53°17′45″ 15.同角的补角相等16.140° 17.90 18.180°;19°38′29″. 19. 20.1或4或6三、解答题21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°22.AM=7cm或3cm23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.第4章 单元测试题2检测时间:45分钟,满分:100分班级 学号 姓名 得分一、填空题:(每空2分,共46分)1.正方体有______条棱,_____个顶点, 个面.2.圆柱的侧面展开图是一个 ,圆锥的侧面展开图是一个 ,棱柱的侧面展开图是一个 。
七年级数学图形的初步认识单元测试卷

第四章 图形的初步认识单元测验试卷初一 班 座号 姓名 成绩(满分100分, 时间90分钟)一. 选择题(共每题4分,共32分)1.①平角是一条直线. ②线段AB 是点A 与点B 的距离.③射线AB 与射线BA 表示同一条射线. ④过一点有且只有一条直线与已知直线平行. ⑤圆柱的侧面是长方形。
以上说法正确的有( )A .0个 B.1个 C.2个 D.3个2.在下列立体图形中,不属于多面体的是( )A .正方体B .三棱柱C .长方体D .圆锥体 3.两个锐角的和( )A .一定是锐角B 一定是直角C 一定是钝角D 可能是钝角、直角或锐角 4.平面上有三点A 、B 、C ,如果AB=8,AC=5,BC=3,则( ) A 点C 在线段AB 上 B 点B 在线段AB 的延长线上C 点C 在直线AB 外D 点C 可能在直线AB 上,也可能在直线AB 外 5.如右图所示,B 、C 是线段AD 上任意两点,M 是AB 的中点,N 是CD 中点,若MN=a ,BC=b ,则线段AD 的长是( ) A 2(a-b ) B 2a-b C a+b D a-b 6.如图,115︒∠=,90AOC ︒∠=,点B 、O 、D 在同一直线上, 则2∠的度数为( )A . 75︒B .15︒C .105︒D .165︒7.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )A 南偏西50度方向B 南偏西40度方向C 北偏东50度方向D 北偏东40度方向8.如图,////,//AB EF DC EG BD , 则图中与1∠相等的角共有( )个A 6个B .5个C .4个 D.2个二. 填空题(3+3+3+4+8=21分)9.不在同一直线上的四点最多能确定 条直线。
10.如右图,点C 是 AOB ∠的边OA 上一点,D 、E 是OB 上两点, 则图中共有 条线段, 条射线, 个小于平角的角.11.如图,点C 是线段AB 上一点,点D 、E 分别是线段AC 、BC 的中点. 如果AB=a,AD=b,其中a>2b,那么CE=A DB MC N ABC DEFGH1ABCDE O A BC D EABCDO1212.(1) ?'2330︒= ︒ 78.36_________'____"︒︒=(2)5245'3246'_________'︒︒︒-= 18.32634'_____︒︒︒+= 13.如图,①如果12∠=∠,那么根据 ,可得 // .得14.如图,AOB ∠为已知角,请画出AOB ∠的平分线OC ,在OC 上任取一点P ,过P 点分别作两边OA 、OB 的垂线段PM 、PN ;用尺子量出PM 、PN 的长,并比较PM 、PN 的大小(请保留作图痕迹)(6分)15.在如图所示,将方格中的图形向右平移3格,再向上平移4格,画出平移后的图形.(3分))16.(1) 一个角的余角比它的补角29还多1︒,求这个角.(2)已知互余两角的差为20︒ ,求这两个角的度数.AB OAB C17.如图,AD=12DB , E 是BC 的中点,BE=1AC=2cm ,求线段DE 的长.ABD18如图,直线//a b ,1(225)x ∠=-︒,2(175)x ∠=-︒,求1,2∠∠的度数.19.在下图中,已知直线AB 和直线CD 被直线GH 所截,交点分别为E 、F 点,AEF EFD ∠=∠.(1)写出//AB CD 的根据;(2)若ME 是AEF ∠的平分线, FN 是EFD ∠的平分线, 则EM 与FN 平行吗?若平行,试写出根据.ABC DEFGMNa b 1 2l20. 如图,已知://AD BC ,且DC AD ⊥于D ,求证:①DC BC ⊥②12180∠+∠=︒21.如图, CD AB ⊥于D , GF AB ⊥于F ,140,250∠=︒∠=︒,求B ∠度数.ABC D 12345A BCD EFG1234。
人教版七年级上册数学《几何图形初步》单元综合检测(带答案)

人教版数学七年级上学期第四章单元测试满分:100分时间:90分钟一、选择题1.有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形是()A. B. C. D.2.用两把常用三角板不可能拼成的角度为()A. B. C. D.3. 如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是( )A. ∠AOD>∠BOCB. ∠AOD<∠BOC;C. ∠AOD=∠BOCD. 无法确定4.如果两个不相等的角的和为,则这两个角可能是()A. 一个小于直角,一个大于直角B. 两个大于直角的角C. 两个小于直角的角D. 以上答案都不对5.已知∠α=35°,那么∠α的余角的补角等于A. 35°B. 65°C. 125°D. 145°6.如图是一个正方体展开图,把展开图折叠成正方体后,”我”字一面的相对面上的字是( )A. 的B. 中C. 国D. 梦7.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是A. 甲B. 乙C. 丙D. 丁8.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有A. 1个B. 2个C. 3个D. 4个二、填空题9.如果点,,在一条直线上,线段,线段,则、两点间的距离是________.10.如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=PB,若剪断后的各段绳子中最长的一段为30cm,则绳子的原长为________ cm..11.如图,从A到B有多条道路,人们通常会走中间的直路,而不走其他的路,这其中的道理是.12.如图,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是_______13.如图所示,已知∠AOB=90°,∠COD=90°,∠AOC︰∠BOD=1︰2,则∠BOD=________.14.如图,M是线段AB的中点,N是线段BC的中点,AB=8cm,BC=6cm,则线段MN=__ cm.三、解答题15. (6分)下面是小马虎解的一道题题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.解:根据题意可画出图,∵∠AOC=∠BOA-∠BOC=70°-15°=55°,∴∠AOC=55°.若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.16.已知∠α=76°,∠β=41°31′.(1)求∠β的余角;(2)求∠α的2倍与∠β的的差.17.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.(1)请你数一数,图中共有多少个小于平角的角?(2)求∠BOD的度数.(3)请通过计算说明OE是否平分∠BOC.18.如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.(1)如果CD=5cm,MN=8cm,求AB的长;(2)如果AB=a,MN=b,求CD的长.19.已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,①∠MON与旋转度数n°有怎样的数量关系?说明理由;②当n为多少时,∠MON为直角?(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OA绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.参考答案一、选择题1.有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形是()A. B. C. D.【答案】B【解析】【分析】根据五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱的面数进行判断.【详解】依题意得,有六个面的立体图形为:①正方体,③四棱柱,④长方体,共有3个.故答案选:B.【点睛】本题考查的知识点是认识立体图形,解题的关键是熟练的掌握立体图形概念.2.用两把常用三角板不可能拼成的角度为()A. B. C. D.【答案】C【解析】【分析】根据两个三角板可拼出的角度有15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,180°【详解】∵三角板的度数为30°,60°,90°;45°,45°,90°∴可拼出的角度有15°,30°,45°,60°,75°,90°105°,120°,135°,150°,180°.故答案选:C.【点睛】本题考查的知识点是角的计算,解题的关键是熟练的掌握角之间的转换.3. 如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是( )A. ∠AOD>∠BOCB. ∠AOD<∠BOC;C. ∠AOD=∠BOCD. 无法确定【答案】C【解析】本题考查了角的大小比较根据题意∠AOC=∠BOD,再根据图得知∠COD为∠AOD与∠BOC的公共角,从而得出答案.∵∠AOC=∠BOD,∠COD为∠AOD与∠BOC的公共角,∴∠AOC+∠COD=∠BOD+∠COD,∴∠AOD=∠BOC,故选C.4.如果两个不相等的角的和为,则这两个角可能是()A. 一个小于直角,一个大于直角B. 两个大于直角的角C. 两个小于直角的角D. 以上答案都不对【答案】A【解析】【分析】根据补角定义,两个不相等的角的和为180°,则这两个角是一个锐角,一个钝角,由此选择答案即可.【详解】∵两个不相等的角的和为180°,∴这两个角是一个锐角(小于直角),一个钝角(大于直角).故答案选:A.【点睛】本题考察的知识点是余角和补角,解题的关键是熟练的掌握余角和补角的定义与计算.5.已知∠α=35°,那么∠α的余角的补角等于A. 35°B. 65°C. 125°D. 145°【答案】C【解析】【分析】根据余角和补角的概念列式计算即可.【详解】解:∵∠α=35°,∴∠α的余角为:90°-35°=55°,∴∠α的余角的补角为:180°-55°=125°,故选:C.【点睛】本题考查的是余角和补角的概念,若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.6.如图是一个正方体展开图,把展开图折叠成正方体后,”我”字一面的相对面上的字是( )A. 的B. 中C. 国D. 梦【答案】D【解析】试题分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,”们”与”中”是相对面,”我”与”梦”是相对面,”的”与”国”是相对面.故选D.考点:正方体相对两个面上的文字.【此处有视频,请去附件查看】7.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是A. 甲B. 乙C. 丙D. 丁【答案】D【解析】解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁.故选D.8.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有A. 1个B. 2个C. 3个D. 4个【答案】C【解析】解:根据角的和差关系可得第一个图形∠α=∠β=45°,根据同角的余角相等可得第二个图形∠α=∠β,根据等角的补角相等可得第三个图形∠α=∠β,第四个图形∠α+∠β=180°,不相等,因此∠α=∠β的图形个数共有3个.故选C.点睛:此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等,等角的余角相等.二、填空题9.如果点,,在一条直线上,线段,线段,则、两点间的距离是________.【答案】或【解析】【分析】根据题意画出图形,根据点C在线段AB上和在线段AB外两种情况进行解答即可.【详解】解:当如图1所示点C在线段AB的外时,∵AB=6cm,BC=8cm,∴AC=6+8=14(cm);当如图2所示点C在线段AB上时,∵AB=6cm,BC=8cm,∴AC=8-6=2(cm).故答案为:14cm或2cm.【点睛】本题考查的是两点间的距离,解答此题时要注意进行分类讨论,不要漏解.10.如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=PB,若剪断后的各段绳子中最长的一段为30cm,则绳子的原长为________ cm..【答案】40或80【解析】解:本题有两种情形:(1)当点A是绳子的对折点时,将绳子展开如图.∵AP=PB,剪断后的各段绳子中最长的一段为30cm,∴BP=30cm,AP=10cm.∴绳子的原长=2AB=80cm;(2)当点B是绳子的对折点时,将绳子展开如图.∵AP=PB,剪断后的各段绳子中最长的一段为30cm,∴2BP=30cm,∴BP=15cm,AP=5cm.∴绳子的原长=2AB=40cm.11.如图,从A到B有多条道路,人们通常会走中间的直路,而不走其他的路,这其中的道理是.【答案】两点之间线段最短【解析】试题分析:根据线段的性质:两点之间线段最短填空即可.解:从A到B有多条道路,人们会走中间的直路,而不会走其他曲折的路,这是因为两点之间,线段最短.故答案为:两点之间,线段最短.考点:线段的性质——两点之间,线段最短12.如图,如果在阳光下你的身影的方向北偏东60°方向,那么太阳相对于你的方向是_______【答案】南偏西60°【解析】【分析】根据方向角的定义即可解答.【详解】由于人相对与太阳与太阳相对于人的方位正好相反,∵在阳光下你的身影的方向北偏东60°方向,∴太阳相对于你的方向是南偏西60°.故答案为:南偏西60°.【点睛】本题考查了方向角的概念,熟知方向角的概念是解答本题的关键.13.如图所示,已知∠AOB=90°,∠COD=90°,∠AOC︰∠BOD=1︰2,则∠BOD=________.【答案】120°【解析】【分析】根据周角的定义及已知条件可得∠AOC+∠BOD=180°,再由∠AOC︰∠BOD=1︰2即可求得∠BOD的度数.【详解】∵∠AOB=90°,∠COD=90°,∴∠AOC+∠BOD=360°-(∠AOB+∠COD)=180°,∵∠AOC︰∠BOD=1︰2,∴∠BOD=2∠AOC,∴∠AOC+2∠AOC=180°,即∠AOC=60°,∴∠BOD=2∠AOC=120°.故答案为:120°.【点睛】本题考查了角的计算,根据平角的定义求得∠AOC+∠BOD=180°是解决问题的关键.14.如图,M是线段AB的中点,N是线段BC的中点,AB=8cm,BC=6cm,则线段MN=__ cm.【答案】7 cm.【解析】【分析】由线段中点的定义知AM=MB=AB=4cm,BN=NC=BC=3cm.然后结合图示中的”MN=MB+BN”来求线段MN的长度.【详解】解:∵M是线段AB的中点,AB=8cm,∴MB=AB=4cm;∵N是线段BC的中点,BC=6cm,∴BN=NC=BC=3cm;∴MN=MB+BN=4+3=7cm.故答案为7.【点睛】本题考查了两点间的距离和线段中点的性质.注意”数形结合”的数学思想在本题中的应用.三、解答题15. (6分)下面是小马虎解的一道题题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.解:根据题意可画出图,∵∠AOC=∠BOA-∠BOC=70°-15°=55°,∴∠AOC=55°.若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.【答案】小马不会得满分的.见解析.【解析】试题分析:在同一平面内,若∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB 的外部.试题解析:如图,当OC在∠AOB的内部时,∠AOC=∠BOA﹣∠BOC=55°,当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,故∠AOC的度数是55°或85°.考点:角的计算.16.已知∠α=76°,∠β=41°31′.(1)求∠β的余角;(2)求∠α的2倍与∠β的的差.【答案】(1)48°29′;(2)131°14′30″.【解析】试题分析:(1)根据余角的定义即可求解;(2)根据题意列出式子求解即可.试题解析:(1)∠β的余角=90°-∠β=90°-41°31′=48°29′.(2)∵∠α=76°,∠β=41°31′,∴2∠α-∠β=2×76°-×41°31′=152°-20°45′30″=131°14′30″.17.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.(1)请你数一数,图中共有多少个小于平角的角?(2)求∠BOD的度数.(3)请通过计算说明OE是否平分∠BOC.【答案】(1)9;(2)155°;(3)OE平分∠BOC.理由见解析.【解析】试题分析:(1)根据角的定义即可解决;(2)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;(3)根据∠COE=∠DOE-∠DOC和∠BOE=∠BOD-∠DOE分别求得∠COE与∠BOE的度数即可说明.试题解析:解:(1)图中小于平角的角有9个.它们分别是:∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB.(2)∵∠AOC=50°,OD平分∠AOC,∴∠DOC=∠AOC=25°,∠BOC=180°﹣∠AOC=130°,∴∠BOD=∠DOC+∠BOC=155°.(3)∵∠DOE=90°,∠DOC=25°,∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.又∵∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,∴∠COE=∠BOE,即OE平分∠BOC.点睛:本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.18.如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.(1)如果CD=5cm,MN=8cm,求AB的长;(2)如果AB=a,MN=b,求CD的长.【答案】(1)线段AB的长为11cm;(2)2b﹣a.【解析】【分析】(1)先根据M,N分别是线段AC,BD的中点,可得MC=AC,DN=BD,再根据MC+CD+DN=MN=8cm,可得MC+DN=8﹣5=3cm,进而可得:AC+BD=2MC+2DN=2×3=6cm,所以AB=AC+CD+BD=AC+BD+CD=6+5=11(cm),(2)根据M,N分别是线段AC,BD的中点,可得CM=AM=AC,BN=DN=BD,再根据AM+BN=MC+DN=AB﹣MN,可得MC+DN=a﹣b,进而可得:CD=MN﹣(MC+DN)=b﹣(a﹣b)=2b﹣a.【详解】(1)M,N分别是线段AC,BD的中点,∴MC=AC,DN=BD,∵MC+CD+DN=MN=8cm,∴MC+DN=8﹣5=3cm,∴AC+BD=2MC+2DN=2×3=6cm,∴AB=AC+CD+BD=AC+BD+CD=6+5=11(cm),即线段AB的长为11cm,(2)M,N分别是线段AC,BD的中点,∴CM=AM=AC,BN=DN=BD,∵AM+BN=MC+DN=AB﹣MN,∴MC+DN=a﹣b,∴CD=MN﹣(MC+DN)=b﹣(a﹣b)=2b﹣a.【点睛】本题主要考查线段的中点性质和线段和差关系,解决本题的关键是要熟练掌握线段中点性质,根据线段和差关系进行求解.19.已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,①∠MON与旋转度数n°有怎样的数量关系?说明理由;②当n为多少时,∠MON为直角?(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OA绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.【答案】(1)25°;(2)①n°+25°,②n=65°;(3)m°+25°.【解析】【分析】(1)如图1,根据OM平分∠AOB,∠AOB=130°,利用角平分线的定义可得:∠AOM=∠AOB=×130°=65°,再根据ON平分∠COD,∠COD=80°,可得∠AON=∠COD=×80°=40°,进而求出∠MON=∠AOM﹣∠AON=65°﹣40°=25°,(2)①如图2中,根据图形中角的和差关系可得:∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,②当∠MON=90°时,由于n°+25°=90°,所以n=65°,(3)如图3中,根据图中角的和差关系可得:∠MON=∠COM﹣∠CON=65°+m°﹣(80°+m°)=m°+25°. 【详解】(1)如图1,∵OM平分∠AOB,∠AOB=130°,∴∠AOM=∠AOB=×130°=65°,∵ON平分∠COD,∠COD=80°,∴∠AON=∠COD=×80°=40°,∴∠MON=∠AOM﹣∠AON=65°﹣40°=25°,(2)①如图2中,∠MON=∠COM﹣∠NOC=65°+n°﹣40°=n°+25°,②当∠MON=90°时,n°+25°=90°,∴n=65°,(3)如图3中,∠MON=∠COM﹣∠CON=65°+m°﹣(80°+m°)=m°+25°.【点睛】本题主要考查角平分线的定义和角的和差关系,解决本题的关键是要熟练掌握角平分线的定义,并能结合图形分析角的和差关系.。
数学七年级上册《几何图形初步》单元综合检测题(含答案)

24.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t=(直接写结果)
(1)若以点C为原点,则点A对应的数是;点B对应的数是.
(2)A,B两点间的距离是;B,C两点间的距离是;A,C之间的距离是.
(3)当原点在处时,三个点到原点的距离之和最小,最小距离是.
20.如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,请求x﹣2y﹣3z的值.
21.∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
故选B.
【点睛】本题考查了余角和补角,正确表示出这个角的补角与余角是解题的关键.
3.在平面内,有两个角∠AOB=60°,∠AOC=30°,OA为两角的公共边,则∠BOC为( )
A.30°B.90°C.30°或90°D.无法确定
【答案】C
【解析】
【分析】
本题是角的计算的多解问题,求解时要注意分情况讨论.
A. 30°B. 90°C. 30°或90°D.无法确定
4.货轮A在航行的过程中发现:客轮B在它的南偏东80°的方向上,同时,在它的北偏东20°的方向上又发现了客轮C,则∠BAC的度数是( )
A.60°B.120°C.100°D.80°
5.如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条”捷径”,”捷径”的数学道理是( )
故选C.
【点睛】本题考查了直线、射线、线段的相关知识,熟练掌握各相关概念是解题的关键.
人教版七年级上册数学《几何图形初步》单元检测题(含答案)

故答案为OF.
【点睛】本题主要考查了数字变化的规律,这类题型难点在于找到其中的规律.
10.已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数
1
2
3
4
线段总条数
3
6
10
15
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2B. 1+2+3+…+n+n+1C. n+1D.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6 cm,BC=4 cm,点C在直线AB上,M,N分别是AC,BC的中点,求MN的长度.”结果会有变化吗?如果有,求出结果.
参考答案
一、选择题(每题3分,共30分)
1.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
A.五条线段,三条射线
B.一条直线,三条线段
C.三条线段,两条射线,一条直线
D.三条线段,三条射线
【答案】C
【解析】
试题分析:由直线、射线及线段的定义、图形知:
本图形有:
线段AB、BC、CA;
射线AD、AE;
直线DE.
即有三条线段,两条射线,一条直线.
故选C.
考点:直线、射线、线段.
5.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是
13.已知线段AB=6 cm,在直线AB上画线段AC=2 cm,则BC的长是_____cm.
14.已知∠α与∠β互余,且∠α=40°,则∠β为_____.
15.立方体木块的表面标有六个字1,2,3,4,5,6,下图是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是______.
人教版七年级上册数学 第四章 几何图形初步 单元测试(含解析)

第四章几何图形初步单元测试一.选择题1.对如图所示几何体的认识正确的是()A.棱柱的底面是四边形B.棱柱的侧面是三角形C.几何体是四棱柱D.棱柱的底面是三角形2.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于()A.点动成线B.线动成面C.面动成体D.以上都不对3.下列说法正确的是()A.延长直线AB到点CB.延长射线AB到点CC.延长线段AB到点CD.射线AB与射线BA是同一条射线4.如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD 上,且EA=1,则BE的长为()A.4B.6或8C.6D.85.下列说法正确的是()A.两点之间的线段,叫做这两点之间的距离B.87'等于1.45°C.射线OA与射线AO表示的是同一条射线D.延长线段AB到点C,使AC=BC6.线段AB=9,点C在线段AB上,且有AC=AB,M是AB的中点,则MC等于()A.3B.C.D.7.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在()A.A区B.B区C.C区D.A、B两区之间8.如图,将一副三角板叠在一起使直角顶点重合于点O,(两块三角板可以在同一平面内自由转动),下列结论一定成立的是()A.∠BOA>∠DOC B.∠BOA﹣∠DOC=90°C.∠BOA+∠DOC=180°D.∠BOC≠∠DOA9.下列说法正确的是()A.射线比直线短B.从同一点引出的两条射线所组成的图形叫做角C.若AP=BP,则P是线段AB的中点D.两点之间的线段叫做这两点之间的距离10.如图,O在直线AB上,OC平分∠DOA(大于90°),OE平分∠DOB,OF⊥AB,则图中互余的角有()对.A.6B.7C.8D.10二.填空题11.若一个六棱柱,则它有条棱,有个面.12.秒针旋转一周时,形成一个圆面,用数学知识可以理解为.13.已知点A、B、C在同一直线上,若AB=10cm,AC=16cm,点M、N分别是线段AB、AC中点,则线段MN的长是.14.如图,线段AB=3,延长AB到点C,使BC=2AB,则AC=.15.如图,已知CD=AD=BC,E、F分别是AC、BC的中点,且BF=40cm,则EF 的长度为cm.16.人们会把弯曲的河道改直,这样能够缩短航程.这样做的道理是.17.如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点,且AB=BC=CD,点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P有个.18.如图,已知A、B是线段EF上两点,EA:AB:BF=1:2:3,M、N分别为EA、BF 的中点,且MN=8cm,则EF长为.19.如图,C、D是线段AB上的两点,E是AC的中点,F是BD的中点,若AB=m,CD =n,则线段EF的长为.20.如图,射线OC,OD在∠AOB内,∠AOB和∠BOC互为补角,.若∠COD比∠BOD大m°(m<30),则∠AOC=°.(用含m的式子表示)三.解答题21.如图所示是一张铁皮.(1)计算该铁皮的面积;(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.22.如图,线段AB=20,BC=15,点M是AC的中点.(1)求线段AM的长度;(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.23.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:(1)图中到小明家距离相同的是哪些地方?(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.24.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.25.如图,C是线段AB上一点,AC=5cm,点p从点A出发沿AB以3cm/s的速度匀速向点B运动,点Q从点C出发沿CB以1cm/s的速度匀速向点B运动,两点同时出发,结果点P比点Q先到3s.(1)求AB的长;(2)设点P、Q出发时间为ts,①求点P与点Q重合时(未到达点B),t的值;②直接写出点P与点Q相距2cm时,t的值.26.线段与角的计算.(1)如图1,已知点C为AB上一点,AC=15cm,CB=AC,若D、E分别为AC、AB 的中点,求DE的长.(2)已知:如图2,∠AOB被分成∠AOC:∠COD:∠DOB=2:3:4,OM平分∠AOC,ON平分∠DOB,且∠MON=90°,求∠AOB的度数.参考答案1.解:如图所示的几何体是三棱柱,它有两个全等的三角形的底面,三个矩形的侧面,因此选项ABC均不符合题意,选项D符合题意;故选:D.2.解:孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于线动成面,故选:B.3.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;D、射线AB与射线BA不是同一条射线,故本选项不符合题意;故选:C.4.解:若E在线段DA的延长线,如图1,∵EA=1,AD=9,∴ED=EA+AD=1+9=10,∵BD=2,∴BE=ED﹣BD=10﹣2=8,若E线段AD上,如图2,EA=1,AD=9,∴ED=AD﹣EA=9﹣1=8,∵BD=2,∴BE=ED﹣BD=8﹣2=6,综上所述,BE的长为8或6.故选:B.5.解:A、应为:连结两点的线段的长度叫做这两点间的距离,故本选项错误;B、87'=60'+27'=1°+()°=1.45°,故本选项正确;C、射线OA的端点是点O,射线AO的端点是点A,所以,它们不是同一条射线,故本选项错误;D、延长线段AB到点C,则AC一定大于BC,不能使AC=BC,故本选项错误.故选:B.6.解:∵AB=9,∴AC=AB=3,∵M是AB的中点,∴AM=AB=∴MC=AM﹣AC=﹣3=故选:B.7.解:∵当停靠点在A区时,所有员工步行到停靠点路程和是:15×100+10×300=4500m,当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000m,当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000m,当停靠点在A、B区之间时,设在A区、B区之间时,设距离A区x米,则所有员工步行路程之和=30x+15(100﹣x)+10(100+200﹣x),=30x+1500﹣15x+3000﹣10x,=5x+4500,∴当x=0时,即在A区时,路程之和最小,为4500米;综上,当停靠点在A区时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在A区.故选:A.8.解:因为是直角三角板,所以∠AOC=∠BOD=90°,所以∠BOA+∠DOC=∠AOC+∠BOC+∠DOC=∠AOC=∠BOD=180°,故选:C.9.解:A.射线和直线不可以比较长短,原说法错误,故本选项不符合题意;B.从同一点引出的两条射线所组成的图形叫做角,原说法正确,故本选项符合题意;C.若点P在线段AB上,AP=BP,则P是线段AB的中点,原说法错误,故本选项不符合题意;D.两点之间的线段的长度叫做这两点之间的距离,原说法错误,故本选项不符合题意;故选:B.10.解:∵OC平分∠DOA,∴∠AOC=∠COD,∵OE平分∠DOB,∴∠DOE=∠BOE,∴∠COE=90°,∴∠AOC+∠BOE=90°,∠AOC+∠DOE=90°,∠COD+∠BOE=90°,∠COD+∠DOE =90°,∠COF+∠EOF=90°,∵OF⊥AB,∴∠AOC+∠COF=90°,∠COD+∠COF=90°,∠BOE+∠EOF=90°,∠BOD+∠DOF =90°,∠DOE+∠EOF=90°,∴互余的角有10对.故选:D.11.解:因为六棱柱上下两个底面是6边形,侧面是6个长方形,所以共有18条棱,8个面;故答案为18,8.12.解:根据点、线、面、体之间的关系可得,线动成面.13.解:(1)如图1,,∵AB=10cm,点M是线段AB的中点,∴AM=10÷2=5(cm);∵AC=16cm,点N是线段AC的中点,∴AN=16÷2=8(cm),∴MN=AM+AN=5+8=13(cm)(2)如图2,,∵AB=10cm,点M是线段AB的中点,∴AM=10÷2=5(cm);∵AC=16cm,点N是线段AC的中点,∴AN=16÷2=8(cm),∴MN=AN﹣AM=8﹣5=3(cm),综上,线段MN的长是13cm或3cm.故答案为:13cm或3cm.14.解:∵AB=3,∴BC=2AB=6,∴AC=AB+BC=3+6=9.故答案为:9.15.解:∵点F是BC的中点,且BF=40cm,∴BC=2BF=80cm,∵CD=AD=BC,∴CD=×80=16cm,AD=64cm,∴AC=AD﹣CD=48cm,∵E、F分别是AC、BC的中点,∴CE=AC=24cm,CF=BF=40cm,∴EF的长度为CE+CF=64cm,故答案为:64.16.解:由线段的性质可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,故答案为:两点之间线段最短.17.解:根据题意可知:当点P经过任意一条线段中点时会发出报警,∵图中共有线段DC、DB、DA、CB、CA、BA,∵BC和AD中点是同一个∴发出警报的可能最多有5个.故答案为5.18.解:∵EA:AB:BF=1:2:3,可以设EA=x,AB=2x,BF=3x,而M、N分别为EA、BF的中点,∴MA=EA,NB=BF,∴MN=MA+AB+BN=x+2x+x=4x ∵MN=8cm,∴4x=8,∴x=2,∴EF=EA+AB+BF=6x=12,∴EF的长为12cm,故答案为:12cm.19.解:∵AB=m,CD=n.∴AB﹣CD=m﹣n,∵E、F分别是AC、DB的中点,∴CE=AC,DF=DB,∴CE+DF=(m﹣n),∴EF=CE+DF+DC=(m﹣n)+n=m+n,故答案为:m+n.20.解:∵∠AOB和∠BOC互为补角,∴∠AOB+∠BOC=180°,∵∠BOD=,∴3∠BOD+∠BOC=180°,即∠BOC=180°﹣3∠BOD,∵∠COD+∠BOD=∠BOC,∴180°﹣3∠BOD=∠COD+∠BOD,∴∠COD+4∠BOD=180°,∵∠COD比∠BOD大m°(m<30),∴∠COD﹣∠BOD=m°,∴∠BOD=()°,∠COD=()°∴∠BOC=()°,∴∠AOB=180°﹣∠BOC=(108﹣)°,∴∠AOC=∠AOB﹣∠BOC=(108﹣)°﹣()°=(36﹣m)°.故答案为(36﹣m).21.解:(1)(1×3+2×3+1×2)×2=22(m2),(2)根据棱柱的展开与折叠,可得可以折叠成长方体的盒子,其长、宽、高分别为3cm,2cm,1cm,因此体积为:1×2×3=6(m3),22.解:(1)线段AB=20,BC=15,∴AC=AB﹣BC=20﹣15=5.又∵点M是AC的中点.∴AM=AC=×5=,即线段AM的长度是.(2)∵BC=15,CN:NB=2:3,∴CN=BC=×15=6.又∵点M是AC的中点,AC=5,∴MC=AC=,∴MN=MC+NC=,即MN的长度是.23.解:(1)因为点C为OP的中点,所以OC=2km,因为OA=2km,所以可得出距小明家距离相同的是学校和公园;(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.24.解:∵OC平分∠AOB,∠BOC=26°,∴∠AOB=2∠BOC=52°.∴∠BOD=180°﹣52°=128°.∵OE平分∠DOB,∴∠BOE=∠DOB=×128°=64°.25.解:(1)设AB=xcm,根据题意可得:(x﹣5)﹣=3,解得:x=12,答:AB的长为12cm;(2)①由题意可得:3t=t+5,解得:t=,故点P与点Q重合时(未到达点B),t的值为;②当点P追上点Q前相距2cm,由题意可得:3t+2=t+5,解得:t=,当追上后相距2cm,由题意可得:3t﹣2=t+5,解得:t=,总上所述:t=或t=.26.解:(1)∵AC=15cm,CB=AC,∴CB=×15=10(cm),∴AB=15+10=25(cm).∵D,E分别为AC,AB的中点,∴AE=BE=AB=12.5cm,DC=AD=AC=7.5cm,∴DE=AE﹣AD=12.5﹣7.5=5(cm);(2)设∠AOC=2x,∠COD=3x,∠DOB=4x,则∠AOB=9x,∵OM平分∠AOC,ON平分∠DOB,∴∠MOC=x,∠NOD=2x,∴∠MON=x+3x+2x=6x,又∵∠MON=90°,∴6x=90°,∴x=15°,∴∠AOB=135°.。
七年级上册数学第4章图形的初步认识单元练习题(含答案)

第4章图形的初步认识检测题(时间:90分钟,满分:100分)一、选择题(每小题3分,共30分)1.下列物体的形状类似于球的是()A.茶杯B.羽毛球C.乒乓球D.白炽灯泡2.正多面体的面数、棱数、顶点数之间存在着一个奇妙的关系,若用F、E. V分别表示正多而体的而数、棱数、顶点数,则有F + V — E = 2,现有一个正多面体共有12条棱,6个顶点,则它的面数F等于()A.6B.8C.12D.203.如果Na与N/?是邻补角,且/a> 很那么Z侄的余角是(A.l(Za+Z/?)B.|ZaC.|(Za-Z/?)D.不能确定4.下列四个立体图形中,主视图为圆的是()。
5.将“创建文明城市”六个字分别写在一个正方体的六个而上,这个正方体的平面展开图如所示, 那么在这个正方体中,和“创”相对的字是( A.文B.明C.城6.如图, 已知直线曲、CD 相交于点。
, ZEOC = 110% 则ZBOD 的大小C.45°D.55QD rH第6题图B.35A.25 共5页8. 下列平而图形不能够国成正方体的是(9. 过平面_匕4, B, C 三点中的任意两点作直线,可作()那么线段OB 的长度是( )二、填空题(每小题3分,共24分)11. 如图,直线CD 相交于点。
,OE 平分匕AOD,若ZBOC = 80°,贝ljZAOE = 12. 直线上的点有—个,射线上的点有—个,线段上的点有—个.13. 两条直线相交有 个交点,三条直线相交最多有 个交点,最少有 个交点.14. 如图,OM 平分ZAOB, ON 平分ZCOD.若NMON= 50。
,ZBOC = 10% 则匕4OD = 15 .如图给出的分别有射线、16.下列表面展开图的立体图形的名称分别是:A.1条B.3条C.1条或3条D.无数条10.在直线[上顺次取4、B 、 C 三点,使得= 5 cm, BC = 3 cm.如果。
是线段AC 的中点,A.2 cmB.0.5 cmC.1.5 cmD.l cmA第11题图直线、线段,其中能相交的图形有 个. 第15题图17.如图,C, D是线段上两点,若CB = 4 cm, DB = 7 cm,且D^L AC的中点,贝脂。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版七年级数学上册图形的认识初步单元检测题姓名:__________班级:__________考号:__________一﹨选择题(本大题共12小题,每小题4分,共48分。
)1.如图,在直线l上有A.B﹨C三点,则图中线段共有()A.1条B.2条C.3条D.4条2.把下列图标折成一个正方体的盒子,折好后与“中”相对的字是()A.祝B.你C.顺D.利3.下列关系式正确的是()A.35.5°=35°5′B.35.5°=35°50′C.35.5°<35°5′ D.35.5°>35°5′4.下面的几何体中,属于棱柱的有()A.1 个B.2 个C.3 个D.4 个5.如图,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为()A.62°B.118°C.72°D.59°6.将如图所示的直角三角形绕直角边AC旋转一周,所得的几何体从正面看是下图中的()A.B.C.D.7.如图,已知直线AB﹨CD相交于点O,OA平分∠EOC,∠EOD=70°,则∠BOD的大小为()A.25°B.35°C.45°D.55°8.如图给出的分别有射线﹨直线﹨线段,其中能相交的图形有()A.①②③④B.①C.②③④D.①③9.用一副三角板(两块)画角,不可能画出的角的度数是()A.15°B.55°C.75°D.135°10.以下3个说法中:①在同一直线上的4点A.B﹨C﹨D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是()A.②③B.③C.①②D.①11.如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )A.两点确定一条直线B.两点确定一条线段C.两点之间,直线最短D.两点之间,线段最短12.如图,在数轴上有A.B﹨C﹨D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A.D两点表示的数的分别为﹣5和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是()A.﹣1 B. 0 C. 1 D. 2二﹨填空题(本大题共6小题,每小题4分,共24分)13.要把一根木条在墙上钉牢,至少需要__________枚钉子.其中的道理是__________.14.如图,OC平分∠BOD,OE平分∠AOD,则与∠COD互余的角是______________________.15.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因.16.如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC=°.17.把两块三角板按如图所示那样拼在一起,那么∠ABC的度数是.18.已知线段AB=2cm,延长AB到点C,使BC=4cm,D为AB的中点,则线段DC=_____________________.三﹨解答题(本大题共8小题,共78分)19.已知∠α与∠β互为补角,且∠β的比∠α大15°,求∠α的余角.20.如图,点C为线段AB上一点,若线段AC=12cm,AC:CB=3:2,D﹨E两点分别为AC﹨AB的中点,求DE的长.21.按要求画图:(1)画直线AC;(2)画线段AB;(3)画射线BC.22.小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);(3)用量角器测出C点相对于点A的方位角.23.如图,已知A.O﹨B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.(1)若∠BOC=62°,求∠DOE的度数;(2)若∠BOC=a°,求∠DOE的度数;(3)图中是否有互余的角?若有请写出所有互余的角.24.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.(1)写出∠AOC与∠BOD的大小关系:,判断的依据是;(2)若∠COF=35°,求∠BOD的度数.25.取一张长方形的纸片,如图①所示,折叠一个角,记顶点A落下的位置为A′,折痕为CD,如图②所示再折叠另一个角,使DB沿DA′方向落下,折痕为DE,试判断∠CDE的大小,并说明你的理由.26.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t >0)秒.(1)写出数轴上点B表示的数__________,点P表示的数__________(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P﹨Q同时出发,问点P运动多少秒时追上点Q?(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.图形的认识初步单元检测题答案解析一﹨选择题1.【分析】根据线段的概念求解.解:图中线段有AB﹨AC﹨BC这3条,故选:C.2.【分析】利用正方体及其表面展开图的特点解题.解:这是一个正方体的平面展开图,共有六个面,其中面“祝”与面“利”相对,面“你”与面“考”相对,面“中”与面“顺”相对.故选C.3.【分析】根据大单位化小单位乘以进率,可得答案.解:A.35.5°=35°30′,35°30′>35°5′,故A错误;B﹨35.5°=35°30′,35°30′<35°50′,故B错误;C﹨35.5°=35°30′,35°30′>35°5′,故C错误;D﹨35.5°=35°30′,35°30′>35°5′,故D正确;故选:D.4.解:从左到右依次是长方体,圆柱,棱柱,棱锥,圆锥,棱柱.故选:C.5. 分析:利用对顶角的定义以及周角定义得出∠AOC的度数.解:∵直线AB和CD相交于点O,∠AOD与∠BOC的和为236°,∴∠AOC=∠BOD==62°.故选A.6. 分析:根据直角三角形绕直角边旋转一周得到的图形是圆锥,再根据圆锥体的主视图解答.解:Rt△ABC绕直角边AC旋转一周得到一圆锥体,圆锥体的主视图是等腰三角形.故选:D.7. 分析:先求出∠EOC=110°,再由OA平分∠EOC求出∠AOC=55°,即可求出∠BOD=∠AOC=55°.解:∵∠EOD=70°,∴∠EOC=180°﹣70°=110°,∵OA平分∠EOC,∴∠AOC=∠EOC=55°,∴∠BOD=∠AOC=55°;故选:D.8. 分析:根据直线是向两方无限延伸的,射线是向一方无限延伸的,线段不能向任何一方无限延伸进行画图可得答案.解:能相交的图形有①③.故选:D.9.分析:解答此题的关键是分清两块三角板的锐角度数的度数分别是多少,然后对应着4个选项再进行组合,看看可能画出的角的度数是多少即可.解:两块三角板的锐角度数分别为:30°,60°;45°,45°用一块三角板的45°角和另一块三角板的30°角组合可画出15°﹨75°角,用一块三角板的直角和和另一块三角板的45°角组合可画出135°角,无论两块三角板怎么组合也不能画出55°角.故选B.10.分析:根据线段的概念,直线的性质和余角﹨补角的定义进行判断.解:①在同一直线上的4点A.B﹨C﹨D只能表示6条不同的线段,故错误;②经过两点有一条直线,并且只有一条直线,正确;③同一个锐角的补角一定大于它的余角,正确.故选A.11. 分析:根据两点之间线段最短即可得出答案.解:因为两点之间线段最短,把弯曲的河道改直,能够缩短航程.故选:D.12.分析:根据A.D两点在数轴上所表示的数,求得AD的长度,然后根据2AB=BC=3CD,求得AB﹨BD的长度,从而找到BD的中点E所表示的数.解:∵|AD|=|6﹣(﹣5)|=11,2AB=BC=3CD,∴AB=1.5CD,∴1.5CD+3CD+CD=11,∴CD=2,∴AB=3,∴BD=8,∴ED=BD=4,∴|6﹣E|=4,∴点E所表示的数是:6﹣4=2.∴离线段BD的中点最近的整数是2.故选D.二﹨填空题13. 分析:根据两点确定一条直线解答.解:把一根木条钉牢在墙上,至少需要两枚钉子,其中的道理是:两点确定一条直线.故答案为:两,两点确定一条直线.14. 分析:答题是首先知道余角的概念,由∠AOD+∠BOD=180°,又知OC平分∠BOD,OE平分∠AOD,故知∠COE=90°.解:∵∠AOD+∠BOD=180°,∵OC平分∠BOD,OE平分∠AOD,∴∠DOE+∠COD=90°,∠DOE=∠AOE,∴与∠COD互余的角是∠DOE和∠AOE.15.分析:根据线段的性质解答即可.解:为抄近路践踏草坪原因是:两点之间线段最短.故答案为:两点之间线段最短.16.【分析】根据∠AOD是∠BOD的补角求得∠AOD的度数,然后根据角平分线的定义求∠AOC的度数.【解答】解:∵∠AOD+∠BOD=180°,∠BOD=40°,∴∠AOD=140°;∵OC平分∠AOD,∴∠AOC=∠COD=∠AOD=70°;故答案是:70.17.分析:∠ABC等于30度角与直角的和,据此即可计算得到.解:∠ABC=30°+90°=120°.故答案是:120°.18.分析:先根据题意找出各点的位置,然后直接计算即可.解:画出图形如下所示:则DC=DB+BC=AB+BC=1+4=5cm.故答案为:5cm.三﹨解答题19.分析:根据补角的定义,互补两角的和为180°,根据题意列出方程组即可求出∠α,再根据余角的定义即可得出结果.解:根据题意及补角的定义,∴,解得,∴∠α的余角为90°﹣∠α=90°﹣63°=27°.故答案为:27°.20. 分析:根据AC:CB=3:2,可得CB的长,根据线段的和差,可得AB的长,根据线段中点的性质,可得AD﹨AE的长,再根据线段的和差,可得答案.解:由AC=12cm,AC:CB=3:2,得CB=8cm,由线段的和差,得BA=AC+BC=12+8=20cm,由D﹨E两点分别为AC﹨AB的中点,得AD=0.5AC=6cm,AE=0.5AB=10cm,由线段的和差,得DE=AE﹣AD=10﹣6=4cm.21.分析:利用直线,射线及线段的定义画图即可.解:如图,22.分析:(1)根据叙述,利用方向角的定义即可作出图形;(2)利用刻度尺测量,然后根据图上1cm等于实际距离40m即可求得实际距离;(3)利用量角器测量即可.解:(1)如图;(2)AC=3.46cm,则C距A的实际距离是:3.46×40=138(m);(3)C点相对于A的方向角是:北偏西75°.23.【分析】(1)OD平分∠AOC,OE平分∠BOC,得出∠DOE=(∠BOC+∠COA),代入数据求得问题;(2)利用(1)的结论,把∠BOC=a°,代入数据求得问题;(3)根据(1)(2)找出互余的角即可.解:(1)∵OD平分∠AOC,OE平分∠BOC,∴∠DOC=∠AOC,∠COE=∠BOC∴∠DOE=∠DOC+∠COE=(∠BOC+∠COA)=×(62°+180°﹣62°)=90°;(2)∠DOE═(∠BOC+∠COA)=×(a°+180°﹣a°)=90°;(3)∠DOA与∠COE互余;∠DOA与∠BOE互余;∠DOC与∠COE互余;∠DOC 与∠BOE互余.24.分析:(1)根据对顶角相等填空即可;(2)首先根据直角由已知角求得它的余角,再根据角平分线的概念求得∠AOE,再利用角的关系求得∠AOC,根据上述结论,即求得了∠BOD.解:(1)相等,对顶角相等;(2)∵∠COE是直角,∠COF=35°∴∠EOF=55°又OF平分∠AOE,∴∠AOE=110°∴∠AOC=20°∴∠BOD=∠AOC=20°.故答案为相等﹨对顶角相等﹨20°.点评:(1)理解邻补角的概念,掌握等角的补角相等的性质;(2)正确求得一个角的余角,熟练运用角平分线表示角之间的倍分关系,再根据角之间的和差关系进行计算.25.分析:根据折叠的原理,可知∠BDE=∠A′DE,∠A′DC=∠ADC.再利用平角为180°,易求得∠CDE=90°.解:∠CDE=90°.理由:∵∠BDE=∠A′DE,∠A′DC=∠ADC,∴∠CDA′=∠ADA′,∠A′DE=∠BDA,∴∠CDE=∠CDA′+∠A′DE,=∠ADA′+∠BDA,=(∠ADA′+∠BDA′),=×180°,=90°.26.解:(1)点B表示的数是﹣6;点P表示的数是8﹣5t,(2)设点P运动x秒时,在点C处追上点Q (如图)则AC=5x,BC=3x,∵AC﹣BC=AB∴5x﹣3x=14…解得:x=7,∴点P运动7秒时,在点C处追上点Q.…(3)没有变化.分两种情况:①当点P在点A.B两点之间运动时:MN=MP+NP=AP+BP=(AP+BP)=AB=7…②当点P运动到点B的左侧时:MN=MP﹣NP=AP﹣BP=(AP﹣BP)=AB=7…综上所述,线段MN的长度不发生变化,其值为7 …(4)式子|x+6|+|x﹣8|有最小值,最小值为14.…。
