4-2洛必达法则
洛必达法则总结归纳

洛必达法则总结归纳
洛必达法则是经济学中一个重要的概念,用于描述市场中不同价格水平下的产品销售量。
它的核心思想是:产品价格与销售量之间存在着相互作用关系,当价格上升时,销售量将会下降;反之,当价格下降时,销售量则会上升。
总结归纳洛必达法则,我们可以得出以下几个关键点:
1. 市场需求的弹性:洛必达法则认为市场需求对价格的反应是弹性的,即当价格变动时,市场需求的反应程度与价格变动幅度成正比。
当价格变化较小时,市场需求的变化也会比较小;反之,当价格变化较大时,市场需求的变化也会比较大。
2. 价格与销售量的相互作用:洛必达法则认为,价格与销售量之间存在着相互作用关系。
当价格上升时,销售量将会下降;反之,当价格下降时,销售量则会上升。
因此,企业需要在制定产品价格时考虑到价格与销售量之间的平衡。
3. 最大化利润的实现:洛必达法则认为,企业应该通过制定合适的价格来最大化其利润。
当价格过高时,销售量会下降,从而减少利润;反之,当价格过低时,虽然销售量会增加,但是利润也会下降。
因此,企业需要通过市场调研等手段来确定商品的最佳价格,以实现最大化利润的目标。
4. 市场竞争的影响:洛必达法则还强调了市场竞争对于产品价格与销售量之间关系的影响。
在竞争激烈的市场中,企业需要通过制定更合适的价格来保持其竞争力,从而在市场中取得更大的份额。
总之,洛必达法则对于企业制定产品价格以及实现最大利润具有很重要的指导意义,企业应该通过市场调研、竞争分析等手段来确定最佳的价格水平。
洛必达法则

00∞∞)(x f )(x F )()(lim )(x F x f x a x ∞→→00∞∞x x x tan lim 0→00bx ax x sin ln sin ln lim 0+→∞∞)(x f )(x F a)(x f ')(x F '0)(≠'x F )()(lim x F x f a x ''→)()(lim )()(lim x F x f x F x f a x a x ''=→→)()(x F x f ''00∞∞)(x f ')(x F '.)()(lim )()(lim )()(lim =''''=''=→→→x F x f x F x f x F x f a x a x a x .)()(lim )()(lim x F x f x F x f x x ''=∞→∞→∞∞x x x tan lim 0→第二节 洛必达法则一、 型及 型未定式解法:洛必达法则定义:如果当(或)时,两个函数 和 都趋于零或都趋于无穷 大,那么极限 可能存在、也可能不存在。
通常把这种极限称为 型及型未定式。
例如: 型 型定理1:设:(1)当时,函数 及 都趋于零;(2)在 点的某去心邻域内, 及 都存在,且 ; (3) 存在(或为无穷大); 那么这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则。
注:(1)如果 仍属 型及 型,且 及 满足定理条件,可以继续使用法则,即(2)当时,该法则仍然成立。
(定理2)(3)当,时的未定式 也有相应的法则。
a x →∞→x a x →∞→x a x →∞→x)()(tan lim 0''=→x x x 原式1sec lim 20x x →=123lim 2331+--+-→x x x x x x 求12333lim 221---=→x x x x 266lim 1-=→x x x 23=266lim 1-→x x x bxax x sin ln sin ln lim 0+→求22111lim xx x -+-=+∞→原式221lim x x x +=+∞→xx x 3tan tan lim 2π→求x x x 3sec 3sec lim 222π→=原式x x x 222cos 3cos lim 31π→=x x x x x sin cos 23sin 3cos 6lim 312--→πx x x 2sin 6sin lim 2π→=x x x 2cos 26cos 6lim 2π→=)0 ( lim >+∞→λλ为正整数,求n e xx n x x n x x n x e nx e x λλλ1lim lim -+∞→+∞→=xn x e x n λλ0!lim ⋅==+∞→ )0( ln lim >+∞→n x x n x 求例1:求解: =1例2: 解:原式注意:(1)上式中 不是未定式,不能使用洛必达法则,否则导致错误的结果。
4-2洛必达法则

1. 0型
步 骤 : 0 1 ,或 0 01
0
例 8 求limxcot2x. (0) x 0
解原 式 lim x (0) lim ( x) x 0tan2x 0 x0 (tan 2x)
lxi m0 2sec12
2x
1. 2
提示与分析: x与cot 2x,哪部分做分母, 要以转化后极限易算为准则.
x (xn ) 无穷大量
lim
x
x nx n1
1
lim
x
nxn
0.
若求导之后出现繁分式,一般应化简后再判
断是否为0型或者型,然后再决定是否能继
0
续用洛必达法则.
π arctan x
例7 求 lim 2
.
(0 )
x
1
0
解
原式
l i m( 2
极限是常数1
1
cosx
4xl imπ sinx(π 2x)
2
1 ( cos x)
4
lim
π
x
(π
2x)
0型 0
2
1 sin x 1
lim
.
4 xπ 2
8
2
2. 型不定式
定 理 如 果 函 数 f ( x )和 g( x )满 足
(1) x a(或 x )时 , f ( x ) , g( x ) ;
lim xln x x 0 1
x0
x
ln x lim x 0 1
x
1
lim x
x
0
1 x2
0,
4-2洛必达法则1211

例
tan x ∞ . ( ) 求 lim π ∞ x → tan 3 x
2
sin x ⋅ cos 3 x 原式 = lim π x → cos x ⋅ sin 3 x
2
sec2 x 解 原式 = lim π 3 sec 2 3 x x→
2
cos 3 x 0 = −lim ( ) π cos x 0 x→
15
二、其它未定式
1. 0 ⋅ ∞, ∞ − ∞型未定式
0 ∞ 型 关键 将其化为洛必达法则可解决的 , 0 ∞ ∞ 1 0⋅ ∞ 型 0⋅ ∞ ⇒ ⋅ ∞ ⇒ 或 0⋅ ∞ ⇒0⋅ 1 ⇒ 0 ⋅ 0 ∞ ∞ 0
求 lim x − 2e x . ( 0 ⋅ ∞ ) 例
x → +∞
ex ∞ ex ∞ 解 原式 = lim 2 ( ) = lim ( ) x → +∞ 2 x ∞ x → +∞ x ∞ ex = lim = +∞ . x → +∞ 2 16
例 求 lim x(
x → +∞
π
2
− arctan x ). ( ∞⋅ 0 )
π
解 原式 = lim 2
x → +∞
− arctan x
1 x 1 − 2 2 x = lim 1 + x = lim 2 =1 x → +∞ 1 x → +∞ 1 + x − 2 x
0 ( ) 0
17
∞−∞ 型
1 1 0 0− 0 ∞− ∞⇒ − ⇒ ⇒ 0 0 0⋅ 0 0
∞ ln sin ax 例 求 lim ( ) . x→0 ln sin bx → ∞ a cos ax ⋅ sin bx a sin bx 解 原式 = lim = lim x →0 b cos bx ⋅ sin ax x →0 b sin ax
洛必达法则原理推导

洛必达法则原理推导洛必达法则原理推导洛必达法则是微积分学中的一种重要理论,它描述了函数在逼近某个点时的极限趋近问题。
这个原理是由法国数学家洛必达在18世纪发明的。
在本文中,我们将通过推导的方式来理解洛必达法则的原理。
在微积分中,洛必达法则的表述是:当函数$f(x)$和$g(x)$在$x=a$处都可导,且$g'(a)$不等于$0$时,如果$\lim_{x\rightarrow a}f(x)=0$且$\lim_{x\rightarrow a}g(x)=0$,则$\lim_{x\rightarrowa}\frac{f(x)}{g(x)}$存在,且有$\lim_{x\rightarrowa}\frac{f(x)}{g(x)}=\frac{f'(a)}{g'(a)}$。
我们可以通过导数的定义来理解洛必达法则。
考虑$f(x)$和$g(x)$在$x=a$处的导数,假设都存在,我们可以将它们展开为下面的形式:$$f'(a) = \lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}$$$$g'(a) = \lim_{x\rightarrow a}\frac{g(x)-g(a)}{x-a}$$由于$\lim_{x\rightarrow a}f(x)=0$和$\lim_{x\rightarrow a}g(x)=0$,我们可以将$f(x)$和$g(x)$展开为泰勒级数:$$f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+...$$$$g(x)=g(a)+g'(a)(x-a)+\frac{g''(a)}{2}(x-a)^2+...$$因为$f(x)$和$g(x)$在$x=a$处可导,所以它们的一阶导数存在,而一阶导数在$x=a$处的值分别是$f'(a)$和$g'(a)$。
洛必达法则洛必达法则

洛必达法则洛必达法则洛必达法则洛必达法则(L'Hospital法则),是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
设(1)当x→a时,函数f(x)及F(x)都趋于零;(2)在点a的去心邻域内,f'(x)及F'(x)都存在且F'(x)≠0;(3)当x→a时lim f'(x)/F'(x)存在(或为无穷大),那么x→a时 lim f(x)/F(x)=lim f'(x)/F'(x)。
再设(1)当x→∞时,函数f(x)及F(x)都趋于零;(2)当|x|>N时f'(x)及F'(x)都存在,且F'(x)≠0;(3)当x→∞时lim f'(x)/F'(x)存在(或为无穷大),那么x→∞时 lim f(x)/F(x)=lim f'(x)/F'(x)。
利用洛必达法则求未定式的极限是微分学中的重点之一,在解题中应注意:①在着手求极限以前,首先要检查是否满足0/0或∞/∞型未定式,否则滥用洛必达法则会出错。
当不存在时(不包括∞情形),就不能用洛必达法则,这时称洛必达法则不适用,应从另外途径求极限。
比如利用泰勒公式求解。
②若条件符合,洛必达法则可连续多次使用,直到求出极限为止。
③洛必达法则是求未定式极限的有效工具,但是如果仅用洛必达法则,往往计算会十分繁琐,因此一定要与其他方法相结合,比如及时将非零极限的乘积因子分离出来以简化计算、乘积因子用等价量替换等等. 泰勒公式(T aylor's formula)泰勒中值定理:若函数f(x)在开区间(a,b)有直到n+1阶的导数,则当函数在此区间内时,可以展开为一个关于(x-x.)多项式和一个余项的和:f(x)=f(x.)+f'(x.)(x-x.)+f''(x.)/2!*(x-x.)^2,+f'''(x.)/3!*(x-x.)^3+……+f(n)(x.) /n!*(x-x.)^n+Rn其中Rn=f(n+1)(ξ)/(n+1)!*(x-x.)^(n+1),这里ξ在x和x.之间,该余项称为拉格朗日型的余项。
4-2洛比达法则
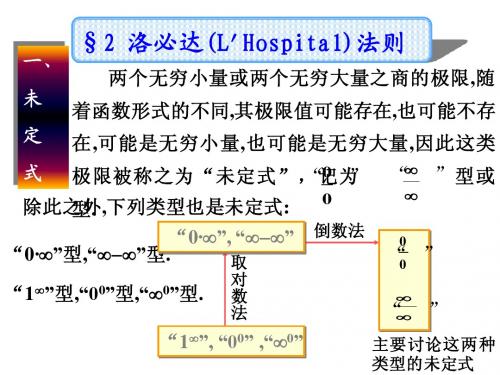
∞ “ ” 型或 ∞
除此之外,下列类型也是未定式 除此之外 下列类型也是未定式: 型. 下列类型也是未定式 ∞−∞” “0·∞”, “∞−∞ ∞ 取 ∞−∞ ∞−∞”型 “0·∞”型,“∞−∞ 型. ∞ 型 ∞−∞ 对 “1∞”型,“00”型,“∞0”型. 型 型 ∞ 型
数 法
0 “ 0
∞ “ ∞
2
极
又如
失效之二 循环
x→ +∞
lim
x 1+ x2
1+ x2 x = lim = lim x→ x→ +∞ +∞ x 1+ x2
解:原极限= lim 原极限
1 1+(1/ x )
2
x→ +∞
=1
春风得意洛 春风得意洛必塔 一招遍摘极限花 可叹英雄亦失手 莫忘前章有妙法
练习
x +sinx lim x→ x −sinx ∞
sinx co 3x s −3sin3x = lim lim = − lim =3 x→ / 2sin3x x→ / 2 ⋅ co x x→ / 2 −sinx π π π s
lnx lim α (α > 0) 例7.求 求 ∞ x→ +∞ x “∞ ”型. 1/ x 1 原极限= 解:原极限 lim 0 α−1 = lim α= x→ α +∞ x x→ α +∞ x ex ex ex 原极限= 例8.计算 lim 2 解:原极限 lim 计算 = lim = +∞ x→ x +∞ x→ 2x x→ +∞ +∞ 2
2 等价无穷小) 等价无穷小 ta 2 x (等价无穷小 n x = lim = lim 0 1− o x→ 1−c s x x→ 1 0 → x2 2 lnx +1− x 例4.计算极限 lim 计算极限
微积分(曹定华)(修订版)课后题答案第四章习题详解

习题 4-11.验证函数f (x )=lnsin x 在[π5π,66]上满足罗尔定理的条件,并求出相应的ξ,使f ′(ξ)=0.解: 显然()ln sin f x x =在5π,66x ⎡⎤⎢⎥⎣⎦上连续,在π5π,66⎛⎫⎪⎝⎭内可导,且π5π()()ln 266f f ==-,满足罗尓定理的条件. 令cos ()cot 0sin xf x x x '===,则π2x =即存在ππ5π(,)66ξα=∈,使()0f ξ'=成立.2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ ?[][][]2(1)()1,;(2)(),;1,10,21sin ,0π(3)()0,π1,exf x f x x x x f x x =-=--<≤⎧=⎨=⎩解: (1) 2()1e x f x =-在[]1,1-上连续,在()1,1-内可导,且(1)1,(1)1,e e f f -=-=- 即 (1)(1)f f-= () f x ∴在[]1,1-上满足罗尓定理的三个条件. 令 2()20e x f x x '==得 0x =, 即存在0(1,1)ξ=∈-,使()0f ξ'=.(2) 101()1112xx f x x x x -≤<⎧==-⎨-≤≤⎩显然()f x 在(0,1),(1,2)内连续,又1111(10)lim ()lim (1)0,(10)lim ()lim (1)0,(10)(10)(1)0,即x x x x f f x x f f x x f f f --++→→→→-==-=+==-=-=+==所以()f x 在1x =处连续,而且22(00)lim ()lim (1)1(0),(20)lim ()lim (1)1(2),x x x x f f x x f f f x x f ++--→→→→+==-==-==-==即()f x 在0x =处右连续,在2x =处左连续,所以()f x 在[]0,2 上连续.又1111()(1)1(1)lim lim 1,11()(1)1(1)lim lim 111x x x x f x f x f x x f x f x f x x --++-→→+→→--'===-----'===--(1)(1)(f f f x -+''∴≠∴在1x =处不可导,从而()f x 在(0,2)内不可导. 又 (0)(2)1f f ==又由 101()112x f x x -<<⎧'=⎨<<⎩ 知 ()0f x '≠综上所述,函数()f x 满足罗尓定理的条件(1),(3)不满足条件(2),没有满足定理结论的ξ. (3) 由0(00)lim sin 0(0)1x f x f +→+==≠=知()f x 在0x =不右连续,() f x ∴在[]0,π上不连续,显然()f x 在()0,π上可导,又(0)1,(π)0f f ==,即(0)(π)f f ≠,且()cos (0,π) f x x x '=∈,取π(0,π)2ξ=∈,有π()cos cos02f ξξ'===.综上所述,函数()f x 满足罗尓定理的条件(2),不满足条件(1),(3),有满足定理结论的ξ,ξ=π2.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数,说明方程()0f x '=有几个实根,并指出它们所在的区间.解: 显然()f x 在[]1,2上连续,在()1,2内可导,且(1)(2)0f f ==,由罗尓定理知,在()1,2内至少存在一点1ξ,使1()0f ξ'=,即()0f x '=在()1,2内至少有一个实根.同理 ()0f x '=在()2,3内也至少有一个实根2ξ.又()0f x '=是二次方程,最多有两个实根,故()0f x '=有两个实根,分别在区间()1,2和()2,3内.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间[0,1]上的正确性.解: 显然3()2f x x x =+在[0,1]上连续,在()0,1内可导,满足拉格朗日中值定理的条件.若令2(1)(0)()32310f f f x x-'=+==-则3x =±,取3ξ=,即存在(0,1)3ξ=,使得(1)(0)()10f f f ξ-=-成立.从而拉格朗日中值定理对函数3()2f x x x =+在[0,1]上成立.5※. 设()f x '在[a ,b ]上连续,在[a ,b ]内可导,f ′(a ) = 0,f ′′(x ) > 0,证明:f ′(a )> f (b )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(在x与x0之间 )
f ( ) f ( x ) im A, 当x x0时, x0 , lim A, l x 0 g' ( ) x x0 g' ( x )
f ( x) f ( ) lim lim A. x x0 g ( x ) x0 g' ( )
3
x sin x 原式 lim 3 x 0 x ( 1 x 1 sin x )
lim x sin x 2x3 1 . 12
x 0
例14 (洛必达法则失效的例题)
x cos x 求 lim . x x
1 sin x lim(1 sin x ). 解 原式 lim x x 1 极限不存在 洛必达法则失效。
例3
求 lim 2
x
arctan x 1 x .
0 型 0
1 2 x2 解 原式 lim 1 x lim 1. 2 x 1 x 1 x 2 x
例4
e e 2 求 lim . x 0 1 cos x
x x
0 型 0
x
e e 解: 原式= l i m x0 sin x
cos x 1 3x2
x 0
sin x 1 lim . x 0 6 x 6
洛必达法则 II
若函数 f ( x) 和 g ( x) 满足:
型
(1) lim f ( x) lim g ( x)
x x0 x x0
(2) 在点 x0 的某去心邻域内均可导, g '( x) 0 且
0 型 0
型
未定式的变形(1)
设 lim f ( x ) 0, lim g( x )
0
g( x ) f ( x ) g( x ) 1 f ( x)
0 0 0
f ( x ) g( x )
f ( x) 1 g( x )
未定式的变形(2)
例1
(1 x ) 1 求 lim . x 0 x
解 原式 lim
(1 x ) x 0 1
0 型 0
1
.
例2
x3 3 x 2 求 lim 3 . 2 x 1 x x x 1
2
0 型 0
3x 3 6x 3 解 原式 lim 2 lim . x 1 3 x 2 x 1 x 1 6 x 2 2
关于洛必达法则 I 之注
在洛必达法则 I中, 极限过程可换为 xx , xx 或 x .
0 - 0
, x , x - ,
洛必达法则 I 的证明
证 定义辅助函数
f ( x ), x x0 f1 ( x ) , x x0 0,
在 U 0 ( x0 , ) 内任取一点 , x
1 原式 lim (1 cos x ) 1. x x
小结
洛必达法则
0 ,1 , 型
0 0
型
f g 1 g 1 f (1 g ) (1 f )
0 型 0 型
f e
g
g ln f
0 型
f f g 1g
思考题 1
1、设 lim f ( x ) 是不定型极限,如果 f ( x ) 的极限不
g( x ), x x0 g1 ( x ) , x x0 0,
在以 x0 与 x 为端点的区间上 ,
则有
f1 ( x ), g1 ( x )满足柯西中值定理的条, 件
f ( x ) f ( x ) f (a ) f ( ) g' ( ) g( x ) g( x ) g(a )
1 x 1 (1 x ) x ] , 当x 0 [ 三、讨论函数 f ( x ) , e 1 e 2 , 当x 0
在点 x 0处 的连续性.
(A)充分条件;
(B)必要条件;
(C)充分必要条件; (D)既非充分也非必要条件 .
e e lim x 0 x sin x
x
sin x
x
lim
2x x2 2x x
lim(e x )
x x 0
1 sin 2 x
已知f ( x)正值且二阶可导,f (0) f '(0) 1, f (sin x) 1 求 lim x 0 ln f ( x)
g( x ) g ( x )
存在,是否 f ( x ) 的极限也一定不存在?举例说明. g( x )
思考题 1 之解答
不一定. 例 f ( x ) x sin x ,
g( x ) x
f ( x ) 1 cos x 显然 lim lim 极限不存在. x g ( x ) x 1 f ( x) x sin x 但 lim lim 1 极限存在. x g ( x ) x x
思考题 2
设 lim f ( x ) lim F ( x ) 0 ,且在点 a 的某邻域中
xa xa
(点 a 可除外) f ( x ) 及F ( x ) 都存在, 且F ( x ) 0 , ,
f ' ( x) f ( x) 则 lim 存在是 lim ' 存在的(B ). x a F ( x ) x a F im (cot x )
x 0 1 ln x
.
型
0
1 ln x
解 取对数得 (cot x )
e
1 ln(cot x ) ln x
,
1 1 2 1 lim ln(cot x ) lim cot x sin x 1 x 0 x 0 ln x x x 1, 原式 e 1 . lim x 0 cos x sin x
将如下三种未定式转化为
0 型
0 0 ln 0 取对数 1 ln 1 0 ln 0
0
0 .
例10
求 lim x .
x x 0
0 型
0
x ln x
0 型
x 0
解
原式 lim e
x 0
e
lim x ln x
4.2 洛必达法则
解决两个无穷小量之比的极限或两 个无穷大量之比的极限的简单而有 效的一种方法.
记号
两个无穷小量之比的极限式称为
0 型未定式 0
两个无穷大量之比的极限式称为
型未定式
洛必达法则 I
0 型 0
若函数 f ( x) 和 g ( x) 满足:
(1) lim f ( x) lim g ( x) 0
型
0 化为 0
解
x sin x 原式 lim x 0 x sin x
型
x sin x lim 2 x 0 x 1 cos x lim x 0 2x sin x lim 0. x 0 2
无穷小量代换 运用洛必达法则
未定式的变形(3)
[ f ( x)]g( x ) e g( x) ln f ( x ) 通过
1 1 0 0
00 00
通过通分或分子有理化及其它变换转化为:
0 型 0
型
例8
求 lim x e .
x 2 x
0 型
2 2x 解 原式 lim lim x 0 x e x e x
例9
1 1 求 lim( ). x 0 sin x x
f '( x) (3) lim A (或 ) x x0 g '( x )
f ( x) f '( x) 则有 lim lim A (或 ) . x x0 g ( x ) x x0 g '( x )
关于洛必达法则 II 之注
在洛必达法则 II 中, 极限过程可换为 x x , x x , x , x - ,
1 x 1 x2
型
e
e
0
ln x lim x 0 1 x
e
x 0
lim
运用罗必达法则
1
例11
求 lim x
x 1 1 1 x
.
1 型
1 ln x 1 x
0 型 0
ln x lim x 1 1 x
解
原式 lim e
x 1
e
洛必达法则
e
1 lim ( x ) x 1 1
- 0 0
或 x .
例6
ln sin ax 求 lim . x 0 ln sin bx
型
a cos ax sin bx cos bx 解 原式 lim lim 1. x 0 b cos bx sin ax x 0 cos ax
例7
tan x 求 lim . tan 3 x x
x
e x e x lim x 0 cos x
2
用了两次洛必达法则
例5
注意:洛必达法则是求未定式的一种有效方法, 与其它求极限方法结合使用,效果更好.
求 lim sin x x x tan x
2
x 0
.
先用无穷小量代换
解 原式 lim
sin x x x
3
x 0
lim
2
型
cos 3 x lim cos x x
2
sin x cos 3 x 解 原式 lim x sin 3 x cos x
2
3 sin3 x lim 3 sin x x
2
其它类型的未定式
0 型 型
1 型
